通常可以将一个网络定义为二元组 $ G = (V,E) $ $ V = \{ {v_1},{v_2},\cdots ,{v_n}\} $ $ E = \{ {e_1},{e_2},\cdots ,{e_n}\} $ . 在时效网络中,若不考虑节点交互关系发生的时长,则在整个网络演化期内的边都可以用三元组 $(i,j,t) $ $ i $ $ j $ $ t $ $ \left( {t,t+N} \right) $ $ T $ $ L = N/T $ $ \{ \left( {t,t+n} \right),\left( {t+n,t+2n} \right),\cdots , \left( {t+(T - 1)n,t+N} \right)\} $ $ \{ {G_1},{G_2},\cdots ,{G_n}\} $ $ (i,j,t,\Delta t) $ $ i $ $ j $ $ t $ $ \Delta t $
[2]
WU L R, QI J Y, SHI N, et al Revealing the relationship of topics popularity and bursty human activity patterns in social temporal networks
[J]. Physica A: Statistical Mechanics and its Applications , 2022 , 588 : 126568
DOI:10.1016/j.physa.2021.126568
[3]
黄强娟. 时序网络结构建模与演化分析研究[D]. 长沙: 国防科技大学, 2019: 3-4.
HUANG Qiang-juan. Research on structure modeling and evolution analysis in temporal network [D]. Changsha: National University of Defense Technology, 2019: 3-4.
[5]
TAYLOR D, MYERS S A, CLAUSET A, et al Eigenvector-based centrality measures for temporal networks
[J]. Multiscale Modeling and Simulation , 2017 , 15 (1 ): 537 - 574
DOI:10.1137/16M1066142
[本文引用: 3]
[7]
胡钢, 许丽鹏, 徐翔 基于时序网络层间同构率动态演化的重要节点辨识
[J]. 物理学报 , 2021 , 70 (10 ): 355 - 366
[本文引用: 1]
HU Gang, XU Li-peng, XU Xiang Evolution of inter-layer isomorphism rate in temporal networks
[J]. Acta Physica Sinica , 2021 , 70 (10 ): 355 - 366
[本文引用: 1]
[8]
JIANG J L, FANG H, LI S Q, et al Identifying important nodes for temporal networks based on the ASAM model
[J]. Physica A: Statistical Mechanics and its Applications , 2022 , 586 : 126455
DOI:10.1016/j.physa.2021.126455
[本文引用: 1]
[9]
TANG J, MUSOLESI M, MASCOLO C, et al. Temporal distance metrics for social network analysis [C]// Proceedings of the 2nd ACM Workshop on Online Social Networks . Barcelona: ACM, 2009: 31-36.
[本文引用: 1]
[12]
刘建国, 任卓明, 郭强, 等 复杂网络中节点重要性排序的研究进展
[J]. 物理学报 , 2013 , 62 (17 ): 9 - 18
DOI:10.7498/aps.62.178901
[本文引用: 2]
LIU Jian-guo, REN Zhuo-ming, GUO Qiang, et al Node importance ranking of complex networks
[J]. Acta Physica Sinica , 2013 , 62 (17 ): 9 - 18
DOI:10.7498/aps.62.178901
[本文引用: 2]
[13]
FREEMAN L C A set of measures of centrality based on betweenness
[J]. Sociometry , 1977 , 40 (1 ): 35 - 41
DOI:10.2307/3033543
[本文引用: 1]
[15]
WANG Z, PEI X, WANG Y, et al. Ranking the key nodes with temporal degree deviation centrality on complex networks [C]// Proceedings of the 29th Chinese Control And Decision Conference (CCDC) . Chongqing: IEEE, 2017: 1484-1489.
[本文引用: 2]
[16]
TAKAGUCHI T, YANO Y, YOSHIDA Y Coverage centralities for temporal networks
[J]. The European Physical Journal B , 2016 , 89 (2 ): 1 - 11
[本文引用: 1]
[17]
YE Z H, ZHAN X X, ZHOU Y Z, et al. Identifying vital nodes on temporal networks: An edge-based k-shell decomposition [C]// Proceedings of the 36th Chinese Control Conference . Dalian: IEEE, 2017: 1402-1407.
[本文引用: 2]
[18]
KITSAK M, GALLOS L K, HAVLIN S, et al Identification of influential spreaders in complex networks
[J]. Nature Physics , 2010 , 6 (11 ): 888 - 893
DOI:10.1038/nphys1746
[本文引用: 1]
[19]
QU C Q, ZHAN X X, WANG G H, et al Temporal information gathering process for node ranking in time-varying networks
[J]. Chaos: An Interdisciplinary Journal of Nonlinear Science , 2019 , 29 (3 ): 033116
DOI:10.1063/1.5086059
[本文引用: 1]
[20]
梁耀洲, 郭强, 殷冉冉, 等 基于排名聚合的时序网络节点重要性研究
[J]. 电子科技大学学报 , 2020 , 49 (4 ): 519 - 523
DOI:10.12178/1001-0548.2019087
[本文引用: 2]
LIANG Yao-zhou, GUO Qiang, YIN Ran-ran, et al Node importance identification for temporal network based on ranking aggregation
[J]. Journal of University of Electronic Science and Technology of China , 2020 , 49 (4 ): 519 - 523
DOI:10.12178/1001-0548.2019087
[本文引用: 2]
[21]
KIPF T N, WELLING M. Semi-supervised classification with graph convolutional networks [EB/OL]. [2017-02-22]. https://arxiv.org/abs/1609.02907.
[本文引用: 2]
[22]
徐冰冰, 岑科廷, 黄俊杰, 等. 图卷积神经网络综述[J]. 计算机学报, 2020, 43(5): 755-780.
[本文引用: 1]
XU Bing-bing, CEN Ke-ting, HUANG Jun-jie, et al. A survey on graph convolutional neural network[ J]. Chinese Journal of Computers , 2020, 43(5): 755-780.
[本文引用: 1]
[23]
LECUN Y, BOTTOU L, BENGIO Y Gradient-based learning applied to document recognition
[J]. Proceedings of the IEEE , 1998 , 86 (11 ): 2278 - 2324
DOI:10.1109/5.726791
[本文引用: 1]
[24]
张林, 程华, 房一泉 基于卷积神经网络的链接表示及预测方法
[J]. 浙江大学学报: 工学版 , 2018 , 52 (3 ): 552 - 559
[本文引用: 1]
ZHANG Lin, CHENG Hua, FANG Yi-quan CNN-based link representation and prediction method
[J]. Journal of Zhejiang University: Engineering Science , 2018 , 52 (3 ): 552 - 559
[本文引用: 1]
[25]
BRUNA J, ZAREMBA W, SZLAM A, et al. Spectral networks and locally connected networks on graphs [EB/OL]. [2014-05-21]. https://arxiv.org/abs/1312.6203.
[本文引用: 1]
[26]
HE K M, ZHANG X, REN S, et al. Deep residual learning for image recognition [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR) . Las Vegas: IEEE, 2016: 770-778.
[本文引用: 1]
[27]
ROZENSHTEIN P, GIONIS A. Temporal pagerank [C]// Proceedings of the Machine Learning and Knowledge Discovery in Databases . Riva del Garda: Springer, 2016: 674-689.
[本文引用: 1]
[28]
BI J L, JIN J, QU C Q, et al Temporal gravity model for important node identification in temporal networks
[J]. Chaos, Solitons and Fractals , 2021 , 147 : 110934
DOI:10.1016/j.chaos.2021.110934
[本文引用: 1]
[29]
GÉNOIS M, VESTERGAARD C L, FOURNET J, et al Data on face-to-face contacts in an office building suggest a low-cost vaccination strategy based on community linkers
[J]. Network Science , 2015 , 3 (3 ): 326 - 347
DOI:10.1017/nws.2015.10
[本文引用: 1]
[30]
KLIMT B, YANG Y M. The enron corpus: a new dataset for email classification research [C]// Proceedings of the European Conference on Machine Learning . Pisa: Springer, 2004: 217-226.
[本文引用: 1]
[35]
AGRESTI A. Analysis of ordinal categorical data [M]. New York: John Wiley and Sons, 2010: 189–190.
[本文引用: 1]
Temporal networks
1
2012
... 时效网络考虑节点之间交互关联关系的时间特征属性,集中分析动态演化条件下网络的拓扑结构和动力学特征,可以更加准确地解释社交通讯信息流与人类活动模式关系、电子和生物病毒传播机制、基因调控激活序列以及脑功能网络时域特征等[1 -4 ] .节点重要性评价方法根据不同视角可分为2类,即分析节点在时间分层网络结构中的局部重要性和节点在网络演化过程中的全局综合重要性. ...
Revealing the relationship of topics popularity and bursty human activity patterns in social temporal networks
0
2022
Dynamics of ranking
1
2022
... 时效网络考虑节点之间交互关联关系的时间特征属性,集中分析动态演化条件下网络的拓扑结构和动力学特征,可以更加准确地解释社交通讯信息流与人类活动模式关系、电子和生物病毒传播机制、基因调控激活序列以及脑功能网络时域特征等[1 -4 ] .节点重要性评价方法根据不同视角可分为2类,即分析节点在时间分层网络结构中的局部重要性和节点在网络演化过程中的全局综合重要性. ...
Eigenvector-based centrality measures for temporal networks
3
2017
... Taylor等[5 ] 通过多层耦合网络分析法构建超邻接矩阵(supra adjacency matrix, SAM)以表征动态时效网络层内和层间连接关系,定义了时效网络基于特征向量的中心性度量指标以及节点重要性的评价指标. 经典的SAM时效网络模型利用共享参数调节层间关系,忽略不同节点层间连接关系的差异性.杨剑楠等[6 ] 引入邻居拓扑重叠系数重新表达节点的层间连接关系,提出基于节点层间相似性的超邻接矩阵(similarity based supra-adja cency matrix, SSAM)改进的时效网络表达方法.胡钢等[7 ] 考虑到跨层网络间的相容相似度问题,定义网络层间逼近关系系数,通过信息集结弥补邻居拓扑重叠系数的不足,提出改进的基于时效网络层间同构率动态演化的超邻接矩阵模型(isomorphism rate based supra adjacency matrix, ISAM),给出节点在各时间层的排序结果. Jiang等[8 ] 考虑节点连接信息递延的非马尔可夫性特征,提出新的增强相似度指数(enhanced similarity index, ESI)来度量相邻层和非相邻层之间的耦合关系,并引入时间衰减因子描述不同时间层内节点间耦合强度,构建出基于衰减的SAM时效网络模型(attenuation based SAM, ASAM). ...
... 文献[5 ]将节点规模为 $ N $ $ T $ $ NT \times NT $
... 时效网络中的节点重要性可以从2个方面进行评价:1)从网络结构性能角度出发,考察节点移除如何影响网络连通性;2)从网络功能性角度出发,考察节点对网络传播效果的影响[6 ] .通过计算网络中所有节点之间的距离倒数之和的均值获得网络效率[32 ] ,可表示静态网络中信息流通的难易程度,并评判网络连通性.时效网络通过替换距离变量,定义时序全局效率[5 ] 指标来衡量信息传播效率,表征网络时序性能: ...
基于层间相似性的时序网络节点重要性研究
3
2018
... Taylor等[5 ] 通过多层耦合网络分析法构建超邻接矩阵(supra adjacency matrix, SAM)以表征动态时效网络层内和层间连接关系,定义了时效网络基于特征向量的中心性度量指标以及节点重要性的评价指标. 经典的SAM时效网络模型利用共享参数调节层间关系,忽略不同节点层间连接关系的差异性.杨剑楠等[6 ] 引入邻居拓扑重叠系数重新表达节点的层间连接关系,提出基于节点层间相似性的超邻接矩阵(similarity based supra-adja cency matrix, SSAM)改进的时效网络表达方法.胡钢等[7 ] 考虑到跨层网络间的相容相似度问题,定义网络层间逼近关系系数,通过信息集结弥补邻居拓扑重叠系数的不足,提出改进的基于时效网络层间同构率动态演化的超邻接矩阵模型(isomorphism rate based supra adjacency matrix, ISAM),给出节点在各时间层的排序结果. Jiang等[8 ] 考虑节点连接信息递延的非马尔可夫性特征,提出新的增强相似度指数(enhanced similarity index, ESI)来度量相邻层和非相邻层之间的耦合关系,并引入时间衰减因子描述不同时间层内节点间耦合强度,构建出基于衰减的SAM时效网络模型(attenuation based SAM, ASAM). ...
... 为了更真实地反映网络连接变化规律,文献[6 ]引入邻居拓扑重叠系数表达层间连接关系,解决SAM模型无法利用可调参数对网络层间连接紧密程度变化进行差异化表达的问题.节点 $ i $
... 时效网络中的节点重要性可以从2个方面进行评价:1)从网络结构性能角度出发,考察节点移除如何影响网络连通性;2)从网络功能性角度出发,考察节点对网络传播效果的影响[6 ] .通过计算网络中所有节点之间的距离倒数之和的均值获得网络效率[32 ] ,可表示静态网络中信息流通的难易程度,并评判网络连通性.时效网络通过替换距离变量,定义时序全局效率[5 ] 指标来衡量信息传播效率,表征网络时序性能: ...
基于层间相似性的时序网络节点重要性研究
3
2018
... Taylor等[5 ] 通过多层耦合网络分析法构建超邻接矩阵(supra adjacency matrix, SAM)以表征动态时效网络层内和层间连接关系,定义了时效网络基于特征向量的中心性度量指标以及节点重要性的评价指标. 经典的SAM时效网络模型利用共享参数调节层间关系,忽略不同节点层间连接关系的差异性.杨剑楠等[6 ] 引入邻居拓扑重叠系数重新表达节点的层间连接关系,提出基于节点层间相似性的超邻接矩阵(similarity based supra-adja cency matrix, SSAM)改进的时效网络表达方法.胡钢等[7 ] 考虑到跨层网络间的相容相似度问题,定义网络层间逼近关系系数,通过信息集结弥补邻居拓扑重叠系数的不足,提出改进的基于时效网络层间同构率动态演化的超邻接矩阵模型(isomorphism rate based supra adjacency matrix, ISAM),给出节点在各时间层的排序结果. Jiang等[8 ] 考虑节点连接信息递延的非马尔可夫性特征,提出新的增强相似度指数(enhanced similarity index, ESI)来度量相邻层和非相邻层之间的耦合关系,并引入时间衰减因子描述不同时间层内节点间耦合强度,构建出基于衰减的SAM时效网络模型(attenuation based SAM, ASAM). ...
... 为了更真实地反映网络连接变化规律,文献[6 ]引入邻居拓扑重叠系数表达层间连接关系,解决SAM模型无法利用可调参数对网络层间连接紧密程度变化进行差异化表达的问题.节点 $ i $
... 时效网络中的节点重要性可以从2个方面进行评价:1)从网络结构性能角度出发,考察节点移除如何影响网络连通性;2)从网络功能性角度出发,考察节点对网络传播效果的影响[6 ] .通过计算网络中所有节点之间的距离倒数之和的均值获得网络效率[32 ] ,可表示静态网络中信息流通的难易程度,并评判网络连通性.时效网络通过替换距离变量,定义时序全局效率[5 ] 指标来衡量信息传播效率,表征网络时序性能: ...
基于时序网络层间同构率动态演化的重要节点辨识
1
2021
... Taylor等[5 ] 通过多层耦合网络分析法构建超邻接矩阵(supra adjacency matrix, SAM)以表征动态时效网络层内和层间连接关系,定义了时效网络基于特征向量的中心性度量指标以及节点重要性的评价指标. 经典的SAM时效网络模型利用共享参数调节层间关系,忽略不同节点层间连接关系的差异性.杨剑楠等[6 ] 引入邻居拓扑重叠系数重新表达节点的层间连接关系,提出基于节点层间相似性的超邻接矩阵(similarity based supra-adja cency matrix, SSAM)改进的时效网络表达方法.胡钢等[7 ] 考虑到跨层网络间的相容相似度问题,定义网络层间逼近关系系数,通过信息集结弥补邻居拓扑重叠系数的不足,提出改进的基于时效网络层间同构率动态演化的超邻接矩阵模型(isomorphism rate based supra adjacency matrix, ISAM),给出节点在各时间层的排序结果. Jiang等[8 ] 考虑节点连接信息递延的非马尔可夫性特征,提出新的增强相似度指数(enhanced similarity index, ESI)来度量相邻层和非相邻层之间的耦合关系,并引入时间衰减因子描述不同时间层内节点间耦合强度,构建出基于衰减的SAM时效网络模型(attenuation based SAM, ASAM). ...
基于时序网络层间同构率动态演化的重要节点辨识
1
2021
... Taylor等[5 ] 通过多层耦合网络分析法构建超邻接矩阵(supra adjacency matrix, SAM)以表征动态时效网络层内和层间连接关系,定义了时效网络基于特征向量的中心性度量指标以及节点重要性的评价指标. 经典的SAM时效网络模型利用共享参数调节层间关系,忽略不同节点层间连接关系的差异性.杨剑楠等[6 ] 引入邻居拓扑重叠系数重新表达节点的层间连接关系,提出基于节点层间相似性的超邻接矩阵(similarity based supra-adja cency matrix, SSAM)改进的时效网络表达方法.胡钢等[7 ] 考虑到跨层网络间的相容相似度问题,定义网络层间逼近关系系数,通过信息集结弥补邻居拓扑重叠系数的不足,提出改进的基于时效网络层间同构率动态演化的超邻接矩阵模型(isomorphism rate based supra adjacency matrix, ISAM),给出节点在各时间层的排序结果. Jiang等[8 ] 考虑节点连接信息递延的非马尔可夫性特征,提出新的增强相似度指数(enhanced similarity index, ESI)来度量相邻层和非相邻层之间的耦合关系,并引入时间衰减因子描述不同时间层内节点间耦合强度,构建出基于衰减的SAM时效网络模型(attenuation based SAM, ASAM). ...
Identifying important nodes for temporal networks based on the ASAM model
1
2022
... Taylor等[5 ] 通过多层耦合网络分析法构建超邻接矩阵(supra adjacency matrix, SAM)以表征动态时效网络层内和层间连接关系,定义了时效网络基于特征向量的中心性度量指标以及节点重要性的评价指标. 经典的SAM时效网络模型利用共享参数调节层间关系,忽略不同节点层间连接关系的差异性.杨剑楠等[6 ] 引入邻居拓扑重叠系数重新表达节点的层间连接关系,提出基于节点层间相似性的超邻接矩阵(similarity based supra-adja cency matrix, SSAM)改进的时效网络表达方法.胡钢等[7 ] 考虑到跨层网络间的相容相似度问题,定义网络层间逼近关系系数,通过信息集结弥补邻居拓扑重叠系数的不足,提出改进的基于时效网络层间同构率动态演化的超邻接矩阵模型(isomorphism rate based supra adjacency matrix, ISAM),给出节点在各时间层的排序结果. Jiang等[8 ] 考虑节点连接信息递延的非马尔可夫性特征,提出新的增强相似度指数(enhanced similarity index, ESI)来度量相邻层和非相邻层之间的耦合关系,并引入时间衰减因子描述不同时间层内节点间耦合强度,构建出基于衰减的SAM时效网络模型(attenuation based SAM, ASAM). ...
1
... Tang等[9 -10 ] 通过时序最短路径定义时序介数中心性和时序紧密度中心性,描述网络演化过程中的消息传递控制机制,提出时效网络节点重要性综合度量方法. Kim等[11 ] 通过跨时间复制节点交互信息表达潜在信息流向,构建基于明显路径流的时效网络模型,提出间隔时间内节点的时序度中心性、时序介数中心性和时序接近中心性指标,将静态网络中的度中心性[12 ] 、介数中心性[13 ] 、接近中心性[14 ] 的概念拓展应用到时效网络中,实现对节点的全局重要性综合评价. Wang等[15 ] 对时序度中心性概念进一步拓展,通过计算时序度中心性偏差,提出时序度偏差中心性指标. Takaguchi等[16 ] 分析现有中心性方法存在时间间隔难以选取调整和计算效率2大瓶颈,将节点和时间戳的组合视为时序节点单元,聚焦时序路径的局部结构,提出时序覆盖中心性(temporal coverage centrality, TCC)和时序边界覆盖中心性(temporal boundary coverage centrality, TBCC),揭示节点中心性值分布的非均匀性. Ye等[17 ] 基于k -核分解[18 ] 在静态网络节点重要性评价问题中的优异表现,提出基于边的k -核分解方法并应用于时效网络,通过计算时间聚合图上节点与其邻域节点间连边的权重和,综合评价节点重要性. Qu等[19 ] 提出适用于时效网络的时序信息收集(temporal information gathering, TIG)过程,探究时序结构信息对节点重要性排序结果的影响. 梁耀洲等[20 ] 引入基于评分矩阵的聚合理论,通过计算节点在各时间层内的排序得分累加和,实现节点重要性的全局综合评价. 通过对静态网络节点中心性度量方法在时效网络上的改进应用,针对全局视角下的节点重要性综合评价问题给出初步解决方案,但方案的排序有效性在具体应用场景数据集上缺少更进一步的量化透视和模型的性能仿真验证. ...
Small-world behavior in time-varying graphs
2
2010
... Tang等[9 -10 ] 通过时序最短路径定义时序介数中心性和时序紧密度中心性,描述网络演化过程中的消息传递控制机制,提出时效网络节点重要性综合度量方法. Kim等[11 ] 通过跨时间复制节点交互信息表达潜在信息流向,构建基于明显路径流的时效网络模型,提出间隔时间内节点的时序度中心性、时序介数中心性和时序接近中心性指标,将静态网络中的度中心性[12 ] 、介数中心性[13 ] 、接近中心性[14 ] 的概念拓展应用到时效网络中,实现对节点的全局重要性综合评价. Wang等[15 ] 对时序度中心性概念进一步拓展,通过计算时序度中心性偏差,提出时序度偏差中心性指标. Takaguchi等[16 ] 分析现有中心性方法存在时间间隔难以选取调整和计算效率2大瓶颈,将节点和时间戳的组合视为时序节点单元,聚焦时序路径的局部结构,提出时序覆盖中心性(temporal coverage centrality, TCC)和时序边界覆盖中心性(temporal boundary coverage centrality, TBCC),揭示节点中心性值分布的非均匀性. Ye等[17 ] 基于k -核分解[18 ] 在静态网络节点重要性评价问题中的优异表现,提出基于边的k -核分解方法并应用于时效网络,通过计算时间聚合图上节点与其邻域节点间连边的权重和,综合评价节点重要性. Qu等[19 ] 提出适用于时效网络的时序信息收集(temporal information gathering, TIG)过程,探究时序结构信息对节点重要性排序结果的影响. 梁耀洲等[20 ] 引入基于评分矩阵的聚合理论,通过计算节点在各时间层内的排序得分累加和,实现节点重要性的全局综合评价. 通过对静态网络节点中心性度量方法在时效网络上的改进应用,针对全局视角下的节点重要性综合评价问题给出初步解决方案,但方案的排序有效性在具体应用场景数据集上缺少更进一步的量化透视和模型的性能仿真验证. ...
... 式中:e 为时序全局效率, $ {d_{i,j}} $ [10 ] . 时序距离指的是时序最短路径,与静态网络中的最短路径不同的是其需要遵循节点连接发生的时间先后顺序. 例如信息从节点 $ i $ $ j $ $ k $ $ i $ $ j $ $ j $ $ k $
Temporal node centrality in complex networks
4
2012
... Tang等[9 -10 ] 通过时序最短路径定义时序介数中心性和时序紧密度中心性,描述网络演化过程中的消息传递控制机制,提出时效网络节点重要性综合度量方法. Kim等[11 ] 通过跨时间复制节点交互信息表达潜在信息流向,构建基于明显路径流的时效网络模型,提出间隔时间内节点的时序度中心性、时序介数中心性和时序接近中心性指标,将静态网络中的度中心性[12 ] 、介数中心性[13 ] 、接近中心性[14 ] 的概念拓展应用到时效网络中,实现对节点的全局重要性综合评价. Wang等[15 ] 对时序度中心性概念进一步拓展,通过计算时序度中心性偏差,提出时序度偏差中心性指标. Takaguchi等[16 ] 分析现有中心性方法存在时间间隔难以选取调整和计算效率2大瓶颈,将节点和时间戳的组合视为时序节点单元,聚焦时序路径的局部结构,提出时序覆盖中心性(temporal coverage centrality, TCC)和时序边界覆盖中心性(temporal boundary coverage centrality, TBCC),揭示节点中心性值分布的非均匀性. Ye等[17 ] 基于k -核分解[18 ] 在静态网络节点重要性评价问题中的优异表现,提出基于边的k -核分解方法并应用于时效网络,通过计算时间聚合图上节点与其邻域节点间连边的权重和,综合评价节点重要性. Qu等[19 ] 提出适用于时效网络的时序信息收集(temporal information gathering, TIG)过程,探究时序结构信息对节点重要性排序结果的影响. 梁耀洲等[20 ] 引入基于评分矩阵的聚合理论,通过计算节点在各时间层内的排序得分累加和,实现节点重要性的全局综合评价. 通过对静态网络节点中心性度量方法在时效网络上的改进应用,针对全局视角下的节点重要性综合评价问题给出初步解决方案,但方案的排序有效性在具体应用场景数据集上缺少更进一步的量化透视和模型的性能仿真验证. ...
... 研究采用“5+1+2”模式,选取5种基于拓扑结构的时效网络节点重要性度量方法、基于动力学随机游走的识别方法、基于排名聚合及引力模型的节点综合重要性度量方法进行性能对比.
2.2.1. 时序度中心性<sup>[<xref ref-type="bibr" rid="b11">11</xref>]</sup> 节点中心性最直接有效的度量指标就是度中心性,节点度值越大表明节点重要性越强. 时序度中心性(temporal degree, TD)将节点度的概念推广到时间维度,得到时效网络中心性度量基准指标: ...
... 式中:
$\; \mu (v) = \dfrac{1}{T}\displaystyle \sum\limits_{t = 1}^T {{D_t}(v)} $ 为节点
$ v $ 时序度值的均值.
2.2.3. 时序接近中心性<sup>[<xref ref-type="bibr" rid="b11">11</xref>]</sup> 接近中心性算法通过计算静态物理路径评估节点重要性,(temporal closeness, TC)则通过引入时序最短路径,拓展应用于时效网络节点重要性评估,时序接近中心性定义的计算式为 ...
... 式中:
$ {\varDelta _{t,j}}(v,u) $ 为在时间间隔
$ i \leqslant t < j $ 内节点
$ v $ 与其他节点间的时序距离.
2.2.4. 时序介数中心性<sup>[<xref ref-type="bibr" rid="b11">11</xref>]</sup> 时序介数中心性(temporal betweeness, TB)通过统计任意两点间的时序最短路径数目,计算经过目标节点的最短路径比例,评估节点重要性程度,具体代数式为 ...
复杂网络中节点重要性排序的研究进展
2
2013
... Tang等[9 -10 ] 通过时序最短路径定义时序介数中心性和时序紧密度中心性,描述网络演化过程中的消息传递控制机制,提出时效网络节点重要性综合度量方法. Kim等[11 ] 通过跨时间复制节点交互信息表达潜在信息流向,构建基于明显路径流的时效网络模型,提出间隔时间内节点的时序度中心性、时序介数中心性和时序接近中心性指标,将静态网络中的度中心性[12 ] 、介数中心性[13 ] 、接近中心性[14 ] 的概念拓展应用到时效网络中,实现对节点的全局重要性综合评价. Wang等[15 ] 对时序度中心性概念进一步拓展,通过计算时序度中心性偏差,提出时序度偏差中心性指标. Takaguchi等[16 ] 分析现有中心性方法存在时间间隔难以选取调整和计算效率2大瓶颈,将节点和时间戳的组合视为时序节点单元,聚焦时序路径的局部结构,提出时序覆盖中心性(temporal coverage centrality, TCC)和时序边界覆盖中心性(temporal boundary coverage centrality, TBCC),揭示节点中心性值分布的非均匀性. Ye等[17 ] 基于k -核分解[18 ] 在静态网络节点重要性评价问题中的优异表现,提出基于边的k -核分解方法并应用于时效网络,通过计算时间聚合图上节点与其邻域节点间连边的权重和,综合评价节点重要性. Qu等[19 ] 提出适用于时效网络的时序信息收集(temporal information gathering, TIG)过程,探究时序结构信息对节点重要性排序结果的影响. 梁耀洲等[20 ] 引入基于评分矩阵的聚合理论,通过计算节点在各时间层内的排序得分累加和,实现节点重要性的全局综合评价. 通过对静态网络节点中心性度量方法在时效网络上的改进应用,针对全局视角下的节点重要性综合评价问题给出初步解决方案,但方案的排序有效性在具体应用场景数据集上缺少更进一步的量化透视和模型的性能仿真验证. ...
... 创建空矩阵 $ {\boldsymbol{A}} $ $ \left( {{{\boldsymbol{A}}^{(1)}},{{\boldsymbol{A}}^{(2)}},\cdots ,{{\boldsymbol{A}}^{(T)}}} \right) $ $ \left( {{G_1},{G_2},\cdots ,{G_T}} \right) $ $ {\boldsymbol{A}} $ [12 ] 能够综合表达节点自身及邻域节点重要性,因此利用特征向量中心性作为节点重要性基本度量指标,即求解超邻接矩阵 $ {\boldsymbol{A}} $ ${\boldsymbol{m}} = \left\{ {m_1},{m_2},\cdots , {m_{NT}} \right\}^{\rm{T}}$ . 将向量 $ {\boldsymbol{m}} $ $ N \times T $ $ {\boldsymbol{W}} = {\left\{ {{w_{i,t}}} \right\}_{N \times T}} $
复杂网络中节点重要性排序的研究进展
2
2013
... Tang等[9 -10 ] 通过时序最短路径定义时序介数中心性和时序紧密度中心性,描述网络演化过程中的消息传递控制机制,提出时效网络节点重要性综合度量方法. Kim等[11 ] 通过跨时间复制节点交互信息表达潜在信息流向,构建基于明显路径流的时效网络模型,提出间隔时间内节点的时序度中心性、时序介数中心性和时序接近中心性指标,将静态网络中的度中心性[12 ] 、介数中心性[13 ] 、接近中心性[14 ] 的概念拓展应用到时效网络中,实现对节点的全局重要性综合评价. Wang等[15 ] 对时序度中心性概念进一步拓展,通过计算时序度中心性偏差,提出时序度偏差中心性指标. Takaguchi等[16 ] 分析现有中心性方法存在时间间隔难以选取调整和计算效率2大瓶颈,将节点和时间戳的组合视为时序节点单元,聚焦时序路径的局部结构,提出时序覆盖中心性(temporal coverage centrality, TCC)和时序边界覆盖中心性(temporal boundary coverage centrality, TBCC),揭示节点中心性值分布的非均匀性. Ye等[17 ] 基于k -核分解[18 ] 在静态网络节点重要性评价问题中的优异表现,提出基于边的k -核分解方法并应用于时效网络,通过计算时间聚合图上节点与其邻域节点间连边的权重和,综合评价节点重要性. Qu等[19 ] 提出适用于时效网络的时序信息收集(temporal information gathering, TIG)过程,探究时序结构信息对节点重要性排序结果的影响. 梁耀洲等[20 ] 引入基于评分矩阵的聚合理论,通过计算节点在各时间层内的排序得分累加和,实现节点重要性的全局综合评价. 通过对静态网络节点中心性度量方法在时效网络上的改进应用,针对全局视角下的节点重要性综合评价问题给出初步解决方案,但方案的排序有效性在具体应用场景数据集上缺少更进一步的量化透视和模型的性能仿真验证. ...
... 创建空矩阵 $ {\boldsymbol{A}} $ $ \left( {{{\boldsymbol{A}}^{(1)}},{{\boldsymbol{A}}^{(2)}},\cdots ,{{\boldsymbol{A}}^{(T)}}} \right) $ $ \left( {{G_1},{G_2},\cdots ,{G_T}} \right) $ $ {\boldsymbol{A}} $ [12 ] 能够综合表达节点自身及邻域节点重要性,因此利用特征向量中心性作为节点重要性基本度量指标,即求解超邻接矩阵 $ {\boldsymbol{A}} $ ${\boldsymbol{m}} = \left\{ {m_1},{m_2},\cdots , {m_{NT}} \right\}^{\rm{T}}$ . 将向量 $ {\boldsymbol{m}} $ $ N \times T $ $ {\boldsymbol{W}} = {\left\{ {{w_{i,t}}} \right\}_{N \times T}} $
A set of measures of centrality based on betweenness
1
1977
... Tang等[9 -10 ] 通过时序最短路径定义时序介数中心性和时序紧密度中心性,描述网络演化过程中的消息传递控制机制,提出时效网络节点重要性综合度量方法. Kim等[11 ] 通过跨时间复制节点交互信息表达潜在信息流向,构建基于明显路径流的时效网络模型,提出间隔时间内节点的时序度中心性、时序介数中心性和时序接近中心性指标,将静态网络中的度中心性[12 ] 、介数中心性[13 ] 、接近中心性[14 ] 的概念拓展应用到时效网络中,实现对节点的全局重要性综合评价. Wang等[15 ] 对时序度中心性概念进一步拓展,通过计算时序度中心性偏差,提出时序度偏差中心性指标. Takaguchi等[16 ] 分析现有中心性方法存在时间间隔难以选取调整和计算效率2大瓶颈,将节点和时间戳的组合视为时序节点单元,聚焦时序路径的局部结构,提出时序覆盖中心性(temporal coverage centrality, TCC)和时序边界覆盖中心性(temporal boundary coverage centrality, TBCC),揭示节点中心性值分布的非均匀性. Ye等[17 ] 基于k -核分解[18 ] 在静态网络节点重要性评价问题中的优异表现,提出基于边的k -核分解方法并应用于时效网络,通过计算时间聚合图上节点与其邻域节点间连边的权重和,综合评价节点重要性. Qu等[19 ] 提出适用于时效网络的时序信息收集(temporal information gathering, TIG)过程,探究时序结构信息对节点重要性排序结果的影响. 梁耀洲等[20 ] 引入基于评分矩阵的聚合理论,通过计算节点在各时间层内的排序得分累加和,实现节点重要性的全局综合评价. 通过对静态网络节点中心性度量方法在时效网络上的改进应用,针对全局视角下的节点重要性综合评价问题给出初步解决方案,但方案的排序有效性在具体应用场景数据集上缺少更进一步的量化透视和模型的性能仿真验证. ...
The centrality index of a graph
1
1966
... Tang等[9 -10 ] 通过时序最短路径定义时序介数中心性和时序紧密度中心性,描述网络演化过程中的消息传递控制机制,提出时效网络节点重要性综合度量方法. Kim等[11 ] 通过跨时间复制节点交互信息表达潜在信息流向,构建基于明显路径流的时效网络模型,提出间隔时间内节点的时序度中心性、时序介数中心性和时序接近中心性指标,将静态网络中的度中心性[12 ] 、介数中心性[13 ] 、接近中心性[14 ] 的概念拓展应用到时效网络中,实现对节点的全局重要性综合评价. Wang等[15 ] 对时序度中心性概念进一步拓展,通过计算时序度中心性偏差,提出时序度偏差中心性指标. Takaguchi等[16 ] 分析现有中心性方法存在时间间隔难以选取调整和计算效率2大瓶颈,将节点和时间戳的组合视为时序节点单元,聚焦时序路径的局部结构,提出时序覆盖中心性(temporal coverage centrality, TCC)和时序边界覆盖中心性(temporal boundary coverage centrality, TBCC),揭示节点中心性值分布的非均匀性. Ye等[17 ] 基于k -核分解[18 ] 在静态网络节点重要性评价问题中的优异表现,提出基于边的k -核分解方法并应用于时效网络,通过计算时间聚合图上节点与其邻域节点间连边的权重和,综合评价节点重要性. Qu等[19 ] 提出适用于时效网络的时序信息收集(temporal information gathering, TIG)过程,探究时序结构信息对节点重要性排序结果的影响. 梁耀洲等[20 ] 引入基于评分矩阵的聚合理论,通过计算节点在各时间层内的排序得分累加和,实现节点重要性的全局综合评价. 通过对静态网络节点中心性度量方法在时效网络上的改进应用,针对全局视角下的节点重要性综合评价问题给出初步解决方案,但方案的排序有效性在具体应用场景数据集上缺少更进一步的量化透视和模型的性能仿真验证. ...
2
... Tang等[9 -10 ] 通过时序最短路径定义时序介数中心性和时序紧密度中心性,描述网络演化过程中的消息传递控制机制,提出时效网络节点重要性综合度量方法. Kim等[11 ] 通过跨时间复制节点交互信息表达潜在信息流向,构建基于明显路径流的时效网络模型,提出间隔时间内节点的时序度中心性、时序介数中心性和时序接近中心性指标,将静态网络中的度中心性[12 ] 、介数中心性[13 ] 、接近中心性[14 ] 的概念拓展应用到时效网络中,实现对节点的全局重要性综合评价. Wang等[15 ] 对时序度中心性概念进一步拓展,通过计算时序度中心性偏差,提出时序度偏差中心性指标. Takaguchi等[16 ] 分析现有中心性方法存在时间间隔难以选取调整和计算效率2大瓶颈,将节点和时间戳的组合视为时序节点单元,聚焦时序路径的局部结构,提出时序覆盖中心性(temporal coverage centrality, TCC)和时序边界覆盖中心性(temporal boundary coverage centrality, TBCC),揭示节点中心性值分布的非均匀性. Ye等[17 ] 基于k -核分解[18 ] 在静态网络节点重要性评价问题中的优异表现,提出基于边的k -核分解方法并应用于时效网络,通过计算时间聚合图上节点与其邻域节点间连边的权重和,综合评价节点重要性. Qu等[19 ] 提出适用于时效网络的时序信息收集(temporal information gathering, TIG)过程,探究时序结构信息对节点重要性排序结果的影响. 梁耀洲等[20 ] 引入基于评分矩阵的聚合理论,通过计算节点在各时间层内的排序得分累加和,实现节点重要性的全局综合评价. 通过对静态网络节点中心性度量方法在时效网络上的改进应用,针对全局视角下的节点重要性综合评价问题给出初步解决方案,但方案的排序有效性在具体应用场景数据集上缺少更进一步的量化透视和模型的性能仿真验证. ...
... 式中:
$ {D_t}(v) $ 为节点
$ v $ 在时间窗
$ {G_t}(i \leqslant t < j) $ 内的度值,
$ \left| V \right| $ 为节点数量.
2.2.2. 时序度中心性偏差值<sup>[<xref ref-type="bibr" rid="b15">15</xref>]</sup> 基于时间窗图模型通过计算各时间窗内的度中心性标准差,时序度中心性偏差值(temporal degree deviation centrality, TDDC)刻画每个节点的时序度值与均值的偏离程度. 偏差值越大,该节点属于网络核心关键节点的可能性越大. 时序度中心性偏差计算为 ...
Coverage centralities for temporal networks
1
2016
... Tang等[9 -10 ] 通过时序最短路径定义时序介数中心性和时序紧密度中心性,描述网络演化过程中的消息传递控制机制,提出时效网络节点重要性综合度量方法. Kim等[11 ] 通过跨时间复制节点交互信息表达潜在信息流向,构建基于明显路径流的时效网络模型,提出间隔时间内节点的时序度中心性、时序介数中心性和时序接近中心性指标,将静态网络中的度中心性[12 ] 、介数中心性[13 ] 、接近中心性[14 ] 的概念拓展应用到时效网络中,实现对节点的全局重要性综合评价. Wang等[15 ] 对时序度中心性概念进一步拓展,通过计算时序度中心性偏差,提出时序度偏差中心性指标. Takaguchi等[16 ] 分析现有中心性方法存在时间间隔难以选取调整和计算效率2大瓶颈,将节点和时间戳的组合视为时序节点单元,聚焦时序路径的局部结构,提出时序覆盖中心性(temporal coverage centrality, TCC)和时序边界覆盖中心性(temporal boundary coverage centrality, TBCC),揭示节点中心性值分布的非均匀性. Ye等[17 ] 基于k -核分解[18 ] 在静态网络节点重要性评价问题中的优异表现,提出基于边的k -核分解方法并应用于时效网络,通过计算时间聚合图上节点与其邻域节点间连边的权重和,综合评价节点重要性. Qu等[19 ] 提出适用于时效网络的时序信息收集(temporal information gathering, TIG)过程,探究时序结构信息对节点重要性排序结果的影响. 梁耀洲等[20 ] 引入基于评分矩阵的聚合理论,通过计算节点在各时间层内的排序得分累加和,实现节点重要性的全局综合评价. 通过对静态网络节点中心性度量方法在时效网络上的改进应用,针对全局视角下的节点重要性综合评价问题给出初步解决方案,但方案的排序有效性在具体应用场景数据集上缺少更进一步的量化透视和模型的性能仿真验证. ...
2
... Tang等[9 -10 ] 通过时序最短路径定义时序介数中心性和时序紧密度中心性,描述网络演化过程中的消息传递控制机制,提出时效网络节点重要性综合度量方法. Kim等[11 ] 通过跨时间复制节点交互信息表达潜在信息流向,构建基于明显路径流的时效网络模型,提出间隔时间内节点的时序度中心性、时序介数中心性和时序接近中心性指标,将静态网络中的度中心性[12 ] 、介数中心性[13 ] 、接近中心性[14 ] 的概念拓展应用到时效网络中,实现对节点的全局重要性综合评价. Wang等[15 ] 对时序度中心性概念进一步拓展,通过计算时序度中心性偏差,提出时序度偏差中心性指标. Takaguchi等[16 ] 分析现有中心性方法存在时间间隔难以选取调整和计算效率2大瓶颈,将节点和时间戳的组合视为时序节点单元,聚焦时序路径的局部结构,提出时序覆盖中心性(temporal coverage centrality, TCC)和时序边界覆盖中心性(temporal boundary coverage centrality, TBCC),揭示节点中心性值分布的非均匀性. Ye等[17 ] 基于k -核分解[18 ] 在静态网络节点重要性评价问题中的优异表现,提出基于边的k -核分解方法并应用于时效网络,通过计算时间聚合图上节点与其邻域节点间连边的权重和,综合评价节点重要性. Qu等[19 ] 提出适用于时效网络的时序信息收集(temporal information gathering, TIG)过程,探究时序结构信息对节点重要性排序结果的影响. 梁耀洲等[20 ] 引入基于评分矩阵的聚合理论,通过计算节点在各时间层内的排序得分累加和,实现节点重要性的全局综合评价. 通过对静态网络节点中心性度量方法在时效网络上的改进应用,针对全局视角下的节点重要性综合评价问题给出初步解决方案,但方案的排序有效性在具体应用场景数据集上缺少更进一步的量化透视和模型的性能仿真验证. ...
... 式中:
$ {\sigma _{t,j}}(s,\;d) $ 为时间间隔内节点
$ s $ 到节点
$ d $ 的最短路径总数,
$ {\sigma _{t,j}}(s,\;d,\;v) $ 为通过节点
$ v $ 的最短路径数量.
2.2.5. 时序<i>k</i>-核分解<sup>[<xref ref-type="bibr" rid="b17">17</xref>]</sup> 时序k -核分解(temporal k -shell decomposition, TK)通过连边权值计算聚合目标节点和邻居节点时序k -核特征,实现时效网络节点重要性度量,聚合权值越大节点越重要. 节点时序k -核计算式为 ...
Identification of influential spreaders in complex networks
1
2010
... Tang等[9 -10 ] 通过时序最短路径定义时序介数中心性和时序紧密度中心性,描述网络演化过程中的消息传递控制机制,提出时效网络节点重要性综合度量方法. Kim等[11 ] 通过跨时间复制节点交互信息表达潜在信息流向,构建基于明显路径流的时效网络模型,提出间隔时间内节点的时序度中心性、时序介数中心性和时序接近中心性指标,将静态网络中的度中心性[12 ] 、介数中心性[13 ] 、接近中心性[14 ] 的概念拓展应用到时效网络中,实现对节点的全局重要性综合评价. Wang等[15 ] 对时序度中心性概念进一步拓展,通过计算时序度中心性偏差,提出时序度偏差中心性指标. Takaguchi等[16 ] 分析现有中心性方法存在时间间隔难以选取调整和计算效率2大瓶颈,将节点和时间戳的组合视为时序节点单元,聚焦时序路径的局部结构,提出时序覆盖中心性(temporal coverage centrality, TCC)和时序边界覆盖中心性(temporal boundary coverage centrality, TBCC),揭示节点中心性值分布的非均匀性. Ye等[17 ] 基于k -核分解[18 ] 在静态网络节点重要性评价问题中的优异表现,提出基于边的k -核分解方法并应用于时效网络,通过计算时间聚合图上节点与其邻域节点间连边的权重和,综合评价节点重要性. Qu等[19 ] 提出适用于时效网络的时序信息收集(temporal information gathering, TIG)过程,探究时序结构信息对节点重要性排序结果的影响. 梁耀洲等[20 ] 引入基于评分矩阵的聚合理论,通过计算节点在各时间层内的排序得分累加和,实现节点重要性的全局综合评价. 通过对静态网络节点中心性度量方法在时效网络上的改进应用,针对全局视角下的节点重要性综合评价问题给出初步解决方案,但方案的排序有效性在具体应用场景数据集上缺少更进一步的量化透视和模型的性能仿真验证. ...
Temporal information gathering process for node ranking in time-varying networks
1
2019
... Tang等[9 -10 ] 通过时序最短路径定义时序介数中心性和时序紧密度中心性,描述网络演化过程中的消息传递控制机制,提出时效网络节点重要性综合度量方法. Kim等[11 ] 通过跨时间复制节点交互信息表达潜在信息流向,构建基于明显路径流的时效网络模型,提出间隔时间内节点的时序度中心性、时序介数中心性和时序接近中心性指标,将静态网络中的度中心性[12 ] 、介数中心性[13 ] 、接近中心性[14 ] 的概念拓展应用到时效网络中,实现对节点的全局重要性综合评价. Wang等[15 ] 对时序度中心性概念进一步拓展,通过计算时序度中心性偏差,提出时序度偏差中心性指标. Takaguchi等[16 ] 分析现有中心性方法存在时间间隔难以选取调整和计算效率2大瓶颈,将节点和时间戳的组合视为时序节点单元,聚焦时序路径的局部结构,提出时序覆盖中心性(temporal coverage centrality, TCC)和时序边界覆盖中心性(temporal boundary coverage centrality, TBCC),揭示节点中心性值分布的非均匀性. Ye等[17 ] 基于k -核分解[18 ] 在静态网络节点重要性评价问题中的优异表现,提出基于边的k -核分解方法并应用于时效网络,通过计算时间聚合图上节点与其邻域节点间连边的权重和,综合评价节点重要性. Qu等[19 ] 提出适用于时效网络的时序信息收集(temporal information gathering, TIG)过程,探究时序结构信息对节点重要性排序结果的影响. 梁耀洲等[20 ] 引入基于评分矩阵的聚合理论,通过计算节点在各时间层内的排序得分累加和,实现节点重要性的全局综合评价. 通过对静态网络节点中心性度量方法在时效网络上的改进应用,针对全局视角下的节点重要性综合评价问题给出初步解决方案,但方案的排序有效性在具体应用场景数据集上缺少更进一步的量化透视和模型的性能仿真验证. ...
基于排名聚合的时序网络节点重要性研究
2
2020
... Tang等[9 -10 ] 通过时序最短路径定义时序介数中心性和时序紧密度中心性,描述网络演化过程中的消息传递控制机制,提出时效网络节点重要性综合度量方法. Kim等[11 ] 通过跨时间复制节点交互信息表达潜在信息流向,构建基于明显路径流的时效网络模型,提出间隔时间内节点的时序度中心性、时序介数中心性和时序接近中心性指标,将静态网络中的度中心性[12 ] 、介数中心性[13 ] 、接近中心性[14 ] 的概念拓展应用到时效网络中,实现对节点的全局重要性综合评价. Wang等[15 ] 对时序度中心性概念进一步拓展,通过计算时序度中心性偏差,提出时序度偏差中心性指标. Takaguchi等[16 ] 分析现有中心性方法存在时间间隔难以选取调整和计算效率2大瓶颈,将节点和时间戳的组合视为时序节点单元,聚焦时序路径的局部结构,提出时序覆盖中心性(temporal coverage centrality, TCC)和时序边界覆盖中心性(temporal boundary coverage centrality, TBCC),揭示节点中心性值分布的非均匀性. Ye等[17 ] 基于k -核分解[18 ] 在静态网络节点重要性评价问题中的优异表现,提出基于边的k -核分解方法并应用于时效网络,通过计算时间聚合图上节点与其邻域节点间连边的权重和,综合评价节点重要性. Qu等[19 ] 提出适用于时效网络的时序信息收集(temporal information gathering, TIG)过程,探究时序结构信息对节点重要性排序结果的影响. 梁耀洲等[20 ] 引入基于评分矩阵的聚合理论,通过计算节点在各时间层内的排序得分累加和,实现节点重要性的全局综合评价. 通过对静态网络节点中心性度量方法在时效网络上的改进应用,针对全局视角下的节点重要性综合评价问题给出初步解决方案,但方案的排序有效性在具体应用场景数据集上缺少更进一步的量化透视和模型的性能仿真验证. ...
... 式中:
$ w_{i,j}^t = \min\; \{ k_s^t(i),k_s^t(j)\} $ 表示在时间窗
$ t $ 中,节点
$ i $ 和节点
$ j $ 间连边的权值;
$ {k}_{s}^{t}(i)、{k}_{s}^{t}(j) $ 分别为节点
$ i $ 和
$ j $ 的
k -shell值.
2.2.6. 排名聚合<sup>[<xref ref-type="bibr" rid="b20">20</xref>]</sup> 基于排名聚合(ranking aggregation, RA)的方法通过制定评分机制,建立各时间窗口内节点的重要性评分矩阵并进行加和计算,根据加和得分获得节点重要性综合排序: ...
基于排名聚合的时序网络节点重要性研究
2
2020
... Tang等[9 -10 ] 通过时序最短路径定义时序介数中心性和时序紧密度中心性,描述网络演化过程中的消息传递控制机制,提出时效网络节点重要性综合度量方法. Kim等[11 ] 通过跨时间复制节点交互信息表达潜在信息流向,构建基于明显路径流的时效网络模型,提出间隔时间内节点的时序度中心性、时序介数中心性和时序接近中心性指标,将静态网络中的度中心性[12 ] 、介数中心性[13 ] 、接近中心性[14 ] 的概念拓展应用到时效网络中,实现对节点的全局重要性综合评价. Wang等[15 ] 对时序度中心性概念进一步拓展,通过计算时序度中心性偏差,提出时序度偏差中心性指标. Takaguchi等[16 ] 分析现有中心性方法存在时间间隔难以选取调整和计算效率2大瓶颈,将节点和时间戳的组合视为时序节点单元,聚焦时序路径的局部结构,提出时序覆盖中心性(temporal coverage centrality, TCC)和时序边界覆盖中心性(temporal boundary coverage centrality, TBCC),揭示节点中心性值分布的非均匀性. Ye等[17 ] 基于k -核分解[18 ] 在静态网络节点重要性评价问题中的优异表现,提出基于边的k -核分解方法并应用于时效网络,通过计算时间聚合图上节点与其邻域节点间连边的权重和,综合评价节点重要性. Qu等[19 ] 提出适用于时效网络的时序信息收集(temporal information gathering, TIG)过程,探究时序结构信息对节点重要性排序结果的影响. 梁耀洲等[20 ] 引入基于评分矩阵的聚合理论,通过计算节点在各时间层内的排序得分累加和,实现节点重要性的全局综合评价. 通过对静态网络节点中心性度量方法在时效网络上的改进应用,针对全局视角下的节点重要性综合评价问题给出初步解决方案,但方案的排序有效性在具体应用场景数据集上缺少更进一步的量化透视和模型的性能仿真验证. ...
... 式中:
$ w_{i,j}^t = \min\; \{ k_s^t(i),k_s^t(j)\} $ 表示在时间窗
$ t $ 中,节点
$ i $ 和节点
$ j $ 间连边的权值;
$ {k}_{s}^{t}(i)、{k}_{s}^{t}(j) $ 分别为节点
$ i $ 和
$ j $ 的
k -shell值.
2.2.6. 排名聚合<sup>[<xref ref-type="bibr" rid="b20">20</xref>]</sup> 基于排名聚合(ranking aggregation, RA)的方法通过制定评分机制,建立各时间窗口内节点的重要性评分矩阵并进行加和计算,根据加和得分获得节点重要性综合排序: ...
2
... 基于上述问题以及超邻接矩阵模型建模时效网络动态演化过程,量化表达节点交互顺序和关联关系,利用图卷积神经网络[21 -22 ] (graph convolutional network, GCN)对图结构数据的处理优势和参数优化能力捕捉空间依赖,构建基于图卷积融合计算的时效网络重要节点辨识模型(identifying critical nodes in temporal networks via SAM and graph convolution, ISGC),聚合节点邻域结构信息和时序特征,在全局维度上实现对时效网络节点重要性的综合评价. ...
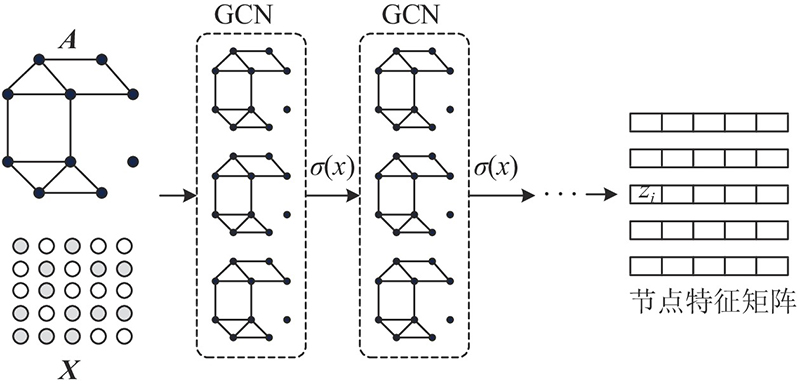
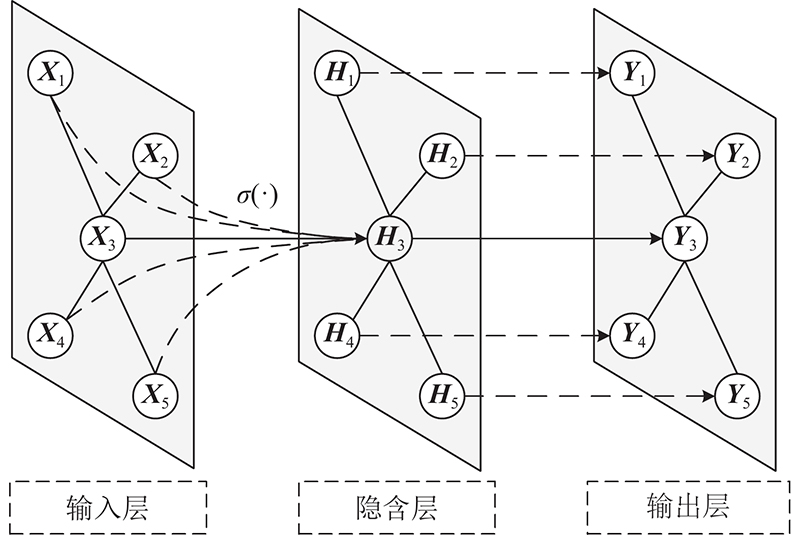
... 卷积神经网络(convolutional neural network, CNN)[23 -24 ] 模型可以利用离散卷积在输入数据空间定义全局共享的卷积核,通过计算中心像素点、相邻像素点的加权和构成特征图,提取局部的空间特征,这只适用于在欧几里德空间,处理图像和规则网格等类型的数据. 对于普遍表达应用的图结构数据,每个节点的局部拓扑结构都存在差异,导致其不再满足平移不变性,无法利用相同尺寸的卷积核执行卷积运算,提取数据拓扑空间特征. Bruna等[25 ] 基于图谱理论利用卷积定理先对谱空间的特征信号做乘法,再通过傅里叶逆变换将信号转换到原空间,对谱域上的图卷积算子进行定义,构建出第一个图卷积神经网络,有效克服图结构数据上不满足平移不变性的局限性. 构造的谱卷积神经网络并不满足局部连接特征,并且计算时空复杂度较高. Kipf等[21 ] 利用一阶Chebyshev多项式作为卷积核,通过参数化设计,有效实现网络局部性,同时大大降低算法时空复杂度,提出图卷积神经网络的空间方法. ...
1
... 基于上述问题以及超邻接矩阵模型建模时效网络动态演化过程,量化表达节点交互顺序和关联关系,利用图卷积神经网络[21 -22 ] (graph convolutional network, GCN)对图结构数据的处理优势和参数优化能力捕捉空间依赖,构建基于图卷积融合计算的时效网络重要节点辨识模型(identifying critical nodes in temporal networks via SAM and graph convolution, ISGC),聚合节点邻域结构信息和时序特征,在全局维度上实现对时效网络节点重要性的综合评价. ...
1
... 基于上述问题以及超邻接矩阵模型建模时效网络动态演化过程,量化表达节点交互顺序和关联关系,利用图卷积神经网络[21 -22 ] (graph convolutional network, GCN)对图结构数据的处理优势和参数优化能力捕捉空间依赖,构建基于图卷积融合计算的时效网络重要节点辨识模型(identifying critical nodes in temporal networks via SAM and graph convolution, ISGC),聚合节点邻域结构信息和时序特征,在全局维度上实现对时效网络节点重要性的综合评价. ...
Gradient-based learning applied to document recognition
1
1998
... 卷积神经网络(convolutional neural network, CNN)[23 -24 ] 模型可以利用离散卷积在输入数据空间定义全局共享的卷积核,通过计算中心像素点、相邻像素点的加权和构成特征图,提取局部的空间特征,这只适用于在欧几里德空间,处理图像和规则网格等类型的数据. 对于普遍表达应用的图结构数据,每个节点的局部拓扑结构都存在差异,导致其不再满足平移不变性,无法利用相同尺寸的卷积核执行卷积运算,提取数据拓扑空间特征. Bruna等[25 ] 基于图谱理论利用卷积定理先对谱空间的特征信号做乘法,再通过傅里叶逆变换将信号转换到原空间,对谱域上的图卷积算子进行定义,构建出第一个图卷积神经网络,有效克服图结构数据上不满足平移不变性的局限性. 构造的谱卷积神经网络并不满足局部连接特征,并且计算时空复杂度较高. Kipf等[21 ] 利用一阶Chebyshev多项式作为卷积核,通过参数化设计,有效实现网络局部性,同时大大降低算法时空复杂度,提出图卷积神经网络的空间方法. ...
基于卷积神经网络的链接表示及预测方法
1
2018
... 卷积神经网络(convolutional neural network, CNN)[23 -24 ] 模型可以利用离散卷积在输入数据空间定义全局共享的卷积核,通过计算中心像素点、相邻像素点的加权和构成特征图,提取局部的空间特征,这只适用于在欧几里德空间,处理图像和规则网格等类型的数据. 对于普遍表达应用的图结构数据,每个节点的局部拓扑结构都存在差异,导致其不再满足平移不变性,无法利用相同尺寸的卷积核执行卷积运算,提取数据拓扑空间特征. Bruna等[25 ] 基于图谱理论利用卷积定理先对谱空间的特征信号做乘法,再通过傅里叶逆变换将信号转换到原空间,对谱域上的图卷积算子进行定义,构建出第一个图卷积神经网络,有效克服图结构数据上不满足平移不变性的局限性. 构造的谱卷积神经网络并不满足局部连接特征,并且计算时空复杂度较高. Kipf等[21 ] 利用一阶Chebyshev多项式作为卷积核,通过参数化设计,有效实现网络局部性,同时大大降低算法时空复杂度,提出图卷积神经网络的空间方法. ...
基于卷积神经网络的链接表示及预测方法
1
2018
... 卷积神经网络(convolutional neural network, CNN)[23 -24 ] 模型可以利用离散卷积在输入数据空间定义全局共享的卷积核,通过计算中心像素点、相邻像素点的加权和构成特征图,提取局部的空间特征,这只适用于在欧几里德空间,处理图像和规则网格等类型的数据. 对于普遍表达应用的图结构数据,每个节点的局部拓扑结构都存在差异,导致其不再满足平移不变性,无法利用相同尺寸的卷积核执行卷积运算,提取数据拓扑空间特征. Bruna等[25 ] 基于图谱理论利用卷积定理先对谱空间的特征信号做乘法,再通过傅里叶逆变换将信号转换到原空间,对谱域上的图卷积算子进行定义,构建出第一个图卷积神经网络,有效克服图结构数据上不满足平移不变性的局限性. 构造的谱卷积神经网络并不满足局部连接特征,并且计算时空复杂度较高. Kipf等[21 ] 利用一阶Chebyshev多项式作为卷积核,通过参数化设计,有效实现网络局部性,同时大大降低算法时空复杂度,提出图卷积神经网络的空间方法. ...
1
... 卷积神经网络(convolutional neural network, CNN)[23 -24 ] 模型可以利用离散卷积在输入数据空间定义全局共享的卷积核,通过计算中心像素点、相邻像素点的加权和构成特征图,提取局部的空间特征,这只适用于在欧几里德空间,处理图像和规则网格等类型的数据. 对于普遍表达应用的图结构数据,每个节点的局部拓扑结构都存在差异,导致其不再满足平移不变性,无法利用相同尺寸的卷积核执行卷积运算,提取数据拓扑空间特征. Bruna等[25 ] 基于图谱理论利用卷积定理先对谱空间的特征信号做乘法,再通过傅里叶逆变换将信号转换到原空间,对谱域上的图卷积算子进行定义,构建出第一个图卷积神经网络,有效克服图结构数据上不满足平移不变性的局限性. 构造的谱卷积神经网络并不满足局部连接特征,并且计算时空复杂度较高. Kipf等[21 ] 利用一阶Chebyshev多项式作为卷积核,通过参数化设计,有效实现网络局部性,同时大大降低算法时空复杂度,提出图卷积神经网络的空间方法. ...
1
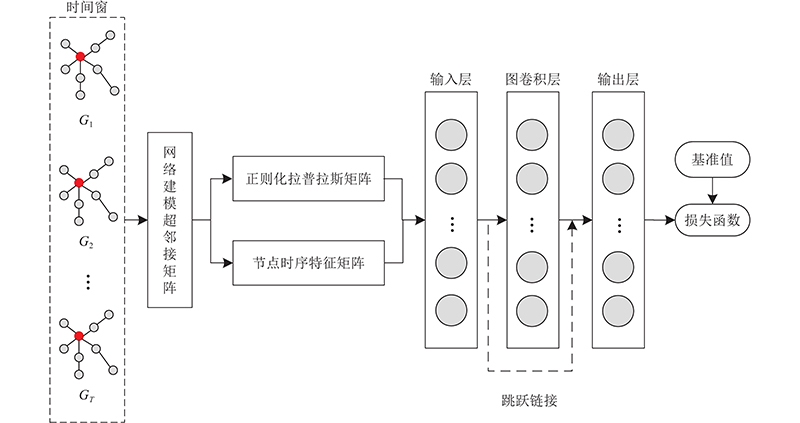
... 在时序特征表达阶段中,通过超邻接矩阵对时效网络进行动态演化建模,表征节点层内和层间连接的时间依赖关系,并计算节点在不同时间层的时序特征属性,构造时序特征矩阵作为下一阶段的输入;在空间信息提取阶段中,根据时效网络数据构建静态聚合网络,通过邻接矩阵描述时效网络的静态聚合拓扑结构以表征空间依赖,并将经过数据预处理后的节点时序特征作为模块共同输入,利用图卷积提取网络空间信息和节点特征,输出节点最终特征序列表示.针对模型训练过程中存在的梯度消失和节点信息丢失问题,设计添加跳跃连接机制(skip connection, SC)[26 ] ,以提升网络表征能力. ISGC模型结构如图1 所示,主要包含3个部分,即输入层、图卷积层和输出层. ...
1
... 式中:
$ g(v,u) $ 为节点
$ v $ 相对于节点
$ u $ 的综合得分,
$ g(v) $ 为
$ v $ 相对于网络其他所有节点的最终评分.
2.2.7. 时序网页排名<sup>[<xref ref-type="bibr" rid="b27">27</xref>]</sup>(temporal page rank, TPR) 将时效网络表示为系列静态图集合,基于网络上的随机游走策略,结合时序信息和动力学提出适用于时效网络的时序PageRank方法来评估节点重要性程度: ...
Temporal gravity model for important node identification in temporal networks
1
2021
... 式中:
$ c({\boldsymbol{z}}|t) $ 为在时间
$ t $ 之前从节点
$ v $ 出发到达
$ u $ 的游走序列集合,
$ c({{\boldsymbol{z}}'}|t) $ 为所有从节点
$ v $ 出发且与游走
$ {\boldsymbol{z}} $ 的路径长度相等的游走数目.
2.2.8. 时序引力模型<sup>[<xref ref-type="bibr" rid="b28">28</xref>]</sup>(temporal gravity model, TGM) 假设节点的中心性取决于对邻居节点的引力大小,必须满足邻居节点在结构和时序距离上都接近目标节点. 将经典静态中心性度量指标及时序扩展视为质量,结合节点之间的时序距离,定义时序引力中心性,实现对节点重要性的综合度量: ...
Data on face-to-face contacts in an office building suggest a low-cost vaccination strategy based on community linkers
1
2015
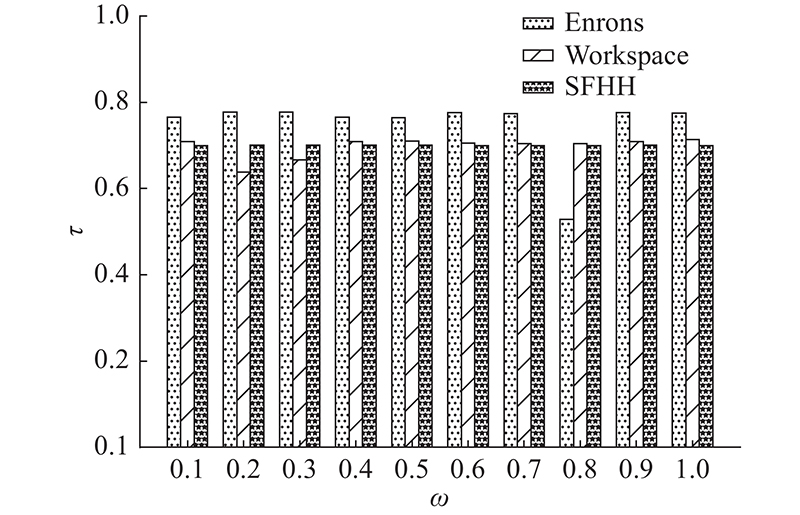
... 为了验证ISGC模型在时效网络节点重要性评价过程中的有效性,选用3个公开实证网络数据集Workspace[29 ] 、Enrons[30 ] 和SFHH[31 ] 进行实验. Workspace是一家法国公司通过移动射频设备获得的公司员工每天面对面的交互数据,时间是2013-6-24—2013-7-3;Enrons是网络科学研究领域最常用的实证网络数据之一,主要包含美国安然公司员工之间的往来邮件数据,时间是1999—2002年,本研究截取其中2001年交互数据子集作为实验数据,SFHH是2009年法国尼斯会议中与会者之间的交互网络. 数据集的基本统计特征信息描述如表1 所示,其中Num为网络节点规模,Win为切分的时间窗口数量,Inter为节点间的交互次数,Static为聚合静态网络节点间的连边数量,During为数据集时间跨度. ...
1
... 为了验证ISGC模型在时效网络节点重要性评价过程中的有效性,选用3个公开实证网络数据集Workspace[29 ] 、Enrons[30 ] 和SFHH[31 ] 进行实验. Workspace是一家法国公司通过移动射频设备获得的公司员工每天面对面的交互数据,时间是2013-6-24—2013-7-3;Enrons是网络科学研究领域最常用的实证网络数据之一,主要包含美国安然公司员工之间的往来邮件数据,时间是1999—2002年,本研究截取其中2001年交互数据子集作为实验数据,SFHH是2009年法国尼斯会议中与会者之间的交互网络. 数据集的基本统计特征信息描述如表1 所示,其中Num为网络节点规模,Win为切分的时间窗口数量,Inter为节点间的交互次数,Static为聚合静态网络节点间的连边数量,During为数据集时间跨度. ...
Can co-location be used as a proxy for face-to-face contacts?
1
2018
... 为了验证ISGC模型在时效网络节点重要性评价过程中的有效性,选用3个公开实证网络数据集Workspace[29 ] 、Enrons[30 ] 和SFHH[31 ] 进行实验. Workspace是一家法国公司通过移动射频设备获得的公司员工每天面对面的交互数据,时间是2013-6-24—2013-7-3;Enrons是网络科学研究领域最常用的实证网络数据之一,主要包含美国安然公司员工之间的往来邮件数据,时间是1999—2002年,本研究截取其中2001年交互数据子集作为实验数据,SFHH是2009年法国尼斯会议中与会者之间的交互网络. 数据集的基本统计特征信息描述如表1 所示,其中Num为网络节点规模,Win为切分的时间窗口数量,Inter为节点间的交互次数,Static为聚合静态网络节点间的连边数量,During为数据集时间跨度. ...
Efficient behavior of small-world networks
1
2001
... 时效网络中的节点重要性可以从2个方面进行评价:1)从网络结构性能角度出发,考察节点移除如何影响网络连通性;2)从网络功能性角度出发,考察节点对网络传播效果的影响[6 ] .通过计算网络中所有节点之间的距离倒数之和的均值获得网络效率[32 ] ,可表示静态网络中信息流通的难易程度,并评判网络连通性.时效网络通过替换距离变量,定义时序全局效率[5 ] 指标来衡量信息传播效率,表征网络时序性能: ...
Attack robustness and centrality of complex networks
1
2013
... 为了检验ISGC方法对节点重要性的排序效果,研究采用节点删除法[33 ] 计算节点删除后时序全局效率与原时序效率的差值 $ {E_v} $
A new measure of rank correlation
1
1938
... 式中: $ {e_v} $ $ e $ [34 -35 ] (Kendall’s $ \tau $ ) 评估模型输出序列和时效全局效率差值序列排序的一致性程度. 一致性程度越高,则模型输出序列排序精准度越高. ...
1
... 式中: $ {e_v} $ $ e $ [34 -35 ] (Kendall’s $ \tau $ ) 评估模型输出序列和时效全局效率差值序列排序的一致性程度. 一致性程度越高,则模型输出序列排序精准度越高. ...