浙江大学学报(工学版)

浙江大学学报(工学版), 2023, 57(5): 883-891 doi: 10.3785/j.issn.1008-973X.2023.05.004

计算机技术与控制工程

基于数字孪生的机身对接精度优化控制方法

赵永胜,, 赵志勇, 李迎, 张涛

1. 北京工业大学 先进制造与智能技术研究所，北京 100020

2. 北京工业大学 先进制造技术北京市重点实验室，北京 100020

3. 北京工业大学 机械工业重型机床数字化设计与测试技术重点实验室，北京 100020

Optimal control method of fuselage docking accuracy based on digital twin

ZHAO Yong-sheng,, ZHAO Zhi-yong, LI Ying, ZHANG Tao

1. Institute of Advanced Manufacturing and Intelligent Technology, Beijing University of Technology, Beijing 100020, China

2. Beijing Key Laboratory of Advanced Manufacturing Technology, Beijing University of Technology, Beijing 100020, China

3. Machinery Industry Key Laboratory of Heavy Machine Tool Digital Design and Testing Technology, Beijing University of Technology, Beijing 100020, China

收稿日期: 2022-09-21  

基金资助: 国家自然科学基金资助项目（52075012）

Received: 2022-09-21  

Fund supported: 国家自然科学基金资助项目（52075012）

作者简介 About authors

赵永胜（1975—），男，教授，博导，从事机床动力学、非线性系统辨识和系统仿真与控制研究.orcid.org/0000-0002-6592-8833.E-mail：yszhao@bjut.edu.cn , E-mail：yszhao@bjut.edu.cn

摘要

针对传统对接方法在缺少现场实测数据支持下的被动调整问题，提出基于数字孪生的机身对接精度优化控制方法.基于数字孪生虚实结合技术，研究机身对接工艺优化反馈控制技术. 搭建融合冗余控制算法和工艺优化策略的数字孪生系统，明确了基于现场实测数据的测量-优化-反馈精度优化流程. 基于有限状态机理论，精准重建数字孪生模型，实现对接过程的监控和精度预测，根据同轴度评价指标完成工艺参数二次设计，将优化后的工艺参数重新下发至物理现场、控制现场进行对接. 对接位姿偏差对比结果表明：对接精度优化控制方法将机身筒段位置偏差降低了60.03%，姿态偏差降低了53.94%.

关键词： 数字孪生 ; 机身对接 ; 模型重构 ; 参数优化 ; 优化控制

Abstract

Aiming at the problem of passive adjustment of traditional docking methods without the support of field measured data, the optimization feedback control technology of fuselage docking process was studied based on the digital twin virtual reality combination technology. A digital twin system integrating the redundant control algorithm and the process optimization strategy was built. The process of measurement-optimization-feedback accuracy optimization based on field measured data was clarified. The digital twin model was accurately reconstructed based on the finite-state machine theory. The monitoring and precision prediction of docking process were realized. The secondary design of process parameters was completed according to the coaxiality evaluation index. The optimized process parameters were redistributed to the physical site to control the on-site docking process. The comparison of the docking position and attitude deviation showed that the optimal control method of the docking accuracy reduced the position deviation of the fuselage barrel by 60.03% and the attitude deviation by 53.94%.

Keywords： digital twin ; fuselage docking ; model reconstruction ; parameter optimization ; optimal control

PDF (1631KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

赵永胜, 赵志勇, 李迎, 张涛. 基于数字孪生的机身对接精度优化控制方法. 浙江大学学报(工学版)[J], 2023, 57(5): 883-891 doi:10.3785/j.issn.1008-973X.2023.05.004

ZHAO Yong-sheng, ZHAO Zhi-yong, LI Ying, ZHANG Tao. Optimal control method of fuselage docking accuracy based on digital twin. Journal of Zhejiang University(Engineering Science)[J], 2023, 57(5): 883-891 doi:10.3785/j.issn.1008-973X.2023.05.004

机身的对接装配是飞机总装的重要环节，装配质量对飞机的寿命和可靠性有很大影响[1]. 传统的飞机对接装配缺乏现场实测数据支持，装配精度低，装配质量一致性差[2]. 为提高机身对接精度，对接自动化是对接装配发展的必然趋势，是提升制造质量重要途径[3]. 近年来，国内外学者在自动对接方面展开大量研究，主要围绕对接偏差传递[4]、累积和优化[5-6]等方面. 国内目前存在的主要问题是对接工艺主要针对理想模型，很少考虑实际驱动误差，难以根据装配现场进行装配优化[7-8].

数字孪生技术的虚实结合和双向数据流通特点，促进飞机对接装配模式的转型[9]，实现了物理空间到数字空间的同步映射，实时监控对接的过程，以及数字空间对物理空间的实时控制. 姜珊等[10]以翼身对接平台为对象，定义了有限状态机的转移机制，通过对数据进行采集和处理，实现调姿对接机构在数字空间的参数化几何建模，建立基于有限状态机的数字孪生几何模型. 张玉良等[11]分析在轨航天器的结构组成，详细介绍面向航天器在轨装配的数字孪生技术内涵，提出通过数据组成实现数字孪生体构建，以此表达在轨航天器的状态. 张入元等[12]提出一种基于数字孪生的在线监控方案，介绍在线监控系统的实施流程，研究基于数字孪生的总装建模和全方位数据采集，根据实时数据更新数字孪生模型，并实现模型可视化以及装对接的在线监控. 张瀚丹等[13]设计基于数字孪生的雕刻机交互平台，详细介绍了各数字孪生镜像模型的构建，利用各种软件实现工作的虚拟调试仿真和动态实时监控，实验结果分析表明，系统具有较高的实时性和准确性. 孙学民等[14]针对汽车发动机缸体单元装配，研究数字孪生的产品全要素建模方法，提出基于知识图谱的工艺优化方法和装配质量的控制策略，搭建数字孪生装配系统平台并进行验证.

传统的对接精度仿真通过建立虚拟模型，采用合适的算法进行仿真，预测对接精度. 飞机的对接装配仿真还需要根据现场实际测量数据重建模型，优化对接工艺，减小因为实际对接现场外界因素造成的对接装配误差. 黄郁雯等[15]针对船体分段结构装配问题，研究分段装配体系，并对船体装配工艺进行规划，开发数字空间和物理空间的信息交互平台，在一定程度上可以解决船体装配过程中的外界干扰因素. 易扬等[16]针对复杂产品在装配精度预测过程中缺乏装配现场实测数据指导的问题，提出基于数字孪生的精准建模方法，在此基础上，结合现场实测数据和多维度误差源对装配过程进行精度预测，并搭建数字孪生装配平台，验证了方法的可行性. 李新等[17]以井下变电所巡检机器人为研究对象，设计基于虚幻引擎4（unreal engine 4，UE4）的数字孪生系统，该系统可以实时接收巡检过程中的检测数据，三维显示井下变电所巡检环境，实现整个巡检过程的智能化. 郭飞燕等[18]对装配工艺优化反馈的各项关键技术进行研究，考虑真实物理拓扑关系构建数字孪生模型，基于面向装配设计的思想，对装配工艺进行规划，根据实际测量数据更新装配偏差，并结合装配过程中的形变信息实现装配公差的优化，在仿真软件中进行柔性装配仿真，验证此技术的可能性.

目前对接装配过程的监控和优化的研究还处于探索阶段，通过数字孪生技术，结合现场实测数据，对装配过程进行监控和工艺优化的全流程落地应用研究较少. 本研究提出基于数字孪生的飞机对接精度优化方法，搭建了基于数字孪生的飞机对接系统平台，该数字孪生系统平台具有虚拟模型重建、实时对接状态监控、对接工艺优化和精准实时控制的功能.

1. 基于数字孪生的机身对接系统框架

面向数字孪生技术在飞机机身对接中的应用，开展基于实时数据采集的数字孪生模型精准重建，融合实测数据和评价指标的工艺优化方法，建成数据采集拟合平台. 基于UE4的可视化监控平台和对接控制平台的系统集成，搭建机身数字孪生对接交互系统，验证基于数字孪生的对接精度优化方法.

基于数字孪生的机身对接系统总体框架如图1所示，基于数字孪生五维模型[19]，搭建机身数字孪生对接控制系统. 基于数字孪生的机身对接系统主要分为3个部分，包括物理层、数据层和孪生层. 物理空间包括对接物理实体、激光跟踪仪和位移传感器等测量系统和数控定位器对接控制系统，物理空间具备位姿偏差信息测量采集功能和对接控制指令的执行功能.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   基于数字孪生的机身对接系统

Fig.1   Fuselage docking system based on digital twin


孪生数据服务层是孪生层模型映射和控制系统构建的关键，数据服务层全方面地包含物理空间的设计制造数据、测量感知数据、虚拟空间数据处理分析数据和参数优化数据等，同时是实现物理空间和数字空间数据传输和交互连接的基础. 通过构建数字空间和物理空间之间的连接，保证高精度测量设备和数字化对接控制技术之间的数据信息双向传输，实现机身的对接闭环反馈.

数字空间孪生层包括物理实体几何数据、约束数据的全要素建模、包含精度评价算法、参数优化算法以及冗余控制算法等对接控制系统. 在此基础上，实现模型重建和三维可视化，并为物理空间的实际对接现场提供控制指令，保证对接持续进行.

2. 基于实时采集的孪生模型重建

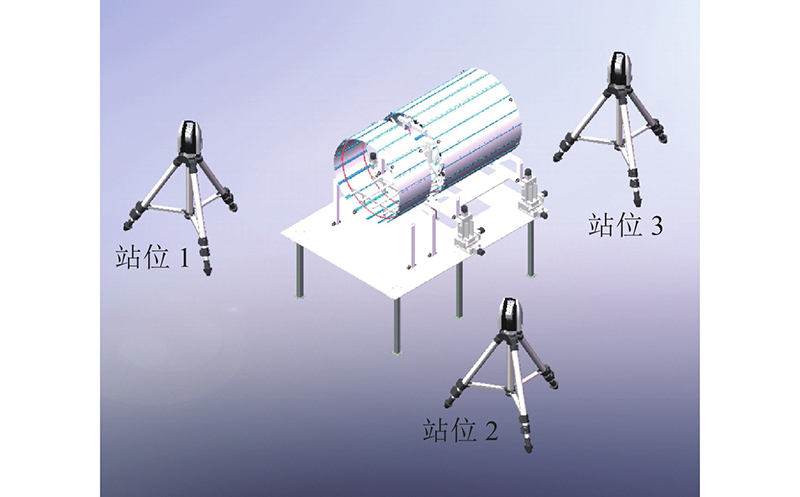
测量网络的构建是孪生模型重建的基础，也是促进飞机对接工艺优化的关键. 根据激光跟踪仪站位设计要求优化测量站位布局，即在能够满足测量需求的前提下，尽量采取最少的站位数量，减小激光跟踪仪的转站误差，提高测量精度[20].

基于对接接触面之间的同轴度、平行度等精度要求，筛选用于构建机身数字孪生模型的关键特征点[21]，安装在靶球基准座. 如图2所示，激光跟踪仪反射镜选用1.5 inch标准球，配合安装在飞机机身上的靶球基准座进行测量. 通过3个站位下的激光跟踪仪分别对机身多个测量基准点进行冗余测量，完成各基准点测量后，根据多站位冗余数据优化解算基准点空间坐标，完成激光跟踪仪坐标系的统一，构建测量网络. 通过激光跟踪仪测量网络的构建，激光跟踪仪转站误差可得到有效控制.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   多站位冗余测量网络

Fig.2   Multi station redundant measurement network


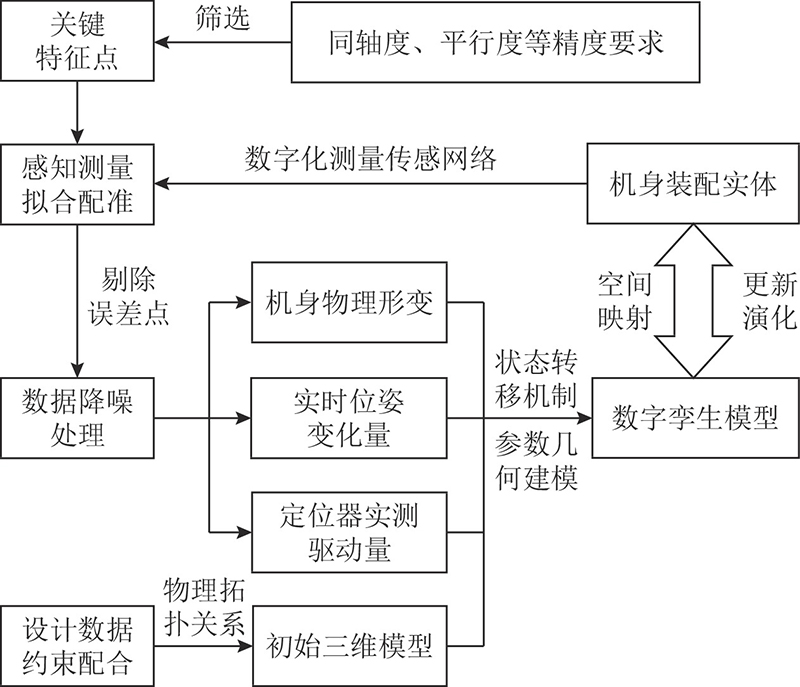
为了使数字孪生模型能表示对接现场的真实物理状态，数据信息需要包括工装设计制造数据和尺寸公差数据、装配完成后零部件真实约束配合数据，以及对接过程中测量设备和传感器测量采集的真实数据等. 首先根据初始设计制造数据建立数字孪生仿真平台三维模型，并根据物理实体真实约束，配合数据对数字孪生模型进行装配约束，保证和物理实体装配约束一致，实现相同的协同控制运动，为实现物理空间实时数据与数字空间模型融合奠定基础.

在物理现场对接过程中，对现场的实际数据进行采集和处理，通过数据处理算法对采集到的数据信息进行降噪处理，去除无效数据，并实时修正机身关键特征点参数，为精准重构数字孪生模型提供信息基础.

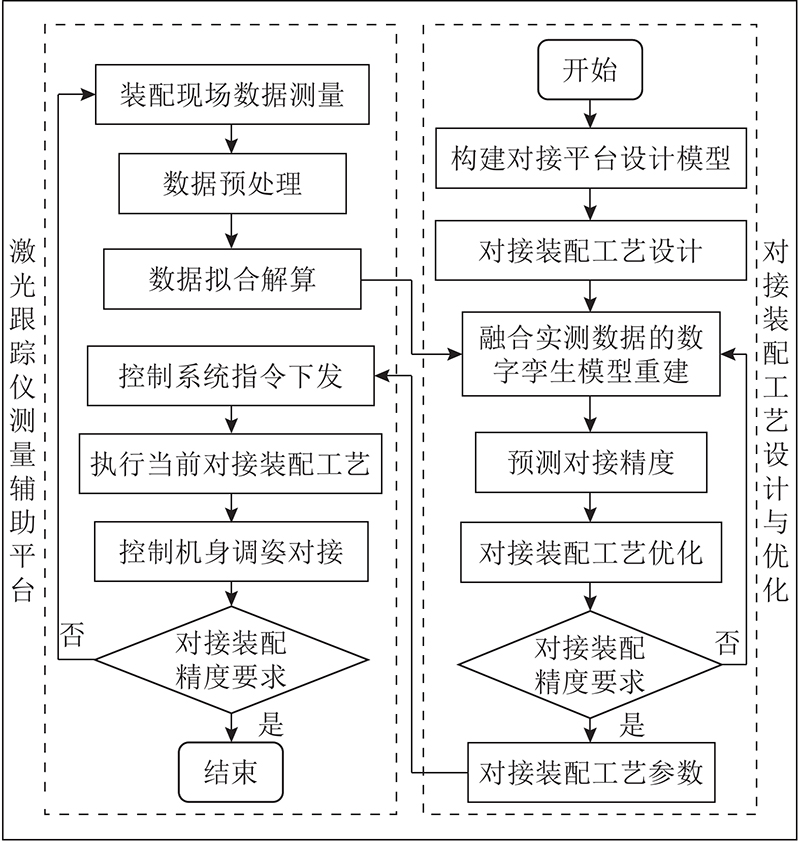
基于数字孪生的模型动态精准重构流程如图3所示，基于有限状态机理论[22-23]，将对接平台数字孪生模型建模过程划分为6个状态，包括3个平移和3个旋转状态. 通过激光跟踪仪测量设备进行实时数据采集，计算机身位姿变化量，得到机身的状态转移指令；通过位移传感器感知定位器驱动轴实际变化量，得到调姿工装的状态转移指令. 结合工装各部件之间的装配约束数据，快速重构机身和调姿工装各定位器零部件模型，构建能反映当前装配过程的几何模型，完成装配现场向数字空间的映射，实现数字孪生模型的参数化几何建模. 在对接装配工艺执行过程中，可实现在线数据检测，同步数字孪生模型，监控对接装配过程，感知运行状态，计算对接装配精度.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   数孪生模型精准重构

Fig.3   Precise reconstruction of digital twin model


3. 基于数字孪生的精度优化控制方法

开展面向对接现场实时测量和主动预测调整的方法研究，基于数字孪生的飞机对接精度优化方法整体流程如图4所示. 根据对接过程中的实测数据进行精度预测，主动优化工艺参数，弥补传统对接方法被动调整的不足，提高机身对接装配精度[24]和装配效率.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   基于数字孪生的飞机对接精度优化流程

Fig.4   Aircraft docking accuracy optimization process based on digital twin


基于数字孪生虚实融合技术，首先在数字空间构建机身对接装配平台几何模型和约束模型，根据初始测量数据初步进行对接装配工艺规划. 在物理空间对接过程中，通过激光跟踪仪实时测量机身特征点坐标，并将其作为模型动态构建的数据来源. 利用数据处理软件进行数据处理和拟合解算，将处理之后的数据上传到数字空间，更新重建数字孪生几何设计模型，并且通过数字孪生体动态描述机身对接过程的实际路径情况，实现数字孪生的从实到虚.

通过现场实时测量数据，重建数字孪生模型，根据精度评价指标预测机身的对接精度，进行工艺优化，对工艺参数进行二次设计. 将优化后的工艺参数下发至对接控制系统，依据优化后的对接工艺指令控制机身完成调姿对接，直至满足精度要求，实现数字孪生的以虚控实，从而实现闭环控制.

基于数字孪生的对接控制系统坐标系如图5所示，首先在激光跟踪仪上建立测量坐标系，并且通过构建测量网络完成激光跟踪仪转站，实现坐标系的统一，以此作为全局坐标系 $ {\text{\{}}O{\text{\} }} $. 以机身对接接触面圆心为原点，轴线矢量方向为y轴，通过原点垂直于对称面方向为x轴，建立固定坐标系 $ \{ F\} $和对接坐标系 $\{ D\} $，机身横截面圆心分别为 ${F_1}、{F_2}、{D_1}、{D_2}$. 通过激光跟踪仪测量拟合机身位姿，得到固定坐标系 $ \{ F\} $在全局坐标系 $ {\text{\{}}O{\text{\} }} $中的位姿为 $ {{\boldsymbol{F}}_{\rm{B}}}{\boldsymbol{ = }}{\left[ {X_{\rm{B}},Y_{\rm{B}},Z_{\rm{B}},\alpha _{\rm{B}},\beta _{\rm{B}},{\gamma _{\rm{B}}}} \right]^{\text{T}}} $，对接坐标系 $\{ D\} $在全局坐标系 $ {\text{\{}}O{\text{\} }} $中的位姿为 ${{\boldsymbol{D}}_{\rm{M}}}{\boldsymbol{ = }}\left[ {X_{\rm{M}}},{Y_{\rm{M}}},{Z_{\rm{M}}},{\alpha _{\rm{M}}}, {\beta _{\rm{M}}},{\gamma _{\rm{M}}} \right]^{\text{T}}$. 将固定机身位姿 ${{\boldsymbol{F}}_{\rm{B}}}$在轴线方向保留20.0 mm余量得到机身理想位姿 $ {{\boldsymbol{D}}_0} $，计算得到位置偏差 ${\boldsymbol{p}}$和姿态偏差 $ {\boldsymbol{a}} $.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   对接控制平台坐标系

Fig.5   Docking control platform coordinate system


采用5次多项式 ${\boldsymbol{f}}(t)$对对接工艺进行初步规划，以此验证基于数字孪生的工艺优化方法. 初始轨迹方程为

$ {\boldsymbol{f}}(t) = {{\boldsymbol{m}}_0}{t^5}+{{\boldsymbol{m}}_1}{t^4}+{{\boldsymbol{m}}_2}{t^3}+{{\boldsymbol{m}}_3}{t^2}+{{\boldsymbol{m}}_4}t+{{\boldsymbol{m}}_5} . $
(1)

边界条件为

$ \left. \begin{gathered} {\boldsymbol{f}}(0) = {{\boldsymbol{D}}_{\rm{M}}}, \\ {\boldsymbol{f}}(T) = {{\boldsymbol{D}}_0} , \\ {\boldsymbol{f}}'(0) = {\bf{0}}, \\ {\boldsymbol{f}}'(T) = {\bf{0}}, \\ {\boldsymbol{f}}''(0) = {\bf{0}}, \\ {\boldsymbol{f}}''(T) = {\bf{0}}. \\ \end{gathered} \right\} $
(2)

联立求解得

$\begin{split} {\boldsymbol{f}}(t) =\;& \frac{{6({{\boldsymbol{D}}_0} - {{\boldsymbol{D}}_{\rm{M}}})}}{{{T^5}}}{t^5}+\frac{{ - 15({{\boldsymbol{D}}_0} - {{\boldsymbol{D}}_{\rm{M}}})}}{{{T^4}}}{t^4}+\\ &\frac{{10({{\boldsymbol{D}}_0} - {{\boldsymbol{D}}_{\rm{M}}})}}{{{T^3}}}{t^3}+{{\boldsymbol{D}}_{\rm{M}}} . \end{split} $
(3)

式中：m为未知数矩阵，t为时间， $T$为对接时间常数（由计算得到）， ${{\boldsymbol{D}}_{\rm{M}}}$为初始实际位姿， $ {\boldsymbol{D}} _0 $为理想目标位姿.

为了验证精度优化控制方法，初步将调姿轨迹按照时间划分为5段，之后分步进行调姿. 根据分步调姿工艺结果，分别计算相应调姿过程中的位姿偏差，最终将各段轨迹通过冗余驱动算法计算出各个定位器的驱动量，驱动定位器实现机身对接[25] .

例如位置调整，假设机身先完成位置调整，再完成姿态调整，则机身通过位置调整后实际位姿 ${{\boldsymbol{D}}_{\rm{M}}}$应和位置调整完成后的理论位姿 ${{\boldsymbol{D}}^{\text{w}}} = \left[ {X_1},{Y_1}, {Z_1},\alpha , \beta ,\gamma \right]^{\text{T}}$重合，得到定位器变换规律为

$ \left[ {{{\boldsymbol{P}}_i}^{\text{w}},1} \right] = \left[ {{{\boldsymbol{P}}_i},1} \right]\left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ {\Delta x}&{\Delta y}&{\Delta z}&1 \end{array}} \right] . $
(4)

式中： ${{\boldsymbol{P}}_{\boldsymbol{i}}} = [{x_i},{y_i},{z_i}]$和 ${{\boldsymbol{P}}_i}^{\text{w}} = [{x_i}^1,{y_i}^1,{z_i}^1]$为位置调整前后定位器坐标.

在位置调整中，当4个定位器匀速运动时不存在调姿工装变形情况，故定位器采用匀速运动即可，令（ $ i = {\text{1}},{\text{2}},{\text{3}},{\text{4}} $）即可得到4个定位器的各轴驱动量.

定位器运动向量矩阵为

$ {\boldsymbol{M}} = \left[ \begin{gathered} {x_{_1}}^1 - {x_{_1}},\;{y_{_1}}^1 - {y_{_1}},\;{z_{_1}}^1 - {z_{_1}} \\ {x_{_2}}^1 - {x_{_2}},\;{y_{_2}}^1 - {y_{_2}},\;{z_{_2}}^1 - {z_{_2}} \\ {x_{_3}}^1 - {x_{_3}},\;{y_{_3}}^1 - {y_{_3}},\;{z_{_3}}^1 - {z_{_3}} \\ {x_{_4}}^1 - {x_{_4}},\;{y_{_4}}^1 - {y_{_4}},\;{z_{_4}}^1 - {z_{_4}} \\ \end{gathered} \right] . $
(5)

在完成一步对接过程后，机身到达 $ {{\boldsymbol{D}}_1}' $（ $ {{\boldsymbol{D}}_1}' $为完成第1段轨迹内的位置调整和姿态调整后的机身实际位姿）. 因为机身薄壁大部件在对接过程中的变形和定位器控制误差等，使得机身对接装配仿真不符合现场实际情况，与理论位置 $ {{\boldsymbol{D}}_1} $比较，存在一定偏差.

基于数字孪生的工艺优化方法在对接过程中实现工艺主动优化，通过数字孪生平台预测对接精度并根据同轴度精度评价指标，对装配质量进行评估. 当不满足精度要求时，重新根据位姿偏差规划对接工艺，完成工艺参数的二次设计，并将工艺指令下发到物理现场对对接过程进行精确控制.

采用直线法评价两机身的同轴度，即通过截面圆心( ${F_1},{F_2},{F_3},{F_4}$)构造一条空间直线，同轴度用该直线的直线度表示：

$ {\phi } = 2{\varphi }. $
(6)

式中： ${\phi }$为同轴度， ${\varphi}$为直线度.

根据同轴度评价指标 $\Delta \phi $验证是否满足精度要求，即 $\Delta \phi \geqslant {\phi }$时，重新拟合得到新的实际位姿 $ {{\boldsymbol{D}}_{\rm{M}}} $，计算相应的位姿偏差，进行工艺规划. 之后将新的工艺参数下发到控制系统中，生成新的控制指令控制定位器实现机身对接，由此形成闭环控制，保证精度要求在误差范围内.

4. 实例验证

4.1. 机身筒段对接验证平台和系统集成

为了验证基于数字孪生的对接精度优化控制方法的可行性，以某民用飞机机身的典型结构缩比模型为例设计了软硬件系统，通过集成的数字孪生对接交互系统建立上位机和物理装配实体的交互连接，从而优化机身对接的精度，具体流程如下.

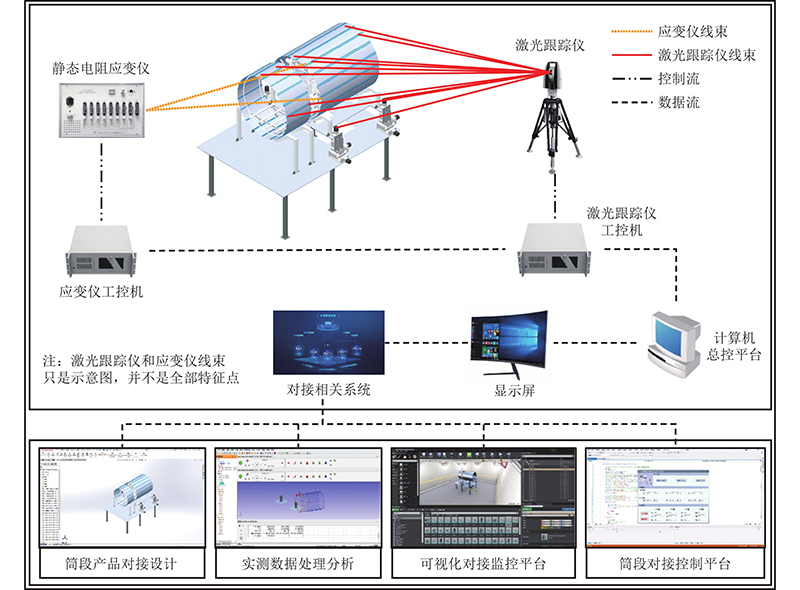
1）围绕物理现场以及对接装配实测数据的采集需求，对物理空间中的测量设备进行规划布局，构建测量辅助网络. 对装配现场测量设备、数据处理软件及仿真监控平台、控制系统等进行集成，从而形成基于数字孪生的机身筒段对接交互系统，如图6所示.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   基于数字孪生的机身筒段对接交互系统

Fig.6   Interactive system of fuselage barrel butt joint based on digital twin


2）通过数据采集处理平台对物理空间机身筒段位姿、电机驱动量等信息进行实时采集，将数据传输到基于UE4的可视化监控平台，精准重建数字孪生模型，以此监控实体的运行状态.

3）在对接过程中，基于对接精度优化策略，进行对接精度仿真预测，根据评价指标评价对接装配工艺的可行性，符合精度要求后将工艺指令下发到运动控制系统平台.

4）通过Visual studio搭建对接控制系统平台，用来控制调姿对接过程的运行和停止，并且能够实时显示电机的驱动量. 经过数据采集处理平台和可视化监控平台，将得到的位姿调整量输入到对接控制系统平台，完成机身对接装配.

4.2. 对接精度优化控制方法验证

某民用飞机机身的典型结构机身筒段缩比模型对接装配现场如图7所示. 实验台主要由机身筒段、固定筒段、位姿测量系统、对接控制系统组成. 固定筒段安装在调姿实验台支架上，移动筒段通过调姿工装安装在由4个定位器组成的并联调姿机构上，两筒段之间的位姿误差没有超过定位器的有效行程.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   机身筒段对接装配现场

Fig.7   Butt joint assembly site of fuselage barrel


利用Leica激光跟踪仪构建调姿测量网络，通过多站位冗余测量网络完成激光跟踪仪转站，固定筒段和机身筒段关键特征点在全局坐标系下的坐标由激光跟踪仪配套软件Spatial Analyzer采集，得到的坐标数据分别如表1、2所示. 根据表中数据，利用最小二乘位姿拟合方法对数据进行拟合求解，计算得到固定筒段的位姿参数 $ {{\boldsymbol{F}}_{\rm{B}}} $=[−141.504，667.189，−284.130，−2.449°，90.471°，10.884°]，机身筒段位姿参数 $ {{\boldsymbol{D}}_{\rm{M}}} $=[−261.706，642.920，−305.994，−1.977°，90.362°，10.381°]. 根据固定筒段的位姿参数在轴线方向保留20.0 mm余量得到机身筒段理想位姿 $ {{\boldsymbol{D}}_0} $=[−161.504，667.189，−284.130，−2.449°，90.471°，10.884°].

表 1   对接前固定筒段坐标

Tab.1  Coordinates of fixed barrel section before docking

序号 $X$/mm $Y$/mm $Z$/mm
1 373.555 214.014 −283.830
2 323.193 489.961 181.887
3 223.150 1027.714 174.355
4 169.474 1276.241 −301.373
5 −39.473 136.544 −283.939
6 −85.010 403.496 181.617
7 −187.961 936.987 183.871
8 −242.197 1195.985 −275.965

新窗口打开| 下载CSV


表 2   对接前机身筒段坐标

Tab.2  Coordinates of fuselage barrel section before docking

序号 $X$/mm $Y$/mm $Z$/mm
1 −165.008 111.734 −298.051
2 −186.030 242.148 51.455
3 −309.740 903.813 168.885
4 −368.699 1138.559 −122.273
5 −1267.995 −92.702 −288.938
6 −1315.942 174.049 176.233
7 −1413.406 710.535 163.508
8 −1464.478 978.906 −294.405

新窗口打开| 下载CSV


根据所提的基于数字孪生的对接精度优化控制方法，在对接过程中，根据实测数据实时监控对接过程，预测对接精度. 超出精度评价指标阈值 $\Delta \phi $=1.0 mm时，优化对接工艺参数，并将优化后的驱动量下发到由C#开发的运动控制系统平台，即可按照编写好的程序更新冗余驱动算法，控制定位器完成机身筒段对接. 机身筒段完成对接后，两筒段对接端面对正，并且两端面销孔基本对齐. 再次测量机身筒段特征点，拟合机身筒段位姿数据，验证对接精度是否满足要求，对接后的机身筒段特征点坐标值如表3所示.

表 3   对接后机身筒段坐标

Tab.3  Coordinates of fuselage barrel section after docking

序号 $X$/mm $Y$/mm $Z$/mm
1 −67.851 134.420 −272.060
2 −86.006 268.002 76.409
3 −208.747 930.715 188.840
4 −270.093 1162.814 −103.943
5 −1170.726 −69.842 −252.045
6 −1214.856 201.168 211.063
7 −1312.421 737.478 194.271
8 −1367.247 1001.686 −265.625

新窗口打开| 下载CSV


通过所提方法完成对接后，根据各特征点的坐标值计算得到本研究对接精度优化机身筒段的位姿参数为 $ {{\boldsymbol{D}}_{\text{Y}}} $=[−161.884，666.843，−284.257，−2.392°，90.458°，10.937°]. 点击复位按钮将机身筒段调整到初始位姿，通过工艺规划和冗余驱动调姿算法进行调姿，在对接过程中不再根据实时测量数据进行反馈调整. 对接完成后，测量拟合得到常规方法机身筒段的位姿参数为 $ {{\boldsymbol{D}}_{\rm{N}}} $=[−162.069，668.316，−283.551，−2.546°，90.438°，10.965°]. 由此得到使用基于数字孪生的对接精度优化控制方法后，对接端面中心位置位姿绝对偏差如图8所示，其中，s为位置偏差，θ为姿态偏差.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   机身筒段对接位姿偏差对比

Fig.8   Comparison of posture deviation of fuselage barrel butt joint


对接位姿偏差对比显示，使用本研究优化方法前后的位姿偏差存在明显变化. 轴线Δ $x$=0.380 mm，Δ $y$=0.346 mm，Δ $z$=0.127 mm，Δ $\alpha $=0.057°，Δ $\;\beta $=0.013°，Δ $\gamma $=0.053°，满足对接精度要求，在一定程度上表明了基于数字孪生的对接精度优化控制系统的可行性.

5. 结　语

1）基于实时数据采集的数字孪生模型精准重建是精度优化控制的基础，通过构建测量网络完成实时数据采集，基于有限状态机理论实现物理现场和数字空间的数据融合，不断更新对接现场的数字孪生模型.

2）通过精度预测和评价指标优化对接工艺参数，并将位姿参数传递到运动控制系统平台，对机身下一步对接进行更精确的控制.

3）以某民用飞机机身的典型结构缩比模型为例，从面向对接现场的数字孪生对接精度优化控制系统验证了本研究方法的可行性. 实验结果表明，所提方法可以提高机身筒段的对接精度.

4）利用数字孪生技术进行实际现场对接过程的监控预测，优化对接工艺指令，对装配过程进行实时控制，从而提高对接精度，此项技术具有一定的通用性. 虽然对数字孪生驱动对接精度优化控制技术的落地应用展开相关研究，只局限于各个模块的集成，未来可以将所有模块统一到可视化管控平台中.

参考文献

梅中义, 黄超, 范玉青

飞机数字化装配技术发展与展望

[J]. 航空制造技术, 2015, 18: 32- 37

[本文引用: 1]

MEI Zhong-yi, HUANG Chao, FAN Yu-qing

Development and prospect of the aircraft digital assembly technology

[J]. Aeronautical Manufacturing Technology, 2015, 18: 32- 37

[本文引用: 1]

文科, 杜福洲, 张铁军, 等

舱段类部件数字化柔性对接系统设计与试验研究

[J]. 航空制造技术, 2017, 60 (11): 24- 31

[本文引用: 1]

WEN Ke, DU Fu-zhou, ZHANG Tie-jun, et al

Research on design and experiment for digital flexible aligning system of cabin components

[J]. Aeronautical Manufacturing Technology, 2017, 60 (11): 24- 31

[本文引用: 1]

许国康

大型飞机自动化装配技术

[J]. 航空学报, 2008, 29 (3): 734- 740

[本文引用: 1]

XU Guo-kang

Automatic assembly technology for large aircraft

[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29 (3): 734- 740

[本文引用: 1]

GUO Jun-kang, LI Bao-tong, LIU Zhi-gang, et al

Integration of geometric variation and part defor-mation into variation propagation of 3D assem-blies

[J]. International Journal of Production Research, 2016, 54 (19): 5708- 5721

DOI:10.1080/00207543.2016.1158881      [本文引用: 1]

XU Song-gang, JOHN K

Statistical geometric computation on tolerances for dimensioning

[J]. Computer Aided Design, 2016, 70 (1): 193- 201

[本文引用: 1]

郭俊康, 李宝童, 洪军, 等

基于误差状态最优估计的精密机床装配调整工艺决策

[J]. 机械工程学报, 2020, 56 (11): 172- 180

DOI:10.3901/JME.2020.11.172      [本文引用: 1]

GUO Jun-kang, LI Bao-tong, HONG Jun, et al

Assembly adjustment process planning of preci-sion machine tools based on optimal estimation of variation propagation

[J]. Journal of Mechanical Engineering, 2020, 56 (11): 172- 180

DOI:10.3901/JME.2020.11.172      [本文引用: 1]

赵欢, 葛东升, 罗来臻, 等. 大型构件自动化柔性对接装配技术综述 [J/OL]. 机械工程学报, 2022, 58: 1–21. http://kns.cnki.net/kcms/detail/11.2187.TH.20220527.1104.039.html.

[本文引用: 1]

ZHAO Huan, GE Dong-sheng, LUO Lai-zhen, et al. Survey of automated flexible docking assembly technology for large-scale components [J/OL]. Journal of Mechanical Engineering, 2022, 58: 1–21. http://kns.cnki.net/kcms/detail/11.2187.TH.20220527.1104.039.html.

[本文引用: 1]

孙惠斌, 颜建兴, 魏小红, 等

数字孪生驱动的航空发动机装配技术

[J]. 中国机械工程, 2020, 31 (7): 833- 841

[本文引用: 1]

SUN Hui-bin, YAN Jian-xing, WEI Xiao-hong, et al

Digital twin-driven aero-engine assembly technology

[J]. China Mechanical Engineering, 2020, 31 (7): 833- 841

[本文引用: 1]

LU Y, LIU C, KEVIN I, et al

Digital twin-driven smart manufacturing: connotation, reference model, applications and research issues

[J]. Robotics and Computer Integrated Manufacturing, 2020, 61: 101837

DOI:10.1016/j.rcim.2019.101837      [本文引用: 1]

姜珊, 王仲奇, 夏松, 等

飞机柔性工装数字孪生几何模型构建方法

[J]. 航空制造技术, 2022, 65 (12): 86- 91

[本文引用: 1]

JIANG Shan, WANG Zhong-qi, XIA Song, et al

Construction method of digital twin geometry mo-del for aircraft flexible tooling

[J]. Aeronautical Manufacturing Technology, 2022, 65 (12): 86- 91

[本文引用: 1]

张玉良, 张佳朋, 王小丹, 等

面向航天器在轨装配的数字孪生技术

[J]. 导航与控制, 2018, 17 (3): 75- 82

[本文引用: 1]

ZHANG Yu-liang, ZHANG Jia-peng, WANG Xiao-dan, et al

Digital twin technology for spacecraft on-orbit assembly

[J]. Navigation and Control, 2018, 17 (3): 75- 82

[本文引用: 1]

张入元, 武殿梁, 黄顺舟

基于数字孪生的总装对接在线监控技术

[J]. 组合机床与自动化加工技术, 2021, (11): 109- 113

[本文引用: 1]

ZHANG Ru-yuan, WU Dian-liang, HUANG Shun-zhou

Online monitoring technology of final assembly docking based on digital twin

[J]. Modular Machine Tool and Automatic Manufacturing Technique, 2021, (11): 109- 113

[本文引用: 1]

张瀚丹, 李康康, 杨豫鹏, 等

基于数字孪生的雕刻机人机交互系统设计

[J]. 计算机测量与控制, 2021, 29 (10): 170- 175

[本文引用: 1]

ZHANG Han-dan, LI Kang-kang, YANG Yu-peng, et al

Design of human-machine interaction system for engraving machine based on digital twin

[J]. Computer Measurement and Control, 2021, 29 (10): 170- 175

[本文引用: 1]

孙学民, 刘世民, 申兴旺, 等

数字孪生驱动的高精密产品智能化装配方法

[J]. 计算机集成制造系统, 2022, 28 (6): 1704- 1716

[本文引用: 1]

SUN Xue-min, LIU Shi-min, SHEN Xing-wang, et al

Digital twin-driven intelligent assembly method for high precision products

[J]. Computer Integrated Manufacturing Systems, 2022, 28 (6): 1704- 1716

[本文引用: 1]

黄郁雯, 李培勇, 唐正, 等

基于数字孪生的船体分段装配规划研究

[J]. 武汉理工大学学报: 交通科学与工程版, 2022, 46 (5): 878- 882

[本文引用: 1]

HUAGN Yu-wen, LI Pei-yong, TAGN Zheng, et al

Ship block structure assembly planning based on digital twin

[J]. Journal of Wuhan University of Technology: Transportation Science and Engineering, 2022, 46 (5): 878- 882

[本文引用: 1]

易扬, 冯锦丹, 刘金山, 等

复杂产品数字孪生装配模型表达与精度预测

[J]. 计算机集成制造系统, 2021, 27 (2): 617- 630

[本文引用: 1]

YI Yang, FENG Jin-dan, LIU Jin-shan, et al

Model expression and accuracy prediction method of digital twin-based assembly for complex products

[J]. Computer Integrated Manufacturing Systems, 2021, 27 (2): 617- 630

[本文引用: 1]

李新, 李飞, 方世巍, 等

基于UE4的井下变电所巡检机器人数字孪生系统

[J]. 煤矿安全, 2021, 52 (11): 130- 133

[本文引用: 1]

LI Xin, LI Fei, FANG Shi-wei, et al

Digital twin system of inspection robot in underground substation based on UE4

[J]. Safety in Coal Mines, 2021, 52 (11): 130- 133

[本文引用: 1]

郭飞燕, 刘检华, 邹方, 等

数字孪生驱动的装配工艺设计现状及关键实现技术研究

[J]. 机械工程学报, 2019, 55 (17): 110- 132

DOI:10.3901/JME.2019.17.110      [本文引用: 1]

GUO Fei-yan, LIU Jian-hua, ZOU Fang, et al

Research on the state-of-art, connotation and key implementation technology of assembly process planning with digital twin

[J]. Journal of Mechanical Engineering, 2019, 55 (17): 110- 132

DOI:10.3901/JME.2019.17.110      [本文引用: 1]

陶飞, 张萌, 程江峰, 等

数字孪生车间: 一种未来车间运行新模式

[J]. 计算机集成制造系统, 2017, 23 (1): 1- 9

[本文引用: 1]

TAO Fei, ZHANG Meng, CHENG Jiang-feng, et al

Digital twin workshop: a new paradigm for future workshop

[J]. Computer Integrated Manufacturing Systems, 2017, 23 (1): 1- 9

[本文引用: 1]

赵建国, 台春雷, 刘哲, 等

飞机装配大尺寸多系统测量场构建及应用

[J]. 航空制造技术, 2022, 65 (5): 63- 67

[本文引用: 1]

ZHAO Jian-guo, TAI Chun-lei, LIU Zhe, et al

Establishment and application of large-volume multi-system measurement field for aircraft assembly

[J]. Aeronautical Manufacturing Technology, 2022, 65 (5): 63- 67

[本文引用: 1]

GUO Fei-yan, ZOU Fang, LIU Jian-hua, et al

Comprehensive identification of aircraft coordina-tion feature based on complete importance modeling and its engineering application

[J]. Assembly Automation, 2018, 38 (4): 398- 411

DOI:10.1108/AA-10-2017-139      [本文引用: 1]

PETER M, LAN E. 基于FSM和Verilog HDL的数字电路设计[M]. 姚世扬, 译. 北京: 机械工业出版社, 2016: 1–15.

[本文引用: 1]

陈哲涵, 杜福洲, 唐晓青

基于关键测量特性的飞机装配检测数据建模研究

[J]. 航空学报, 2012, 33 (11): 2143- 2152

[本文引用: 1]

CHEN Zhe-han, DU Fu-zhou, TANG Xiao-qing

Key measurement haracteristics based inspection data modeling for aircraft assembly

[J]. Acta Aero-nautica et Astronautica Sinica, 2012, 33 (11): 2143- 2152

[本文引用: 1]

洪军, 郭俊康, 刘志刚, 等

基于状态空间模型的精密机床装配精度预测与调整工艺

[J]. 机械工程学报, 2013, 49 (6): 114- 121

DOI:10.3901/JME.2013.06.114      [本文引用: 1]

HONG Jun, GUO Jun-kang, LIU Zhi-gang, et al

Assembly accuracy prediction and adjustment process modeling of precision machine tool based on state space model

[J]. Journal of Mechanical Engineering, 2013, 49 (6): 114- 121

DOI:10.3901/JME.2013.06.114      [本文引用: 1]

王思知, 刘伦乾, 朱春伟, 等

机身装配中自动定位器调姿算法研究

[J]. 机电工程术, 2019, 48 (7): 63- 67

[本文引用: 1]

WANG Si-zhi, LIU Lun-qian, ZHU Chun-wei, et al

Research on positioning algorithm of automatic positioner in fuselage assembly

[J]. Mechanical and Electrical Engineering Technology, 2019, 48 (7): 63- 67

[本文引用: 1]

/

〈 〉