近年来,国内外学者对叠合板拼缝的受弯性能进行大量的试验研究和理论分析. 徐天爽等[3]通过试验对比研究传统式拼缝和整体式拼缝叠合板的受弯性能,建议合理的整体式拼缝构造形式,得到整体式拼缝叠合板的受弯性能优于传统式拼缝叠合板. 丁克伟等[4]提出新型的拼缝结构形式,在拼缝两侧增加多功能限位器,增强了拼缝处的弯矩传递性能. 通过试验验证了该种拼缝形式能够达到现浇板的受力性能水平. 崔士起等[5]通过试验对比研究5种分离式接缝叠合板的受弯性能,分析接缝位置、接缝数量及现浇层厚度对垂直接缝方向叠合板抗弯刚度的影响. 余泳涛等[6]研究单缝密拼叠合板的受弯性能,分析桁架钢筋叠合板拼缝处的传力机理. 结果表明,在拼缝处设置桁架钢筋,可以提高叠合板垂直于拼缝方向的刚度和承载力. Stehle等[7]通过试验研究密拼叠合板的受弯性能,与规范公式进行比较,验证了密拼拼缝的连接形式能够可靠地应用于双向叠合板上.
参考JGJ 1—2014《装配式混凝土结构技术规程》[8]的叠合板构造要求,创新研发了新型的凹槽拼缝连接叠合板,特点为在预制底板的板侧开槽,在预制板跨中拼接处的凹槽内放置连接钢筋,与板侧受力钢筋相搭接. 这种连接方式在兼具叠合板可靠性能的基础上,提升了叠合板在生产、运输吊装和现场施工中的便捷性. 通过足尺试验对比,研究整体现浇板、后浇带连接叠合板及凹槽拼缝连接叠合板的受弯性能,包括开裂弯矩、极限承载力、裂缝开展情况、变形延性和破坏特征等. 建立相应的有限元模型,对比分析不同凹槽尺寸及C型、D型凹槽拼缝连接叠合板试件的受弯性能差异. 基于已验证的有限元模型,研究D型凹槽拼缝连接叠合板受弯性能的主要影响参数,明确叠合板凹槽拼缝连接的合理设计.
1. 试验概况
1.1. 试件设计
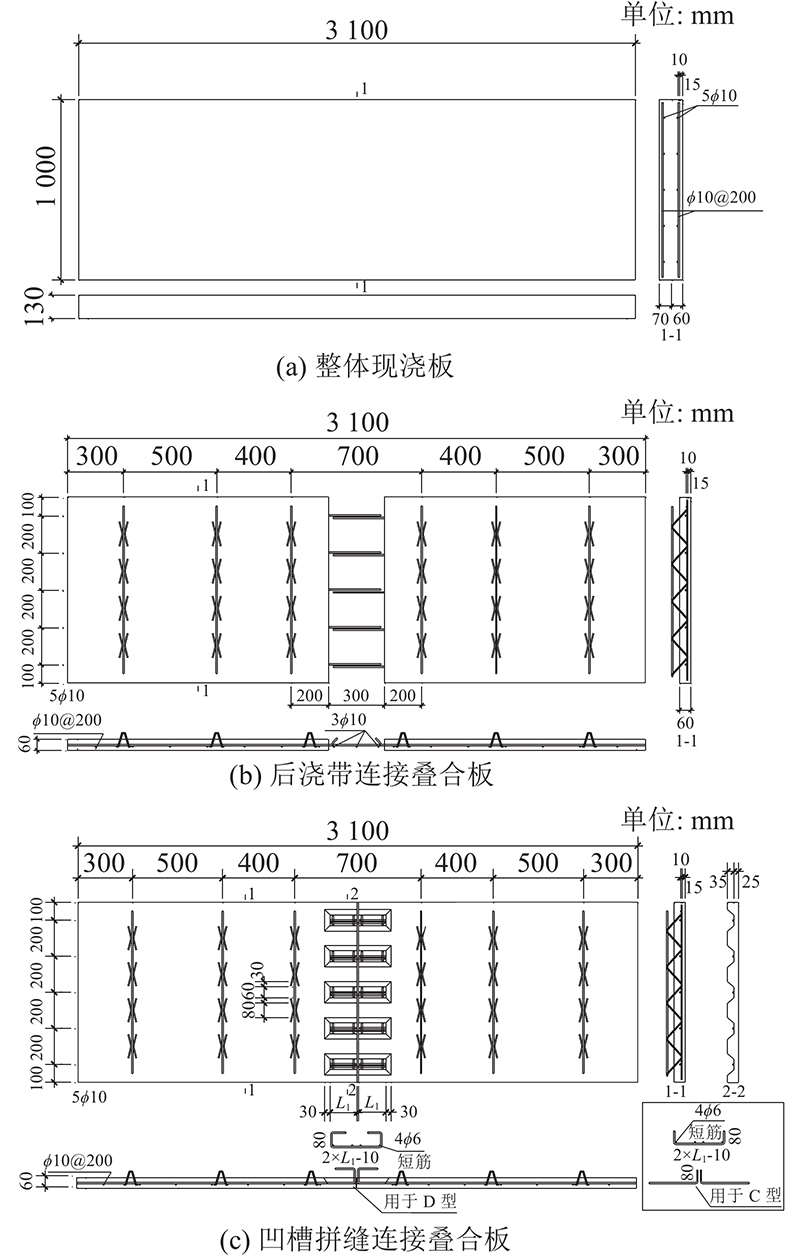
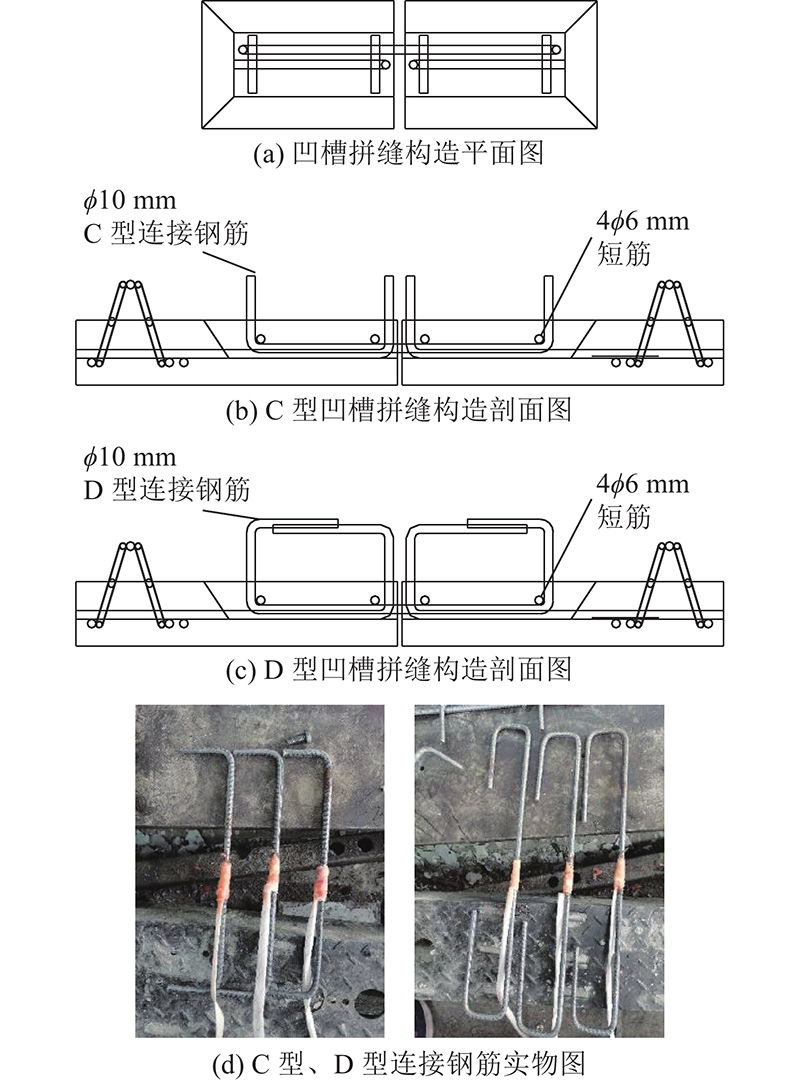
共设计8个试件,开展足尺受弯性能试验,其中整体现浇板试件1个、后浇带连接叠合板试件1个和凹槽拼缝连接叠合板试件6个(主要考虑连接钢筋类型和凹槽长度2个参数). 各试件长度为3 100 mm,宽度为1 000 mm,厚度为130 mm,预制板厚度为60 mm,现浇层厚度为70 mm,试件的几何尺寸和配筋如图1、表1所示. 其中L为叠合板的长度,W为叠合板的宽度,L1为凹槽长度. 试件的现浇层和预制层的横向分布钢筋均为5ϕ10 mm,受力纵筋均为ϕ10 mm@200 mm,混凝土保护层厚度为15 mm. 在预制底板侧开槽,将预制板受力纵筋弯折90°(C型)或环形弯折(D型),在2块预制板拼接处的凹槽内放置C型或D型连接钢筋进行搭接,最后浇筑混凝土后浇层. C型、D型凹槽拼缝的构造详图如图2所示.
图 1
表 1 板试件的几何尺寸和配筋
Tab.1
| 编号 | 试件类型 | 配筋 | L/mm | W/mm | 钢筋连接方式 | L1/mm |
| A | 整体现浇 | ϕ10 mm@200 mm | 3 100 | 1 000 | — | — |
| B | 后浇带连接 | ϕ10 mm@200 mm | 3 100 | 1 000 | — | — |
| C1 | 凹槽拼缝 | ϕ10 mm@200 mm | 3 100 | 1 000 | C型连接 | 100 |
| C2 | 凹槽拼缝 | ϕ10 mm@200 mm | 3 100 | 1 000 | C型连接 | 200 |
| C3 | 凹槽拼缝 | ϕ10 mm@200 mm | 3 100 | 1 000 | C型连接 | 300 |
| D1 | 凹槽拼缝 | ϕ10 mm@200 mm | 3 100 | 1 000 | D型连接 | 100 |
| D2 | 凹槽拼缝 | ϕ10 mm@200 mm | 3 100 | 1 000 | D型连接 | 200 |
| D3 | 凹槽拼缝 | ϕ10 mm@200 mm | 3 100 | 1 000 | D型连接 | 300 |
图 2
1.2. 材料力学性能
采用同一批次的混凝土原材料,浇筑2组(共6个)100 mm×100 mm×100 mm的混凝土立方体试块,用于抗压试验,测定混凝土的力学性能参数. 参考《混凝土结构设计规范》[9](GB 50010—2010)中的计算公式,计算得到立方体抗压强度fcu = 40.6 MPa,混凝土弹性模量Ec = 32.5 GPa,混凝土轴心抗拉强度ft = 2.4 MPa,混凝土轴心抗压强度fc = 26.8 MPa.
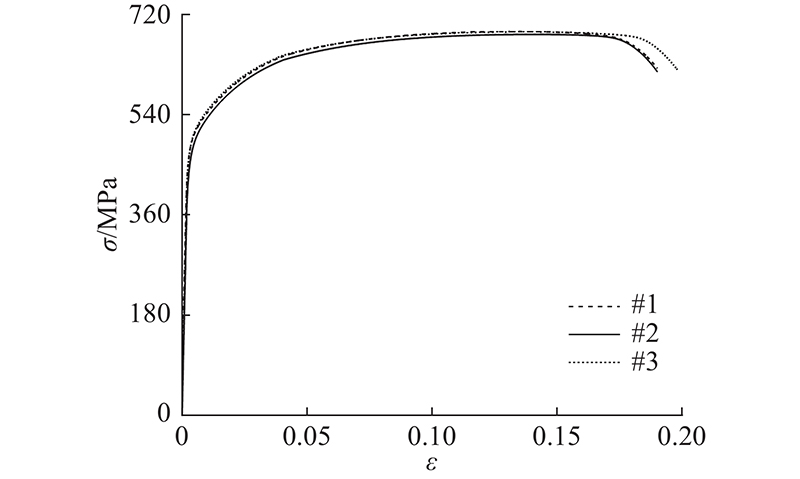
叠合板试件的受力钢筋采用直径为10 mm的HRB400钢筋,抽取同批次的ϕ10 mm的3根钢筋进行拉伸试验. 通过试验测得的钢筋弹性模量Es = 197.6 GPa,钢筋抗拉屈服强度fy = 430.1 MPa,钢筋抗拉极限强度fu = 684.5 MPa和最大力总延伸率Agt = 29.6%,钢筋的拉伸应力
图 3
1.3. 试验加载及量测方案
图 4
图 4 叠合板试件受弯试验加载装置图
Fig.4 Loading device diagram of flexural test for composite slab specimen
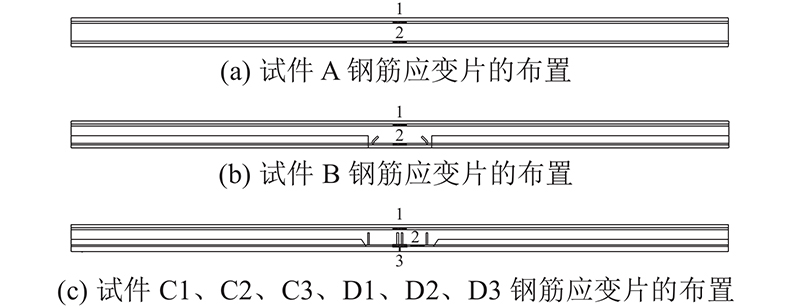
叠合板试件受弯试验量测的内容如下. 1)位移计布置在1/4跨、跨中、3/4跨及两边支座处,如图4(b)所示,用于测量叠合板的位移和支座沉降. 2)在叠合板上、下表面共布置10片应变片,用于监测叠合板的裂缝开展情况;在叠合板上、下表面的跨中位置各布置3片,下表面跨中两侧间隔0.4 m处对称布置2片,1/4跨、3/4跨处布置2片. 3)在各试件跨中板面及板底受力纵筋的跨中位置布置应变片#1、#2,在凹槽拼缝连接叠合板的C型、D型连接钢筋位置布置应变片#3,用于量测钢筋应变数据. 为了提高应变数据的可读性,对应变测点进行简化,简化后的应变测点图如图5所示. 4)采用CK102型裂缝宽度检测仪,测量裂缝宽度.
图 5
2. 试验结果分析
2.1. 试验现象
图 6
图 7
根据各试件的破坏状态可以看出,当凹槽拼缝连接叠合板的拼缝处锚固长度不足时,叠合面易发生撕裂,沿叠合面撕裂的范围内连接钢筋的锚固长度进一步减小,无法进行有效传力,导致试件出现脆性破坏. 应增加钢筋锚固长度来控制叠合面的撕裂破坏,保证预制板及拼缝处的连接钢筋和受力纵筋有效传力.
2.2. 荷载-跨中挠度的对比分析
图 8
表 2 试件受弯承载力的试验结果
Tab.2
| 试件 编号 | (kN·m) | (kN·m) | | (kN·m) | (kN·m) | | mm |
| A | 7.1 | 7.6 | 1.07 | 14.5 | 25.6 | 1.76 | 241.39 |
| B | 7.1 | 7.2 | 1.01 | 14.5 | 26.8 | 1.85 | 242.73 |
| C1 | 7.2 | 4.8 | 0.67 | 12.8 | 11.2 | 0.87 | 26.49 |
| C2 | 7.2 | 7.2 | 1.00 | 12.8 | 21.2 | 1.65 | 75.02 |
| C3 | 7.2 | 7.2 | 1.00 | 12.8 | 21.6 | 1.69 | 80.46 |
| D1 | 7.2 | 6.0 | 0.83 | 12.8 | 12.0 | 0.94 | 32.74 |
| D2 | 7.2 | 8.0 | 1.11 | 12.8 | 21.6 | 1.69 | 99.36 |
| D3 | 7.2 | 8.4 | 1.17 | 12.8 | 23.2 | 1.81 | 119.56 |
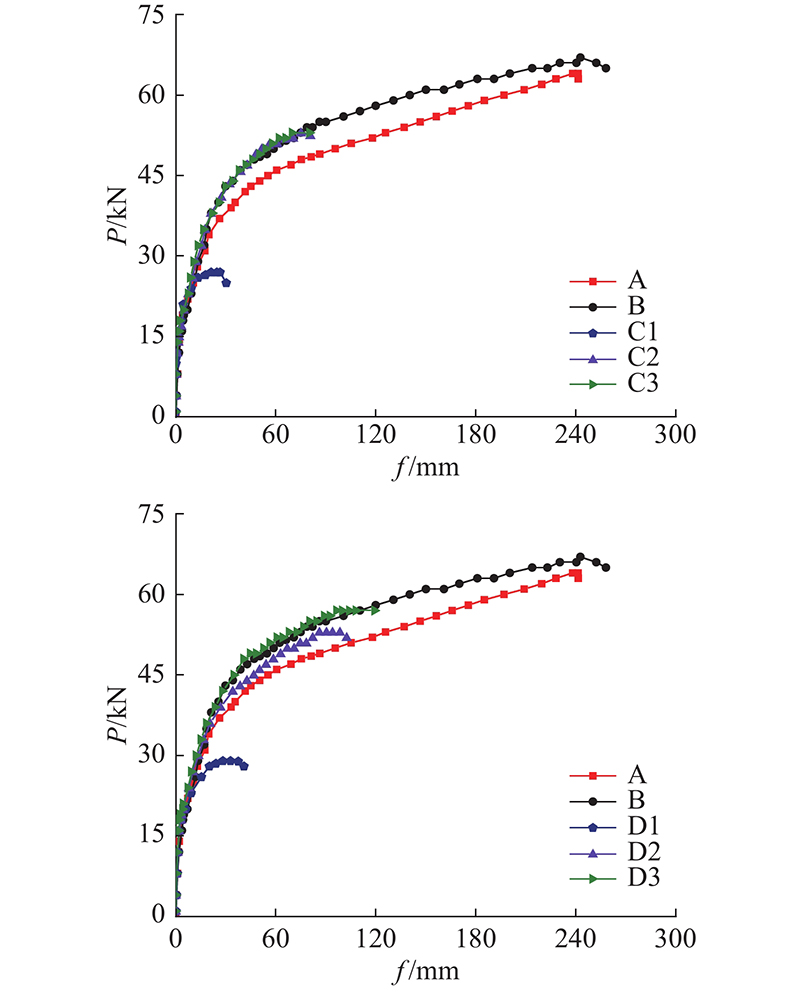
1)后浇带连接叠合板试件B的极限承载力为67 kN,较整浇板试件A的极限承载力64 kN大4.7%. 最大跨中挠度为242.73 mm,与整浇板试件A的最大跨中挠度241.39 mm相近,受弯性能与整浇板基本相似.
2)试件C1、C2、C3的极限承载力分别为28、53、54 kN,较整浇板试件A分别小56.3%、17.2%、15.6%. 最大跨中挠度分别为26.49、75.02、80.46 mm,较整浇板试件A分别小89.0%、68.9%、66.7%. 相较于整浇板和后浇带连接叠合板,凹槽拼缝连接叠合板的极限承载力和延性均有不同程度的降低.
3)试件D1、D2、D3的极限承载力分别为30、54、58 kN,较整浇板试件A分别小53.1%、15.6%、9.3%. 最大跨中挠度分别为32.74、99.36、119.56 mm,较整浇板试件A分别小86.4%、58.8%、50.4%. 随着凹槽长度的增加,凹槽拼缝连接叠合板的受弯承载力和延性得到了有效的提高. 相较于C型连接,D型连接凹槽拼缝叠合板的受弯性能更好.
2.3. 裂缝发展及对比分析
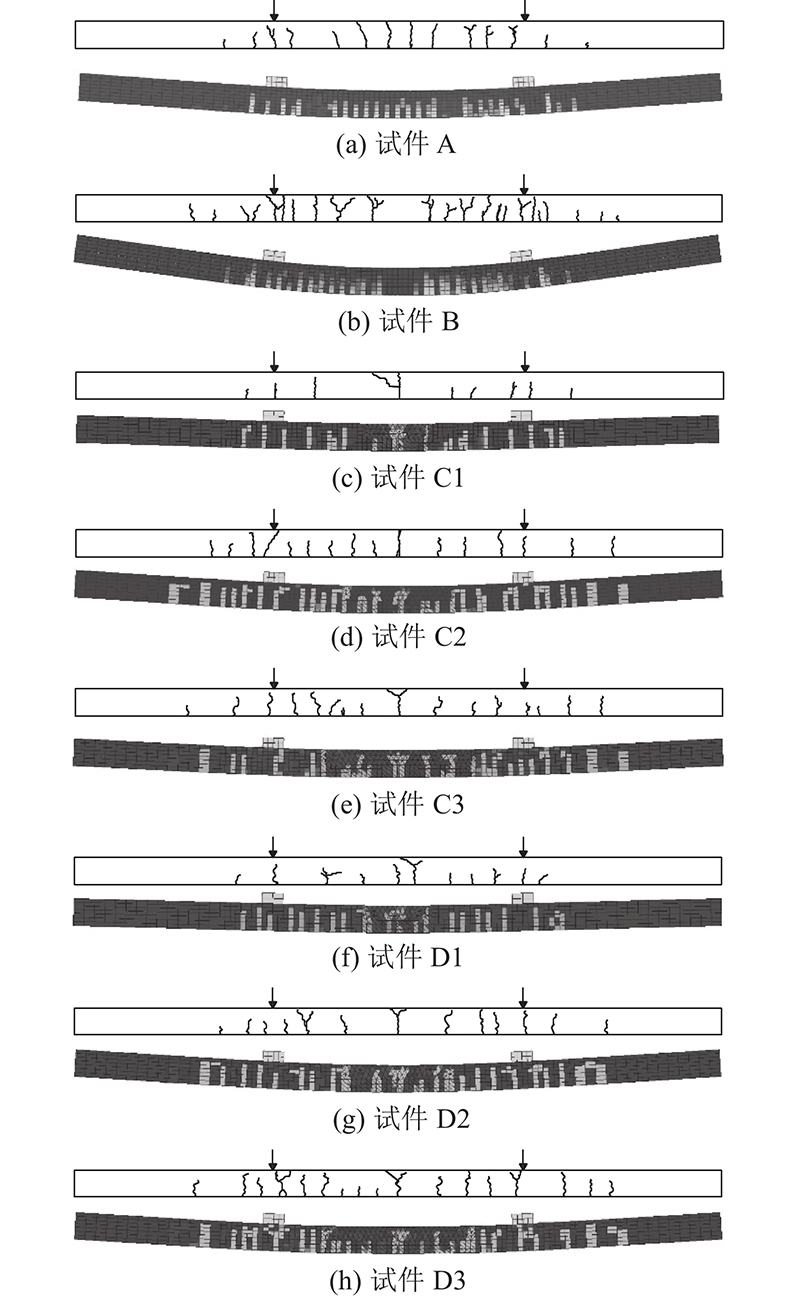
叠合板试件的板底及板侧裂缝分布图如图7所示. 当试件A的跨中弯矩达到7.6 kN∙m时,第1条裂缝出现在纯弯段;试件破坏时共14条裂缝,分布在板跨中两侧−840~900 mm,板底裂缝分布均匀且宽度较小. 当试件B的跨中弯矩达到7.2 kN∙m时,后浇带两侧位置首先开裂;试件破坏时共20条裂缝,分布在叠合板跨中两侧−990~1 050 mm,后浇带两侧裂缝宽度较宽,其他裂缝宽度较小.
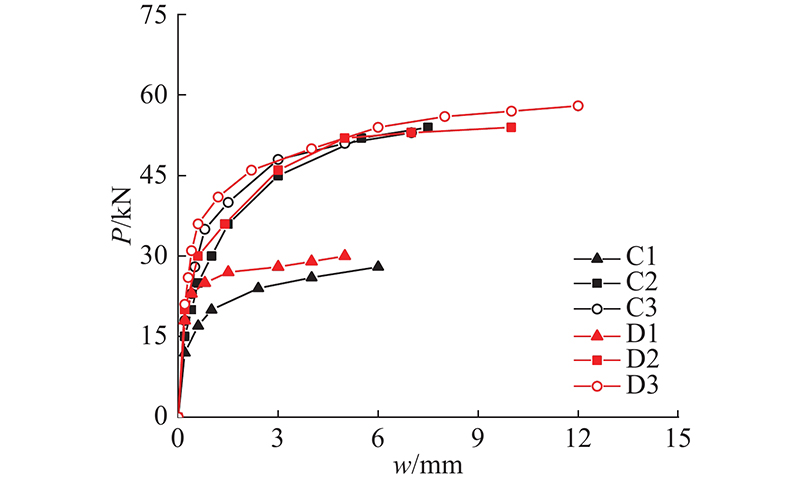
凹槽拼缝连接叠合板试件预制板拼缝宽度随荷载变化的曲线如图9所示. 图中,w为预制板拼缝宽度. 当试件C1的跨中弯矩达到4.8 kN∙m时,裂缝首先在拼缝处出现;当达到极限承载力时,试件拼缝最大宽度为7.2 mm;试件破坏时共有9条裂缝,分布在叠合板跨中两侧−740~820 mm. 当试件C2的跨中弯矩达到6.0 kN∙m时,裂缝首先在拼缝处出现;当达到极限承载力时,试件拼缝最大宽度为7.5 mm;试件破坏时共有16条裂缝,分布在叠合板跨中两侧−900~1 030 mm. 当试件C3的跨中弯矩达到7.2 kN∙m时,裂缝首先在拼缝处出现;当达到极限承载力时,试件拼缝最大宽度为7.2 mm;试件破坏时共有16条裂缝,分布在叠合板跨中两侧−1020~970 mm.
图 9
当试件D1的跨中弯矩达到6.0 kN∙m时,裂缝首先在拼缝处出现;当达到极限承载力时,试件拼缝最大宽度为5.0 mm;试件破坏时共有11条裂缝,分布在叠合板跨中两侧−780~720 mm. 当试件D2的跨中弯矩达到8.0 kN∙m时,裂缝首先在拼缝处出现;当达到极限承载力时,试件拼缝最大宽度为9.5 mm;试件破坏时共有13条裂缝,分布在叠合板跨中两侧−850~1 000 mm. 当试件D3的跨中弯矩达到8.4 kN∙m时,裂缝首先在拼缝处出现;当达到极限承载力时,试件拼缝最大宽度为12.0 mm;试件破坏时共有15条裂缝,分布在叠合板跨中两侧−970~1 020 mm.
对比分析整体现浇板、后浇带连接叠合板及凹槽拼缝连接叠合板试件的裂缝分布情况,可得如下结论. 各试件的裂缝主要呈竖向开展,有分叉现象,叠合板的预制底板侧与现浇侧的裂缝发展及分布基本一致,二者的协同工作性能较好. 整浇板试件板底裂缝分布均匀且宽度较小. 后浇带连接叠合板试件位于后浇带两侧的裂缝宽度较宽,其他裂缝宽度较小. 凹槽拼缝连接叠合板试件的裂缝主要集中在跨中拼缝处且宽度较大,选用D型连接钢筋和增加凹槽长度的方式增大了拼缝处钢筋锚固长度,可以改善裂缝沿板长方向的分布情况,有效控制裂缝的开展.
2.4. 钢筋应变
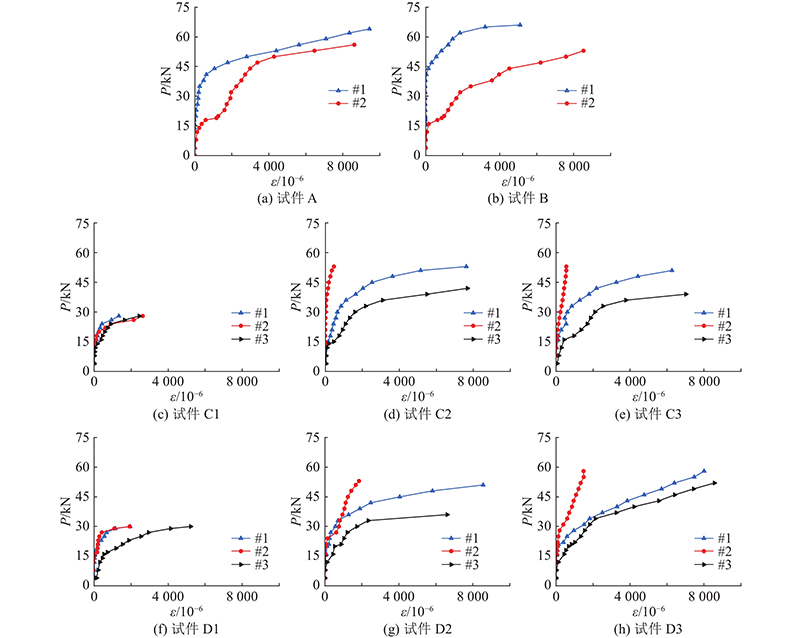
图 10
从图10可得如下结论. 1)在试验过程中,整体现浇板板底纵筋和后浇带连接叠合板的预制层纵筋首先发生屈服. 2)凹槽拼缝连接叠合板跨中凹槽拼接处的C型(D型)连接钢筋首先发生屈服,直至试件破坏,凹槽拼缝连接叠合板的预制层纵筋跨中位置未发生屈服. 3)在试件开裂后,相较于D型连接,C型连接凹槽拼缝连接叠合板试件的钢筋应变发展更快,钢筋屈服时的荷载较小. 对比3组凹槽长度可知,随着凹槽长度的增加,凹槽拼缝连接叠合板试件的钢筋应变发展变缓,钢筋屈服时的荷载增大.
3. 理论分析
3.1. 材料本构模型
叠合板试件由钢筋和混凝土2种材料组成. 合理选取钢筋和混凝土材料的本构模型,对分析叠合板试件的受弯性能较重要.
3.1.1. 混凝土本构模型
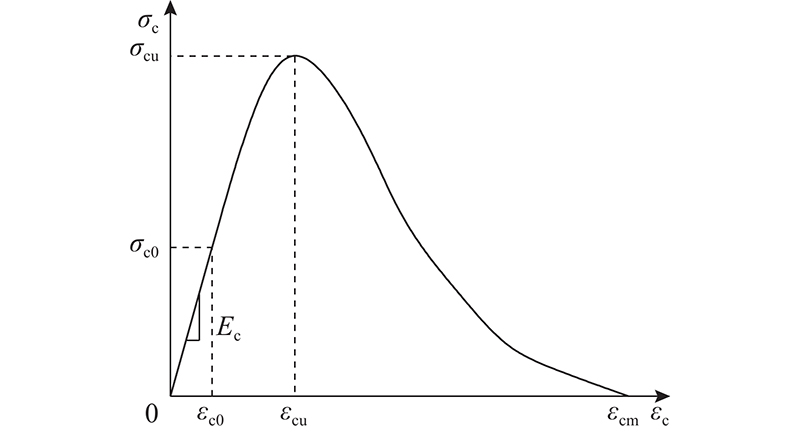
图 11
图 11 混凝土的单轴受压应力-应变曲线
Fig.11 Uniaxial compression stress-strain curve of concrete
式中:Ec为混凝土弹性模量,根据
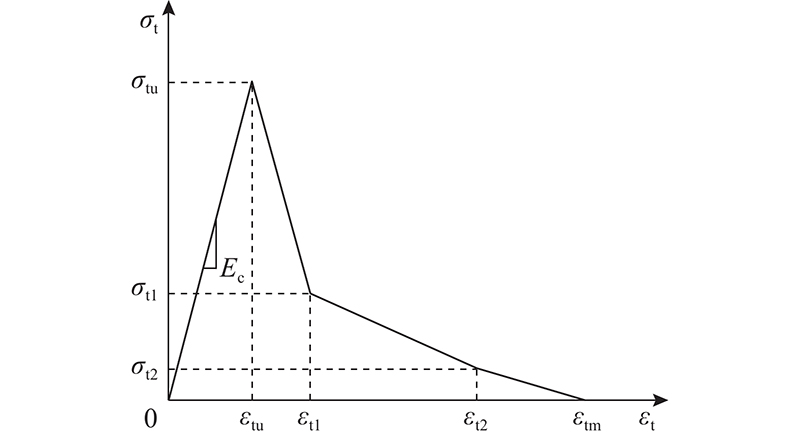
混凝土的受拉应力
图 12
式中:
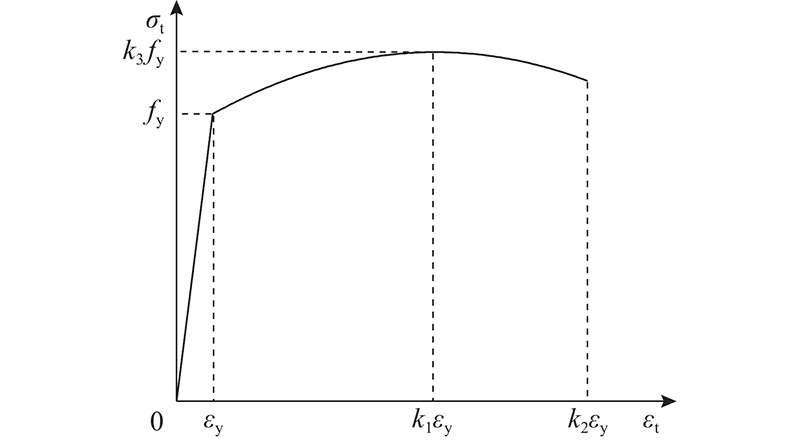
3.1.2. 钢筋本构模型
图 13
式中:k1为峰值应变和屈服应变的比值,k2为极限应变和屈服应变的比值,k3为峰值应力和屈服应力的比值.
3.2. 理论计算
整体现浇板、后浇带连接叠合板及凹槽拼缝连接叠合板开裂弯矩的计算遵从《混凝土结构设计规范》[9],根据截面形式的不同,截面抵抗矩塑性影响系数的取值不同. 开裂弯矩值的计算公式为
式中:
叠合板正截面受弯承载力按矩形截面计算,采用GB 50010—2010中的公式计算,假定叠合面不发生滑移,正截面符合平截面假定. 受弯承载力的计算公式为
式中:
为了防止试件发生超筋破坏,受压区高度须满足
式中:As为受拉钢筋的横截面积,as为受拉区纵向钢筋合力点至截面受拉边缘的距离.
按照实际材料性能试验所得的数据,计算各试件的开裂弯矩和极限弯矩. 计算时考虑板的自重,各理论计算结果与试验数据如表2所示. 可知,除脆性破坏试件C1、D1,其他试件的开裂弯矩理论计算值略低于或等于试验测得的数值,极限弯矩的理论计算值较试验测得的数值偏小,依据现行相关设计规范所计算的结果偏保守.
4. 有限元分析
4.1. 有限元模型
为了研究凹槽拼缝连接叠合板的受弯性能并验证模拟方法的准确性,采用ABAQUS数值模拟软件,建立8个叠合板试件的有限元模型. 分析各试件受弯加载过程中的力学性能,与叠合板受弯承载力的试验结果进行对比分析.
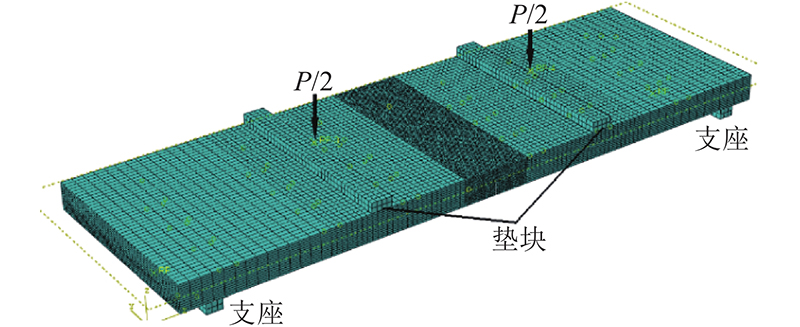
建立的有限元模型几何尺寸与试验试件保持一致. 为了避免在有限元分析过程中出现数值奇异的问题,将刚性垫板设置在叠合板的加载位置和支座处. 混凝土单元采用8节点6面体三维空间线性缩减积分单元C3D8R,由于凹槽拼缝连接叠合板的凹槽部分形状不规则,不便于划分六面体网格,采用C3D10十结点二次四面体单元. 钢筋采用2节点三维桁架单元T3D2. 经过反复试算与收敛性测试,混凝土网格划分尺寸如下. 厚度方向:70 mm后浇层划分4层,60 mm预制层划分3层;宽度方向:单元长度为25 mm;长度方向:对于叠合板试件A、B,跨中两侧800 mm的区域网格较密,单元长度为25 mm,两侧区域网格较疏,单元长度为50 mm. 对于凹槽拼缝连接叠合板试件,由于凹槽处形状不规则,采用四面体单元,单元长度为25 mm. 钢筋单元网格划分尺寸为50 mm. 以试件C1为例,凹槽拼缝连接叠合板的有限元模型如图14所示.
图 14
模型采用嵌入式约束方式,模拟钢筋与混凝土的相互作用. 对于叠合板新旧混凝土叠合面的约束有2种方法:1)考虑新旧混凝土界面的应力,界面引入接触;2)认为预制层和叠合层之间变形协调,不产生相对滑移,采用Tie约束. 由于预制底板表面的人工凿毛处理和钢筋桁架使叠合板在发生受弯破坏之前不会发生剪切破坏,故模型上、下表面的新老混凝土交界面采用Tie约束. 在试验过程中观测到凹槽拼缝连接叠合板的跨中拼缝发生撕裂,为了精确模拟能量迅速在跨中释放,在竖向跨中拼缝处引入接触,接触模型采用经典库仑摩擦模型. 为了确保求解过程的收敛,采用位移加载的方式.
4.2. 模型材料参数
钢筋材料采用标准塑性模型. 螺纹钢筋的本构关系采用上述的受拉应力-应变关系曲线,根据材料力学性能试验的结果可知,钢筋模型参数的取值如表3所示.
表 3 钢筋模型的参数
Tab.3
| 钢筋 | Es/GPa | fy/MPa | εy | k1 | k2 | k3 |
| ϕ10 mm | 197.6 | 430.1 | 0.0022 | 63.6 | 89.5 | 1.59 |
4.3. 有限元分析结果
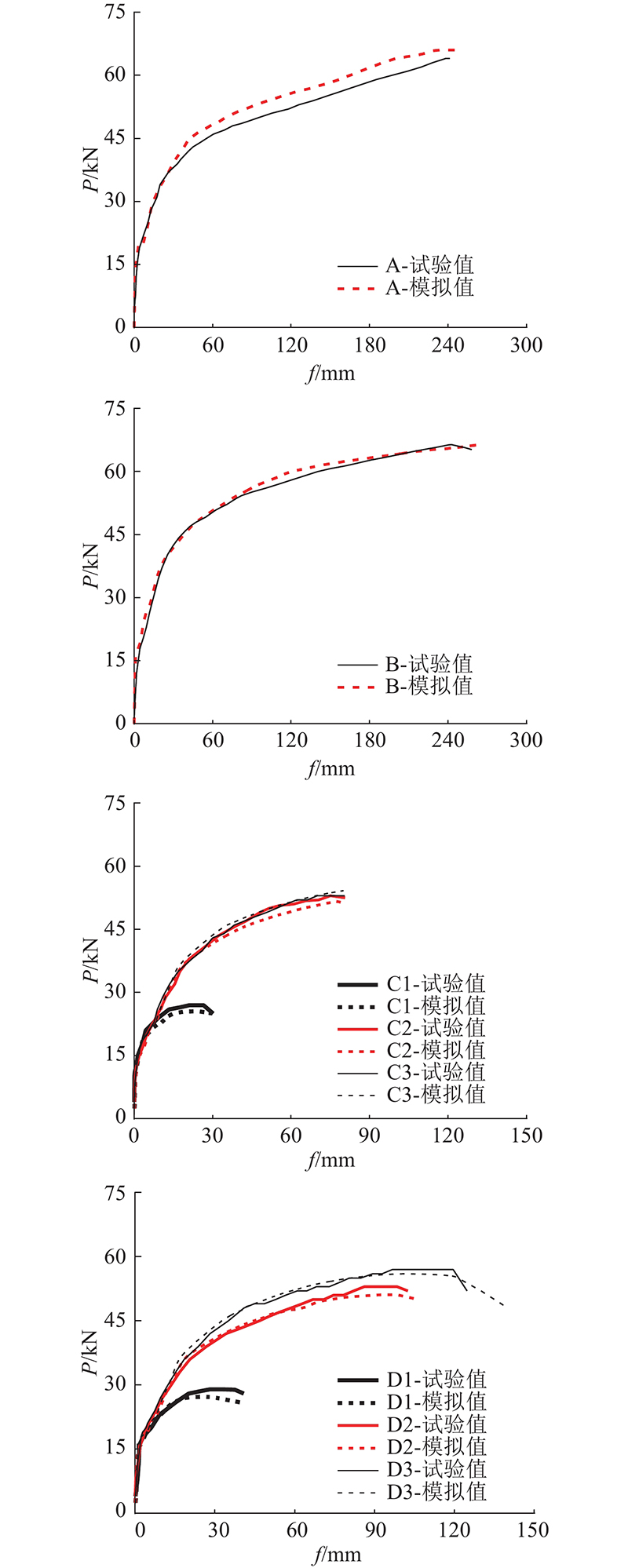
图 15
图 15 试件荷载-跨中挠度曲线的对比
Fig.15 Comparison of load-mid-span deflection curve of specimen
表 4 叠合板试件的数值模拟结果
Tab.4
| 试件规格 | | | | | | | | | |
| A | 8.0 | 7.6 | 0.95 | 26.4 | 25.6 | 0.97 | 248.36 | 241.39 | 0.97 |
| B | 7.6 | 7.2 | 0.95 | 26.4 | 26.8 | 1.02 | 264.53 | 242.73 | 0.92 |
| C1 | 4.4 | 4.8 | 1.09 | 10.5 | 11.2 | 1.07 | 26.81 | 26.49 | 0.98 |
| C2 | 6.9 | 7.2 | 1.05 | 20.8 | 21.2 | 1.02 | 77.05 | 75.02 | 0.97 |
| C3 | 6.9 | 7.2 | 1.05 | 21.6 | 21.6 | 1.00 | 80.36 | 80.46 | 1.00 |
| D1 | 6.0 | 6.0 | 1.00 | 11.2 | 12.0 | 1.07 | 30.33 | 32.74 | 1.08 |
| D2 | 7.6 | 8.0 | 1.05 | 20.6 | 21.6 | 1.05 | 98.18 | 99.36 | 1.01 |
| D3 | 7.6 | 8.4 | 1.10 | 22.3 | 23.2 | 1.04 | 120.12 | 119.56 | 0.99 |
建立的有限元模型的荷载-跨中挠度曲线、受弯承载力及跨中挠度等均与试验结果吻合较好,因此可以较准确地预测叠合板试件的受弯性能.
图 16
图 17
5. 参数分析
以凹槽长度为300 mm的D型连接凹槽拼缝连接叠合板(试件D3)为例,建立有限元模型,分析连接钢筋配筋率、叠合层厚度及凹槽深度对D型连接凹槽拼缝连接叠合板受弯性能的影响.
5.1. 连接钢筋配筋率
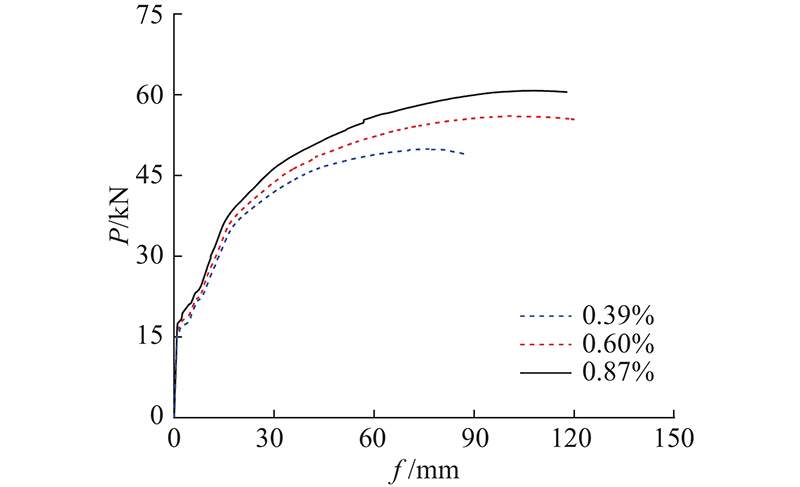
分别选取连接钢筋直径为8、10和12 mm进行叠合板受弯承载力分析,得到如图18所示的不同连接钢筋配筋率的荷载-跨中挠度曲线.
图 18
图 18 不同连接钢筋配筋率叠合板的荷载-跨中挠度曲线
Fig.18 Load-mid-span deflection curves of composite slabs with different connecting reinforcement ratios
从图18可得如下结论. 1)叠合板屈服前的荷载-跨中挠度曲线斜率相差不大,增大连接钢筋配筋率对叠合板的抗弯刚度和开裂弯矩影响不明显. 2)连接钢筋配筋率为0.39%、0.60%和0.87%的凹槽拼缝连接叠合板的受弯承载力分别为50、56和62 kN,配筋率由0.60%增加到0.87%,受弯承载力提高了11%. 增大连接钢筋直径,有效提高了凹槽拼缝连接叠合板的受弯承载力. 加强拼缝配筋后的凹槽拼缝连接叠合板的受弯承载力较整浇板仅降低3%左右.
5.2. 叠合层厚度
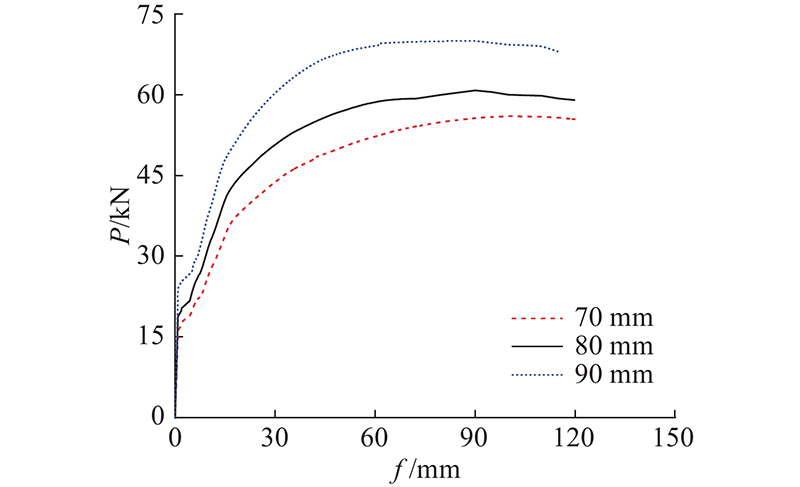
分别选取叠合层厚度为70、80、90 mm,开展叠合板受弯承载力分析,得到如图19所示的不同叠合层厚度的荷载-跨中挠度曲线.
图 19
图 19 不同叠合层厚度的叠合板荷载-跨中挠度曲线
Fig.19 Load-mid-span deflection curves of composite slabs with different thicknesses of laminated layer
从图19可得如下结论. 1)随着叠合层厚度的增加,叠合板的抗弯刚度逐步提高,叠合层厚度为70、80、90 mm的凹槽拼缝连接叠合板开裂弯矩分别为7.6、8.4、10 kN∙m,与叠合层厚度为70 mm的叠合板相比,开裂弯矩分别提高了11%、31%. 2)叠合层厚度为70、80、90 mm的凹槽拼缝连接叠合板受弯承载力分别为56、61、70 kN,与叠合层厚度为70 mm的叠合板相比,受弯承载力分别提高了9%和25%. 在保持预制层厚度不变的情况下,增加叠合层厚度可以显著提高叠合板的开裂弯矩和受弯承载力,但在实际工程应用中,应综合考虑受力、经济和效率等因素,合理选择叠合层厚度.
5.3. 凹槽深度
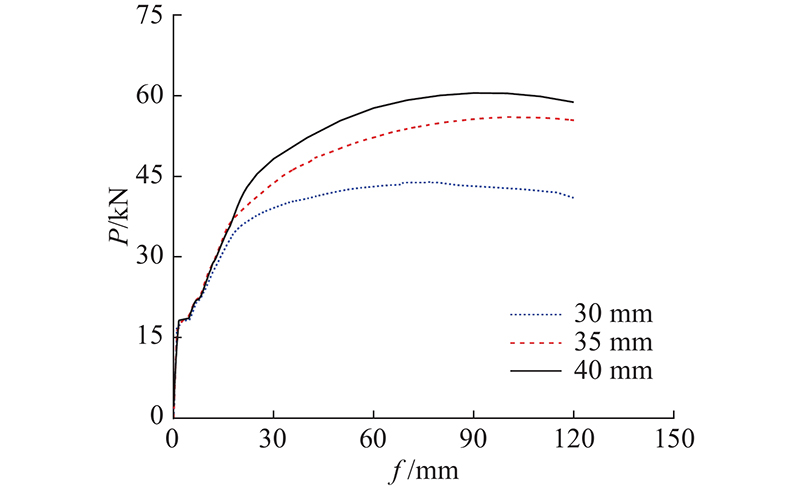
分别选取预制层凹槽深度为30、35、40 mm,开展叠合板受弯承载力分析,得到如图20所示的不同凹槽深度的荷载-跨中挠度曲线.
图 20
图 20 不同凹槽深度的叠合板荷载-跨中挠度曲线
Fig.20 Load-mid-span deflection curves of composite slabs with different groove depths
从图20可得如下结论. 1)叠合板屈服前的荷载-跨中挠度曲线的斜率相差不大,增大预制层凹槽深度对叠合板的抗弯刚度和开裂弯矩影响较小. 2)预制层凹槽深度为30、35、40 mm的凹槽拼缝连接叠合板的受弯承载力分别为44、56、60 kN. 随着凹槽深度的增大,叠合板的受弯承载力有明显提高. 3)在保证混凝土保护层厚度的前提下,合理增加凹槽深度可以增大拼缝处连接钢筋的截面有效高度,提升拼缝连接的受弯性能,同时增强了叠合层与预制层之间的咬合力,避免叠合板沿叠合面发生撕裂破坏.
6. 结 论
(1)后浇带连接叠合板的受弯承载力和最大跨中挠度与整浇板相近,后浇带两侧裂缝宽度较宽,其他裂缝宽度相对较小. 凹槽拼缝连接叠合板的受弯承载力略低于整浇板和后浇带连接叠合板,拼缝处的裂缝宽度较大,其余裂缝宽度较小.
(2)凹槽长度为100 mm的叠合板发生脆性破坏. 凹槽长度为200和300 mm的叠合板表现出良好的受弯性能. 通过增加凹槽长度,增大连接钢筋锚固长度,抑制叠合面发生撕裂破坏,保证拼缝处连接钢筋和受力纵筋有效传力,提升叠合板的受弯性能.
(3)相较于C型连接,D型凹槽拼缝连接叠合板的受弯承载力、裂缝开展情况及变形延性等受弯性能更好,环形弯折的连接钢筋对叠合板受弯过程中主裂缝的开展起到了抑制作用.
(4)连接钢筋配筋率、叠合层厚度及凹槽深度是影响D型连接凹槽拼缝连接叠合板受弯性能的重要因素. 根据有限元分析结果可知,增大连接钢筋配筋率可以有效地提高叠合板的受弯承载力. 保持预制层厚度不变,增大叠合层厚度,可以显著提高叠合板的受弯承载力. 在保证混凝土保护层厚度的前提下,合理设置凹槽深度可以提升拼缝连接的受弯性能.
参考文献
新型叠合板拼缝构造措施的试验研究及有限元分析
[J].DOI:10.13204/j.gyjz201502012 [本文引用: 1]
Experimental study and finite element analysis of the new type of composite slab joint structure measures
[J].DOI:10.13204/j.gyjz201502012 [本文引用: 1]
双向叠合板拼缝传力性能的试验研究
[J].DOI:10.3969/j.issn.1002-8528.2003.06.004 [本文引用: 1]
Experimental study on joint force transmission performance of two-way composite plate
[J].DOI:10.3969/j.issn.1002-8528.2003.06.004 [本文引用: 1]
一种新型拼缝结构的叠合板受力机理及试验研究
[J].DOI:10.15951/j.tmgcxb.2015.10.009 [本文引用: 1]
Mechanical mechanism and experimental study of composite plate with a new type of joint structure
[J].DOI:10.15951/j.tmgcxb.2015.10.009 [本文引用: 1]
分离式接缝叠合板垂直接缝方向抗弯刚度的试验及计算方法研究
[J].DOI:10.14006/j.jzjgxb.2018.09.009 [本文引用: 1]
Research on test and calculation method of bending stiffness of vertical joint of separated joint composite plate
[J].DOI:10.14006/j.jzjgxb.2018.09.009 [本文引用: 1]
单缝密拼钢筋混凝土叠合板受弯性能试验研究
[J].DOI:10.14006/j.jzjgxb.2019.04.003 [本文引用: 1]
Experimental study on flexural behavior of single joint close fitting reinforced concrete composite slab
[J].DOI:10.14006/j.jzjgxb.2019.04.003 [本文引用: 1]
Performance of joints in reinforced concrete slabs for two-way spanning action
[J].
Stress-strain relationship of high-strength concrete in compression
[J].DOI:10.1061/(ASCE)0899-1561(1996)8:2(70) [本文引用: 2]
Behavior of reinforced concrete columns under variable axial loads: analysis
[J].
Ultimate strength behavior of sandwich pipes filled with steel fiber reinforced concrete
[J].DOI:10.1016/j.oceaneng.2012.07.033 [本文引用: 1]
Finite element analysis of punching shear of concrete slabs using damaged plasticity model in ABAQUS
[J].DOI:10.1016/j.engstruct.2015.04.016 [本文引用: 1]
A plastic-damage model for concrete
[J].DOI:10.1016/0020-7683(89)90050-4 [本文引用: 1]