采用有限元分析方法对套筒灌浆连接接头进行研究,不仅能够获得丰富的试验数据,还能够对套筒内部灌浆料的受力状态进行全程观测. 根据钢筋建模方式的不同,目前国内外相关研究中建立的接头有限元模型主要有4种:1)元素尺度模型;2)线尺度模型;3)棒尺度模型;4)肋尺度模型. 元素尺度模型是抽象的等效模型,该模型中接头没有实体,整个接头等效为1组应力-应变关系,特点是计算效率高,易于收敛,适用于套筒灌浆连接预制构件的模拟[5-6]. 线尺度模型是混合单元模型,该模型中,钢筋和套筒分别采用梁单元和壳单元来建模,灌浆料采用实体单元. 相比于全实体模型,该方法在保证计算精度的同时,能够在一定程度上提高计算效率[7]. 在棒尺度模型中,整个接头全部采用实体单元建模,是全实体模型. 其中钢筋以表面光滑的圆柱体建模,钢筋和灌浆料间的黏结作用通过接触面上的“接触模型”来定义. 棒尺度模型的特点是易于建模和网格划分,能够较好地反映接头试验的实际情况,因此被广泛采用[8-12]. 肋尺度模型是全实体模型,该模型考虑钢筋肋的几何外形,用实体单元对钢筋肋进行建模,能够模拟钢筋肋和灌浆料间的机械咬合作用[13]. 由于建模过程复杂,计算收敛难度大,相关研究较少[14-16].
在套筒灌浆连接接头的数值模拟中,存在许多不足. 除元素尺度模型外,所有模型都通过“接触模型”定义不同材料间的相互作用,但相关参数的设置几乎全凭经验. 不同接触模型的参数差别较大,模型的通用性差. 对于有限元计算结果,仅对接头模型的荷载-位移曲线和套筒个别测点的应变进行验证,无法保证模型的准确性. 除此之外,现有的接头模型都不够精细,无法对灌浆料的开裂和破坏机理进行模拟,无法反映接头的微观工作机理.
本文提出套筒灌浆连接接头的精细化建模方法. 采用DIANA 10.3有限元软件,根据文献[17]建立接头试件的肋尺度精细化有限元模型. 利用有限元分析方法,研究接头的连接性能和灌浆料的开裂、破坏过程.
1. 试验概况
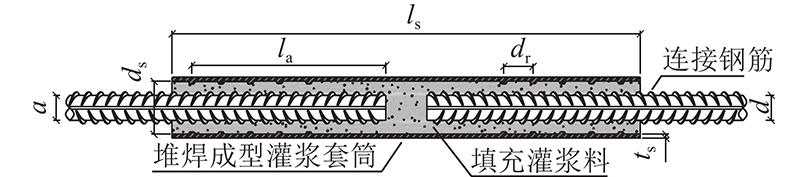
表 1 接头试件的几何参数
Tab.1
| 编号 | 钢筋 | 灌浆套筒 | 破坏模式 | ||||||
| d/mm | la/mm | ls/mm | N | dr/mm | ds/mm | ts/mm | |||
| A1 | 25 | 100 | 380 | 5 | 25 | 43 | 4 | 拔出破坏 | |
| A2 | 25 | 150 | 380 | 5 | 25 | 43 | 4 | 拉断破坏 | |
| B1 | 25 | 125 | 430 | 5 | 30 | 43 | 4 | 拔出破坏 | |
| B2 | 25 | 175 | 430 | 5 | 30 | 43 | 4 | 拉断破坏 | |
| C1 | 25 | 150 | 480 | 6 | 30 | 43 | 4 | 拔出破坏 | |
| C2 | 25 | 200 | 480 | 6 | 30 | 43 | 4 | 拉断破坏 | |
图 1
表 2 钢筋和套筒的材料性能参数
Tab.2
| 类别 | Es/MPa | fy/MPa | fu/MPa | A/% |
| 钢筋-I | 2.00×105 | 435 | 585 | 22.3 |
| 钢筋-II | 2.00×105 | 435 | 625 | 26.4 |
| 套筒 | 2.06×105 | 390 | 505 | 21.0 |
图 2
图 3
2. 精细有限元模型建立
2.1. 材料本构模型
图 4
图 5
现阶段灌浆料尚无成熟的材料本构模型,本文采用混凝土总应变裂缝模型中的Thorenfeldt受压本构模型和Hordijk受拉本构模型,对灌浆料的受压和受拉性能进行模拟,相关的力学参数按表3取值.
表 3 灌浆料的本构模型参数
Tab.3
| 参数 | 数值 |
| 弹性模量Ec | 23 GPa |
| 泊松比ν | 0.2 |
| 抗压强度fcm | 80.2 MPa |
| 抗拉强度ftm | 4 MPa |
| 断裂能Gf | 0.161 N/mm |
Thorenfeldt[20]受压本构模型按下式取值.
式中:σc、εc分别为灌浆料的压应力和压应变;fcm为灌浆料的抗压强度,对应的应变为峰值应变εcm,其值均为负. 本构曲线如图6所示.
图 6
Hordijk受拉本构模型[20]按下式取值:
式中:
图 7
2.2. 单元选取和网格划分
试件中采用的25钢筋表面布有倾斜且肋高渐变的月牙肋,其复杂的几何外形不利于有限元建模. 在有限元模型中,将钢筋肋简化为一系列平行环肋,环肋截面为梯形. 尺寸参考规范GB/T 1499.2—2018[21],梯形截面的上、下底和高分别为1.00、2.62和1.40 mm. 套筒肋建模采用相同的简化方法,梯形截面的上、下底和高分别为4.00、6.88和2.50 mm.
图 8
在钢筋-灌浆料接触界面和灌浆料-套筒接触界面上,通过耦合不同材料单元在重合节点处的自由度,建立3种材料间的连接,如图8所示,不再另外设置“接触单元”. 建立的肋尺度精细化有限元模型仅通过单轴应力状态下的材料本构模型,即可反映套筒灌浆连接接头在单向拉伸荷载下的力学响应,避免了“接触模型”的经验性设置,大大提高了模型的通用性.
3. 有限元分析结果
3.1. 模型验证
表 4 接头试件的有限元分析结果与试验结果的对比
Tab.4
| 试件 | | | δ′/mm | δ′/δ | 破坏模式 |
| A1 | 233.16 | 1.03 | 7.61 | 1.23 | 拔出破坏(√) |
| A2 | 241.55 | 0.99 | 10.94 | 0.78 | 拉断破坏(√) |
| B1 | 241.09 | 0.99 | 11.98 | 0.96 | 拔出破坏(√) |
| B2 | 241.30 | 0.98 | 10.22 | 0.74 | 拉断破坏(√) |
| C1 | 241.74 | 0.98 | 11.66 | 1.03 | 拉断破坏(×) |
| C2 | 256.57 | 0.97 | 12.46 | 0.76 | 拉断破坏(√) |
图 9
图 9 试件破坏时的钢筋Von Mises应变云图
Fig.9 Nephograms of rebar Von Mises strain at failure moment
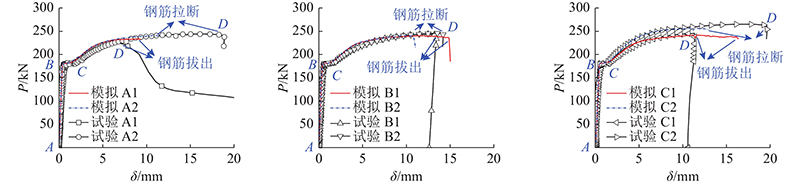
如图10所示为试件荷载-位移曲线的模拟结果与试验结果对比. 可见,两者的曲线吻合较好,所有曲线均表现出明显的弹性段(A-B)、屈服段(B-C)和强化段(C-D),表明有限元模型能够准确地反映接头试件在轴向拉力下的宏观力学响应.
图 10
图 10 荷载-位移曲线模拟结果与试验结果对比
Fig.10 Comparison of load-displacement curves between results of FE analyses and experiments
如图11所示为不同荷载下钢筋轴向应变ε沿轴向的分布曲线对比,实心点和虚心点曲线分别表示模拟结果和试验结果. 可知,模拟得到的钢筋应变分布规律与试验类似:钢筋轴向应变从自由端(套筒中部)向加载端(套筒端部)递增,应变沿轴向方向的增长率在套筒端部附近略大于锚固段内部,锚固长度越大,这种应变增长率的差别越明显. 在钢筋屈服前,加载端和自由端的钢筋应变与试验值较接近,其余位置的应变模拟值稍小. 考虑到试验中应变测量可能受到的干扰,利用有限元模拟得到的钢筋应变分布结果是可以接受的.
图 11
图 11 钢筋轴向应变分布的模拟结果与试验结果对比
Fig.11 Comparison of rebar axial strain distribution between results of FE analysis and experiments
如图12所示为不同荷载下套筒轴向应变沿轴向方向的分布曲线对比,实心点和虚心点曲线分别表示模拟结果和试验结果. 可知,两者不仅具有相同的分布规律,且各个测点的应变基本相同,表明该模型能够准确地反映套筒的细部受力状态和变形情况. 图12中的套筒应变试验分布曲线表明,套筒的轴向应变从两端向中部递增,且应变沿轴向方向的增长梯度逐渐减小,直至套筒中部,应变增长趋于平缓,套筒应变基本不变. 在钢筋屈服后,由于钢筋的伸长和变细,套筒端部处的钢筋与灌浆料间不再紧密接触,出现黏结劣化. 套筒端部的应变随着荷载水平的提高不再增加,在极限荷载下端部应变甚至出现明显下降,说明套筒的有效约束面发生内移[23]. 对比图12中套筒应变的模拟分布曲线表明,该精细有限元模型能够反映这一现象.
图 12
图 12 套筒轴向应变分布的模拟结果与试验结果对比
Fig.12 Comparison of sleeve axial strain distribution between results of FE analysis and experiments
以上对比结果表明,接头试件的肋尺度精细化有限元模型不仅能够反映试件在轴向拉力下的宏观力学性能,而且能够反映试件中钢筋和套筒的细部受力状态和变形情况以及套筒的有效约束面内移现象,可以用于接头的一般力学性能和微观工作机理的深入研究.
3.2. 灌浆料破坏过程及裂缝开展
图 13
图 14
图 15
在钢筋屈服后(180 kN),钢筋肋和套筒肋处均出现不同程度的裂缝. 钢筋肋处裂缝的宽度和长度沿钢筋向外递增,裂缝最宽处达到0.1 mm. 套筒肋处裂缝的宽度和长度沿套筒向外递减,最大裂缝宽度约为0.04 mm. 在套筒中部纯灌浆段观察到2条水平裂缝. 在极限荷载(234 kN)下,套筒端部发生明显的楔形破坏,同时观察到灌浆键(钢筋肋之间的灌浆料)的剪切破坏,破坏区域约占锚固段的1/2. 在该破坏区域,原本分布在套筒肋上斜面处的裂缝已经消失;在灌浆键未破坏区域,裂缝依然存在. 说明灌浆键的剪切破坏会导致钢筋的机械咬合作用失效,灌浆料的应力传递效率降低,最终造成套筒有效约束面内移.
如图16所示为试件A2的灌浆料主拉应变云图,裂缝开展过程和分布规律与A1类似,但极限荷载下灌浆键剪切破坏的范围比A1小,约占锚固段的1/3. 说明增加钢筋锚固长度能够有效地提高接头的连接性能,在套筒灌浆连接接头设计中,可以通过增大钢筋锚固长度来提高接头承载力. 在试件A2的纯灌浆段,由于较短的纯灌浆段长度,该处未观察到水平裂缝.
图 16
从试件A1和A2的裂缝开展规律可知,锚固区灌浆料中的裂缝均为斜向分布的圆锥状裂缝,与接头轴向的夹角约为30°~45°,这是灌浆料中形成的锥面斜压杆的分布角度. 套筒端部和钢筋自由端是灌浆料的2个薄弱点,裂缝开展较早且宽度较大.
在钢筋和灌浆料接触面上,裂缝从套筒端部和钢筋自由端2处相向发展;在灌浆料和套筒的接触面上,裂缝从套筒中部开始逐渐向端部发展. 锚固段中部是套筒的主要约束区域,裂缝开展和灌浆键破坏发展最迟,增大锚固长度可以有效地减小锚固段中部区域灌浆料的开裂.
3.3. 套筒环向应变的分布
图 17
图 17 灌浆套筒径向约束的隔离体示意图
Fig.17 Free body diagram for radial confinement of sleeve
图 18
从图18可知,从套筒端部至中点区域内,套筒环向应变沿轴向方向先增大再保持一段长度后又迅速增大,且锚固长度越长,环向应变增长过程中的保持阶段范围越大. 对比不同试件保持长度内的应变可知,在保持阶段末的环向负应变较之前稍低,说明套筒该点处的环向收缩变形较其他位置要小,这是钢筋自由端处灌浆料锥面斜压杆在分界点处对套筒的挤压造成的. 对于试件A1、B1和C1,分界点在位于应变片D附近,该处对应套筒内壁从中点向两端方向的第1、2道环肋之间,如图18(a)、(c)和(e)所示. 对于试件A2、B2和C2,分界点位于应变片C附近,该处对应套筒内壁从中点往两端至第1道环肋之间,如图18(b)、(d)和(f)所示. 由此可知,在试件A1、B1和C1中,灌浆料锥面斜压杆作用范围为应变片D至套筒端部区域. 套筒从中点向两端的第1道环肋处于该作用范围以外,故此道环肋对套筒中灌浆料的止推作用无法充分发挥. 对钢筋采用套筒灌浆连接时,在套筒内壁设置环肋有利于灌浆料形成锥面斜压杆效应,既能防止灌浆料沿轴向向套筒端部滑移,又能约束灌浆料沿径向膨胀开裂. 为了保证所有套筒环肋都能生效,设计时应将套筒环肋布置在灌浆料锥形斜压杆作用范围以内,如试件A2、B2和C2所示. 对于本实验而言,当从套筒中点向外布置环肋时,第1道环肋应距离锚固钢筋端部至少30 mm,该距离在数值上约为1倍钢筋直径.
由图18(a)、(c)和(e)可知,试件A1、B1和C1的环向应变分布曲线在套筒中部的纯灌浆段有一个明显的平台段,因为该区域钢筋传递给套筒的拉拔力不再增加,套筒由于泊松效应形成的环向负应变不再增加,沿轴向方向形成平台段分布. 这种平台段分布对于套筒灌浆连接接头来说是不利的,因为该区域的灌浆料无法形成锥面斜压杆应力传递机制,降低了接头的应力传递效率. 在套筒灌浆连接接头设计中,套筒中部的纯灌浆段不应过长,对于该堆焊成型灌浆套筒,20 mm较理想.
4. 结 论
(1)建立的肋尺度精细化有限元模型能够模拟带肋钢筋的机械咬合作用,反映接头试件的破坏模式、极限承载力、荷载-位移曲线以及钢筋和套筒的轴向应变分布规律,避免了“接触模型”及相关参数的经验性设置.
(2)钢筋锚固区灌浆料中的裂缝均为斜向分布的圆锥状裂缝,与接头轴向的夹角约为30°~45°. 增大锚固长度,可以有效地减小锚固段中部区域灌浆料的开裂.
(3)灌浆键的剪切破坏会导致钢筋的机械咬合作用失效,破坏区域灌浆料的应力传递效率降低. 与钢筋自由端齐平的套筒肋无法充分发挥对灌浆料的止推作用,中部纯灌浆段无法形成锥面斜压杆应力传递机制,在套筒灌浆连接接头设计中应避免这2种情况.
参考文献
Performance and confining mechanism of grouted deformed pipe splice under tensile load
[J].
Bond stress-slip characteristics of reinforcing bars in grout-filled coupling steel sleeves
[J].
Mechanical characteristics of grout-filled coupling sleeves of electric resistance welded steel tube under uniaxial tensile loads
[J].
灌浆套筒连接装配式梁柱节点精细有限元模型
[J].
High-precision finite element model of prefabricated reinforced concrete beam-column joint with grout sleeve
[J].
Effective stress-strain relationship for grouted sleeve connection: modeling and experimental verification
[J].
新型12mm钢筋灌浆套筒连接力学性能试验研究及有限元分析
[J].
Experimental research and finite element analysis of the mechanical properties of 12 millimeter steel bar grouting sleeve connection
[J].
Non-proprietary bar splice sleeve for precast concrete construction
[J].
Experimental and numerical investigation on mechanical properties of grouted-sleeve splices
[J].DOI:10.1016/j.conbuildmat.2020.120441
变形灌浆套筒连接性能试验研究及有限元分析
[J].
Experimental study and finite element analysis on behavior of deformed grout-filled pipe splice
[J].
灌浆套筒连接构件的有限元分析
[J].
Finite element analysis of grouting coupler connection member
[J].
装配式新型灌浆套筒接头设计及有限元分析
[J].
Design and finite element analysis of assembled grouted deformed pipe splice
[J].
Effect of tapered head sleeve structural parameters on grouting connection joints deformation
[J].DOI:10.1061/(ASCE)MT.1943-5533.0003174 [本文引用: 1]
Modelling the response of tapered head sleeve connection under tensile load using finite element method
[J].
考虑表面肋参数的钢-连续纤维复合筋与灌浆套筒界面性能研究
[J].
Study on bond performance between steel-FRP (fiber reinforced polymer) composite bars and grouted sleeves considering influence of surface ribs
[J].
Stress-strain curves for hot-rolled steels
[J].
单向拉伸荷载下堆焊成型套筒灌浆连接性能试验研究
[J].
Experimental study on connection performance of grouted welded sleeve under uniaxial tensile load
[J].