针对电力电子系统的参数优化设计问题,传统的优化算法主要有目标规划法、约束法、权重法以及最大最小法等,它们通常是将多个目标合并为1个目标函数[1-3],需要多次迭代,所求得的最优解没有可比性,在处理维数高且非线性的复杂问题时存在明显不足. 有关电力电子系统的研究考虑从多个角度进行综合性能优化,但多个优化指标可能相互冲突并具有很大的提升空间,通常采用多目标优化技术来解决该问题[4]. 遗传算法为典型的多目标优化算法,其解集在空间上形成的曲线可以清楚地反映多个冲突问题之间相互妥协的耦合关系,这条曲线即为Pareto前沿,通过评价各解的优劣获得多目标优化问题的最优解[5]. Srinivas等[6]基于Pareto支配关系提出非支配排序遗传算法(non-dominated sorting genetic algorithm,NSGA),采用共享小生境技术进行临界层选择,尽可能维持个体的多样分布. 由于NSGA存在非支配排序复杂度高、父代最优解易丢失以及共享小生境技术实现复杂等问题,Deb等[7]引入快速非支配排序、精英选择策略和个体拥挤距离等方法设计出NSGA-II,迅速成为研究热点[8-10].针对NSGA-II不仅在计算过程中存在种群分布不均匀、收敛速度较慢的缺点,而且在逆变器参数优化设计中,存在多数未考虑多个目标同时优化的问题. 本研究提出兼顾种群分布性和收敛性的超平面NSGA-II(hyperplane NSGA-II,HP-NSGA-II),用于实现双输入双降压型逆变器(dual-input dual-buck inverter,DIDBI)系统多个参数优化设计,在保持粒子分布性的同时能够保留收敛性较好的粒子,有益于提高全局收敛速度,有效弥补NSGA-II的缺陷.
在电力电子系统运行时,有源功率器件的导通压降、导通时间、关断时间均不为零,会产生相应的功率损耗. 当器件导通时,饱和压降和导通电阻会产生通态损耗;当器件在开通和关断的瞬间,电流电压不为零相交的暂态过程会产生开关损耗. 利用多目标优化算法并根据各元器件的体积和总损耗来选取器件,忽略漏感等线路寄生参数的影响,准确计算各开关器件的功率损耗对优化结果非常重要[11]. 王康等[12]提出同时优化该变换器的功率损耗、物理尺寸和成本的多目标优化方法,得到综合性能最优的器件组合方案,实现低压开关槽式变换器的效率、面积和成本达到折中最优. 谐波畸变率(total harmonic distortion,THD)同样可以通过多目标优化算法进行优化,Mohammadi等[13]提出细菌觅食优化算法,通过对无源谐波滤波器的经济布置和尺寸调整,可以同时将总电压THD和有功功率损耗降至最低. 在实际工程应用中,应尽量减小电力电子设备体积,实现小型化,因此体积优化也成为参数设计的趋势.
1. DIDBI优化目标函数
1.1. DIDBI拓扑结构
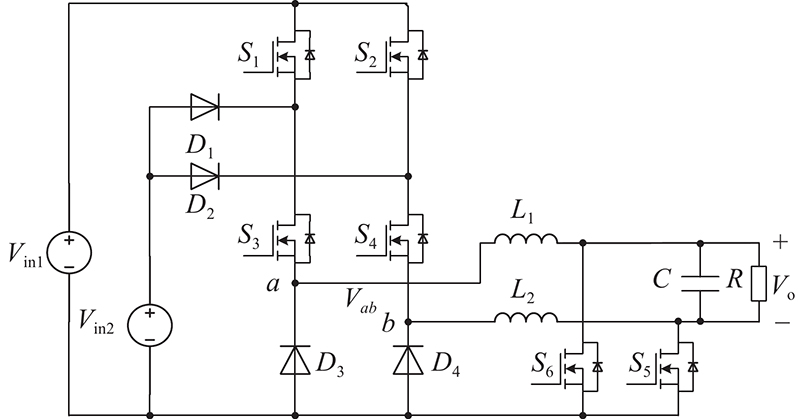
DIDBI应用于单相115 V/400 Hz交流电,默认功率为1 kW,拓扑结构如图1所示. 该逆变器中S1~S4为高频管,S5、S6为低频管,电感L1、L2和电容C共同构成滤波电路,拓扑为对称结构,设定L1=L2=L. 图中的DIDBI有2个并联的双输入降压型高频脉冲电压源单元[17]. 正向降压式变换Buck电路由S1、S3、S5、D1、D3和L1组成,负向Buck电路由S2、S4、S6、D2、D4和L2组成,正反向Buck电路分别在输出电压Vo的正负半周交替运行. 在正半周期中,开关S1,S3和S5调制工作,其他开关保持关断状态. 在负半周期中,开关S2,S4和S6调制工作,其他开关关断. 根据开关状态组合逆变器电压源单元的桥臂中点a、b共产生5种电压电平Vab,即±Vin1、±Vin2、0. 当Vab的输出电压为高电平时,由高压直流输入端口Vin1为逆变器供电. 当Vab的输出电压为低电平时,由低压直流输入端口Vin2为逆变器供电.
图 1
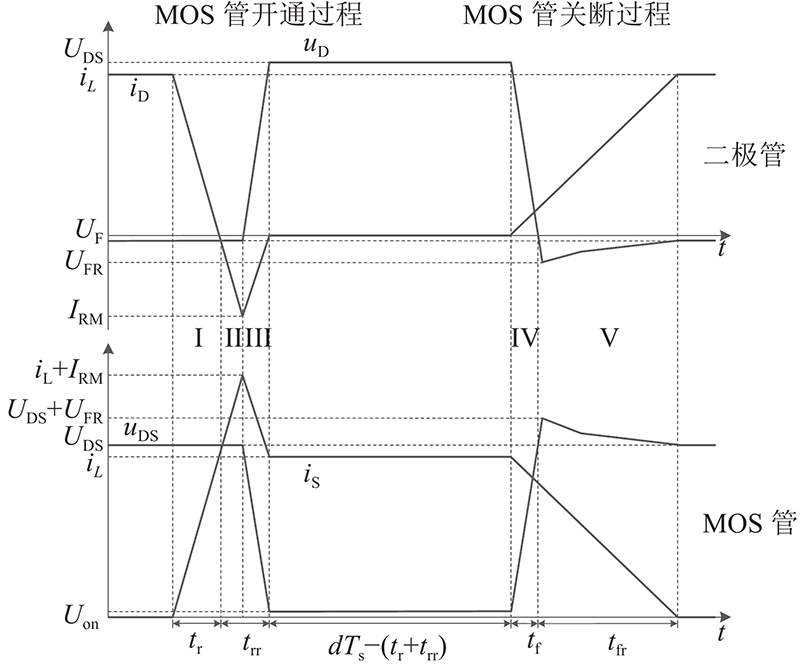
1.2. 开关器件功率损耗计算
图 2
二极管关断一次损耗WD-off的计算式为
MOS管关断一次损耗WS-off的计算式为
二极管开通一次损耗WD-on的计算式为
设Ts为MOS管的开关周期,d为占空比,RDS为漏源间的导通电阻,则MOS管导通时间为dTs,二极管续流时间为(1−d)Ts. 由此可得MOS管的通态损耗WSR和二极管的通态损耗WDR的计算式分别为
在Vo>Vin2阶段,MOS管S3始终导通,MOS管S1导通时,D1截止;关断时,D1导通. 该阶段需计算S3的通态损耗,并根据式(1)~(6)计算S1、D1的损耗,此阶段持续时间为ta,开关频率为fs,S1开关次数为N1=fsta,MOS管S1、S3以及开关管D1损耗表达式分别为
在0<Vo<Vin2阶段,MOS管S3和二极管D1开通时,D3截止;关断时,D3开通,同样可以计算S3、D3的损耗,此阶段持续时间为tb,S3开关次数为N2=fstb. 由于D1在此阶段不存在反向偏置,可忽略D1的开关损耗,只考虑其通态损耗,此阶段D1损耗表达式为
开关器件S3和D3损耗表达式分别为
MOS管S5在输出电压的正半周期内始终导通,S5的通态损耗表达式为
考虑正负半周期的对称性,得到单个周期内DIDBI功率器件的总损耗表达式为
DIDBI功率器件的功率损耗表达式为
1.3. DIDBI输入输出向量与THD函数
输出电压THD的表达式为[19]
式中:H为特定阶数,Un、U1为谐波基波分量有效值. 反向传播(back propagation,BP)神经网络是误差可反向传播的前馈网络,可学习非线性的输入-输出映射关系. 本研究采用BP神经网络分析DIDBI输出电压THD,输入为DIDBI滤波电容C、滤波电感L和开关频率fs这3个系统参数,输出为DIDBI输出电压THD. 输入和输出向量表示为
1.4. 滤波元件体积评价函数
在实际工程应用中,优化设计应尽量减少逆变器的体积,其中体积最大部件主要为滤波元件中的电感. 假设DIDBI电感电流与输出电流相同,输出电流基波有效值为
式中:wC为电容的单位权重因子,电容与电感相比体积差距较大,因此wC通常很小.
2. DIDBI约束条件分析
DIDBI中LC低通滤波器可以滤除高次谐波分量,使输出电压接近所需正弦波,因此在优化设计过程中,须对滤波电路的阻频特性、无功功率要素进行约束,均表示为含有系统参数C、L、fs的不等式.
2.1. 滤波器谐振频率
2.2. 电感电流纹波
较强的电流纹波除大幅增加逆变器滤波电感的磁芯损耗之外,还将导致更大的电流峰值. 结合工程经验并考虑到电感体积的影响,限制电感上电流纹波最大值ΔiL-max为输出电流峰值的1%~5%. 单极性SPWM续流阶段滤波电容电压约为输出电压Vo,基本全加在逆变侧电感L1两端,得到
续流阶段前一模态是直流低压输入源Vin2供电,输出电压Vo计算式为
结合式(21)、(22),推出电感上电流纹波最大值ΔiL-max计算式为
DIDBI具有五电平的特点,直流低压输入源Vin2=28 V,系统参数的设计要满足最差环境,因此选择[d(1-d)]max=0.25,得到含有L、fs的约束条件为
2.3. 滤波器无功功率
滤波器的无功功率影响逆变器对电源容量的利用效率. 由于逆变器输出以基波为主,忽略占比很小的谐波分量,无功功率可以简化为
式中:ω1为基波角频率,
逆变器的有功功率包括逆变器输出功率Po和开关管损耗功率Ploss,忽略相对较小的功率损耗,限定逆变器功率因数不低于0.98[22]
将式(27)代入式(26),得到L、C的约束条件为
3. 基于HP-NSGA-II的DIDBI系统参数优化
3.1. 基于HP-NSGA-II的临界层个体超平面构建
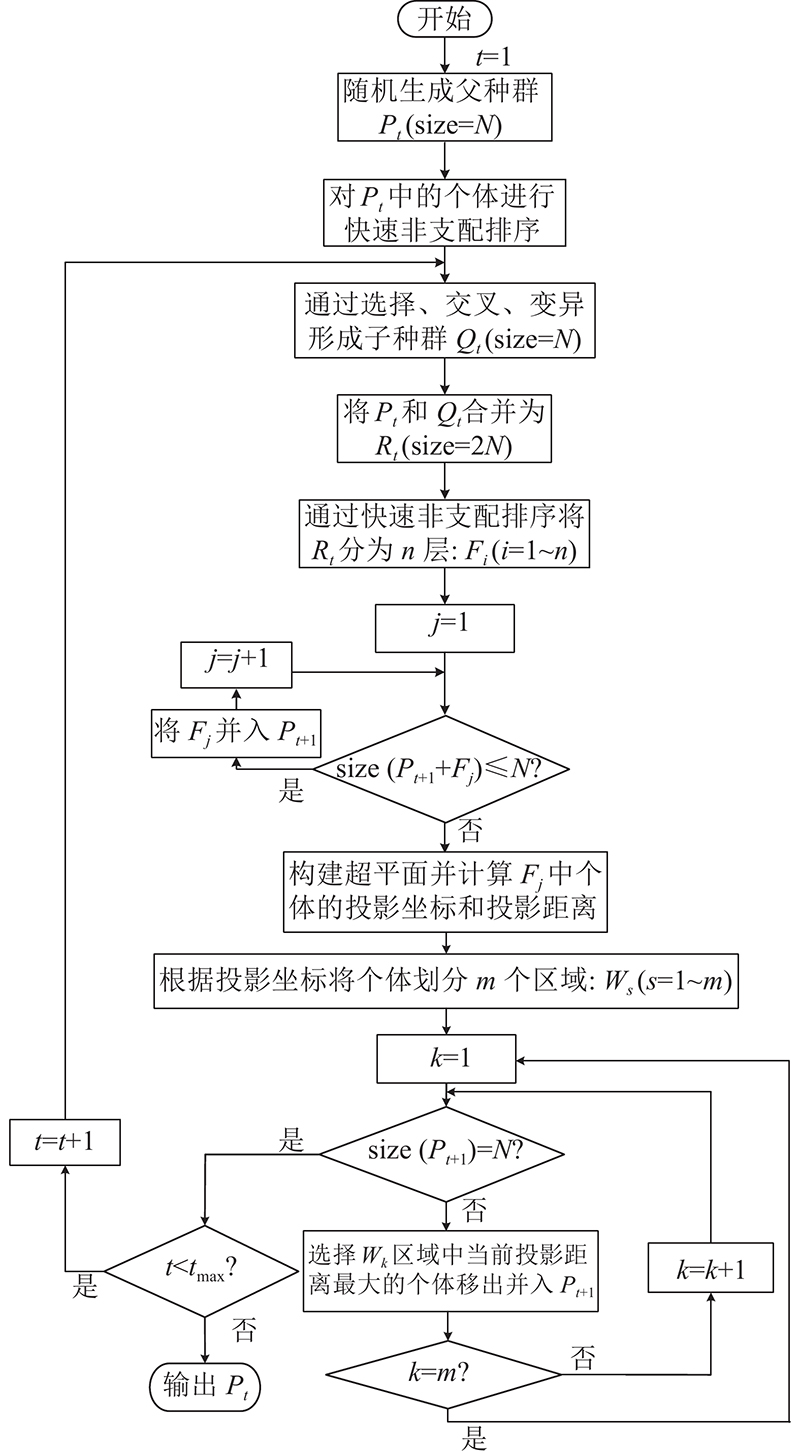
考虑种群分布性和收敛性,提出HP-NSGA-II. 在种群进化过程中,利用成绩标量函数(achievement scalarizing function,ASF)将多目标优化问题转化为极大极小问题,求得多目标方向上的极值点,反映种群边缘分布情况,极值点集合构成临界层个体的超平面. 以超平面的法向量为种群进化趋势,获得临界层个体在此平面的投影,投影坐标可以观测到个体之间的聚集分布程度,投影距离体现个体沿法向量的进化程度. 综合投影坐标和距离在临界层选择下一代个体,推进种群朝着分布均匀且收敛良好的前沿最优解进化.
图 3
图 3 超平面第二代非支配排序遗传算法的流程图
Fig.3 Flow chart of hyperplane non-dominated sorting genetic algorithm II
式中:x为种群中个体,M为目标数,v为目标方向的权重向量,fi(x)为个体x对应第i个优化目标值. M−1维超平面表达式可由M个极值点求得,个体x到超平面的投影坐标f′(x)和投影距离d的表达式[24]分别为
式中:w为超平面法向量,f(x)为个体x对应的优化目标值,b为超平面的截距,
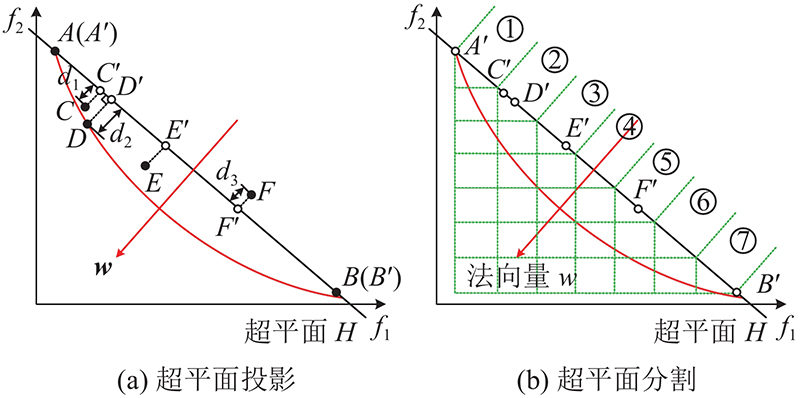
超平面的建立由投影和分割组成,如图4所示. 投影过程中,输入为临界层的所有个体P、目标数量M以及目标方向权重向量的集合v,输出为个体投影坐标f'(x)集合与个体投影距离d集合. 图4(a)中,点A~F为临界层的5个个体,图中曲线为理想Pareto前沿,直线H为1维超平面,w为超平面法向量. 区域分割过程中,输入为临界层的所有个体P、目标数量M以及各维度分割区域数N,输出为区域编号集合、区域个体集合以及区域个体的投影距离集合. 图4(b)中,以极值点为边界范围,对超平面以一定间隔进行区域分割,将投影点划分到对应区域中,将极值点A',B'之间的超平面等分为7个区域. 图4(a)中,位于超平面两侧个体的投影距离符号不同,记原点侧为正,另一侧为负. C、D、F的投影点分别为C'、D'、F',投影距离d1、d2为正,d3为负,d2 > d1,认为D比C进化程度更优,收敛性更好. 按照区域所属个体数量升序进行选择,每个区域选择1个当前投影距离最大的个体. 图4(b)中区域2选择投影距离更大、进化程度更优的个体D,放入下一代种群,同时将此个体从区域中删除. 对这些区域进行多轮选择,直到满足下一代种群数量要求. 为了保护种群边缘分布,极值点不参与比较,直接选入下一代种群.
图 4
图 4 基于超平面第二代非支配排序遗传算法的临界层个体超平面构建
Fig.4 Hyperplane construction of critical layer individual based on hyperplane non-dominated sorting genetic algorithm II
3.2. HP-NSGA-II性能测试
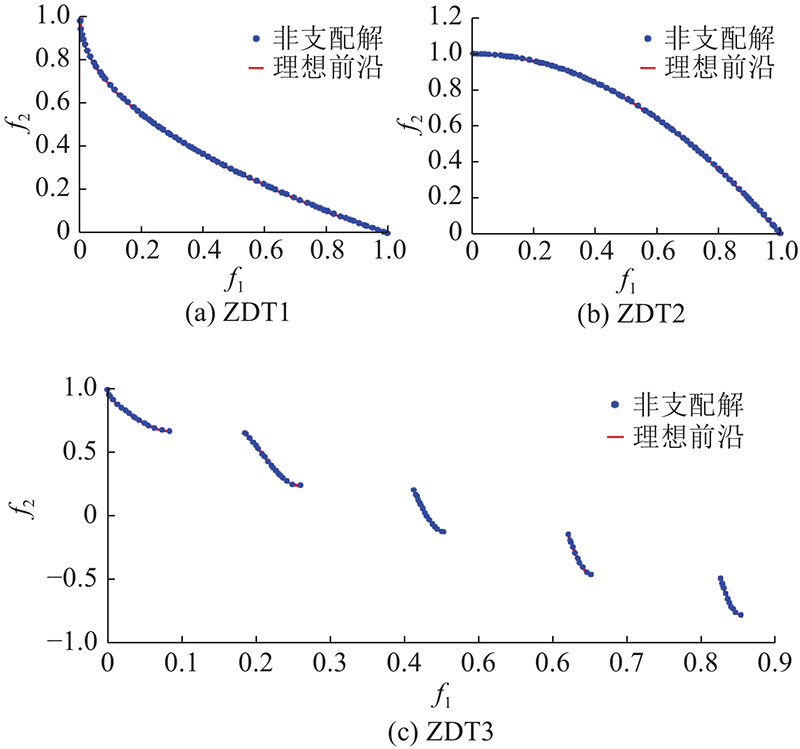
采用零延性变换(zero-ductility transition, ZDT)多目标测试函数对HP-NSGA-II进行简单的性能测试,检验HP-NSGA-II在面对不同前沿时寻找最优解的能力,测试结果如图5所示,ZDT1为凸前沿,ZDT2为凹前沿,ZDT3为非连续前沿,均代表Pareto前沿特征. 种群大小为100,迭代次数为50,色点代表HP-NSGA-II进化得到的非支配解,曲线代表真实的Pareto前沿. 在50次迭代后,得到的非支配解均匀地分布于整个真实前沿轮廓,图中无论是凸前沿、凹前沿,还是非连续前沿,优化都达到理想效果.
图 5
图 5 超平面第二代非支配排序遗传算法的性能测试实验
Fig.5 Performance test experiment of hyperplane non-dominated sorting genetic algorithm II
3.3. 优化过程中的染色体编码和种群初始化
结合优化目标函数和分析的约束条件,DIDBI系统参数优化的染色体编码和种群初始化步骤如下.
1)将约束条件中的式(20)、(24)和(28)中包含L、C、fs的表达式,用设计变量a、b、q代替,得到3个变量的取值范围:
2)根据式(32),一组在规定范围内取值的a、b、q,可以唯一确定一组系统参数L、C、fs. 因此选择a、b、q进行染色体编码,可以满足约束条件. 第i条染色体Xi是包含3个基因,即ai、bi和qi的基因链.
初始化种群时,每条染色体所包含的基因a、b和q在(32)所示的各自初始范围内随机生成,组合形成个体数为N的染色体群,父代种群Pt.
3.4. 系统参数优化结果比较与分析
利用NSGA-Ⅱ、γ-NSGA-Ⅱ和HP-NSGA-II分别对DIDBI系统参数进行多目标优化,NSGA-II在进化过程中默认所有优化目标同样重要. γ-NSGA-Ⅱ按照目标重要度顺序进行“对向量γ降维-快速非支配排序分层-选择个体进入下一代”的重复操作,使种群在多个目标不同重要度的影响下朝着更重要目标、优化效果更好的方向进化[16],详细流程不赘述.
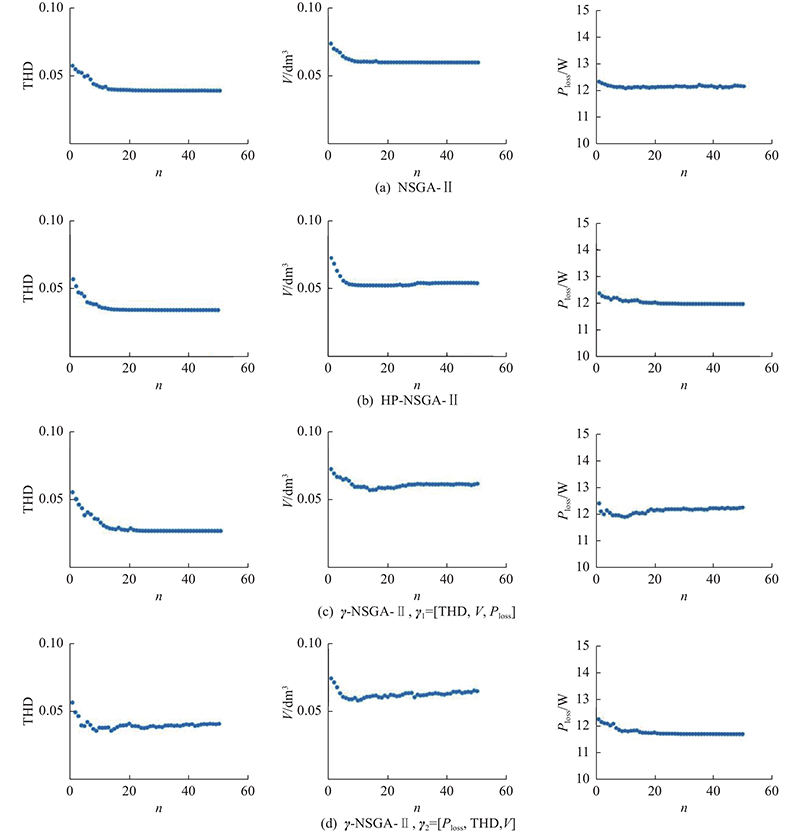
设置初始父代种群大小为100,种群中每条染色体的优劣分别由各目标函数式(16)、(18)、(19)的计算结果来评价. 设置交叉概率为0.8,突变概率为0.2,经过50次迭代,各代Pareto解集3个优化目标平均值如图6所示. 图中,n为迭代次数. 与图6(a)相比,图6(b)的3个优化目标收敛速度更快、效果更好. 说明随着种群中非支配个体数量的增加,HP-NSGA-II兼顾分布性及个体收敛程度,而NSGA-II收敛速度慢. 图6(c)中,在[THD, V,Ploss]条件下,Ploss在进化后期呈略微上升趋势,使得THD和V在进化过程中降低. 与图6(a)、(b)相比,γ-NSGA-Ⅱ牺牲了重要度较低的Ploss的小部分进化,使得重要度较高的THD进化效果更好,可以满足对THD要求严格而对功率损耗要求不高的用户需求. 图(d)中,在[Ploss, THD,V]条件下,最不重要的优化目标函数值V在进化后期呈略微上升趋势,使Ploss值降到更低,这满足以功率损耗低最优的用户需求. 综上所述,当目标重要度向量不同时,γ-NSGA-Ⅱ优化结果总是优于NSGA-II和HP-NSGA-II的优化结果;在目标重要度向量相同时,HP-NSGA-II的优化结果整体优于NSGA-II.
图 6
图 6 第二代非支配排序遗传算法改进前后各目标函数值进化过程
Fig.6 Evolution process of each objective function values before and after improvement of non-dominated sorting genetic algorithm II
为了进一步验证各算法的进化效果,在上述情况下分别进行10轮进化,每轮迭代50次. NSGA-II与2种改进算法的第50代Pareto解集中3个目标的平均值对比如表1所示. 由表观察10轮遗传结果的平均值可知,HP-NSGA-II整体优化效果优于NSGA-II,γ-NSGA-Ⅱ使优化结果有所侧重. 在[THD, VL,Ploss]条件下,重要度最高的目标为THD,其平均值为0.029,是3种情况下THD的最小值. 重要度最低的目标为Ploss,其平均值为12.36 W,是3种情况下的最大值. 同理,在[Ploss, THD,VL]条件下,Ploss是3种情况下最小值,VL数值最大,可见,HP-NSGA-II各个目标优化效果较为均衡,γ-NSGA-Ⅱ使重要度高的目标优化效果更好,重要度低的目标优化效果较差. 与NSGA-Ⅱ相比,HP-NSGA-II的收敛速度更快. 在高维(维数>3)多目标优化中,目标空间的复杂度增加,如何平衡解集的收敛性和分布性成为该优化问题中的难点,HP-NSGA-II具有收敛速度快、寻优精度高且稳定性的优点,因此更适用于此类高维且复杂的优化问题的求解.γ-NSGA-Ⅱ相比之下,允许用户根据实际情况及时调整目标重要度向量,适用于优化目标重要度不同的实际场合.
表 1 算法改进前后第50代Pareto解集对比
Tab.1
| 编号 | NSGA-Ⅱ | HP-NSGA-II | γ-NSGA-Ⅱ,γ1 = [THD, VL,Ploss] | γ-NSGA-Ⅱ,γ2 = [Ploss, THD,VL] | |||||||||||
| THD | V/dm3 | Ploss/W | THD | V/dm3 | Ploss/W | THD | V/dm3 | Ploss/W | THD | V/dm3 | Ploss/W | ||||
| 1 | 0.041 | 0.060 | 12.27 | 0.036 | 0.055 | 12.01 | 0.028 | 0.061 | 12.41 | 0.040 | 0.064 | 11.78 | |||
| 2 | 0.043 | 0.064 | 12.30 | 0.034 | 0.057 | 12.16 | 0.030 | 0.063 | 12.33 | 0.039 | 0.065 | 11.71 | |||
| 3 | 0.040 | 0.058 | 12.28 | 0.035 | 0.054 | 12.05 | 0.029 | 0.062 | 12.30 | 0.042 | 0.064 | 11.77 | |||
| 4 | 0.039 | 0.059 | 12.23 | 0.035 | 0.052 | 12.05 | 0.029 | 0.059 | 12.41 | 0.041 | 0.066 | 11.82 | |||
| 5 | 0.042 | 0.057 | 12.25 | 0.037 | 0.055 | 12.02 | 0.030 | 0.059 | 12.41 | 0.043 | 0.067 | 11.69 | |||
| 6 | 0.040 | 0.060 | 12.20 | 0.036 | 0.053 | 12.01 | 0.028 | 0.061 | 12.39 | 0.042 | 0.068 | 11.75 | |||
| 7 | 0.041 | 0.062 | 12.25 | 0.033 | 0.051 | 12.06 | 0.030 | 0.058 | 12.35 | 0.044 | 0.064 | 11.76 | |||
| 8 | 0.042 | 0.060 | 12.26 | 0.036 | 0.054 | 12.02 | 0.030 | 0.059 | 12.37 | 0.041 | 0.066 | 11.83 | |||
| 9 | 0.042 | 0.058 | 12.31 | 0.037 | 0.053 | 12.08 | 0.031 | 0.063 | 12.32 | 0.042 | 0.065 | 11.80 | |||
| 10 | 0.041 | 0.059 | 12.24 | 0.035 | 0.050 | 12.09 | 0.029 | 0.062 | 12.33 | 0.041 | 0.063 | 11.77 | |||
| 平均 | 0.041 | 0.060 | 12.26 | 0.035 | 0.053 | 12.05 | 0.029 | 0.061 | 12.36 | 0.042 | 0.065 | 11.77 | |||
4. 实验研究
根据DIDBI在航空领域的性能需求和适用环境,选择THD=0.028 91、V=0.059 47 dm3、Ploss=12.393 3 W的目标函数值对应解为Pareto实际解. 因此,与实际解对应的染色体为
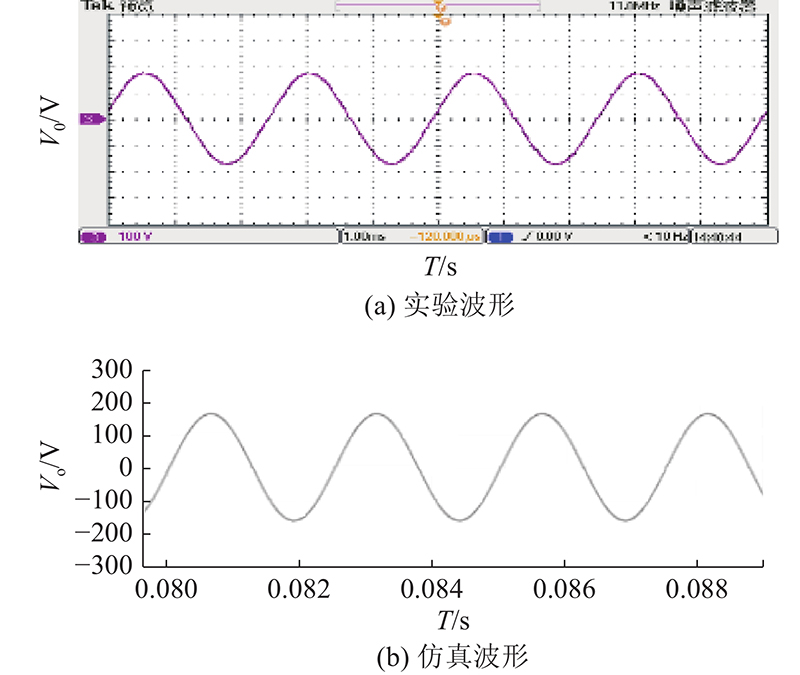
将式(34)代入式(32)计算得到逆变器的参数C=1.2446×10−6 F、L=2.5712×10−4 H、fs=4.9003×104 Hz,进行标称量选择:C=1 μF、L=0.3 mH、fs=50 kHz. 将该系统参数重新代入各目标的函数式演算出的目标函数值为THD=0.029 06、V=0.065 63 dm3、Ploss=12.423 2 W,与最优解目标函数值相差无几. 按照上述标称参数搭建1 kW的DIDBI样机,如图7所示. 其中输入高直流电压为180 V,低直流电压为28 V. 在Simulink电路模型中对输出电压进行仿真验证,实验波形与仿真波形如图8所示. 图中,Vo为输出电压,T为时间. 可以看出,电压波形平滑,输出良好. 对输出电压THD进行仿真和实验数据分析,得到输出电压THD的仿真值为2.91%,实验值为2.48%. 2个值基本吻合,均未超过7%,满足技术最低标准要求. 实验值较仿真值低的原因是仿真时没有考虑漏感引起.
图 7
图 8
图 8 双输入双降压型逆变器的输出电压波形
Fig.8 Output voltage waveforms of dual-input dual-buck inverter
5. 结 论
(1)将HP-NSGA-II应用于DIDBI系统参数多目标优化设计,以开关损耗Ploss、输出电压总谐波失真THD和滤波元件体积V为目标函数,开展与NSGA-II、γ-NSGA-II的对比分析. 观察10轮迭代的3个优化目标平均值,与NSGA-II相比,HP-NSGA-II的THD、V和Ploss,分别减小14.6%、11.7%与8.2%,优化效果明显,收敛速度更快.
(2)当重要度向量为[THD, V,Ploss]时,HP-NSGA-II的THD比γ-NSGA-II的THD高17.1%,HP-NSGA-II的V和Ploss分别比γ-NSGA-II的V和Ploss低13.1%和2.5%. 可见,γ-NSGA-Ⅱ更适用于优化目标重要度不同的实际场合. HP-NSGA-II使各目标的进化效果均衡,能够满足对高维多目标优化中所有目标值进行共同优化的需求.
(3)在DIDBI样机上开展实验研究,输出电压THD的仿真值和实验值均未超过7%,满足技术最低标准的要求,证实设计有效.
(4)HP-NSGA-II可以为其他变换器系统参数优化设计提供一定参考与指导.
(5)本研究只考虑电路参数,没有考虑控制策略,下一步将针对不同的控制策略开展对应参数优化方法的研究.
参考文献
LLCC谐振滤波器在高频正弦波逆变器中的优化设计
[J].
Parameters optimization and design of LLCC resonant converter in high frequency sinusoidal inverter
[J].
塑料机油冷却器盖加强筋参数的多目标优化
[J].
Multi-objective optimization of ribs design parameters for plastic oil cooler cover
[J].
An optimization design method of low frequency resonant filter based on NSGA-II
[J].
Harmonic analysis of hybrid renewable microgrids comprising optimal design of passive filters and uncertainties
[J].DOI:10.1016/j.jpgr.2018.07.023 [本文引用: 1]
Multiobjective function optimization using nondominated sorting genetic algorithms
[J].DOI:10.1162/evco.1994.2.3.221 [本文引用: 1]
A fast and elitist multiobjective genetic algorithm: NSGA-II
[J].DOI:10.1109/4235.996017 [本文引用: 2]
基于无重访NSGA-Ⅱ算法的配电网多目标重构
[J].
Multi-objective distribution network reconfiguration based on non-revisiting NSGA-II algorithm
[J].
基于NSGA-Ⅱ算法的ECPT系统PID参数寻优及输出稳压控制
[J].
Evolutionary multi-objective optimization of PID parameters for output voltage regulation in ECPT system based on NSGA-Ⅱ
[J].
基于剩余能量熵的供水管网可靠性优化设计
[J].
Reliability optimization design of water distribution system based on surplus energy entropy
[J].
低压开关槽式变换器多目标优化
[J].
Multi-objective optimization of switched-tank converter for low-voltage applications
[J].
Bacterial foraging optimization and adaptive version for economically optimum sitting, sizing and harmonic tuning orders setting of LC harmonic passive power filters in radial distribution systems with linear and nonlinear loads
[J].DOI:10.1016/j.asoc.2015.01.021 [本文引用: 1]
一种双直流输入多电平双Buck逆变器
[J].
A dual-DC-input multi-level dual-buck inverter
[J].
Multi-objective optimization design of a notch filter based on improved NSGA-II for conducted emissions
[J].DOI:10.1109/ACCESS.2020.2991576 [本文引用: 2]
A Family of dual-buck inverters with an extended low-voltage DC-input port for efficiency improvement based on dual-input pulsating voltage-source cells
[J].
高效非隔离单相并网MOSFET逆变器拓扑及控制策略
[J].DOI:10.3969/j.issn.1000-6753.2016.13.010 [本文引用: 1]
Topology and control strategy for high-efficient non-isolated single-phase grid-connected MOSFET inverter
[J].DOI:10.3969/j.issn.1000-6753.2016.13.010 [本文引用: 1]
三相四桥臂逆变器输出滤波器的优化设计
[J].
The optimal design of the output filter for three-phase four-leg inverter
[J].
基于虚拟电阻的PWM逆变器LC输出滤波器的研究
[J].
Research on PWM inverter LC output filter based on virtual resistance
[J].
Achievement scalarizing function sorting for strength Pareto evolutionary algorithm in many-objective optimization
[J].DOI:10.1007/s00521-020-05398-1 [本文引用: 1]