Development of a simplified bond stress–slip model for bonded FRP–concrete interfaces
1
2014
... 复合材料界面层的损伤破坏是导致其结构整体失效的重要因素之一. 在实际工程中,界面层的破坏可由多种荷载情况造成,如切向荷载、法向荷载以及复合型荷载. 复合材料界面层损伤破坏的力学机理复杂,破坏模式多样,因此建立能够准确描述界面破坏机理的理论模型是学术界和工程界共同关注的焦点[1-2]. ...
Progressive damage modeling of composite materials subjected to mixed mode cyclic loading using cohesive zone model
1
2020
... 复合材料界面层的损伤破坏是导致其结构整体失效的重要因素之一. 在实际工程中,界面层的破坏可由多种荷载情况造成,如切向荷载、法向荷载以及复合型荷载. 复合材料界面层损伤破坏的力学机理复杂,破坏模式多样,因此建立能够准确描述界面破坏机理的理论模型是学术界和工程界共同关注的焦点[1-2]. ...
Towards modeling of reinforced concrete members with externally bonded fiber-reinforced polymer composites
1
2003
... 通过试验准确分析并研究界面层的非线性损伤断裂机理有较大困难,因此理论模型分析和数值模拟成为研究界面层力学性能的重要手段. Wong等[3-5]采用内聚力模型(cohesive zone model, CZM)模拟界面层的非线性损伤破坏现象. 在假定损伤仅在界面内产生及扩展的前提下,内聚力模型将界面中的牵引力与界面上下表面的相对位移进行关联,以模拟界面层的黏结滑移关系[6]. 有关CZM的研究通常假定牵引力与相对位移间的损伤关系是弹性的[7],即牵引力在初始状态下呈弹性增长,直至达到起始损伤强度,损伤演化才开始,牵引力降低直至为零. 内聚力理论模型大多基于“牵引力准则”定义[8-9]. 在一维单一方向荷载下(法向或切向),CZM中牵引力与相对位移的本构关系相对简单直接,且过往研究中采用的单向本构较为类似[10]. 在复合加载下,CZM本构根据不同的损伤表达方式可分为独立(decoupled)损伤模型和耦合(coupled)损伤模型[11]. 独立损伤模型在各加载方向上的损伤标量相互独立[12],但此模型存在2个明显的缺陷: 1)某一方向上的损伤标量仅与该方向的加载历史有关,与其他方向上的加载历史无关2)界面的整体破坏通过特定的破坏准则控制,在数值模型实现过程中可能存在不连续性问题. 对于耦合损伤模型,一种常用的方法是对法向和切向的相对位移进行耦合,形成有效相对位移,进而计算单一损伤标量[7];另一种方法是耦合各向的能量,推导定义单一损伤标量. 例如Needleman等[8-9]通过对耦合的势能表达式进行关于各向位移差的偏导,得到切向和法向的牵引力,进而得到单一损伤标量. 此方法仅可用于相对位移单调增长且混合模态比恒定的状况下损伤的定义,在卸载及循环加载时并不适用. 为了解决这一问题,Nairn等[13]提出从“强度理论”角度重新定义破坏模型. 在复合加载下,基于强度理论的内聚力模型(strength theory cohesive zone model, ST-CZM)不需要定义特定的破坏准则,其混合模态破坏面由各方向上相互独立的强度模型决定,混合模态比在加载和卸载过程中随加载历史改变. ST-CZM的提出很好地解决了上述各种CZM模型中存在的问题,且ST-CZM在准脆性材料断裂模拟复合材料界面层损伤模拟中具有一定的应用前景. ...
Stress transfer and fracture propagation in different kinds of adhesive joints
0
2002
Fracturing behaviors of FRP-strengthened concrete structures
1
2003
... 通过试验准确分析并研究界面层的非线性损伤断裂机理有较大困难,因此理论模型分析和数值模拟成为研究界面层力学性能的重要手段. Wong等[3-5]采用内聚力模型(cohesive zone model, CZM)模拟界面层的非线性损伤破坏现象. 在假定损伤仅在界面内产生及扩展的前提下,内聚力模型将界面中的牵引力与界面上下表面的相对位移进行关联,以模拟界面层的黏结滑移关系[6]. 有关CZM的研究通常假定牵引力与相对位移间的损伤关系是弹性的[7],即牵引力在初始状态下呈弹性增长,直至达到起始损伤强度,损伤演化才开始,牵引力降低直至为零. 内聚力理论模型大多基于“牵引力准则”定义[8-9]. 在一维单一方向荷载下(法向或切向),CZM中牵引力与相对位移的本构关系相对简单直接,且过往研究中采用的单向本构较为类似[10]. 在复合加载下,CZM本构根据不同的损伤表达方式可分为独立(decoupled)损伤模型和耦合(coupled)损伤模型[11]. 独立损伤模型在各加载方向上的损伤标量相互独立[12],但此模型存在2个明显的缺陷: 1)某一方向上的损伤标量仅与该方向的加载历史有关,与其他方向上的加载历史无关2)界面的整体破坏通过特定的破坏准则控制,在数值模型实现过程中可能存在不连续性问题. 对于耦合损伤模型,一种常用的方法是对法向和切向的相对位移进行耦合,形成有效相对位移,进而计算单一损伤标量[7];另一种方法是耦合各向的能量,推导定义单一损伤标量. 例如Needleman等[8-9]通过对耦合的势能表达式进行关于各向位移差的偏导,得到切向和法向的牵引力,进而得到单一损伤标量. 此方法仅可用于相对位移单调增长且混合模态比恒定的状况下损伤的定义,在卸载及循环加载时并不适用. 为了解决这一问题,Nairn等[13]提出从“强度理论”角度重新定义破坏模型. 在复合加载下,基于强度理论的内聚力模型(strength theory cohesive zone model, ST-CZM)不需要定义特定的破坏准则,其混合模态破坏面由各方向上相互独立的强度模型决定,混合模态比在加载和卸载过程中随加载历史改变. ST-CZM的提出很好地解决了上述各种CZM模型中存在的问题,且ST-CZM在准脆性材料断裂模拟复合材料界面层损伤模拟中具有一定的应用前景. ...
A unified cohesive zone model for simulating adhesive failure of composite structures and its parameter identification
1
2017
... 通过试验准确分析并研究界面层的非线性损伤断裂机理有较大困难,因此理论模型分析和数值模拟成为研究界面层力学性能的重要手段. Wong等[3-5]采用内聚力模型(cohesive zone model, CZM)模拟界面层的非线性损伤破坏现象. 在假定损伤仅在界面内产生及扩展的前提下,内聚力模型将界面中的牵引力与界面上下表面的相对位移进行关联,以模拟界面层的黏结滑移关系[6]. 有关CZM的研究通常假定牵引力与相对位移间的损伤关系是弹性的[7],即牵引力在初始状态下呈弹性增长,直至达到起始损伤强度,损伤演化才开始,牵引力降低直至为零. 内聚力理论模型大多基于“牵引力准则”定义[8-9]. 在一维单一方向荷载下(法向或切向),CZM中牵引力与相对位移的本构关系相对简单直接,且过往研究中采用的单向本构较为类似[10]. 在复合加载下,CZM本构根据不同的损伤表达方式可分为独立(decoupled)损伤模型和耦合(coupled)损伤模型[11]. 独立损伤模型在各加载方向上的损伤标量相互独立[12],但此模型存在2个明显的缺陷: 1)某一方向上的损伤标量仅与该方向的加载历史有关,与其他方向上的加载历史无关2)界面的整体破坏通过特定的破坏准则控制,在数值模型实现过程中可能存在不连续性问题. 对于耦合损伤模型,一种常用的方法是对法向和切向的相对位移进行耦合,形成有效相对位移,进而计算单一损伤标量[7];另一种方法是耦合各向的能量,推导定义单一损伤标量. 例如Needleman等[8-9]通过对耦合的势能表达式进行关于各向位移差的偏导,得到切向和法向的牵引力,进而得到单一损伤标量. 此方法仅可用于相对位移单调增长且混合模态比恒定的状况下损伤的定义,在卸载及循环加载时并不适用. 为了解决这一问题,Nairn等[13]提出从“强度理论”角度重新定义破坏模型. 在复合加载下,基于强度理论的内聚力模型(strength theory cohesive zone model, ST-CZM)不需要定义特定的破坏准则,其混合模态破坏面由各方向上相互独立的强度模型决定,混合模态比在加载和卸载过程中随加载历史改变. ST-CZM的提出很好地解决了上述各种CZM模型中存在的问题,且ST-CZM在准脆性材料断裂模拟复合材料界面层损伤模拟中具有一定的应用前景. ...
Mixed-mode cohesive-zone models for fracture of an adhesively bonded polymer–matrix composite
2
2006
... 通过试验准确分析并研究界面层的非线性损伤断裂机理有较大困难,因此理论模型分析和数值模拟成为研究界面层力学性能的重要手段. Wong等[3-5]采用内聚力模型(cohesive zone model, CZM)模拟界面层的非线性损伤破坏现象. 在假定损伤仅在界面内产生及扩展的前提下,内聚力模型将界面中的牵引力与界面上下表面的相对位移进行关联,以模拟界面层的黏结滑移关系[6]. 有关CZM的研究通常假定牵引力与相对位移间的损伤关系是弹性的[7],即牵引力在初始状态下呈弹性增长,直至达到起始损伤强度,损伤演化才开始,牵引力降低直至为零. 内聚力理论模型大多基于“牵引力准则”定义[8-9]. 在一维单一方向荷载下(法向或切向),CZM中牵引力与相对位移的本构关系相对简单直接,且过往研究中采用的单向本构较为类似[10]. 在复合加载下,CZM本构根据不同的损伤表达方式可分为独立(decoupled)损伤模型和耦合(coupled)损伤模型[11]. 独立损伤模型在各加载方向上的损伤标量相互独立[12],但此模型存在2个明显的缺陷: 1)某一方向上的损伤标量仅与该方向的加载历史有关,与其他方向上的加载历史无关2)界面的整体破坏通过特定的破坏准则控制,在数值模型实现过程中可能存在不连续性问题. 对于耦合损伤模型,一种常用的方法是对法向和切向的相对位移进行耦合,形成有效相对位移,进而计算单一损伤标量[7];另一种方法是耦合各向的能量,推导定义单一损伤标量. 例如Needleman等[8-9]通过对耦合的势能表达式进行关于各向位移差的偏导,得到切向和法向的牵引力,进而得到单一损伤标量. 此方法仅可用于相对位移单调增长且混合模态比恒定的状况下损伤的定义,在卸载及循环加载时并不适用. 为了解决这一问题,Nairn等[13]提出从“强度理论”角度重新定义破坏模型. 在复合加载下,基于强度理论的内聚力模型(strength theory cohesive zone model, ST-CZM)不需要定义特定的破坏准则,其混合模态破坏面由各方向上相互独立的强度模型决定,混合模态比在加载和卸载过程中随加载历史改变. ST-CZM的提出很好地解决了上述各种CZM模型中存在的问题,且ST-CZM在准脆性材料断裂模拟复合材料界面层损伤模拟中具有一定的应用前景. ...
... [7];另一种方法是耦合各向的能量,推导定义单一损伤标量. 例如Needleman等[8-9]通过对耦合的势能表达式进行关于各向位移差的偏导,得到切向和法向的牵引力,进而得到单一损伤标量. 此方法仅可用于相对位移单调增长且混合模态比恒定的状况下损伤的定义,在卸载及循环加载时并不适用. 为了解决这一问题,Nairn等[13]提出从“强度理论”角度重新定义破坏模型. 在复合加载下,基于强度理论的内聚力模型(strength theory cohesive zone model, ST-CZM)不需要定义特定的破坏准则,其混合模态破坏面由各方向上相互独立的强度模型决定,混合模态比在加载和卸载过程中随加载历史改变. ST-CZM的提出很好地解决了上述各种CZM模型中存在的问题,且ST-CZM在准脆性材料断裂模拟复合材料界面层损伤模拟中具有一定的应用前景. ...
A continuum model for void nucleation by inclusion debonding
2
1987
... 通过试验准确分析并研究界面层的非线性损伤断裂机理有较大困难,因此理论模型分析和数值模拟成为研究界面层力学性能的重要手段. Wong等[3-5]采用内聚力模型(cohesive zone model, CZM)模拟界面层的非线性损伤破坏现象. 在假定损伤仅在界面内产生及扩展的前提下,内聚力模型将界面中的牵引力与界面上下表面的相对位移进行关联,以模拟界面层的黏结滑移关系[6]. 有关CZM的研究通常假定牵引力与相对位移间的损伤关系是弹性的[7],即牵引力在初始状态下呈弹性增长,直至达到起始损伤强度,损伤演化才开始,牵引力降低直至为零. 内聚力理论模型大多基于“牵引力准则”定义[8-9]. 在一维单一方向荷载下(法向或切向),CZM中牵引力与相对位移的本构关系相对简单直接,且过往研究中采用的单向本构较为类似[10]. 在复合加载下,CZM本构根据不同的损伤表达方式可分为独立(decoupled)损伤模型和耦合(coupled)损伤模型[11]. 独立损伤模型在各加载方向上的损伤标量相互独立[12],但此模型存在2个明显的缺陷: 1)某一方向上的损伤标量仅与该方向的加载历史有关,与其他方向上的加载历史无关2)界面的整体破坏通过特定的破坏准则控制,在数值模型实现过程中可能存在不连续性问题. 对于耦合损伤模型,一种常用的方法是对法向和切向的相对位移进行耦合,形成有效相对位移,进而计算单一损伤标量[7];另一种方法是耦合各向的能量,推导定义单一损伤标量. 例如Needleman等[8-9]通过对耦合的势能表达式进行关于各向位移差的偏导,得到切向和法向的牵引力,进而得到单一损伤标量. 此方法仅可用于相对位移单调增长且混合模态比恒定的状况下损伤的定义,在卸载及循环加载时并不适用. 为了解决这一问题,Nairn等[13]提出从“强度理论”角度重新定义破坏模型. 在复合加载下,基于强度理论的内聚力模型(strength theory cohesive zone model, ST-CZM)不需要定义特定的破坏准则,其混合模态破坏面由各方向上相互独立的强度模型决定,混合模态比在加载和卸载过程中随加载历史改变. ST-CZM的提出很好地解决了上述各种CZM模型中存在的问题,且ST-CZM在准脆性材料断裂模拟复合材料界面层损伤模拟中具有一定的应用前景. ...
... [8-9]通过对耦合的势能表达式进行关于各向位移差的偏导,得到切向和法向的牵引力,进而得到单一损伤标量. 此方法仅可用于相对位移单调增长且混合模态比恒定的状况下损伤的定义,在卸载及循环加载时并不适用. 为了解决这一问题,Nairn等[13]提出从“强度理论”角度重新定义破坏模型. 在复合加载下,基于强度理论的内聚力模型(strength theory cohesive zone model, ST-CZM)不需要定义特定的破坏准则,其混合模态破坏面由各方向上相互独立的强度模型决定,混合模态比在加载和卸载过程中随加载历史改变. ST-CZM的提出很好地解决了上述各种CZM模型中存在的问题,且ST-CZM在准脆性材料断裂模拟复合材料界面层损伤模拟中具有一定的应用前景. ...
Void nucleation by inclusion debonding in a crystal matrix
2
1999
... 通过试验准确分析并研究界面层的非线性损伤断裂机理有较大困难,因此理论模型分析和数值模拟成为研究界面层力学性能的重要手段. Wong等[3-5]采用内聚力模型(cohesive zone model, CZM)模拟界面层的非线性损伤破坏现象. 在假定损伤仅在界面内产生及扩展的前提下,内聚力模型将界面中的牵引力与界面上下表面的相对位移进行关联,以模拟界面层的黏结滑移关系[6]. 有关CZM的研究通常假定牵引力与相对位移间的损伤关系是弹性的[7],即牵引力在初始状态下呈弹性增长,直至达到起始损伤强度,损伤演化才开始,牵引力降低直至为零. 内聚力理论模型大多基于“牵引力准则”定义[8-9]. 在一维单一方向荷载下(法向或切向),CZM中牵引力与相对位移的本构关系相对简单直接,且过往研究中采用的单向本构较为类似[10]. 在复合加载下,CZM本构根据不同的损伤表达方式可分为独立(decoupled)损伤模型和耦合(coupled)损伤模型[11]. 独立损伤模型在各加载方向上的损伤标量相互独立[12],但此模型存在2个明显的缺陷: 1)某一方向上的损伤标量仅与该方向的加载历史有关,与其他方向上的加载历史无关2)界面的整体破坏通过特定的破坏准则控制,在数值模型实现过程中可能存在不连续性问题. 对于耦合损伤模型,一种常用的方法是对法向和切向的相对位移进行耦合,形成有效相对位移,进而计算单一损伤标量[7];另一种方法是耦合各向的能量,推导定义单一损伤标量. 例如Needleman等[8-9]通过对耦合的势能表达式进行关于各向位移差的偏导,得到切向和法向的牵引力,进而得到单一损伤标量. 此方法仅可用于相对位移单调增长且混合模态比恒定的状况下损伤的定义,在卸载及循环加载时并不适用. 为了解决这一问题,Nairn等[13]提出从“强度理论”角度重新定义破坏模型. 在复合加载下,基于强度理论的内聚力模型(strength theory cohesive zone model, ST-CZM)不需要定义特定的破坏准则,其混合模态破坏面由各方向上相互独立的强度模型决定,混合模态比在加载和卸载过程中随加载历史改变. ST-CZM的提出很好地解决了上述各种CZM模型中存在的问题,且ST-CZM在准脆性材料断裂模拟复合材料界面层损伤模拟中具有一定的应用前景. ...
... -9]通过对耦合的势能表达式进行关于各向位移差的偏导,得到切向和法向的牵引力,进而得到单一损伤标量. 此方法仅可用于相对位移单调增长且混合模态比恒定的状况下损伤的定义,在卸载及循环加载时并不适用. 为了解决这一问题,Nairn等[13]提出从“强度理论”角度重新定义破坏模型. 在复合加载下,基于强度理论的内聚力模型(strength theory cohesive zone model, ST-CZM)不需要定义特定的破坏准则,其混合模态破坏面由各方向上相互独立的强度模型决定,混合模态比在加载和卸载过程中随加载历史改变. ST-CZM的提出很好地解决了上述各种CZM模型中存在的问题,且ST-CZM在准脆性材料断裂模拟复合材料界面层损伤模拟中具有一定的应用前景. ...
Coupled cohesive zone models for mixed-mode fracture: a comparative study
1
2015
... 通过试验准确分析并研究界面层的非线性损伤断裂机理有较大困难,因此理论模型分析和数值模拟成为研究界面层力学性能的重要手段. Wong等[3-5]采用内聚力模型(cohesive zone model, CZM)模拟界面层的非线性损伤破坏现象. 在假定损伤仅在界面内产生及扩展的前提下,内聚力模型将界面中的牵引力与界面上下表面的相对位移进行关联,以模拟界面层的黏结滑移关系[6]. 有关CZM的研究通常假定牵引力与相对位移间的损伤关系是弹性的[7],即牵引力在初始状态下呈弹性增长,直至达到起始损伤强度,损伤演化才开始,牵引力降低直至为零. 内聚力理论模型大多基于“牵引力准则”定义[8-9]. 在一维单一方向荷载下(法向或切向),CZM中牵引力与相对位移的本构关系相对简单直接,且过往研究中采用的单向本构较为类似[10]. 在复合加载下,CZM本构根据不同的损伤表达方式可分为独立(decoupled)损伤模型和耦合(coupled)损伤模型[11]. 独立损伤模型在各加载方向上的损伤标量相互独立[12],但此模型存在2个明显的缺陷: 1)某一方向上的损伤标量仅与该方向的加载历史有关,与其他方向上的加载历史无关2)界面的整体破坏通过特定的破坏准则控制,在数值模型实现过程中可能存在不连续性问题. 对于耦合损伤模型,一种常用的方法是对法向和切向的相对位移进行耦合,形成有效相对位移,进而计算单一损伤标量[7];另一种方法是耦合各向的能量,推导定义单一损伤标量. 例如Needleman等[8-9]通过对耦合的势能表达式进行关于各向位移差的偏导,得到切向和法向的牵引力,进而得到单一损伤标量. 此方法仅可用于相对位移单调增长且混合模态比恒定的状况下损伤的定义,在卸载及循环加载时并不适用. 为了解决这一问题,Nairn等[13]提出从“强度理论”角度重新定义破坏模型. 在复合加载下,基于强度理论的内聚力模型(strength theory cohesive zone model, ST-CZM)不需要定义特定的破坏准则,其混合模态破坏面由各方向上相互独立的强度模型决定,混合模态比在加载和卸载过程中随加载历史改变. ST-CZM的提出很好地解决了上述各种CZM模型中存在的问题,且ST-CZM在准脆性材料断裂模拟复合材料界面层损伤模拟中具有一定的应用前景. ...
Mixed-mode fracture analyses of plastically-deforming adhesive joints
1
2001
... 通过试验准确分析并研究界面层的非线性损伤断裂机理有较大困难,因此理论模型分析和数值模拟成为研究界面层力学性能的重要手段. Wong等[3-5]采用内聚力模型(cohesive zone model, CZM)模拟界面层的非线性损伤破坏现象. 在假定损伤仅在界面内产生及扩展的前提下,内聚力模型将界面中的牵引力与界面上下表面的相对位移进行关联,以模拟界面层的黏结滑移关系[6]. 有关CZM的研究通常假定牵引力与相对位移间的损伤关系是弹性的[7],即牵引力在初始状态下呈弹性增长,直至达到起始损伤强度,损伤演化才开始,牵引力降低直至为零. 内聚力理论模型大多基于“牵引力准则”定义[8-9]. 在一维单一方向荷载下(法向或切向),CZM中牵引力与相对位移的本构关系相对简单直接,且过往研究中采用的单向本构较为类似[10]. 在复合加载下,CZM本构根据不同的损伤表达方式可分为独立(decoupled)损伤模型和耦合(coupled)损伤模型[11]. 独立损伤模型在各加载方向上的损伤标量相互独立[12],但此模型存在2个明显的缺陷: 1)某一方向上的损伤标量仅与该方向的加载历史有关,与其他方向上的加载历史无关2)界面的整体破坏通过特定的破坏准则控制,在数值模型实现过程中可能存在不连续性问题. 对于耦合损伤模型,一种常用的方法是对法向和切向的相对位移进行耦合,形成有效相对位移,进而计算单一损伤标量[7];另一种方法是耦合各向的能量,推导定义单一损伤标量. 例如Needleman等[8-9]通过对耦合的势能表达式进行关于各向位移差的偏导,得到切向和法向的牵引力,进而得到单一损伤标量. 此方法仅可用于相对位移单调增长且混合模态比恒定的状况下损伤的定义,在卸载及循环加载时并不适用. 为了解决这一问题,Nairn等[13]提出从“强度理论”角度重新定义破坏模型. 在复合加载下,基于强度理论的内聚力模型(strength theory cohesive zone model, ST-CZM)不需要定义特定的破坏准则,其混合模态破坏面由各方向上相互独立的强度模型决定,混合模态比在加载和卸载过程中随加载历史改变. ST-CZM的提出很好地解决了上述各种CZM模型中存在的问题,且ST-CZM在准脆性材料断裂模拟复合材料界面层损伤模拟中具有一定的应用前景. ...
A consistent energy-based cohesive zone model to simulate delamination between differently oriented plies
1
2022
... 通过试验准确分析并研究界面层的非线性损伤断裂机理有较大困难,因此理论模型分析和数值模拟成为研究界面层力学性能的重要手段. Wong等[3-5]采用内聚力模型(cohesive zone model, CZM)模拟界面层的非线性损伤破坏现象. 在假定损伤仅在界面内产生及扩展的前提下,内聚力模型将界面中的牵引力与界面上下表面的相对位移进行关联,以模拟界面层的黏结滑移关系[6]. 有关CZM的研究通常假定牵引力与相对位移间的损伤关系是弹性的[7],即牵引力在初始状态下呈弹性增长,直至达到起始损伤强度,损伤演化才开始,牵引力降低直至为零. 内聚力理论模型大多基于“牵引力准则”定义[8-9]. 在一维单一方向荷载下(法向或切向),CZM中牵引力与相对位移的本构关系相对简单直接,且过往研究中采用的单向本构较为类似[10]. 在复合加载下,CZM本构根据不同的损伤表达方式可分为独立(decoupled)损伤模型和耦合(coupled)损伤模型[11]. 独立损伤模型在各加载方向上的损伤标量相互独立[12],但此模型存在2个明显的缺陷: 1)某一方向上的损伤标量仅与该方向的加载历史有关,与其他方向上的加载历史无关2)界面的整体破坏通过特定的破坏准则控制,在数值模型实现过程中可能存在不连续性问题. 对于耦合损伤模型,一种常用的方法是对法向和切向的相对位移进行耦合,形成有效相对位移,进而计算单一损伤标量[7];另一种方法是耦合各向的能量,推导定义单一损伤标量. 例如Needleman等[8-9]通过对耦合的势能表达式进行关于各向位移差的偏导,得到切向和法向的牵引力,进而得到单一损伤标量. 此方法仅可用于相对位移单调增长且混合模态比恒定的状况下损伤的定义,在卸载及循环加载时并不适用. 为了解决这一问题,Nairn等[13]提出从“强度理论”角度重新定义破坏模型. 在复合加载下,基于强度理论的内聚力模型(strength theory cohesive zone model, ST-CZM)不需要定义特定的破坏准则,其混合模态破坏面由各方向上相互独立的强度模型决定,混合模态比在加载和卸载过程中随加载历史改变. ST-CZM的提出很好地解决了上述各种CZM模型中存在的问题,且ST-CZM在准脆性材料断裂模拟复合材料界面层损伤模拟中具有一定的应用前景. ...
A re-evaluation of mixed-mode cohesive zone modeling based on strength concepts instead of traction laws
4
2021
... 通过试验准确分析并研究界面层的非线性损伤断裂机理有较大困难,因此理论模型分析和数值模拟成为研究界面层力学性能的重要手段. Wong等[3-5]采用内聚力模型(cohesive zone model, CZM)模拟界面层的非线性损伤破坏现象. 在假定损伤仅在界面内产生及扩展的前提下,内聚力模型将界面中的牵引力与界面上下表面的相对位移进行关联,以模拟界面层的黏结滑移关系[6]. 有关CZM的研究通常假定牵引力与相对位移间的损伤关系是弹性的[7],即牵引力在初始状态下呈弹性增长,直至达到起始损伤强度,损伤演化才开始,牵引力降低直至为零. 内聚力理论模型大多基于“牵引力准则”定义[8-9]. 在一维单一方向荷载下(法向或切向),CZM中牵引力与相对位移的本构关系相对简单直接,且过往研究中采用的单向本构较为类似[10]. 在复合加载下,CZM本构根据不同的损伤表达方式可分为独立(decoupled)损伤模型和耦合(coupled)损伤模型[11]. 独立损伤模型在各加载方向上的损伤标量相互独立[12],但此模型存在2个明显的缺陷: 1)某一方向上的损伤标量仅与该方向的加载历史有关,与其他方向上的加载历史无关2)界面的整体破坏通过特定的破坏准则控制,在数值模型实现过程中可能存在不连续性问题. 对于耦合损伤模型,一种常用的方法是对法向和切向的相对位移进行耦合,形成有效相对位移,进而计算单一损伤标量[7];另一种方法是耦合各向的能量,推导定义单一损伤标量. 例如Needleman等[8-9]通过对耦合的势能表达式进行关于各向位移差的偏导,得到切向和法向的牵引力,进而得到单一损伤标量. 此方法仅可用于相对位移单调增长且混合模态比恒定的状况下损伤的定义,在卸载及循环加载时并不适用. 为了解决这一问题,Nairn等[13]提出从“强度理论”角度重新定义破坏模型. 在复合加载下,基于强度理论的内聚力模型(strength theory cohesive zone model, ST-CZM)不需要定义特定的破坏准则,其混合模态破坏面由各方向上相互独立的强度模型决定,混合模态比在加载和卸载过程中随加载历史改变. ST-CZM的提出很好地解决了上述各种CZM模型中存在的问题,且ST-CZM在准脆性材料断裂模拟复合材料界面层损伤模拟中具有一定的应用前景. ...
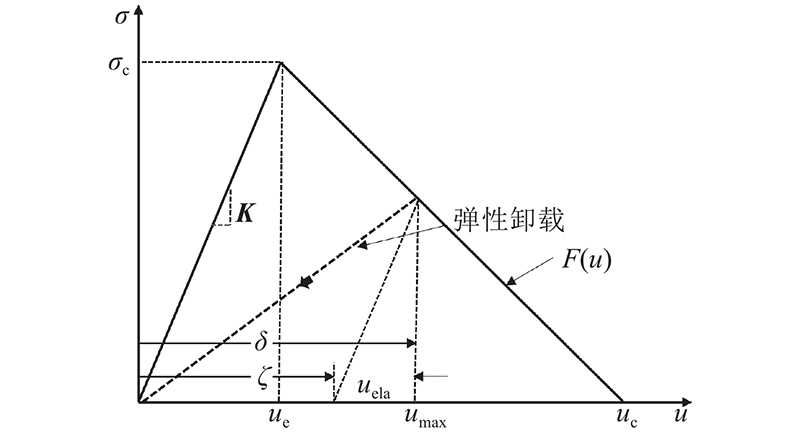
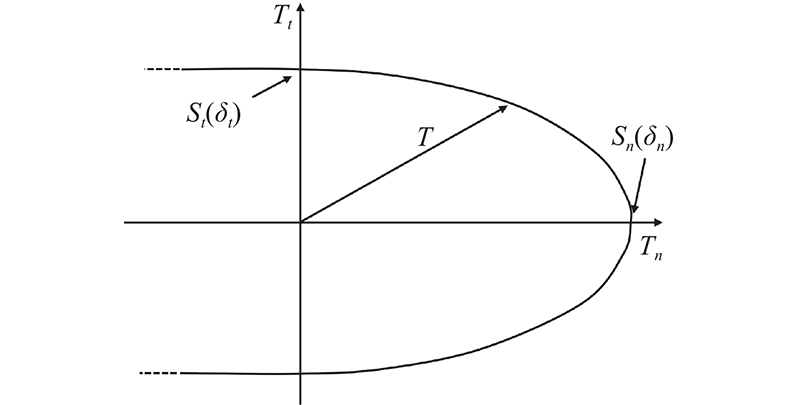
... 一维单一方向荷载下 $ F(u) $与 $ S(\delta ) $仅存在语义表达上的差异,但在混合模态推导过程中,二者差异显著,且区分F(u)与 $ S(\delta ) $的定义非常重要[13]. 在复合加载状态下,此推导过程须分别定义代表法向和切向的独立强度[15]. 牵引力矩阵 $ {\boldsymbol{T}} $和应变能矩阵 $ {\boldsymbol{U}} $关于相对位移矩阵、损伤矩阵的表达式为 ...
... 将式(21)、(22)分别以泰勒级数展开,在增量中仅保留一阶项[13],分别得到 ...
... 式中: $ \delta _{\rm{m}}^{\rm{f}} $为混合模态相对位移[20], $ \delta _{\rm{m}}^{\max } $为混合模态破坏位移, $ \delta _{\rm{m}}^{\rm{o}} $为混合模态损伤起始位移. 由式可知,只有当 $ \delta _{\rm{m}}^{\max }/\delta _{\rm{m}}^{\rm{o}} $不变时,混合模态比的变化才不会影响损伤的定义. 否则当损伤产生时,刚度矩阵出现突变[13]. ST-CZM没有这个缺陷,表明ST-CZM相较自带单元拥有更灵活的耦合方式. ...
基于内聚力理论的二维二次界面单元在ABAQUS中的UEL程序实现
1
2019
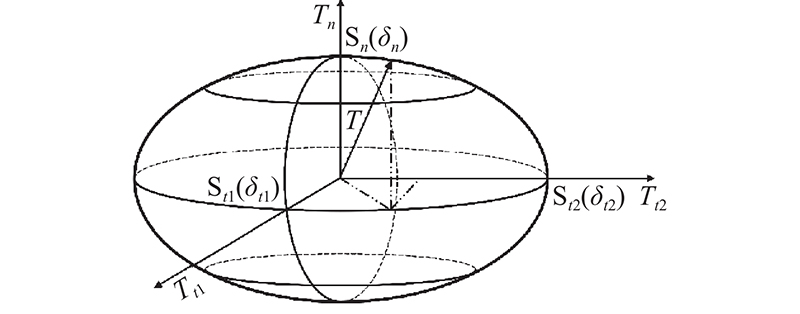
... 本研究拓展二维强度理论,得到基于强度理论的三维内聚力模型. 在此基础上,使用Abaqus平台的用户单元子程序(user-defined element, UEL)[14]进行有限元实现. 建立3个验证模型,模拟多种破坏模式,验证模型的有效性和准确性,将STM-CZM应用于FRP-混凝土试件的单剪试验和四点弯曲梁试验数值模型中,模拟现实试验的复杂情况. ...
基于内聚力理论的二维二次界面单元在ABAQUS中的UEL程序实现
1
2019
... 本研究拓展二维强度理论,得到基于强度理论的三维内聚力模型. 在此基础上,使用Abaqus平台的用户单元子程序(user-defined element, UEL)[14]进行有限元实现. 建立3个验证模型,模拟多种破坏模式,验证模型的有效性和准确性,将STM-CZM应用于FRP-混凝土试件的单剪试验和四点弯曲梁试验数值模型中,模拟现实试验的复杂情况. ...
相场断裂模型分步算法在ABAQUS中的实现
1
2016
... 一维单一方向荷载下 $ F(u) $与 $ S(\delta ) $仅存在语义表达上的差异,但在混合模态推导过程中,二者差异显著,且区分F(u)与 $ S(\delta ) $的定义非常重要[13]. 在复合加载状态下,此推导过程须分别定义代表法向和切向的独立强度[15]. 牵引力矩阵 $ {\boldsymbol{T}} $和应变能矩阵 $ {\boldsymbol{U}} $关于相对位移矩阵、损伤矩阵的表达式为 ...
相场断裂模型分步算法在ABAQUS中的实现
1
2016
... 一维单一方向荷载下 $ F(u) $与 $ S(\delta ) $仅存在语义表达上的差异,但在混合模态推导过程中,二者差异显著,且区分F(u)与 $ S(\delta ) $的定义非常重要[13]. 在复合加载状态下,此推导过程须分别定义代表法向和切向的独立强度[15]. 牵引力矩阵 $ {\boldsymbol{T}} $和应变能矩阵 $ {\boldsymbol{U}} $关于相对位移矩阵、损伤矩阵的表达式为 ...
Application of scaled boundary finite element method for delamination analysis of composite laminates using cohesive zone modelling
4
2020
... 经典验证模型分别为Garg等[16]的双悬臂梁模型(double cantilever beam, DCB)、固定比率混合模型(fixed ratio mixed mode, FRMM)以及Park等[17]的混合模态弯曲模型(mixed mode bending, MMB). 将ST-CZM与传统双线性内聚力模型及试验数据进行对比. 内聚力单元的界面参数如表1[18]所示. 表中, ${\sigma _{\rm{I}}}$为法向峰值应力, ${u_{\rm{eI}}}$为法向损伤起始位移, ${K_{\rm{I}}}$为法向初始刚度, ${G_{\rm{I}}}$为法向断裂能, ${\sigma _{\rm{II}}}$为切向峰值应力, ${u_{\rm{eII}}}$为切向损伤起始位移, ${K_{\rm{II}}}$为切向初始刚度, ${G_{\rm{II}}}$为切向断裂能. 验证算例模型的各项材料参数如表2所示[16]. 表中, ${E_{{\text{11}}}}$、 ${E_{{\text{22}}}}$、 ${E_{{\text{33}}}}$分别为3个方向的弹性模量, ${G_{{\text{12}}}}$、 ${G_{{\text{13}}}}$、 ${G_{{\text{23}}}}$分别为3个方向的切变模量, ${v_{{\text{12}}}}$、 ${v_{{\text{13}}}}$、 ${v_{{\text{23}}}}$分别为3个方向的泊松比. ...
... [16]. 表中, ${E_{{\text{11}}}}$、 ${E_{{\text{22}}}}$、 ${E_{{\text{33}}}}$分别为3个方向的弹性模量, ${G_{{\text{12}}}}$、 ${G_{{\text{13}}}}$、 ${G_{{\text{23}}}}$分别为3个方向的切变模量, ${v_{{\text{12}}}}$、 ${v_{{\text{13}}}}$、 ${v_{{\text{23}}}}$分别为3个方向的泊松比. ...
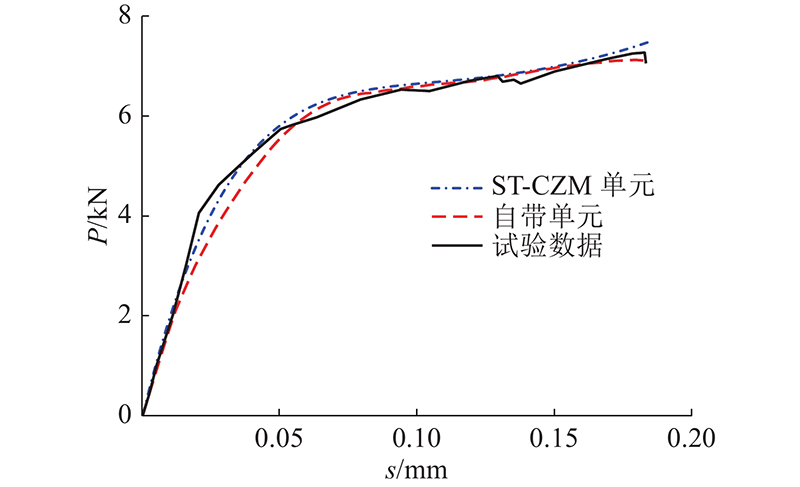
... DCB数值模型试件尺寸如图4所示,数值模型边界条件按试验实际取用[16]. 如图5所示为DCB采用ST-CZM计算的数值结果与Abaqus自带双线性内聚力单元结果、试验数据的对比图. 图中, ${P}$为荷载, ${s}$为张开位移,DCB模型计算结果使用自带单元模拟,所得峰值相较于实验结果误差为4.44%,ST-CZM相较于实验结果误差为0.41%. 明显ST-CZM对峰值的预测更接近试验的实际情况,其对损伤阶段的预测符合试验的破坏模式. ...
... FRMM的几何尺寸与DCB的几何尺寸相同,边界条件不同. FRMM上端受到荷载作用,下端不受约束. FRMM的边界条件按试验实际取用,如图6所示[16]. 如图7所示为FRMM采用ST-CZM计算的数值结果与自带双线性内聚力单元以及LS-DYNA[19]模拟结果的对比图. 可以看出,3种结果破坏模式相近,三者峰值强度相差不超过2 N,但LS-DYNA计算得到的结果曲线与其余2条相差较大. 原因是LS-DYNA求解采用显示动力学算法模拟静态加载时得到的结果,因此受加载速率影响较大[19]. ...
Computational implementation of the PPR potential-based cohesive model in ABAQUS: educational perspective
4
2012
... 经典验证模型分别为Garg等[16]的双悬臂梁模型(double cantilever beam, DCB)、固定比率混合模型(fixed ratio mixed mode, FRMM)以及Park等[17]的混合模态弯曲模型(mixed mode bending, MMB). 将ST-CZM与传统双线性内聚力模型及试验数据进行对比. 内聚力单元的界面参数如表1[18]所示. 表中, ${\sigma _{\rm{I}}}$为法向峰值应力, ${u_{\rm{eI}}}$为法向损伤起始位移, ${K_{\rm{I}}}$为法向初始刚度, ${G_{\rm{I}}}$为法向断裂能, ${\sigma _{\rm{II}}}$为切向峰值应力, ${u_{\rm{eII}}}$为切向损伤起始位移, ${K_{\rm{II}}}$为切向初始刚度, ${G_{\rm{II}}}$为切向断裂能. 验证算例模型的各项材料参数如表2所示[16]. 表中, ${E_{{\text{11}}}}$、 ${E_{{\text{22}}}}$、 ${E_{{\text{33}}}}$分别为3个方向的弹性模量, ${G_{{\text{12}}}}$、 ${G_{{\text{13}}}}$、 ${G_{{\text{23}}}}$分别为3个方向的切变模量, ${v_{{\text{12}}}}$、 ${v_{{\text{13}}}}$、 ${v_{{\text{23}}}}$分别为3个方向的泊松比. ...
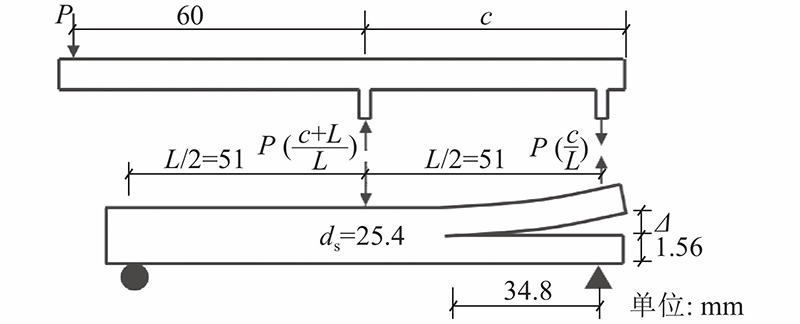
... MMB几何尺寸及边界条件如图8所示[17]. 图中, $\varDelta $为开口位移;L为试件的长度;L=102 mm;单梁高1.56 mm;ds为试件厚度,ds=25.4 mm. 如图9所示为采用ST-CZM计算的数值结果与基于势能的内聚单元模型(potential-based cohesive zone model, PPR)单元[17]的结果、解析解的对比图,其中解析解基于线性梁理论以及线弹性断裂力学得到. 可以看出,MMB计算结果中使用PPR单元所得峰值相较于解析解误差为4.07%,自带单元相较于解析解误差为11.35%,ST-CZM相较于解析解误差为3.1%. ST-CZM对峰值的预测与Park等[17]的结果相近,且破坏模式相同,损伤阶段结果与解析解符合较好. 当改变MMB的界面单元参数时(如修改 ${\sigma _{\rm{I}}}$=80 MPa),使用Abaqus自带CZM单元无法收敛. 原因在于加载过程中MMB的混合模态比是变化的,自带单元很难灵活应对. 自带单元对损伤的定义式[20]为 ...
... [17]的结果、解析解的对比图,其中解析解基于线性梁理论以及线弹性断裂力学得到. 可以看出,MMB计算结果中使用PPR单元所得峰值相较于解析解误差为4.07%,自带单元相较于解析解误差为11.35%,ST-CZM相较于解析解误差为3.1%. ST-CZM对峰值的预测与Park等[17]的结果相近,且破坏模式相同,损伤阶段结果与解析解符合较好. 当改变MMB的界面单元参数时(如修改 ${\sigma _{\rm{I}}}$=80 MPa),使用Abaqus自带CZM单元无法收敛. 原因在于加载过程中MMB的混合模态比是变化的,自带单元很难灵活应对. 自带单元对损伤的定义式[20]为 ...
... [17]的结果相近,且破坏模式相同,损伤阶段结果与解析解符合较好. 当改变MMB的界面单元参数时(如修改 ${\sigma _{\rm{I}}}$=80 MPa),使用Abaqus自带CZM单元无法收敛. 原因在于加载过程中MMB的混合模态比是变化的,自带单元很难灵活应对. 自带单元对损伤的定义式[20]为 ...
Mixed-mode bending method for delamination testing
3
1990
... 经典验证模型分别为Garg等[16]的双悬臂梁模型(double cantilever beam, DCB)、固定比率混合模型(fixed ratio mixed mode, FRMM)以及Park等[17]的混合模态弯曲模型(mixed mode bending, MMB). 将ST-CZM与传统双线性内聚力模型及试验数据进行对比. 内聚力单元的界面参数如表1[18]所示. 表中, ${\sigma _{\rm{I}}}$为法向峰值应力, ${u_{\rm{eI}}}$为法向损伤起始位移, ${K_{\rm{I}}}$为法向初始刚度, ${G_{\rm{I}}}$为法向断裂能, ${\sigma _{\rm{II}}}$为切向峰值应力, ${u_{\rm{eII}}}$为切向损伤起始位移, ${K_{\rm{II}}}$为切向初始刚度, ${G_{\rm{II}}}$为切向断裂能. 验证算例模型的各项材料参数如表2所示[16]. 表中, ${E_{{\text{11}}}}$、 ${E_{{\text{22}}}}$、 ${E_{{\text{33}}}}$分别为3个方向的弹性模量, ${G_{{\text{12}}}}$、 ${G_{{\text{13}}}}$、 ${G_{{\text{23}}}}$分别为3个方向的切变模量, ${v_{{\text{12}}}}$、 ${v_{{\text{13}}}}$、 ${v_{{\text{23}}}}$分别为3个方向的泊松比. ...
... 基于强度理论的内聚力模型验证算例黏结单元参数[18] ...
... Material parameters for cohesive elements in verification models for strength theory cohesive zone model[18] ...
Cohesive zone length in numerical simulations of composite delamination
2
2008
... FRMM的几何尺寸与DCB的几何尺寸相同,边界条件不同. FRMM上端受到荷载作用,下端不受约束. FRMM的边界条件按试验实际取用,如图6所示[16]. 如图7所示为FRMM采用ST-CZM计算的数值结果与自带双线性内聚力单元以及LS-DYNA[19]模拟结果的对比图. 可以看出,3种结果破坏模式相近,三者峰值强度相差不超过2 N,但LS-DYNA计算得到的结果曲线与其余2条相差较大. 原因是LS-DYNA求解采用显示动力学算法模拟静态加载时得到的结果,因此受加载速率影响较大[19]. ...
... [19]. ...
2
... MMB几何尺寸及边界条件如图8所示[17]. 图中, $\varDelta $为开口位移;L为试件的长度;L=102 mm;单梁高1.56 mm;ds为试件厚度,ds=25.4 mm. 如图9所示为采用ST-CZM计算的数值结果与基于势能的内聚单元模型(potential-based cohesive zone model, PPR)单元[17]的结果、解析解的对比图,其中解析解基于线性梁理论以及线弹性断裂力学得到. 可以看出,MMB计算结果中使用PPR单元所得峰值相较于解析解误差为4.07%,自带单元相较于解析解误差为11.35%,ST-CZM相较于解析解误差为3.1%. ST-CZM对峰值的预测与Park等[17]的结果相近,且破坏模式相同,损伤阶段结果与解析解符合较好. 当改变MMB的界面单元参数时(如修改 ${\sigma _{\rm{I}}}$=80 MPa),使用Abaqus自带CZM单元无法收敛. 原因在于加载过程中MMB的混合模态比是变化的,自带单元很难灵活应对. 自带单元对损伤的定义式[20]为 ...
... 式中: $ \delta _{\rm{m}}^{\rm{f}} $为混合模态相对位移[20], $ \delta _{\rm{m}}^{\max } $为混合模态破坏位移, $ \delta _{\rm{m}}^{\rm{o}} $为混合模态损伤起始位移. 由式可知,只有当 $ \delta _{\rm{m}}^{\max }/\delta _{\rm{m}}^{\rm{o}} $不变时,混合模态比的变化才不会影响损伤的定义. 否则当损伤产生时,刚度矩阵出现突变[13]. ST-CZM没有这个缺陷,表明ST-CZM相较自带单元拥有更灵活的耦合方式. ...
Overcoming the convergence difficulty of cohesive zone models through a Newton-Raphson modification technique
1
2020
... 纤维增强复合材料(fiber reinforced polymer, FRP)加固钢筋混凝土结构的技术应用范围广、研究历史长、破坏模式复杂,与黏结界面损伤力学模型的研究联系紧密[21-22]. 选取几组典型的FRP-混凝土试验作为实用算例,验证ST-CZM的可靠性. 所建单剪试验数值模型及四点弯曲梁试验数值模型分别代表素混凝土和钢筋混凝土试件试验,参照Zhang等[23-24]的试验进行结果对比. 采用的界面参数如表3所示. ...
Cohesive zone model prediction of debonding failure in CFRP-to-steel bonded interface with a ductile adhesive
1
2022
... 纤维增强复合材料(fiber reinforced polymer, FRP)加固钢筋混凝土结构的技术应用范围广、研究历史长、破坏模式复杂,与黏结界面损伤力学模型的研究联系紧密[21-22]. 选取几组典型的FRP-混凝土试验作为实用算例,验证ST-CZM的可靠性. 所建单剪试验数值模型及四点弯曲梁试验数值模型分别代表素混凝土和钢筋混凝土试件试验,参照Zhang等[23-24]的试验进行结果对比. 采用的界面参数如表3所示. ...
Experimental and numerical investigation of debonding process of the FRP plate-concrete interface
3
2019
... 纤维增强复合材料(fiber reinforced polymer, FRP)加固钢筋混凝土结构的技术应用范围广、研究历史长、破坏模式复杂,与黏结界面损伤力学模型的研究联系紧密[21-22]. 选取几组典型的FRP-混凝土试验作为实用算例,验证ST-CZM的可靠性. 所建单剪试验数值模型及四点弯曲梁试验数值模型分别代表素混凝土和钢筋混凝土试件试验,参照Zhang等[23-24]的试验进行结果对比. 采用的界面参数如表3所示. ...
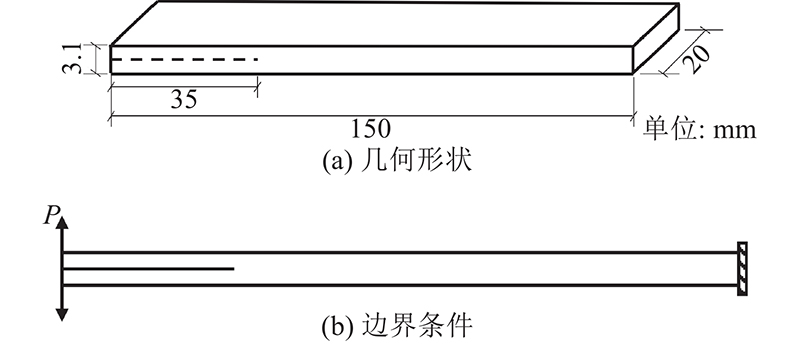
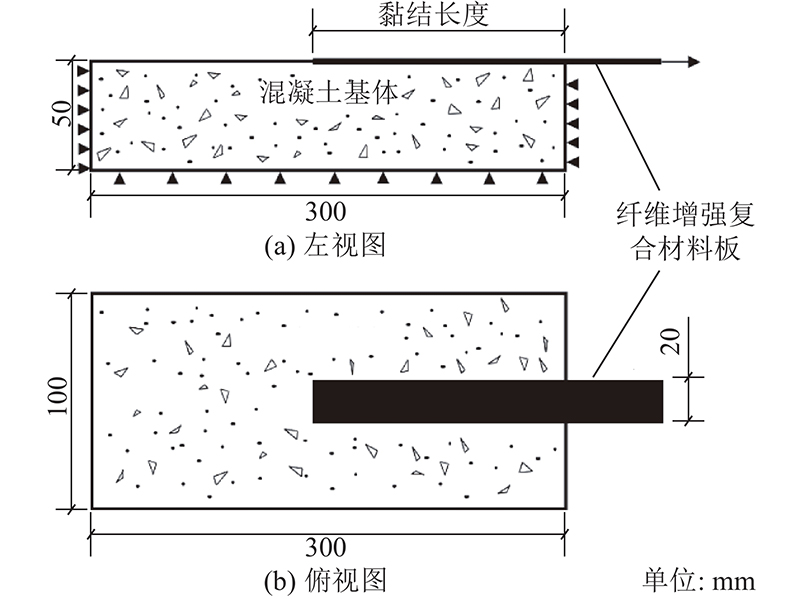
... 剪切拉拔是常见的研究FRP-混凝土界面的试验方法[25-26]. 选取单剪试验结果[23]与数值模型对照,以确定ST-CZM在单一模态下的可靠性. 素混凝土数值模型长300 mm,宽100 mm,高50 mm. 标准测试得到的试件抗压强度为29.3 MPa. FRP板数值模型厚度为2 mm, FRP试件测试得到的拉伸强度为4.1 GPa,弹性模量为256 GPa,黏结长度为180 mm,黏结宽度为20 mm. 文献[27]~[29]中的试验也采用类似试件. 试件几何尺寸如图10所示,数值模型一切边界条件按照试验实际取用[23]. ...
... [23]. ...
Effect of load distribution on IC debonding in FRP-strengthened RC beams: full-scale experiments
10
2018
... 纤维增强复合材料(fiber reinforced polymer, FRP)加固钢筋混凝土结构的技术应用范围广、研究历史长、破坏模式复杂,与黏结界面损伤力学模型的研究联系紧密[21-22]. 选取几组典型的FRP-混凝土试验作为实用算例,验证ST-CZM的可靠性. 所建单剪试验数值模型及四点弯曲梁试验数值模型分别代表素混凝土和钢筋混凝土试件试验,参照Zhang等[23-24]的试验进行结果对比. 采用的界面参数如表3所示. ...
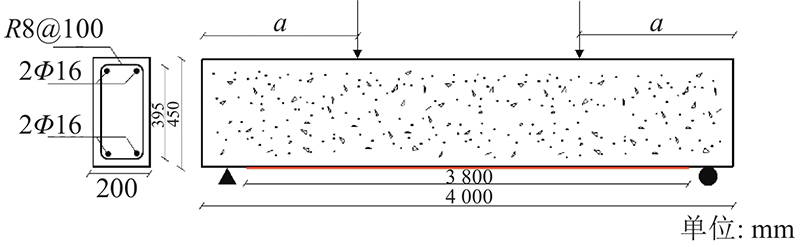
... FRP-混凝土梁黏结界面的失效主要是跨中局部脱黏导致的[30-32]. 采用的四点弯曲梁试验模型根据Fu等[24]的试验确定,混凝土内嵌钢筋. 圆柱体抗压强度为47 MPa,四点弯曲梁混凝土试件的长4 000 mm,宽200 mm,高450 mm. 加强钢筋采用2根16 mm受拉钢筋和2根16 mm受压钢筋,采用8 mm箍筋,箍筋间距为100 mm. 底部粘贴的FRP板长3 800 mm,宽100 mm,厚0.999 mm,试件几何尺寸如图13所示. 图中,a为加载点与试件边缘的距离. 将a=1 250 mm的参考试件命名为L2D1250,a=1 750 mm的参考试件命名为L2D1750. ...
... L2D1250试验裂缝图[24] ...
... Experimental crack patterns of L2D1250[24] ...
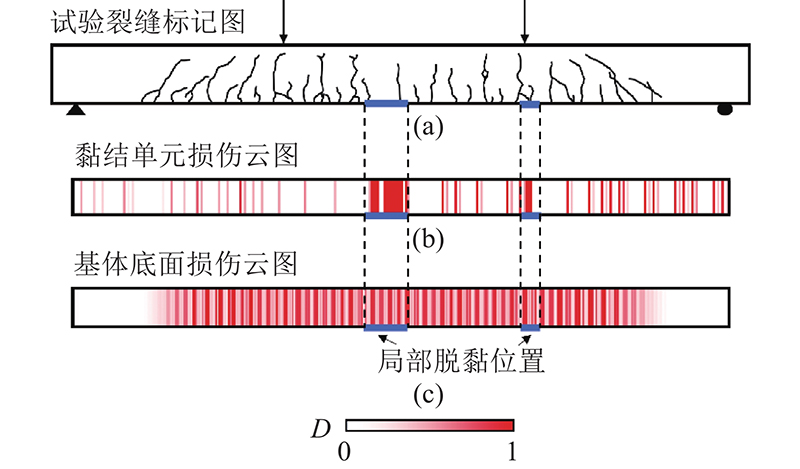
... L2D1250局部脱黏标记图[24] ...
... Local debonding positions plot of L2D1250[24] ...
... L2D1750试验裂缝图[24] ...
... Experimental crack patterns of L2D1750[24] ...
... L2D1750局部脱黏标记图[24] ...
... Local debonding positions plot of L2D1750[24] ...
Shear strengthening of reinforced concrete beams using externally-bonded aluminum alloy plates: an experimental study
1
2016
... 剪切拉拔是常见的研究FRP-混凝土界面的试验方法[25-26]. 选取单剪试验结果[23]与数值模型对照,以确定ST-CZM在单一模态下的可靠性. 素混凝土数值模型长300 mm,宽100 mm,高50 mm. 标准测试得到的试件抗压强度为29.3 MPa. FRP板数值模型厚度为2 mm, FRP试件测试得到的拉伸强度为4.1 GPa,弹性模量为256 GPa,黏结长度为180 mm,黏结宽度为20 mm. 文献[27]~[29]中的试验也采用类似试件. 试件几何尺寸如图10所示,数值模型一切边界条件按照试验实际取用[23]. ...
A new single-shear set-up for stable debonding of FRP–concrete joints
1
2009
... 剪切拉拔是常见的研究FRP-混凝土界面的试验方法[25-26]. 选取单剪试验结果[23]与数值模型对照,以确定ST-CZM在单一模态下的可靠性. 素混凝土数值模型长300 mm,宽100 mm,高50 mm. 标准测试得到的试件抗压强度为29.3 MPa. FRP板数值模型厚度为2 mm, FRP试件测试得到的拉伸强度为4.1 GPa,弹性模量为256 GPa,黏结长度为180 mm,黏结宽度为20 mm. 文献[27]~[29]中的试验也采用类似试件. 试件几何尺寸如图10所示,数值模型一切边界条件按照试验实际取用[23]. ...
A general strength model for fiber bundle composites under transverse tension or interlaminar shear
1
2019
... 剪切拉拔是常见的研究FRP-混凝土界面的试验方法[25-26]. 选取单剪试验结果[23]与数值模型对照,以确定ST-CZM在单一模态下的可靠性. 素混凝土数值模型长300 mm,宽100 mm,高50 mm. 标准测试得到的试件抗压强度为29.3 MPa. FRP板数值模型厚度为2 mm, FRP试件测试得到的拉伸强度为4.1 GPa,弹性模量为256 GPa,黏结长度为180 mm,黏结宽度为20 mm. 文献[27]~[29]中的试验也采用类似试件. 试件几何尺寸如图10所示,数值模型一切边界条件按照试验实际取用[23]. ...
混凝土弹塑性损伤本构模型参数及其工程应用
0
2015
混凝土弹塑性损伤本构模型参数及其工程应用
0
2015
碳纤维增强塑料布与混凝土基层粘结行为研究
1
2007
... 剪切拉拔是常见的研究FRP-混凝土界面的试验方法[25-26]. 选取单剪试验结果[23]与数值模型对照,以确定ST-CZM在单一模态下的可靠性. 素混凝土数值模型长300 mm,宽100 mm,高50 mm. 标准测试得到的试件抗压强度为29.3 MPa. FRP板数值模型厚度为2 mm, FRP试件测试得到的拉伸强度为4.1 GPa,弹性模量为256 GPa,黏结长度为180 mm,黏结宽度为20 mm. 文献[27]~[29]中的试验也采用类似试件. 试件几何尺寸如图10所示,数值模型一切边界条件按照试验实际取用[23]. ...
碳纤维增强塑料布与混凝土基层粘结行为研究
1
2007
... 剪切拉拔是常见的研究FRP-混凝土界面的试验方法[25-26]. 选取单剪试验结果[23]与数值模型对照,以确定ST-CZM在单一模态下的可靠性. 素混凝土数值模型长300 mm,宽100 mm,高50 mm. 标准测试得到的试件抗压强度为29.3 MPa. FRP板数值模型厚度为2 mm, FRP试件测试得到的拉伸强度为4.1 GPa,弹性模量为256 GPa,黏结长度为180 mm,黏结宽度为20 mm. 文献[27]~[29]中的试验也采用类似试件. 试件几何尺寸如图10所示,数值模型一切边界条件按照试验实际取用[23]. ...
Intermediate crack-induced debonding in RC beams and slabs
1
2003
... FRP-混凝土梁黏结界面的失效主要是跨中局部脱黏导致的[30-32]. 采用的四点弯曲梁试验模型根据Fu等[24]的试验确定,混凝土内嵌钢筋. 圆柱体抗压强度为47 MPa,四点弯曲梁混凝土试件的长4 000 mm,宽200 mm,高450 mm. 加强钢筋采用2根16 mm受拉钢筋和2根16 mm受压钢筋,采用8 mm箍筋,箍筋间距为100 mm. 底部粘贴的FRP板长3 800 mm,宽100 mm,厚0.999 mm,试件几何尺寸如图13所示. 图中,a为加载点与试件边缘的距离. 将a=1 250 mm的参考试件命名为L2D1250,a=1 750 mm的参考试件命名为L2D1750. ...
1
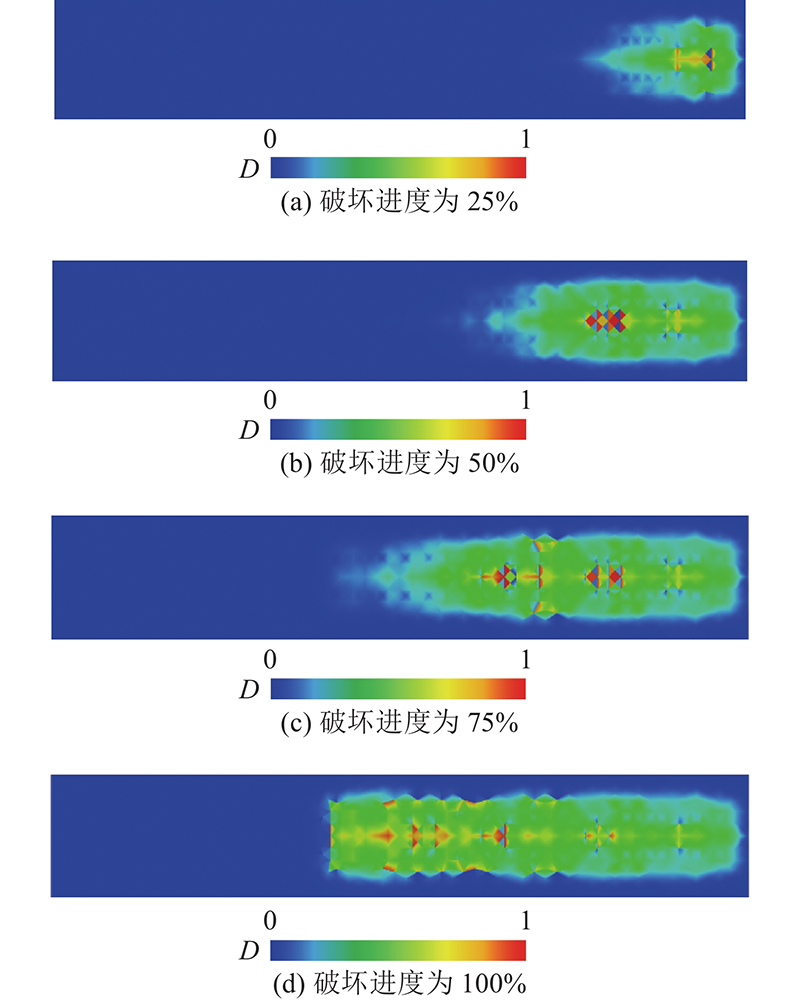
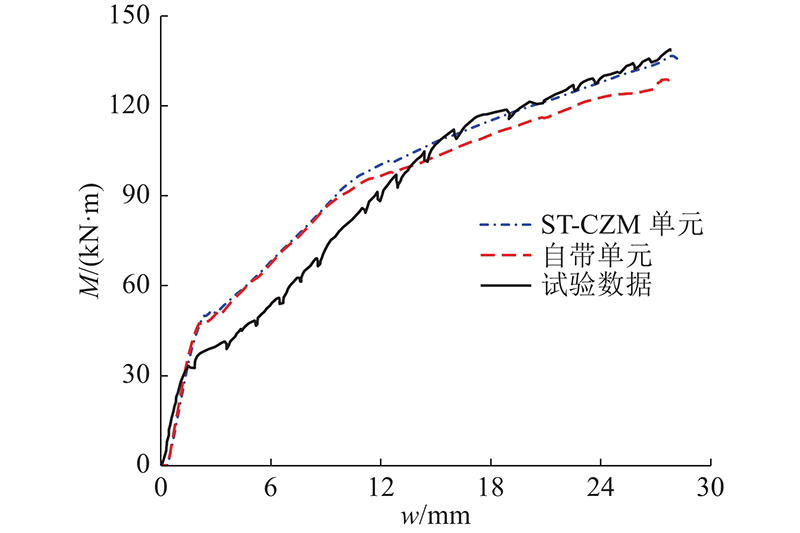
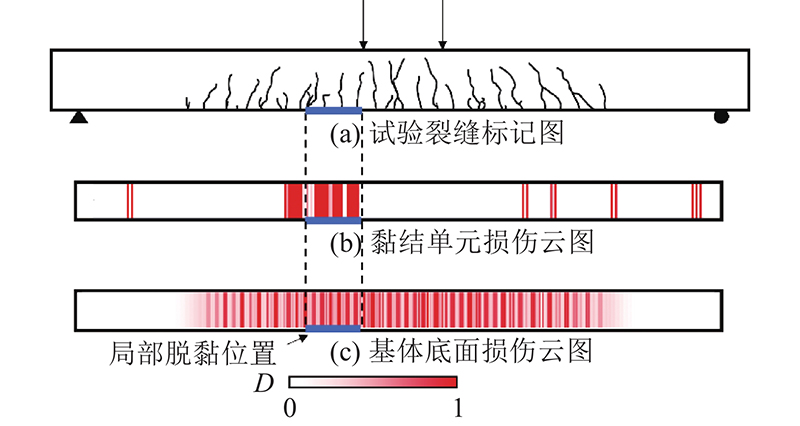
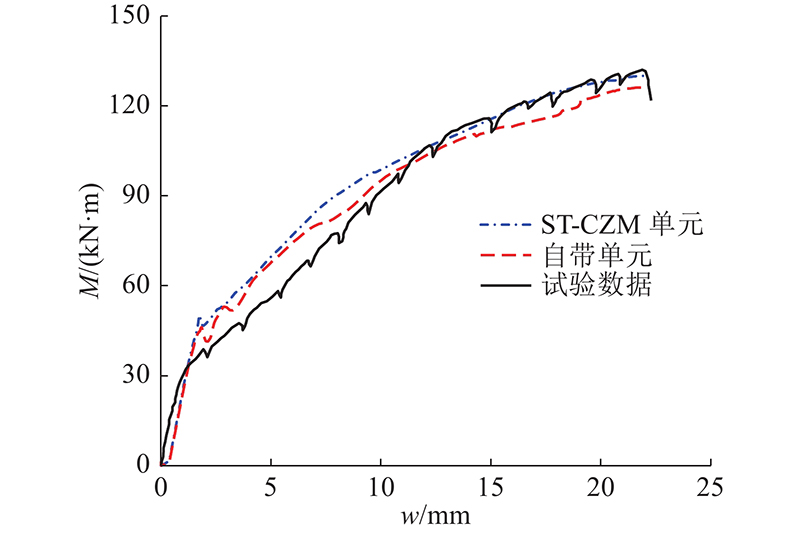
... 模型L2D1750采用的自带单元与L2D1250的相同. L2D1750试验的试验裂缝图、局部脱黏标记图以及模拟损伤云图分别如图18~20所示. 其中图19(b)、(c)分别为黏结单元损伤云图和基体损伤云图,得到云图的方法与L2D1250相同. 观察图19可以得到,试验得到的局部脱黏位置与ST-CZM预测的黏结单元最早出现集中损伤的位置接近. 如图21所示为L2D1750的试件分别采用自带单元、ST-CZM单元的模拟结果与试验结果的对比图. 分析可以得到1)试件破坏过程可以明显地划分为3阶段. 阶段1为斜率几乎不变的弹性阶段;阶段2开始损伤出现,曲线的斜率第1次减小,混凝土内部钢筋和FRP逐渐发挥加强作用;阶段3混凝土裂缝基本成形,斜率第2次减小. 观察模拟结果可以得出,自带单元对界面强度的估计值偏低,且计算结果更不稳定. 2)通过对比图18~20的结果可以看出,试验结果和数值结果的裂缝发展趋势接近. 分析原因,受到弯矩作用,在裂缝向上发展之前混凝土下半部分已经完全破坏,这是裂缝的相互作用导致的最终破坏结果[31]. 3)数值模型中破坏集中的位置与试验得到的局部脱黏位置接近. 局部脱黏是导致 FRP 最终的脱落和失效的主要原因. FRP-混凝土黏结界面的破坏模式复杂,传统模型在这种模式下想要准确得到局部脱黏的位置有比较大的困难,而ST-CZM能够较准确地复现试验的破坏情况. 这也是本研究实现的ST-CZM的优越性之一. ...
Debonding failure along a softening FRP-to-concrete interface between two adjacent cracks in concrete members
2
2007
... FRP-混凝土梁黏结界面的失效主要是跨中局部脱黏导致的[30-32]. 采用的四点弯曲梁试验模型根据Fu等[24]的试验确定,混凝土内嵌钢筋. 圆柱体抗压强度为47 MPa,四点弯曲梁混凝土试件的长4 000 mm,宽200 mm,高450 mm. 加强钢筋采用2根16 mm受拉钢筋和2根16 mm受压钢筋,采用8 mm箍筋,箍筋间距为100 mm. 底部粘贴的FRP板长3 800 mm,宽100 mm,厚0.999 mm,试件几何尺寸如图13所示. 图中,a为加载点与试件边缘的距离. 将a=1 250 mm的参考试件命名为L2D1250,a=1 750 mm的参考试件命名为L2D1750. ...
... 过于靠近的加载端可能会影响试验以及模拟的结果[32],本研究建立加载跨度较大的L2D1750,直观表现具有多种破坏模式的复合模态下的界面破坏情况. ...