聚类是数据挖掘与机器学习中的一项基本任务，旨在无先验信息的情况下，分析数据样本之间的关系，将相似的样本分到同一簇，使得簇内的样本相似度高，簇间的样本相似度低. 由于其具有无需人工标注的优势，聚类也已经成功应用于图像处理、人脸识别、推荐系统等现实应用中. 得益于深度学习^[1]的蓬勃发展，许多研究者开始将深度学习的思想应用到聚类领域^[2]，并取得了巨大的成功.

Xie等^[3]提出了深度嵌入聚类(deep embedded clustering, DEC)，通过在联合优化的特征空间中对一组数据点进行聚类来学习特征表示. Guo等^[4]引入了重构损失来改进DEC.

基于自编码器(auto-encoders, AE)^[5]的方法在学习低维表征时只考虑了数据本身的属性信息，很少考虑数据之间的拓扑结构. 而拓扑结构往往揭示了数据之间潜在的相似性，能为学习低维表征提供有价值的指导^[6]. 因此，能同时集成拓扑结构和节点属性的图卷积神经网络(graph convolutional network, GCN)^[7]引起了许多研究者的关注. 基于以上工作的启发，Wang等^[8]提出了一个目标导向的属性图聚类网络. 之后，Bo等^[9]设计了信息传递算子和双重自监督学习机制，将AE和GCN模块统一到一个框架中.

尽管现有的深度聚类方法已经从不同方面进行了改进，但它们仍然普遍存在以下一个或多个问题：1) 大多数的方法只考虑了图的全局表示和节点表示是否来自同一个网络，并未探索节点属性信息和节点表示之间的关系，而节点的属性信息往往包含着关于节点的核心信息，研究它们之间的关联性有助于学习到的低维表征捕获更多有用的判别信息. 2) 现有的大多数方法只考虑了直接相连的邻居节点，由于图的稀疏性，2个相似度较高的节点可能没有边直接相连，如果没有考虑它们之间的关系，将会削弱低维表征的可靠性^[10]. 3)现有方法无法从不精准的预测标签中获益. 虽然部分预测标签存在错误，但具有高置信度的预测标签可以传播有用的信息，指导低维表征的学习.

针对深度聚类相关研究的局限性，本研究提出一种高阶互信息最大化与伪标签指导的深度聚类模型(high-order mutual information maximization and pseudo-label guided deep clustering, HMIPDC). 1) 该模型通过高阶互信息最大化策略和自注意力机制充分融合图中的多种信息，借此生成可靠的低维表征，进而利用基于深度散度的聚类损失函数(deep divergence-based clustering, DDC)^[11]和伪标签来迭代优化聚类目标. 2)利用多跳邻近矩阵更为准确地捕捉节点之间的拓扑相关性，并结合自注意力机制帮助目标节点更加合理地聚合邻居节点. 然后采用一种动态信息融合机制对学到的低维表征中的图结构和属性信息进一步融合. 3) 提出一种新颖的自监督训练策略. 该策略首先使用DDC算法来衡量聚类损失，然后从模型迭代过程产生的预测标签中选择置信度较高的标签，并将其作为伪标签来对模型进行反向监督，从而提升聚类性能.

近年来，得益于GCN强大的表示能力，广大的研究人员探索了用GCN同时提取图结构和节点属性的深度聚类方法^[12-13]. Kipf等^[14]利用GCN作为编码器来聚合邻居节点的属性信息并形成特征表示，然后使用内积解码器来重构图的邻接矩阵. Kou等^[15]则通过引入自监督模块，让模型能够学习到更有利于后续聚类任务的节点表示.

考虑到GCN的过度平滑问题并没有得到较好的缓解，Tu等^[16]提出了一个深度融合聚类网络(deep fusion clustering network, DFCN)，该模型通过一个信息融合模块来整合和细化从AE和改进的图自编码器学到的低维表征，并采用三重自监督机制来优化聚类分配. Liu等^[17]从样本和特征级别引入双重信息相关减少机制来减少冗余信息的影响，保留更多的判别特征. 但是这些方法都没有对模型学习到的预测标签进行区分，导致很多错误的标签被用来指导低维表征的学习，降低了聚类效果.

互信息(mutual information,MI)^[18]是衡量2个随机变量之间依赖程度的一种度量方式. 其中，高互信息表明2个随机变量之间的相关性较大，零互信息表明2个随机变量之间是相互独立的. 由于MI的特性，许多研究人员试图将MI的思想运用到无监督学习领域. 得益于深度学习强大的计算能力，Belghazi等^[18]提出了一种高效计算深度神经网络输入与输出之间MI的方法. 为了充分利用图像中丰富的结构和属性信息，Hjelm等^[19]通过训练编码器模型使用互信息神经网络估计来最大化输入和局部表示之间的互信息.

由于图数据在现实世界中普遍存在，研究者们试图将深度信息最大化（deep InfoMax，DIM）的想法从图像迁移到图中，如深度图信息最大化(deep graph infomax, DGI)^[20]通过对全局信息的提取来最大化全局表示和节点表示之间的MI，进而学习到有利于后续聚类任务的低维表征. Molaei等^[12]通过利用最大团来学习图表示的信息最大化方法. 然而这些方法并未充分利用原始图的节点属性信息和图嵌入后的相关信息，这样不利于发现节点之间潜在的属性关联关系，使得表征学习缺乏相关的指导，降低了低维表征的质量.

给定一个具有 $K$个聚类中心的属性图 ${{G = }}\{ V,\varSigma ,{\boldsymbol{F}}\} $. 其中， $V = \{ {{\boldsymbol{v}}_1},{{\boldsymbol{v}}_2}, \cdots ,{{\boldsymbol{v}}_n}\} $为图的节点集合； $\varSigma $为边集合， $\xi $为边的条数； ${\boldsymbol{F}} = \left[ {{{\boldsymbol{f}}_1},{{\boldsymbol{f}}_2}, \cdots ,{{\boldsymbol{f}}_n}} \right] \in {{\bf{R}}^{n \times d}}$表示节点的属性矩阵， ${{\boldsymbol{f}}_i}$表示节点 ${{\boldsymbol{v}}_i}$的属性向量， $d$为节点维度， $n$为图中的节点个数. 该图的拓扑结构可以用邻接矩阵 $ {\boldsymbol{A}}{\text{ = }}{\left[ {{a_{ij}}} \right]_{n \times n}} \in {{\bf{R}}^{n \times n}} $来表示. 本研究使用的数据集都是不带权重的无向图，如果节点 ${{\boldsymbol{v}}_i}$和节点 ${{\boldsymbol{v}}_j}$之间有边直接相连，则 ${a_{ij}} = 1$，否则 ${a_{ij}} = 0$.

定义1 　互信息^[21]. 给定2个随机变量 $X$和 $Y$，则它们之间的互信息定义如下：

(1) $ I(X;Y) = H(X)+H(Y) - H(X,Y). $

式中： $H(X)$为熵， $H(X|Y)$为条件熵， $H(X,Y)$为 $X$和 $Y$的联合分布的熵.

定义2 　高阶互信息^[22]. 高阶互信息是对大于等于3个随机变量之间的互信息的一种描述. 可以用类似于互信息的定义来表示高阶互信息，其定义如下：

(2) $ I\left( {{X_1};{X_2}; \cdots ;{X_n}} \right) = \sum\limits_{i = 1}^n {{{( - 1)}^{i+1}}\sum\limits_{{j_1} < \cdots < {j_i}} {H\left( {{X_{{j_1}}},{X_{{j_2}}}, \cdots ,{X_{{j_i}}}} \right)} } . $

式中： $ H\left( {{X_{{j_1}}},{X_{{j_2}}}, \cdots ,{X_{{j_i}}}} \right) $为 $ {X_{{j_1}}},{X_{{j_2}}}, \cdots ,{X_{{j_i}}} $联合分布的熵， $ \displaystyle\sum\limits_{{j_1} < \cdots < {j_i}} {H\left( {{X_{{j_1}}},{X_{{j_2}}}, \cdots ,{X_{{j_i}}}} \right)} $为遍历随机变量的组合.

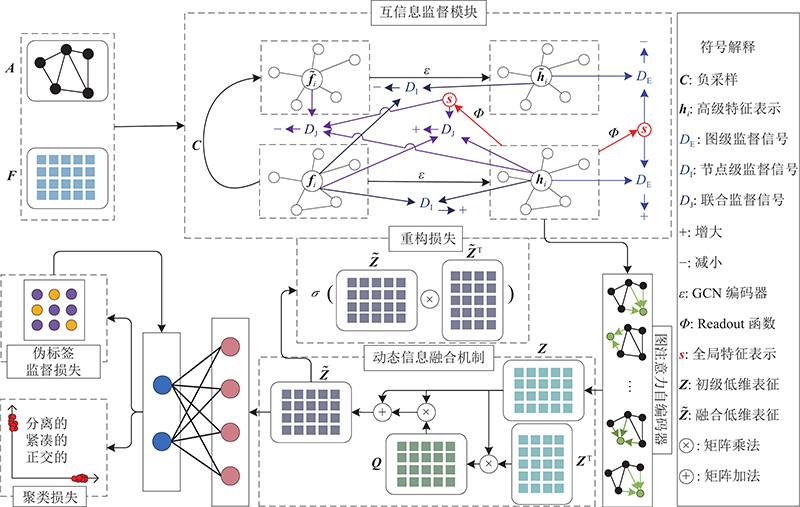
HMIPDC模型首先利用互信息监督模块对高级特征表示 ${{\boldsymbol{h}}_i}$、节点属性信息 ${{\boldsymbol{f}}_i}$和全局特征表示 ${\boldsymbol{s}}$三者之间的相关性进行判断，并通过最大化它们之间的互信息来保证模型可以从原始输入中获取更有用的信息；其次引入了图注意力自编码器，使模型在训练过程中能够依据邻居节点对于目标节点的重要程度来分配不同权重并聚合邻居节点，从而学习到合理的低维表征；然后使用一种动态信息融合机制对学习到的低维表征进一步精炼；最后通过最小化目标函数来获得更好的聚类性能. HMIPDC模型框架如图1所示.

为了充分挖掘图中节点之间的相关性，让网络提取到更适合下游任务的低维表征，采用一种高阶互信息最大化策略^[21]，通过将高级特征表示 ${{\boldsymbol{h}}_i}$、全局特征表示 ${\boldsymbol{s}}$和节点属性向量 $ {{\boldsymbol{f}}_i} $这3个随机变量之间的互信息最大化以实现在同质属性网络上的表征学习.

通过不断聚合与目标节点 ${{\boldsymbol{v}}_i}$直接相连的邻居节点进行表征学习. 具体来说，引入GCN编码器 $\varepsilon$来得到 ${{\boldsymbol{h}}_i}$：

(3) $ \varepsilon \left( {{\boldsymbol{F}},{\boldsymbol{A}}} \right) = {\boldsymbol{H}} = {{\rm{ReLU}}} \left( {{{{\hat{\boldsymbol D}}}^{ - {1}/{2}}}{\hat{\boldsymbol A}}{{{\hat{\boldsymbol D}}}^{ - {1}/{2}}}{\boldsymbol{FW}}} \right). $

式中： ${\hat{\boldsymbol A}} = {\boldsymbol{A}}+w{\boldsymbol{I}}$， ${\boldsymbol{I}}$为单位对角矩阵，相当于给每个节点增加自连接关系，保证目标节点在聚合其邻居节点时能考虑到自身的属性信息， $w$为自连接的权重，越大的权重表明节点本身在生成 ${{\boldsymbol{h}}_i}$的过程中起着越重要的作用； $ {\hat{\boldsymbol D}} $为保存每个节点的度的矩阵， ${\hat d_{ii}} = {\displaystyle\sum}_j{{\hat a}_{ij}} $为节点 ${{\boldsymbol{v}}_i}$对应的度， ${\hat a_{ij}}$为矩阵 ${\hat{\boldsymbol A}}$第 $i$行第 $j$列的元素； ${{\rm{ReLU}}} $为线性整流函数； ${\boldsymbol{W}}$为可训练的权重矩阵.

选择 $ {\boldsymbol{H}}$中所有节点属性的平均值作为 ${{\rm{Readout}}} $函数 $\varPhi $：

(4) $ {\boldsymbol{s}} = \varPhi ({\boldsymbol{H}}) = \frac{1}{n}\sum\limits_{i = 1}^n {{{\boldsymbol{h}}_i}} . $

式中： ${{\boldsymbol{h}}_i}$为矩阵 ${\boldsymbol{H}}$的第 $i$行向量.

由于考虑的是3个随机变量之间的互信息，故有

(5) $ \begin{split} I({X_1};\;&{X_2};{X_3}) = \\ & H({X_1})+H({X_2})+H({X_3}) - \\ & H({X_1},{X_2}) - H({X_1},{X_3}) - \\ & H({X_2},{X_3}){\text+}H({X_1},{X_2},{X_3}) = \\ & I({X_1};{X_2})+I({X_1};{X_3}) - I({X_1};{X_2},{X_3}). \end{split}\qquad\qquad$

式中： $ I({X_1};{X_2},{X_3}) $为 ${X_1}$的分布与 $({X_2},{X_3})$的联合分布之间的互信息. 将需要计算的3个随机变量代入式(5)可以得到

(6) $ I({{\boldsymbol{h}}_i};{\boldsymbol{s}};{{\boldsymbol{f}}_i}) = I({{\boldsymbol{h}}_i};{\boldsymbol{s}})+I({{\boldsymbol{h}}_i};{{\boldsymbol{f}}_i}) - I({{\boldsymbol{h}}_i};{\boldsymbol{s}},{{\boldsymbol{f}}_i}). $

式中： $I({{\boldsymbol{h}}_i};{\boldsymbol{s}})$考虑了图级监督信号，即节点的低维表征和全局表示之间的互信息； $I({{\boldsymbol{h}}_i};{{\boldsymbol{f}}_i})$考虑了节点级监督信号，即节点的低维表征和节点属性之间的互信息； $ I({{\boldsymbol{h}}_i};{\boldsymbol{s}},{{\boldsymbol{f}}_i}) $则考虑了节点级监督信号和图级监督信号之间的相互作用.

进一步考虑高阶互信息：

(7) $ {L_{{\rm{mi}}}} = {\lambda _{\rm{E}}}I({{\boldsymbol{h}}_i};{\boldsymbol{s}})+{\lambda _{\rm{I}}}I({{\boldsymbol{h}}_i};{{\boldsymbol{f}}_i})+{\lambda _{\rm{J}}}I({{\boldsymbol{h}}_i};{\boldsymbol{s}},{{\boldsymbol{f}}_i}). $

式中： ${\lambda _{\rm{E}}}、{\lambda _{\rm{I}}}、{\lambda _{\rm{J}}}$为可以调整的平衡系数.

1）对于 $ I\left( {{{\boldsymbol{h}}_i};{\boldsymbol{s}}} \right) $. 依照DGI的设定可以得到

(8) $ {L}_{{\rm{E}}}=E\text{ }[\mathrm{ln}\;{{{D}}}_{{\rm E}}({{\boldsymbol{h}}}_{i},{\boldsymbol{s}})]+E\text{ }[\mathrm{ln}\;(1-{{{D}}}_{{\rm{E}}}({\tilde{{\boldsymbol{h}}}}_{i},{\boldsymbol{s}}))]. $

式中： $ E $表示期望； $ {{\tilde{\boldsymbol h}}_i} $为来自负网络 $\tilde G$的高级特征表示，它先通过一个显式的腐蚀函数 $ C\text{ }:\tilde{G}\text{=}C(G) $对原始网络 $G$的属性矩阵 ${\boldsymbol{F}}$的行进行随机打乱，从而得到负网络 $\tilde G$，然后再使用 $\tilde G$提供的负样本生成 $ {{\tilde{\boldsymbol h}}_i} $； $ {{{D}}_{\rm{E}}} $为图级监督信号的判别器， $ {{{D}}_{\rm{E}}}({{\boldsymbol{h}}_i},{\boldsymbol{s}}) $为使用双线性评分函数对 $ ({{\boldsymbol{h}}_i},{\boldsymbol{s}}) $进行评分.

2）对于 $ I({{\boldsymbol{h}}_i};{{\boldsymbol{f}}_i}) $. 将式(8)中的 $ {\boldsymbol{s}} $替换为 $ {{\boldsymbol{f}}_i} $：

(9) $ {L}_{{\rm{I}}}=E\text{ }[\mathrm{ln}\;{{{D}}}_{{\rm{I}}}({{\boldsymbol{h}}}_{i},{{\boldsymbol{f}}}_{i})]+E\text{ }[\mathrm{ln}\;(1-{{{D}}}_{{\rm{I}}}({\tilde{{\boldsymbol{h}}}}_{i},{{\boldsymbol{f}}}_{i}))]. $

式中： $ {{D}_{\rm{I}}} $为节点级监督信号的判别器.

3）对于 $ I({{\boldsymbol{h}}_i};{\boldsymbol{s}},{{\boldsymbol{f}}_i}) $. 通过 $\tilde G$中的属性矩阵 ${\tilde{\boldsymbol F}}$让编码器 $\varepsilon $更好地捕捉 $ ({{\boldsymbol{h}}_i},{\boldsymbol{s}},{{\boldsymbol{f}}_i}) $这3个随机变量之间的互信息，尤其是 ${\boldsymbol{s}}$和 $ {{\boldsymbol{f}}_i} $之间的互信息，这是图级信号和节点级信号都没有考虑到的，由此可以得到

(10) $ {L}_{{\rm{J}}}=E\text{ }[\mathrm{ln}\;{{{D}}}_{{\rm{J}}}({{\boldsymbol{h}}}_{i},{\boldsymbol{s}},{{\boldsymbol{f}}}_{i})]+E\text{ }[\mathrm{ln}\;(1-{{{D}}}_{{\rm{J}}}({{{\boldsymbol{h}}}}_{i},{\boldsymbol{s}},{\tilde{{\boldsymbol{f}}}}_{i}))]. $

式中： $ {{{D}}_{\rm{J}}} $为监督联合信号的判别器， ${{\tilde{\boldsymbol f}}_i}$为矩阵 ${\tilde{\boldsymbol F}}$中第 $i$行的向量.

4）最终的监督信号以最大化以下公式为目标：

(11) $ {L}_{{\rm{mi}}}\text{}={\lambda }_{{\rm{E}}}{L}_{{\rm{E}}}+{\lambda }_{{\rm{I}}}{L}_{{\rm{I}}}\text{}+{\lambda }_{{\rm{J}}}{L}_{{\rm{J}}}. $

为了更好地利用邻近信息和节点的属性信息，采用图自编码器(graph auto-encoder, GAE)^[14]作为主框架来学习低维表征；同时将GAE中的GCN模块替换为图注意力网络(graph attention networks, GAT)^[23]的图注意力层，以此来构成图注意力自编码器. 这样就可以将原本GCN的标准化函数替换为使用注意力权重的邻居节点特征聚合函数，通过计算目标节点与邻居节点之间的“注意力系数”，让图神经网络更加关注重要的邻居节点.

为了判断每个邻居节点对于目标节点的重要程度，在逐层图注意力策略中对不同邻居节点表示赋予不同的权重：

(12) $ {\boldsymbol{z}}_i^{l+1} = \sigma \left( {\sum\limits_{j \in {N_i}} {{\alpha _{ij}}{\boldsymbol{Wz}}_j^l} } \right). $

式中： ${\boldsymbol{z}}_j^l$为节点 ${{\boldsymbol{v}}_j}$在第 $l$层所对应的特征向量； $ {\boldsymbol{z}}_i^{l+1} $为以节点 ${{\boldsymbol{v}}_i}$为目标节点生成的第 $l+1$层的特征向量，这是经过一个以自注意力机制为核心的操作后生成的； ${\alpha _{ij}}$为注意力系数，表示邻居节点 ${{\boldsymbol{v}}_j}$对于目标节点 ${{\boldsymbol{v}}_i}$的重要程度； $ {N_i} $为节点 $ {{\boldsymbol{v}}_i} $的邻居节点集合； $\sigma $为非线性激活函数； ${\boldsymbol{W}}$为作用到每个邻居节点的权重矩阵. 为了计算 ${\alpha _{ij}}$，从拓扑距离和属性信息2个方面来衡量邻居节点对于目标节点的重要性.

1）拓扑距离. 邻居节点通过邻边来表示目标节点. 为了更好地挖掘图中节点之间的相关性，在图注意力自编码器中使用 $t$跳邻居节点来获得一个多跳邻近矩阵：

(13) $ {\boldsymbol{M}} = ({\boldsymbol{B}}+{{\boldsymbol{B}}^2}+ \cdots +{{\boldsymbol{B}}^t})/t. $

式中： $t$为可调整的参数，可以根据数据集的稀疏性和复杂程度进行相应调整，本研究将其设置为2； ${\boldsymbol{B}}$为转移矩阵，如果目标节点 $ {{\boldsymbol{v}}_i} $和邻居节点 ${{\boldsymbol{v}}_j}$之间有边相连，则 ${b_{ij}} = 1/{d_i}$，否则 ${b_{ij}} = 0$， ${d_i}$为目标节点 ${{\boldsymbol{v}}_i}$的度； ${{\boldsymbol{B}}^t}$为 ${\boldsymbol{B}}$的 $t$次方； ${m_{ij}}$为节点 ${{\boldsymbol{v}}_i}$和节点 ${{\boldsymbol{v}}_j}$在 $t$跳内的拓扑相关性，即如果 ${m_{ij}} > 0$，表示节点 ${{\boldsymbol{v}}_i}$和节点 ${{\boldsymbol{v}}_j}$之间具有相关性，值越大表示相关性越大.

2）属性信息. 注意力系数 ${\alpha _{ij}}$可以用一个单层前馈神经网络 $ \phi $来表示：

(14) $ {\phi _{ij}} = {{\boldsymbol{e}}^{\rm{T}}}({\boldsymbol{W}}{{\boldsymbol{f}}_i},{\boldsymbol{W}}{{\boldsymbol{f}}_j}). $

式中： $ {{\boldsymbol{f}}_i} $和 ${{\boldsymbol{f}}_j}$分别为节点 ${{\boldsymbol{v}}_i}$和节点 ${{\boldsymbol{v}}_j}$的属性特征， $ {{\boldsymbol{e}}^{\rm{T}}} $为共享的权重向量的转置.

为了使原来没有可比性的数据变得具有可比性，同时又能保持不同数据之间的相对关系，采用 ${{\rm{softmax}}} $函数对邻域 $ u \in {N_i} $的注意力系数进行归一化：

(15) $ {\alpha _{ij}} = {{{\rm{softmax}}} _j}\;({\phi _{ij}}) = \frac{{\exp\; ({\phi _{ij}})}}{{\displaystyle\sum\nolimits_{u \in {N_i}} {\exp \;({\phi _{iu}})} }}. $

再加上拓扑权重 ${\boldsymbol{M}}$和非线性激活函数 $ \delta $，注意力系数 $ {\alpha _{ij}} $可以表示为

(16) $ {\alpha _{ij}} = \frac{{\exp \;(\delta {m_{ij}}{\phi _{ij}})}}{{\displaystyle\sum\nolimits_{u \in {N_i}} {\exp \;(\delta {m_{iu}}{\phi _{iu}})} }}. $

为了进一步提炼从图注意力自编码器中学习到的初级低维表征 ${\boldsymbol{Z}}$中的图结构和节点属性信息，提出了一种动态信息融合机制，该机制由自相关学习机制和跳跃连接组成.

1）使用自相关学习机制让 ${\boldsymbol{Z}}$融合节点属性空间中的非局部关系.

计算自相关系数矩阵并进行归一化得到 ${\boldsymbol{Q}}$：

(17) $ {q_{ij}} = \frac{{\exp\; {{({\boldsymbol{Z}}{{\boldsymbol{Z}}^{\rm{T}}})}_{ij}}}}{{\displaystyle\sum\limits_{u = 1}^n {\exp \;{{({\boldsymbol{Z}}{{\boldsymbol{Z}}^{\rm{T}}})}_{iu}}} }}. $

探讨节点之间的全局相关性来修改 ${\boldsymbol{Z}}$，得到节点的全局特征表示：

(18) $ {{\boldsymbol{Z}}_{\rm{q}}} = {\boldsymbol{QZ}}. $

2）为了保证样本空间在进行多次变换后，仍能保持其核心特征，采用跳跃连接让节点信息可以通过动态信息融合机制顺利传递：

(19) $ {\tilde{\boldsymbol Z}} = \beta {{\boldsymbol{Z}}_{\rm{q}}}+{\boldsymbol{Z}}. $

式中： $\tilde {\boldsymbol{Z}} \in {{\bf{R}}^{n \times d'}}$为融合低维表征， $d'$为嵌入维度； $\beta $为可学习的权重系数，将其初始化为0，并在网络训练时使用梯度下降法自动学习权重.

由于 $\tilde {\boldsymbol{Z}}$已经包含了属性和结构信息，选择内积解码器来预测节点之间的连接：

(20) $ {\tilde a_{ij}} = {{\rm{sigmoid}}} \;({{\tilde{\boldsymbol z}}_i}{{\tilde{\boldsymbol z}}_j}^{\rm{T}}). $

式中： ${\tilde a_{ij}}$为 $G$重构后的邻接矩阵 $\tilde {\boldsymbol{A}}$中第 $i$行第 $j$列的元素， ${{\tilde{\boldsymbol z}}_i}$为融合低维表征矩阵 ${\tilde{\boldsymbol Z}}$中的第 $i$行向量.

HMIPDC的目标函数由3个部分组成，即图注意力自编码器的重构损失、聚类损失以及伪标签监督损失.

通过二元交叉熵计算 ${\boldsymbol{A}}$和 $\tilde {\boldsymbol{A}}$之间的差值，并最小化其差值来逐步降低重构误差：

(21) $ {L_{{\rm{re}}}} = - \frac{1}{n}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{a_{ij}} \ln\; \left( {{{\tilde a}_{ij}}} \right)+\left( {1 - {a_{ij}}} \right) \ln\; \left( {1 - {{\tilde a}_{ij}}} \right)} } . $

通过降低重构误差可以尽可能地保留数据固有的局部结构.

使用DDC^[11]算法来衡量聚类损失，该算法用概率密度函数对每个簇进行建模并优化聚类分配，然后采用信息论中的CS散度(Cauchy-Schwarz divergence)来最大化它们的概率密度函数之间的差异，使得网络能够通过梯度下降方法优化其权重并学习输入图的内在簇结构.

其聚类损失函数主要由3个损失项组成.

1）第1个损失项主要考虑数据聚类在低维表征空间的可分离性和紧凑性约束，其源自CS散度的多重概率密度函数泛化，用来保证不同簇中的节点之间的相似度较小，而同一簇中的节点之间的相似度尽可能的大. 第1个损失项表达式如下：

(22) $ {L_1}{\text{ }} = \sum\limits_{i = 1}^{K - 1} {\sum\limits_{j > i}^K {\frac{{{\tilde{\boldsymbol z}}_i^{\rm{T}}{\boldsymbol{U}}{{{\tilde{\boldsymbol z}}}_j}}}{{\sqrt {{\tilde{\boldsymbol z}}_i^{\rm{T}}{\boldsymbol{U}}{{{\tilde{\boldsymbol z}}}_i}{\tilde{\boldsymbol z}}_j^{\rm{T}}{\boldsymbol{U}}{{{\tilde{\boldsymbol z}}}_j}} }}} } . $

式中： ${\boldsymbol{U}}$为采用 ${u_{ij}} = \exp\; ({{ - ||{{{\tilde{\boldsymbol z}}}_i} - {{{\tilde{\boldsymbol z}}}_j}|{|^2}} \mathord{\left/ {\vphantom {{ - ||{{{\tilde{\boldsymbol z}}}_i} - {{{\tilde{\boldsymbol z}}}_j}|{|^2}} {{{(2\ell )}^2}}}} \right. } {{{(2\ell )}^2}}})$计算得到的核相似度矩阵， $\ell $为高斯核带宽，它是通过基于学习表示的统计信息计算得到的，默认值为0.15.

2）第2个损失项要求不同节点的聚类分配在低维特征空间是向量正交的，从而避免聚类结果陷入局部最优解，防止聚类划分结构的退化；当且仅当矩阵的内积为零时，簇分配向量是正交的. 第2个损失项表达式如下：

(23) $ {L_2} = {{\rm{triu}}}\; \left( {{\tilde{\boldsymbol Z}}{{{\tilde{\boldsymbol Z}}}^{\rm{T}}}} \right). $

式中： $ {{\rm{triu}}}\; \left( \cdot \right) $为矩阵上三角元素的总和.

3）第3个损失项试图把簇分配向量推向标准单纯形空间的拐角附近，通过位于标准单纯形拐角处的理想聚类中心中的相似点分组来分离数据点. 第3个损失项表达式如下：

(24) $ {L_3} = \sum\limits_{i = 1}^{K - 1} {\sum\limits_{j > i}^K {\frac{{{\boldsymbol{m}}_i^{\rm{T}}{\boldsymbol{U}}{{\boldsymbol{m}}_j}}}{{\sqrt {{\boldsymbol{m}}_i^{\rm{T}}{\boldsymbol{U}}{{\boldsymbol{m}}_i}{\boldsymbol{m}}_j^{\rm{T}}{\boldsymbol{U}}{{\boldsymbol{m}}_j}} }}} } . $

式中： ${m_{ij}} = \exp\; ( - ||{{\tilde{\boldsymbol z}}_i} - {{\boldsymbol{l}}_j}|{|^2})$， ${{\boldsymbol{l}}_j}$为 $ {{\bf{R}}^k} $中第 $j$个笛卡尔基向量.

4）模型训练期间的聚类损失可以表示为这3个损失项的总和：

(25) $ {L_{{\rm{ddc}}}} = {L_1}+{L_2}+{L_3}. $

伪标签监督损失函数^[24]的设计同时兼顾了正伪标签和负伪标签.

1）获取伪标签.

直接从每次模型训练的预测标签中选择正伪标签：

(26) $ \tilde y_k^{(i)} = 1\left[ {p_k^{(i)} > {\gamma _{\rm{p}}}} \right]. $

式中： $\tilde y_k^{(i)}$为节点 ${{\boldsymbol{v}}_i}$是否属于第 $k$类的伪标签； $p_k^{(i)}$为节点 ${{\boldsymbol{v}}_i}$在模型预测时，最大概率所在的类是第 $k$类的概率； ${\gamma _{\rm{p}}}$为正伪标签的阈值，其值域为 $\left( {0,1.0} \right)$； $1\left[ \cdot \right]$为指示方程，如果 $ p_k^{(i)} > {\gamma _{\rm{p}}} $，则结果为1，否则为0. 式(26)直接将满足 $ p_k^{(i)} > {\gamma _{\rm{p}}} $的节点 ${{\boldsymbol{v}}_i}$选取为正伪标签，表明节点 ${{\boldsymbol{v}}_i}$属于第 $k$类.

用相似的方法从模型预测的结果中选择负伪标签：

(27) $ \bar y_k^{(i)} = 1\left[ {p_k^{(i)} < {\gamma _{\rm{n}}}} \right]. $

式中： $ {\gamma _{\rm{n}}} $为负伪标签的阈值，其值域为 $\left( {0,1.0} \right)$，并且 $ {\gamma _{\rm{n}}} < {\gamma _{\rm{p}}} $. 式(27)直接将满足 $ p_k^{(i)} < {\gamma _{\rm{n}}} $的节点选取为负伪标签，表明节点 ${{\boldsymbol{v}}_i}$不属于第 $k$类.

使用 $\theta _k^{(i)}$将正伪标签和负伪标签整合起来，用来指导节点 ${{\boldsymbol{v}}_i}$的预测标签能否被用于指导训练模型：

(28) $ \theta _k^{(i)} = 1\left[ {p_k^{(i)} > {\gamma _{\rm{p}}}} \right]+1\left[ {p_k^{(i)} < {\gamma _{\rm{n}}}} \right]. $

2）计算伪标签监督损失.

使用交叉熵损失来表示正伪标签监督损失：

(29) $ {L_{\rm{p}}} = - \frac{1}{{{\partial _{{\rm{pn}}}}}}\sum\limits_{k = 1}^K {\theta _k^{(i)}\tilde y_k^{(i)}\ln } \;(\hat y_k^{(i)}). $

式中： $ {\partial _{{\rm{pn}}}} = \displaystyle\sum\nolimits_k {\theta _k^{(i)}} $为从预测标签中选择的伪标签总数， $ \hat y_k^{(i)} $为模型预测时节点 ${{\boldsymbol{v}}_i}$在第 $k$类的输出概率.

借用正伪标签的交叉熵损失函数设计出负伪标签的损失函数：

(30) $ {L_{\rm{n}}} = - \frac{1}{{{\partial _{{\rm{pn}}}}}}\sum\limits_{k = 1}^K {\theta _k^{(i)}(1 - \bar y_k^{(i)})\ln } \;(1 - \hat y_k^{(i)}). $

结合式(29)、(30)的损失函数，得到最终的伪标签监督损失：

(31) $ {L_{{\rm{pn}}}} = - \frac{1}{{{\partial _{{\rm{pn}}}}}}\sum\limits_{k = 1}^K {\theta _k^{(i)}\left[ {\tilde y_k^{(i)}\ln\; (\hat y_k^{(i)})+(1 - \bar y_k^{(i)})\ln\; (1 - \hat y_k^{(i)})} \right]} . $

联合式(21)、(25)、(31)，得到最终进行优化的目标函数：

(32) $ L = {L_{{\rm{re}}}}+\eta {L_{{\rm{ddc}}}}+\mu {L_{{\rm{pn}}}}. $

式中： $ \eta $和 $ \mu $为超参数，是用来平衡这3种损失函数的权衡参数.

为了评估HMIPDC的有效性，在ACM^[9]、Citeseer^[9]、DBLP^[9]、和AMAP^[17]4个公开的数据集上对不同方法进行大量实验. 这些数据集的一些统计信息如表1所示.

为了证明HMIPDC的优越性，本研究选择了8种聚类方法作为基线方法，包括1种使用原始数据的传统聚类方法(K-means^[25])，2种基于AE的深度聚类方法(AE^[5]、IDEC^[3])，2种基于GCN的深度图聚类方法(GAE^[14]、DAEGC^[8])以及3种融合多种信息的深度图聚类方法(SDCN^[9]、DFCN^[16]、DCRN^[17]). 上述基线方法的介绍如下.

1）K-means^[25]：一种基于原始数据的传统聚类方法，先为节点分配初始的聚类中心，并通过不断的迭代来优化聚类.

2）AE^[5]：一种分2步走的深度聚类方法，先用自编码器学习到低维表征，再将其用于后续的聚类任务.

3）IDEC^[4]：一种联合深度聚类方法，通过同时学习低维表征和聚类分配来迭代优化聚类目标.

4）GAE^[14]：一种使用GCN来学习低维表征的深度图聚类方法.

5）DAEGC^[8]：通过引入自注意力机制来学习低维表征，并使用聚类损失来监督图聚类过程.

6）SDCN^[9]：有效地联合AE和GCN模块来更好地学习低维表征，并设计了一个双重自监督机制来监督聚类过程，指导整个模型的优化.

7）DFCN^[16]：设计了一种基于相关性来学习结构与属性信息的融合模块，用来合并AE和GAE学到的低维表征，并提出了一种三重自监督机制为信息融合提供可靠的指导.

8）DCRN^[17]：通过双重方式来降低信息的相关性，从而提升特征区分能力，并且引入了传播正则化来缓解表示崩溃，使得网络能够以浅层网络结构获得长距离信息.

类似以前的聚类研究^[17]，采用4种常用的评价指标来评估模型的聚类性能，即聚类准确率(accuracy, ACC)^[26]、规范化互信息(normalized mutual information, NMI)^[27]、调整兰德指数(adjusted Rand index, ARI)^[15]和macro F1-score(F1)^[28]. 对于每种评价指标，数值越高意味着聚类效果越好.

所有的实验都是基于Pytorch深度学习框架实现并完成的，并且运行在Ubuntu 18.04.6上，使用的CPU是i9-11900K，GPU是NVIDIAGeForce RTX 3090. 对于DAEGC，按照原始论文^[8]的设置处理论文实验所涉及的各种参数和实验环境，借此来重现源代码；为了防止出现极端情况，将该论文实验重复运行了10次并获得平均值和相应的标准差. 对于其他的基线方法，直接使用DCRN中列出的相应结果. 对于HMIPDC，ACM使用学习率为0.001的Adam^[29]算法来优化高级特征表示，Citeseer、DBLP和AMAP使用的学习率为0.0001，并且都采用提前停止策略来避免过拟合，之后再将所有数据集的学习率修改为0.01来进一步优化模型. 根据参数敏感性测试的结果，将所有数据集里用于平衡损失函数的超参数 $ \mu $、 $\eta $分别设置为0.01、1.0；嵌入维度 $d'$统一设置为128. 通过模型训练的结果不断调整超参数 $ {\gamma _{\rm{n}}} $、 $ {\gamma _{\rm{p}}} $的大小，最终得到：ACM的超参数 $ {\gamma _{\rm{n}}} $、 $ {\gamma _{\rm{p}}} $设置为0.6、0.2；Citeseer的超参数 $ {\gamma _{\rm{n}}} $、 $ {\gamma _{\rm{p}}} $设置为0.9、0.3；DBLP的超参数 $ {\gamma _{\rm{n}}} $、 $ {\gamma _{\rm{p}}} $设置为0.7、0.2；AMAP的超参数 $ {\gamma _{\rm{n}}} $、 $ {\gamma _{\rm{p}}} $设置为0.5、0.1.

HMIPDC和8种基线方法在4个数据集上的聚类结果如表2所示. 表中，加粗的字体表示最优的结果. 根据表2中的结果，得到以下观察.

1）在4个数据集中，HMIPDC相较于其他基线方法在4个评价指标上都有较佳的性能表现. 例如在DBLP数据集中，HMIPDC在ACC、NMI、ARI和F1上分别超过了最佳基线方法0.68%、0.46%、1.79%和0.48%.

2）K-means、AE和IDEC方法在各个指标上都跟HMIPDC相距甚远. 这是因为它们仅仅考虑了节点属性信息来进行聚类，忽略了图结构对于后续聚类任务的影响. 相对而言，HMIPDC同时整合了图结构和节点属性信息，将其统一到一个框架中提取低维表征，并不断优化聚类目标，进而大大提升了聚类效果.

3）虽然SDCN和DFCN方法有效整合了图结构和节点属性信息，但是它们将编码器部分学到的属性信息过度引入到潜在空间中，使得低维表征包含了很多冗余信息，降低了低维表征的质量. 而HMIPDC则采用高阶互信息最大化策略来探索低维表征和节点属性信息之间的关系，使得获得的表征更具有辨别力.

4）相较于最佳的基线方法DCRN，HMIPDC在许多指标上也有不错的性能提升. DCRN虽然通过对齐软分配分布和目标分布来指导网络学习，但是它并没有对模型学习到的预测标签进行区分，导致很多错误的标签被用来指导学习，降低了聚类效果. 相反，HMIPDC使用伪标签技术将置信度较高的样本加入到自监督学习中，减少了错误的标签信息对于后续表征学习的影响，提高了聚类性能.

通过消融实验来证明互信息监督模块和伪标签技术在HMIPDC中的重要性，进一步表明HMIPDC模型的有效性. 首先以由图注意力自编码器和DDC聚类损失为主要部分构成的一个框架作为基线(AD)，因为它是HMIPDC模型进行训练的一个主体框架. AD-MI、AD-PL和AD-MI-PL分别表示添加了互信息监督模块、伪标签技术和两者都添加的方法. 消融研究结果如表3所示. 表中，加粗的字体表示最优的结果.

由表3可以看出：1）AD-MI和AD-PL在4个数据集上的所有指标都优于AD. 这表明互信息监督模块和伪标签技术确实能提升聚类效果. 2）AD-MI-PL在4个数据集上的所有指标都优于AD、AD-MI和AD-PL. 原因在于AD-MI-PL在利用高阶互信息学到低维表征后，选取了高置信度的预测标签作为伪标签来进行自监督学习，通过不断地迭代优化，使得生成的低维表征更易于后续的聚类任务. 3）特别地，在AMAP数据集中，AD-MI-PL相较于AD在ACC、NMI、ARI和F1这4个评价指标上分别有了8.16%、7.85%、11.06%和9.62%的提升，这主要得益于AD-MI-PL通过高阶互信息和伪标签有效地整合了图结构和节点属性信息，使得提取到的低维表征拥有原始图的核心特征，从而让聚类性能在大规模图上有极大的提升.

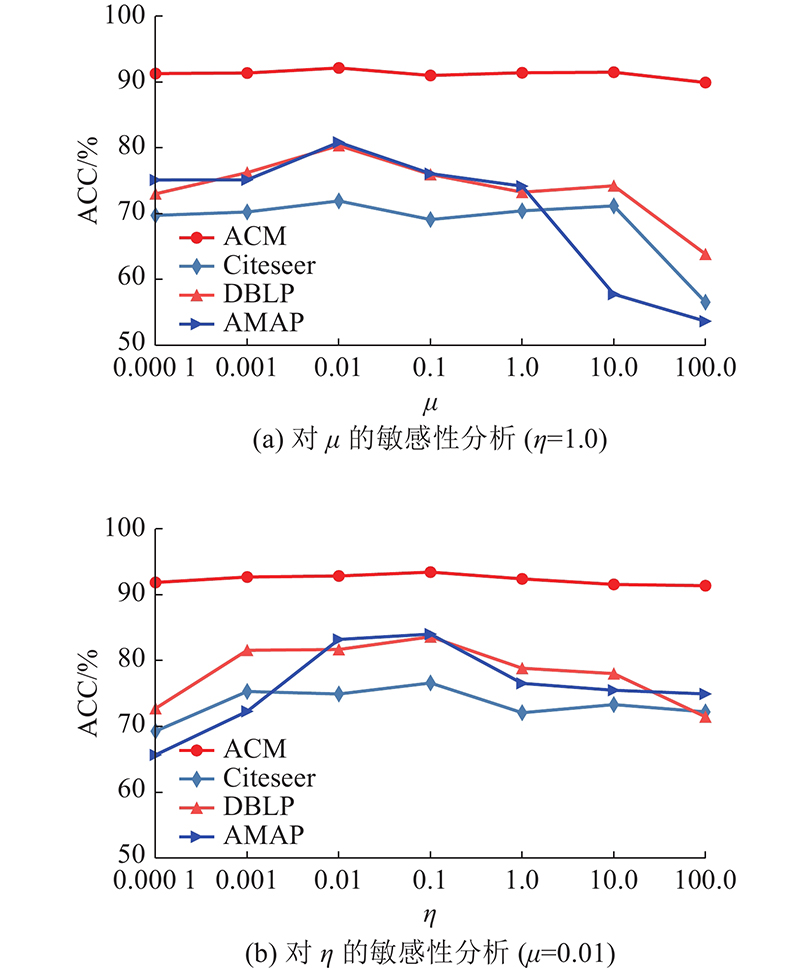
通过4个数据集中的ACC来探讨HMIPDC对目标函数的权衡超参数 $\mu $和 $\eta $的敏感性. 具体来说，固定 $\eta = 1.0$，修改 $\mu $的值；固定 $\mu = 0.01$，修改 $ \eta $的值，其结果如图2所示. 可以看出，ACM数据集对于 $\mu $和 $ \eta $的变化都不敏感，具有较好的稳定性；在Citeseer、DBLP和AMAP中，虽然HMIPDC的性能在一定程度上会受参数变化的影响，但是当 $\mu \in \left[ {0.001,1.0} \right]$、 $\eta \in \left[ 0.1, 10.0 \right]$时仍有较好的稳定性；设置 $\mu = 0.01$和 $ \eta = 1.0 $是较合理的，因为这时模型具有较高的ACC.

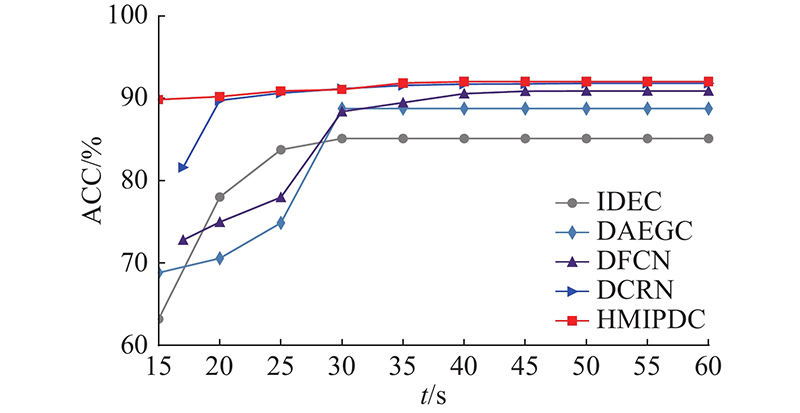
为了探究模型的训练时间对于聚类效果的影响，在ACM数据集中，记录了IDEC、DAEGC、DFCN、DCRN和HMIPDC这5种方法在不同训练时间t的ACC，结果如图3所示. 可以看出，相较于其他4种方法，HMIPDC在所有的训练时间都能保持较高的ACC. 特别地，如果训练时间不足30 s，由于其他4种方法都须先耗费一定的时间对模型进行不同程度的预训练，导致模型的ACC在训练初期表现不佳；而HMIPDC并不需要进行预训练，模型能有更多时间进行本身的优化，从而获得较高的ACC.

为了更加直观地验证HMIPDC的有效性，在ACM数据集上，将IDEC、SDCN、DFCN、DCRN和HMIPDC使用t-分布随机邻域嵌入(t-distributed stochastic neighbor embedding, t-SNE)^[30]算法将模型学习到的低维表征投影到二维空间并进行可视化，可视化结果如图4所示. 图中，不同的颜色表示不同的簇. 可以看出，较于原始数据，每种模型方法都有不错的可视化结果. 对于图4(b)、(c)，虽然不同颜色之间有明显的边界，但是它们每种颜色的内部混杂了许多其他颜色的节点，说明它们生成的低维表征还不能较好地区分不同类别的节点. 对于图4(d)、(e)，虽然同一颜色的点能彼此靠近，但是每种颜色的边界却不清晰，导致它们不能较好地区分不同类别的相似节点. 图4(f)的可视化结果最好，同种颜色的点紧密地聚集在一起，不同颜色的点彼此分离，表明HMIPDC生成的低维表征具有更清晰的结构，可以更好地揭示数据之间的内在聚类结构.

提出一种高阶互信息最大化与伪标签指导的深度聚类模型HMIPDC，该模型通过高阶互信息最大化策略充分利用图的拓扑结构和节点的属性信息，从原始图中获得更有价值的节点特征. 采用了一种结合多跳邻近矩阵的自注意力机制，驱使目标节点在进行聚合操作时能够关注重要的邻居节点，从而有效克服数据稀疏性和复杂性对聚类结果的影响. 为了减少训练过程出现的噪声影响，HMIPDC使用DDC聚类损失函数来衡量聚类性能，并从模型的聚类预测结果中选取置信度较高的样本作为伪标签，用于指导低维表征的学习，进而实现更优的聚类性能. 在4个数据集上进行的聚类任务、消融研究、参数敏感性分析、实验时间分析和聚类可视化分析，充分表明了HMIPDC聚类性能的有效性和优越性.

本研究只是在同质属性网络中进行深度聚类研究. 在未来的工作中，将会进一步考虑拥有不同类型节点的异质信息网络^[31]，尝试利用异质信息网络中丰富的语义信息来完成聚类任务. 另外，现实世界中的图数据大多数都存在缺失，如何在有缺失的数据中有效地进行聚类任务也将是下一步的研究重点.