时间列数据是按某一给定采样频率,对某一过程进行监测得到的一段实值数据波形,随时间戳变化连续记录,不受系统环境之类的因素影响[1]. 近年来,随着信息技术的发展,时间序列的应用越来越广泛,如灾害监测、安全分析、金融商业等领域[2],无时无刻都在产生大量带有时间属性的数据. 如何对时间序列进行高效分类[3-4]是流式数据事件分析和数据挖掘的基础,也是领域研究的热点和难点. 以矿山灾害监测预警系统为例,利用部署在矿山周围的传感器对微震数据进行实时存储,矿山灾害事件通常会持续几秒至几十秒,每个灾害均为时间序列事件,对这些灾害事件进行类型划分[5],有利于归纳总结各种类型灾害的特征,对于灾害数据分析和灾害救援工作都具有非常重要的意义.
针对上述问题,本研究提出基于Gram矩阵[9]的T-CNN时间序列分类方法,在保留时序性的基础上,改进CNN模型在全连接层的平方损失函数[10],提高分类的准确性和效率. 主要贡献如下:1)针对时间序列矩阵转换后损失时间属性的问题,提出基于Gram矩阵的转化方法,将时间序列无损转换为时间域图像,并采用小波阈值去噪法滤除正态背景噪声[11-12];2)在将转换后的时间域图像输入到卷积神经网络后,为了加快网络收敛速率,在卷积层引入Toeplitz[13]卷积核矩阵,实现矩阵乘积替换传统卷积运算;3)在此基础上,提出T-CNN分类模型,在全连接层引入Triplet网络[14]思想,计算同类间与不同类间的相似度,优化CNN模型的损失函数,从而加快模型收敛速率,提高分类的准确性.
1. 相关工作
目前,国内外学者对时间序列分类方法进行了深入研究,取得了一定的研究成果,主要包括基于符号化聚合近似、基于时间域距离、基于Shapelet、基于深度学习的时间序列分类方法.
在基于符号化聚合近似的分类方面,Fang等[15]提出基于符号化聚合近似(symbolic aggregate approximation,SAX)的方法进行分类,将序列进行分段,每一段转化为一个对应的字母,统计字母出现的频率进行分类,该方法利用了聚合思想,对时间序列进行有效降维,可以提高分类的速率,但牺牲了时间序列的大量数据点,分类的准确性不高; El-Shorbagy等[16]提出基于时间序列数据趋势转折点(trend turning points,TTP)的分类方法,通过提取时间序列本身的趋势特征,将具有相同趋势的序列为一类,该方法须对每段时间序列的极值点、拐点之类的特征点进行统计分析,对特定规律的数据集分类有较好的效果,但对于数据规模大的数据集和趋势变化剧烈的数据集,分类效果较差.
在基于时间域距离的分类方面,Vianna等[17]提出基于时间域距离(time domain distance,TDD)的时间序列分类方法,通过计算不同序列之间的欧式距离来反映时间序列之间的相似性,距离越近相似性越高,该方法只使用距离公式,计算简单分类快速,总体的分类准确性较低;Cheng等[18]提出基于间隔的支持向量机(support vector machine, SVM)分类方法,该方法将时间序列划分为等长的间隔,计算每个间隔的均值和标准差后,使用支持向量机进行分类。虽然该方法使用了分类器,有助于提高分类效率,但该方法将时间序列看作普通离散数据点集,损失了时间属性,导致分类准确性不高.
本研究针对上述问题,提出基于Gram矩阵的T-CNN时间序列分类方法,使用Gram矩阵将时间序列无损地转换为时间域图像,保留了时间序列的时序性,并提出基于卷积神经网络的T-CNN分类模型,优化模型损失函数,提高分类的准确性和效率.
2. 时间序列的Gram矩阵转换
定义1 时间序列. 设
定义2 时间序列事件. 由时间序列中超过阈值范围第1个异常点发起,并持续一段时间的连续异常数据的集合,表示为
由以上定义可知,时间序列事件均具有时间属性. 针对现有时间序列矩阵转换方法损失时间属性的问题,通过时间序列的Gram时间域图像无损转换法,实现时间序列的全信息无损转换.
2.1. 正态噪声滤除
Gram矩阵转换后的时间域图像直方图会呈现正态分布,正态噪声(多为高斯噪声)的存在会直接影响时间域图像转换的准确性. 因此,在使用Gram矩阵转换时间序列前先进行数据预处理,用小波阈值去噪法滤除数据中携带的正态背景噪声.
去噪步骤如下:1) 信号的小波分解. 选择一个小波并确定一个小波分解的层次
时间序列事件中同类事件通常具有相同的特征规律,但由于事件发生的位置及强度都不相同,感知到的事件数据均不在同一尺度下. 因此,使用时间序列归一化公式,使数据各个特征维度对目标函数的影响权重一致. 数据归一化公式如下:
式中:
2.2. 基于Gram矩阵的时间域图像转换
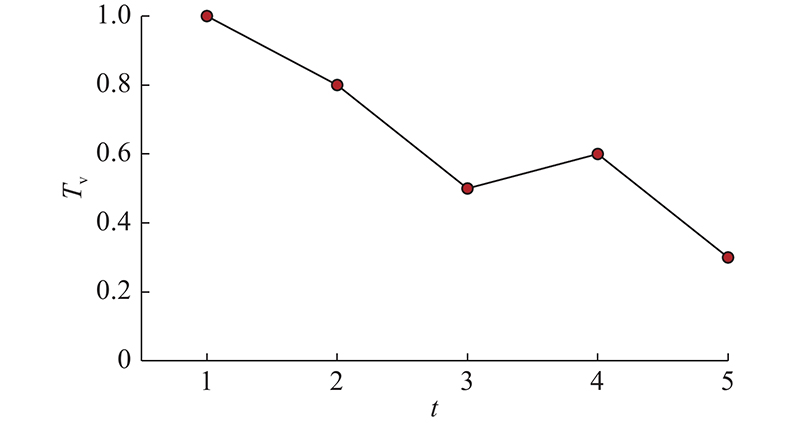
由于时间序列存在时序性,按照时间先后顺序呈现不同的规律分布. 时间序列的时序性是决定其分类类别的重要属性. 因此,引入Gram矩阵进行时间域图像转换,在保留时间序列时序性的同时,无损地将时间序列片段转换为
Gram矩阵是由每一对向量的内积按如下形式构成的矩阵:
式中:
式中:
图 1
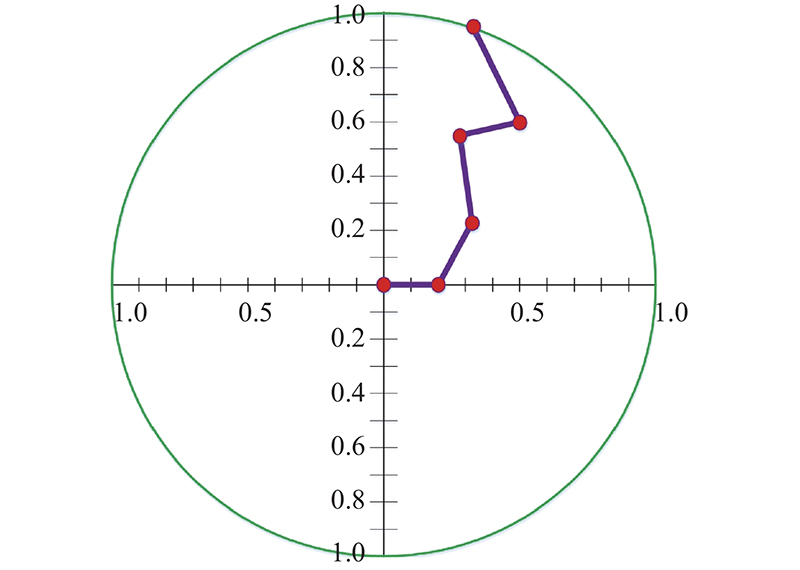
对时间序列
式中:
图 2
当
图 3
3. 时间域图像的T-CNN分类方法
将时间序列转化为Gram时间域图像,之后将其作为输入矩阵输进卷积神经网络中进行分类. 针对卷积神经网络存在卷积层计算复杂、训练速度慢的问题[26],提出基于Toeplitz矩阵乘积的方法来替换卷积层的卷积运算,并在损失函数中引入Triplet网络思想提高分类的效率和准确性.
3.1. 基于Toeplitz矩阵乘积的卷积运算
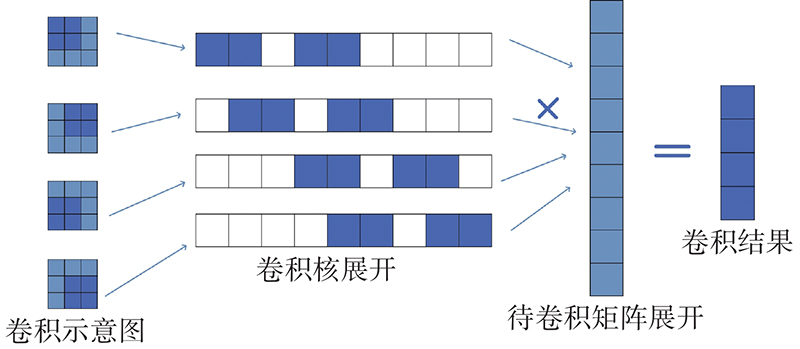
传统卷积运算如图4左侧所示,其中深色的方块代表卷积核矩阵,当卷积时,卷积核在待卷积图像上按设定步长依次移动,与卷积核重和的图像部分,相应进行乘积计算,直到卷积核遍历完整个图像,得到的矩阵即为卷积结果,计算复杂度极高. 针对该问题,引入Toeplitz矩阵乘积来替换卷积运算.
图 4
图 4 Toeplitz矩阵转换过程示意图
Fig.4 Schematic diagram of Toeplitz matrix transformation process
定义3 Toeplitz矩阵. 每条自左上至右下的斜线上的元素相同的矩阵为Toeplitz矩阵,具有
如图4所示为Toeplitz矩阵转换过程示意图. 把卷积核矩阵按输入图像的行序依次展开,与输入图像重合部分卷积核直接保留,其他部分用零填充,卷积核每按步长移动一次得到新的卷积核展开矩阵,这些矩阵共同构成组合矩阵,即Toeplitz矩阵. 将输入图像按行序依次展开为列向量,Toeplitz矩阵的每行与列向量的乘积就等价于原始的一次卷积核卷积,使Toeplitz矩阵的乘积替换卷积运算.
3.1.1. Toeplitz卷积核矩阵构建
要将卷积计算替换为Toeplitz矩阵乘积的运算,首先须将卷积核矩阵H构建为Toeplitz卷积核矩阵Ht. 给出任意卷积核矩阵H:
其对应的Toeplitz卷积核矩阵构建步骤如下.
1) 将卷积核矩阵的每一行元素生成一个小Toeplitz矩阵,卷积核矩阵尺寸为
2) 将步骤1)中得到
步骤1)中举的例子由式(9)得到
3.1.2. Toeplitz矩阵的卷积运算
由3.1.1得到Toeplitz卷积核矩阵
式中:
例如,
基于Toeplitz矩阵的卷积运算可以得到
再按
通过Toeplitz矩阵的乘积可以有效地替换卷积运算. 在时间复杂度方面,输入图像尺寸为
3.2. T-CNN模型分类
CNN网络的全连接层在进行收敛运算时,须使用损失函数进行约束. 在训练模型的损失函数中引入Triplet网络思想,构建T-CNN模型进行时间序列分类.
设由
式中:
CNN使用梯度下降法对
式中:
式中:
由式(14)和(15)可以看出,在每次反向迭代中,
式中:
在基于Triplet网络的T-CNN模型的损失函数中,加入同类间特征差异函数和不同类间特征差异函数,使权值调整的过程参数更快提取差异较大的特征.
4. 实验分析
实验数据集采用矿山微震大数据平台产生的10万条时间序列数据,感知器采样频率为1000条/s. 数据集包含3种类型的矿山微震信号的时间序列事件波形. 训练集规模占总数据集的40%,测试集规模占总数据集的60%,模型训练框架为Tensorflow,实验软硬件环境如表1所示.
表 1 实验软硬件环境
Tab.1
| 环境 | 配置 |
| CPU | Intel Core(TM)i7-7500U |
| 内存 | 8 GB |
| 硬盘容量 | 1 TB |
| 操作系统 | Windows 8.1 (64bit) |
| 编程语言 | Java |
| JDK版本 | 1.7.0_45 |
为了防止局部过收敛,卷积神经网络结构设置2层卷积层. 卷积层1采用大小为
4.1. 模型迭代次数对比
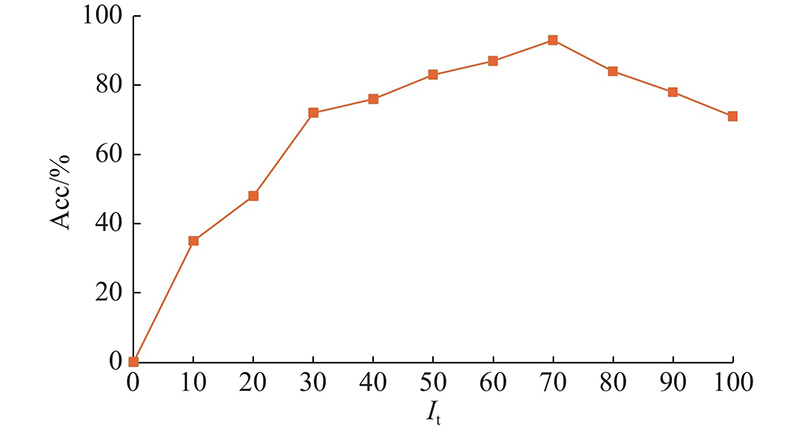
T-CNN模型通过不断前向传导调节模型至最优状态,其中主要可调参数为学习率和迭代次数. 此实验过程中设置学习率为0.005,调节迭代次数. 如图5所示为不同迭代次数下时间域图像分类准确性的变化,准确率为分类正确的样本数占总体样本数的比例. 图中,It为迭代次数,Acc为分类准确率. 可以看出,当迭代次数在40次以内时,分类总准确性提高较快;当迭代次数为40~70次时,分类总准确性提高幅度变缓;当迭代次数为70次时,分类总准确性最高,约为93%;当迭代次数大于70次时,分类总准确性下降. 由此得知,迭代次数的增加在一定范围内能提高分类精度,但超过范围后会导致模型过拟合,分类准确性下降.
图 5
4.2. 分类准确率对比
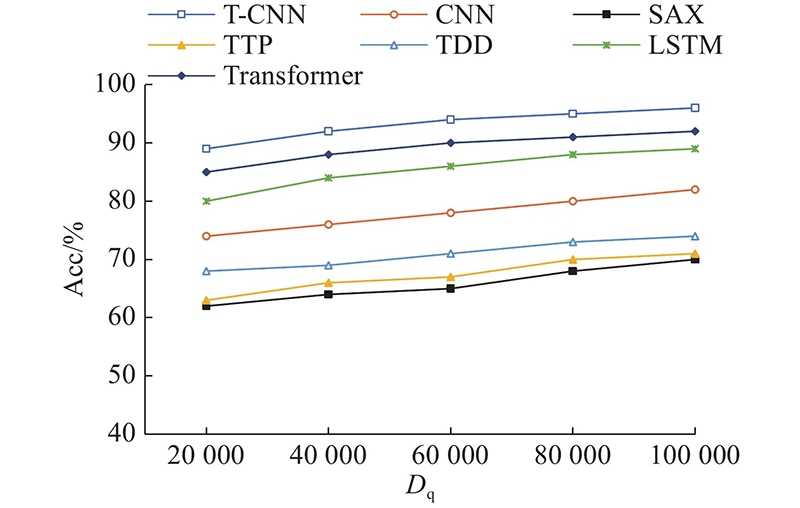
如图6所示为分类模型分类准确率对比图. 图中,Dq为数据量. 对比方法为符号化聚合近似SAX方法[15]、趋势转折点TTP方法[16]、时间域距离TDD方法[17]、CNN模型方法[20]、门控机制的LSTM模型[21]和多头自注意力机制的Transformer模型[22]. 其中,SAX采用每5个数据点聚合成一个符号;TTP选取包括最大值在内的最大3个转折点和包括最小值在内的最小3个转折点;TDD设定距离阈值为0.5;CNN模型结构和参数设置和T-CNN模型相同;LSTM隐藏层数目为512;Transformer采用默认设置. 后续实验都采用上述实验参数设置. 由图6可知,随着数据量的增加,7种方法分类准确率都在提高后趋于平缓. T-CNN模型由于使用Gram矩阵将时间序列转换为时间域图像,可以完整的保留时间序列的属性,分类准确率要明显好于其他方法.
图 6
图 6 不同分类模型分类准确率对比图
Fig.6 Comparison of classification accuracy of different classification models
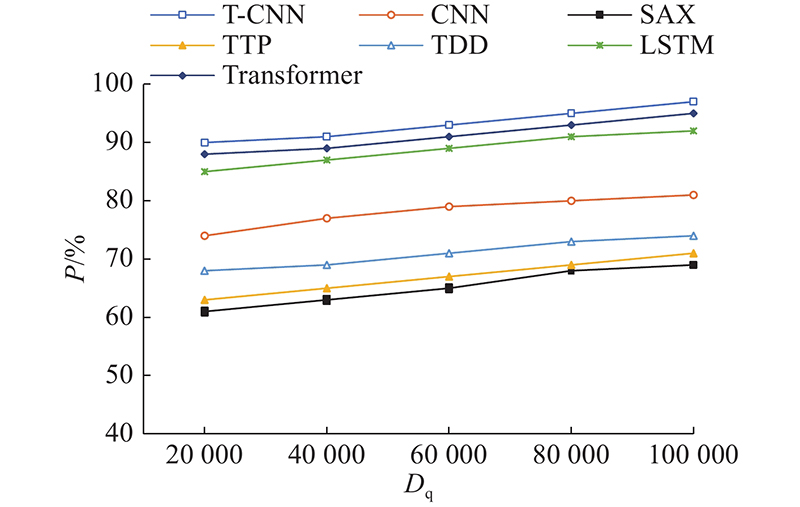
4.3. 分类精确率对比
精确率为预测为某类别的样本数中真正为此类样本的占比,表达式如下:
式中:
图 7
图 7 不同分类模型分类精确率对比图
Fig.7 Comparison of classification precision of different classification models
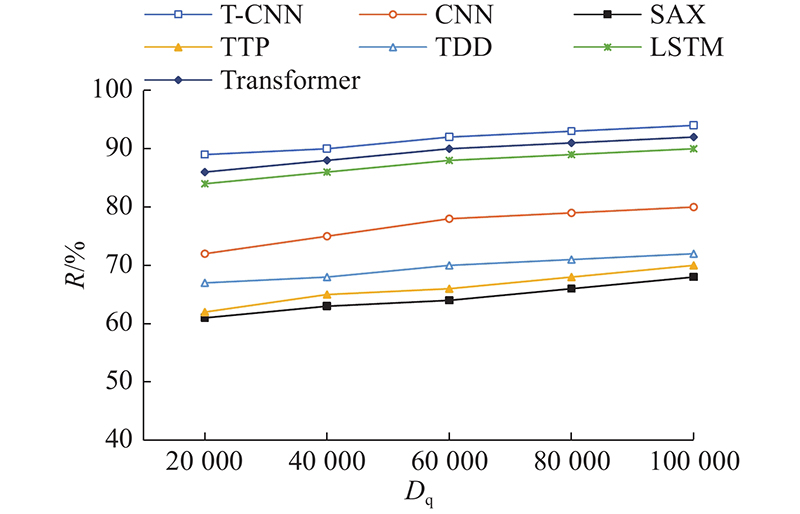
4.4. 分类查全率对比
查全率为某一类别样本中被检测出来的占比:
图 8
图 8 不同分类模型分类查全率对比图
Fig.8 Comparison of classification recall of different classification models
4.5. F1值对比
F1值是精确率和查全率的调和平均:
图 9
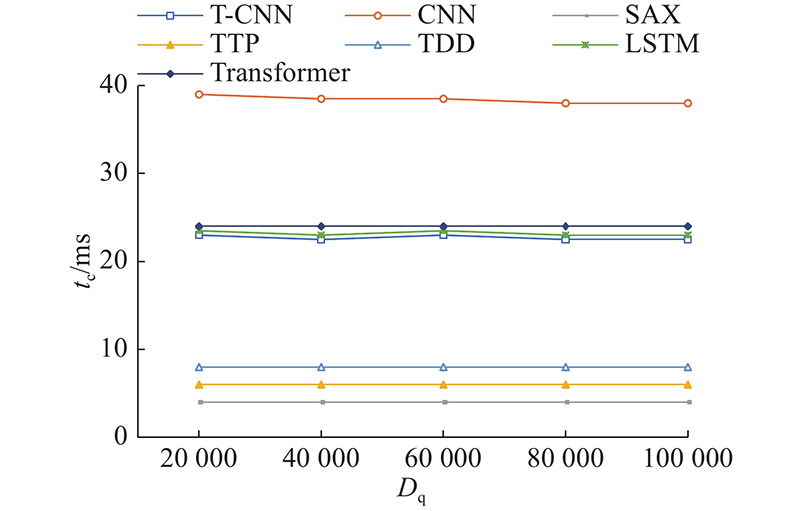
4.6. 分类效率对比
如图10所示为T-CNN、SAX[15]、TTP[16]、TDD[17]、CNN[20]、LSTM[21]和Transformer[22]7种方法对单个时间序列进行分类的效率对比图. 图中,tc为分类时间. 可以看出,随着数据量的增加,T-CNN和CNN模型加快收敛速度,分类时间会有所减少. SAX采用聚合思想,在对时间序列分段后,变为字母序列再分类,牺牲了分类的准确性,因此分类速度最快. TTP须寻找极值点和转折点,比SAX分类慢. TDD要对所有数据点进行距离计算,分类时间比SAX和TTP要多. CNN模型由于卷积运算和参数不断迭代计算,分类速率最慢. 而T-CNN模型在卷积层使用Toeplitz矩阵计算,并改进损失函数,收敛速率加快,相对CNN模型减少了近50%的分类时间.
图 10
图 10 不同分类模型分类效率对比图
Fig.10 Comparison of classification efficiency of different classification models
4.7. Toeplitz卷积与传统卷积运行时间对比
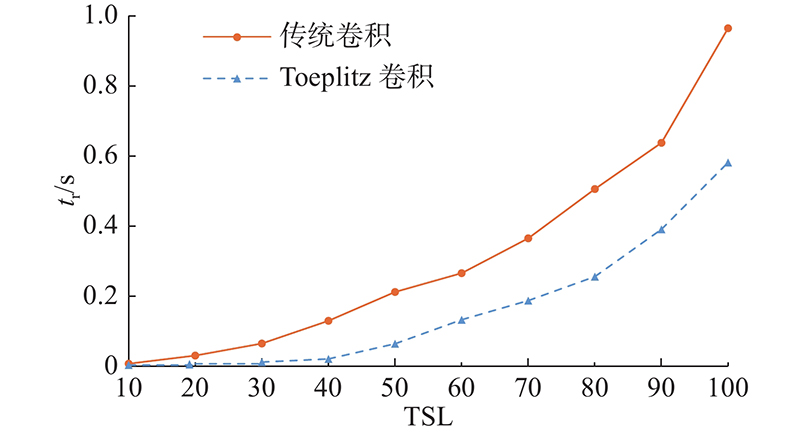
对基于Toeplitz矩阵乘积卷积和传统卷积进行运算时间对比,实验过程中取
图 11
图 11 Toeplitz卷积与传统卷积运行时间对比图
Fig.11 Comparison of Toeplitz convolution and traditional convolution running time
5. 结 语
基于Gram矩阵的T-CNN时间序列分类方法对时间序列用小波阈值去噪后,使用Gram矩阵将时间序列无损转换为时间域图像;将时间域图像作为输入矩阵输入到T-CNN模型进行分类,在卷积层中引入Toeplitz卷积核矩阵,用2个矩阵的乘积替换卷积运算;在全连接层引入Triplet网络思想中同类和不同类图片的输出差值来改进CNN的损失函数. 实验表明,基于Gram矩阵的T-CNN时间序列分类方法在分类的准确率、精确率、查全率、F1值上均优于现有方法. 但在基于Gram矩阵转化时间序列进行分类时,须对时间序列进行分段截取处理,下一步将考虑在连续时间序列流上进行相似的分类方法.
参考文献
A review on outlier/anomaly detection in time series data
[J].
基于聚类和探测精英引导的蜻蜓算法
[J].
Dragonfly algorithm based on clustering and detection elite guidance
[J].
Guest editorial for special issue on time series classification
[J].DOI:10.1109/JAS.2019.1911741 [本文引用: 1]
Future of oil and gas trade of Kazakhstan in the European Union context: application of time series analysis
[J].DOI:10.2478/vjbsd-2020-0011 [本文引用: 1]
Multistage identification method for real-time abnormal events of streaming data
[J].
A novel trend based SAX reduction technique for time series
[J].DOI:10.1016/j.eswa.2019.04.026 [本文引用: 1]
InterpretTime: a new approach for the systematic evaluation of neural-network interpretability in time series classification
[J].
卷积神经网络研究综述
[J].DOI:10.11897/SP.J.1016.2017.01229 [本文引用: 1]
Review of convolutional neural network
[J].DOI:10.11897/SP.J.1016.2017.01229 [本文引用: 1]
On the computational completeness of matrix simple semi-conditional grammars
[J].
Emulated order identification for models of big time series data
[J].DOI:10.1002/sam.11504 [本文引用: 1]
A coupled convolutional neural network for small and densely clustered ship detection in SAR images
[J].
面向时空图建模的图小波卷积神经网络模型
[J].DOI:10.13328/j.cnki.jos.006170 [本文引用: 1]
Graph wavelet convolutional neural network for spatiotemporal graph modeling
[J].DOI:10.13328/j.cnki.jos.006170 [本文引用: 1]
Asymptotic spectra of large matrices coming from the symmetrization of Toeplitz structure functions and applications to preconditioning
[J].
Two-stage method based on triplet margin loss for pig face recognition
[J].DOI:10.1016/j.compag.2022.106737 [本文引用: 1]
A new mining framework with piecewise symbolic spatial clustering
[J].
Numerical investigation of mixed convection of nanofluid flow in a trapezoidal channel with different aspect ratios in the presence of porous medium
[J].
Time-domain distance protection of transmission lines based on the conic section general equation
[J].DOI:10.1016/j.jpgr.2021.107740 [本文引用: 6]
Sparse multi-output Gaussian processes for online medical time series prediction
[J].DOI:10.1186/s12911-020-1069-4 [本文引用: 1]
融合选择提取与子类聚类的快速Shapelet发现算法
[J].DOI:10.13328/j.cnki.jos.005912 [本文引用: 1]
Fast Shapelet discovery algorithm combining selective extraction and subclass clustering
[J].DOI:10.13328/j.cnki.jos.005912 [本文引用: 1]
融合时间序列与卷积神经网络的网络谣言检测
[J].
Network rumor detection combining time series and convolutional neural network
[J].
State-of-health estimation and remaining useful life for lithium-ion battery based on deep learning with Bayesian hyperparameter optimization
[J].
Time series forecasting and classification models based on recurrent with attention mechanism and generative adversarial networks
[J].DOI:10.3390/s20247211 [本文引用: 6]
Hybrid LSTM-transformer model for emotion recognition from speech audio files
[J].DOI:10.1109/ACCESS.2022.3163856 [本文引用: 1]
Time-series averaging using constrained dynamic time warping with tolerance
[J].DOI:10.1016/j.patcog.2017.08.015 [本文引用: 1]
Distributed fast Shapelet transform: a big data time series classification algorithm
[J].DOI:10.1016/j.ins.2018.10.028 [本文引用: 1]
A deep learning framework for time series classification using relative position matrix and convolutional neural network
[J].DOI:10.1016/j.neucom.2019.06.032 [本文引用: 1]
基于改进快速区域卷积神经网络的视频SAR运动目标检测算法研究
[J].DOI:10.11999/JEIT200630 [本文引用: 1]
Research on video SAR moving target detection algorithm based on improved faster region-based CNN
[J].DOI:10.11999/JEIT200630 [本文引用: 1]