现有的矩阵变换器输入侧谐振抑制方法主要包括被动阻尼法[15-17]和主动阻尼法[18-21]两大类. 前者引入结构简单的电阻,能够起到阻尼系统谐振的目的. 阻尼电阻对系统的性能影响较大,如何兼顾谐振抑制、高频段谐波衰减及系统损耗是被动阻尼法的核心问题. 主动阻尼法采用算法实现谐振的抑制,许宇翔等[18]提出采集输出侧电流中高频谐波分量至输出侧闭环控制,以实现矩阵变换器的输入谐振抑制. Lei等[19]提出基于电流预测策略的谐振抑制新型方法. 陆松等[20]提出通过反馈滤波电感电流与滤波电容电压中的高频量至闭环控制中的谐振方法. Nunokawa等[21]提出基于复杂框架下的矩阵变换器谐振抑制方法,该方法通过高通滤波器(HPF)采集输入侧中主要频率点附近的多个谐波电流,但HPF的过渡带较长,容易引入谐振点频率段外的无用信号,是开环的控制方法,静态与动态性能不足.
针对矩阵变换器输入侧谐振问题及现有抑制方法存在的缺陷,本文综合多个参数约束条件,获取滤波电感和电容的最优参数值,将抑制谐振点附近的谐波作为被动阻尼法中阻尼电阻的设计依据. 将该方法的思想进行拓展,提出采用陷波滤波器(notch filter)提取滤波电容电压中特定谐波至闭环控制,以有效地抑制输入谐振点附近的谐波电流. 通过仿真结果验证了所提方法的有效性.
1. 矩阵变换器输入侧谐振产生的原因分析
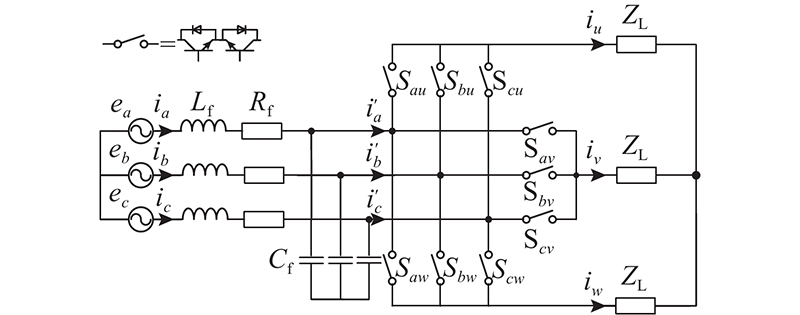
如图1所示为常规的三相-三相矩阵变换器(3-3MC)拓扑结构. 图中,ea、eb和ec分别为三相输入电压,ia、ib和ic分别为三相输入电流,Lf、Rf分别为滤波电感及等效电阻,Cf为滤波电容,
图 1
图 1 三相-三相矩阵变换器拓扑图
Fig.1 Topology of three-phase to three-phase matrix converter
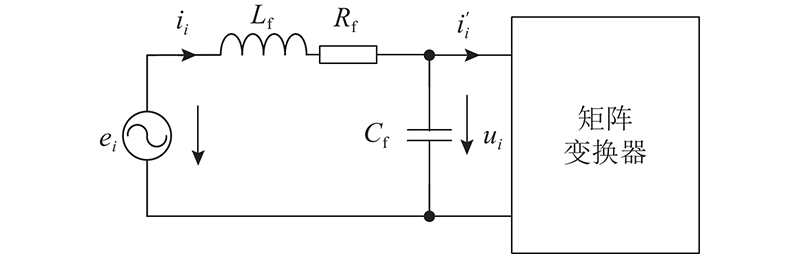
假设输入为三相对称电压信号,输出为三相对称负载,则3-3MC可以等效为3个独立的单相-单相矩阵变换器,输入侧等效电路如图2所示.
图 2
对于该等效电路,采用基尔霍夫电压定律,可得矩阵变换器输入侧电压与电流之间相互关系的时域表达式:
式中:ui (i = a、b、c)为输入端滤波电容电压,ii为输入电流,
对式(1)进行拉氏变换,可得s域下输入滤波器中电压与电流相互关系的表达式:
由式(2)可得,输入电流与输入电压、输入端电流之间的s函数关系式为
由式(3)可得,该s函数分母中固有频率
分析式(4)可知,在无阻尼电阻的情况下,滤波器中Cf ≪ Lf,滤波电感等效电阻Rf ≪ 1 Ω,则阻尼系数ξ' ≈ 0,因此矩阵变换器输入LC滤波器是近似二阶无阻尼系统,输入电压与输入端电流中谐振频率点附近的谐波容易激发产生输入谐振电流.
2. 被动阻尼法的实现
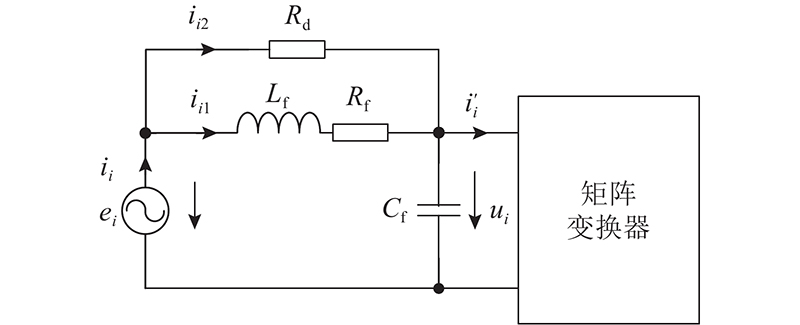
为了抑制输入LC滤波器引起的输入电流谐振,一般采用在滤波电感Lf或滤波电容Cf上并联或串联电阻的方式. 综合考虑谐振抑制效果和系统损耗降低等,常采用在电感上安装阻尼电阻Rd的被动阻尼法抑制谐振,等效电路如图3所示.
图 3
图 3 被动阻尼法下的输入侧等效电路图
Fig.3 Equivalent circuit diagram of input side based on passive damping method
从图3可知,输入LC滤波器中电压与电流相互关系的时域表达式为
式中:ii1、ii2分别为滤波电感和阻尼电阻的支路电流,Rd为阻尼电阻.
对式(5)进行拉氏变换可知,s域下输入LC滤波器中电压与电流相互关系的表达式为
由式(6)可得,输入电流与输入电压、输入端电流之间的s函数关系式为
由于滤波电感的等效电阻Rf ≪Rd,则此时ωn和图3所示滤波器的阻尼系数ξ的表达式分别为
从式(8)可知,在输入电感上并联Rd后,增大了ξ,但ωn几乎没有改变,因此系统的稳定性得到了提升. 在被动阻尼法中引入Rd后,ξ与Rd成反比. 如何设计合适的Rd使得ξ达到合理的水平,可以实现在不明显影响高频谐波衰减能力的同时,抑制了输入电流中谐振点附近谐波电流的幅值,这是被动阻尼法中参数优化设计的关键.
3. 矩阵变换器输入滤波器的优化设计
3.1. 滤波器参数的优化设计方法
1) 截止频率fc取值为开关频率fs的1/10~1/5,且大于输入频率fi的10倍.
2) 滤波器的ξ取值为
3) 滤波电感上的基波压降不超过输入电压的3%.
4) Rd的功率损耗小于最大功率的0.5%.
5) 滤波电容的功耗不超过最大功率的5%.
为了提高滤波器在开关频率点处的高频谐波抑制能力,童诚[17]定义滤波器的fc为fs的1/5~1/2. 为了减少引入Rd后高频段衰减能力不足带来的高频谐波抑制效果的下降,将fc取为fs (10 kHz)的1/10~1/5,fc大于fi(50 Hz)的10倍. 综合上述条件,约束条件1)中截止频率设为500~2 000 Hz.
输入电压的幅值为
滤波电容电感与fc之间的关系如下:
由式(9)和约束条件1)可得,滤波电感的理论值为Lf = 1.8 mH. 由于常见的滤波电感取值为0.5~3.0 mH,一般步进为0.5 mH,因此实际滤波电感取为1.5 mH,则此时系统的实际截止频率为948 Hz,即符合约束条件1)的要求.
根据电感上电流与电压之间的关系,输入LC滤波器中电感上电压uL(t)的表达式为
式中:Im为输入电流的幅值. 矩阵变换器最大输入功率Pi = 2 000 W,输入电压幅值Em =
从式(10)可知,电感引起的压降与输入电压幅值之比为
从式(11)可知,电感引起的压降比λu = 2.6% < 3%,即符合约束条件3)的要求.
阻尼电阻的损耗表达式为
从式(12)可得ξ =
输入滤波电容上的损耗表达式为
从式(13)可得,Pc与Pi的比值为
从式(14)可知,电容功耗与最大输入功率的比值为λc = 3.6% < 5%,符合约束条件5)的要求.
3.2. 阻尼电阻的设计步骤
现有输入性能方面的规定包括:国家标准GB/T14549-93和国际电工委员会IEC技术分会颁布的标准IEC6100-3-2. 前者规定了输入电流和滤波电容电压总谐波畸变率(THD)均小于5%,各奇数次谐波含有率小于3%. 后者规定了设备中输入电流奇数次谐波含量,由于谐振频率为948 Hz,该频率为基波频率的19次,以10%的滤波电感误差、5%的电容误差为例,谐振频率为882~1 197 Hz,即谐振频率段为基波的16~24次谐波. 假设输入电流中无偶数次倍谐波和3的倍数次谐波,需要研究并分析所设计的阻尼电阻对输入电流中13、17、19、23和25次共5个特定谐波的抑制效果,作为衡量阻尼电阻抑制谐振效果的依据之一.
抑制不同次谐振电流的理想阻尼电阻计算表达式为
式中:ii为标准IEC6100-3-2规定的第i次谐波电流含量的上限,λi为经快速傅里叶变换(FFT)分析后的第i次谐波电流的实际含有率,i0为基波电流幅值.
标准IEC6100-3-2对输入电流谐波含量进行限定,其中13~25次谐波含量规定如下:13次谐波含量i13 = 0.21 A,17次谐波含量i17 = 0.132 A,19次谐波含量i19 = 0.118 A,23次谐波含量i23 = 0.098 A,25次谐波含量i25 = 0.09 A. 无阻尼条件(Rd = +∞) 下的仿真参数如表1所示. 若输出电流设定值为6.5 A,则输入电流中13~25次谐波电流含有率分别为:λ13 = 5.86%、λ17 = 13.98%、λ19 = 119.7%、λ23 = 18.98%、λ25 = 10.76%,基波电流幅值为i0 = 1.661 A. 从式(15)可得,输入侧13~25次谐波对应的Rd分别如下:Rd_13 = 17.405 Ω,Rd_17= 37.872 Ω,Rd_19 = 150.104 Ω,Rd_23 = 9.987 Ω,Rd_25 = 12.381 Ω. 根据约束条件2)的要求,当Rd = 150.104 Ω时,滤波器的ξ < 0.1,该电阻的取值情况不作考虑,只需考虑其他4个理想阻尼电阻附近的实际阻尼电阻对输入谐振抑制的效果. 9.987~37.872 Ω的常见电阻系列如下:10、15、20、22、30、33 Ω. 可知, Rd可以选择10、15和33 Ω,取上述3种不同的实际阻尼电阻进行仿真,对输入性能进行对比分析.
表 1 矩阵变换器的仿真参数
Tab.1
| 参数 | 数值 |
| 输入电压幅值Em /V | |
| 输入电压频率fi /Hz | 50 |
| 滤波电感Lf /mH | 1.5 |
| 滤波电感等效电阻Rf /Ω | 0.075 |
| 滤波电容Cf /μF | 18.8 |
| 输出电流设定值Io* /A | 3.5/6.5 |
| 输出频率fo /Hz | 70 |
| 负载电感L /mH | 7.5 |
| 负载电阻R /Ω | 20 |
| 开关频率fs /kHz | 10 |
由上述分析可得,滤波器的设计步骤如下.
1)按照3.1节的约束条件设计滤波电感与电容,依据元件的易购性,选择合适的滤波电容与电感.
2)根据谐振频率,选择需要抑制的特定谐波频率. 利用仿真软件中的FFT分析模块,获得无阻尼电阻情况下输入电流谐振点附近的主要谐波电流含有率λi与基波电流幅值i0.
3)通过国际标准IEC6100-3-2获得上述谐振点附近主要谐波电流含量的上限,根据式(15)计算获得抑制不同谐波电流的理想阻尼电阻.
4)将理论计算的阻尼电阻与表2对照,获得可选的多个实际阻尼电阻.
表 2 不同阻尼电阻下输入电流中谐振点附近谐波含量
Tab.2
| Io*/A | Rd/Ω | ηi / % | ||||
| i = 13 | i = 17 | i = 19 | i = 23 | i = 25 | ||
| 3.5 | 10 | 0.31 | 0.22 | 0.03 | 0.12 | 0.07 |
| 3.5 | 15 | 0.49 | 0.10 | 0.28 | 0.13 | 0.06 |
| 3.5 | 33 | 0.35 | 0.19 | 0.65 | 0.26 | 0.07 |
| 6.5 | 10 | 0.09 | 0.03 | 0.05 | 0.06 | 0.03 |
| 6.5 | 15 | 0.10 | 0.06 | 0.04 | 0.05 | 0.03 |
| 6.5 | 33 | 0.10 | 0.15 | 0.28 | 0.26 | 0.10 |
5)分析不同阻尼电阻条件下矩阵变换器的输入与输出性能,以不低于标准GB/T 14549-93和IEC 6100-3-2的要求,选取最优输入性能下的实际阻尼电阻.
4. 特定谐波消除法的双闭环控制策略
4.1. 特定谐波段频率的确定及提取方法的改善
提出采用Notch Filter对输入端电压谐振点附近的特定谐波量进行提取,该滤波器的传递函数为
其中,Q为品质因数,用以限制陷波点的宽度,仿真中Q取为500.
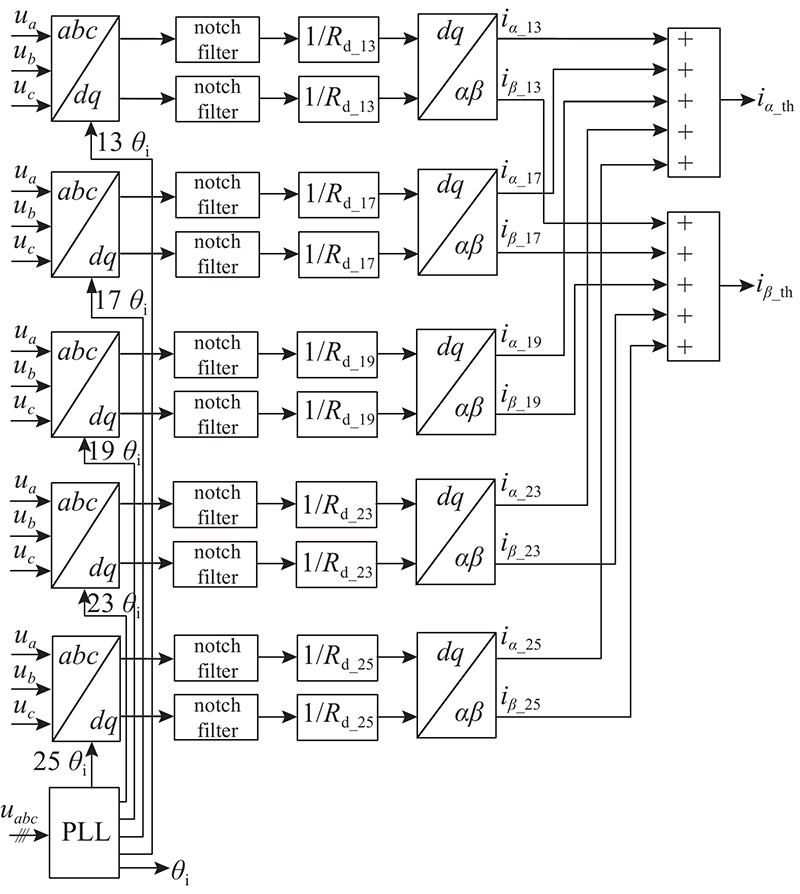
如图4所示为特定谐波提取模块框图. 图中,iαβ_13、iαβ_17、iαβ_19、iαβ_23和iαβ_ 25分别为矩阵变换器滤波电容电流中的13、17、19、23和25次谐波在αβ坐标系下的值.
图 4
4.2. 闭环控制策略的实现
对式(1)进行abc/dq坐标变换,可得矩阵变换器在同步旋转dq轴下的输入微分方程为
双闭环控制系统以输入电流ia、ib和ic的dq轴分量id和iq为控制对象,矩阵变换器三相输入端电流
因为dq轴分量都为直流量,稳态时各变量的微分都为零,令式(18)的微分量为零,得到dq轴下的稳态方程为
根据电流前馈解耦原则,忽略滤波电容电压dq轴分量ud和uq与输入电压dq轴分量ed和eq之间的差异,可得以输入电流的dq轴分量id、iq作为控制对象的电流内环方程式:
式中:kp和ki分别为电流内环PI调节器的比例和积分系数.
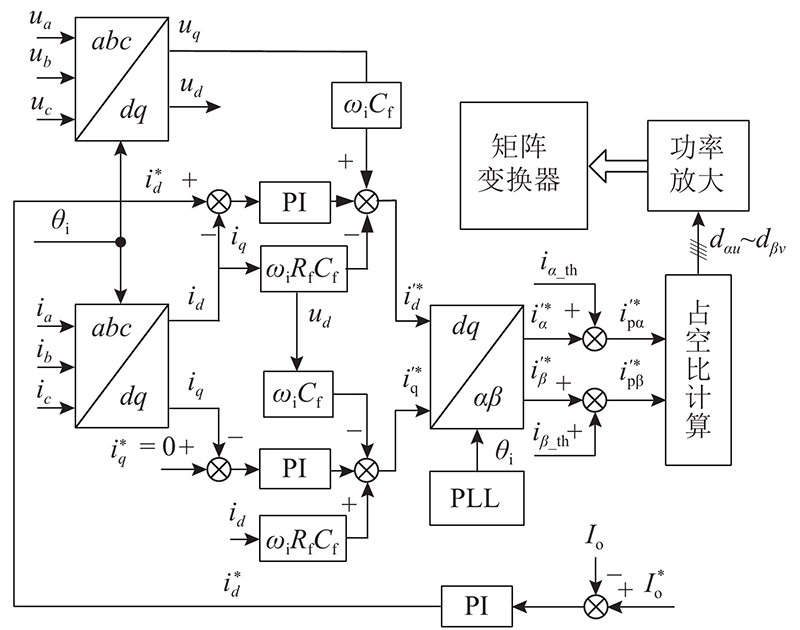
图 5
图 5 基于特定谐波消除法的双闭环控制策略框图
Fig.5 Block diagram of double closed loop control strategy based on specific harmonic elimination method
5. 仿真研究与分析
图 6
如表2所示为当
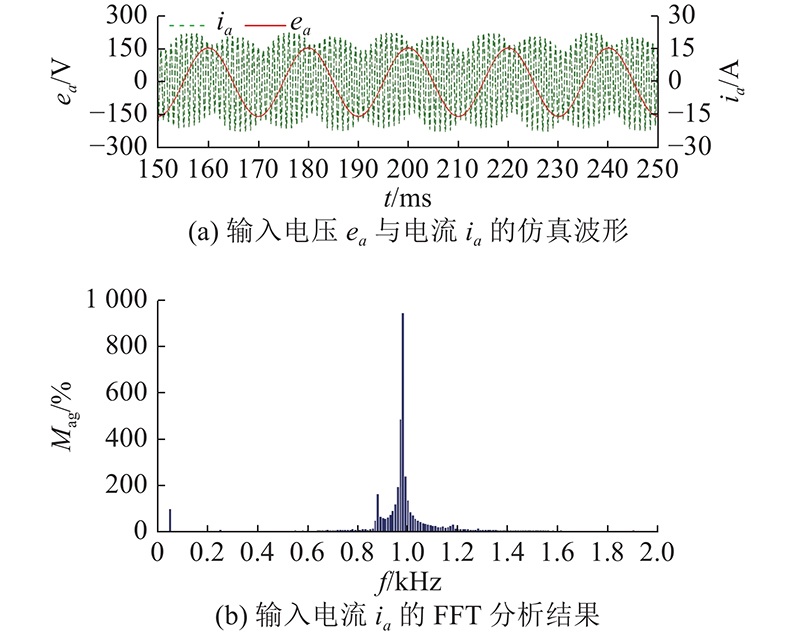
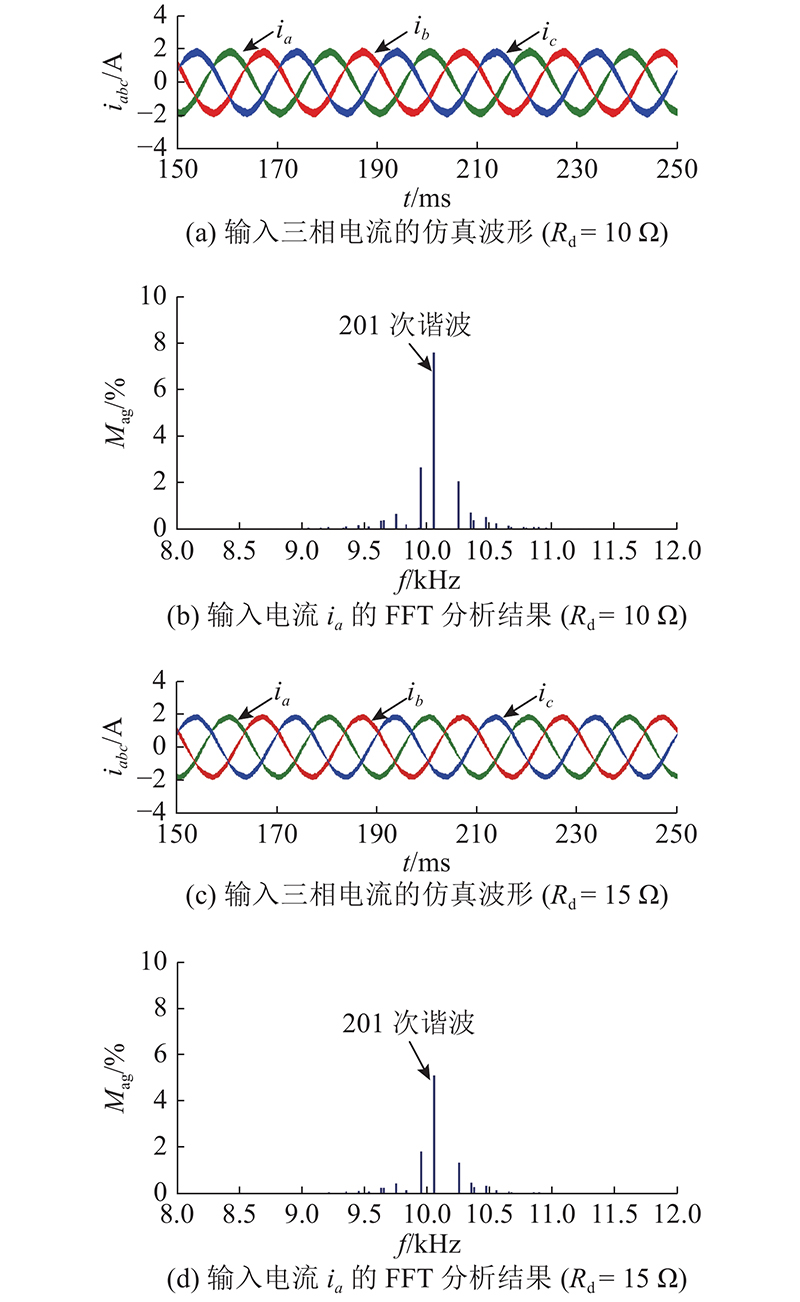
如图7所示为当
图 7
图 7 不同阻尼电阻条件下输入的静态仿真结果
Fig.7 Static simulation results of input side under different Rd
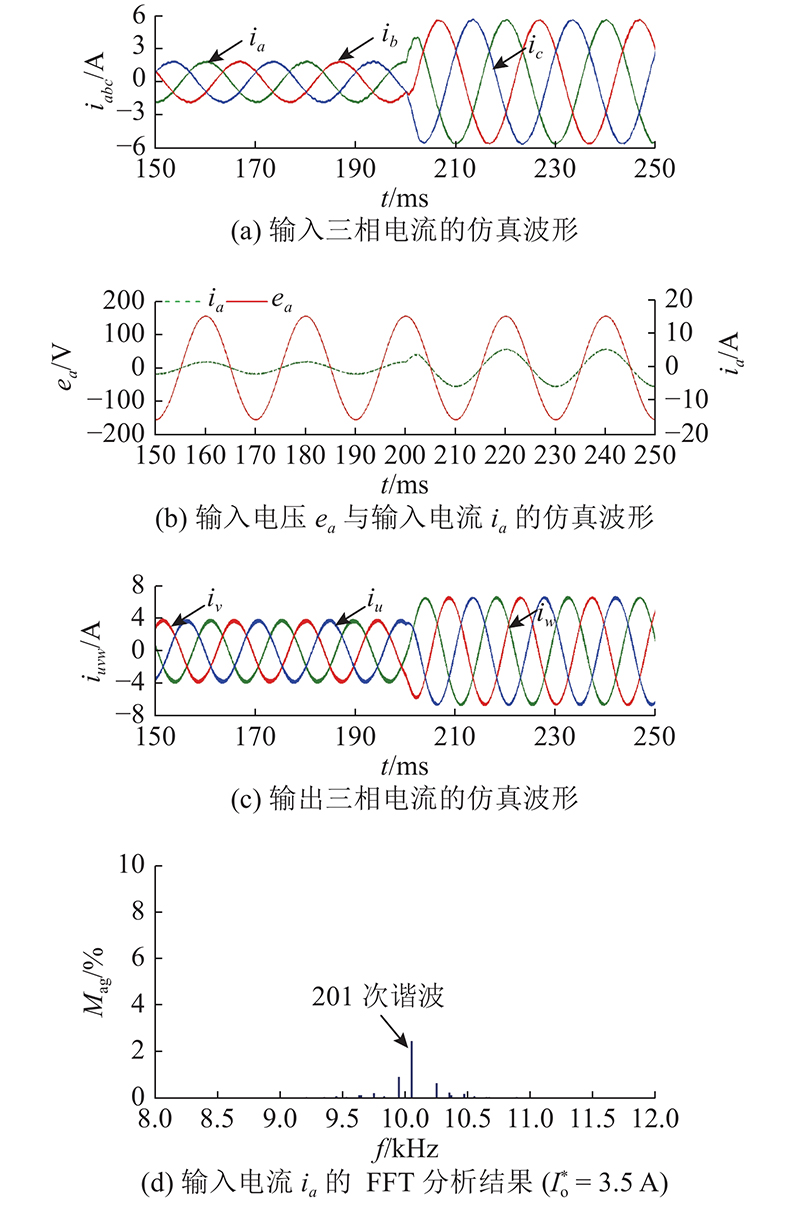
图 8
图 8 输入与输出的动态仿真结果(Rd= 33 Ω)
Fig.8 Dynamic simulation results of input and output (Rd = 33 Ω)
如图9所示为基于特定谐波消除法的双闭环控制策略下的输入与输出动态仿真结果. 图中,200 ms时,输出电流设定值由3.5 A切换到6.5 A. 被动阻尼法中,Rd = 150.104 Ω时的滤波器阻尼系数ξ < 0.1,则 图4中反馈系数Rd_19=150.104 Ω修正为ξ = 0.1时的值,即Rd_19 = 46 Ω. 在被动阻尼法中,若Rd = 17.405、9.987或12.381 Ω,则输入性能不满足国标GB/T14549-93规定3%的上限,因此图4中Rd_i的取值为:Rd_13 = Rd_17 = Rd_23 =Rd_25 = 37.872 Ω,Rd_19 = 46 Ω. 从图9(a)可知,输入电流正弦度得到了进一步提升;从图9(b)可知,由于双闭环控制中的电流内环q轴电流取值为
图 9
图 9 特定谐波消除法的动态仿真结果
Fig.9 Dynamic simulation results of specific harmonic elimination method
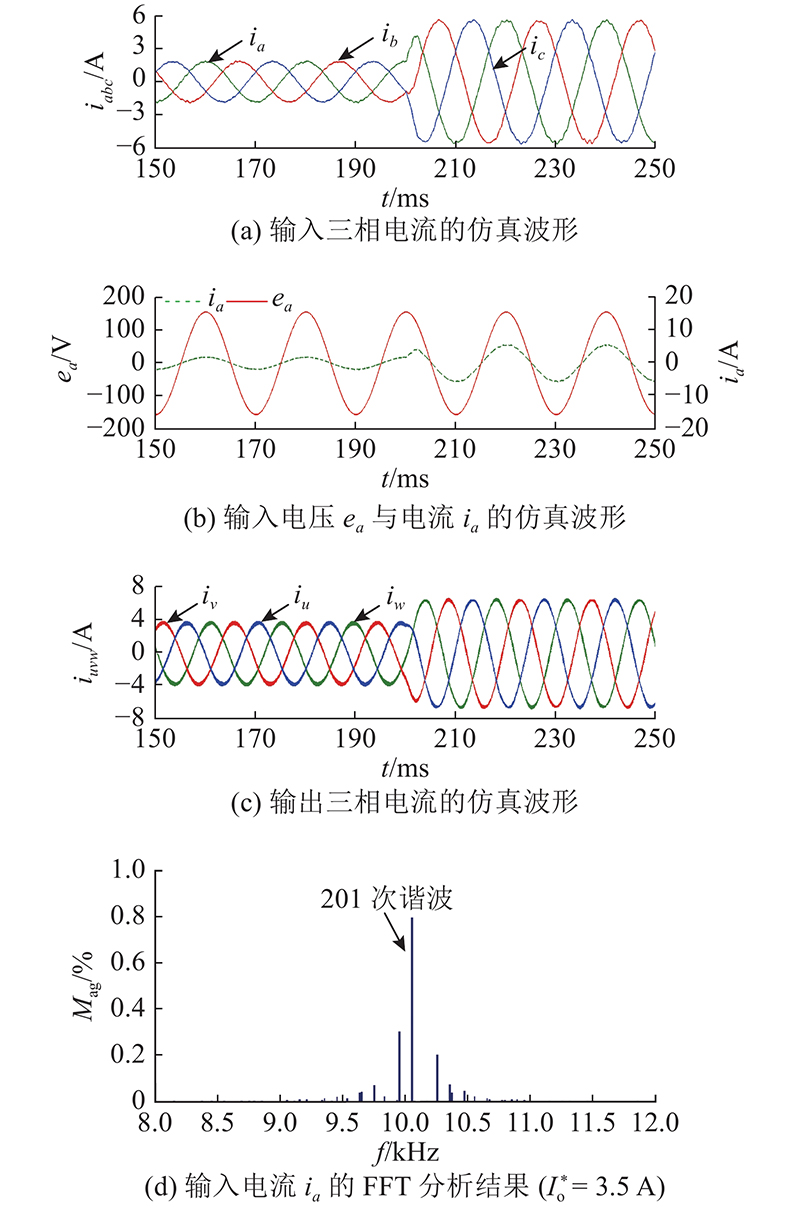
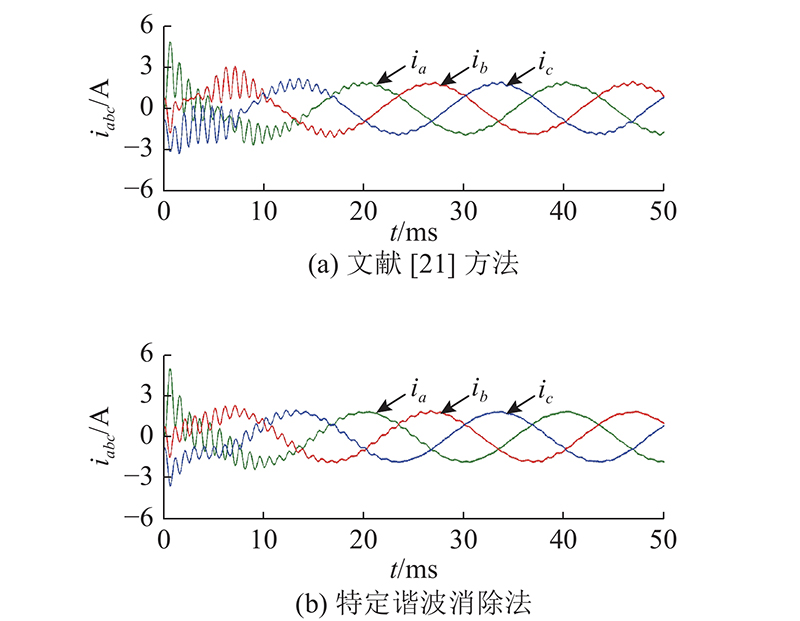
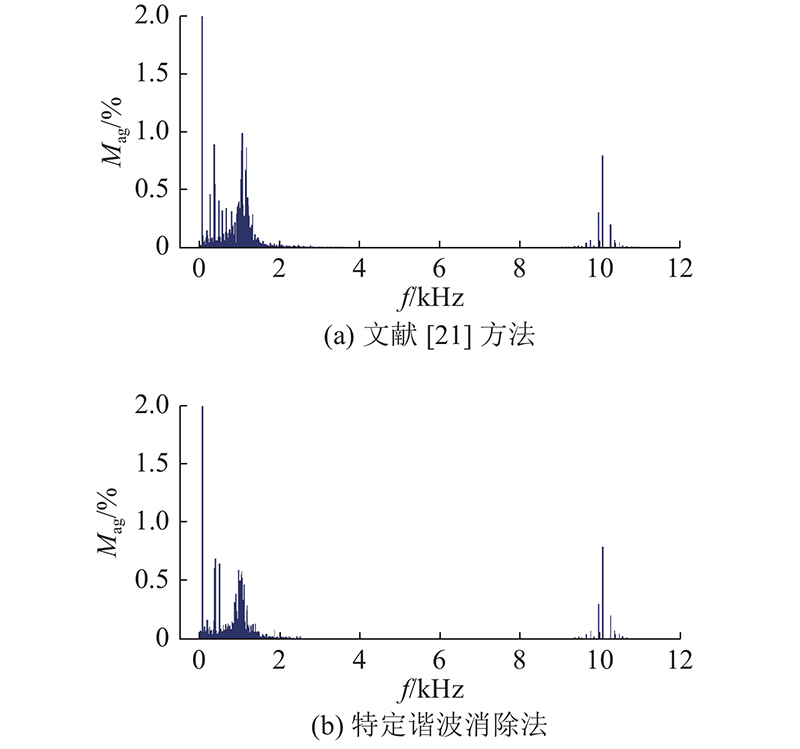
如图10、11所示分别为Nunokawa等[21]所提的HPF方法与本文所提的特定谐波消除法的输入三相电流仿真波形及ia的FFT仿真结果,其中HPF的时间常数T = 3 ms. 从图10(a)、(b)可知,2种方法均能够在较短时间内抑制输入谐振. 由于Nunokawa等[21]采用了过渡带较长的HPF提取谐振点附近谐波电压,谐振电流的衰减时间较本文方法的时间长,收敛速率较后者低. 从图11(a)、(b)可知,采用本文方法,稳态输入电流ia的THD从1.98%下降到1.51%,输入侧性能得到进一步的改善. 由此可见,采用本文的控制策略较文献[21]方法具有更低的THD,对应抑制的谐波主要集中在谐振点附近.
图 10
图 10 不同方法下输入三相电流的瞬态仿真结果
Fig.10 Dynamic simulation results of input three-phase current under different methods
图 11
图 11 不同方法下输入电流ia的仿真分析结果(Io*= 3.5 A)
Fig.11 Simulation results of input current ia under different methods (Io* = 3.5 A)
表 3 不同方法下输入电流中主要谐波含量
Tab.3
| Io*/A | 谐振抑制方法 | ηi /% | ||||
| i = 13 | i = 17 | i = 19 | i = 23 | i = 25 | ||
| 3.5 | 方法1 | 0.35 | 0.19 | 0.65 | 0.26 | 0.07 |
| 3.5 | 方法2 | 0.08 | 0.31 | 0.59 | 0.25 | 0.11 |
| 6.5 | 方法1 | 0.10 | 0.15 | 0.28 | 0.08 | 0.10 |
| 6.5 | 方法2 | 0.18 | 0.16 | 0.33 | 0.12 | 0.05 |
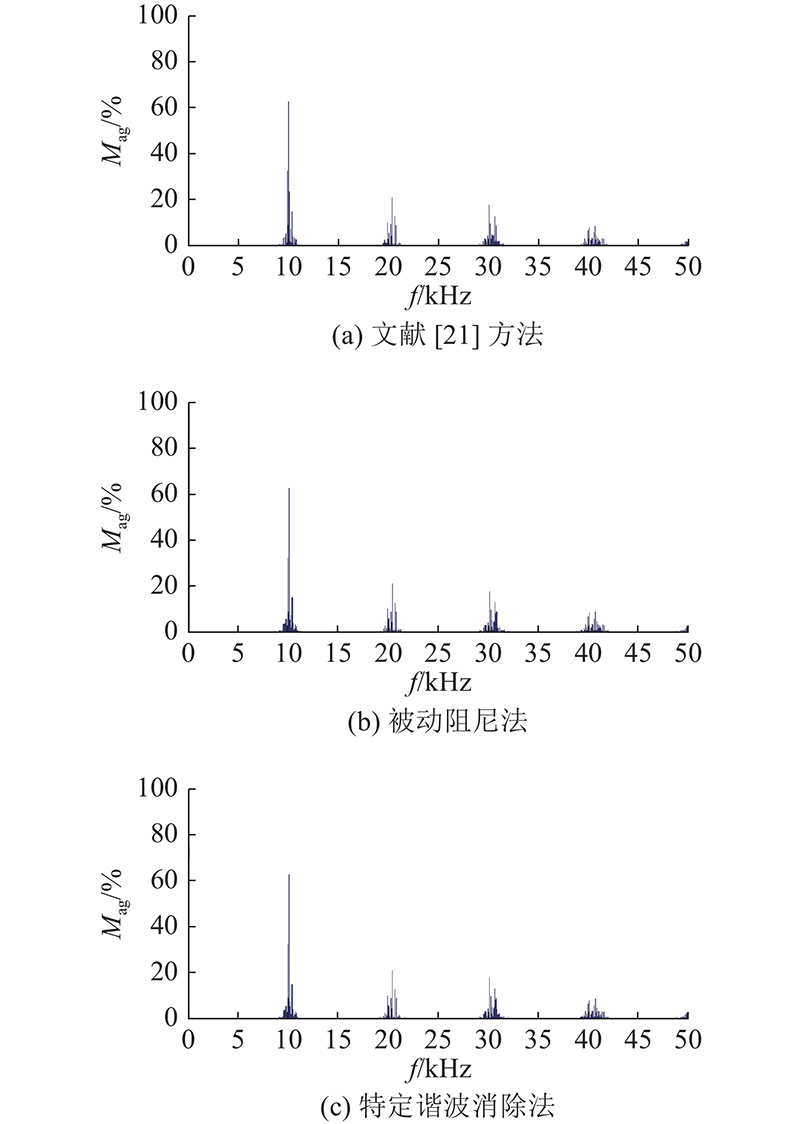
图 12
图 12 不同方法下输出相电压uu的仿真结果
Fig.12 Simulation results of output phase voltage uu under different methods
6. 结 语
本文根据截止频率、理想阻尼系数、电感压降、系统损耗及器件的易购性等多个约束条件,设计矩阵变换器输入LC滤波器,将谐振点附近特定谐波的抑制作为阻尼电阻优化设计的依据. 通过将特定谐波抑制的思想进行延伸,提出基于特定谐波抑制消除方法的矩阵变换器双闭环控制策略,给出该算法中参数的优化设置方法. 通过仿真,将现有方法与所提方法进行对比分析. 仿真结果表明,所提的基于特定谐波消除的输入LC滤波器参数优化与主动谐振抑制方法具有如下特点.
(1)利用所提的方法,能够使输入电流中谐振点附近典型谐波含有率和THD值均下降至标准范围内.
(2)LC滤波器的参数优化设计方法实现简单,能够较好地兼顾谐振点附近谐波的抑制与高频段谐波的衰减,硬件成本低,整机的经济性较好.
(3)基于特定谐波消除的主动谐振抑制控制策略具有算法灵活、谐振电流衰减时间较现有文献的时间短的优点.
参考文献
Generalized double line voltage synthesis strategy for three-to-N phase matrix converter
[J].DOI:10.1049/iet-pel.2017.0487 [本文引用: 1]
传统矩阵变换器最小相位误差空间矢量过调制策略
[J].
Minimum phase error space-vector over-modulation strategy of conventional matrix converter
[J].
抑制矩阵变换器共模电压的间接调制改进方法
[J].
Improved indirect modulation methods for suppressing the common-mode voltage of matrix converter
[J].
矩阵变换器混合型换流策略
[J].
Hybrid commutation strategy for matrix converter
[J].
应用于高压低频输电的H桥级联型矩阵变换器环流机理分析
[J].
Circulating current analysis of cascaded H-bridge matrix converter for high voltage low-frequency AC transmission
[J].
A three-level T-type indirect matrix converter based on the third-harmonic injection technique
[J].DOI:10.1109/JESTPE.2017.2666418
基于FTC的BBMC调速控制策略及参数优化
[J].
BBMC speed control strategy and parameter optimization based on FTC
[J].
三相四桥矩阵变换器非平衡负载运行特性研究
[J].
Research on the capacity of four-leg matrix converter with unbalanced load
[J].
双级矩阵变换器功率开关开路故障的分析与诊断
[J].
Analysis and diagnosis of open-circuited switch faults in two-stage matrix converter
[J].
Open-circuit fault analysis and diagnosis for indirect matrix converter
[J].DOI:10.1109/JESTPE.2017.2772788 [本文引用: 1]
双级矩阵变换器驱动永磁同步电机的混合非线性控制系统
[J].
Hybrid nonlinear control system of permanent magnet synchronous motor driven by two stage matrix converter
[J].
矩阵变换器-永磁同步电机系统直接转矩控制转矩波动抑制策略
[J].
Torque ripple reduction in matrix converter-fed permanent magnet synchronous motor driven by direct torque control
[J].
矩阵式隔离型双向AC-DC变换器控制策略
[J].
Bidirectional and isolated AC-DC converter based on reduced matrix converter
[J].
基于模型预测控制的三相−一相矩阵变换器偏磁控制
[J].
Research on bias control of 3 phase-1 phase matrix converter based on model predictive control
[J].
矩阵变换器输入滤波器设计与研究
[J].
Analysis and design of input filter in matrix converter
[J].
矩阵变换器阻尼输入滤波器的优化设计
[J].DOI:10.3969/j.issn.1001-2095.2014.04.009 [本文引用: 1]
Optimized design of damped input filter of matrix converter
[J].DOI:10.3969/j.issn.1001-2095.2014.04.009 [本文引用: 1]
多模块矩阵变换器改进型线电压合成闭环控制策略研究
[J].
Research on closed loop control strategy of the improved line voltage synthesis for multi-modular matrix converter
[J].
Predictive power control of matrix converter with active damping function
[J].DOI:10.1109/TIE.2016.2541599 [本文引用: 1]
基于滤波器状态反馈的矩阵变换器网侧电流闭环策略
[J].DOI:10.3969/j.issn.1000-6753.2016.07.008 [本文引用: 1]
A grid current closed-loop control strategy for matrix converter based on states feedback of filter
[J].DOI:10.3969/j.issn.1000-6753.2016.07.008 [本文引用: 1]