当船舶和海洋结构物产生大幅参数共振时,会使结构遭受破坏和失效而导致人员和财产损失. 1998年10月,一艘超巴拿马型C11级集装箱船在迎浪海况中航行时发生了幅值达35o~40o的参数横摇运动,导致甲板上的集装箱大量损坏[1]. 参数横摇可发生在随浪[2]、迎浪[3-4]和斜浪[5]航行的船舶上. Yu 等[6]通过检测纵摇和横摇的频率差来判断是否会发生参数横摇. Liu等[7]利用基于雷诺平均Navier-Stokes方程的计算流体力学(computational fluid dynamics, CFD)程序模拟预测了内倾舰艇在迎浪规则波中的参数横摇. Ghamari等[8]采用数值模拟和物理实验的方法,研究了渔船在无航速和有航速2种情况下的参数横摇. 其中数值模拟中Froude-Krylov(F-K)力和静水回复力的非线性影响通过积分到船体瞬时湿表面实现. 海洋浮式平台同样存在参数共振问题[9-10]. Yang等[11]通过数值模拟分析了锚泊缆绳、立管和阻尼对Spar平台参数稳定性的影响. Yang等[12]分析了不规则波中Spar平台几何形状对参数纵摇的影响. Jang等[13]采用与文献[8]类似的方法对极地Spar平台进行数值模拟,发现当波浪频率等于2倍纵摇/横摇固有频率时有参数共振产生,当波浪频率为垂荡固有频率的2倍时,观察到垂荡参数共振.
波浪能作为可再生能源,对其进行开发利用,对保障能源安全、实现可持续发展具有重要意义. 在已有的波浪能利用技术中,固定式振荡水柱(oscillating water column, OWC)[14]或浮式OWC[15-16]是重要的波浪能转换装置,某些小型浮式OWC型装置已成功为航标提供电力供给[17]. Gomes等[18]对松弛锚泊的Spar型OWC波浪能转换装置进行时域数值模拟和模型试验,发现当波浪周期为一半横摇/纵摇固有周期时会产生参数共振. 为了预测参数共振,Giorgi等[19]利用非线性F-K模型模拟文献[18]中的装置,结果表明,参数共振产生时,波能俘获效率下降53%. 另一类受研究者关注的是浮式点吸收波浪能转换装置[20-22],Tarrant等[23]采用F-K模型对双体式垂荡点吸收装置Wavebob进行数值模拟,假设动力输出(power take-off, PTO)机构阻尼力与2个物体间的相对垂荡速度成正比. 本研究认为,在发生大幅参数横摇/纵摇情况下,Wavebob装置PTO阻尼力应修改为与2个物体间的轴向相对速度成正比. 垂荡式点吸收装置只能俘获垂荡方向的波浪能,而多自由度波能转换装置能够比垂荡式点吸收装置俘获更多的能量[24-25].
本研究 1)提出由浮体和承载结构组成的多自由度波浪能装置,承载结构与固定平台铰接,垂向PTO、纵摇PTO及横摇PTO分别用于俘获浮体沿铰接承载结构轴向滑动、浮体纵荡和纵摇及浮体横荡和横摇方向的能量. 2)利用势流理论建立该装置的频域和时域仿真模型. 3)探讨装置发生参数激励运动的原因,分析波高、周期、各PTO阻尼系数等对参数共振及波能俘获效率的影响.
1. 多自由度波浪能装置介绍
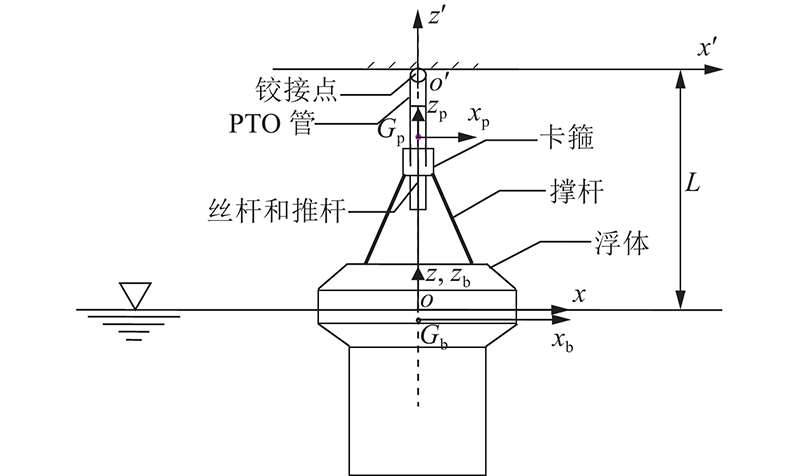
如图1所示,多自由度波浪能转换装置由浮体组合结构(包括浮体、卡箍和撑杆)和承载结构(包括管状壳体、丝杆、推杆及内部构件)组成. 将垂向PTO机构安装在承载壳体内,并简称此管状承载结构为PTO管. 图中,oxyz为空间固定坐标系,原点o位于静水面,z轴垂直向上;Gbxbybzb为固连于浮体的坐标系,原点Gb位于浮体重心处;Gpxpypzp为固连于PTO管的坐标系,原点Gp位于PTO管重心处;o′x′y′z′为固连于铰接点的坐标系,L为铰接点离水面高度. 在PTO管外侧设置滑轨,在通过撑杆与浮体固定相连卡箍的上下端设置滑轮,使卡箍能够沿PTO管上的滑轨滑动. 推杆的作用是将浮体的运动传递到滚珠丝杆机构的螺母上,使浮体组合结构能够沿PTO管往复运动,进而带动与发电机相连的丝杆旋转以捕获浮体沿PTO管滑动方向的能量. PTO管上端与固定平台铰接,并分别与纵摇和横摇方向的PTO机构连接,俘获浮体纵荡与纵摇方向、横荡与横摇方向的能量. 当装置的纵摇和横摇运动幅值较小时,垂向PTO用于俘获浮体垂荡运动方向的能量.
图 1
图 1 多自由度轴对称型波浪能装置示意图及坐标系
Fig.1 Diagram and coordinate systems of multiple degrees of freedom wave energy converter with axial symmetry
本研究所提装置总共有3个PTO机构,每个PTO机构均有独立的发电机与之相连. 无论装置的横摇运动和纵摇运动如何变化,与垂向PTO连接的发电机均能正常发电,但参数横摇、参数纵摇会引起垂向发电机输出功率的减小,因此有必要采取措施抑制参数激励运动. 遭遇随浪或迎浪海况时,与垂向PTO连接的发电机和安装在纵摇铰接轴上的发电机可以正常发电. 遭遇横浪海况时,与垂向PTO连接的发电机和安装在横摇铰接轴上的发电机可以正常发电. 遭遇斜浪海况时3个发电机均可以正常发电. 因此本研究所提装置能够同时俘获浮体多个运动自由度方向的能量.
2. 运动方程
2.1. 线性频域运动方程
由于PTO管铰接约束下的装置无首摇运动,在线性规则波作用下浮体相对于自身重心位置做频率为ω的五自由度简谐运动
式中:ξj(t)为t时刻浮体重心位置j自由度的运动位移,ξj0为复振幅. PTO管绕铰接点o′作横摇(j=4)和纵摇(j=5) 2种自由度运动,且浮体与PTO管具有相同的纵/横摇运动. 装置的运动幅值通过拉格朗日运动方程求解:
式中:Ek为装置动能,EP为势能,ED为负载阻尼吸收的能量;
式中:
式中:mb为包括浮体、撑杆和卡箍在内的组合浮体质量,mp为PTO管质量,
将式(4)代入式(10),得到各自由度方向的平均输出功率. 为了最大化各PTO的平均输出功率,式(10)对Bpj求导,并令导数等于零,得到各PTO对应的最佳负载阻尼系数Boptj. 令Kpj=0,有
对本垂直轴对称波浪能装置而言,利用频域方法求解时,通过式(11)可以很方便地求出各自由度对应的线性最佳负载阻尼系数Boptj(j=3, 4, 5).
2.2. 时域运动方程
若波浪能装置发生参数激励运动,则大幅值的纵摇或横摇运动将影响装置的输出功率和波浪能俘获效率. 由于线性频域运动方程无法分析参数激励运动,对于可能产生参数共振的非线性系统须采用时域方法求解,利用Cummins方程描述辐射力. 设组合浮体为结构1,PTO管为结构2,则将浮体的时域运动方程表示为
式中:
式中:
相对于平衡位置,定义浮体沿PTO管向上滑动时的位移Δl为正,有
式中:
垂向PTO作用在结构1的阻尼力Fp1在固定坐标系x、y和z方向的分量
垂向PTO、横摇PTO及纵摇PTO作用在结构2上的阻尼力/力矩Fp2中各分量
装置由2个结构组成,2个结构体间的接触力传递通过设置刚度系数很大的护舷实现[26],使得浮体和PTO管具有同步的横摇和纵摇运动. 时域运动方程采用AQWA-NAUT模块求解,其中与发电机相连的PTO负载力和流体黏性力的计算在User Force程序中编写,使用Fortran编译动态链接库文件(.dll)实现外部载荷的定义和调用.
3. 波能俘获宽度比
设垂直轴对称浮体水线面处直径为D,规则波中直径D范围内的入射波平均功率为
式中:k为波数;d为水深;H为波高,H=2ζa. 采用频域方法求解时,规则波作用下各PTO机构俘获的平均功率Pmj由式(10)计算得到. 采用时域方法求解时,垂向PTO、横摇PTO和纵摇PTO各自俘获的平均功率分别表示为
式中:Tw为波浪周期. 式(20)表示在2个波浪周期范围内求各PTO的平均输出功率,目的是考虑参数共振的影响,因为参数激励运动主要发生在波浪频率为2倍纵摇或横摇固有频率及其附近频率范围. 将各PTO俘获的输出功率相加得到装置总的输出功率PT。各PTO对应的波能俘获宽度比
式(20)得到的结果为发电机前端的功率,即式(21)计算的俘获宽度比是没有考虑发电机本身效率时的结果,也称为一次转换效率,且在求解运动方程式(12)、(13)时忽略丝杆摩擦损失的影响. 装置总波能俘获宽度比定义为各PTO的波能俘获宽度比之和。
4. 结果分析
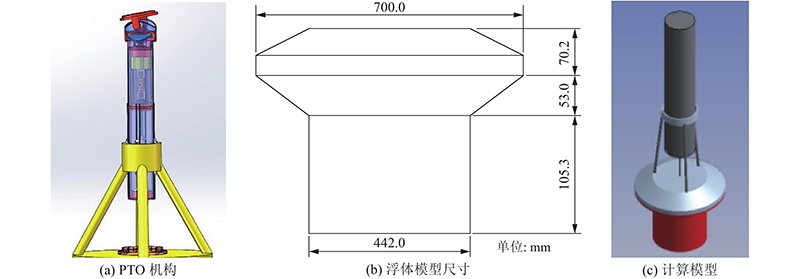
如图2所示,根据缩尺比为1∶4的多向联动复合PTO机构,建立装置水动力性能数值仿真模型. 取计算水深为1.6 m,模型吃水为0.43 m,静浮时浮体重心在空间固定坐标系下的垂向坐标
图 2
4.1. 垂向PTO阻尼系数的影响
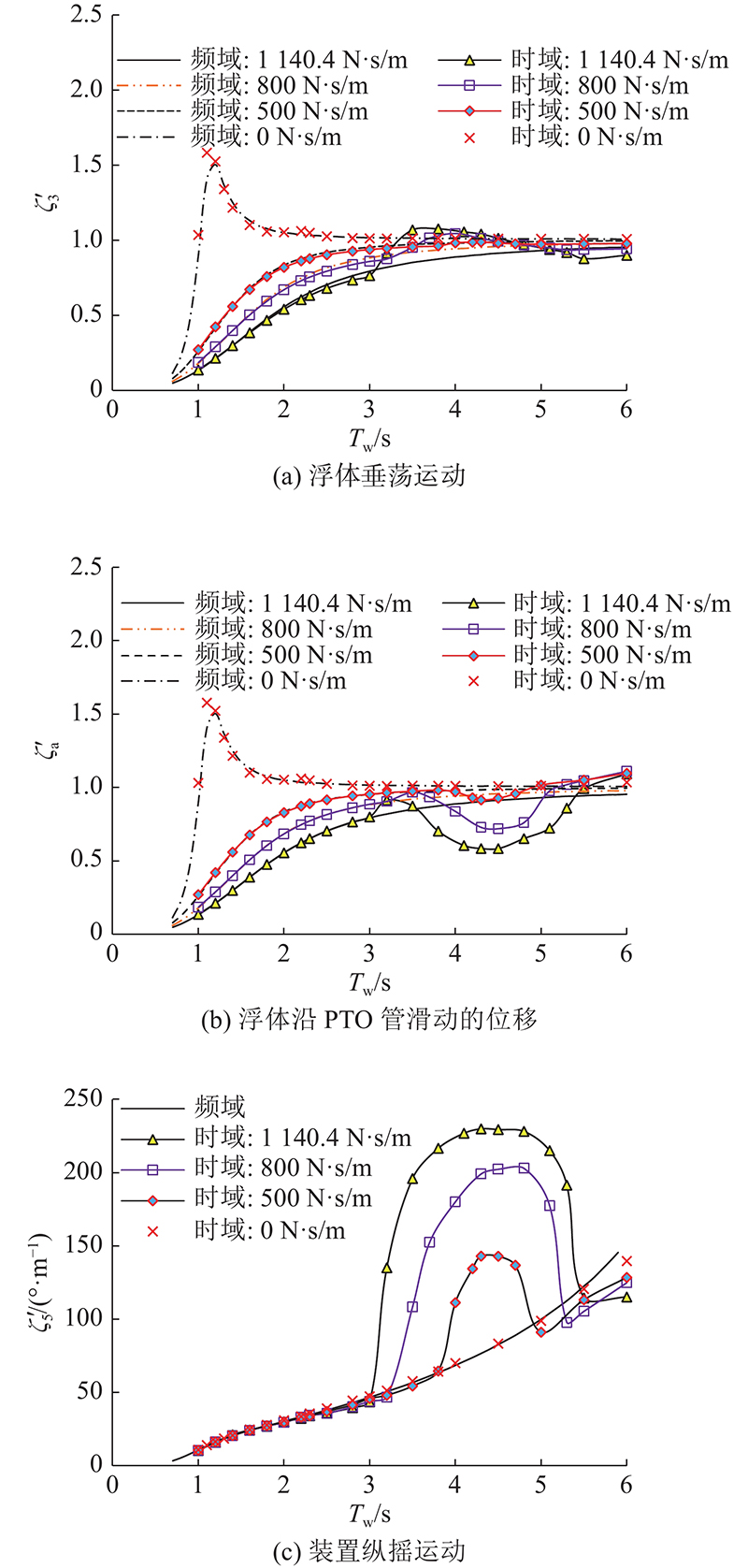
基于线性的频域方法无法模拟参数共振问题,而时域方法可以处理非线性力的作用. 为了寻找参数激励运动发生的原因,时域方法中的F-K力和静水力均采用线性方法计算,因此所有流体作用力项均是线性的,且假设垂向PTO的阻尼力与浮体沿PTO管的滑行速度成正比. 在线性波作用下的装置也有可能产生大幅值参数共振,由式(17)可知,此时垂向PTO力分解到水平和垂直方向时,须保留非线性项的贡献. 为了探讨垂向PTO的负载阻尼系数对装置运动响应的影响,取随浪工况,波高为0.2 m进行数值模拟,只有垂向PTO连接负载,纵摇和横摇PTO皆无负载. 取Bp3=0、500、800、1 140.4 N·s/m进行数值仿真,其中Bp3=1 140.4 N·s/m为周期2.5 s时垂荡方向的最佳负载阻尼系数.
如图3所示为采用时域计算方法得到的装置运动响应与频域结果的比较。图中,
图 3
图 3 垂向负载阻尼系数对装置运动响应的影响
Fig.3 Effect of vertical power take-off damping coefficient on motion response of converter
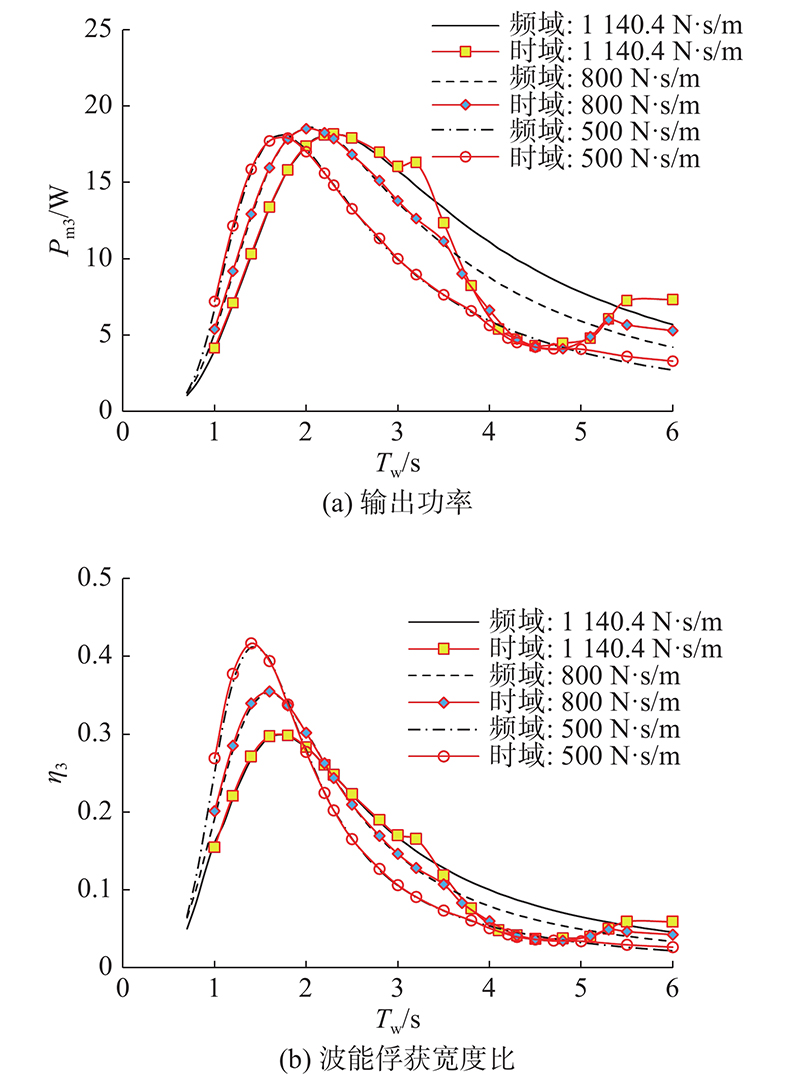
图 4
图 4 垂向负载阻尼系数对装置垂向动力输出机构输出功率及波能俘获宽度比的影响
Fig.4 Effect of vertical power take-off damping coefficient on output power and wave energy capture width ratio of vertical power take-off mechanism
4.2. 波高的影响
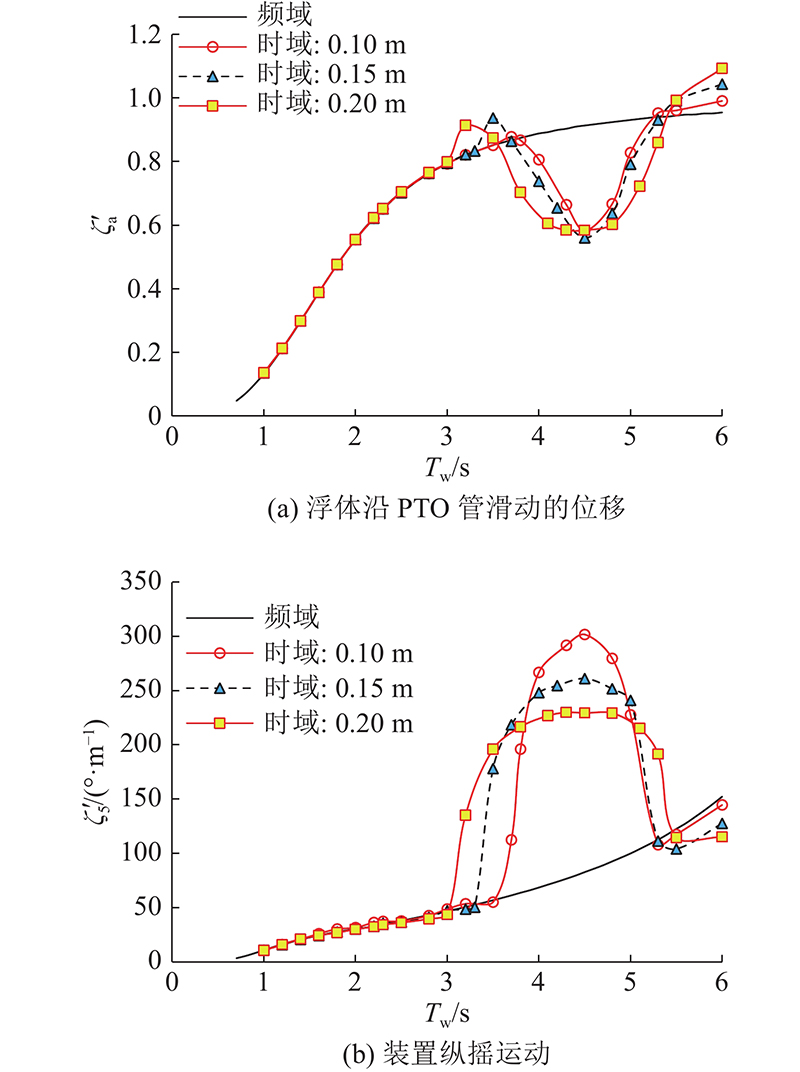
随浪工况,垂向PTO连接负载,纵摇PTO和横摇PTO皆无负载,取模型周期2.5 s时垂荡方向的最佳负载阻尼系数Bp3=Bopt3=1 140.4 N·s/m,并取H=0.1、0.15、0.2 m共 3种波高进行数值模拟. 如图5所示为3种波高对应的浮体沿PTO管滑动位移和装置纵摇运动频率响应函数随波浪周期的变化曲线. 基于线性方程的频域方法所得频率响应函数在Bp3、Bp5一定的情况下不随波高变化,因此只有1条曲线. 在Bp3一定的情况下,由Bp3引起的参数纵摇的频率范围随波高增大而变宽,而纵摇频率响应函数的最大值随波高增大而降低. 如图6所示为3种波高对应的垂向PTO的平均输出功率和波能俘获宽度比随周期变化的曲线. 由图5、6可知,大幅值参数纵摇运动导致浮体沿PTO管滑动的位移变小,造成垂向PTO的输出功率降低,且随着波高增大,发生参数共振的区域向高频(短周期)方向扩展. 当波高为0.1 m时,与频域结果比较,在参数共振区浮体沿PTO管的滑动位移幅值、垂向PTO的输出功率及波能俘获宽度比均下降.
图 5
图 6
图 6 波高对垂向动力输出机构输出功率及波能俘获宽度比的影响
Fig.6 Effect of wave height on output power and wave energy capture width ratio of vertical power take-off mechanism
4.3. 纵摇PTO阻尼系数的影响
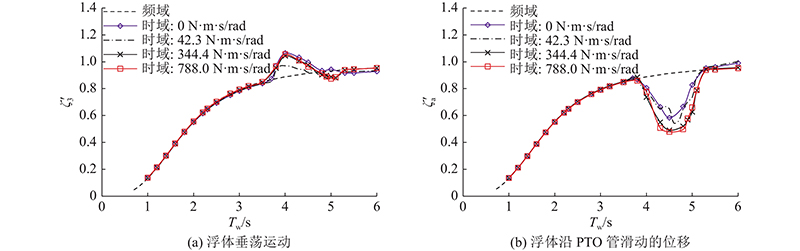
随浪工况,垂向PTO和纵摇PTO皆连接负载用于多自由度波能发电,横摇PTO无负载. 取Tw=2.5 s时垂荡方向的最佳负载阻尼系数Bp3=Bopt3=1 140.4 N·s/m,波高H=0.1 m和纵摇PTO阻尼系数Bp5=0、42.3、344.4、788.0 N·m·s/rad进行数值模拟. Bp5=42.3、344.4、788.0 N·m·s/rad分别对应Tw=8.0、4.5、2.5 s时纵摇方向的最佳负载阻尼系数.
如图7所示为3种Bp5对应的装置运动频率响应函数随波浪周期的变化曲线。图中,
图 7
图 7
图 7 纵摇负载阻尼系数对装置运动响应的影响
Fig.7 Effect of pitch power take-off damping on motion response of converter
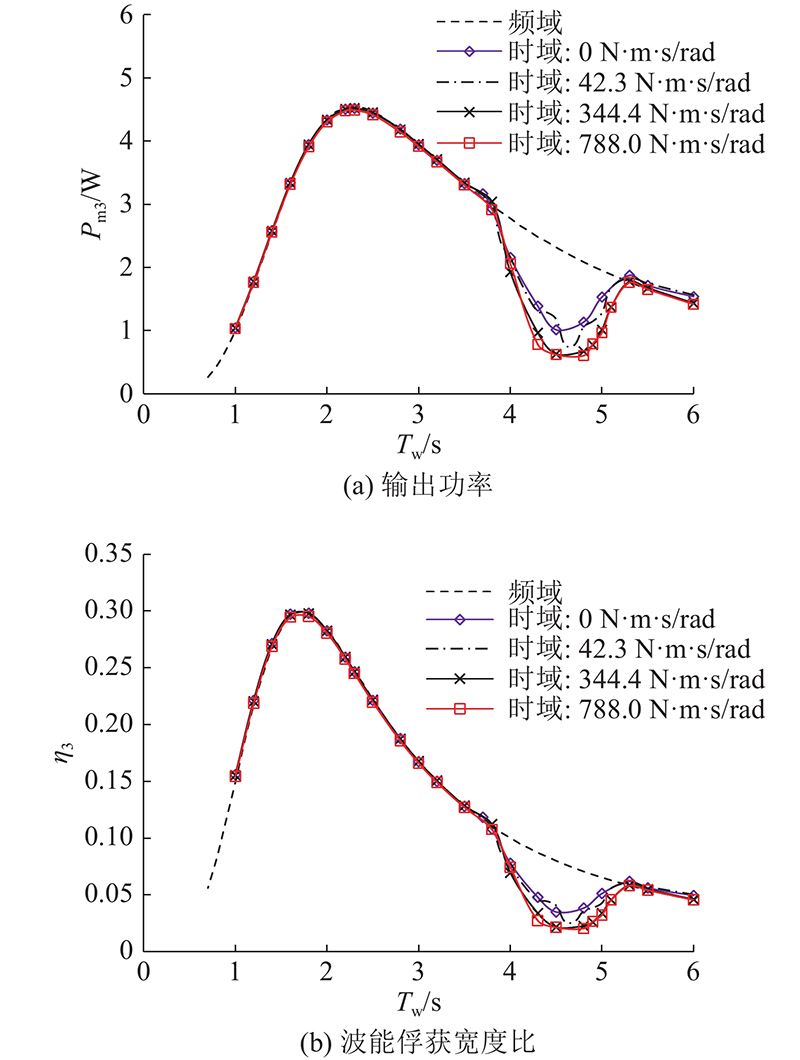
图 8
图 8 纵摇负载阻尼系数对垂向动力输出机构输出功率及波能俘获宽度比的影响
Fig.8 Effect of pitch power take-off damping on output power and wave energy capture width ratio of vertical power take-off mechanism
图 9
图 9 纵摇负载阻尼系数对纵摇动力输出机构的输出功率及波能俘获宽度比的影响
Fig.9 Effect of pitch power take-off damping on output power and wave energy capture width ratio of pitch power take-off mechanism
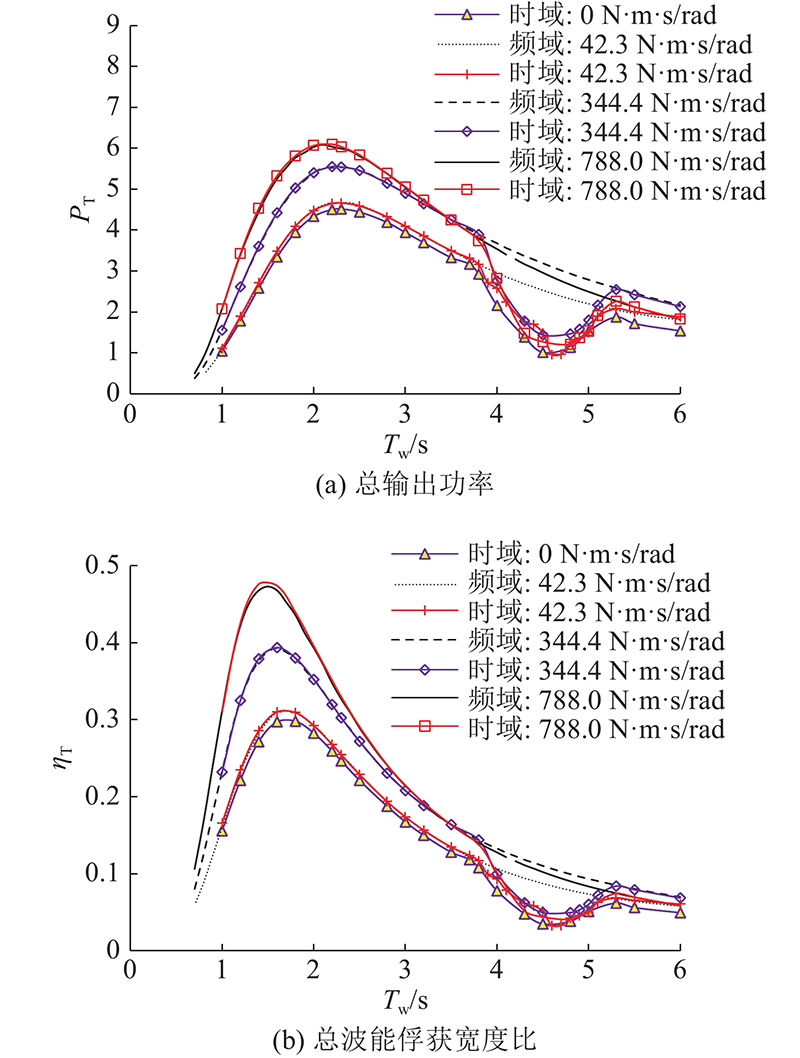
如图10所示为装置总输出功率PT和总波能俘获宽度比
图 10
图 10 纵摇负载阻尼系数对总输出功率及总波能俘获宽度比的影响
Fig.10 Effect of pitch power take-off damping on total output power and total wave energy capture width ratio
4.4. 参数共振的抑制
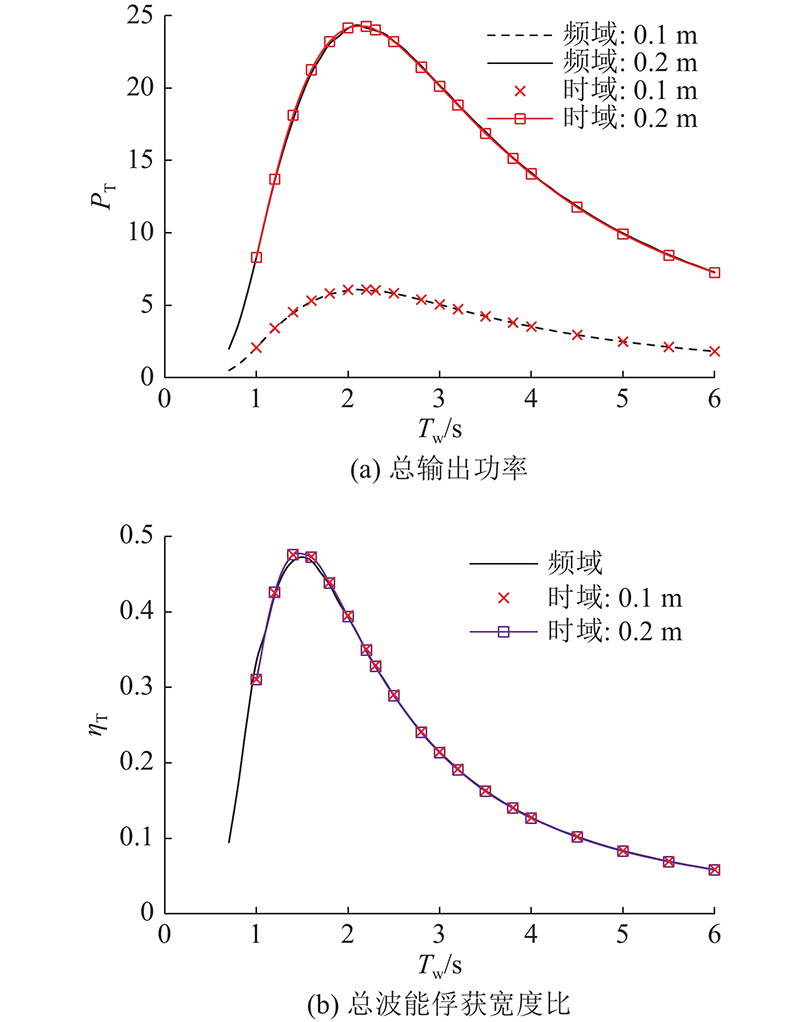
随浪工况,取Tw=2.5 s时垂荡方向的最佳负载阻尼系数Bp3=Bopt3=1 140.4 N·s/m,纵/横摇PTO阻尼系数Bp4=Bp5=Bopt5=788.0 N·m·s/rad,波高H=0.1 、0.2 m进行数值模拟. 随浪工况时的横摇PTO不发电,对横摇施加PTO阻尼力矩的目的是抑制参数横摇. 如图11所示为参数共振得到抑制后总输出功率和总波能俘获宽度比随周期变化的曲线. 可以看出,参数共振得到抑制后,时域与频域曲线吻合良好.
图 11
图 11 参数共振抑制后的总输出功率及总波能俘获宽度比
Fig.11 Total output power and total wave energy capture width ratio after parametric resonance suppression
5. 结 论
(1)采用线性势流理论建立由浮体和PTO管组成的轴对称型多自由度波浪能装置的频域计算模型. 模型可以简化成3个单自由度方程,具有简单快速的计算优势. 建立时域计算模型,假设垂向PTO阻尼力与浮体沿PTO管滑动的速度成正比,纵/横摇方向PTO阻尼力矩与纵/横摇的角速度成正比,在将垂向PTO力分解到水平和垂直方向时,保留非线性项作用以评估参数激励运动. 研究结果表明,在没有产生参数激励运动的频率范围,时域计算结果与频域结果吻合良好.
(2)随浪工况,纵摇PTO和横摇PTO皆不连负载,只有在垂向PTO施加负载阻尼用于俘获波浪能的过程中,在波浪频率为2倍横摇/纵摇固有频率附近范围,有严重的参数纵摇运动,此时的参数横摇幅值较小,且随时间的变化不规则. 当有参数共振时,浮体沿PTO管滑动的位移减小,导致垂向PTO的输出功率及波能俘获宽度比下降. 发生参数纵摇运动的频率范围随波高和垂向PTO阻尼系数Bp3的增大而变宽;当有参数纵摇时,纵摇运动频率响应函数的最大值随波高增大而降低,随Bp3的增大而增大. 随着波高和Bp3的增大,参数共振的区域向高频(短周期)方向扩展. 随浪工况,横摇PTO不连负载,在垂向PTO和纵摇PTO连接负载用于多自由度获能的过程中,纵摇PTO阻尼系数Bp5较小时,参数纵摇和参数横摇运动同时发生;Bp5较大时,参数纵摇受到抑制,但发生较大幅值的参数横摇运动. 参数纵摇受到抑制情况下的参数横摇运动幅值大于参数纵摇和横摇同时产生时的参数横摇幅值.
(3)随浪工况,对纵摇PTO和横摇PTO均施加一定大小的PTO阻尼力矩系数时,能够有效抑制参数共振. 随浪工况,与垂向PTO单独获能比较,纵摇PTO和垂向PTO同时获能时的总输出功率及总波能俘获宽度比均有所提升.
(4)本研究只分析了规则波中的参数激励运动及对波能俘获能力的影响,后续计划针对随机波中的问题开展进一步研究.
参考文献
An investigation of head-sea parametric rolling and its influence on container lashing systems
[J].DOI:10.5957/mt1.2003.40.1.1 [本文引用: 1]
Stochastic rolling motion of ships in following seas
[J].DOI:10.1016/j.oceaneng.2011.03.008 [本文引用: 1]
规则迎浪中船舶参数横摇的三维时域预报方法研究
[J].DOI:10.3969/j.issn.1007-7294.2016.12.002 [本文引用: 1]
Study on a 3D time-domain method to predict parametric rolling of a ship in regular head seas
[J].DOI:10.3969/j.issn.1007-7294.2016.12.002 [本文引用: 1]
Experimental and numerical investigations of ship parametric rolling in regular head waves
[J].DOI:10.1007/s13344-018-0045-6 [本文引用: 1]
斜浪中参强激励横摇运动的数值模拟与解析分析
[J].DOI:10.3969/j.issn.1000-4882.2015.z1.016 [本文引用: 1]
Numerical and analytical research on forcedly-parametrically excited rolling of ships in oblique seas
[J].DOI:10.3969/j.issn.1000-4882.2015.z1.016 [本文引用: 1]
Model experiments on the early detection and rudder stabilization of KCS parametric roll in head waves
[J].DOI:10.1007/s00773-017-0463-9 [本文引用: 1]
CFD prediction of full-scale ship parametric roll in head wave
[J].DOI:10.1016/j.oceaneng.2021.109180 [本文引用: 1]
Numerical and experimental study on the parametric roll resonance for a fishing vessel with and without forward speed
[J].DOI:10.1016/j.apor.2020.102272 [本文引用: 2]
Parametric resonance analyses for spar platform in irregular waves
[J].DOI:10.1007/s13344-018-0025-x [本文引用: 1]
深吃水半潜式平台参数共振研究
[J].DOI:10.16483/j.issn.1005-9865.2016.01.003 [本文引用: 1]
Study on parametric resonance of a deep draft semi-submersible platform
[J].DOI:10.16483/j.issn.1005-9865.2016.01.003 [本文引用: 1]
Coupled dynamic analysis for wave interaction with a truss spar and its mooring line/riser system in time domain
[J].DOI:10.1016/j.oceaneng.2011.11.002 [本文引用: 1]
Effect of hull geometry on parametric resonances of spar in irregular waves
[J].DOI:10.1016/j.oceaneng.2015.03.006 [本文引用: 1]
Mathieu instability of Arctic spar by nonlinear time-domain simulations
[J].DOI:10.1016/j.oceaneng.2019.02.029 [本文引用: 1]
Experimental hydrodynamic investigation of a fixed offshore oscillating water column device
[J].DOI:10.1016/j.apor.2019.01.036 [本文引用: 1]
Model testing of an oscillating water column spar-buoy wave energy converter isolated and in array: motions and mooring forces
[J].DOI:10.1016/j.energy.2016.07.007 [本文引用: 1]
Economic assessment of wave power boat based on the performance of “Mighty Whale” and BBDB
[J].DOI:10.1016/j.rser.2017.08.051 [本文引用: 1]
海洋波浪能浮标发展现状及前景
[J].
Development status and prospect of ocean wave energy buoy
[J].
Time-domain simulation of a slack-moored floating oscillating water column and validation with physical model tests
[J].DOI:10.1016/j.renene.2019.11.159 [本文引用: 2]
Detecting parametric resonance in a floating oscillating water column device for wave energy conversion: numerical simulations and validation with physical model tests
[J].DOI:10.1016/j.apenergy.2020.115421 [本文引用: 1]
Site-specific modeling of self-reacting point absorber in real wave spectrum
[J].DOI:10.1016/j.oceaneng.2021.109736 [本文引用: 1]
Analysis and wave tank verification of the performance of point absorber WECs with different configurations
[J].
Power absorption modeling and optimization of a point absorbing wave energy converter using numerical method
[J].DOI:10.1115/1.4027409 [本文引用: 1]
Investigation on parametrically excited motions of point absorbers in regular waves
[J].DOI:10.1016/j.oceaneng.2015.10.041 [本文引用: 1]
Hydrodynamic performance and power absorption of a multi-freedom buoy wave energy device
[J].DOI:10.1016/j.oceaneng.2018.12.005 [本文引用: 1]
Influence of the shape of a buoy on the efficiency of its dual-motion wave energy conversion
[J].DOI:10.1016/j.energy.2020.118998 [本文引用: 1]