(1) $ \begin{split} & \mathop {\arg \min } \limits_{\boldsymbol{f}} \;\Biggr(\dfrac{1}{2}\left\| { \displaystyle\sum\limits_{d = 1}^D {{\boldsymbol{x}}_t^d} *{{\boldsymbol{f}}^d} - {\boldsymbol{y}}} \right\|_2^2 + \dfrac{1}{2} \displaystyle\sum\limits_{d = 1}^D {\left\| {{\boldsymbol{w}} \cdot {{\boldsymbol{f}}^d}} \right\|_2^2} + \Biggr.\\[-2pt]& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Biggr.\dfrac{\mu }{2}\left\| {{\boldsymbol{f}} - {{\boldsymbol{f}}_{t - 1}}} \right\|_2^2\Biggr) . \end{split} $
[1]
黄月平, 李小锋, 杨小冈, 等 基于相关滤波的视觉目标跟踪算法新进展
[J]. 系统工程与电子技术 , 2021 , 43 (8 ): 2051 - 2065
DOI:10.12305/j.issn.1001-506X.2021.08.05
[本文引用: 1]
HUANG Yue-ping, LI Xiao-feng, YANG Xiao-gang, et al Advances in visual object tracking algorithm based on correlation filter
[J]. Systems Engineering and Electronics , 2021 , 43 (8 ): 2051 - 2065
DOI:10.12305/j.issn.1001-506X.2021.08.05
[本文引用: 1]
[2]
BOLME D S, BEVERIDGE J R, DRAPER B A, et al. Visual object tracking using adaptive correlation filters [C]// 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010: 2544-2550.
[本文引用: 1]
[3]
HENRIQUES J F, CASEIRO R, MARTINS P, et al High-speed tracking with kernelized correlation filters
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2015 , 37 (3 ): 583 - 596
DOI:10.1109/TPAMI.2014.2345390
[本文引用: 4]
[4]
DANELLJAN M, KHAN F S, FELSBERG M, et al. Adaptive color attributes for real-time visual tracking [C]// 2014 IEEE Conference on Computer Vision and Pattern Recognition. Columbus: IEEE, 2014: 1090-1097.
[本文引用: 1]
[5]
WANG N Y, SHI J P, YEUNG D Y, et al. Understanding and diagnosing visual tracking systems [C]// 2015 IEEE International Conference on Computer Vision. Santiago: IEEE, 2015: 3101-3109.
[本文引用: 1]
[7]
熊昌镇, 王润玲, 邹建成 基于多高斯相关滤波的实时跟踪算法
[J]. 浙江大学学报:工学版 , 2019 , 53 (8 ): 1488 - 1495
[本文引用: 1]
XIONG Chang-zhen, WANG Run-ling, ZOU Jian-cheng Real-time tracking algorithm based on multiple Gaussian-distirbution correlation filters
[J]. Journal of Zhejiang University: Engineering Science , 2019 , 53 (8 ): 1488 - 1495
[本文引用: 1]
[8]
GALOOGAHI H K, FAGG A, LUCEY S. Learning backg- round-aware correlation filters for visual tracking [C]// 2017 IEEE International Conference on Computer Vision. Venice: IEEE, 2017: 1144-1152.
[本文引用: 4]
[9]
DANELLJAN M, HÄGER G, KHAN F S, et al. Learning spatially regularized correlation filters for visual tracking [C]// 2015 IEEE International Conference on Computer Vision . Santiago: IEEE, 2015: 4310-4318.
[本文引用: 4]
[10]
LI F, TIAN C, ZUO W M, et al. Learning spatial-temporal regularized correlation filters for visual tracking [C]// 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 4904-4913.
[本文引用: 5]
[11]
尹明锋, 薄煜明, 朱建良, 等. 基于通道可靠性的多尺度背景感知相关滤波跟踪算法[J]. 光学学报. 2019, 39(5): 0515002.
[本文引用: 2]
YIN Ming-feng, BO Yu-ming, ZHU Jian-liang, et al. Multi-scale context-aware correlation filter tracking algorithm based on channel reliability [J]. Acta Optica Sinica, 2019, 39(5): 0515002.
[本文引用: 2]
[12]
LU X K, MA C, NI B B, et al Adaptive region proposal with channel regularization for robust object tracking
[J]. IEEE Transactions on Circuits and Systems for Video Technology , 2021 , 31 (4 ): 1268 - 1282
DOI:10.1109/TCSVT.2019.2944654
[本文引用: 1]
[13]
XU T Y , FENG Z H, WU X J, et al. Joint group feature selection and discriminative filter learning for robust visual obj-ect tracking [C]// 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019: 7950-7960.
[本文引用: 2]
[14]
YE J J, FU C H, LIN F L, et al Multi-regularized correlation filter for UAV tracking and self-localization
[J]. IEEE Transactions on Industrial Electronics , 2021 , 6004 - 6014
[本文引用: 1]
[15]
WANG M M, LIU Y, HUANG Z Y. Large margin object tracking with circulant feature maps [C]// 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017: 4800-4808.
[本文引用: 1]
[16]
HUANG Z Y, FU C H, LI Y M, et al. Learning aberrance repressed correlation filters for real-time UAV tracking [C]// Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019: 2891-2900.
[本文引用: 4]
[17]
LI Y M, FU C H, DING F Q, et al. AutoTrack: towards high-performance visual tracking for UAV with automatic spatio-temporal regularization [C]// 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020: 11920-11929.
[本文引用: 4]
[18]
姜文涛, 刘晓璇, 涂潮, 等 空间异常适应性的目标跟踪
[J]. 模式识别与人工智能 , 2021 , 34 (5 ): 473 - 484
DOI:10.16451/j.cnki.issn1003-6059.202105010
[本文引用: 1]
JIANG Wen-tao, LIU Xiao-xuan, TU Chao, et al Spatially abnormal adaptive target tracking
[J]. Pattern Recognition and Artificial Intelligence , 2021 , 34 (5 ): 473 - 484
DOI:10.16451/j.cnki.issn1003-6059.202105010
[本文引用: 1]
[19]
BOYD S, PARIKH N, CHU E, et al Distributed optimization and statistical learning via the alternating direction method of multipliers
[J]. Foundations and Trends in Machine Leaning , 2010 , 3 (1 ): 1 - 122
DOI:10.1561/2200000016
[本文引用: 1]
[20]
WU Y, LIM J, YANG M H Object tracking benchmark
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2015 , 37 (9 ): 1834 - 1848
DOI:10.1109/TPAMI.2014.2388226
[本文引用: 1]
[21]
LIANG P P, BLASCH E, LING H B. Encoding color info- rmation for visual tracking: algorithms and benchmark [J]. IEEE Transactions on Image Processing, 2015, 24(12): 5630-5644.
[本文引用: 1]
[22]
MUELLER M, SMITH N, GHANEM B. A benchmark and simulator for UAV tracking [C]// 2016 European Conference on Computer Vision. Amsterdam: Springer, 2016: 445–461.
[本文引用: 1]
[23]
MA C, HUANG J B, YANG X, et al. Hierarchical convolutional features for visual tracking [C]// 2015 IEEE International Conference on Computer Vision . Santiago: IEEE, 2015: 3074-3082.
[本文引用: 3]
[24]
QI Y, ZHANG S, QIN L, et al. Hedged deep tracking [C]// 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 4303-4311.
[本文引用: 3]
[25]
DANELLJAN M, HÄGER G, KHAN F S, et al. Convolutional features for correlation filter based visual tracking [C]// 2015 IEEE International Conference on Computer Vision Workshop. Santiago: IEEE, 2015: 621-629.
[本文引用: 2]
[26]
DANELLJAN M, BHAT G, KHAN F S, et al. ECO: efficient convolution operators for tracking [C]// 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017: 6931-6939.
[本文引用: 3]
[27]
DANELLJAN M, HÄGER G, KHAN F S, et al. Adaptive decontamination of the training set: a unified formulation for discriminative visual tracking [C]// 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas : IEEE, 2016: 1430-1438.
[本文引用: 3]
[28]
MA C, YANG X K, ZAHNG C Y, et al. Long-term correlation tracking [C]// 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015: 5388-5396.
[本文引用: 3]
[29]
MA H Y, ACTON S T, LIN Z L SITUP: scale invariant tracking using average peak-to-correlation energy
[J]. IEEE Transactions on Image Processing , 2020 , 29 : 3546 - 3557
DOI:10.1109/TIP.2019.2962694
[本文引用: 3]
[30]
MA H Y, LIN Z L, ACTON S T FAST: fast and accurate scale estimation for tracking
[J]. IEEE Signal Processing Letters , 2020 , 27 : 161 - 165
DOI:10.1109/LSP.2019.2963147
[本文引用: 3]
[31]
FU C H, XU J T, LIN F L, et al Object saliency-aware dual regularized correlation filter for real-time aerial tracking
[J]. IEEE Transactions on Geoscience and Remote Sensing , 2020 , 58 (12 ): 8940 - 8951
DOI:10.1109/TGRS.2020.2992301
[本文引用: 3]
[32]
BERTINETTO L, VALMADRE J, HENRIQUES J F, et al. Fully-convolutional siamese networks for object tracking [C]// 2016 European Conference on Computer Vision . Amsterdam: Springer, 2016: 850-865.
[本文引用: 1]
基于相关滤波的视觉目标跟踪算法新进展
1
2021
... 目标跟踪是高层计算机视觉处理技术的重要基石,在智能视觉导航、智能视频监控、人机交互等军事及民用领域应用广泛[1 ] . 基于相关滤波的目标跟踪算法由于其精度高、鲁棒性好,受到相关学者关注. 相比于生成式目标跟踪算法,判别式目标跟踪算法充分考虑背景信息,提高了分类的准确性. Bolme等[2 ] 提出最小输出误差平方和跟踪算法(minimum output sum of squared error, MOSSE),将通信领域的相关滤波引入目标跟踪,通过傅里叶变换将时域的复杂运算转换到频域进行加速求解,算法速度高达669 帧/s. Henriques等[3 ] 提出核相关滤波目标跟踪算法(kernelized correlation filters, KCF),将核函数以及多通道的梯度方向直方图(histogram of oriented gradient, HOG)特征引入相关滤波跟踪器,不但增强了模型的判别能力,而且保持了较快的跟踪速度. Danelljan等[4 ] 将颜色(color name, CN)特征引入相关滤波框架以更好应对跟踪过程中的光照变化. Wang等[5 ] 提出理解和诊断视觉跟踪系统,通过实验发现特征提取在目标跟踪过程中发挥着重要的作用. 目标跟踪算法常用的手工特征包括HOG、CN. HOG特征通过计算图像局部区域的方向梯度表达目标,有效描述目标的轮廓和形状信息;CN特征包含图像的色彩信息,对目标形变、旋转具有很好的适应性. 汤张泳等[6 ] 提出多空间分辨率自适应特征融合的目标跟踪算法,在时空正则相关滤波算法(spatial-temporal regularized correlation filters, STRCF)框架下使用更深的网络提取深度特征,进一步提升跟踪的鲁棒性和鉴别性. 由于汤张泳等[6 ] 所提算法的平均速度约为4帧/s,不能满足实时性的要求. 熊昌镇等[7 ] 提出的多高斯相关滤波器融合的目标跟踪算法,采用稀疏卷积特征表达目标,能够有效应对遮挡、形变挑战,但未区分高维特征的有效性. ...
基于相关滤波的视觉目标跟踪算法新进展
1
2021
... 目标跟踪是高层计算机视觉处理技术的重要基石,在智能视觉导航、智能视频监控、人机交互等军事及民用领域应用广泛[1 ] . 基于相关滤波的目标跟踪算法由于其精度高、鲁棒性好,受到相关学者关注. 相比于生成式目标跟踪算法,判别式目标跟踪算法充分考虑背景信息,提高了分类的准确性. Bolme等[2 ] 提出最小输出误差平方和跟踪算法(minimum output sum of squared error, MOSSE),将通信领域的相关滤波引入目标跟踪,通过傅里叶变换将时域的复杂运算转换到频域进行加速求解,算法速度高达669 帧/s. Henriques等[3 ] 提出核相关滤波目标跟踪算法(kernelized correlation filters, KCF),将核函数以及多通道的梯度方向直方图(histogram of oriented gradient, HOG)特征引入相关滤波跟踪器,不但增强了模型的判别能力,而且保持了较快的跟踪速度. Danelljan等[4 ] 将颜色(color name, CN)特征引入相关滤波框架以更好应对跟踪过程中的光照变化. Wang等[5 ] 提出理解和诊断视觉跟踪系统,通过实验发现特征提取在目标跟踪过程中发挥着重要的作用. 目标跟踪算法常用的手工特征包括HOG、CN. HOG特征通过计算图像局部区域的方向梯度表达目标,有效描述目标的轮廓和形状信息;CN特征包含图像的色彩信息,对目标形变、旋转具有很好的适应性. 汤张泳等[6 ] 提出多空间分辨率自适应特征融合的目标跟踪算法,在时空正则相关滤波算法(spatial-temporal regularized correlation filters, STRCF)框架下使用更深的网络提取深度特征,进一步提升跟踪的鲁棒性和鉴别性. 由于汤张泳等[6 ] 所提算法的平均速度约为4帧/s,不能满足实时性的要求. 熊昌镇等[7 ] 提出的多高斯相关滤波器融合的目标跟踪算法,采用稀疏卷积特征表达目标,能够有效应对遮挡、形变挑战,但未区分高维特征的有效性. ...
1
... 目标跟踪是高层计算机视觉处理技术的重要基石,在智能视觉导航、智能视频监控、人机交互等军事及民用领域应用广泛[1 ] . 基于相关滤波的目标跟踪算法由于其精度高、鲁棒性好,受到相关学者关注. 相比于生成式目标跟踪算法,判别式目标跟踪算法充分考虑背景信息,提高了分类的准确性. Bolme等[2 ] 提出最小输出误差平方和跟踪算法(minimum output sum of squared error, MOSSE),将通信领域的相关滤波引入目标跟踪,通过傅里叶变换将时域的复杂运算转换到频域进行加速求解,算法速度高达669 帧/s. Henriques等[3 ] 提出核相关滤波目标跟踪算法(kernelized correlation filters, KCF),将核函数以及多通道的梯度方向直方图(histogram of oriented gradient, HOG)特征引入相关滤波跟踪器,不但增强了模型的判别能力,而且保持了较快的跟踪速度. Danelljan等[4 ] 将颜色(color name, CN)特征引入相关滤波框架以更好应对跟踪过程中的光照变化. Wang等[5 ] 提出理解和诊断视觉跟踪系统,通过实验发现特征提取在目标跟踪过程中发挥着重要的作用. 目标跟踪算法常用的手工特征包括HOG、CN. HOG特征通过计算图像局部区域的方向梯度表达目标,有效描述目标的轮廓和形状信息;CN特征包含图像的色彩信息,对目标形变、旋转具有很好的适应性. 汤张泳等[6 ] 提出多空间分辨率自适应特征融合的目标跟踪算法,在时空正则相关滤波算法(spatial-temporal regularized correlation filters, STRCF)框架下使用更深的网络提取深度特征,进一步提升跟踪的鲁棒性和鉴别性. 由于汤张泳等[6 ] 所提算法的平均速度约为4帧/s,不能满足实时性的要求. 熊昌镇等[7 ] 提出的多高斯相关滤波器融合的目标跟踪算法,采用稀疏卷积特征表达目标,能够有效应对遮挡、形变挑战,但未区分高维特征的有效性. ...
High-speed tracking with kernelized correlation filters
4
2015
... 目标跟踪是高层计算机视觉处理技术的重要基石,在智能视觉导航、智能视频监控、人机交互等军事及民用领域应用广泛[1 ] . 基于相关滤波的目标跟踪算法由于其精度高、鲁棒性好,受到相关学者关注. 相比于生成式目标跟踪算法,判别式目标跟踪算法充分考虑背景信息,提高了分类的准确性. Bolme等[2 ] 提出最小输出误差平方和跟踪算法(minimum output sum of squared error, MOSSE),将通信领域的相关滤波引入目标跟踪,通过傅里叶变换将时域的复杂运算转换到频域进行加速求解,算法速度高达669 帧/s. Henriques等[3 ] 提出核相关滤波目标跟踪算法(kernelized correlation filters, KCF),将核函数以及多通道的梯度方向直方图(histogram of oriented gradient, HOG)特征引入相关滤波跟踪器,不但增强了模型的判别能力,而且保持了较快的跟踪速度. Danelljan等[4 ] 将颜色(color name, CN)特征引入相关滤波框架以更好应对跟踪过程中的光照变化. Wang等[5 ] 提出理解和诊断视觉跟踪系统,通过实验发现特征提取在目标跟踪过程中发挥着重要的作用. 目标跟踪算法常用的手工特征包括HOG、CN. HOG特征通过计算图像局部区域的方向梯度表达目标,有效描述目标的轮廓和形状信息;CN特征包含图像的色彩信息,对目标形变、旋转具有很好的适应性. 汤张泳等[6 ] 提出多空间分辨率自适应特征融合的目标跟踪算法,在时空正则相关滤波算法(spatial-temporal regularized correlation filters, STRCF)框架下使用更深的网络提取深度特征,进一步提升跟踪的鲁棒性和鉴别性. 由于汤张泳等[6 ] 所提算法的平均速度约为4帧/s,不能满足实时性的要求. 熊昌镇等[7 ] 提出的多高斯相关滤波器融合的目标跟踪算法,采用稀疏卷积特征表达目标,能够有效应对遮挡、形变挑战,但未区分高维特征的有效性. ...
... 2)基于手工特征的相关滤波算法:KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] . ...
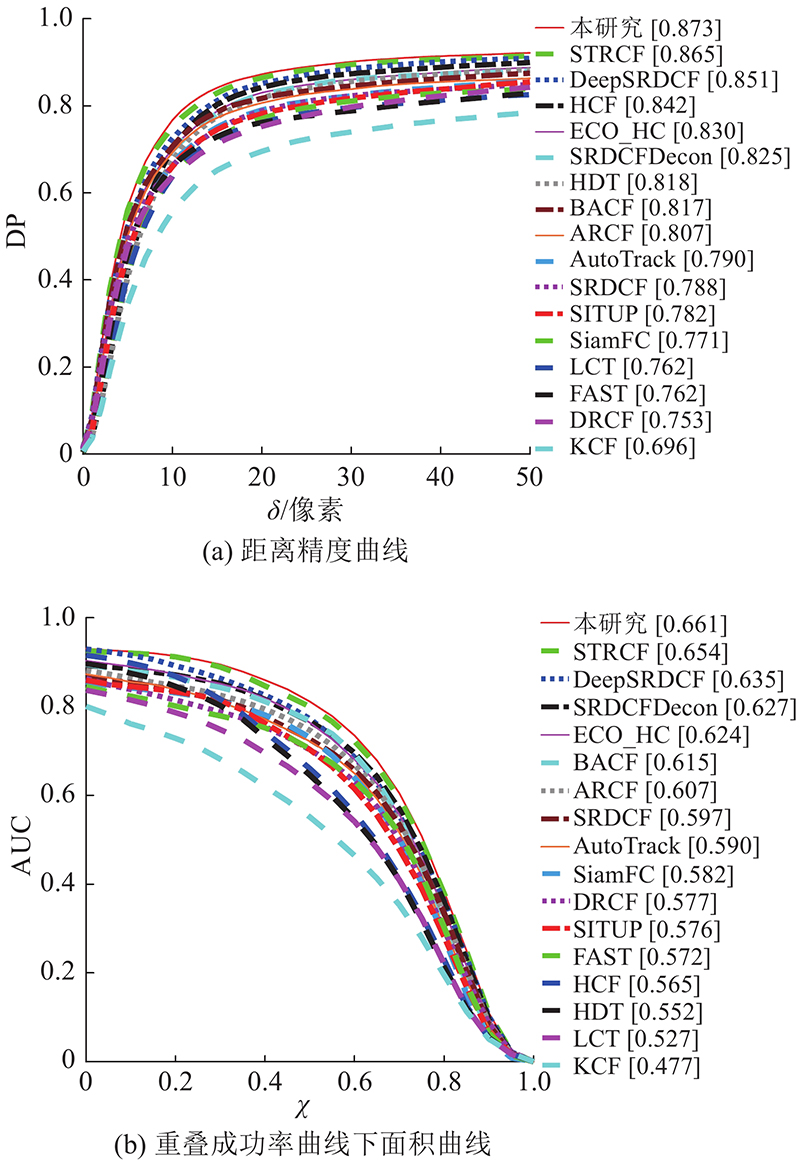
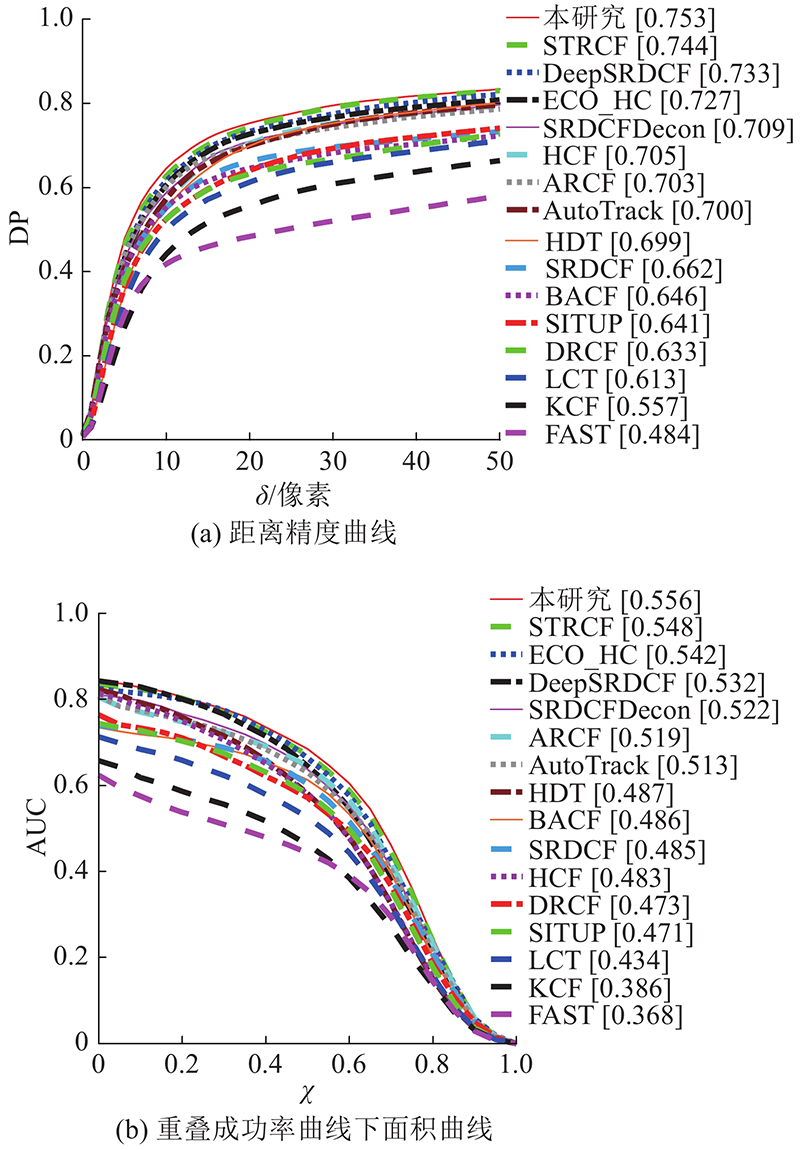
... 为了进一步测试本研究算法在更具挑战性的数据集上的跟踪效果,选取TempleColor128数据集进行验证. 对比更多优秀的算法,主要包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、DeepSRDCF[25 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 以及近年优秀的跟踪算法ARCF[16 ] 、AutoTrack[17 ] 、SITUP[29 ] 、FAST[30 ] 、DRCF[31 ] . 如图5 所示,为不同算法在TempleColor128数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在TempleColor128数据集获得最高的DP、AUC,分别为75.3%、55.6%. 相比于基线算法STRCF,DP和AUC分别提高了0.9%、0.8%. ...
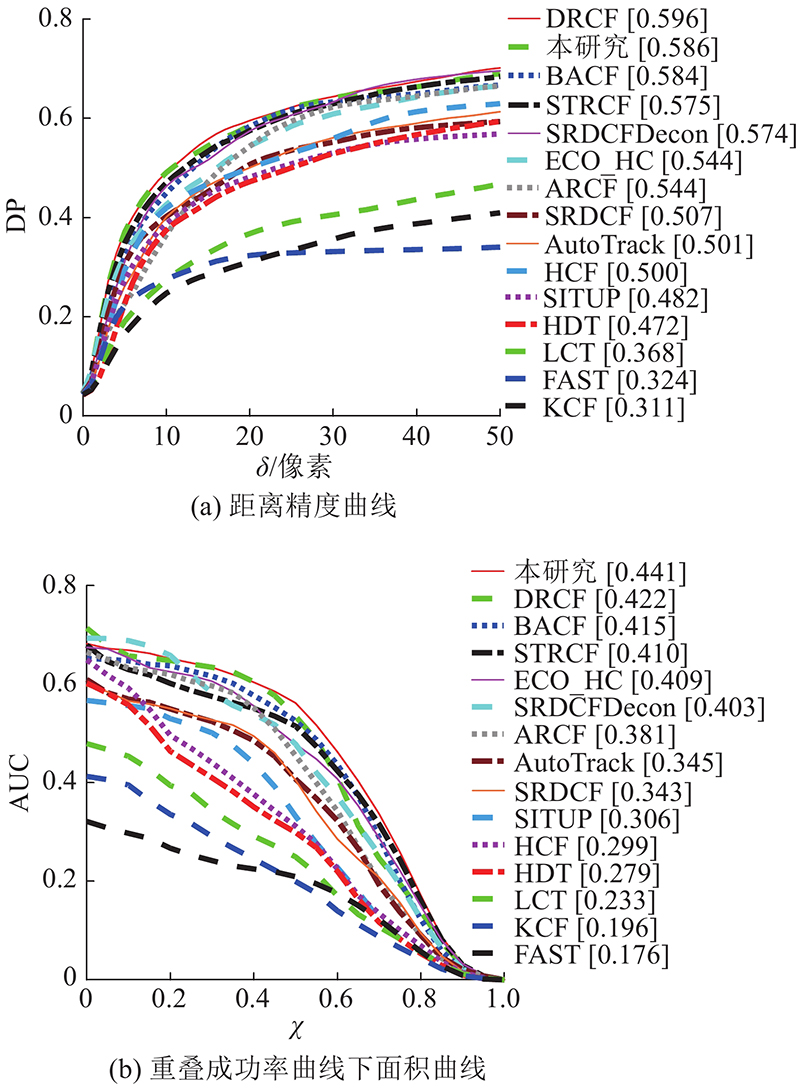
... 为了验证本研究算法在无人机航拍数据集上的适用性,选取UAV20L数据集长时视频序列进行测试. 对比算法包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] 以及适用于无人机领域的优秀算法ARCF[16 ] 、AutoTrack[17 ] 、DRCF[31 ] . 如图6 所示为不同算法在UAV20L数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在UAV20L数据集上获得第2高的DP,为58.6%; 同时获得第1高的AUC,为44.1%. 相比于STRCF,本研究算法的DP、AUC分别提高1.1%和3.1%. DRCF在UAV20L数据集上获得较高的DP和AUC. 主要原因是DRCF利用显著性检测算法构建双重正则项,使边界效应得到有效缓解. ...
1
... 目标跟踪是高层计算机视觉处理技术的重要基石,在智能视觉导航、智能视频监控、人机交互等军事及民用领域应用广泛[1 ] . 基于相关滤波的目标跟踪算法由于其精度高、鲁棒性好,受到相关学者关注. 相比于生成式目标跟踪算法,判别式目标跟踪算法充分考虑背景信息,提高了分类的准确性. Bolme等[2 ] 提出最小输出误差平方和跟踪算法(minimum output sum of squared error, MOSSE),将通信领域的相关滤波引入目标跟踪,通过傅里叶变换将时域的复杂运算转换到频域进行加速求解,算法速度高达669 帧/s. Henriques等[3 ] 提出核相关滤波目标跟踪算法(kernelized correlation filters, KCF),将核函数以及多通道的梯度方向直方图(histogram of oriented gradient, HOG)特征引入相关滤波跟踪器,不但增强了模型的判别能力,而且保持了较快的跟踪速度. Danelljan等[4 ] 将颜色(color name, CN)特征引入相关滤波框架以更好应对跟踪过程中的光照变化. Wang等[5 ] 提出理解和诊断视觉跟踪系统,通过实验发现特征提取在目标跟踪过程中发挥着重要的作用. 目标跟踪算法常用的手工特征包括HOG、CN. HOG特征通过计算图像局部区域的方向梯度表达目标,有效描述目标的轮廓和形状信息;CN特征包含图像的色彩信息,对目标形变、旋转具有很好的适应性. 汤张泳等[6 ] 提出多空间分辨率自适应特征融合的目标跟踪算法,在时空正则相关滤波算法(spatial-temporal regularized correlation filters, STRCF)框架下使用更深的网络提取深度特征,进一步提升跟踪的鲁棒性和鉴别性. 由于汤张泳等[6 ] 所提算法的平均速度约为4帧/s,不能满足实时性的要求. 熊昌镇等[7 ] 提出的多高斯相关滤波器融合的目标跟踪算法,采用稀疏卷积特征表达目标,能够有效应对遮挡、形变挑战,但未区分高维特征的有效性. ...
1
... 目标跟踪是高层计算机视觉处理技术的重要基石,在智能视觉导航、智能视频监控、人机交互等军事及民用领域应用广泛[1 ] . 基于相关滤波的目标跟踪算法由于其精度高、鲁棒性好,受到相关学者关注. 相比于生成式目标跟踪算法,判别式目标跟踪算法充分考虑背景信息,提高了分类的准确性. Bolme等[2 ] 提出最小输出误差平方和跟踪算法(minimum output sum of squared error, MOSSE),将通信领域的相关滤波引入目标跟踪,通过傅里叶变换将时域的复杂运算转换到频域进行加速求解,算法速度高达669 帧/s. Henriques等[3 ] 提出核相关滤波目标跟踪算法(kernelized correlation filters, KCF),将核函数以及多通道的梯度方向直方图(histogram of oriented gradient, HOG)特征引入相关滤波跟踪器,不但增强了模型的判别能力,而且保持了较快的跟踪速度. Danelljan等[4 ] 将颜色(color name, CN)特征引入相关滤波框架以更好应对跟踪过程中的光照变化. Wang等[5 ] 提出理解和诊断视觉跟踪系统,通过实验发现特征提取在目标跟踪过程中发挥着重要的作用. 目标跟踪算法常用的手工特征包括HOG、CN. HOG特征通过计算图像局部区域的方向梯度表达目标,有效描述目标的轮廓和形状信息;CN特征包含图像的色彩信息,对目标形变、旋转具有很好的适应性. 汤张泳等[6 ] 提出多空间分辨率自适应特征融合的目标跟踪算法,在时空正则相关滤波算法(spatial-temporal regularized correlation filters, STRCF)框架下使用更深的网络提取深度特征,进一步提升跟踪的鲁棒性和鉴别性. 由于汤张泳等[6 ] 所提算法的平均速度约为4帧/s,不能满足实时性的要求. 熊昌镇等[7 ] 提出的多高斯相关滤波器融合的目标跟踪算法,采用稀疏卷积特征表达目标,能够有效应对遮挡、形变挑战,但未区分高维特征的有效性. ...
多空间分辨率自适应特征融合的相关滤波目标跟踪算法
2
2020
... 目标跟踪是高层计算机视觉处理技术的重要基石,在智能视觉导航、智能视频监控、人机交互等军事及民用领域应用广泛[1 ] . 基于相关滤波的目标跟踪算法由于其精度高、鲁棒性好,受到相关学者关注. 相比于生成式目标跟踪算法,判别式目标跟踪算法充分考虑背景信息,提高了分类的准确性. Bolme等[2 ] 提出最小输出误差平方和跟踪算法(minimum output sum of squared error, MOSSE),将通信领域的相关滤波引入目标跟踪,通过傅里叶变换将时域的复杂运算转换到频域进行加速求解,算法速度高达669 帧/s. Henriques等[3 ] 提出核相关滤波目标跟踪算法(kernelized correlation filters, KCF),将核函数以及多通道的梯度方向直方图(histogram of oriented gradient, HOG)特征引入相关滤波跟踪器,不但增强了模型的判别能力,而且保持了较快的跟踪速度. Danelljan等[4 ] 将颜色(color name, CN)特征引入相关滤波框架以更好应对跟踪过程中的光照变化. Wang等[5 ] 提出理解和诊断视觉跟踪系统,通过实验发现特征提取在目标跟踪过程中发挥着重要的作用. 目标跟踪算法常用的手工特征包括HOG、CN. HOG特征通过计算图像局部区域的方向梯度表达目标,有效描述目标的轮廓和形状信息;CN特征包含图像的色彩信息,对目标形变、旋转具有很好的适应性. 汤张泳等[6 ] 提出多空间分辨率自适应特征融合的目标跟踪算法,在时空正则相关滤波算法(spatial-temporal regularized correlation filters, STRCF)框架下使用更深的网络提取深度特征,进一步提升跟踪的鲁棒性和鉴别性. 由于汤张泳等[6 ] 所提算法的平均速度约为4帧/s,不能满足实时性的要求. 熊昌镇等[7 ] 提出的多高斯相关滤波器融合的目标跟踪算法,采用稀疏卷积特征表达目标,能够有效应对遮挡、形变挑战,但未区分高维特征的有效性. ...
... [6 ]所提算法的平均速度约为4帧/s,不能满足实时性的要求. 熊昌镇等[7 ] 提出的多高斯相关滤波器融合的目标跟踪算法,采用稀疏卷积特征表达目标,能够有效应对遮挡、形变挑战,但未区分高维特征的有效性. ...
多空间分辨率自适应特征融合的相关滤波目标跟踪算法
2
2020
... 目标跟踪是高层计算机视觉处理技术的重要基石,在智能视觉导航、智能视频监控、人机交互等军事及民用领域应用广泛[1 ] . 基于相关滤波的目标跟踪算法由于其精度高、鲁棒性好,受到相关学者关注. 相比于生成式目标跟踪算法,判别式目标跟踪算法充分考虑背景信息,提高了分类的准确性. Bolme等[2 ] 提出最小输出误差平方和跟踪算法(minimum output sum of squared error, MOSSE),将通信领域的相关滤波引入目标跟踪,通过傅里叶变换将时域的复杂运算转换到频域进行加速求解,算法速度高达669 帧/s. Henriques等[3 ] 提出核相关滤波目标跟踪算法(kernelized correlation filters, KCF),将核函数以及多通道的梯度方向直方图(histogram of oriented gradient, HOG)特征引入相关滤波跟踪器,不但增强了模型的判别能力,而且保持了较快的跟踪速度. Danelljan等[4 ] 将颜色(color name, CN)特征引入相关滤波框架以更好应对跟踪过程中的光照变化. Wang等[5 ] 提出理解和诊断视觉跟踪系统,通过实验发现特征提取在目标跟踪过程中发挥着重要的作用. 目标跟踪算法常用的手工特征包括HOG、CN. HOG特征通过计算图像局部区域的方向梯度表达目标,有效描述目标的轮廓和形状信息;CN特征包含图像的色彩信息,对目标形变、旋转具有很好的适应性. 汤张泳等[6 ] 提出多空间分辨率自适应特征融合的目标跟踪算法,在时空正则相关滤波算法(spatial-temporal regularized correlation filters, STRCF)框架下使用更深的网络提取深度特征,进一步提升跟踪的鲁棒性和鉴别性. 由于汤张泳等[6 ] 所提算法的平均速度约为4帧/s,不能满足实时性的要求. 熊昌镇等[7 ] 提出的多高斯相关滤波器融合的目标跟踪算法,采用稀疏卷积特征表达目标,能够有效应对遮挡、形变挑战,但未区分高维特征的有效性. ...
... [6 ]所提算法的平均速度约为4帧/s,不能满足实时性的要求. 熊昌镇等[7 ] 提出的多高斯相关滤波器融合的目标跟踪算法,采用稀疏卷积特征表达目标,能够有效应对遮挡、形变挑战,但未区分高维特征的有效性. ...
基于多高斯相关滤波的实时跟踪算法
1
2019
... 目标跟踪是高层计算机视觉处理技术的重要基石,在智能视觉导航、智能视频监控、人机交互等军事及民用领域应用广泛[1 ] . 基于相关滤波的目标跟踪算法由于其精度高、鲁棒性好,受到相关学者关注. 相比于生成式目标跟踪算法,判别式目标跟踪算法充分考虑背景信息,提高了分类的准确性. Bolme等[2 ] 提出最小输出误差平方和跟踪算法(minimum output sum of squared error, MOSSE),将通信领域的相关滤波引入目标跟踪,通过傅里叶变换将时域的复杂运算转换到频域进行加速求解,算法速度高达669 帧/s. Henriques等[3 ] 提出核相关滤波目标跟踪算法(kernelized correlation filters, KCF),将核函数以及多通道的梯度方向直方图(histogram of oriented gradient, HOG)特征引入相关滤波跟踪器,不但增强了模型的判别能力,而且保持了较快的跟踪速度. Danelljan等[4 ] 将颜色(color name, CN)特征引入相关滤波框架以更好应对跟踪过程中的光照变化. Wang等[5 ] 提出理解和诊断视觉跟踪系统,通过实验发现特征提取在目标跟踪过程中发挥着重要的作用. 目标跟踪算法常用的手工特征包括HOG、CN. HOG特征通过计算图像局部区域的方向梯度表达目标,有效描述目标的轮廓和形状信息;CN特征包含图像的色彩信息,对目标形变、旋转具有很好的适应性. 汤张泳等[6 ] 提出多空间分辨率自适应特征融合的目标跟踪算法,在时空正则相关滤波算法(spatial-temporal regularized correlation filters, STRCF)框架下使用更深的网络提取深度特征,进一步提升跟踪的鲁棒性和鉴别性. 由于汤张泳等[6 ] 所提算法的平均速度约为4帧/s,不能满足实时性的要求. 熊昌镇等[7 ] 提出的多高斯相关滤波器融合的目标跟踪算法,采用稀疏卷积特征表达目标,能够有效应对遮挡、形变挑战,但未区分高维特征的有效性. ...
基于多高斯相关滤波的实时跟踪算法
1
2019
... 目标跟踪是高层计算机视觉处理技术的重要基石,在智能视觉导航、智能视频监控、人机交互等军事及民用领域应用广泛[1 ] . 基于相关滤波的目标跟踪算法由于其精度高、鲁棒性好,受到相关学者关注. 相比于生成式目标跟踪算法,判别式目标跟踪算法充分考虑背景信息,提高了分类的准确性. Bolme等[2 ] 提出最小输出误差平方和跟踪算法(minimum output sum of squared error, MOSSE),将通信领域的相关滤波引入目标跟踪,通过傅里叶变换将时域的复杂运算转换到频域进行加速求解,算法速度高达669 帧/s. Henriques等[3 ] 提出核相关滤波目标跟踪算法(kernelized correlation filters, KCF),将核函数以及多通道的梯度方向直方图(histogram of oriented gradient, HOG)特征引入相关滤波跟踪器,不但增强了模型的判别能力,而且保持了较快的跟踪速度. Danelljan等[4 ] 将颜色(color name, CN)特征引入相关滤波框架以更好应对跟踪过程中的光照变化. Wang等[5 ] 提出理解和诊断视觉跟踪系统,通过实验发现特征提取在目标跟踪过程中发挥着重要的作用. 目标跟踪算法常用的手工特征包括HOG、CN. HOG特征通过计算图像局部区域的方向梯度表达目标,有效描述目标的轮廓和形状信息;CN特征包含图像的色彩信息,对目标形变、旋转具有很好的适应性. 汤张泳等[6 ] 提出多空间分辨率自适应特征融合的目标跟踪算法,在时空正则相关滤波算法(spatial-temporal regularized correlation filters, STRCF)框架下使用更深的网络提取深度特征,进一步提升跟踪的鲁棒性和鉴别性. 由于汤张泳等[6 ] 所提算法的平均速度约为4帧/s,不能满足实时性的要求. 熊昌镇等[7 ] 提出的多高斯相关滤波器融合的目标跟踪算法,采用稀疏卷积特征表达目标,能够有效应对遮挡、形变挑战,但未区分高维特征的有效性. ...
4
... 训练样本不真实将导致边界效应的产生,使滤波器的判别能力降低. Galoogahi等[8 ] 提出的背景感知相关滤波算法(background-aware correlation filters, BACF)引入裁剪矩阵,在扩大的搜索区域上裁剪样本,保证了样本质量,有效缓解了边界效应. Danelljan等[9 ] 提出的空间正则相关滤波算法(spatially regularized discriminative correlation filters, SRDCF)采用扩大搜索区域的方式获得大量样本,通过固定的空间正则权重惩罚滤波器系数缓解边界效应. Li等[10 ] 提出的STRCF在SRDCF的基础上引入时间约束,防止滤波器模型退化,进一步提升了跟踪器的性能. 相比传统的相关滤波算法,以上扩大搜索区域的方法引入更多的背景信息,使滤波器更容易从环境中学习,降低了跟踪结果的可信度. 在目标函数中引入异常抑制正则项,及时抑制跟踪过程中出现的异常,将提高目标跟踪的鲁棒性. ...
... 2)基于手工特征的相关滤波算法:KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] . ...
... 为了进一步测试本研究算法在更具挑战性的数据集上的跟踪效果,选取TempleColor128数据集进行验证. 对比更多优秀的算法,主要包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、DeepSRDCF[25 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 以及近年优秀的跟踪算法ARCF[16 ] 、AutoTrack[17 ] 、SITUP[29 ] 、FAST[30 ] 、DRCF[31 ] . 如图5 所示,为不同算法在TempleColor128数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在TempleColor128数据集获得最高的DP、AUC,分别为75.3%、55.6%. 相比于基线算法STRCF,DP和AUC分别提高了0.9%、0.8%. ...
... 为了验证本研究算法在无人机航拍数据集上的适用性,选取UAV20L数据集长时视频序列进行测试. 对比算法包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] 以及适用于无人机领域的优秀算法ARCF[16 ] 、AutoTrack[17 ] 、DRCF[31 ] . 如图6 所示为不同算法在UAV20L数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在UAV20L数据集上获得第2高的DP,为58.6%; 同时获得第1高的AUC,为44.1%. 相比于STRCF,本研究算法的DP、AUC分别提高1.1%和3.1%. DRCF在UAV20L数据集上获得较高的DP和AUC. 主要原因是DRCF利用显著性检测算法构建双重正则项,使边界效应得到有效缓解. ...
4
... 训练样本不真实将导致边界效应的产生,使滤波器的判别能力降低. Galoogahi等[8 ] 提出的背景感知相关滤波算法(background-aware correlation filters, BACF)引入裁剪矩阵,在扩大的搜索区域上裁剪样本,保证了样本质量,有效缓解了边界效应. Danelljan等[9 ] 提出的空间正则相关滤波算法(spatially regularized discriminative correlation filters, SRDCF)采用扩大搜索区域的方式获得大量样本,通过固定的空间正则权重惩罚滤波器系数缓解边界效应. Li等[10 ] 提出的STRCF在SRDCF的基础上引入时间约束,防止滤波器模型退化,进一步提升了跟踪器的性能. 相比传统的相关滤波算法,以上扩大搜索区域的方法引入更多的背景信息,使滤波器更容易从环境中学习,降低了跟踪结果的可信度. 在目标函数中引入异常抑制正则项,及时抑制跟踪过程中出现的异常,将提高目标跟踪的鲁棒性. ...
... 2)基于手工特征的相关滤波算法:KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] . ...
... 为了进一步测试本研究算法在更具挑战性的数据集上的跟踪效果,选取TempleColor128数据集进行验证. 对比更多优秀的算法,主要包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、DeepSRDCF[25 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 以及近年优秀的跟踪算法ARCF[16 ] 、AutoTrack[17 ] 、SITUP[29 ] 、FAST[30 ] 、DRCF[31 ] . 如图5 所示,为不同算法在TempleColor128数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在TempleColor128数据集获得最高的DP、AUC,分别为75.3%、55.6%. 相比于基线算法STRCF,DP和AUC分别提高了0.9%、0.8%. ...
... 为了验证本研究算法在无人机航拍数据集上的适用性,选取UAV20L数据集长时视频序列进行测试. 对比算法包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] 以及适用于无人机领域的优秀算法ARCF[16 ] 、AutoTrack[17 ] 、DRCF[31 ] . 如图6 所示为不同算法在UAV20L数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在UAV20L数据集上获得第2高的DP,为58.6%; 同时获得第1高的AUC,为44.1%. 相比于STRCF,本研究算法的DP、AUC分别提高1.1%和3.1%. DRCF在UAV20L数据集上获得较高的DP和AUC. 主要原因是DRCF利用显著性检测算法构建双重正则项,使边界效应得到有效缓解. ...
5
... 训练样本不真实将导致边界效应的产生,使滤波器的判别能力降低. Galoogahi等[8 ] 提出的背景感知相关滤波算法(background-aware correlation filters, BACF)引入裁剪矩阵,在扩大的搜索区域上裁剪样本,保证了样本质量,有效缓解了边界效应. Danelljan等[9 ] 提出的空间正则相关滤波算法(spatially regularized discriminative correlation filters, SRDCF)采用扩大搜索区域的方式获得大量样本,通过固定的空间正则权重惩罚滤波器系数缓解边界效应. Li等[10 ] 提出的STRCF在SRDCF的基础上引入时间约束,防止滤波器模型退化,进一步提升了跟踪器的性能. 相比传统的相关滤波算法,以上扩大搜索区域的方法引入更多的背景信息,使滤波器更容易从环境中学习,降低了跟踪结果的可信度. 在目标函数中引入异常抑制正则项,及时抑制跟踪过程中出现的异常,将提高目标跟踪的鲁棒性. ...
... 初始的步长参数 $ {\gamma ^{(0)}}=10 $ $ {\gamma ^{\max }}=100 $ $ \sigma =1.2$ . 时间正则惩罚参数 $ \;\mu $ $\; \rho $ $ \lambda $ [10 ] 相同. ...
... 2)基于手工特征的相关滤波算法:KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] . ...
... 为了进一步测试本研究算法在更具挑战性的数据集上的跟踪效果,选取TempleColor128数据集进行验证. 对比更多优秀的算法,主要包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、DeepSRDCF[25 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 以及近年优秀的跟踪算法ARCF[16 ] 、AutoTrack[17 ] 、SITUP[29 ] 、FAST[30 ] 、DRCF[31 ] . 如图5 所示,为不同算法在TempleColor128数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在TempleColor128数据集获得最高的DP、AUC,分别为75.3%、55.6%. 相比于基线算法STRCF,DP和AUC分别提高了0.9%、0.8%. ...
... 为了验证本研究算法在无人机航拍数据集上的适用性,选取UAV20L数据集长时视频序列进行测试. 对比算法包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] 以及适用于无人机领域的优秀算法ARCF[16 ] 、AutoTrack[17 ] 、DRCF[31 ] . 如图6 所示为不同算法在UAV20L数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在UAV20L数据集上获得第2高的DP,为58.6%; 同时获得第1高的AUC,为44.1%. 相比于STRCF,本研究算法的DP、AUC分别提高1.1%和3.1%. DRCF在UAV20L数据集上获得较高的DP和AUC. 主要原因是DRCF利用显著性检测算法构建双重正则项,使边界效应得到有效缓解. ...
2
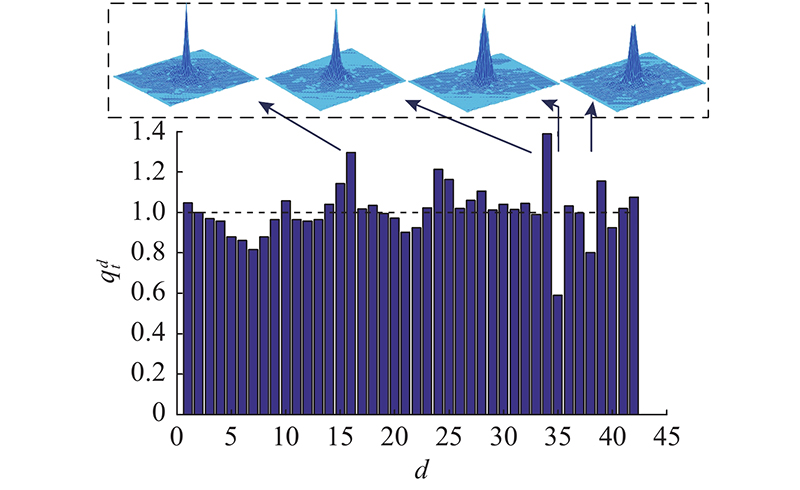
... 文献[11 ]~[13 ]的研究表明,不同特征通道对目标位置估计的贡献不同. 尹明锋等[11 ] 采用通道可靠性系数衡量相关滤波器响应图的置信度,并将其应用于多通道响应图融合,实现目标的精确定位. Lu等[12 ] 提出在目标跟踪过程中,一些特征通道对前景目标敏感,另一些通道对背景、噪声敏感,通过在目标函数中引入 $ {l_1} $ [13 ] 提出空间特征选择和通道特征选择融合的相关滤波算法,通过将个体变量分配到具有一定视觉意义的特定群组,实现空间域和通道域的特征选择,突出具有增强判别力的特征. Ye等[14 ] 利用通道可靠性正则项,在训练阶段联合滤波器模板优化通道权重,实现通道权重的自动分配. ...
... [11 ]采用通道可靠性系数衡量相关滤波器响应图的置信度,并将其应用于多通道响应图融合,实现目标的精确定位. Lu等[12 ] 提出在目标跟踪过程中,一些特征通道对前景目标敏感,另一些通道对背景、噪声敏感,通过在目标函数中引入 $ {l_1} $ [13 ] 提出空间特征选择和通道特征选择融合的相关滤波算法,通过将个体变量分配到具有一定视觉意义的特定群组,实现空间域和通道域的特征选择,突出具有增强判别力的特征. Ye等[14 ] 利用通道可靠性正则项,在训练阶段联合滤波器模板优化通道权重,实现通道权重的自动分配. ...
2
... 文献[11 ]~[13 ]的研究表明,不同特征通道对目标位置估计的贡献不同. 尹明锋等[11 ] 采用通道可靠性系数衡量相关滤波器响应图的置信度,并将其应用于多通道响应图融合,实现目标的精确定位. Lu等[12 ] 提出在目标跟踪过程中,一些特征通道对前景目标敏感,另一些通道对背景、噪声敏感,通过在目标函数中引入 $ {l_1} $ [13 ] 提出空间特征选择和通道特征选择融合的相关滤波算法,通过将个体变量分配到具有一定视觉意义的特定群组,实现空间域和通道域的特征选择,突出具有增强判别力的特征. Ye等[14 ] 利用通道可靠性正则项,在训练阶段联合滤波器模板优化通道权重,实现通道权重的自动分配. ...
... [11 ]采用通道可靠性系数衡量相关滤波器响应图的置信度,并将其应用于多通道响应图融合,实现目标的精确定位. Lu等[12 ] 提出在目标跟踪过程中,一些特征通道对前景目标敏感,另一些通道对背景、噪声敏感,通过在目标函数中引入 $ {l_1} $ [13 ] 提出空间特征选择和通道特征选择融合的相关滤波算法,通过将个体变量分配到具有一定视觉意义的特定群组,实现空间域和通道域的特征选择,突出具有增强判别力的特征. Ye等[14 ] 利用通道可靠性正则项,在训练阶段联合滤波器模板优化通道权重,实现通道权重的自动分配. ...
Adaptive region proposal with channel regularization for robust object tracking
1
2021
... 文献[11 ]~[13 ]的研究表明,不同特征通道对目标位置估计的贡献不同. 尹明锋等[11 ] 采用通道可靠性系数衡量相关滤波器响应图的置信度,并将其应用于多通道响应图融合,实现目标的精确定位. Lu等[12 ] 提出在目标跟踪过程中,一些特征通道对前景目标敏感,另一些通道对背景、噪声敏感,通过在目标函数中引入 $ {l_1} $ [13 ] 提出空间特征选择和通道特征选择融合的相关滤波算法,通过将个体变量分配到具有一定视觉意义的特定群组,实现空间域和通道域的特征选择,突出具有增强判别力的特征. Ye等[14 ] 利用通道可靠性正则项,在训练阶段联合滤波器模板优化通道权重,实现通道权重的自动分配. ...
2
... 文献[11 ]~[13 ]的研究表明,不同特征通道对目标位置估计的贡献不同. 尹明锋等[11 ] 采用通道可靠性系数衡量相关滤波器响应图的置信度,并将其应用于多通道响应图融合,实现目标的精确定位. Lu等[12 ] 提出在目标跟踪过程中,一些特征通道对前景目标敏感,另一些通道对背景、噪声敏感,通过在目标函数中引入 $ {l_1} $ [13 ] 提出空间特征选择和通道特征选择融合的相关滤波算法,通过将个体变量分配到具有一定视觉意义的特定群组,实现空间域和通道域的特征选择,突出具有增强判别力的特征. Ye等[14 ] 利用通道可靠性正则项,在训练阶段联合滤波器模板优化通道权重,实现通道权重的自动分配. ...
... [13 ]提出空间特征选择和通道特征选择融合的相关滤波算法,通过将个体变量分配到具有一定视觉意义的特定群组,实现空间域和通道域的特征选择,突出具有增强判别力的特征. Ye等[14 ] 利用通道可靠性正则项,在训练阶段联合滤波器模板优化通道权重,实现通道权重的自动分配. ...
Multi-regularized correlation filter for UAV tracking and self-localization
1
2021
... 文献[11 ]~[13 ]的研究表明,不同特征通道对目标位置估计的贡献不同. 尹明锋等[11 ] 采用通道可靠性系数衡量相关滤波器响应图的置信度,并将其应用于多通道响应图融合,实现目标的精确定位. Lu等[12 ] 提出在目标跟踪过程中,一些特征通道对前景目标敏感,另一些通道对背景、噪声敏感,通过在目标函数中引入 $ {l_1} $ [13 ] 提出空间特征选择和通道特征选择融合的相关滤波算法,通过将个体变量分配到具有一定视觉意义的特定群组,实现空间域和通道域的特征选择,突出具有增强判别力的特征. Ye等[14 ] 利用通道可靠性正则项,在训练阶段联合滤波器模板优化通道权重,实现通道权重的自动分配. ...
1
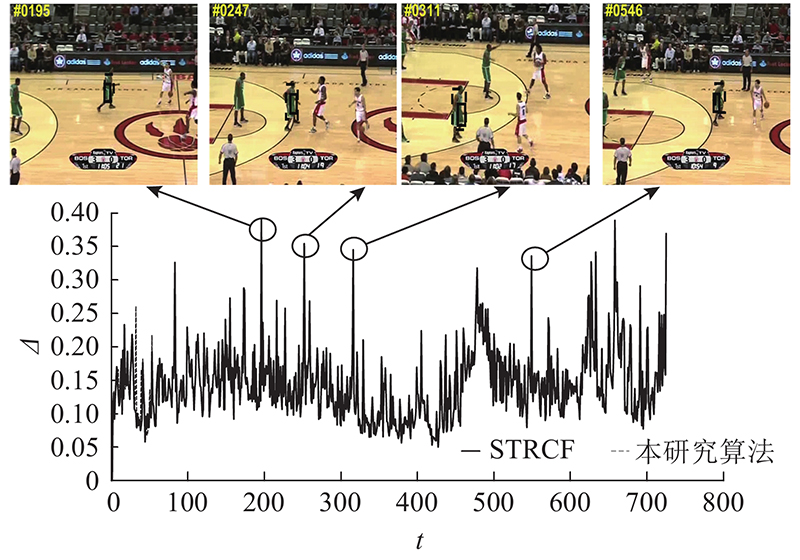
... Wang等[15 ] 提出高置信度的模型更新策略,引入新的判据指标平均峰值相关能量(average peak to correlation energy, APCE)来判断响应图的质量. 当APCE突然减小时,即目标发生遮挡或者丢失时,选择不更新模型,避免模型漂移. Huang等[16 ] 提出具有畸变抑制的目标跟踪算法(aberrance repressed correlation filters, ARCF),引入畸变抑制项约束响应图突变,进一步提升了跟踪器的性能. Li等[17 ] 提出的自适应时空正则目标跟踪算法,充分利用局部和全局响应图的变化实现自适应时空正则,无需复杂的参数调节,能够更好地应对跟踪过程中的挑战. 姜文涛等[18 ] 提出空间异常适应性的目标跟踪算法,通过对比学习到的响应图模型与当前帧的响应图,生成对应的置信分数,影响模型的学习过程. ...
4
... Wang等[15 ] 提出高置信度的模型更新策略,引入新的判据指标平均峰值相关能量(average peak to correlation energy, APCE)来判断响应图的质量. 当APCE突然减小时,即目标发生遮挡或者丢失时,选择不更新模型,避免模型漂移. Huang等[16 ] 提出具有畸变抑制的目标跟踪算法(aberrance repressed correlation filters, ARCF),引入畸变抑制项约束响应图突变,进一步提升了跟踪器的性能. Li等[17 ] 提出的自适应时空正则目标跟踪算法,充分利用局部和全局响应图的变化实现自适应时空正则,无需复杂的参数调节,能够更好地应对跟踪过程中的挑战. 姜文涛等[18 ] 提出空间异常适应性的目标跟踪算法,通过对比学习到的响应图模型与当前帧的响应图,生成对应的置信分数,影响模型的学习过程. ...
... 3) 适合于无人机领域,基于手工特征的相关滤波算法:ARCF[16 ] 、AutoTrack[17 ] 、DRCF[31 ] . ...
... 为了进一步测试本研究算法在更具挑战性的数据集上的跟踪效果,选取TempleColor128数据集进行验证. 对比更多优秀的算法,主要包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、DeepSRDCF[25 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 以及近年优秀的跟踪算法ARCF[16 ] 、AutoTrack[17 ] 、SITUP[29 ] 、FAST[30 ] 、DRCF[31 ] . 如图5 所示,为不同算法在TempleColor128数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在TempleColor128数据集获得最高的DP、AUC,分别为75.3%、55.6%. 相比于基线算法STRCF,DP和AUC分别提高了0.9%、0.8%. ...
... 为了验证本研究算法在无人机航拍数据集上的适用性,选取UAV20L数据集长时视频序列进行测试. 对比算法包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] 以及适用于无人机领域的优秀算法ARCF[16 ] 、AutoTrack[17 ] 、DRCF[31 ] . 如图6 所示为不同算法在UAV20L数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在UAV20L数据集上获得第2高的DP,为58.6%; 同时获得第1高的AUC,为44.1%. 相比于STRCF,本研究算法的DP、AUC分别提高1.1%和3.1%. DRCF在UAV20L数据集上获得较高的DP和AUC. 主要原因是DRCF利用显著性检测算法构建双重正则项,使边界效应得到有效缓解. ...
4
... Wang等[15 ] 提出高置信度的模型更新策略,引入新的判据指标平均峰值相关能量(average peak to correlation energy, APCE)来判断响应图的质量. 当APCE突然减小时,即目标发生遮挡或者丢失时,选择不更新模型,避免模型漂移. Huang等[16 ] 提出具有畸变抑制的目标跟踪算法(aberrance repressed correlation filters, ARCF),引入畸变抑制项约束响应图突变,进一步提升了跟踪器的性能. Li等[17 ] 提出的自适应时空正则目标跟踪算法,充分利用局部和全局响应图的变化实现自适应时空正则,无需复杂的参数调节,能够更好地应对跟踪过程中的挑战. 姜文涛等[18 ] 提出空间异常适应性的目标跟踪算法,通过对比学习到的响应图模型与当前帧的响应图,生成对应的置信分数,影响模型的学习过程. ...
... 3) 适合于无人机领域,基于手工特征的相关滤波算法:ARCF[16 ] 、AutoTrack[17 ] 、DRCF[31 ] . ...
... 为了进一步测试本研究算法在更具挑战性的数据集上的跟踪效果,选取TempleColor128数据集进行验证. 对比更多优秀的算法,主要包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、DeepSRDCF[25 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 以及近年优秀的跟踪算法ARCF[16 ] 、AutoTrack[17 ] 、SITUP[29 ] 、FAST[30 ] 、DRCF[31 ] . 如图5 所示,为不同算法在TempleColor128数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在TempleColor128数据集获得最高的DP、AUC,分别为75.3%、55.6%. 相比于基线算法STRCF,DP和AUC分别提高了0.9%、0.8%. ...
... 为了验证本研究算法在无人机航拍数据集上的适用性,选取UAV20L数据集长时视频序列进行测试. 对比算法包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] 以及适用于无人机领域的优秀算法ARCF[16 ] 、AutoTrack[17 ] 、DRCF[31 ] . 如图6 所示为不同算法在UAV20L数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在UAV20L数据集上获得第2高的DP,为58.6%; 同时获得第1高的AUC,为44.1%. 相比于STRCF,本研究算法的DP、AUC分别提高1.1%和3.1%. DRCF在UAV20L数据集上获得较高的DP和AUC. 主要原因是DRCF利用显著性检测算法构建双重正则项,使边界效应得到有效缓解. ...
空间异常适应性的目标跟踪
1
2021
... Wang等[15 ] 提出高置信度的模型更新策略,引入新的判据指标平均峰值相关能量(average peak to correlation energy, APCE)来判断响应图的质量. 当APCE突然减小时,即目标发生遮挡或者丢失时,选择不更新模型,避免模型漂移. Huang等[16 ] 提出具有畸变抑制的目标跟踪算法(aberrance repressed correlation filters, ARCF),引入畸变抑制项约束响应图突变,进一步提升了跟踪器的性能. Li等[17 ] 提出的自适应时空正则目标跟踪算法,充分利用局部和全局响应图的变化实现自适应时空正则,无需复杂的参数调节,能够更好地应对跟踪过程中的挑战. 姜文涛等[18 ] 提出空间异常适应性的目标跟踪算法,通过对比学习到的响应图模型与当前帧的响应图,生成对应的置信分数,影响模型的学习过程. ...
空间异常适应性的目标跟踪
1
2021
... Wang等[15 ] 提出高置信度的模型更新策略,引入新的判据指标平均峰值相关能量(average peak to correlation energy, APCE)来判断响应图的质量. 当APCE突然减小时,即目标发生遮挡或者丢失时,选择不更新模型,避免模型漂移. Huang等[16 ] 提出具有畸变抑制的目标跟踪算法(aberrance repressed correlation filters, ARCF),引入畸变抑制项约束响应图突变,进一步提升了跟踪器的性能. Li等[17 ] 提出的自适应时空正则目标跟踪算法,充分利用局部和全局响应图的变化实现自适应时空正则,无需复杂的参数调节,能够更好地应对跟踪过程中的挑战. 姜文涛等[18 ] 提出空间异常适应性的目标跟踪算法,通过对比学习到的响应图模型与当前帧的响应图,生成对应的置信分数,影响模型的学习过程. ...
Distributed optimization and statistical learning via the alternating direction method of multipliers
1
2010
... 式(4)是凸函数,可以利用交替方向乘子法(alternating direction method of multipliers, ADMM)[19 ] 获得全局最优解. 引入辅助变量,令 $ {\boldsymbol{f}} $ $ {\boldsymbol{g}} $
Object tracking benchmark
1
2015
... 选取OTB2015[20 ] 、TempleColor128[21 ] 、UAV20L[22 ] 3个公开数据集对跟踪算法的整体性能进行测试和评估. OTB2015数据集由100个完全注释的视频序列组成. 这些视频序列包含11种不同的挑战属性. TempleColor128数据集由128个彩色视频序列组成. UAV20L数据集由20个长时视频序列组成,这些视频序列从具有各种挑战的低空无人机上捕获. ...
1
... 选取OTB2015[20 ] 、TempleColor128[21 ] 、UAV20L[22 ] 3个公开数据集对跟踪算法的整体性能进行测试和评估. OTB2015数据集由100个完全注释的视频序列组成. 这些视频序列包含11种不同的挑战属性. TempleColor128数据集由128个彩色视频序列组成. UAV20L数据集由20个长时视频序列组成,这些视频序列从具有各种挑战的低空无人机上捕获. ...
1
... 选取OTB2015[20 ] 、TempleColor128[21 ] 、UAV20L[22 ] 3个公开数据集对跟踪算法的整体性能进行测试和评估. OTB2015数据集由100个完全注释的视频序列组成. 这些视频序列包含11种不同的挑战属性. TempleColor128数据集由128个彩色视频序列组成. UAV20L数据集由20个长时视频序列组成,这些视频序列从具有各种挑战的低空无人机上捕获. ...
3
... 1)基于深度特征的相关滤波算法:HCF[23 ] 、HDT[24 ] 、DeepSRDCF[25 ] . ...
... 为了进一步测试本研究算法在更具挑战性的数据集上的跟踪效果,选取TempleColor128数据集进行验证. 对比更多优秀的算法,主要包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、DeepSRDCF[25 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 以及近年优秀的跟踪算法ARCF[16 ] 、AutoTrack[17 ] 、SITUP[29 ] 、FAST[30 ] 、DRCF[31 ] . 如图5 所示,为不同算法在TempleColor128数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在TempleColor128数据集获得最高的DP、AUC,分别为75.3%、55.6%. 相比于基线算法STRCF,DP和AUC分别提高了0.9%、0.8%. ...
... 为了验证本研究算法在无人机航拍数据集上的适用性,选取UAV20L数据集长时视频序列进行测试. 对比算法包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] 以及适用于无人机领域的优秀算法ARCF[16 ] 、AutoTrack[17 ] 、DRCF[31 ] . 如图6 所示为不同算法在UAV20L数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在UAV20L数据集上获得第2高的DP,为58.6%; 同时获得第1高的AUC,为44.1%. 相比于STRCF,本研究算法的DP、AUC分别提高1.1%和3.1%. DRCF在UAV20L数据集上获得较高的DP和AUC. 主要原因是DRCF利用显著性检测算法构建双重正则项,使边界效应得到有效缓解. ...
3
... 1)基于深度特征的相关滤波算法:HCF[23 ] 、HDT[24 ] 、DeepSRDCF[25 ] . ...
... 为了进一步测试本研究算法在更具挑战性的数据集上的跟踪效果,选取TempleColor128数据集进行验证. 对比更多优秀的算法,主要包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、DeepSRDCF[25 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 以及近年优秀的跟踪算法ARCF[16 ] 、AutoTrack[17 ] 、SITUP[29 ] 、FAST[30 ] 、DRCF[31 ] . 如图5 所示,为不同算法在TempleColor128数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在TempleColor128数据集获得最高的DP、AUC,分别为75.3%、55.6%. 相比于基线算法STRCF,DP和AUC分别提高了0.9%、0.8%. ...
... 为了验证本研究算法在无人机航拍数据集上的适用性,选取UAV20L数据集长时视频序列进行测试. 对比算法包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] 以及适用于无人机领域的优秀算法ARCF[16 ] 、AutoTrack[17 ] 、DRCF[31 ] . 如图6 所示为不同算法在UAV20L数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在UAV20L数据集上获得第2高的DP,为58.6%; 同时获得第1高的AUC,为44.1%. 相比于STRCF,本研究算法的DP、AUC分别提高1.1%和3.1%. DRCF在UAV20L数据集上获得较高的DP和AUC. 主要原因是DRCF利用显著性检测算法构建双重正则项,使边界效应得到有效缓解. ...
2
... 1)基于深度特征的相关滤波算法:HCF[23 ] 、HDT[24 ] 、DeepSRDCF[25 ] . ...
... 为了进一步测试本研究算法在更具挑战性的数据集上的跟踪效果,选取TempleColor128数据集进行验证. 对比更多优秀的算法,主要包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、DeepSRDCF[25 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 以及近年优秀的跟踪算法ARCF[16 ] 、AutoTrack[17 ] 、SITUP[29 ] 、FAST[30 ] 、DRCF[31 ] . 如图5 所示,为不同算法在TempleColor128数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在TempleColor128数据集获得最高的DP、AUC,分别为75.3%、55.6%. 相比于基线算法STRCF,DP和AUC分别提高了0.9%、0.8%. ...
3
... 2)基于手工特征的相关滤波算法:KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] . ...
... 为了进一步测试本研究算法在更具挑战性的数据集上的跟踪效果,选取TempleColor128数据集进行验证. 对比更多优秀的算法,主要包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、DeepSRDCF[25 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 以及近年优秀的跟踪算法ARCF[16 ] 、AutoTrack[17 ] 、SITUP[29 ] 、FAST[30 ] 、DRCF[31 ] . 如图5 所示,为不同算法在TempleColor128数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在TempleColor128数据集获得最高的DP、AUC,分别为75.3%、55.6%. 相比于基线算法STRCF,DP和AUC分别提高了0.9%、0.8%. ...
... 为了验证本研究算法在无人机航拍数据集上的适用性,选取UAV20L数据集长时视频序列进行测试. 对比算法包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] 以及适用于无人机领域的优秀算法ARCF[16 ] 、AutoTrack[17 ] 、DRCF[31 ] . 如图6 所示为不同算法在UAV20L数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在UAV20L数据集上获得第2高的DP,为58.6%; 同时获得第1高的AUC,为44.1%. 相比于STRCF,本研究算法的DP、AUC分别提高1.1%和3.1%. DRCF在UAV20L数据集上获得较高的DP和AUC. 主要原因是DRCF利用显著性检测算法构建双重正则项,使边界效应得到有效缓解. ...
3
... 2)基于手工特征的相关滤波算法:KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] . ...
... 为了进一步测试本研究算法在更具挑战性的数据集上的跟踪效果,选取TempleColor128数据集进行验证. 对比更多优秀的算法,主要包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、DeepSRDCF[25 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 以及近年优秀的跟踪算法ARCF[16 ] 、AutoTrack[17 ] 、SITUP[29 ] 、FAST[30 ] 、DRCF[31 ] . 如图5 所示,为不同算法在TempleColor128数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在TempleColor128数据集获得最高的DP、AUC,分别为75.3%、55.6%. 相比于基线算法STRCF,DP和AUC分别提高了0.9%、0.8%. ...
... 为了验证本研究算法在无人机航拍数据集上的适用性,选取UAV20L数据集长时视频序列进行测试. 对比算法包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] 以及适用于无人机领域的优秀算法ARCF[16 ] 、AutoTrack[17 ] 、DRCF[31 ] . 如图6 所示为不同算法在UAV20L数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在UAV20L数据集上获得第2高的DP,为58.6%; 同时获得第1高的AUC,为44.1%. 相比于STRCF,本研究算法的DP、AUC分别提高1.1%和3.1%. DRCF在UAV20L数据集上获得较高的DP和AUC. 主要原因是DRCF利用显著性检测算法构建双重正则项,使边界效应得到有效缓解. ...
3
... 2)基于手工特征的相关滤波算法:KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] . ...
... 为了进一步测试本研究算法在更具挑战性的数据集上的跟踪效果,选取TempleColor128数据集进行验证. 对比更多优秀的算法,主要包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、DeepSRDCF[25 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 以及近年优秀的跟踪算法ARCF[16 ] 、AutoTrack[17 ] 、SITUP[29 ] 、FAST[30 ] 、DRCF[31 ] . 如图5 所示,为不同算法在TempleColor128数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在TempleColor128数据集获得最高的DP、AUC,分别为75.3%、55.6%. 相比于基线算法STRCF,DP和AUC分别提高了0.9%、0.8%. ...
... 为了验证本研究算法在无人机航拍数据集上的适用性,选取UAV20L数据集长时视频序列进行测试. 对比算法包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] 以及适用于无人机领域的优秀算法ARCF[16 ] 、AutoTrack[17 ] 、DRCF[31 ] . 如图6 所示为不同算法在UAV20L数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在UAV20L数据集上获得第2高的DP,为58.6%; 同时获得第1高的AUC,为44.1%. 相比于STRCF,本研究算法的DP、AUC分别提高1.1%和3.1%. DRCF在UAV20L数据集上获得较高的DP和AUC. 主要原因是DRCF利用显著性检测算法构建双重正则项,使边界效应得到有效缓解. ...
SITUP: scale invariant tracking using average peak-to-correlation energy
3
2020
... 2)基于手工特征的相关滤波算法:KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] . ...
... 为了进一步测试本研究算法在更具挑战性的数据集上的跟踪效果,选取TempleColor128数据集进行验证. 对比更多优秀的算法,主要包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、DeepSRDCF[25 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 以及近年优秀的跟踪算法ARCF[16 ] 、AutoTrack[17 ] 、SITUP[29 ] 、FAST[30 ] 、DRCF[31 ] . 如图5 所示,为不同算法在TempleColor128数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在TempleColor128数据集获得最高的DP、AUC,分别为75.3%、55.6%. 相比于基线算法STRCF,DP和AUC分别提高了0.9%、0.8%. ...
... 为了验证本研究算法在无人机航拍数据集上的适用性,选取UAV20L数据集长时视频序列进行测试. 对比算法包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] 以及适用于无人机领域的优秀算法ARCF[16 ] 、AutoTrack[17 ] 、DRCF[31 ] . 如图6 所示为不同算法在UAV20L数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在UAV20L数据集上获得第2高的DP,为58.6%; 同时获得第1高的AUC,为44.1%. 相比于STRCF,本研究算法的DP、AUC分别提高1.1%和3.1%. DRCF在UAV20L数据集上获得较高的DP和AUC. 主要原因是DRCF利用显著性检测算法构建双重正则项,使边界效应得到有效缓解. ...
FAST: fast and accurate scale estimation for tracking
3
2020
... 2)基于手工特征的相关滤波算法:KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] . ...
... 为了进一步测试本研究算法在更具挑战性的数据集上的跟踪效果,选取TempleColor128数据集进行验证. 对比更多优秀的算法,主要包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、DeepSRDCF[25 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 以及近年优秀的跟踪算法ARCF[16 ] 、AutoTrack[17 ] 、SITUP[29 ] 、FAST[30 ] 、DRCF[31 ] . 如图5 所示,为不同算法在TempleColor128数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在TempleColor128数据集获得最高的DP、AUC,分别为75.3%、55.6%. 相比于基线算法STRCF,DP和AUC分别提高了0.9%、0.8%. ...
... 为了验证本研究算法在无人机航拍数据集上的适用性,选取UAV20L数据集长时视频序列进行测试. 对比算法包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] 以及适用于无人机领域的优秀算法ARCF[16 ] 、AutoTrack[17 ] 、DRCF[31 ] . 如图6 所示为不同算法在UAV20L数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在UAV20L数据集上获得第2高的DP,为58.6%; 同时获得第1高的AUC,为44.1%. 相比于STRCF,本研究算法的DP、AUC分别提高1.1%和3.1%. DRCF在UAV20L数据集上获得较高的DP和AUC. 主要原因是DRCF利用显著性检测算法构建双重正则项,使边界效应得到有效缓解. ...
Object saliency-aware dual regularized correlation filter for real-time aerial tracking
3
2020
... 3) 适合于无人机领域,基于手工特征的相关滤波算法:ARCF[16 ] 、AutoTrack[17 ] 、DRCF[31 ] . ...
... 为了进一步测试本研究算法在更具挑战性的数据集上的跟踪效果,选取TempleColor128数据集进行验证. 对比更多优秀的算法,主要包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、DeepSRDCF[25 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 以及近年优秀的跟踪算法ARCF[16 ] 、AutoTrack[17 ] 、SITUP[29 ] 、FAST[30 ] 、DRCF[31 ] . 如图5 所示,为不同算法在TempleColor128数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在TempleColor128数据集获得最高的DP、AUC,分别为75.3%、55.6%. 相比于基线算法STRCF,DP和AUC分别提高了0.9%、0.8%. ...
... 为了验证本研究算法在无人机航拍数据集上的适用性,选取UAV20L数据集长时视频序列进行测试. 对比算法包括KCF[3 ] 、BACF[8 ] 、SRDCF[9 ] 、STRCF[10 ] 、HCF[23 ] 、HDT[24 ] 、ECO_HC[26 ] 、SRDCFDecon[27 ] 、LCT[28 ] 、SITUP[29 ] 、FAST[30 ] 以及适用于无人机领域的优秀算法ARCF[16 ] 、AutoTrack[17 ] 、DRCF[31 ] . 如图6 所示为不同算法在UAV20L数据集上2个定量分析指标的对比结果. 可以看出,本研究算法在UAV20L数据集上获得第2高的DP,为58.6%; 同时获得第1高的AUC,为44.1%. 相比于STRCF,本研究算法的DP、AUC分别提高1.1%和3.1%. DRCF在UAV20L数据集上获得较高的DP和AUC. 主要原因是DRCF利用显著性检测算法构建双重正则项,使边界效应得到有效缓解. ...
1
... 4)基于端到端学习的目标跟踪算法:SiamFC[32 ] . ...