污水管网入流入渗(rainfall derived inflow and infiltration, RDII)指在雨污分流体制下,降雨导致的污水管网流量增加的现象,它是污水管网健康状况的一项重要指标[1]. 据统计,我国4 000多座污水处理厂中约有1 000座进水COD在150 mg/L以下,污水管网存在入渗入流现象[2]. 在多雨地区,入流入渗量达到了旱季流量的数倍,甚至达到总降雨量的50%[3-4],严重影响了污水管网的正常运行[5-7]和污水处理工艺稳定性[8]. 入流和入渗是2个独立的过程,反应的是2种不同的管网健康问题,因此,准确的识别一场降雨中的入流和入渗可以让管网检修人员做出针对性的修复措施,当入流和入渗同时存在时,二者往往难以区分[9]. 传统的基于假设和经验的水量平衡法[10-12]主观性较强,精度不足;基于现场调查的研究方法(如示踪检测法[13-14]、标记物回收[15]、CCTV[16-18]等)受制于较高的人力和财力成本无法大规模实施,结果不具备可迁移性[19];基于在线监测的方法根据水量平衡[20]和物质守恒[21-22]2个基本规律,可以对单场次降雨的入流入渗进行定量评估和定位分析,但难以区分入流和入渗这2个独立的过程. 为了解决上述问题,基于H市乡镇地区对降雨强度和污水管网水位流速8个月的监测数据,提出了一个可以根据实时数据进行动态率的降雨入流入渗模型,它耦合了产流过程和入流入渗过程,经过实时降雨监测数据对模型参数的率定,实现了入流和入渗的精准识别和量化,对评估污水管网健康状况起到了重要的技术支撑.
1. 研究区域与监测设备
本研究以H市的乡镇区域(如图1所示)为研究对象,进行8个月的降雨强度、检查井水位、流速在线监测. H市的乡镇区域该区域面积约为0.4 km2,平均旱季日流量为128 t/d,约40%的区域为产生污废水的居民区,另有60%的区域为绿化和农田区域;雨水通过雨水沟就近汇入农田和河道,污水管网只收集居民污水进入小型污水处理终端,属于分流制系统. 根据浙江省地方规范《农村生活污水处理技术规范》DB 33/T 868—2012计算,该区域日用水量为98 t/d,结合该区域临近河道,地下水位较高,居民浇灌农田等情况,在旱季污水管网可能已经存在一定程度的入流入渗. 根据以往的终端运维记录,在一些强降雨天气下终端收集到的污废水流量甚至达到旱季流量的数倍.
图 1
图 1 研究区域示意图
(检查井23上游的汇水区域为区域A,检查井21上游的汇水区域为区域B) Schematic diagram of study site
研究区域的污水管网的各处检查井处总共安装了4台超声液位监测设备和2台流速监测设备,并在管网终端提升井处安装1台静压液位计和1台翻斗式雨量计,如表1所示,所有数据的监测间隔均为5 min.
表 1 监测设备分布情况
Tab.1
| 检查井编号 | 静压液位计 | 超声液位计 | 流速计 | 雨量计 | |||
| 28 | √ | √ | |||||
| 23 | √ | √ | |||||
| 45 | √ | ||||||
| 21 | √ | √ | |||||
| 15 | √ | ||||||
2. 计算方法
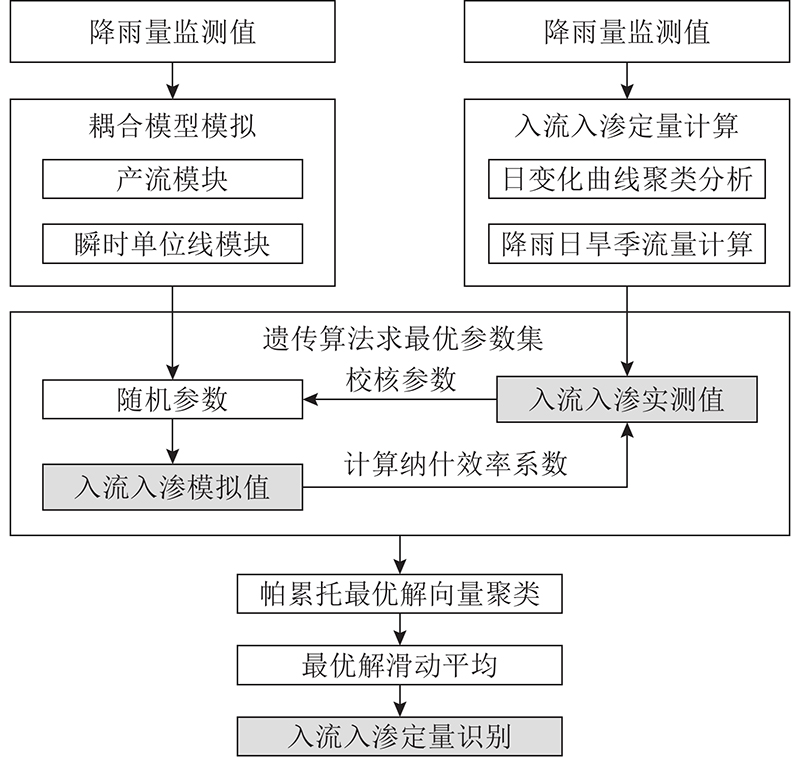
为定量识别污水管网入流入渗量,提出以下研究思路:1)分析旱季无雨日的监测指标日变化规律,计算雨天的入渗入流量;2)将降雨数据划分为训练集和测试集. 对于训练集,以降雨强度和随机产生的参数向量为输入,经过产流模块和入流入渗模块,最终得到监测断面上游入渗和入流的模拟结果,以最大化纳什效率系数为目标,通过遗传算法对参数向量进行校准;3)对历场降雨校核的帕累托最优参数向量进行聚类,选择最优参数集;4)将降雨分为大、中、小3类,每一类通过指数滑动平均法融合历场最优参数集,用测试集的结果验证模型和参数的有效性. 综上,本研究技术路线如图2所示.
图 2
2.1. 旱季监测数据周期性分析
对于一个服务人口相对稳定的乡镇居民污水管网系统,监测流量日变化曲线具有一定的规律. 找到这个周期性规律,是进行入流入渗定量分析的前提条件. 由于研究区域采用分布式污水处理方案,一个村落的污水就近进入小型污水处理设施,污水管网规模较小,易受个别农户用水影响,因此旱季的监测值波动较大. 为了找到旱季水力水质的日变化规律,在经过基本的数据清洗、平滑之后,对旱季的日变化曲线进行z-score标准化处理的公式如下:
式中:t为一天中的时刻(本文中每5min为一个时刻,下文同),Y为一天中最后一个时刻,N为一天内监测值的数量,
图 3
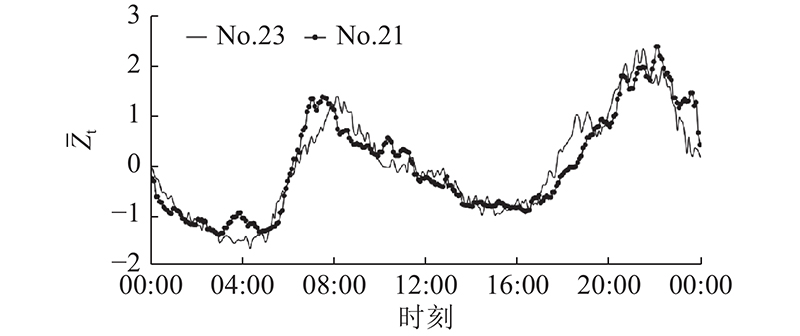
图 3 No.23监测断面旱季日流量聚类示例
Fig.3 Example of dry weather daily flow clustering at monitoring section No.23
图 4
式中:
2.2. 入流入渗定量计算
根据主聚类平均后的标准化值,结合最近n天的旱季流量数据(
式中:
式中:
2.3. 产流模块
产流模块主要考虑降雨形成的与入流入渗相关的径流过程. 根据研究区域的下垫面性质,将研究区域的土地分为2类:一类是不透水的表面,包括屋顶和沥青路面,面积用
式中:
对于绿化和农田区域
式中:
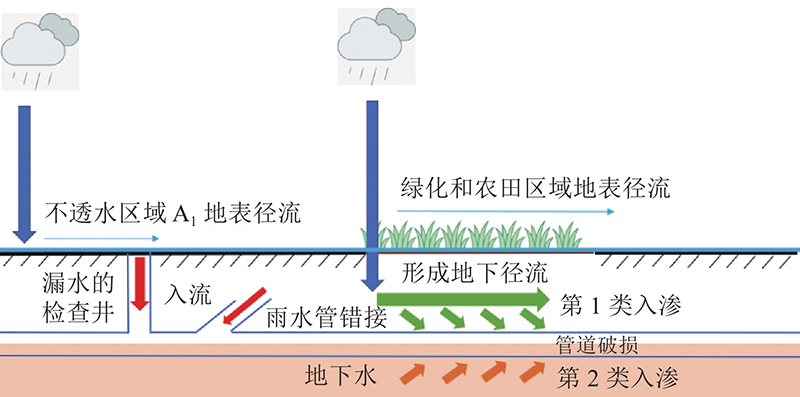
这部分径流将通过单位线的计算,以一定比例转化成入流. 入渗过程则与整个研究区域的下渗和地下径流有关. 经过对多场降雨数据的研究,将入渗的来源分为2类:第1类入渗为包气带内的表层流径流导致的,这部分径流量
式中:
第2类入渗则是降雨导致地下水位抬升,如果地下水位抬升到达管网的埋设深度,将会通过破损的管段进入污水管网,这部分入渗流量可以用达西公式估算:
式中:
式中:M为一固定的系数,
式中:
图 5
图 5 研究区域入流入渗过程示意图
Fig.5 Schematic presentation of inflow and Infiltration in study area
2.4. 瞬时单位线模块
式中:
入流和入渗瞬时值可以通过瞬时单位线和雨强的卷积计算得出:
式中:
2.5. 遗传算法率定参数
将研究区域按照上下游关系划为2个区域,区域A和区域B. 对2个区域在上述产流过程和入流入渗过程中的待定参数进行率定. 需要率定的参数包括:
1) 产流相关的参数:土壤稳定下渗率
式中:
式中:
式中:
优化问题的目标为
监测期间共监测到21场降雨的有效数据,选择其中15场作为训练集校核模型中的数据,剩余6场作为测试集验证模型的有效性. 训练集每一场降雨
在率定过程中,发现耦合模型的最优参数集与降雨强度有着一定的相关性,降雨强度相近的场次最优参数集相近,相反的是降雨强度差异较大的场次最优参数相差也较大. 为了让拟合效果更加精准,将训练集划分为大(H)、中(M)、小降雨(L)3类,划分标准参考ZHANG[25]在类似研究中的划分:总降雨量20 mm以下的降雨划分为小降雨,20 ~80 mm为中降雨、80 mm以上为大降雨. 对于3类降雨分别进行率定过程如下:为了最大程度地利用历史数据,减少偶然误差对模型的扰动,采用指数滑动平均法对最优参数集进行修正. 以小型降雨事件为例:训练集共有
式中:
3. 结果与讨论
3.1. 结果比较与分析
表 2 大、中、小降雨事件最优参数集
Tab.2
| | | | | | ||
| H | 7.52 | 61.66 | 17.74 | 0.08 | 4.0 | |
| M | 6.55 | 63.10 | 15.05 | 0.06 | 5.2 | |
| L | 5.81 | 65.48 | 14.72 | 0.02 | 1.3 | |
| | | | | | | |
| H | 2.77 | 13.39 | 0.35 | 7.67 | 55.63 | 0.94 |
| M | 2.90 | 10.53 | 0.35 | 16.20 | 56.93 | 0.39 |
| L | 1.03 | 8.13 | 0.74 | 10.27 | 59.43 | 0.02 |
| | | | | | | |
| H | 3.11 | 3.95 | 0.11 | 8.08 | 57.44 | 0.20 |
| M | 4.52 | 4.85 | 0.28 | 9.80 | 31.84 | 0.52 |
| L | 1.28 | 12.12 | 0.48 | 5.46 | 22.26 | 0.70 |
表 3 测试集降雨事件验证结果
Tab.3
| 降雨 事件 | Ptotal/mm | 区域 编号 | RateRDI/% | RateRII/% | E | RMSE/ (m3/h−1) |
| L1 | 17.2 | A | 8.03 | 3.02 | 0.86 | 0.60 |
| B | 3.21 | 1.47 | 0.80 | 0.35 | ||
| L2 | 16.6 | A | 7.92 | 3.40 | 0.89 | 0.90 |
| B | 3.08 | 1.78 | 0.75 | 0.52 | ||
| M1 | 45.4 | A | 8.02 | 6.33 | 0.81 | 1.47 |
| B | 4.41 | 3.86 | 0.85 | 0.61 | ||
| M2 | 41.2 | A | 8.16 | 5.00 | 0.85 | 2.19 |
| B | 4.74 | 2.66 | 0.79 | 0.72 | ||
| H1 | 73.8 | A | 9.04 | 12.70 | 0.73 | 0.99 |
| B | 4.81 | 6.42 | 0.78 | 0.74 | ||
| H2 | 223.2 | A | 8.10 | 12.5 | 0.65 | 2.92 |
| B | 3.92 | 6.03 | 0.79 | 0.74 |
从表3中看出,对于6场降雨事件,纳什效率系数在0.65~0.86,相比于ZHANG[25]的瞬时单位线法(纳什效率系数为−7.07~0.62)有了显著的提升,纳什效率系数在数值上等于决策系数(R2). 与ZHANG[1]基于神经网络的方法(R2在0.4 472~0.9 146)相比,所提出的模型在精度下限上有所提升. 详细分析3类降雨的模拟结果:1)小型降雨结果分析. 在小型降雨事件中,大部分额外的管道流量都是水泥屋顶和沥青路面收集到的雨水造成的入流,入渗量可以忽略不计. 由于雨量较小,难以形成包气带内的表层流径流,即第一类入渗的来源. 土壤蓄水容量也没有达到
图 6
综上,随着降雨量的增大,入渗的比例逐步增加,入流入渗的总比例也在增大. 同时从表2也不难看出,区域A的入流和入渗都比区域B严重,因此,在检修的时候应对A区域进行重点检修.
3.2. 模型适用性讨论
1)旱季监测数据周期性分析的适用性. 从图4可以看出,日变化曲线居民的生活规律有着明显的关系. 对于商业区和工业区的周期性分析也可以采用类似的方法,有所不同的是商业区和工业区的排水模式更多地取决于分布更为集中的大用户,具体规律需要根据实测的数据和现场资料具体分析.
4. 结 论
(1)通过建立产流过程、入流入渗过程的耦合模型,从总流量中区分出入流和入渗2个独立过程,发现并解释了随着降雨量增加入渗比例逐渐增加的现象. 经过多场次降雨数据的校核,测试集纳什效率系数在0.65~0.86,相比传统方法精度有所提高,相比于机器学习等黑箱模型,所提出的方法具有更好的可解释性,可以根据地区调查和经验指定耦合模型参数的取值,也可根据该参数的物理意义评估模型的合理性.
(2)借助所提出的耦合模型,决策者可以在管网设计阶段预设参数估算入流入渗预留量;在运维阶段根据降雨预报估算入流入渗,进行雨季的预警调度;在管网检修前对管网健康状况进行针对性预评估.
参考文献
Comparative study of AI based methods–application of analyzing inflow and infiltration in sanitary sewer sub catchments: 15
[J].DOI:10.3390/su12156254 [本文引用: 2]
Monitoring the performance of a storm water separating manifold with distributed temperature sensing
[J].DOI:10.2166/wst.2012.152 [本文引用: 1]
River water intrusion as a source of inflow into the sanitary sewer system
[J].DOI:10.2166/wst.2020.516 [本文引用: 1]
Groundwater infiltration otential (GWIP) as an aid to determining the cause of dilution of waste water
[J].DOI:10.1016/j.jhydrol.2016.09.020
Investigating transitions of centralized water infrastructure to decentralized solutions – an integrated approach
[J].DOI:10.1016/j.proeng.2014.02.171 [本文引用: 1]
Quantifying rainfall-derived inflow and infiltration in sanitary sewer systems based on conductivity monitoring
[J].DOI:10.1016/j.jhydrol.2018.01.002 [本文引用: 3]
地下水渗入排污管道的定量方法
[J].
Quantitative methods for ground water infiltration into sewer system
[J].
Infiltration and inflow in combined sewer systems: long-term analysis
[J].
Infiltration in sewer systems: comparison of measurement methods
[J].DOI:10.2166/wst.2005.0079 [本文引用: 1]
Isotopic tracing of clear water sources in an urban sewer: a combined water and dissolved sulfate stable isotope approach
[J].
Stable isotopes applied as water tracers in column and field studies
[J].DOI:10.1016/j.orggeochem.2009.07.006 [本文引用: 1]
Development of radio frequency identification (RFID) sensors suitable for smart monitoring applications in sewer systems
[J].DOI:10.1016/j.watres.2021.117107 [本文引用: 1]
A deep learning based framework for an automated defect detection system for sewer pipes
[J].DOI:10.1016/j.autcon.2019.102967 [本文引用: 1]
Automated sewer pipeline inspection using computer vision techniques
[J].
Processing of DTS monitoring results: automated detection of illicit connections
[J].DOI:10.2166/wpt.2013.037 [本文引用: 1]
Assessment and pathway determination for rainfall-derived inflow and infiltration in sanitary systems: a case study
[J].DOI:10.1080/1573062X.2019.1700289 [本文引用: 1]
Assessing the severity of rainfall derived infiltration and inflow and sewer deterioration based on the flux stability of sewage markers
[J].
Normalization of wastewater quality to estimate infiltration/inflow and mass flows of metals
[J].DOI:10.1061/(ASCE)EE.1943-7870.0001120 [本文引用: 1]
The form of the instantaneous unit hydrograph
[J].
Uncertainty analysis of a pollutant hydrograph model in assessing inflow and infiltration of sanitary sewer systems
[J].DOI:10.1016/j.jhydrol.2019.04.011 [本文引用: 1]