在地下工程施工时,岩石通常会经历反复加卸载过程,如巷道开挖施工、边坡开挖加固等[1-2]. 由于岩石在循环荷载作用下的强度和变形规律与静态荷载作用下有显著不同,因此研究循环加卸载条件下的岩石力学特性具有重要意义. 尤明庆等[3]在进行大理岩试样循环加卸载试验时,发现循环加卸载可以使大理岩试样强度提高5%~10%,并将这种现象定义为循环加载强化作用. 徐速超等[4]在开展矽卡岩单轴循环加卸载试验时,发现多次循环加卸载后试块强度增幅达到了15%~20%. 李春阳等[5]对花岗岩试块开展恒下限和恒差值的单轴循环加卸载试验,发现花岗岩试块强度分别提升了18.7%、13.2%. 学者们通过室内试验和声发射等方法研究发现,循环加载强化作用的发生一是由于前期循环加卸载对岩石内部结构的调整和压密[6],二是由于岩石新生裂隙面剪切滑移产生碎屑,填充到附近孔隙,提高了裂隙面间的摩擦能力,进而提升了岩石表观强度[7]. 岩石宏观力学特性取决于内部裂纹的细观力学响应[8],常规试验方法仅能从宏观角度分析岩石破坏机理,无法从细观角度进行深层次剖析.
近年来,数值方法已成为研究岩石细观结构的重要手段,颗粒流法已经实现对脆性岩石材料微裂纹行为的有效模拟[9]. Cundall等[10]在离散元理论基础上提出颗粒流法并研发配套的PFC软件(particle flow code,PFC),颗粒流法从细观角度采用圆形颗粒作为计算单元,模拟介质的运动及其相互作用,通过求解平面内的平动和转动方程来确定每一时刻颗粒的位置和速度,再现介质基本特性随应力环境的变化[11]. 因此,该方法特别适用于从岩石细观角度研究宏观力学特性. Potyondy[12]在PFC软件中引入等效晶质模型(grain-based model,GBM),模拟了晶质岩石(如花岗岩、大理岩等)的细观结构. 周喻等[13]通过GBM模型从细观角度揭示了岩石在加载条件下的破裂机制与强度特性. 胡训建等[14]基于等效晶质模型建模的方法实现了对花岗岩细观结构的重建,开展了花岗岩常规三轴压缩试验的研究. Shi等[15]采用离散元方法,研究了矿物配比和微裂隙分布对岩石宏观力学性能的影响. 学者们对岩石细观、宏观结构与力学特性的深入研究,证明了GBM模型对于模拟晶质细观结构的可行性.
为了探究循环加载强化作用对花岗岩细观破坏的影响及作用机理,基于离散元方法,建立了可表征花岗岩循环加载强化作用的GBM强化模型. 通过单轴循环加卸载试验和数值计算结果的对比分析,验证了该模型在花岗岩循环加载强化作用研究中的适用性和可靠性,借助该模型研究了循环加载强化作用对花岗岩细观破坏的影响机制.
1. 花岗岩GBM模型建立
1.1. 研究对象
图 1
表 1 不同矿物成分的质量分数
Tab.1
| 矿物成分 | ωc/% | 矿物成分 | ωc/% | |
| 石英 | 45.64 | 云母 | 6.75 | |
| 斜长石 | 23.02 | 其他矿物 | 0.40 | |
| 钾长石 | 24.19 | — | — |
1.2. GBM模型建立
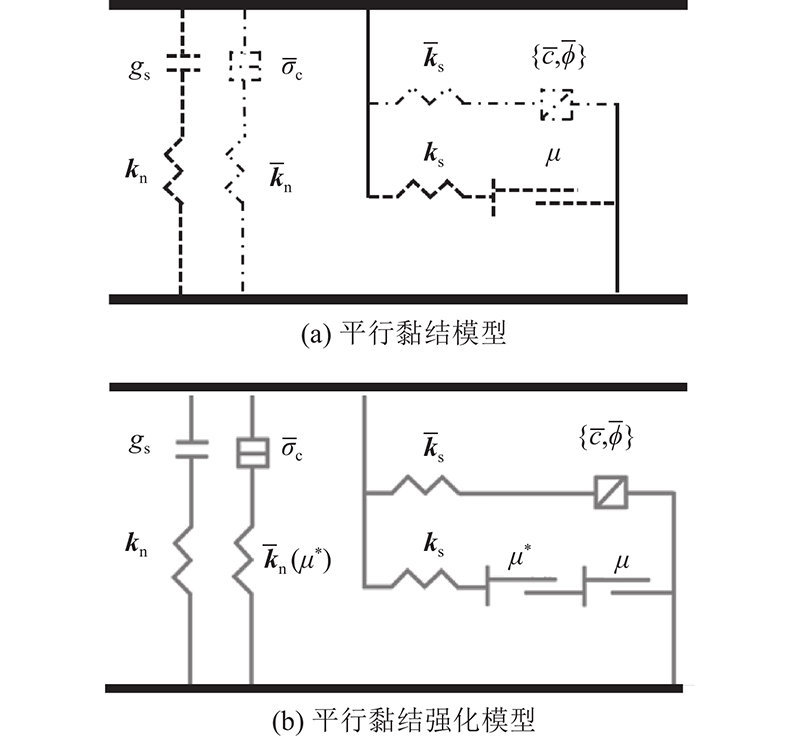
Zhou等[16]证明平行黏结模型(linear parallel bond model)和光滑节理模型(smooth-joint contact model)相组合的方法可以再现脆性岩石的实际破坏过程. 因此,采用平行黏结模型和光滑节理模型分别模拟晶体内部和边界的方法,在PFC2D中构建GBM模型,如图2所示. 具体步骤如下:1)按照岩石试样衍射结果中所含各种矿物颗粒的粒径与质量分数生成模型初始试样;2)计算并存储每个接触两边的矿物颗粒所围成的闭合空间体的形心位置;3)连接矿物之间的每个接触所储存的2个形心坐标,形成几何线;4)删除矿物颗粒,得到矿物颗粒的晶质网络;5)以更小的和能表征矿物颗粒内部力学行为的颗粒重新生成模型;6)对新生成颗粒按照晶质网络几何体进行颗粒和接触的分组.
图 2
1.3. 花岗岩GBM模型参数标定
室内实验中仅做单轴压缩处理的试块,称为原状试块,经过循环加卸载后再进行单轴压缩的试块称为预处理试块。在离散元模拟中,原状试块通过建立GBM模型模拟,预处理试块通过建立GBM强化模型模拟。本研究采用位移控制加载方式,以0.02 mm/min的速率对3组花岗岩试块开展单轴压缩试验,选取接近平均值的试验结果作为典型样本进行分析. 所得岩石单轴压缩峰值应力分别为160.20、159.25、160.85 MPa,取平均值160.10 MPa视为原状花岗岩试块峰值强度. 为了使建立的GBM模型与实际岩样拥有相同或相近的宏观力学性质,采用试错法[18]对细观参数进行标定. 先对模型赋予一组假定的细观参数,进行单轴压缩试验,将模拟结果与室内试验结果进行对比分析,对细观参数不断调试,直至GBM模型和室内试验所获得的岩样宏观力学性质一致. 为了减少运行时间,对GBM模型的参数标定进行相关简化,模型中矿物边界的细观参数是相同的. 表2为GBM模型细观参数,ωc为矿物所占比例,Rmin为最小半径,Rmax为最大半径,ρ为密度,E为弹性模量,
表 2 GBM模型细观参数表
Tab.2
| 种类 | 颗粒基本参数 | 晶体内部细观参数 | 晶体边界细观参数 | |||||||||||||||
| ωc/ % | Rmin/ mm | Rmax / mm | ρ/ (kg·m−3) | E/ GPa | | MPa | c/ MPa | φ/ (°) | μ | (GPa·m−1) | (GPa·m−1) | MPa | MPa | φ/ (°) | μ | |||
| 石英 | 46 | 0.2 | 1.8 | 2 650 | 6.64 | 1 | 82.67 | 82.67 | 50 | 0.5 | 3×1011 | 6.25×1010 | 72.4 | 123.6 | 20 | 0.4 | ||
| 长石 | 47 | 0.5 | 1.8 | 2 600 | 5.13 | 2 | 103.6 | 103.60 | 35 | 0.5 | ||||||||
| 云母 | 7 | 0.5 | 1.8 | 3 050 | 3.14 | 2 | 62.00 | 62.00 | 30 | 0.5 | ||||||||
表 3 原状试块与GBM模型宏观参数
Tab.3
| 项目 | σu/MPa | E/GPa | εu |
| 原状试块 | 160.1 | 16.0 | 0.012 5 |
| GBM模型 | 163.6 | 15.7 | 0.011 6 |
图 3
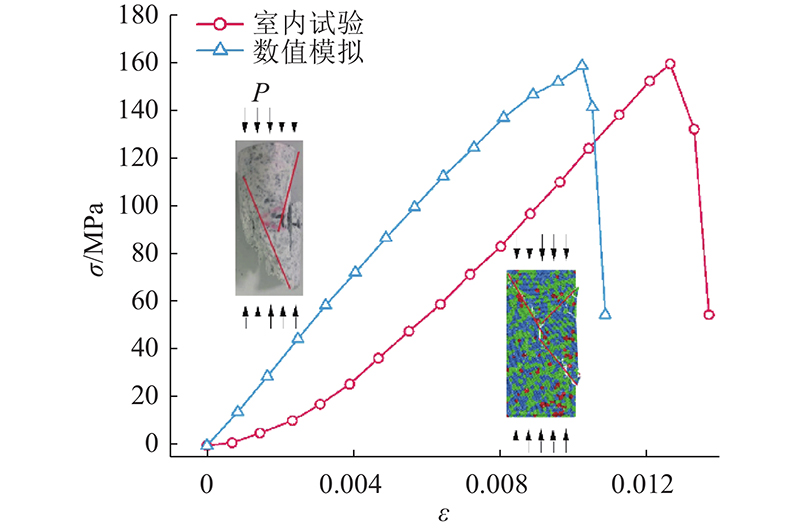
图 3 原状试块与GBM模型应力-应变曲线对比
Fig.3 Comparison of σ-ε curves between undisturbed specimens and GBM
2. 花岗岩GBM强化模型
2.1. 花岗岩室内循环加卸载试验
图 4
图 5
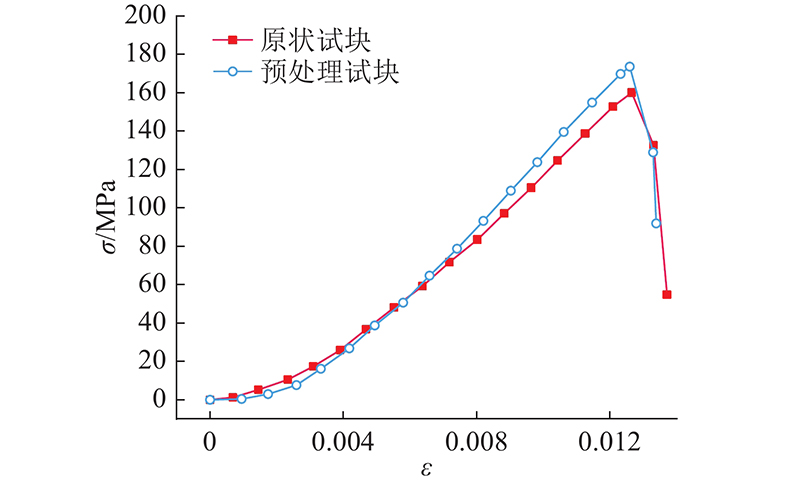
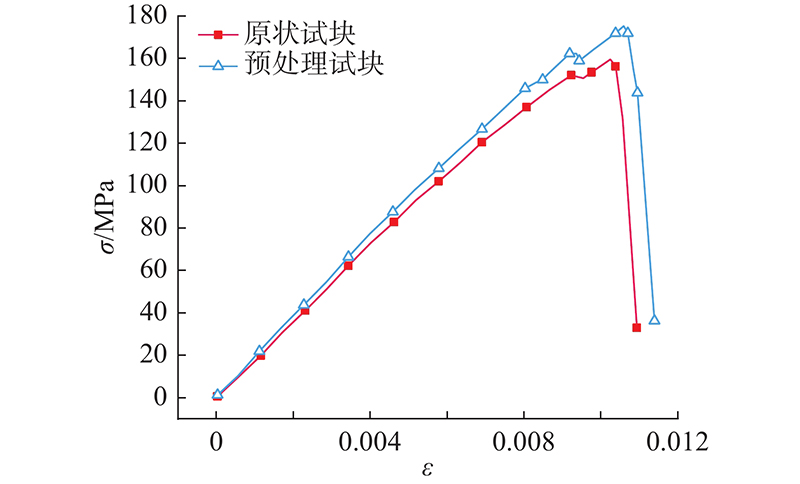
图 5 原状试块与预处理试块应力-应变曲线
Fig.5 Stress-strain curves between undisturbed specimens and pretreatment specimens
2.2. GBM强化模型
2.2.1. GBM强化模型基本假定
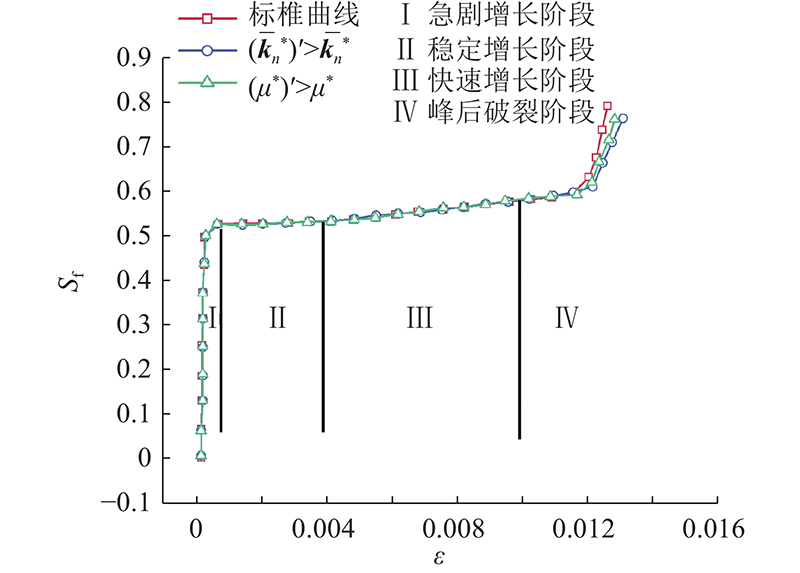
针对岩石循环加载强化作用的宏观力学表现,通过控制模型内部矿物颗粒自锁效应范围以及增大黏结强度,对GBM模型进行相应改进,基于以下假设建立GBM强化模型. 具体假设如下:1)岩石矿物颗粒自锁效应在GBM强化模型中体现为颗粒之间接触数量、接触的刚度值和摩擦系数的变化;2)自锁效应仅影响颗粒接触作用,部分颗粒出现基础滑动趋势,但颗粒间不会发生相对滑移;3)在GBM强化模型中,岩石自锁效应程度是有限的,当试块内部发生自锁效应的接触数量达到某一阈值时,强化效应停止;4)以GBM强化模型中发生强化的接触数量与总接触数量之比,表征岩石发生自锁强化效应的程度,即强化系数(strengthening factor)Sf. 当Sf达到某一特定阈值
式中:
5)在矿物颗粒完全破碎前,GBM模型已经失效,因此不考虑矿物颗粒破碎对局部结构的改变.
2.2.2. 平行黏结模型的强化
平行黏结模型平行键可视为一组具有恒定法向刚度和剪切刚度的弹簧,相对于球体颗粒仅能传递外力作用,黏结位置可以传递外力和力矩. 线性平行键合模型提供2种界面行为:1)第1种界面相当于线性模型,不抵抗相对旋转,无法传递力矩作用,只能通过摩擦系数对剪切力施加库伦极限来调节颗粒间相对滑动,如图6(a)“短划线”组合元件所示,gs为时间步开始时颗粒与颗粒之间的表面间隙,Φ为平行黏结模型内的摩擦角,kn为接触位置法向刚度. 对于GBM强化模型,当触发矿物颗粒自锁效应时,通过增加强化摩擦系数来增强接触位置抗剪强度:
图 6
式中:
之后根据该位置处剪切力的模与抗剪强度之间的数量关系来更新该位置处线性剪切力
式中:
2)第2种界面称为平行键,平行键黏结时可以抵抗相对旋转,直至应力超过强度极限,黏结键断裂,此时界面不承受任何载荷. 如图6(a)中“点-划线”组合元件所示. 对于GBM强化模型适用的接触位置,通过强化法向刚度来增大模型的法向张力:
式中:
对于GBM强化模型适用的接触位置,切向刚度受法向刚度影响:
式中:
线性剪切力更新遵循以下定律:
式中:
平行黏结强化模型主要由s和Sf控制的开关以及与原模型并联的强化部分(
控制GBM强化模型的主要参数有Sf、
图 7
2.3. 强化阈值 $S_{\text{f}}^ * $
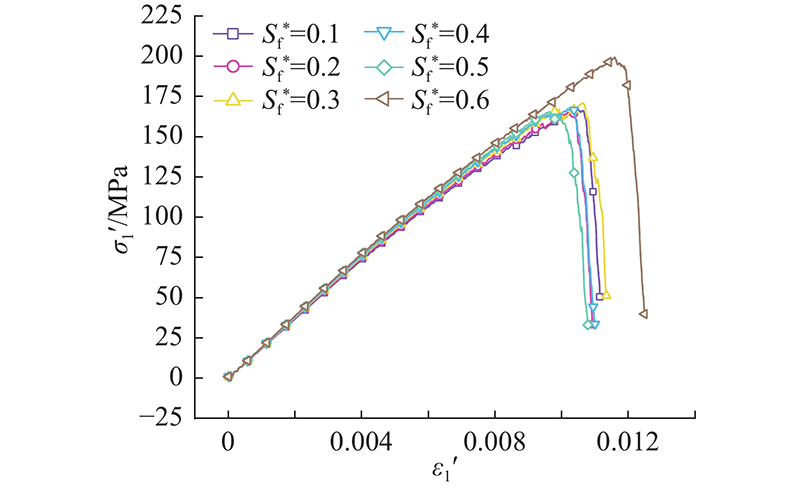
为了探究
图 8
图 8
不同
Fig.8
Stress-strain curve of grain-based reinforcement model with different
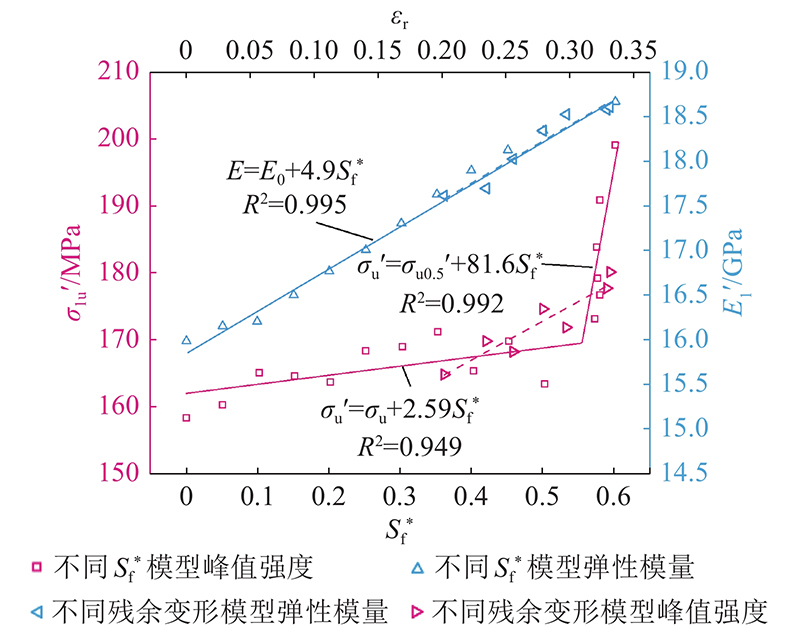
图 9
图 9
GBM强化模型峰值强度、弹性模量随
Fig.9
Variation curves of peak strength and elastic modulus of grain-based reinforcement model with
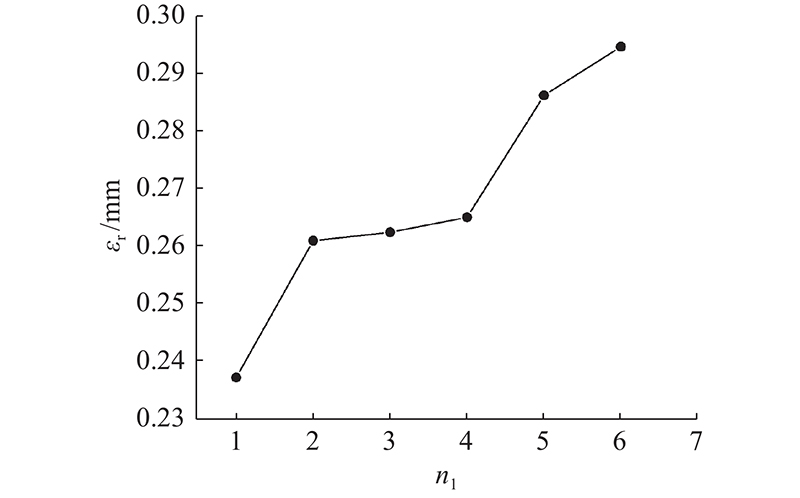
相同循环加卸载路径处理后的试块,残余变形存在差异性. 选取不同残余变形的试块构建GBM强化模型开展单轴压缩试验. 残余变形与弹性模量呈现明显的线性相关,与峰值强度的线性相关性不强,但呈现正相关. 残余变形、
2.4. GBM强化模型细观参数校准
依据室内试验结果,采用试错法不断校准
表 4 原状试块与预处理试块宏观参数试验值与模拟值
Tab.4
| 项目 | 原状试块 | 预处理试块 | |||
| σ0u /MPa | E0 /GPa | | | ||
| 试验值 | 160.1 | 16.0 | 174.6 | 18.3 | |
| 模拟值 | 159.9 | 16.0 | 175.3 | 18.6 | |
图 10
图 10 GBM模型与GBM强化模型应力-应变曲线
Fig.10 Stress-strain curves between GBM and grain-based reinforcement model
图 11
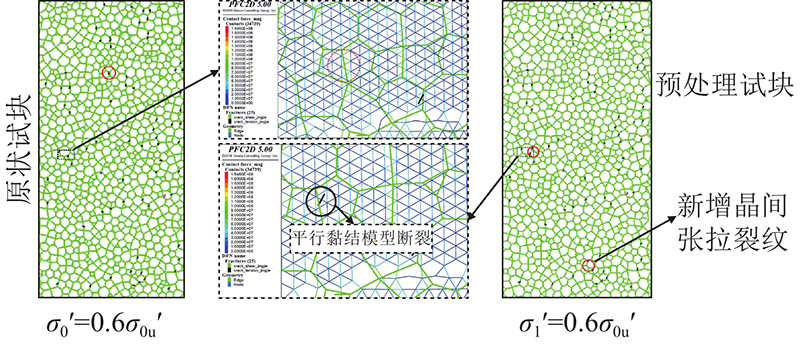
图 11 预处理试块与GBM强化模型宏观破坏特征
Fig.11 Macroscopic failure characteristics of pretreatment specimens and grain-based reinforcement model
3. 花岗岩细观破坏机理
3.1. 预处理试块峰前阶段细观破坏机理
初始阶段(
图 12
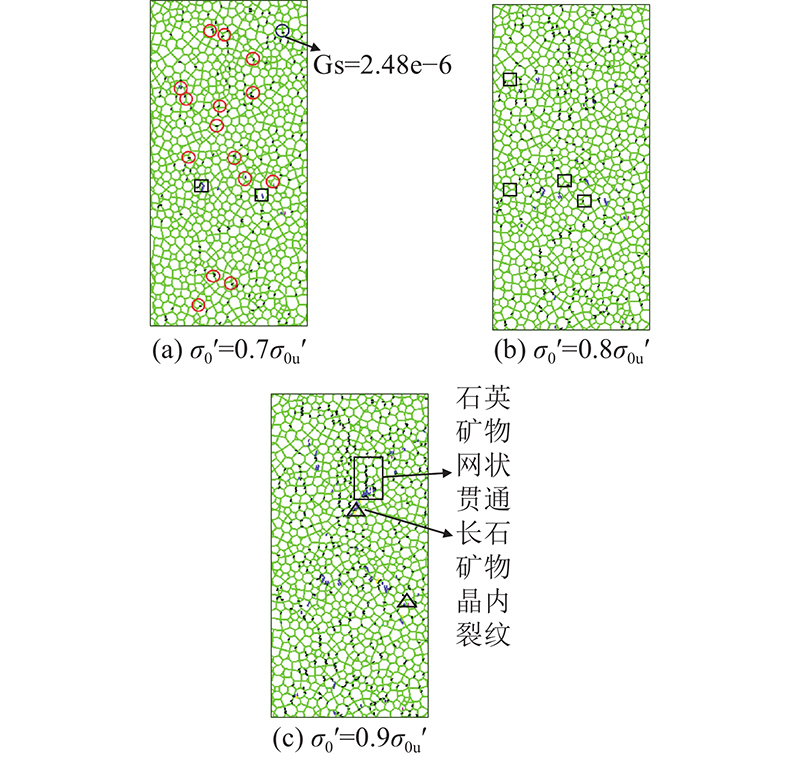
原状试块与预处理试块峰前应各应力水平微裂纹分布如图13、14所示,在图13中,代表性黑云母晶内裂纹用圆形圈出,代表性石英晶内裂纹用矩形框出,代表性长石晶内裂纹用三角形框处. 当
图 13
图 13 GBM模型峰前不同应力水平微裂纹分布
Fig.13 Distribution of pre-peak microcracks at different stress levels in GBM
图 14
图 14 GBM强化模型峰前不同应力水平微裂纹分布
Fig.14 Distribution of pre-peak microcracks at different stress levels in grain-based reinforcement model
3.2. 预处理试块峰值及峰后阶段细观破坏机理
图 15
图 15 GBM模型峰值应力及峰后阶段微裂纹分布
Fig.15 GBM peak stress and post-peak microcrack distribution
图 16
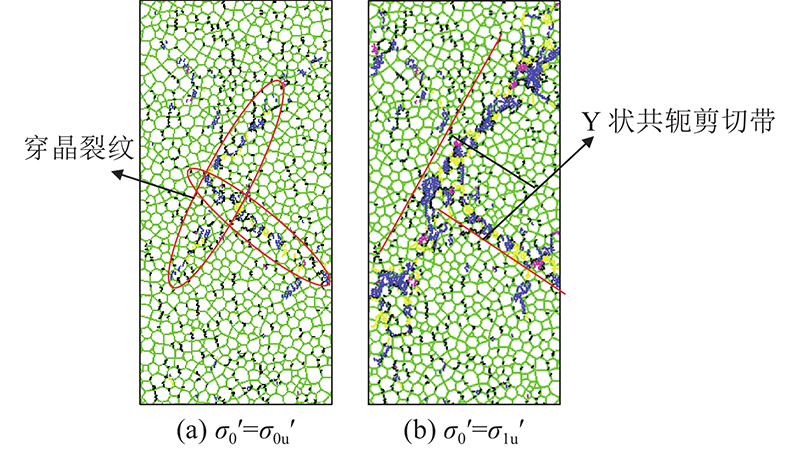
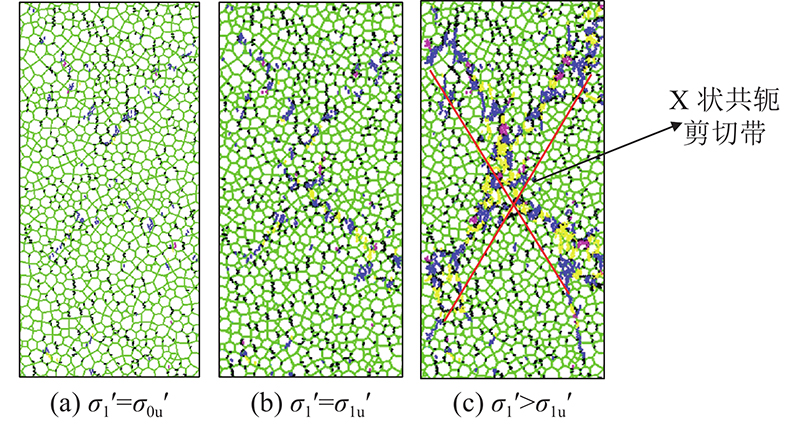
图 16 GBM强化模型峰值应力及峰后阶段微裂纹分布
Fig.16 Grain-based reinforcement model peak stress and post-peak microcrack distribution
当
3.3. 裂纹变化特征
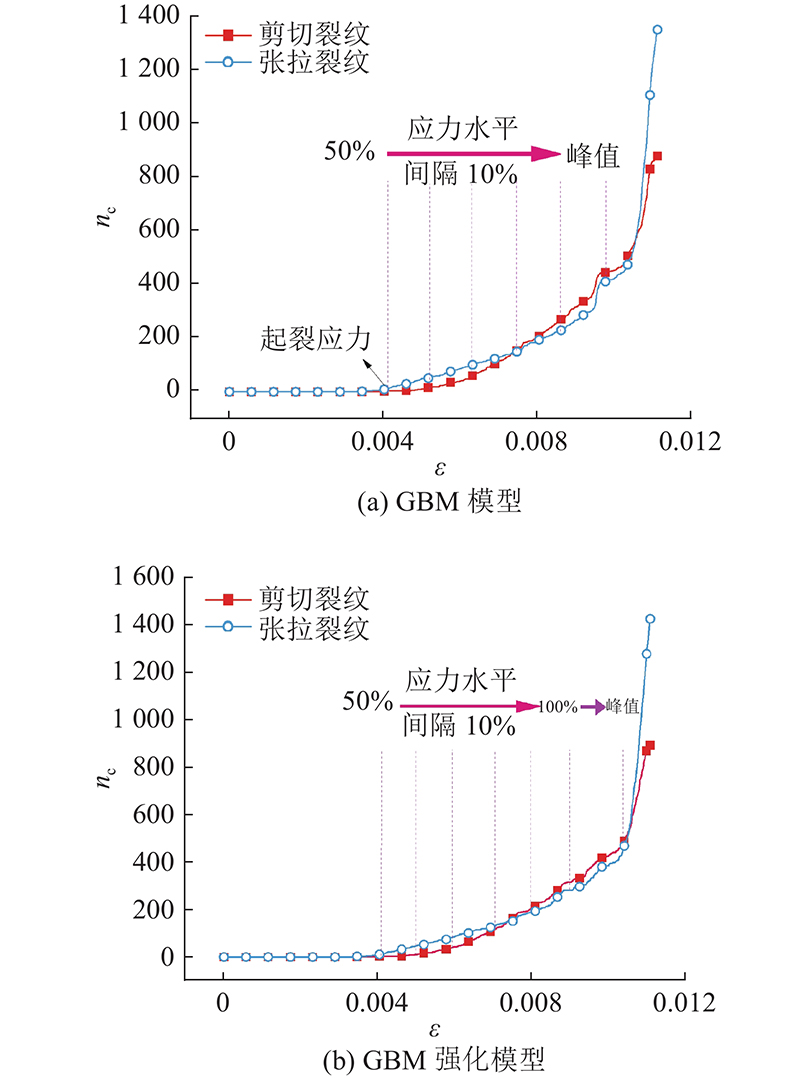
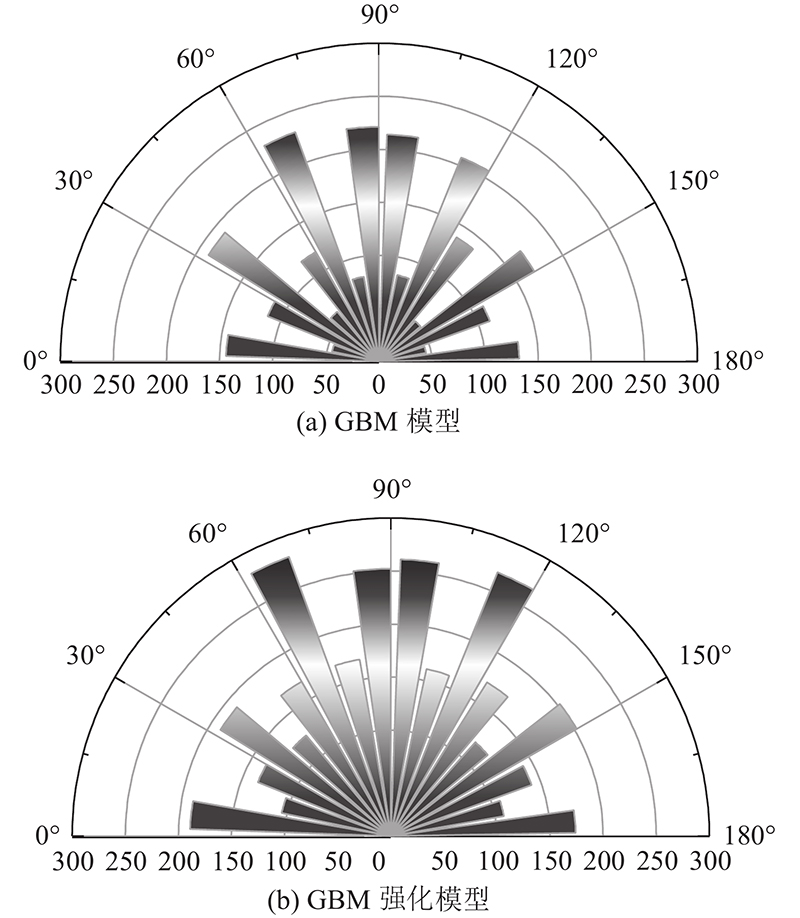
2种模型张拉、剪切裂纹数量变化如图17所示,nc为裂纹数量,裂纹倾角方向及各倾角方向裂纹数量如图18所示. 当达到起裂应力时,2种裂纹同时出现,张拉裂纹增长速度远超剪切裂纹. 随着应力水平提高,张拉裂纹保持匀速缓慢增长,剪切裂纹增呈现指数型增长. 当应力水平达到0.8
图 17
图 17 GBM强化模型裂纹数量随应变的变化曲线
Fig.17 Variation curve of grain-based reinforcement model crack number with strain
图 18
图 18 GBM强化模型裂纹分布特征
Fig.18 Grain-based reinforcement model crack distribution characteristics
4. 峰值强度波动分析
表 5
Tab.5
| | na | ne | |||||||
| nt | ns | nt | ns | ||||||
| 石英 | 长石 | 云母 | 石英 | 长石 | |||||
| 0.5 | 30 | 4 | 0 | 0 | 1 | 0 | 0 | ||
| 0.6 | 65 | 25 | 3 | 0 | 2 | 0 | 0 | ||
| 0.7 | 101 | 73 | 15 | 1 | 3 | 3 | 0 | ||
| 0.8 | 133 | 165 | 36 | 4 | 4 | 16 | 0 | ||
| 0.9 | 182 | 268 | 75 | 11 | 7 | 31 | 1 | ||
| 1.0 | 243 | 418 | 224 | 71 | 15 | 73 | 6 | ||
表 6
Tab.6
| | na | ne | |||||||
| nt | ns | nt | ns | ||||||
| 石英 | 长石 | 云母 | 石英 | 长石 | |||||
| 0.5 | 30 | 4 | 0 | 0 | 1 | 0 | 0 | ||
| 0.6 | 66 | 26 | 3 | 0 | 2 | 0 | 0 | ||
| 0.7 | 102 | 74 | 18 | 2 | 2 | 3 | 0 | ||
| 0.8 | 130 | 160 | 37 | 4 | 4 | 13 | 0 | ||
| 0.9 | 185 | 269 | 89 | 11 | 8 | 32 | 1 | ||
| 1.0 | 243 | 441 | 239 | 80 | 25 | 77 | 4 | ||
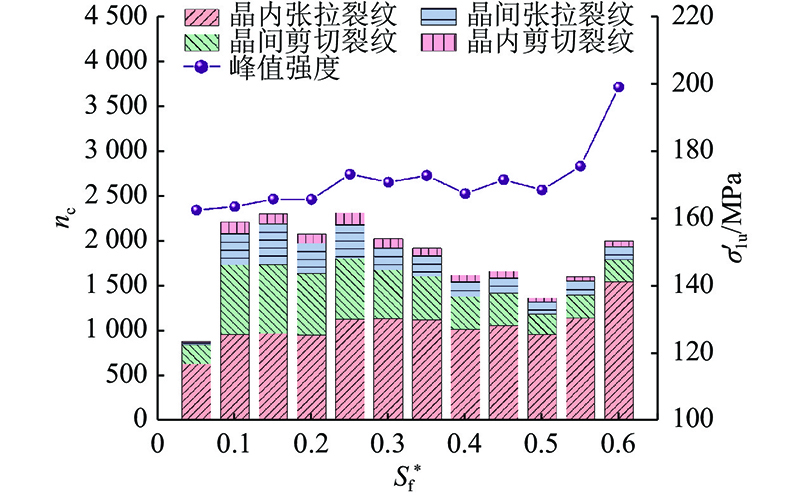
当
图 19
图 19 破坏裂纹数量与峰值强度随强化系数阈值的变化
Fig.19
Variation of nc and
5. 结 论
依据循环加载强化作用的宏观解释对GBM模型平行黏结模型和光滑节理模型进行相应改进,构建了GBM强化模型,对强化参数进行了敏感性分析,为研究循环加载强化作用对脆性岩石不同加载路径细观破坏提供了新方法. 揭示了循环加载强化作用对花岗岩试块单轴压缩过程细观破坏的影响机制. 主要得到以下结论:
(1)在峰前应力阶段,预处理试块由于自锁效应发生试块内应力集中现象,张拉、剪切裂纹的出现时间、生长速度、发育数量与原状试块出现差异. 晶间接触位置出现张拉裂纹,石英、云母和长石相继出现以张拉裂纹为主的晶内裂纹,晶内裂纹总数较原状试块更少,石英、长石依次成为承载主体.
(2)在峰后应力阶段,前期强化作用所积蓄的剪切能量得到释放,长石出现大量密集晶内裂纹. 同时,应力传递至共轭破坏带外的晶间、晶内接触,失效范围扩大,最终导致试块破坏. 长石内部出现密集裂纹是试块失稳的主要标志.
(3)应力集中现象导致长石周边矿物张拉裂纹的扩展程度不同,矿物失效出现差异性. 这种矿物差异性失效引起长石矿物破坏路径改变,造成试块峰值应力随强化系数增大呈现波动性增长.
参考文献
开挖扰动下巷道围岩细观力学行为分析
[J].DOI:10.13347/j.cnki.mkaq.2017.03.051 [本文引用: 1]
Mesomechanics behavior analysis of surrounding rock under roadway excavation disturbance
[J].DOI:10.13347/j.cnki.mkaq.2017.03.051 [本文引用: 1]
爆破开挖扰动下锚固节理岩质边坡位移突变特征与能量机理
[J].
Displacement mutation characteristics and energy mechanisms of anchored jointed rock slopes under blasting excavation disturbance
[J].
大理岩试样循环加载强化作用的试验研究
[J].DOI:10.19636/j.cnki.cjsm42-1250/o3.2008.01.010 [本文引用: 1]
Experimental research on strengthening under cyclic loading of marble samples
[J].DOI:10.19636/j.cnki.cjsm42-1250/o3.2008.01.010 [本文引用: 1]
矽卡岩单轴循环加卸载试验及声发射特性研究
[J].DOI:10.3969/j.issn.1000-7598.2009.10.006 [本文引用: 1]
Experimental study of skarn under uniaxial cyclic loading and unloading test and acoustic emission characteristics
[J].DOI:10.3969/j.issn.1000-7598.2009.10.006 [本文引用: 1]
花岗岩单轴循环加卸载试验及声发射特性研究
[J].DOI:10.13436/j.mkjx.201611027 [本文引用: 2]
Experimental test and acoustic emission characteristics of granite under uniaxial cyclic loading and unloading conditions
[J].DOI:10.13436/j.mkjx.201611027 [本文引用: 2]
脆性岩石单轴循环加卸载试验及断裂损伤力学特性研究
[J].
Experimental test and fracture damage mechanical characteristics of brittle rock under uniaxial cyclic loading and unloading conditions
[J].
循环加卸载下花岗岩强度变形及声发射特征
[J].DOI:10.16198/j.cnki.1009-640X.2018.02.010 [本文引用: 1]
Strength and deformation along with acoustic emission characteristics of granite under cyclic loading and unloading
[J].DOI:10.16198/j.cnki.1009-640X.2018.02.010 [本文引用: 1]
簇平行黏结模型中微观参数对宏观参数影响的量纲研究
[J].DOI:10.13722/j.cnki.jrme.2014.02.008 [本文引用: 1]
Dimensional analysis of effects of microscopic parameters on macroscopic parameters for clumpparallel-bond model
[J].DOI:10.13722/j.cnki.jrme.2014.02.008 [本文引用: 1]
A discrete numerical model for granular assemblies
[J].
颗粒流方法及PFC2D程序
[J].DOI:10.3969/j.issn.1000-7598.2000.03.020 [本文引用: 1]
The method of particle flow and PFC2D code
[J].DOI:10.3969/j.issn.1000-7598.2000.03.020 [本文引用: 1]
A bonded-particle model for rock
[J].DOI:10.1016/j.ijrmms.2004.09.011 [本文引用: 1]
等效晶质模型及岩石力学特征细观研究
[J].DOI:10.13722/j.cnki.jrme.2015.03.008 [本文引用: 1]
An equivalent crystal model for mesoscopic behaviour of rock
[J].DOI:10.13722/j.cnki.jrme.2015.03.008 [本文引用: 1]
细观结构的非均质性对花岗岩强度及变形影响的颗粒流模拟
[J].
Influence of meso-structure heterogeneity on granite strength and deformation with particle flow code
[J].
Calibration of micro-scaled mechanical parameters of granite based on a bonded-particle model with 2D particle flow code
[J].
Novel grain-based model for simulation of brittle failure of alxa porphyritic granite
[J].DOI:10.1016/j.enggeo.2019.02.005 [本文引用: 1]
颗粒流(PFC5.0)数值模拟技术及应用
[J].
Particle Flow Code(PFC5.0)
[J].