盾构隧道管片结构是由多环管片和纵横向螺栓连接构成的预制装配式混凝土结构,广泛应用于城市隧道工程领域[1-2]. 在隧道施工和运营过程中,管片结构主要承受外部土压力、地下水压力、地面超载以及开挖动态工况等外部围压作用. 作为隧道外部结构的支撑体系,在外部围压作用下管片结构的力学承载性能和破坏模式对于隧道的整体安全保障至关重要[3-5]. 国内外对于盾构隧道管片的力学承载性能及破坏模式的研究主要从理论分析、数值计算和模型试验3个方面展开[6-13]. 黄伟明等[6]基于弹性地基曲梁理论和状态空间法,在围压作用下推导获得管片结构的内力和变形解析解,并进行数值模拟验证. Do等[7]基于共轭梁理论,引入接头转动弹簧影响至管片结构刚度矩阵,提出一种分析隧道管片结构的超静定反应法(hyperstatic reaction method, HRM)数值解,以考虑沿隧道边界管片接缝变形的任意分布. Lee等[8]基于梁弹簧模型,推导出预测圆形管片结构内力和位移分布的力法方程理论解,并讨论了接头刚度对管片力学性能的影响. 刘洪清等[9]研究不同管片接头间隙、螺栓倾斜角等细部构造因素下,单环管片结构的接头挠度、接头弯矩等静力有限元响应,并与实验结果进行对比. 汪亦显等[10]考虑管片接头张合状态,对盾构隧道管片及接头螺栓的受力和变形进行研究,认为纵向接头螺栓主要承受压力作用. Zhou等[11]通过大型缩尺模型试验,研究了高静水压作用下不同拼装方式对管片力学特性的影响,发现弯矩峰值位置与错缝拼装的方式有关. 张力等[12]对管片接头进行负弯矩下的抗弯模型试验,表明在高轴压下接头螺栓变形模式以弯曲为主. 巩一凡等[13]基于足尺模型试验,开展类矩形盾构隧道管片接头的抗剪切性能研究,总结出管片错台变形的“四阶段”变化规律.
上述研究主要集中于管片结构的内力和变形特性、接头弹簧刚度和拼接方式影响、抗弯和抗剪承载试验以及强度验算等方面. 由于管片结构是由预制构件装配形成的整体体系,在极端工况条件下整体结构的过大变形及失稳破坏都会成为影响结构使用和承载的重要因素[14-15]. 从整体性能角度出发,按概率极限状态方法进行管片结构设计,以考虑在极端工况条件下盾构管片结构的非线性稳定承载性能就显得尤为重要,目前关于这方面的相关研究相对较少[16-17]. 郭瑞等[16]针对大断面盾构隧道,采用非线性有限元法对管片结构的整体稳定性能进行数值模拟和缩尺模型试验研究,并提出结构失稳破坏的判定建议. 柳献等[17]针对类矩形盾构隧道结构,采用双重非线性(几何非线性、材料非线性)分析进行极限工况下的稳定承载试验和数值模拟研究.
本研究针对盾构隧道管片结构,首先基于壳-弹簧简化计算模型和外部围压荷载模式,提出考虑初始椭圆度缺陷的管片非线性稳定极限承载性能计算方法;接着建立三维有限元数值模型,通过线性屈曲分析获得理想状态下管片的极限承载力和屈曲变形模式;进一步分析椭圆度缺陷的几何计算理论取值,分别引入横长轴和斜长轴初始椭圆度缺陷,就多组缺陷幅值在不同土体侧压力、土体抗力和接头抗弯等参数工况下对于管片非线性极限荷载的影响展开参数敏感性研究,同时对比分析整体式和衬砌式管片的极限荷载;最后,提出含初始椭圆度缺陷的管片极限稳定承载力的工程设计取值建议.
1. 极限承载力计算理论
1.1. 计算模型的简化
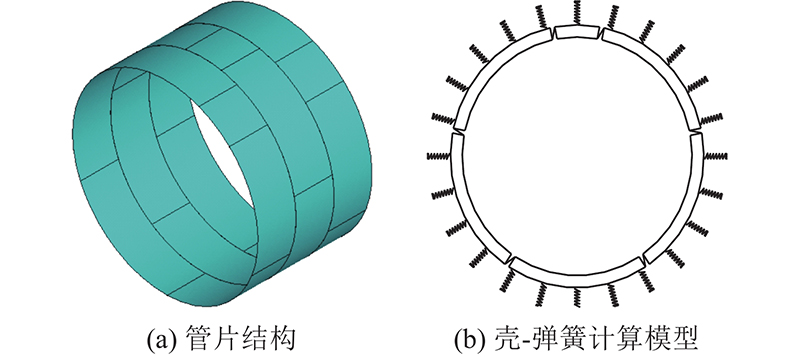
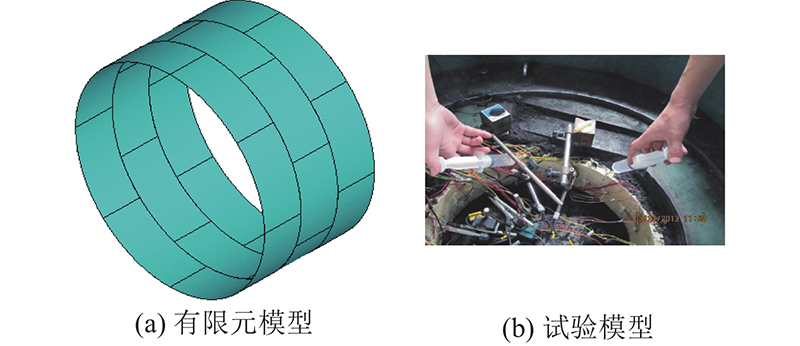
1.1.1. 管片结构
图 1
1.1.2. 壳-弹簧计算模型
管片结构的计算模型采用壳-弹簧模型,其中管片为三维有限元壳单元,管片环向接头、纵向接头为转动弹簧单元,如图1(b)所示. 环向、纵向接头弹簧单元分别沿管片的纵缝、环缝布置在对应节点对上,各组节点允许较小间隙. 土体抗力作用采用双向接地弹簧单元模拟,沿管片整环布置,该弹簧在每个方向均只能受压,不能受拉.
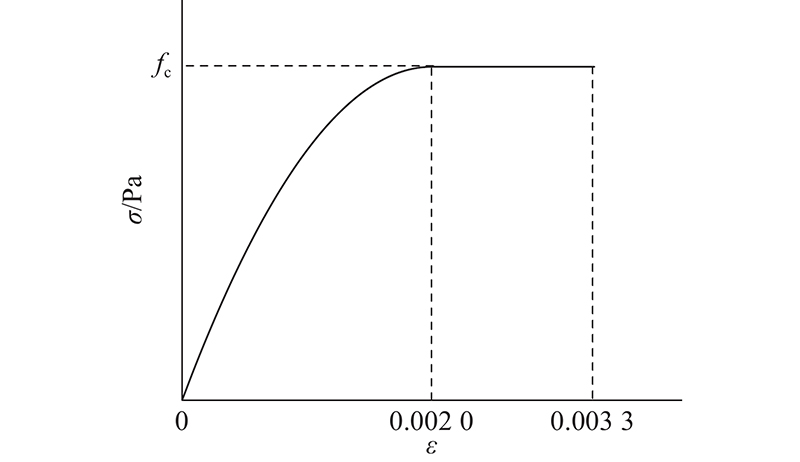
1.1.3. 混凝土材料模型
图 2
式中:
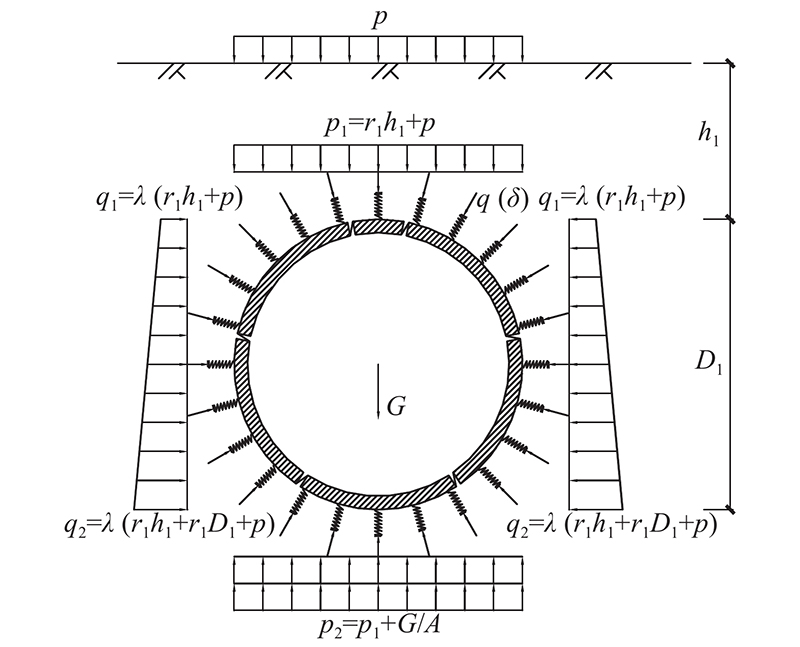
1.2. 荷载模式的处理
图3所示为管片的外部围压荷载模式,其中
图 3
1.2.1. 顶部、底部土压力
管片顶部土压力
式中:
式中:A为管片下半部分的表面积,
1.2.2. 侧向土压力
管片侧向土压力通过土体侧压力系数与对应位置侧向土压力的乘积获得,一般考虑水土合算;管片顶部、底部埋深处的侧向土压力
式中:
1.3. 参数的取值区间
1.3.1. 土体侧压力系数
考虑到软弱黏土地层条件进行分析,对应土体侧压力系数
| 土体 | N | | k/(MN·m−3) |
| 极软黏土 | [0, 2] | [0.65, 0.75] | [0, 1.0] |
| 软黏土 | [2, 4] | [0.55, 0.65] | [1.0, 5.0] |
| 中硬黏土 | [4, 8] | [0.45, 0.55] | [5.0, 10.0] |
1.3.2. 土体抗力系数
式中:
1.3.3. 接头抗弯刚度
管片接头处的力学特性涉及到接触等复杂因素,为简化分析一般通过转角
1.4. 非线性承载力计算
1)设置几何、材料双重非线性,建立管片结构的三维数值分析模型;
2)引入管片初始缺陷变形形式,并给定不同的缺陷幅值;
3)求解多组缺陷幅值下,管片的荷载-位移变化路径曲线;
4)对不同缺陷幅值下稳定极限荷载按平缓收敛或急剧下降突变时相近竖向位移的对应极值点荷载系数进行取值,以便比较不同缺陷幅值对极限荷载系数的影响;
5)采用插值方法,求解不同缺陷幅值下荷载系数的误差百分比,以获得缺陷幅值对承载力的影响程度.
采用荷载系数来对稳定极限承载力进行定量判断,荷载系数α定义为实际加载时荷载F与第2.1节正常使用时荷载F0的比值,即α=F/F0. 对应管片结构的非线性极限承载也是采用极限荷载系数进行定量判断.
2. 有限元分析模型及验证
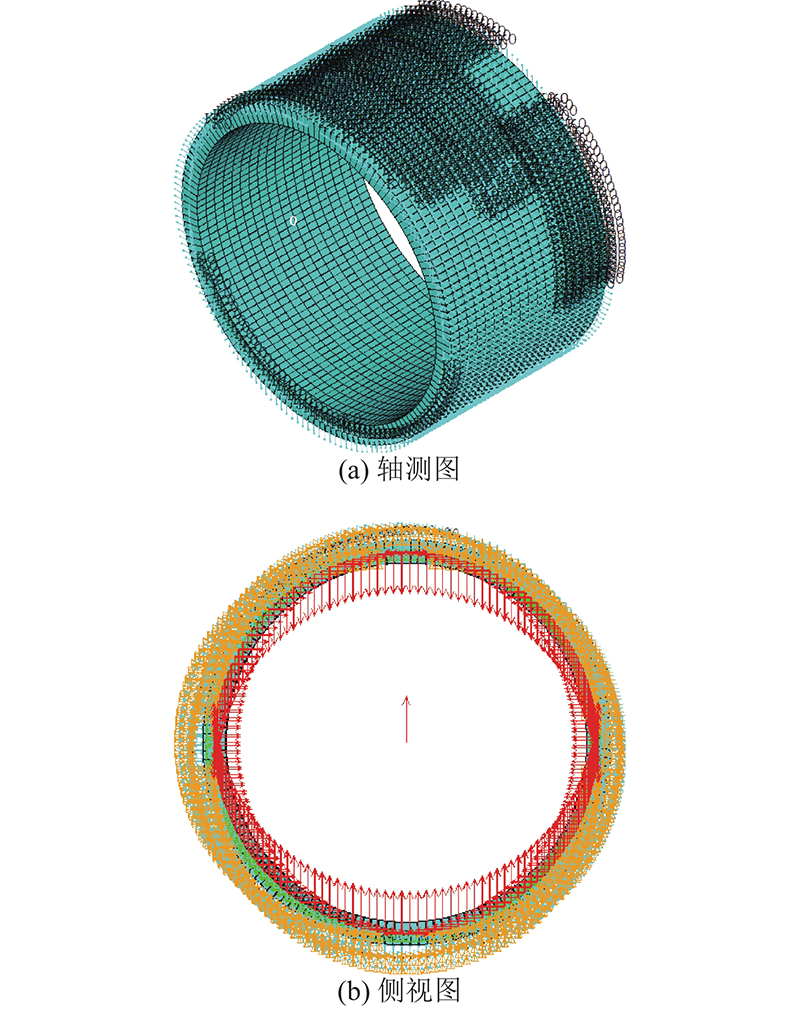
2.1. 有限元模型的建立
选取典型的盾构管片结构进行分析,外直径D1=6.20 m,壁厚t=0.35 m,幅宽B=1.20 m;管片单环沿圆周由6块组成(即1块封顶块22.5°、2块邻接块67.5°和3块标准块67.5°),管片相邻环的错缝转动角
图 4
图 4 管片围压承载有限元分析模型
Fig.4 Finite element analysis model of confining pressure sbearing for segment
2.2. 模型验证
采用文献[16]所述的管片结构极限失稳破坏试验结果,对本研究的壳-弹簧有限元模型进行验证. 文献[16]中管片缩尺模型的相似比为20∶1,对应实体管片结构由三环管片构成,D1=10.8 m,t=0.5 m;B=2.0 m;管片单环沿圆周由8块弧形混凝土预制块组成(即1块封顶块片17°、2块邻接块49°、5块标准块49°),
表 2 有限元模型和试验模型的极限位移比较
Tab.2
| 土体 | | k /(MN·m−3) | Δ /mm | |
| 有限元模型 | 试验模型 | |||
| 极软黏土 | 0.7 | 1.0 | 128.0 | 80.0~120.0 |
| 软黏土 | 0.6 | 2.5 | 95.0 | |
| 中硬黏土 | 0.5 | 5.0 | 67.0 | |
图 5
由表2可知,有限元计算得到的极软黏土、软黏土、中硬黏土中管片结构的极限位移Δ分别为128.0、95.0和67.0 mm,与试验模型得到的管片失稳破坏时的极限位移80.0~120.0 mm较为接近,从而验证了本研究有限元模型的合理性和准确性.
2.3. 线性屈曲分析
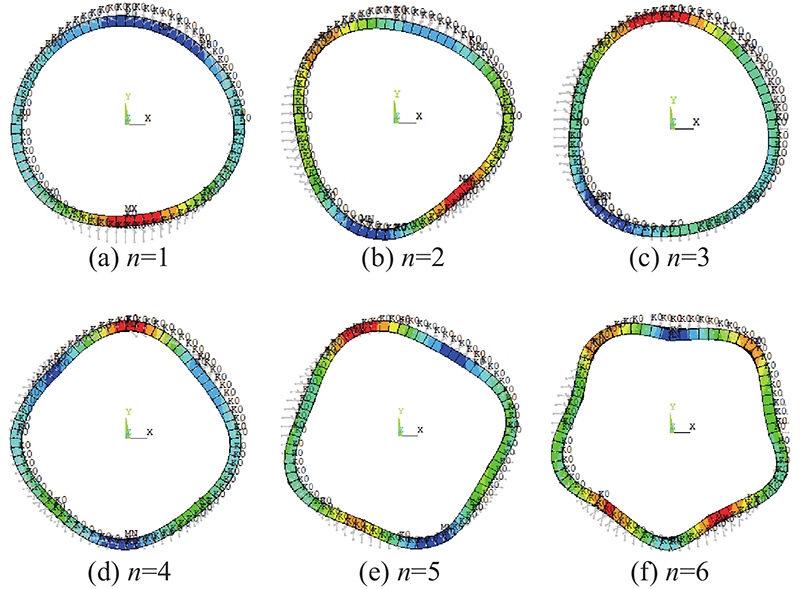
线性屈曲分析计算简单,思路清晰,可以直观获得线性稳定极限荷载系数和对应的管片失稳模态,有益于初步认识管片结构的整体稳定性能. 取初始切线模量
表 3 前10阶线性极限荷载系数
Tab.3
| n | α | n | α | |
| 1 | 24.663 | 6 | 83.973 | |
| 2 | 34.193 | 7 | 85.491 | |
| 3 | 39.705 | 8 | 115.360 | |
| 4 | 52.653 | 9 | 115.510 | |
| 5 | 58.892 | 10 | 120.350 |
图 6
本节线性屈曲分析及图6的失稳模态变形是在线性条件(即:几何线性、材料线性)下得到的管片失稳变形形式;实际由于管片结构承载时的几何非线性、材料非线性效应,稳定极限承载性能一般要比线性屈曲分析时小得多根据壳结构稳定理论,初始几何缺陷一般可视为多个低阶屈曲模态的线性组合,因而本节给出前6阶屈曲模态变形形式. 由于实际盾构管片更多的是采用椭圆度进行整体变形判定,主要针对椭圆度缺陷进行影响分析,椭圆度缺陷本质上也可视为多个线性屈曲模态的组合形式,本节线性屈曲分析较为简单且模态变形较为直观,因而本节研究与第3章的椭圆度缺陷理论、第4章的非线性稳定分析均是相关连的,且具有一定的参考价值. 此外,椭圆度缺陷也并非唯一的整体缺陷形式,针对整体模态缺陷形式和局部缺陷形式等的影响分析将在后续研究中进一步考虑.
3. 椭圆度缺陷的形式和取值
3.1. 椭圆度缺陷计算理论
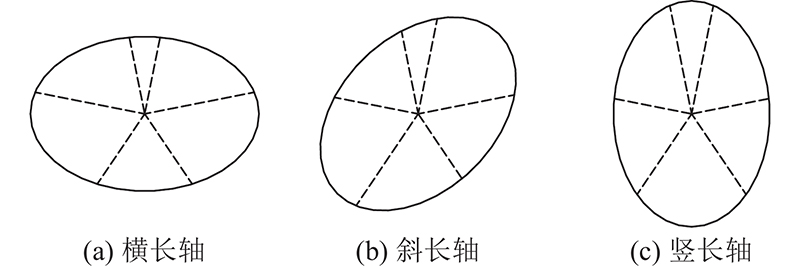
根据管片的不同椭圆长轴倾斜角
图 7
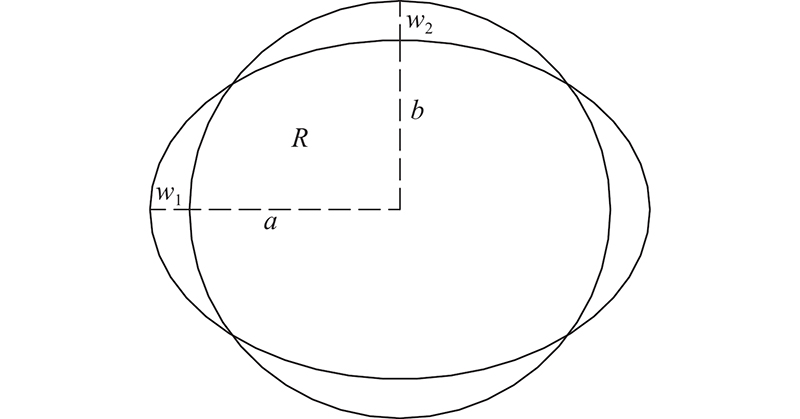
图8为管片出现整体椭圆度缺陷前、后的几何形变图. 根据管片整体形变之前的圆周长和整体形变之后的椭圆周长不变原则,即为
图 8
式中:a、b分别为椭圆长半轴、短半轴的长度,R为圆半径,w1、w2分别为椭圆长轴、短轴的形变缺陷.式(6)简化为
根据规范GB 50446《盾构法隧道施工及验收规范》[22],管片的椭圆度为
由式(6)、(8),可得
若定义椭圆度缺陷对应的缺陷幅值w为椭圆长半轴与短半轴的长度之差,即为
3.2. 椭圆度缺陷的取值
关于椭圆度缺陷,GB 50446《盾构法隧道施工及验收规范》[22]指出施工组装时管片椭圆度缺陷的最大限值是外直径的6‰,即椭圆度缺陷不大于6‰时均认为管片是合格的;因而在实际工程中存在大量有椭圆度变形的管片案例,而为精确圆形管片案例的反而较少. 考虑到掘进施工过程由于受力不均可能产生的错位和形变等劣化因素,取椭圆度e=0(无缺陷)、5.5‰、11.0‰、22.0‰和33.0‰,对应的缺陷幅值为w=0(无缺陷)、13.75、27.50、55.00和82.50 mm,以进一步考虑初始椭圆度缺陷的影响,这是较为合理可行的. 为简化起见,对应椭圆度均取整记为e=0(无缺陷)、5‰、10‰、20‰和30‰进行表示.
4. 椭圆度缺陷对管片极限承载力的影响
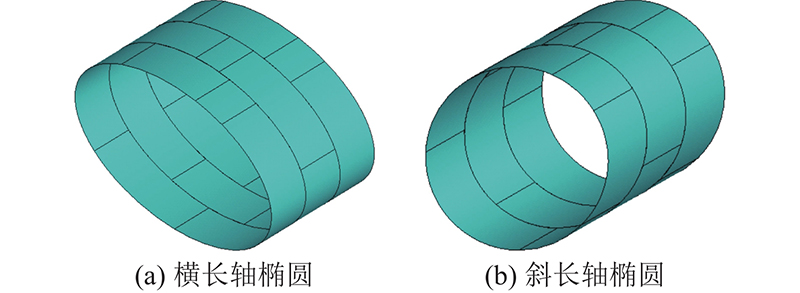
在实际工程中,横长轴椭圆缺陷和斜长轴椭圆缺陷是2种最容易出现的典型缺陷形式,对应管片结构模型见图9,其中最大缺陷变形按椭圆度30‰的15倍进行放大示意,以更为直观地观察得其变形模式. 本章主要针对这2种情况进行分析.
图 9
图 9 含椭圆度缺陷的管片有限元模型(变形放大15倍)
Fig.9 Segment model with elliptic imperfection (deformation magnified 15 times)
4.1. 横长轴椭圆度缺陷的影响
4.1.1. 初始椭圆度(缺陷幅值)的影响
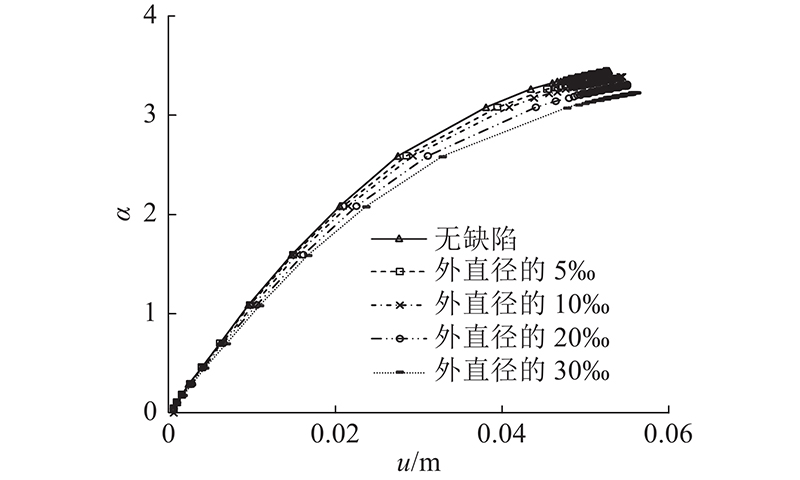
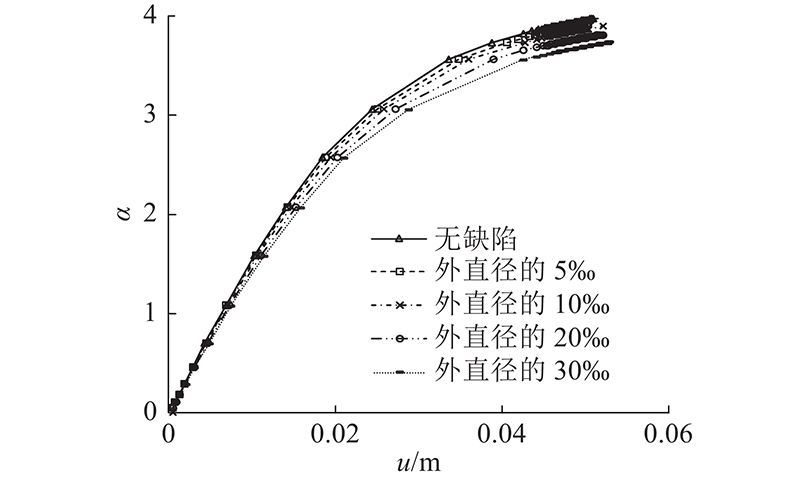
图 10
图 10 管片外部围压荷载系数-顶部中心节点竖向位移曲线
Fig.10 External confining pressure load factor-vertical displacement of top central node curves for segment
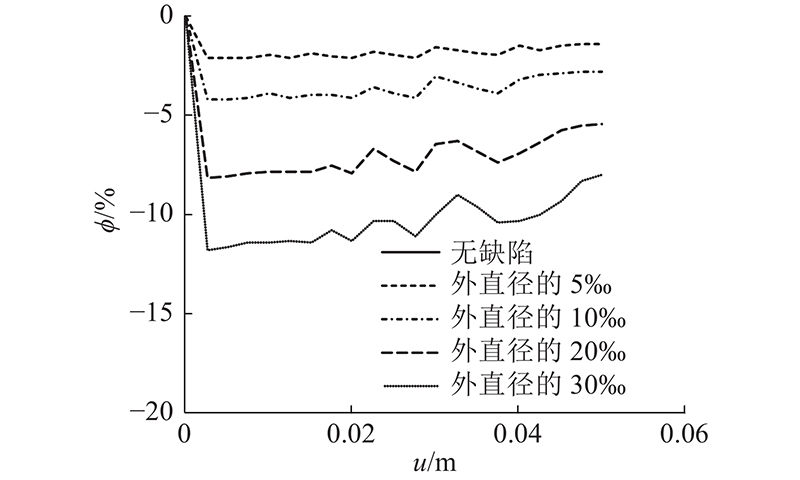
图 11
图 11 管片外部围压荷载系数误差百分比-顶部中心节点竖向位移曲线
Fig.11 Error percentage of external confining pressure load factor-vertical displacement of top central node curves for segment
由图10可知,不同椭圆度缺陷均对结构荷载系数为不利作用,即降低结构承载力. 不同椭圆度缺陷e时,荷载系数α随着竖向位移u增大呈现线性迅速增大、非线性平缓增大和趋于平缓收敛的变化过程. 为了便于比较,不同椭圆度缺陷e下的极限荷载系数α0可按平缓收敛时相同竖向位移的对应极值点荷载系数统一取值,因此本例中e=0(无缺陷)、5‰、10‰、20‰和30‰时,极限荷载系数α0分别为3.458、3.410、3.363、3.274和3.188,具备较好的非线性整体稳定性能.
由图11可知,在不同椭圆度缺陷e时,误差百分比绝对值φ(即缺陷对极限荷载系数α0的影响程度)随着竖向位移u的增大呈现迅速增大、平缓波动的变化过程. 本例中当e=5‰、10‰、20‰和30‰时,极限荷载系数对应的误差百分比分别为−1.37%、−2.73%、−5.32%和−7.80%,即含缺陷时极限荷载系数相对无缺陷时的折减系数分别为0.986 3、0.972 7、0.946 8和0.922 0. 因此,椭圆度缺陷对管片的极限承载力有着不可忽略的影响,折减系数可按最不利工况并取整为0.90.
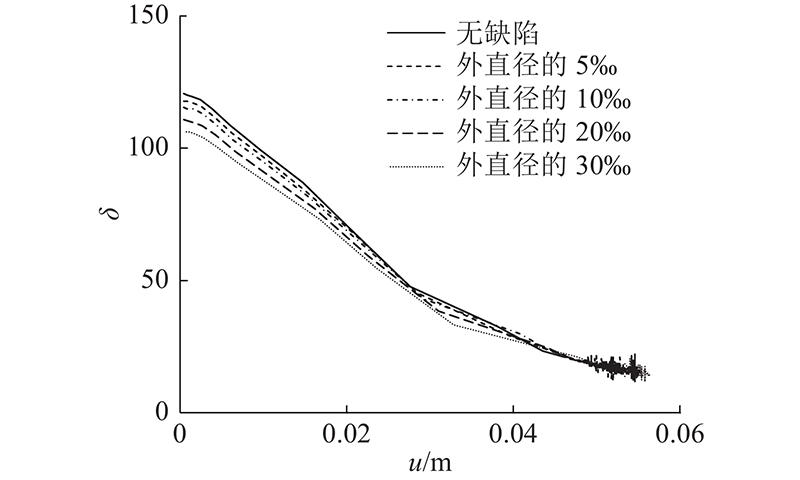
图 12
图 12 管片外部围压荷载系数斜率-顶部中心节点竖向位移曲线
Fig.12 Slope of external confining pressure load factor-vertical displacement of top central node curves for segment
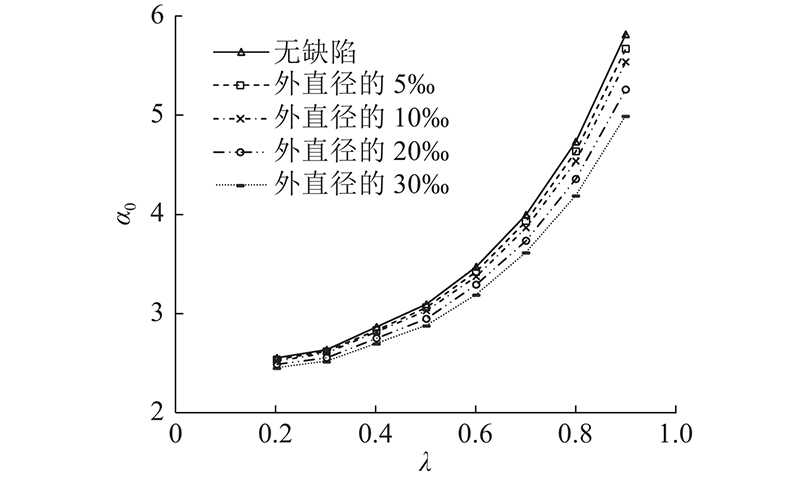
4.1.2. 土体侧压力系数的影响
基于2.1节所述管片的有限元分析模型,取土体侧压力系数
图 13
图 13 管片外部围压极限荷载系数-土体侧压力系数曲线
Fig.13 External confining pressure ultimate load factor-lateral pressure coefficient of soil curves for segment
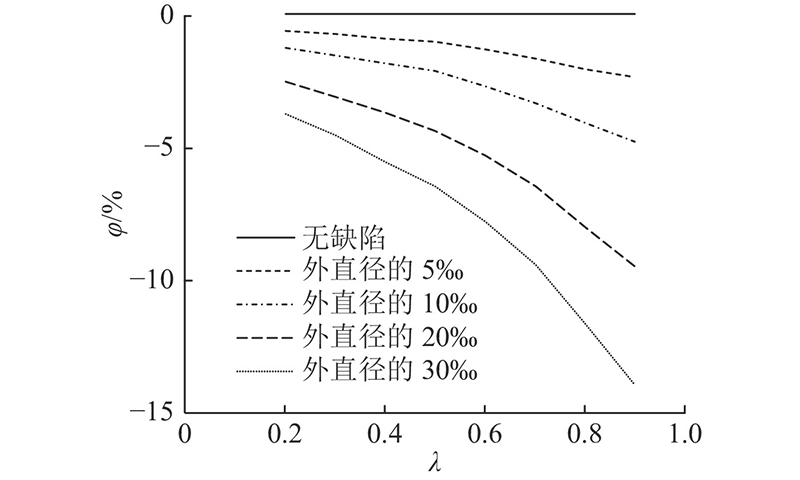
图 14
图 14 管片外部围压极限荷载系数误差百分比-土体侧压力系数曲线
Fig.14 Error percentage of external confining pressure ultimate load factor-lateral pressure coefficient of soil curves for segment
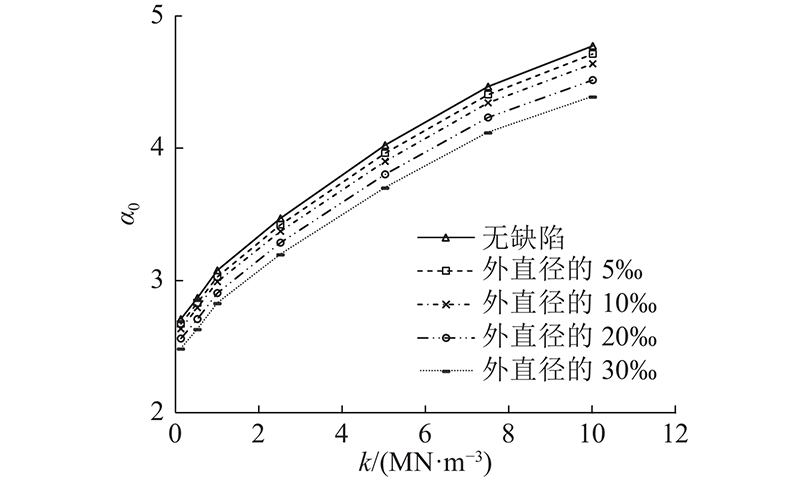
4.1.3. 土体抗力系数的影响
图 15
图 15 管片外部围压极限荷载系数-土体抗力系数曲线
Fig.15 External confining pressure ultimate load factor-soil resistance coefficient curves for segment
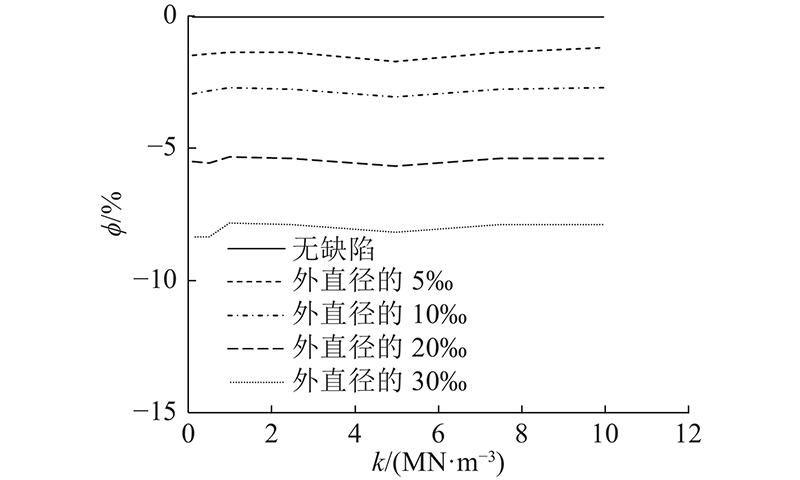
图 16
图 16 管片外部围压极限荷载系数误差百分比-土体抗力系数曲线
Fig.16 Error percentage of external confining pressure ultimate load factor-soil resistance coefficient curves for segment
由图15可知,在不同椭圆度缺陷e时,随着土体抗力系数k的增大,土体约束增大,极限荷载系数α0总体也呈现逐渐增大的趋势,具体分为迅速增大(k<5.0 MN/m3)和缓慢增大(k≥5.0 MN/m3)的过程.
由图16可知,在不同椭圆度缺陷e时,误差百分比绝对值的均随着土体抗力系数k的增大,变化幅度较小,此时椭圆度缺陷对稳定荷载作用微小. 土体抗力系数增大后,管片的周圈约束为同步增强,因而极限荷载系数将减缓提高,对应椭圆度缺陷的敏感性则变化不大,从而导致结构稳定性能的稳步增强. 当椭圆度缺陷为e=0~30‰时,极限荷载系数降低的误差百分比范围为−8.28%~ 0%,折减系数可考虑最不利工况并取整为0.90;其中当e≥20‰时,误差百分比已超过5%,此时缺陷已具有一定影响.
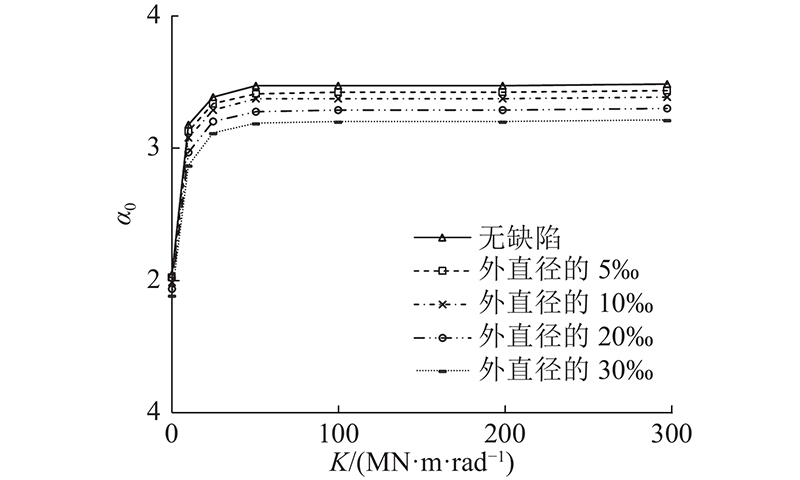
4.1.4. 接头抗弯刚度的影响
图 17
图 17 管片外部围压极限荷载系数-接头抗弯刚度
Fig.17 External confining pressure ultimate load factor-bending stiffness of joint curves for segment
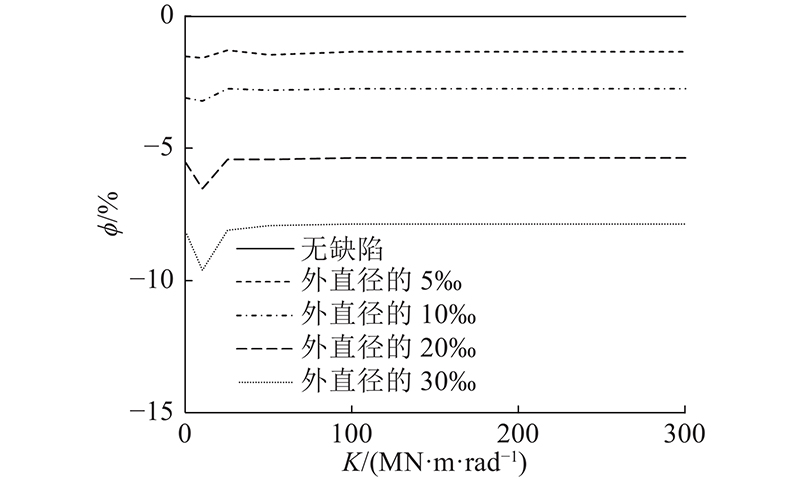
图 18
图 18 管片外部围压极限荷载系数误差百分比-接头抗弯刚度曲线
Fig.18 Error percentage of external confining pressure ultimate load factor-bending stiffness of joint curves for segment
由图17可知,在不同椭圆度缺陷e时,随着K的增大,管片自身刚度提高,极限荷载系数α0总体呈现逐渐增大的趋势,具体分为迅速增大(K<50 MN·m/rad)和趋于平稳(K≥50 MN·m/rad)的过程. 当K≥50 MN·m/rad,不同缺陷幅值下,接头抗弯刚度K的增大对极限承载力的提高贡献微小. 当接头抗弯刚度K接近或超过接头处K方向转动连续的壳结构时,接头抗弯刚度的增大不会引起整体管片刚度的继续增大;此处K方向转动连续的壳结构并不等同于整体式管片.
由图18可知,不同椭圆度缺陷e时,误差百分比绝对值均随着接头抗弯刚度K的增大,经历小幅波动(K<50 MN·m/rad)、趋于平稳(K≥50 MN·m/rad)的过程. 当椭圆度缺陷为e=0~30‰时,极限荷载系数降低的误差百分比范围为−9.51%~0%,折减系数可取为0.90;尤其当e≥20‰时,误差百分比已超过5%,此时缺陷影响一般不可忽略.
4.1.5. 整体式管片近似求解
当接头抗弯刚度较大(
图 19
图 19 整体式管片外部围压极限荷载系数-顶部中心节点竖向位移曲线
Fig.19 External confining pressure ultimate load factor-vertical displacement of top central node curves for intergral segment
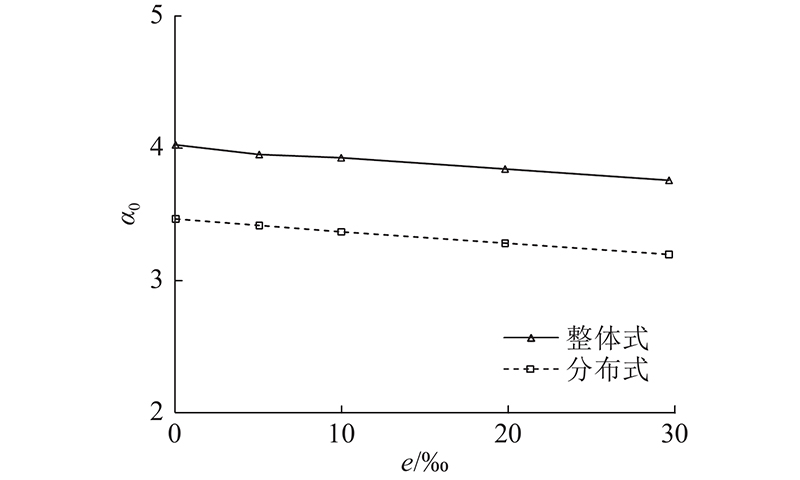
图 20
图 20 整体式、衬砌式管片的外部围压极限荷载系数-椭圆度缺陷幅值曲线比较
Fig.20 Comparison of external confining pressure ultimate load factor-elliptic imperfection amplitude curves for intergral and lining segments
图 21
图 21 整体式、衬砌式管片的外部围压极限荷载系数误差百分比-椭圆度缺陷幅值曲线比较
Fig.21 Comparison of error percentage of external confining pressure ultimate load factor-elliptic imperfection amplitude curves for intergral and lining segments
表 4 整体式、衬砌式管片的外部围压极限荷载系数和误差百分比的比较
Tab.4
| 椭圆度缺陷w (‰) | α0 | ||
| φ1 | φ2 | φ2/φ1 | |
| 0 | 3.99 | 3.46 | 0.84~0.86 |
| 5 | 3.94 | 3.41 | |
| 10 | 3.90 | 3.36 | |
| 20 | 3.81 | 3.27 | |
| 30 | 3.73 | 3.19 | |
表 4
Tab.4
| 椭圆度缺陷w (‰) | 误差百分比/% | |||
| (φ1−φ10)/φ10 | φ1/φ10 | (φ2−φ20)/φ20 | φ2/φ20 | |
| 0 | 0 | 0.935~1.000 | 0 | 0.922~1.000 |
| 5 | −1.89 | −1.37 | ||
| 10 | −2.39 | −2.73 | ||
| 20 | −4.41 | −5.32 | ||
| 30 | −6.52 | −7.80 | ||
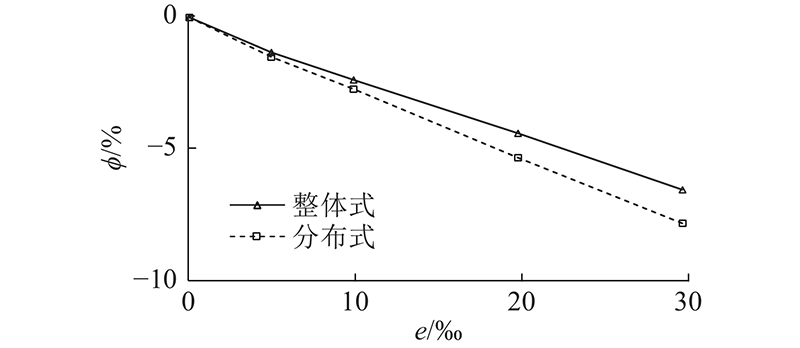
由图19可知,在不同椭圆度缺陷e时,整体式管片的荷载系数α随竖向位移u增大的变化趋势与衬砌式管片类似. 由图20和表4可知,整体式、衬砌式的极限荷载系数φ1、φ2均随着椭圆度缺陷e增大而逐渐降低;不同椭圆度缺陷时,φ2/φ1的比值约为0.84~0.86. 因此,工程中近似计算时,按整体式快速计算获得的极限荷载系数可按最不利工况并取整为折减系数0.85,以求解接近实际的衬砌式极限荷载系数. 由图21可知,在不同椭圆度缺陷e时,整体式、衬砌式的极限荷载系数相比对应无缺陷时,限荷载系数的误差百分比绝对值均是逐渐增大;且衬砌式的增大幅度更为明显,即衬砌式的极限荷载系数降低影响对于椭圆度缺陷e增大变化更为敏感. 含缺陷整体式、衬砌式的极限荷载系数相对对应无缺陷时的折减系数最小分别为0.935、0.922. 因此,工程计算中考虑椭圆度缺陷影响时,整体式、衬砌式计算获得的极限荷载系数,均可考虑最不利工况并取整为0.90的折减系数. 此处并未考虑土体侧压力系数变化的影响,故实际折减系数可根据实际情况取0.85~0.90.
4.2. 斜长轴椭圆度缺陷的影响
在实际工程中,由于管片四周围压的不对称性,椭圆度缺陷的长轴可能呈现一定倾斜角
图 22
图 22 管片外部围压极限荷载系数-长轴倾斜角曲线比较
Fig.22 Comparison of external confining pressure ultimate load factor-inclination angle of major axis curves for segment
图 23
图 23 管片外部围压极限荷载系数误差百分比-长轴倾斜角曲线比较
Fig.23 Comparison of error percentage of external confining pressure ultimate load factor-inclination angle of major axis curves for segment
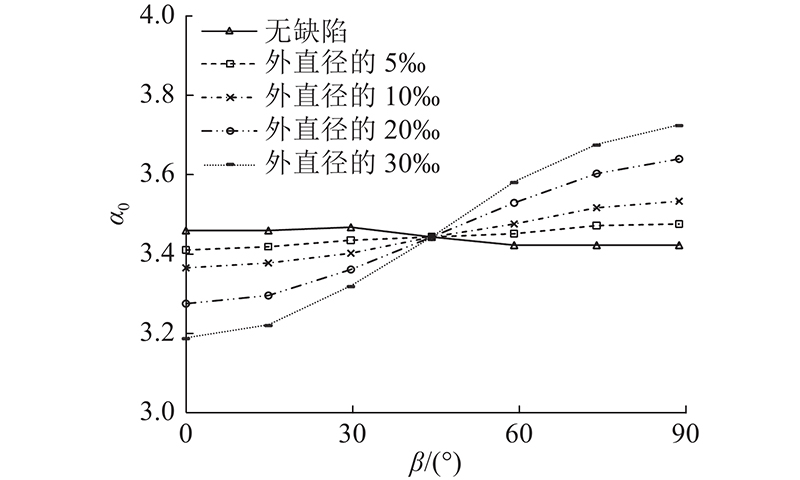
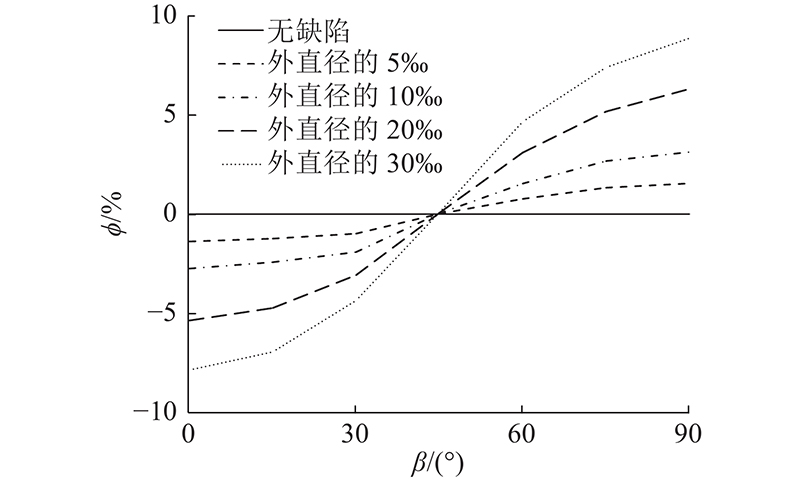
由图22可知,对于无椭圆度缺陷(e=0)情况,随着长轴倾斜角
由图23可知,当有椭圆度缺陷(e >0)时,随着长轴倾斜角
5. 含椭圆度缺陷管片承载力取值建议
5.1. 含椭圆度缺陷计算的承载力取值建议
对于横长轴椭圆缺陷和斜长轴椭圆缺陷(考虑不利效应
5.2. 整体式近似计算的承载力取值建议
在工程中近似计算按整体式管片快速求解获得的极限荷载系数可取0.85折减系数,以获得接近实际的衬砌式管片极限荷载系数. 当考虑椭圆度缺陷的影响时,整体式、衬砌式管片求解获得的极限荷载系数,均可根据实际情况再取0.85~0.90折减系数,以保障管片结构设计的安全性能.
6. 结 论
初始椭圆度缺陷是判定管片结构整体形变缺陷的一个重要指标,针对椭圆度缺陷e≤30‰时,对管片非线性稳定性能影响展开研究,主要结论如下:
(1)不同横长轴椭圆度缺陷均为不利作用,且缺陷越大,不利约明显;不同椭圆度缺陷时,荷载系数随位移的变化均为迅速增大、平缓增大和趋于收敛,极限荷载系数约为3.458~3.188,非线性承载性能较好;而误差百分比绝对值的变化均为迅速增大、平缓波动,最大约为7.80%.
(2)随着土体侧压力系数
(3)在工程设计时,按整体式管片快速求的极限荷载系数时可取折减系数0.85;考虑椭圆度缺陷影响时,整体式、衬砌式求解可再取折减系数0.85~0.90.
(4)对于工程中常见的斜长轴椭圆度缺陷(长轴倾斜角
(5)针对椭圆度缺陷对管片非线性极限稳定承载性能的影响进行参数化研究,结果对管片极限承载力的设计取值具有较好的实用参考价值. 未来将进一步考虑实际外界因素下的非对称围压荷载、实际管片错台或转动缺陷模式,进行管片的破坏模式和承载机理研究.
参考文献
城市盾构隧道数字化智能建造发展概述
[J].
Innovations in the development of digital and intelligent construction of urban shield tunnels
[J].
盾构法修建地铁隧道的技术现状与展望
[J].DOI:10.3969/j.issn.0258-2724.2015.01.015 [本文引用: 1]
Review and pospects on constructing technologies of metro tunnels using shield tunnelling method
[J].DOI:10.3969/j.issn.0258-2724.2015.01.015 [本文引用: 1]
地表超载作用下盾构隧道劣化机理与特性
[J].DOI:10.11779/CJGE201707002 [本文引用: 1]
Mechanisms and characteristics for deterioration of shield tunnels under surface surcharge
[J].DOI:10.11779/CJGE201707002 [本文引用: 1]
基于断裂力学的盾构隧道管片结构开裂破损机制探讨
[J].DOI:10.13722/j.cnki.jrme.2015.1003
Breaking mechanism of segmented lining in shield tunnel based on fracture mechanics
[J].DOI:10.13722/j.cnki.jrme.2015.1003
围压对错缝拼装管片衬砌结构力学性能的影响
[J].
The influence of confining pressure on the mechanical properties of staggered assembling segment lining structure
[J].
基于弹性地基曲梁理论的盾构隧道管片分析方法
[J].
Structural analysis of shield tunnel lining using theory of curved beam resting on elastic foundation
[J].
A new numerical approach to the hyperstatic reaction method for segmental tunnel linings
[J].
An analytical solution for a jointed shield-driven tunnel lining
[J].
盾构隧道管片及纵向接头力学性能数值模拟研究
[J].
Numerical investigation on the mechanical behavior of shield tunnel segment and their longitudinal joint
[J].
盾构隧道衬砌管片接头张合状态力学模型及数值模拟
[J].
Mechanical model and numerical simulation for patulous-occlusive situation of joint of shield tunnel lining segment
[J].
Model test on structural behaviour of underwater shield tunnel with large cross-section considering assembling modes
[J].DOI:10.4028/www.scientific.net/AMR.243-249.3560 [本文引用: 1]
盾构隧道管片接头破坏特征及损伤特性试验研究
[J].
Experimental study on failure behaviors and damage characteristics of segmental joints of shield tunnels
[J].
大断面类矩形盾构隧道管片接头极限抗剪切承载力试验研究
[J].
Experimental study on the ultimate shear bearing capacity of segment joint in shield tunnel with large quasi-rectangular cross-section
[J].
混凝土管片极限承载力计算模型及其模拟分析
[J].
Computational models and numerical simulations for ultimate bearing capacity of concrete segments
[J].
混凝土管片接头极限承载力特性的实验
[J].DOI:10.3969/j.issn.2095-7262.2020.02.019 [本文引用: 2]
Experimental study on characteristics behind ultimate bearing capacity of concrete segment joints
[J].DOI:10.3969/j.issn.2095-7262.2020.02.019 [本文引用: 2]
盾构隧道管片衬砌结构稳定性研究
[J].DOI:10.3969/j.issn.1001-7372.2015.06.011 [本文引用: 10]
Study on stability of segment lining structure for shield tunnel
[J].DOI:10.3969/j.issn.1001-7372.2015.06.011 [本文引用: 10]
类矩形盾构隧道结构极限承载力分析
[J].
Ultimate bearing capacity analysis of quasi-rectangular shield tunnel structure
[J].
近距离桥桩与地铁隧道相互影响研究及展望
[J].
Research and prospect of interaction between close bridge pile and metro tunnel
[J].
盾构穿越对既有地铁隧道影响研究现状与展望
[J].
Research status and prospect of shield tunneling on preexisting metro tunnels
[J].
复合地层盾构隧道管片施工病害特征及成因分析
[J].
Disease characteristics and causes analysis of segments of shield tunnels in composite stratum during construction
[J].
Condition assessment of shield tunnel using a new indicator: the tunnel serviceability index
[J].
Analysis of the influence of soft soil grouting on the metro tunnel based on field measurement
[J].DOI:10.1108/EC-08-2018-0350 [本文引用: 1]
北京地铁运营隧道病害状态分析
[J].DOI:10.15951/j.tmgcxb.2017.06.012 [本文引用: 1]
Analysis on defects of operational metro tunnels in beijing
[J].DOI:10.15951/j.tmgcxb.2017.06.012 [本文引用: 1]
Comprehensive health assessment of shield tunnel structure based on prototype experiment
[J].DOI:10.1007/s11771-018-3771-2 [本文引用: 1]