自振频率是梁式结构最重要的基本参数之一，对梁式结构的损伤监测和识别^[1-2]方面的研究具有重要的价值. 传统方法对桥梁结构的疲劳研究主要是从挠度、刚度、应变等静力特性展开^[3-11]；在承受疲劳荷载直至失效的过程中，梁式结构的性能退化势必会导致以自振频率为主的动力参数的演变^[12-15]. 将结构疲劳问题与自振频率演变联系起来，开展疲劳历程自振频率的解析计算和试验研究，有助于揭示预应力混凝土(PC)梁的疲劳损伤演变及失效机理.

目前，部分学者研究了结构性能退化与模态参数的关联性^[16-18]. Gheorghiu等^[16]研究RC梁在疲劳历程中的模态特性变化，发现扭转和横向频率的降低幅度小于纵向频率. 周宏宇等^[18]开展基于基频法的预应力混凝土箱梁多级变幅疲劳试验，结果表明，疲劳动刚度和静刚度的退化规律相同，疲劳荷载上限值是桥梁结构疲劳刚度退化的重要因素. 可见，梁式结构自振频率的疲劳演变研究没有得到充分的研究，需要进一步的探索. 在对梁式结构自振频率开展疲劳分析时，需要考虑3类梁理论对解析结果的影响，分别是Euler梁、Timoshenko梁及抛物线型布筋的预应力梁. Euler梁仅考虑横向平面弯曲振动的形式，在工程中得到了广泛应用；对于高跨比较大或采用了对切应力比较敏感的材料的梁，剪切变形和转动惯量对自振频率的影响不可忽略，这类梁的振动分析需要采用Timoshenko梁理论. 对于有黏结PC梁，预应力筋是完全灌筑的，整个预应力筋长度方向均有混凝土加强，预应力与混凝土中的压力相平衡，梁体的势能不会受到预应力筋中预应力的影响，因此预应力不会引起结构自振频率的改变^[19]. 由于无黏结PC梁，预应力筋在全梁段范围是自由的，仅在梁端部锚固端受到预加应力的作用，需要根据预应力筋的布筋方式和偏心与否进行具体分析^[20-21].

本文以微梁段隔离体受力分析为基础，理论推导抛物线型布筋的无黏结PC梁疲劳历程自振频率的计算公式. 基于公式对比和算例研究，分析Euler梁、Timoshenko梁和PC梁这3类梁理论频率演变、退化规律和频率修正系数的差别. 通过对重载铁路用预应力混凝土缩尺模型T梁进行疲劳试验和动力测试，分析疲劳历程实测自振频率的退化规律，对比分析3类梁理论频率计算公式的适用性.

给定预应力筋的布置形状呈二次抛物线型的PC简支梁，如图1(a)所示. 图中，L₀为计算长度，EI(x)和ρA(x) 分别为沿轴线方向的抗弯刚度和质量；f₀为预应力筋在梁端和跨中的高度差（失高），恒为正；e为预应力筋在梁端的偏心距，以向上为正，向下为负. 在考虑疲劳效应后，梁的尺寸、材料和受力特征如图1(b)所示，疲劳梁的横向振动位移u(x, t)为随x和t连续变化的函数. 本文公式中的下标N表示疲劳循环次数. 对于梁的自由振动，p_N(x,t) =0.

如图1(b)所示，取梁左端的形心位置处为坐标原点，二次抛物线型预应力筋的线型函数为

(1) $ {y_{\text{c}}}\left( x \right){\text{ = }}\frac{{4{f_0}x\left( {{L_0} - x} \right)}}{{L_0^2}} - e. $

在对梁进行张拉预应力后，梁体将产生反拱，用y(x)表示梁的反拱，则张拉完成后预应力筋的形状函数为y_c(x)-y(x). 在振动过程中，忽略梁体与预应力筋在轴向的耦合作用力，仅考虑梁体与预应力筋垂直于轴向的耦合作用力. 将预应力梁分解为预应力筋和梁体相互耦合的2个体系，如图1(b)所示.

在疲劳一定次数后，对于梁的静力平衡状态，取梁上任意位置x处的梁和预应力筋微段为隔离体，隔离体的受力情况如图2所示.

根据预应力筋的竖向力平衡条件、梁体竖向力平衡条件及梁体的力矩平衡条件，可得

$\tag{2-a} {F_{{\text{p}},N}}\frac{{{{\text{d}}^2}\left[ {{y_{\rm{c}}}\left( x \right) - y\left( x \right)} \right]}}{{{\text{d}}{x^2}}}{\text{d}}x+{g_N}\left( x \right){\text{d}}x = 0, $

$ \tag{2-b}{\text{d}}{Q_N}\left( x \right)+\bar m\left( {x,N} \right)g{\text{d}}x+{p_N}\left( x \right){\text{d}}x - {g_N}\left( x \right){\text{d}}x = 0, $

$\tag{2-c} {\text{d}}{M_N}\left( x \right)+{F_{{\text{p}},N}}{\text{d}}y\left( x \right) - {Q_N}\left( x \right){\text{d}}x = 0. $

结合梁的初等变形理论，可得PC梁的静力平衡方程：

(3) $ \begin{split} &\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}\left[ {EI\left( {x,N} \right)\frac{{{{\text{d}}^2}y\left( x \right)}}{{{\text{d}}{x^2}}}} \right]+{F_{{\text{p}},N}}\frac{{{{\text{d}}^2}{y_{\rm{c}}}\left( x \right)}}{{{\text{d}}{x^2}}}+\\ &{p_N}\left( x \right)+ \bar m\left( {x,N} \right)g = 0. \end{split} $

式中：F_p,N为预应力， $\bar m$为整个预应力梁的质量密度，g为重力加速度，g_N(x)为预应力筋对梁体的反作用力. 只分析等截面梁无外荷载p_N(x)的静力状态情况，抗弯刚度EI和质量密度ρA沿轴线方向均为常量，则将式(3)中的EI(x,N)和ρA(x,N)改写为EI(N)和ρA(N). 当引入疲劳作用时，给定以下假设：1）梁的质量不随疲劳循环过程而变化，只考虑抗弯刚度随着疲劳循环过程而退化；2）在疲劳循环过程中，梁的整体抗弯刚度沿长度方向为常量. 定义疲劳作用下的抗弯刚度退化比：

(4) $ \varphi (N) = {{EI(N)} \mathord{\left/ {\vphantom {{EI(N)} {E{I_0}}}} \right. } ({E{I_0}})}. $

式中：EI₀为梁的初始抗弯刚度. 在混凝土梁的疲劳过程中，随着损伤的产生与发展，抗弯刚度EI作为一个整体在疲劳过程中退化. 为了便于计算，在梁疲劳直至破坏的过程中，作为整体退化的抗弯刚度EI中的截面惯性矩I作为主要退化参数， $\bar E$作为不随疲劳次数变化的等效弹性模量，与通常所指的弹性模量E区别开. 可以得到下式：

(5) $ EI(N) = E{I_0}\varphi (N){\text{ = }}\bar E{I_0}\varphi (N). $

将式(5)代入式(3)，可得

(6) $ \bar E{I_0}\varphi \left( N \right)\frac{{{{\text{d}}^4}y\left( x \right)}}{{{\text{d}}{x^4}}}+{F_{{\text{p}},N}}\frac{{{{\text{d}}^2}{y_{\rm{c}}}\left( x \right)}}{{{\text{d}}{x^2}}}+\bar m\left( N \right)g = 0. $

当预应力梁发生振动时，设整体产生以向下为正方向的振动位移u(x,t)，则振动中梁的竖向位移为

(7) $ {u}_{\text{b}}\left(x,t\right)=\;y\left(x\right)-u\left(x,t\right). $

预应力筋的竖向位移为

(8) $ {u}_{\text{p}}\left(x,t\right) =\;{y}_{\text{c}}\left(x\right)-y\left(x\right)+u\left(x,t\right). $

此时，预应力产生水平分量增量ΔF_p,N，梁与预应力筋的相互作用力的增值为g'(x,t). 对微段隔离体进行振动受力分析，如图3所示. 图中，梁和预应力筋的惯性力分别为df_{Ib, N}(x,t)=f_{Ib, N} (x,t)dx和df_{Ip, N}(x, t)=f_Ip,N(x, t)dx，大小分别为

$\tag{9-a}{f_{{\text{Ib, }}N}}\left( {x,t} \right){\text{ = }}{m_{\text{b}}}\left( {x,N} \right)\frac{{{\partial ^2}{u_{\text{b}}}\left( {x,t} \right)}}{{\partial {t^2}}}, $

$ \tag{9-b}{f_{{\text{Ip, }}N}}\left( {x,t} \right){\text{ = }}{m_{\text{p}}}\left( {x,N} \right)\frac{{{\partial ^2}{u_{\text{p}}}\left( {x,t} \right)}}{{\partial {t^2}}}. $

式中：m_p和m_b分别为预应力筋和梁体的质量， ${m_{\rm{p}}}+{m_{\rm{b}}} = \bar m$. 根据预应力筋的竖向力平衡条件、梁体竖向力平衡条件及梁体的力矩平衡条件，联立可得抛物线型布筋预应力梁的自由振动方程表达式：

(10) $ \begin{split} &\frac{{{\partial ^2}}}{{\partial {x^2}}}\left[ {EI\left( {x,N} \right)\frac{{{\partial ^2}u\left( {x,t} \right)}}{{\partial {x^2}}}} \right]+\bar m\left( {x,N} \right)\frac{{{\partial ^2}u\left( {x,t} \right)}}{{\partial {t^2}}} - \\ &\Delta {F_{{\text{p}},N}}\frac{{{{\text{d}}^2}{y_{\text{c}}}\left( x \right)}}{{{\text{d}}{x^2}}} = 0. \end{split} $

根据前文假设，可以得到引入疲劳作用的抛物线型布筋PC梁的自由振动控制方程：

(11) $ \bar E{I_0}\varphi \left( N \right)\frac{{{\partial ^4}u\left( {x,t} \right)}}{{\partial {x^4}}}+\bar m\frac{{{\partial ^2}u\left( {x,t} \right)}}{{\partial {t^2}}} - \Delta {F_{{\text{p}},N}}\frac{{{{\text{d}}^2}{y_{\text{c}}}\left( x \right)}}{{{\text{d}}{x^2}}} = 0. $

可见，式（11）的前2项为梁的弯曲固有振动项，最后1项为预应力的贡献.

在对式(20)进行求解前，分析自由振动过程中的预应力变化量ΔF_p,N，预应力的变化量可以表示为预应力筋长度的变化，通过几何推导和运算可得

(12) $ \Delta {F_{{\text{p}},N}}{\text{ = }}\frac{{{E_{\text{p}}}{A_{\text{p}}}\Delta {L_{{\text{p}},N}}}}{{{L_{{\text{p}},N}}}}{\text{ = }}\frac{{{E_{\text{p}}}{A_{\text{p}}}}}{{{F_{{\text{p}},N}}{L_{{\text{p}},N}}}}\int_0^{{L_0}} {{g_N}\left( x \right)u\left( {x,t} \right)} {\text{d}}x. $

式(12)具有能量守恒的物理意义^[22]，静力状态下疲劳梁与预应力筋的相互作用力g_N(x)可以由式(3)、(2-a)求得，进而可得ΔF_p,N.

对式(1)求二阶导数，则有

(13) $ \frac{{{{\text{d}}^2}{y_{\text{c}}}}}{{{\text{d}}{x^2}}} = - \frac{{8{f_0}}}{{L_0^2}}. $

结合式(6)，分析等截面梁无外荷载p_N(x)的情况，则有

(14) $ \bar E{I_0}\varphi \left( N \right)\frac{{{{\text{d}}^4}y\left( x \right)}}{{{\text{d}}{x^4}}}{\text{ = }} - \bar mg + \frac{{8{F_{{\text{p}},N}}{f_0}}}{{L_0^2}}. $

对式（14）进行积分，考虑如下所示的边界条件：

$ \left. {\begin{array}{*{20}{c}} \begin{gathered} y\left( 0 \right) = 0, \\ y\left( {{L_0}} \right) = 0, \\ \end{gathered} \\ {\bar E{I_0}\varphi \left( N \right)\dfrac{{{{\text{d}}^2}y\left( x \right)}}{{{\text{d}}{x^2}}}{\text{ = }}{F_{{\text{p}},N}}e.} \end{array}} \right\} $

求解可得y(x)的表达式，代入式(2-a)，可得

$ {g_N}\left( x \right) = \frac{{8{F_{{\text{p}},N}}{f_0}}}{{L_0^2}}+\frac{{{F_{{\text{p}},N}}^2e}}{{\bar E{I_0}\varphi \left( N \right)}}+ $

(15) $ \qquad \quad \frac{{{F_{{\text{p}},N}}}}{{2\bar E{I_0}\varphi \left( N \right)}}\left( { - \bar mg+\frac{{8{F_{{\text{p}},N}}{f_0}}}{{L_0^2}}} \right)\left( {{x^2} - {L_0}x} \right).$

式（15）说明预应力筋与梁体之间的相互作用力是不均匀的，呈二次抛物线分布.

对于简支梁，采用分离变量法，假设梁横向自由振动位移按如下形式随时间简谐变化：

(16) $ u( {x,t} ) = {A_j}\sin \frac{{j{\text{π}} x}}{{{L_0}}}\sin\; (\omega t);\; j = 1,2,\cdots,\infty . $

将式(15)、(16)代入式(12)，可得

(17) $ \Delta {F_{{\text{p}},N}}{\text{ = }}\beta {A_j}\sin\; (\omega t). $

式中：

(18) $ \begin{split} &\;\beta {\text{ = }}\frac{{{E_{\text{p}}}{A_{\text{p}}}}}{{{L_{{\text{p}},N}}}}\left[ {1 - {{\left( { - 1} \right)}^j}} \right] \times\\ &\left[ \frac{{8{f_0}}}{{j{\text{π}} {L_0}}}+\frac{{{F_{{\text{p}},N}}e{L_0}}}{{j{\text{π}} \bar E{I_0}\varphi \left( N \right)}} - \frac{{L_0^3}}{{{j^3}{{\text{π}} ^3}\bar E{I_0}\varphi \left( N \right)}}\left( { - \bar mg+\frac{{8{F_{{\text{p}},N}}{f_0}}}{{L_0^2}}} \right) \right] . \end{split}$

下面采用Galerkin法求解PC梁的自振频率. 结合引入疲劳作用的PC梁自由振动控制方程式(11)，可以列出Galerkin方程：

(19) $ \int_0^{{L_0}} {\left[ {\bar E{I_0}\varphi \left( N \right)\frac{{{\partial ^4}u}}{{\partial {x^4}}} - \bar m{\omega ^2}u - \Delta {F_{{\text{p}},N}}\frac{{{{\text{d}}^2}{y_{\text{c}}}}}{{{\text{d}}{x^2}}}} \right]{\text{δ}} u{\text{d}}x} = 0. $

将式(13)、(17)、(18)代入式(19)，推导得到

(20) $ {\sin ^2}\;(\omega t){\text{δ}} {A_j} \times \int_0^{{L_0}} {\left\{ \left[ {\bar E{I_0}\varphi \left( N \right){{\left( {\frac{{j{\text{π}} }}{{{L_0}}}} \right)}^4} - \bar m{\omega ^2}} \right]{\sin ^2}\frac{{j{\text{π}} x}}{{{L_0}}} +\frac{{8\beta {f_0}}}{{L_0^2}}\sin \frac{{j{\text{π}} x}}{{{L_0}}} \right\}{\text{d}}x} = 0. $

由于 ${\sin ^2}\;(\omega t){\text{δ}} {A_j} \ne 0$，对式(20)积分，结合式(18)后整理，可得如下所示的引入疲劳作用的抛物线型布筋PC梁自振频率计算公式：

(21) $ {w_{{\text{P}}j}}{\text{ = }}\frac{1}{2}{j^2}{\text{π}} \sqrt {\frac{{\bar E{I_0}\varphi \left( N \right)}}{{\bar mL_0^4}}} \sqrt {1+\frac{{16{f_0}{L_0}{E_{\text{p}}}{A_{\text{p}}}{{\left[ {1 - {{\left( { - 1} \right)}^j}} \right]}^2}}}{{{j^6}{{\text{π}} ^6}\bar E{I_0}\varphi \left( N \right){L_{{\text{p}},N}}}}\left[ {8{f_0}+\frac{{\bar mgL_0^4}}{{{j^2}{{\text{π}} ^2}\bar E{I_0}\varphi \left( N \right)}}+\frac{{{F_{{\text{p}},N}}L_0^2}}{{\bar E{I_0}\varphi \left( N \right)}}\left( {e - \frac{{8{f_0}}}{{{j^2}{{\text{π}} ^2}}}} \right)} \right]} ; \; j=1,2,\cdots,\infty. $

引入疲劳作用的Euler梁和Timoshenko梁理论频率的计算公式^[13]分别如下：

(22) $ {w_{{\text{E}}j}}{\text{ = }}\frac{1}{2}{j^2}{\text{π}} \sqrt {\frac{{\bar E{I_0}\varphi \left( N \right)}}{{\rho AL_0^4}}} ; \; j=1,2,\cdots,\infty. $

(23) $ \left. {\begin{split} &{w_{{\text{T}}j}}=\\ &\frac{1}{2}{j^2}{\text{π}} \sqrt {\frac{{\bar E{I_0}\varphi \left( N \right)}}{{\rho AL_0^4}}} \left[ {1 - \frac{1}{2}{{\left( {\frac{{j{\text{π}} }}{{{L_0}}}} \right)}^2}\left( {\frac{{{I_0}\varphi \left( N \right)}}{A}} \right)\left( {1+\frac{{\bar E}}{{\kappa '\bar G}}} \right)} \right];\; \\ &j=1,2,\cdots,\infty. \end{split} } \right\}$

式中： $\kappa' $为截面的有效剪切系数. 对比式(21)~(23)，可以得到

(24) $ {w_{{\text{T}}j}}{\text{ = }}{\eta _{\text{T}}} {w_{{\text{E}}j}}, $

(25) $ \begin{split} \\ {w_{{\text{P}}j}}{\text{ = }}{\eta _{\text{P}}} {w_{{\text{E}}j}}, \end{split} $

(26) $ {\eta _{\text{T}}}{\text{ = }}1 - \frac{1}{2}{\left( {\frac{{j{\text{π}} }}{{{L_0}}}} \right)^2}\left( {\frac{{{I_0}\varphi \left( N \right)}}{A}} \right)\left( {1+\frac{{\bar E}}{{\kappa '\bar G}}} \right), $

(27) $ \begin{split} &{\eta _{\text{P}}}{\text{ = }} \left\{1+\frac{{16{f_0}{L_0}{E_{\text{p}}}{A_{\text{p}}}{{\left[ {1 - {{\left( { - 1} \right)}^j}} \right]}^2}}}{{{j^6}{{\text{π}} ^6}\bar E{I_0}\varphi \left( N \right){L_{{\text{p}},N}}}}\times \right.\\ &\left.\left[ {8{f_0}+\frac{{\bar mgL_0^4}}{{{j^2}{{\text{π}} ^2}\bar E{I_0}\varphi \left( N \right)}}+\frac{{{F_{{\text{p}},N}}L_0^2}}{{\bar E{I_0}\varphi \left( N \right)}}\left( {e - \frac{{8{f_0}}}{{{j^2}{{\text{π}} ^2}}}} \right)} \right] \right\}^{1/2} . \end{split} $

式中：η_T和η_P分别为Timoshenko梁和PC梁相对于Euler梁的频率修正系数，不仅与梁截面尺寸和材料参数有关，而且随着疲劳次数的变化而改变；η_T为剪切变形和转动惯量对梁自振频率的修正系数；η_P为抛物线型布筋的预应力对自振频率的修正系数.

从式(22)可以看出，对于Euler梁，影响w_Ej的参数主要是φ(N)，说明疲劳历程自振频率随着抗弯刚度的变化而变化. 对于Timoshenko梁疲劳历程自振频率，除了Euler梁w_Ej的基础贡献外，剪转效应的影响主要体现在η_T，且η_T随着 $\kappa '$的减小而呈现出单调递减的趋势，说明随着截面有效剪切系数的减小，Timoshenko梁理论对Euler梁的理论频率修正程度越大，剪转效应对梁疲劳过程自振频率的影响越大.

对于抛物线型偏心布筋的PC梁，预应力的影响主要体现在η_P. 当模态阶次为偶数时，η_P = 0，说明抛物线型布筋的预应力不影响整个疲劳历程中梁的偶数阶频率. 对于奇数阶频率，η_P与φ(N)成反比.

考虑跨度L₀ = 4 000 mm的矩形混凝土梁，矩形截面宽为100 mm，高为200 mm. 混凝土材料弹性模量E_c = 32 500 N/mm²，容重为25 kN/m³，考虑矩形截面面积后，梁的质量线密度ρ = 0.5 kN/m.

由于w_Ej的影响参数为φ(N)，等幅疲劳作用下梁疲劳抗弯刚度呈现出“3阶段”退化规律，假设φ(N)的退化规律遵循下述模式^[4]：

(28) $ \varphi {\text{ = }}1 - 0.160 \times \left[ {1 - \frac{{1 - {{\left( {{N \mathord{\left/ {\vphantom {N {{N_{\text{f}}}}}} \right. } {{N_{\text{f}}}}}} \right)}^{0.341}}}}{{{{\left( {1 - {N \mathord{\left/ {\vphantom {N {{N_{\text{f}}}}}} \right. } {{N_{\text{f}}}}}} \right)}^{0.820}}}}} \right]. $

式中：N_f为梁的疲劳寿命，N/N_f为梁的循环寿命比.

对于Timoshenko梁理论，给定混凝土泊松比ν = 0.2，切变模量 $\bar G$的疲劳演变与 $ \bar E $一致，关系为 $ \bar E = 2\bar G\left( {1+\nu } \right) $. $\kappa '$可由下式求得^[23]：

(29) $ \kappa ' = \frac{A}{{{I^2}}}\int_A {\frac{{{S^2}}}{{{b^2}}}} {\text{d}}A. $

式中：S为面积矩. 对于矩形截面， $\kappa '$ = 6/5.

对于PC梁理论，给定预应力筋的材料参数：预应力筋采用1束7 $\phi $5 mm钢绞线，截面面积A_p = 139 mm²；弹性模量E_p = 1.95×10⁵ MPa. 采用抛物线型预应力筋，预应力参数设置为e = 0 mm，f₀ = 70 mm，F_p,N = 100 kN.

计算得到3类梁的前3阶自振频率疲劳演变，如图4所示. 图中，w₁、w₂、w₃分别为1、2、3阶频率. 对比Euler梁和Timoshenko梁的理论频率可知，由于考虑了剪切变形和转动惯量的影响，疲劳过程自振频率总是比Euler梁小，随着模态阶次的增大，两者之间的差别增大. 在实际工程中，应考虑剪切变形和转动惯量对高阶频率的降低效应.

从式(21)可见，抛物线型布筋的预应力不影响整个疲劳历程中梁的偶数阶频率，因此图4未给出预应力梁的第2阶频率演变曲线. 对比PC梁和Euler梁的第1、3阶自振频率疲劳演变可知，由于预应力的作用，梁疲劳过程的频率均比Euler理论计算结果大；随着阶次的增大，频率增大的幅度逐渐降低. 对于第3阶频率，增大的幅度仅达到10⁻² Hz的数量级，几乎可以忽略不计；对于更高阶频率，增大幅度更小. 在实际工程中，基频被广泛利用，因此在具有偏心布筋的预应力梁结构中，应考虑预应力对基频的增强效应.

定义疲劳作用下频率的退化比：

(30) $ \gamma (N) = w(N)/{w_0}. $

式中：w₀为初始自振频率，w(N)为疲劳循环N次后的自振频率. 如图5所示为3类梁前3阶频率退化曲线的对比. 可以看出，Euler梁理论频率的退化速率总大于Timoshenko梁和PC梁奇数阶频率的退化速率. 对于Timoshenko梁，第1阶频率的退化幅度最大，第2阶频率次之，第3阶频率的退化幅度最小. 随着模态阶次的增大，Timoshenko梁频率退化比逐渐增大，退化幅度逐渐减小. 对于预应力梁，由于预应力不影响偶数阶频率，图5(b)中PC梁的第2阶频率退化曲线与Euler梁的频率退化曲线重合. PC梁的第1阶频率的退化幅度最小，第3阶频率次之，说明随着奇数阶频率阶次的增大，退化幅度逐渐增大，退化曲线逐渐接近Euler梁理论退化曲线.

Timoshenko梁的频率理论计算结果比Euler梁的理论计算结果小，本质上是因为η_T的存在. 根据式(26)可得η_T，呈现出如图6所示的三维变化关系. 可以看出，η_T随着模态阶次的增大而减小，表明剪切变形和转动惯量对梁结构高阶频率的影响更大. 随着疲劳次数的增大，梁各阶η_T逐渐增大，说明在经过一定的疲劳次数后，剪切变形和转动惯量对梁自振频率的影响有所减小. η_T增大的趋势没有影响Timoshenko梁疲劳历程自振频率的整体退化，说明η_T对自振频率的增大贡献，没有φ(N)对w_Ej的退化贡献大. 该规律与作者前期研究^[4]所得到的结论一致.

PC梁的奇数阶频率计算结果较Euler梁的理论计算结果大，本质上是因为η_P的存在. 根据式(27)可得疲劳过程中η_P的发展曲线，如图7所示.

在疲劳过程中，对于奇数阶频率，随着疲劳次数的增加，η_P逐渐增大，说明预应力作用加强了对梁自振频率的增大效应. 这种增强作用不会对梁整体的性能退化带来本质的改变. 这是因为w_Pj是以w_Ej为基础，乘以η_P而得到的. 虽然η_P随着疲劳次数的增长表现出增大趋势，但由于w_Ej的降低程度更大，导致w_Pj整体上表现出递减的走势，如图5所示.

对于奇数阶频率，虽然η_P都呈现出增大的趋势，但增大的程度较小，其中第1阶频率增大的程度达到10⁻³的数量级，第3阶为10⁻⁶的数量级，更高奇数阶频率增大的程度甚至更小. 随着奇数阶模态阶次的增大，η_P的增大程度逐渐减小，这解释了图5(b)所示的“随着奇数阶频率阶次的增大，频率退化比逐渐减小，退化曲线逐渐接近Euler梁理论退化曲线”的现象.

将重载铁路用预应力混凝土T梁作为实验对象，制作了5根5.5 m长的缩尺模型T梁^[24-25]，模型梁的尺寸、配筋布置如图8所示. 实体梁模型如图9(a)所示.

选取的模型梁的试验参数设置如表1所示. 表中，σ_con为张拉控制应力，N_pt为考虑预应力损失后的理论有效预应力，P_min和P_max分别为疲劳荷载的下限和上限，ΔP为疲劳荷载幅值. 根据不同的预应力度，将所有梁分为2组. 每组选取1根梁进行极限承载力试验，确定疲劳试验所需的静力极限荷载P_u；其余的用于等幅疲劳试验.

在常规的疲劳试验过程中加入模态测试，以获取疲劳历程中模型梁的自振频率. 模态测试采用敲击法. 敲击法利用敲击锤对每次停机静载后的试验梁进行敲击，通过单点激励，运用多点采集的方法采集加速度信号. 每次试验进行3次模态测试，每次采样时间约为200 s. 利用东华DH5922动态信号采集分析仪及配套传感器，开展加速度信号采集. 在梁上等长位置上，布置14个压电式加速度传感器. 信号采集频率为1 kHz，对采集信号进行快速傅里叶变换（FFT），FFT块长为8 192. 以梁PCB-MPD-CFL-1疲劳试验前的动测试验为例，对采集的加速度信号（见图9(b)）进行FFT变换，得到频响函数. 开展模态识别，得到前3阶频率分别为27.344、75.543和141.933 Hz.

混凝土弹性模量根据混凝土试块材料试验测得（见表1），混凝土材料试验与模型梁疲劳试验同时开展. 切变模量G近似通过E = 2G(1+ν)计算得到，其中ν = 0.2；试验模型梁质量密度近似取ρ = 2 500 kg/m³；疲劳历程中截面惯性矩的计算，根据挠度推算得到的梁刚度与E相除近似得到. 其他模型尺寸及预应力参数的选择是在设计参数的基础上，采用实际施工成型的尺寸. $\kappa '$可以由式(29)计算得到. 对于T字型截面， $\kappa '$可以按下式取值：

(31) $ \kappa ' = A/A_{1}. $

式中：A为梁截面面积，A₁为梁腹板面积. 本例中， $\kappa '$约为3.804.

实测的刚度退化比如图10所示. 计算得到的模型梁理论频率如表2所示（以梁PCB-MPD-CFL-1为例）. 表中，w_e为实测频率，括号中的数值为理论频率与实测频率的偏差.

Euler梁和预应力梁理论频率的计算结果较接近，但与实测结果的偏差较大. 仅第1阶频率在合理范围内，除了疲劳破坏后的第1阶频率偏差达到15%，在疲劳过程中基本不超过10%. 由于考虑了剪转效应对理论频率的修正，基于Timoshenko梁理论的第2、3阶理论频率较Euler梁和预应力梁有了较大的降低. 第1、3阶频率的偏差普遍约为15%，第2阶频率的偏差稍大，基本上小于20%，个别点偏差达到22%.

虽然Timoshenko梁的频率理论计算结果更接近试验结果，但第2阶频率存在一定的偏差，主要原因如下. 1）在实验模态分析方面，通过将模型梁放置在两端铰支座上的方式实现简支边界条件，自由度未达到简支梁应有的自由度约束，可能是导致结果偏差的原因之一. 混凝土梁施工水平导致梁体不密实、测试环境噪声的干扰、测试及传感仪器都是产生误差的原因. 2）在计算模型方面，剪转效应和预应力效应的耦合作用对计算模型的修正未能予以考虑，设置了疲劳历程轴向等刚度的计算模式，未考虑疲劳过程中由于裂缝的产生和分布导致的局部刚度不均匀的因素，因此会对理论计算结果产生影响. 3）在理论参数方面，各个试验梁的尺寸参数、材料力学参数具有一定的离散性，会影响计算结果的准确性. 可以看出，虽然所研究的试验梁对象布置了无黏结预应力筋，但预应力对自振频率的影响较小，基于Timoshenko梁理论的算法更加接近试验结果.

疲劳试验梁实测频率γ_e的疲劳演变曲线如图11所示. 可以看出，实测自振频率随着疲劳进程而降低，自振频率的演变基本呈现出以下3阶段退化的规律：1）在疲劳初期，随着裂缝的产生，梁刚度急剧下降，各阶频率呈现急剧下降的现象；2）在疲劳中期，呈现出较稳定的衰减阶段；3）在疲劳末期，梁频率有大幅度的下降. 在疲劳作用下，第1阶频率的频率退化幅度最大，第2阶频率次之，第3阶频率的频率退化幅度最小. 该规律与基于Timoshenko梁理论的计算结果较吻合，Timoshenko梁理论计算结果表现出比实测结果更小的离散性（见图5）. 由于影响Euler梁疲劳过程自振频率的因素只有φ(N)，Euler梁的前3阶理论频率退化比相等，不能支撑试验结果. Timoshenko梁理论考虑了剪切变形与转动惯量的影响，对各阶频率的修正，尤其是高阶频率的修正，使得疲劳历程理论频率更接近实测值，由此可见Timoshenko梁理论在疲劳历程频率计算方面具有优势.

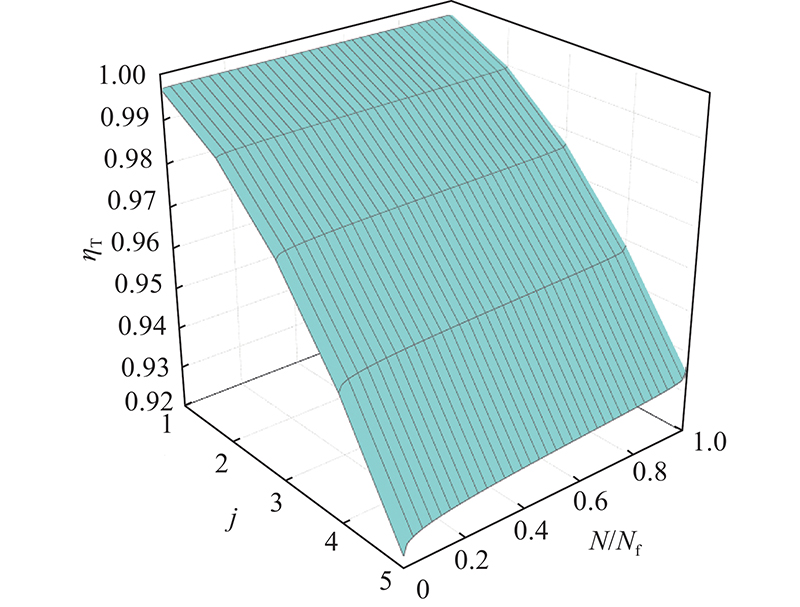
由于在外部激励的模态测试中，通常识别出的第1阶频率具有一定的准确性. 通过比较不同疲劳荷载幅值和不同预应力度下的第1阶频率退化规律，得到如图12所示的曲线.

从图12(a)可知，对于预应力度相等的试验梁，荷载幅值较大的梁的频率退化速率比荷载幅值较小的梁的退化速率大. 从图12(b)可见，对于疲劳荷载幅值基本相等的试验梁，预应力度较大的梁的频率退化速率比预应力度较小的梁的退化速率小，可见预应力的存在对梁疲劳损伤过程有一定的抑制作用. 对于不同试验梁的第1阶频率，从疲劳初期过渡到疲劳中期的频率阈值各不相同，该频率退化比为0.91~0.95. 当频率退化比达到基本确定的退化阈值时，试验梁进入疲劳末期，梁频率有大幅度的下降. 该阈值大约为0.88. 该规律与刚度退化规律相似.

计算得到的η_T如图11所示. 可知，η_T的发展规律与算例得到的结果基本一致，此处不再详述. 由于高阶频率修正系数的降低程度更大，说明剪切变形和转动惯量对高阶频率的影响较低阶更大，这是Timoshenko梁理论频率（尤其是对于高阶频率）更接近实测频率的原因.

在现有的静力学变形计算方面，对于高跨比不大的梁，通常采用Euler梁理论进行挠度计算或刚度验算，已证明Euler梁理论的计算精度满足工程需要. 在动力学方面，基频作为最重要的模态参数而受到广泛重视，各国的桥梁规范中基频的计算采用Euler梁理论. 从本文的试验分析可知，对于基频，采用Euler梁、Timoshenko梁和偏心布筋预应力梁这3种理论得到的计算结果偏差都较小，因此采用Euler梁理论可以满足计算精度，计算过程简便，参数少. 随着模态测试在结构监测与损伤识别领域中的广泛使用，对结构的第2、3阶甚至更高阶模态的需求增大，因此需要准确地识别高阶频率. 在这种情况下，建议采用提出的基于Timoshenko梁理论的高阶频率修正计算方法.

（1）本文推导了偏心布筋的后张拉无黏结预应力梁的疲劳历程自振频率计算公式. 结果显示，抛物线型布筋的预应力不影响整个疲劳历程中梁的偶数阶频率.

（2）Euler梁的理论频率退化速率总是大于Timoshenko梁和PC梁奇数阶频率的退化速率. 随着模态阶次的增大，Timoshenko梁频率的退化幅度逐渐减小. 随着奇数阶频率阶次的增大，预应力梁频率的退化幅度逐渐增大，逐渐接近Euler梁的理论退化曲线.

（3）对于预应力度相等的梁，随着疲劳荷载幅值的增大，梁的第1阶频率退化速率增大. 对于疲劳荷载幅值基本相等的梁，随着预应力度的增大，梁的第1阶频率退化速率减小.

（4）在实际工程中，在具有偏心布筋的无黏结预应力梁结构中，应注意预应力对基频的增强效应. Timoshenko梁理论体现出了对疲劳历程高阶频率修正计算方面的优势.

考虑剪转效应影响的Timoshenko梁理论与预应力相耦合的疲劳历程自振频率数值解析，是今后的研究重点.