An AOIMLS enhanced LIBEM and for solving 3D thermo-elastic problems and non-homogeneous heat conduction problems with heat generation
1
2021
... 准脆性材料(如混凝土、岩石)的热传导问题在工程应用中常见且重要 [1]. 在实际工程中,由于温差普遍存在,热传导几乎时刻在发生[2]. 传热引起温度的变化可能会改变材料的性能与力学行为[3],甚至导致材料失效破坏. 在混凝土结构中,温度由于与早龄期的水化过程息息相关而影响混凝土性能演化[4]当混凝土结构遇到温度在短时间变化剧烈[5] 的情况时,过大的温度梯度会导致结构热开裂. 在地热能源开发中,将冷水循环注入储热层引发岩石裂缝[6],增加了储层的渗透性,对生产有着积极影响. 在核废料处理中,由于衰变释放的热量导致岩石产生裂缝可能会引起放射性物质泄漏[7]. ...
Analysis of three-dimensional anisotropic heat conduction problems on thin domains using an advanced boundary element method
1
2018
... 准脆性材料(如混凝土、岩石)的热传导问题在工程应用中常见且重要 [1]. 在实际工程中,由于温差普遍存在,热传导几乎时刻在发生[2]. 传热引起温度的变化可能会改变材料的性能与力学行为[3],甚至导致材料失效破坏. 在混凝土结构中,温度由于与早龄期的水化过程息息相关而影响混凝土性能演化[4]当混凝土结构遇到温度在短时间变化剧烈[5] 的情况时,过大的温度梯度会导致结构热开裂. 在地热能源开发中,将冷水循环注入储热层引发岩石裂缝[6],增加了储层的渗透性,对生产有着积极影响. 在核废料处理中,由于衰变释放的热量导致岩石产生裂缝可能会引起放射性物质泄漏[7]. ...
Effect of high temperature on physical and mechanical properties of granite
1
2018
... 准脆性材料(如混凝土、岩石)的热传导问题在工程应用中常见且重要 [1]. 在实际工程中,由于温差普遍存在,热传导几乎时刻在发生[2]. 传热引起温度的变化可能会改变材料的性能与力学行为[3],甚至导致材料失效破坏. 在混凝土结构中,温度由于与早龄期的水化过程息息相关而影响混凝土性能演化[4]当混凝土结构遇到温度在短时间变化剧烈[5] 的情况时,过大的温度梯度会导致结构热开裂. 在地热能源开发中,将冷水循环注入储热层引发岩石裂缝[6],增加了储层的渗透性,对生产有着积极影响. 在核废料处理中,由于衰变释放的热量导致岩石产生裂缝可能会引起放射性物质泄漏[7]. ...
A meso-scale analysis of the hygro-thermo-chemical characteristics of early-age concrete
1
2019
... 准脆性材料(如混凝土、岩石)的热传导问题在工程应用中常见且重要 [1]. 在实际工程中,由于温差普遍存在,热传导几乎时刻在发生[2]. 传热引起温度的变化可能会改变材料的性能与力学行为[3],甚至导致材料失效破坏. 在混凝土结构中,温度由于与早龄期的水化过程息息相关而影响混凝土性能演化[4]当混凝土结构遇到温度在短时间变化剧烈[5] 的情况时,过大的温度梯度会导致结构热开裂. 在地热能源开发中,将冷水循环注入储热层引发岩石裂缝[6],增加了储层的渗透性,对生产有着积极影响. 在核废料处理中,由于衰变释放的热量导致岩石产生裂缝可能会引起放射性物质泄漏[7]. ...
The "Chunnel" fire. I: chemoplastic softening in rapidly heated concrete
1
1999
... 准脆性材料(如混凝土、岩石)的热传导问题在工程应用中常见且重要 [1]. 在实际工程中,由于温差普遍存在,热传导几乎时刻在发生[2]. 传热引起温度的变化可能会改变材料的性能与力学行为[3],甚至导致材料失效破坏. 在混凝土结构中,温度由于与早龄期的水化过程息息相关而影响混凝土性能演化[4]当混凝土结构遇到温度在短时间变化剧烈[5] 的情况时,过大的温度梯度会导致结构热开裂. 在地热能源开发中,将冷水循环注入储热层引发岩石裂缝[6],增加了储层的渗透性,对生产有着积极影响. 在核废料处理中,由于衰变释放的热量导致岩石产生裂缝可能会引起放射性物质泄漏[7]. ...
1
... 准脆性材料(如混凝土、岩石)的热传导问题在工程应用中常见且重要 [1]. 在实际工程中,由于温差普遍存在,热传导几乎时刻在发生[2]. 传热引起温度的变化可能会改变材料的性能与力学行为[3],甚至导致材料失效破坏. 在混凝土结构中,温度由于与早龄期的水化过程息息相关而影响混凝土性能演化[4]当混凝土结构遇到温度在短时间变化剧烈[5] 的情况时,过大的温度梯度会导致结构热开裂. 在地热能源开发中,将冷水循环注入储热层引发岩石裂缝[6],增加了储层的渗透性,对生产有着积极影响. 在核废料处理中,由于衰变释放的热量导致岩石产生裂缝可能会引起放射性物质泄漏[7]. ...
Geological storage of high level nuclear waste
1
2011
... 准脆性材料(如混凝土、岩石)的热传导问题在工程应用中常见且重要 [1]. 在实际工程中,由于温差普遍存在,热传导几乎时刻在发生[2]. 传热引起温度的变化可能会改变材料的性能与力学行为[3],甚至导致材料失效破坏. 在混凝土结构中,温度由于与早龄期的水化过程息息相关而影响混凝土性能演化[4]当混凝土结构遇到温度在短时间变化剧烈[5] 的情况时,过大的温度梯度会导致结构热开裂. 在地热能源开发中,将冷水循环注入储热层引发岩石裂缝[6],增加了储层的渗透性,对生产有着积极影响. 在核废料处理中,由于衰变释放的热量导致岩石产生裂缝可能会引起放射性物质泄漏[7]. ...
Effect of heat treatment on dynamic properties of selected rock types taken from the Salt Range in Pakistan
1
2018
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
Thermal conductivity of thermally damaged Beishan granite under uniaxial compression
1
2019
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
An experimental study on tensile characteristics of granite rocks exposed to different high-temperature treatments
1
2019
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
Simulation of the thermal stress in mass concrete using a thermal stress measuring device
1
2009
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
Ceramic nuclear fuel fracture modeling with the extended finite element method
1
2020
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
Elastic crack growth in finite elements with minimal remeshing
1
1999
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
The particle finite element method (PFEM) in thermo-mechanical problems
1
2016
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
Multiphysics phase-field modeling of quasi-static cracking in urania ceramic nuclear fuel
1
2020
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
Peridynamic simulation of thermal failure behaviors in rocks subjected to heating from boreholes
1
2019
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
Numerical investigation on the cooling-related mechanical properties of heated Australian Strathbogie granite using discrete element method
1
2020
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
A coupled thermo-mechanical discontinuum model for simulating rock cracking induced by temperature stresses
1
2015
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
The novel boundary integral equation with adaptive orthogonal IMLS based line integration method for cracked domains under thermal stress
1
2020
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
A new 2D continuous-discontinuous heat conduction model for modeling heat transfer and thermal cracking in quasi-brittle materials
1
2021
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
模拟岩体失效全过程的连续?非连续变形体离散元方法及应用
0
2011
模拟岩体失效全过程的连续?非连续变形体离散元方法及应用
0
2011
岩石破坏全过程的连续?离散耦合分析方法
1
2011
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
岩石破坏全过程的连续?离散耦合分析方法
1
2011
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
A novel thermo-mechanical coupling approach for thermal fracturing of rocks in the three-dimensional FDEM
1
2020
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
Analysis of the failure process by using the lattice discrete element method in the Abaqus environment
1
2020
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
Solution of problems of elasticity by the framework method
1
1941
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
Continuum modeling of three-dimensional truss-like space structures
3
1978
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
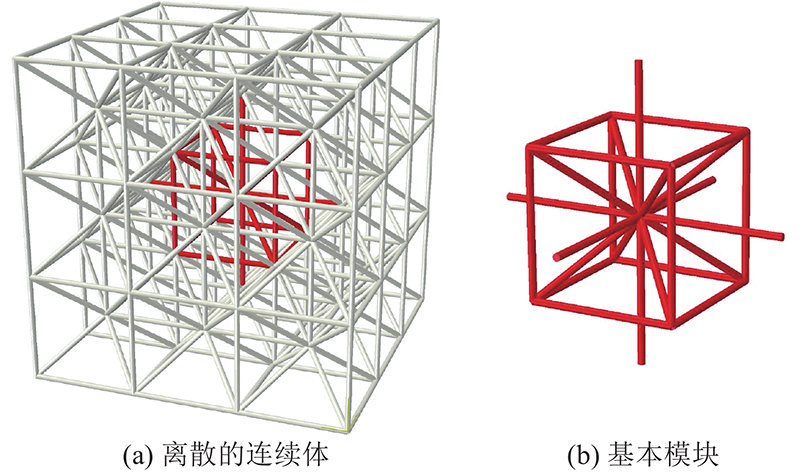
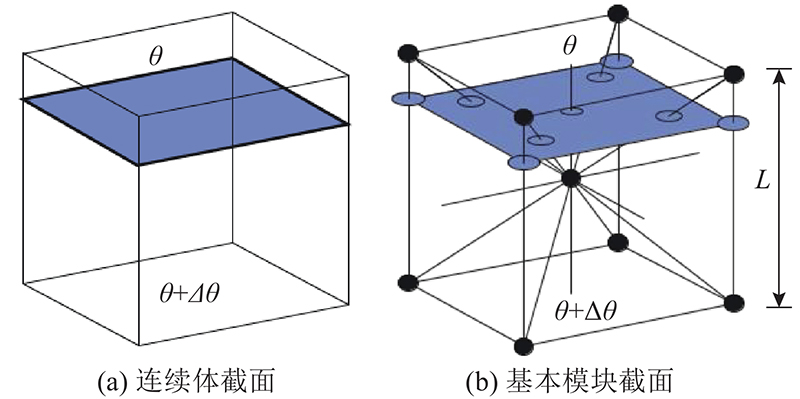
... LDEM的基本原理是将连续体离散为质量集中于两端的、在空间周期性排列的杆单元,本研究采用Nayfeh等[26]提出的LDEM模式. 如图1所示,离散化采用的基本立方体模块由20根杆单元(分为2类:纵向杆、对角杆)与9个节点组成,相邻2个基本模块的体心节点由1根纵向杆单元连接. 杆单元仅在轴向承受荷载,每个节点有3个自由度,表示为位移矢量的3个分量. 假定立方体模块对应的连续体边长为L,纵向杆单元长度Ll=L,对角杆单元长度 $ {L_{\text{d}}} = \sqrt 3 L/2 $. 基本模块整体质量mall与连续体质量相等,即mall=ρL3,其中ρ为连续体密度由于体心节点在模块内部,角节点为8个模块共有,得到体心节点质量mcen=ρL3/2,角节点质量mcor=ρL3/16. 杆单元的横截面积由整体刚度等效计算,在各项同性材料中,纵向杆单元与对角杆单元的等效轴向刚度[26]分别为 ...
... [26]分别为 ...
Introduction of imperfections in the cubic mesh of the truss-like discrete element method
2
2014
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
... 原型LDEM采用牛顿第二定律对每个节点进行求解[27],在此基础上引入杆单元中由于温度产生的内力,在节点上有 ...
Analysis of reinforced concrete plates subjected to impact employing the truss-like discrete element method
2
2015
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
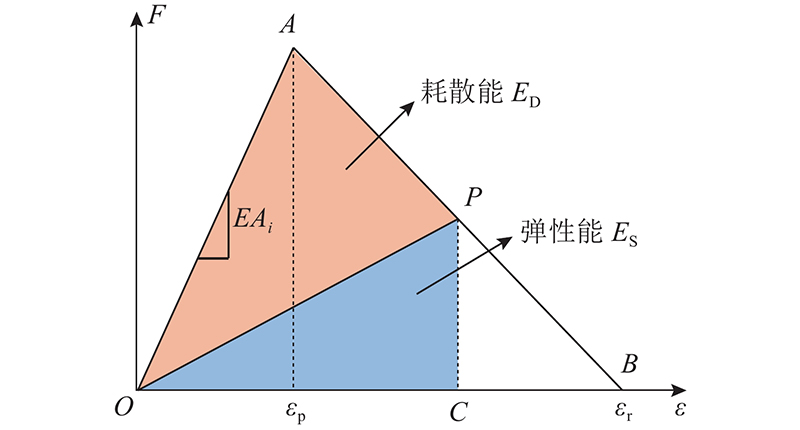
... LDEM使用Kosteski等[28]引入的双线性本构模型,以体现拉伸时微裂纹形成与扩展过程中杆单元承载能力的不可逆损伤. 在压缩载荷的情况下,材料表现为线性弹性. 压缩载荷导致材料失效视为由间接牵引作用造成,其抗压极限强度通常比抗拉强度大5~10倍. 双线性本构模型的荷载−应变曲线如图4所示. 图中,段OA斜率杆单元等效刚度EAi;点A对应的εp为临界应变,表示微裂纹开始形成前的最大应变;点B对应的εr为极限应变,即杆单元失效去除时的应变. 在AB上取任意点P表示杆单元发生损伤但未完全失效,区域OAP的面积ED为发生损伤时所耗散的能量密度,区域OPC的面积Es为杆单元中剩余的弹性能量密度. 当总能量完全耗散,即OAP与OAB重合时,杆单元去除,宏观裂纹产生. ...
Dynamic fracture analysis of concrete or rock plates by means of the discrete element method
1
2009
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
The size effect in quasi-brittle materials: experimental and numerical analysis
1
2017
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
A lattice approach to model flow in cracked concrete
1
2009
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
Simulation of chloride diffusion in cracked concrete with different crack patterns
1
2016
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
Simulation of chloride diffusivity for cracked concrete based on RBSM and truss network model
1
2008
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
2
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
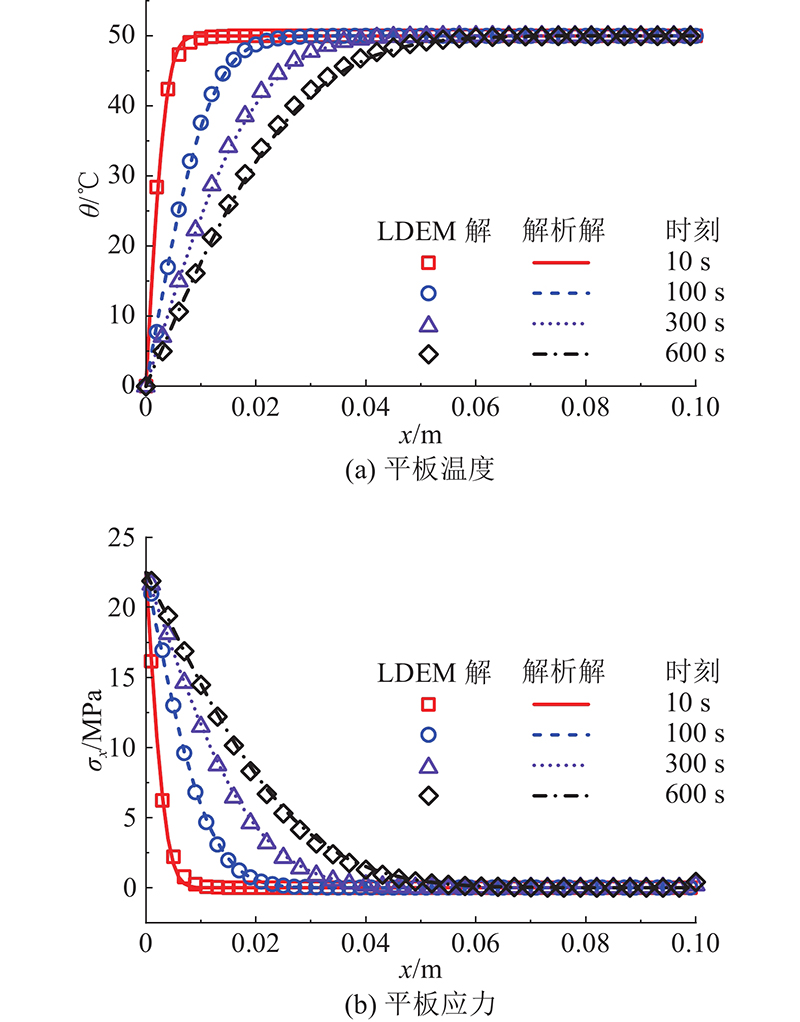
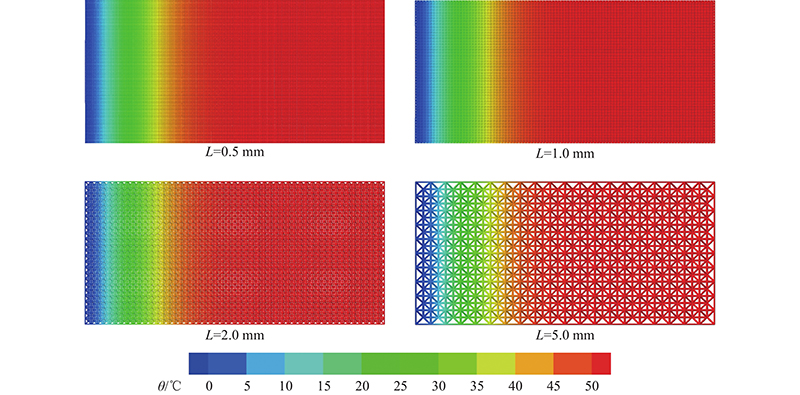
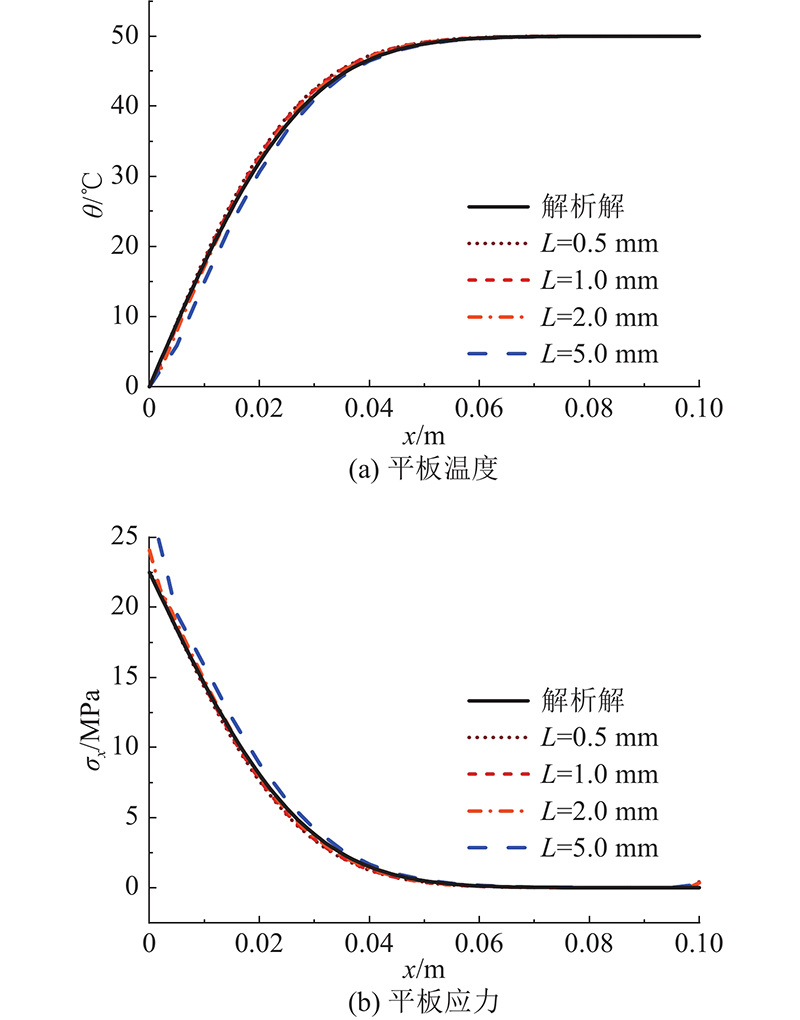
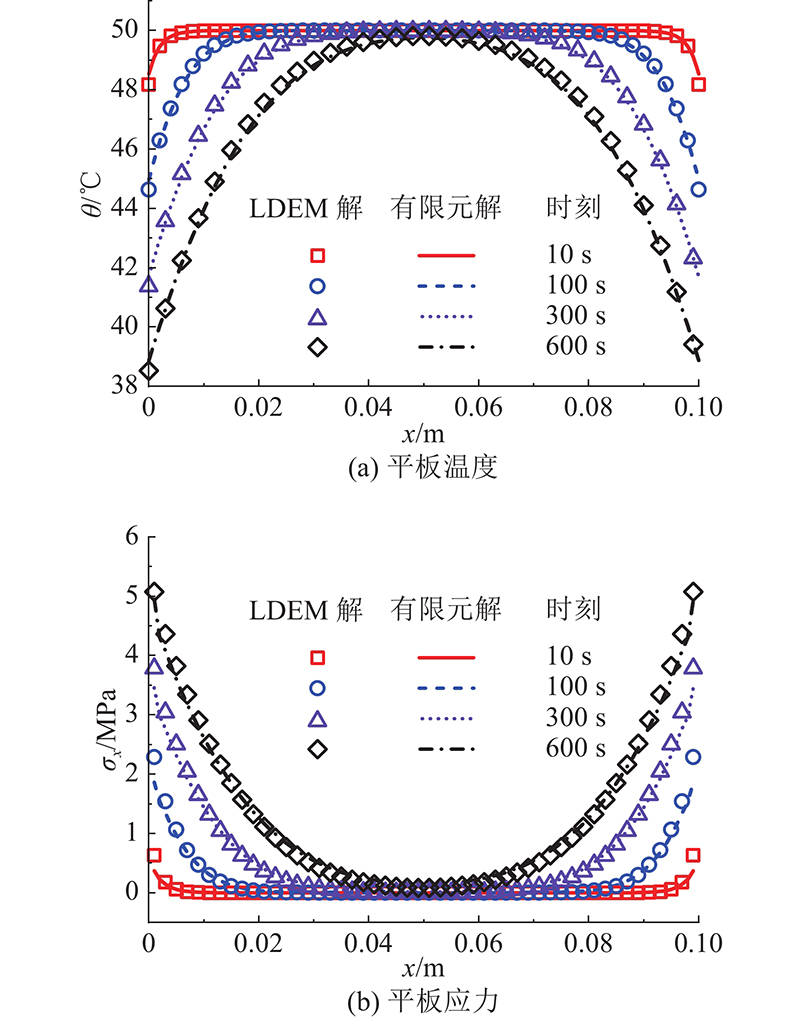
... 式中:D为导温系数,D=k/ρc. 该问题的理论解[34]为 ...
2
... 学者们采用多种试验技术研究准脆性材料的热力学性能[8],如声发射技术(acoustic emission technology,AE)[9]、扫描电镜(scanning electron microscope,SEM)[10]、热应力装置(thermal stress device,TSD)[11]等. 物理试验耗费时间且难以观察热开裂过程中裂纹的萌生与扩展. 为了解决这些问题,数值模拟方法被运用于探索准脆性材料的热开裂机理中. 热开裂数值模拟方法大致分为连续介质模型、非连续介质模型和连续−离散耦合模型. 连续介质模型扩展了有限元法(extended finite element method,XFEM)[12-13]与颗粒有限元法(particle finite element method,PFEM)[14],在解决模拟热开裂问题中被广泛采用. 虽然包括相场方法[15]和近场动力学(peridynamics,PD)[16]在内的先进连续介质方法被运用到准脆性材料热开裂模拟中,但是多数连续介质模型难以处理多裂纹问题. 如离散元法(discrete element method,DEM)[17]、非连续变形分析(discontinuous deformation analysis,DDA)[18-19]的非连续介质模型和以连续−离散耦合方法(finite and discrete element method,FDEM)为代表的连续−离散耦合模型[20-22]能够处理多裂纹问题,缺点是计算量较大,效率低[23]. 格构离散单元法(lattice discrete element method,LDEM)运用格构模型改进标准DEM,大大提高了计算效率[24]. 基于Hrennikoff[25]提出的格构框架思想,Nayfeh等[26]将杆单元构成的基本模块离散连续体结构为LDEM原型. LDEM经过不断改进[27],已经被成功运用于混凝土[28]、岩石[29]、复合材料[30]等结构开裂的计算中. Grassl[31]基于格构思想提出开裂混凝土中的物质流动模型,Wang等[32-33]运用经典格构模型研究氯离子扩散行为,吴迪[34]采用二维格构模型分析混凝土中的热传导问题,均说明格构模型具有计算物质传输与传热的潜力. ...
... 式中:D为导温系数,D=k/ρc. 该问题的理论解[34]为 ...
Experimentally validated meso-scale fracture modelling of mortar using output from micromechanical models
1
2020
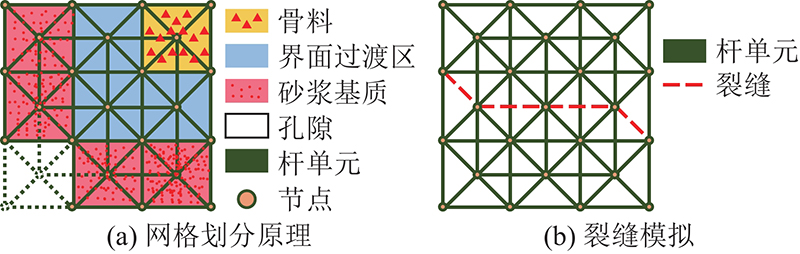
... LDEM适用于多相混合的含孔材料,其离散连续体的过程基于连续体的各相空间分布进行[35]. 以混凝土为例,如图2所示,将连续体划分为空间中的立方体元胞,并依据元胞的空间位置判断其材料属性,将整体区分为骨料、砂浆、界面过渡区(ITZ)与孔隙组成的多相结构. 在元胞的角点与体心生成节点,并将节点集按照LDEM基本模块的排布方式通过杆单元进行连接,根据杆单元所属元胞赋予相应的材料参数. 位于孔隙元胞内的节点不参与单元划分,在模型中形成初始缺陷. LDEM模拟裂纹的形成与扩展是通过在一定开裂准则下的杆单元损伤去除进行的. 在每步计算中,达到极限条件的杆单元将从整体结构中删除,相邻节点不再连续,之后再进入下步计算. ...
Concrete cover requirements for FRP reinforced members in hot climates
2
2005
... 数值模拟以Abdalla[36]进行的钢筋混凝土结构在高温影响下的热开裂物理试验为基础. 混凝土中钢筋通常由线膨胀系数较高的钢材制成,在均匀温升时混凝土保护层产生压力,引起开裂. 试验采用由2种材料构成的同轴圆柱,如图10所示. 图中,a为内芯半径,b为钢筋混凝土整体半径,r为保护层内任意一点到圆心的距离. 模拟采用的热力学参数如表1所示,建立LDEM计算模型,采用0.001 m的LDEM模块进行网格划分. 本研究将模拟以1 ℃/s的速率使试件从0 ℃均匀加热至100 ℃的过程,并将LDEM计算得到的开裂模式对比试验的开裂模式. Abdalla[36]给出的钢筋混凝土材料不均匀性热开裂问题环向应力解析解为 ...
... [36]给出的钢筋混凝土材料不均匀性热开裂问题环向应力解析解为 ...
Ultrasonic imaging and acoustic emission monitoring of thermally induced microcracks in Lac du Bonnet granite
2
1993
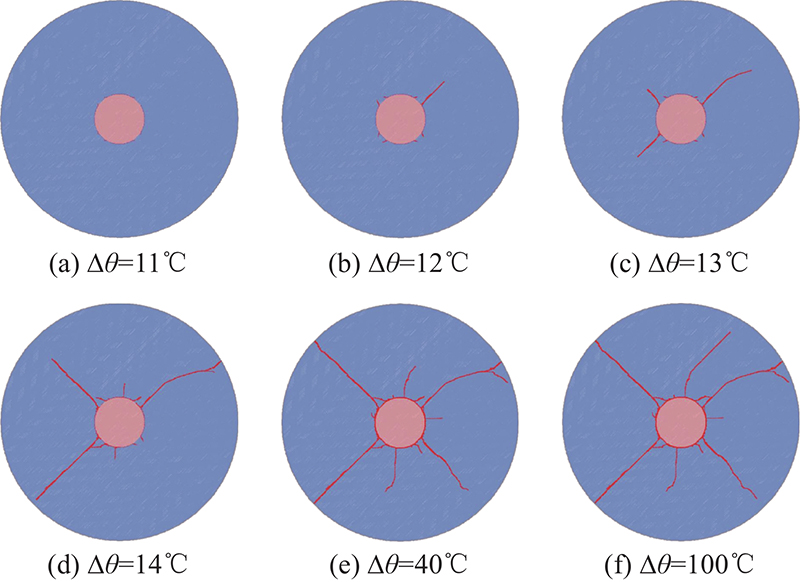
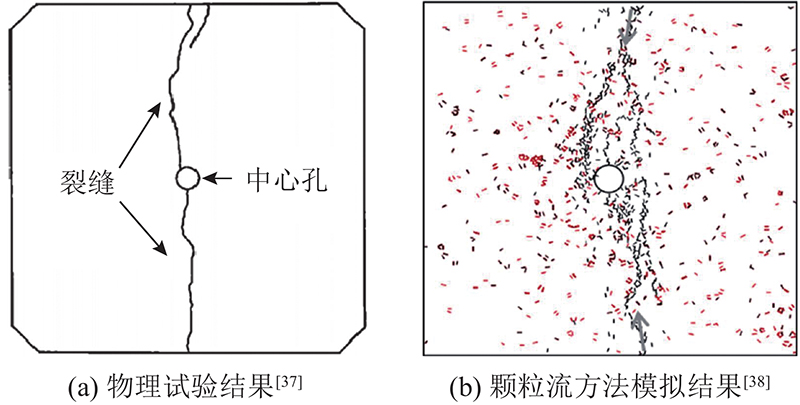
... 验证基于Jansen等[37]进行的方形花岗岩热开裂试验. 试件为边长15 cm的正方形,中心钻孔直径为1 cm,采用0.05 cm的LDEM模块划分网格. 法向约束试件的上下边界,左右为自由边界. 试件的初始温度以及四周的温度边界条件均为20 ℃,加热中心孔,使其温度在1 h内由20 ℃均匀上升至200 ℃. 热力学参数与试验中花岗岩参数保持一致,如表2所示. 计算结果如图13所示,随着中心孔温度的升高,热由孔向四周边界传递. 孔附近的岩石由于温度较高,发生较大的热膨胀变形,外边界附近岩石温升幅度较小,体积膨胀较小. 由于上下边界的法向约束作用,岩石内部的体积膨胀引起的拉伸变形只能在水平方法发生,在上下边界产生较大的拉应力. 随着加热过程的进行,先是在试件上下边缘产生拉伸破坏裂纹,之后上下裂纹同时向着中心孔延伸. 由于中心孔为加热源,附近温度梯度较大,产生的变形不一致,孔周围产生细小的裂纹. 开裂模式与如图14所示的方形花岗岩热开裂试验结果[37]和颗粒流模拟[38]得到的开裂过程一致. ...
... [37]和颗粒流模拟[38]得到的开裂过程一致. ...
Thermal influence on mechanical properties of granite: a microcracking perspective
1
2016
... 验证基于Jansen等[37]进行的方形花岗岩热开裂试验. 试件为边长15 cm的正方形,中心钻孔直径为1 cm,采用0.05 cm的LDEM模块划分网格. 法向约束试件的上下边界,左右为自由边界. 试件的初始温度以及四周的温度边界条件均为20 ℃,加热中心孔,使其温度在1 h内由20 ℃均匀上升至200 ℃. 热力学参数与试验中花岗岩参数保持一致,如表2所示. 计算结果如图13所示,随着中心孔温度的升高,热由孔向四周边界传递. 孔附近的岩石由于温度较高,发生较大的热膨胀变形,外边界附近岩石温升幅度较小,体积膨胀较小. 由于上下边界的法向约束作用,岩石内部的体积膨胀引起的拉伸变形只能在水平方法发生,在上下边界产生较大的拉应力. 随着加热过程的进行,先是在试件上下边缘产生拉伸破坏裂纹,之后上下裂纹同时向着中心孔延伸. 由于中心孔为加热源,附近温度梯度较大,产生的变形不一致,孔周围产生细小的裂纹. 开裂模式与如图14所示的方形花岗岩热开裂试验结果[37]和颗粒流模拟[38]得到的开裂过程一致. ...
热膨胀系数时变性对混凝土温度应力仿真影响
2
2019
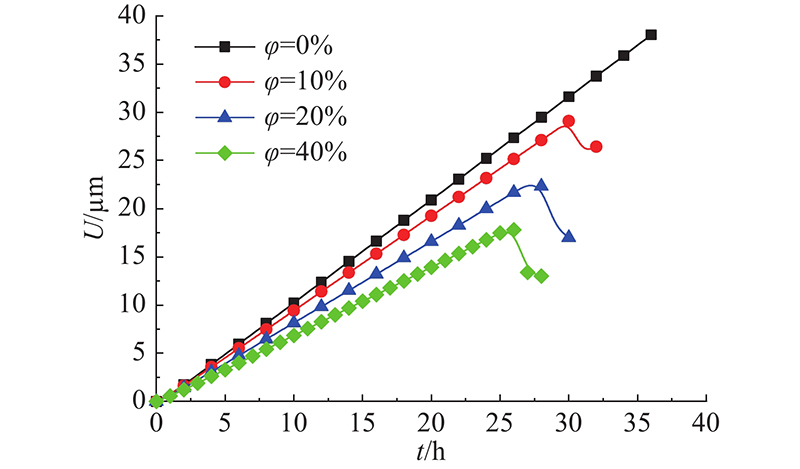
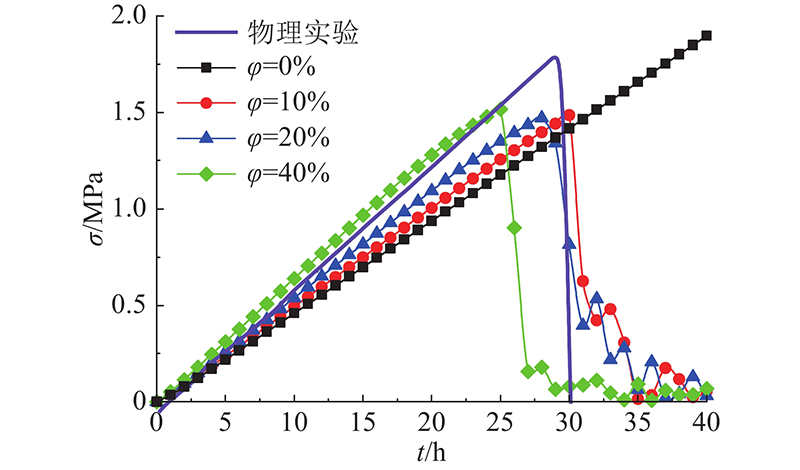
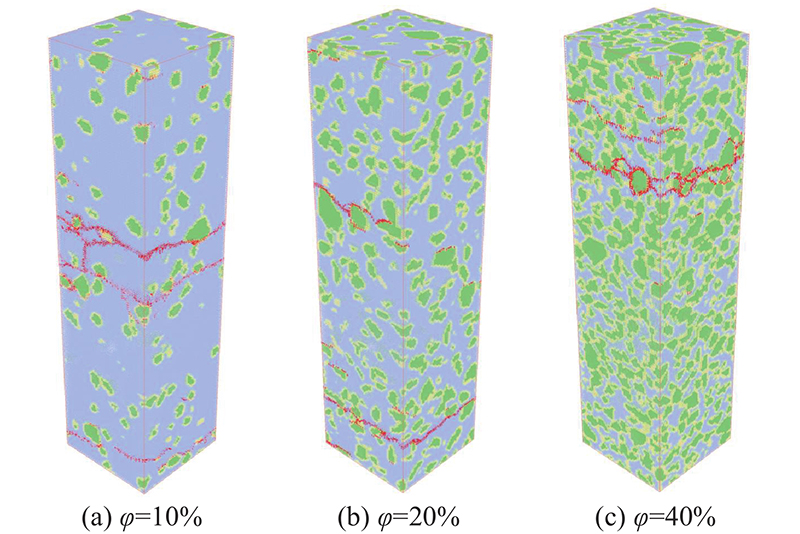
... 温度应力试验机(temperature-stress testing machine,TSTM)是测试混凝土在单轴约束下抗裂性能的装置,卢春鹏等[39]采用TSTM分析早龄期混凝土的温度应力,本研究基于此实验进行仿真. 混凝土配合比与文献[39]的温度应力试验保持一致,水灰比为0.43,单位立方米材料用量分别为水125 kg、水泥189 kg、粉煤灰102 kg、砂672 kg、小石637 kg、中石 637 kg. 混凝土骨料体积分数ϕ ≈40%. 为了研究细观结构对混凝土热开裂的影响,设置不同骨料体积分数ϕ =0%、10%、20%. 考虑到计算成本与骨料投放,试件尺寸选取试验试件中部位置,为600 mm×150 mm×150 mm. 模型骨料投放如图15所示. 以3 mm的LDEM模块划分混凝土模型,并将骨料外层模块作为界面过渡区(interface transition zone, ITZ). 仿真过程:当混凝土7 d养护龄期时,法向约束混凝土试件上下边界,在初温30 ℃的试件四周进行强制降温使其内部温度以1 ℃/h的速率降温直至开裂破坏. 热力学参数参考文献[40],如表3所示. ...
... 采用TSTM分析早龄期混凝土的温度应力,本研究基于此实验进行仿真. 混凝土配合比与文献[39]的温度应力试验保持一致,水灰比为0.43,单位立方米材料用量分别为水125 kg、水泥189 kg、粉煤灰102 kg、砂672 kg、小石637 kg、中石 637 kg. 混凝土骨料体积分数ϕ ≈40%. 为了研究细观结构对混凝土热开裂的影响,设置不同骨料体积分数ϕ =0%、10%、20%. 考虑到计算成本与骨料投放,试件尺寸选取试验试件中部位置,为600 mm×150 mm×150 mm. 模型骨料投放如图15所示. 以3 mm的LDEM模块划分混凝土模型,并将骨料外层模块作为界面过渡区(interface transition zone, ITZ). 仿真过程:当混凝土7 d养护龄期时,法向约束混凝土试件上下边界,在初温30 ℃的试件四周进行强制降温使其内部温度以1 ℃/h的速率降温直至开裂破坏. 热力学参数参考文献[40],如表3所示. ...
热膨胀系数时变性对混凝土温度应力仿真影响
2
2019
... 温度应力试验机(temperature-stress testing machine,TSTM)是测试混凝土在单轴约束下抗裂性能的装置,卢春鹏等[39]采用TSTM分析早龄期混凝土的温度应力,本研究基于此实验进行仿真. 混凝土配合比与文献[39]的温度应力试验保持一致,水灰比为0.43,单位立方米材料用量分别为水125 kg、水泥189 kg、粉煤灰102 kg、砂672 kg、小石637 kg、中石 637 kg. 混凝土骨料体积分数ϕ ≈40%. 为了研究细观结构对混凝土热开裂的影响,设置不同骨料体积分数ϕ =0%、10%、20%. 考虑到计算成本与骨料投放,试件尺寸选取试验试件中部位置,为600 mm×150 mm×150 mm. 模型骨料投放如图15所示. 以3 mm的LDEM模块划分混凝土模型,并将骨料外层模块作为界面过渡区(interface transition zone, ITZ). 仿真过程:当混凝土7 d养护龄期时,法向约束混凝土试件上下边界,在初温30 ℃的试件四周进行强制降温使其内部温度以1 ℃/h的速率降温直至开裂破坏. 热力学参数参考文献[40],如表3所示. ...
... 采用TSTM分析早龄期混凝土的温度应力,本研究基于此实验进行仿真. 混凝土配合比与文献[39]的温度应力试验保持一致,水灰比为0.43,单位立方米材料用量分别为水125 kg、水泥189 kg、粉煤灰102 kg、砂672 kg、小石637 kg、中石 637 kg. 混凝土骨料体积分数ϕ ≈40%. 为了研究细观结构对混凝土热开裂的影响,设置不同骨料体积分数ϕ =0%、10%、20%. 考虑到计算成本与骨料投放,试件尺寸选取试验试件中部位置,为600 mm×150 mm×150 mm. 模型骨料投放如图15所示. 以3 mm的LDEM模块划分混凝土模型,并将骨料外层模块作为界面过渡区(interface transition zone, ITZ). 仿真过程:当混凝土7 d养护龄期时,法向约束混凝土试件上下边界,在初温30 ℃的试件四周进行强制降温使其内部温度以1 ℃/h的速率降温直至开裂破坏. 热力学参数参考文献[40],如表3所示. ...
基于性能演变理论的混凝土细观损伤特性研究
1
2018
... 温度应力试验机(temperature-stress testing machine,TSTM)是测试混凝土在单轴约束下抗裂性能的装置,卢春鹏等[39]采用TSTM分析早龄期混凝土的温度应力,本研究基于此实验进行仿真. 混凝土配合比与文献[39]的温度应力试验保持一致,水灰比为0.43,单位立方米材料用量分别为水125 kg、水泥189 kg、粉煤灰102 kg、砂672 kg、小石637 kg、中石 637 kg. 混凝土骨料体积分数ϕ ≈40%. 为了研究细观结构对混凝土热开裂的影响,设置不同骨料体积分数ϕ =0%、10%、20%. 考虑到计算成本与骨料投放,试件尺寸选取试验试件中部位置,为600 mm×150 mm×150 mm. 模型骨料投放如图15所示. 以3 mm的LDEM模块划分混凝土模型,并将骨料外层模块作为界面过渡区(interface transition zone, ITZ). 仿真过程:当混凝土7 d养护龄期时,法向约束混凝土试件上下边界,在初温30 ℃的试件四周进行强制降温使其内部温度以1 ℃/h的速率降温直至开裂破坏. 热力学参数参考文献[40],如表3所示. ...
基于性能演变理论的混凝土细观损伤特性研究
1
2018
... 温度应力试验机(temperature-stress testing machine,TSTM)是测试混凝土在单轴约束下抗裂性能的装置,卢春鹏等[39]采用TSTM分析早龄期混凝土的温度应力,本研究基于此实验进行仿真. 混凝土配合比与文献[39]的温度应力试验保持一致,水灰比为0.43,单位立方米材料用量分别为水125 kg、水泥189 kg、粉煤灰102 kg、砂672 kg、小石637 kg、中石 637 kg. 混凝土骨料体积分数ϕ ≈40%. 为了研究细观结构对混凝土热开裂的影响,设置不同骨料体积分数ϕ =0%、10%、20%. 考虑到计算成本与骨料投放,试件尺寸选取试验试件中部位置,为600 mm×150 mm×150 mm. 模型骨料投放如图15所示. 以3 mm的LDEM模块划分混凝土模型,并将骨料外层模块作为界面过渡区(interface transition zone, ITZ). 仿真过程:当混凝土7 d养护龄期时,法向约束混凝土试件上下边界,在初温30 ℃的试件四周进行强制降温使其内部温度以1 ℃/h的速率降温直至开裂破坏. 热力学参数参考文献[40],如表3所示. ...