拉、吊索是缆索承重桥中重要的承重构件. 长期服役桥梁的拉、吊索遭受腐蚀介质侵蚀出现病害并进行维修更换的案例层出不穷,极端荷载作用下桥梁发生断索的报道也屡见不鲜. 2007年3月,车辆交通事故和火灾致使Mezcala斜拉桥1根斜拉索断裂、多根斜拉索严重受损. 2011年10月,运营10年的Kutai-Kartanegara悬索桥由1根吊索断裂引发吊索连续破坏[1], 事故造成11人死亡30多人失踪.
缆索承重桥的拉、吊索突然断裂后,剩余结构的内力、刚度将重新分配,并伴随着显著的动力效应. 相比于房屋建筑领域在承重构件失效和结构抵抗连续倒塌方面提出详细的设计规程,现有规范对桥梁断索仅给出指导性规定. 美国后张法预应力协会(post-tension institution,PTI)[2]给出2种计算斜拉桥断索响应的方法:1)拟动力分析方法,采用静力分析方法加上2. 0的动力放大系数;2)动力分析方法,可以更加准确地模拟断索产生的动力效应. 学者们针对缆索承重桥断索的研究结果表明,在拟动力分析中,所有截面和构件采用相同的动力放大系数并不合理,动力分析方法计算获得的结构断索响应更能反映真实情况[3-4]. 采用动力方法计算索构件断裂动力响应时不可避免地涉及2个关键问题:1)如何选用合理的吊索断裂模拟方法;2)如何确定结构断索动力响应的影响因素. 吴庆雄等[5]采用接触碰撞和单元删除的方式,模拟拱桥吊杆断裂的动力过程. 张羽等[6]采用删除拉索单元的方法,分析斜拉桥拉索连续断裂过程中主梁、拉索及索塔的动力响应. 学者们针对缆索承重桥断索响应动力效应影响因素的研究结果表明,吊索断裂持续时间Δt是影响结构断索响应动力放大系数最显著的因素. Ruiz-Teran等[7]以上承式悬带桥为例,针对断索时间的作用效应进行参数化分析,得出若Δt<1/100的结构基本周期,则结构断索动力响应可以达到最大值. Zhou等[8]在研究斜拉桥断索动力响应时假设Δt=0.01 s. 邱文亮等[9]分析了Δt以及失效吊索拉力损失函数对悬索桥断索响应动力效应的影响. 该研究发现,当Δt<1/10的断索点主缆局部振动周期时,悬索桥断索响应动力效应达到最大且趋于稳定,失效吊索拉力损失与Δt呈线性关系时,结构断索响应动力效应最小.
悬索桥与斜拉桥、拱桥的结构形式不同,分析断索动力响应时,除了断裂吊索的冲击作用外,还应考虑断索后主缆局部振动产生的影响. 主缆局部振动对悬索桥断索动力响应计算结果影响的研究基本处于空白. 基于上述问题,对悬索桥断索动力分析过程中影响主缆局部振动的因素开展模型参数研究.
1. 断索模拟方法及有限元模型
1.1. 悬索桥断索过程模拟方法
悬索桥作为多自由度结构,其基本动力学控制方程可以写为
式中:
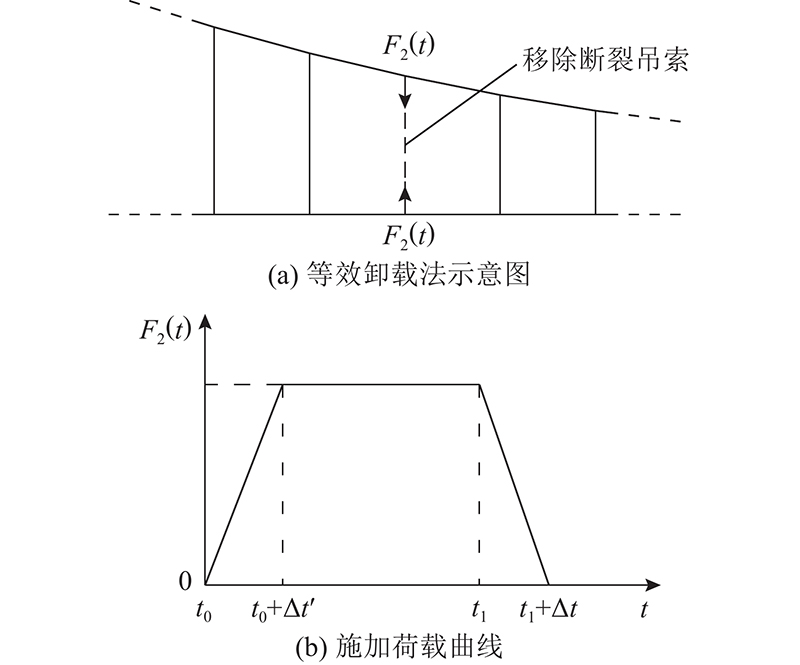
图 1
图 1 等效卸载法模拟悬索桥吊索断裂
Fig.1 Hanger-breakage event simulating through unloading equivalent force method
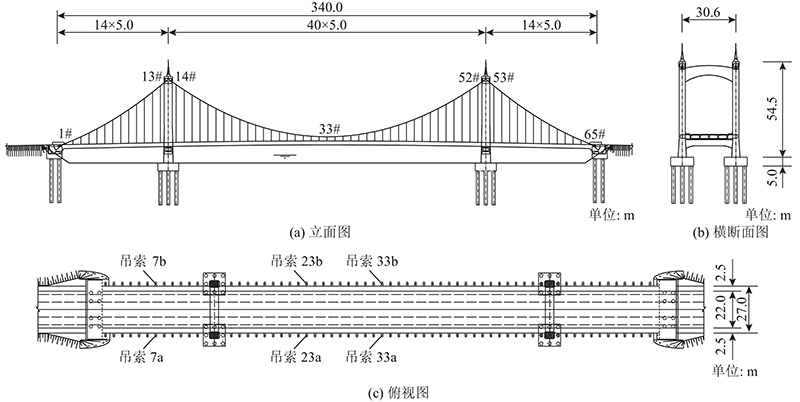
1.2. 工程概况
图 2
图 3
1.3. 有限元模型
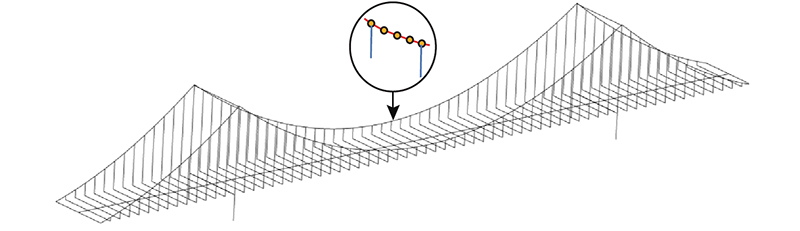
如图4所示,利用软件Abaqus2020建立“鱼骨”动力计算模型. 主梁、横梁以及桥塔采用空间梁单元模拟,以考虑扭转质量和扭转刚度. 在悬索桥静力分析和整体结构动力分析时,主缆通常被视为无抗弯刚度的构件,有限元模型中采用桁架单元模拟. 考虑主缆抗弯刚度时,主缆用梁单元模拟. 吊索索夹使用质量单元模拟,质量集中在索夹所在主缆节点上. 索夹1#到9#、57#到65#的质量均为1 200 kg,索夹10#到17#、49#到56#质量均为1 600 kg,索夹18#到48#质量均为1 000 kg. 模型忽略群桩基础对动力分析的影响,在索塔底部施加固结约束. 依据支座布置类型,在梁底施加相应自由度约束. 在进行断索动力分析时,仅考虑恒载作用,模型除考虑自重荷载外,附加桥面二期铺装和附属物荷载集度为108 kN/m,主缆上保护层荷载集度为0.37 kN/m. 结构1阶振型为主梁竖弯,频率为 0.446 Hz,结构14 阶振型为主梁扭转,频率为1.474 Hz.
图 4
在大跨桥梁非线性分析中,阻尼设置对结构动力响应尤为重要.一般采用与结构质量矩阵
式中:ξ 为结构模态阻尼比,
2. 断索响应计算结果及影响因素
2.1. 单根吊索断裂结构动力响应分析
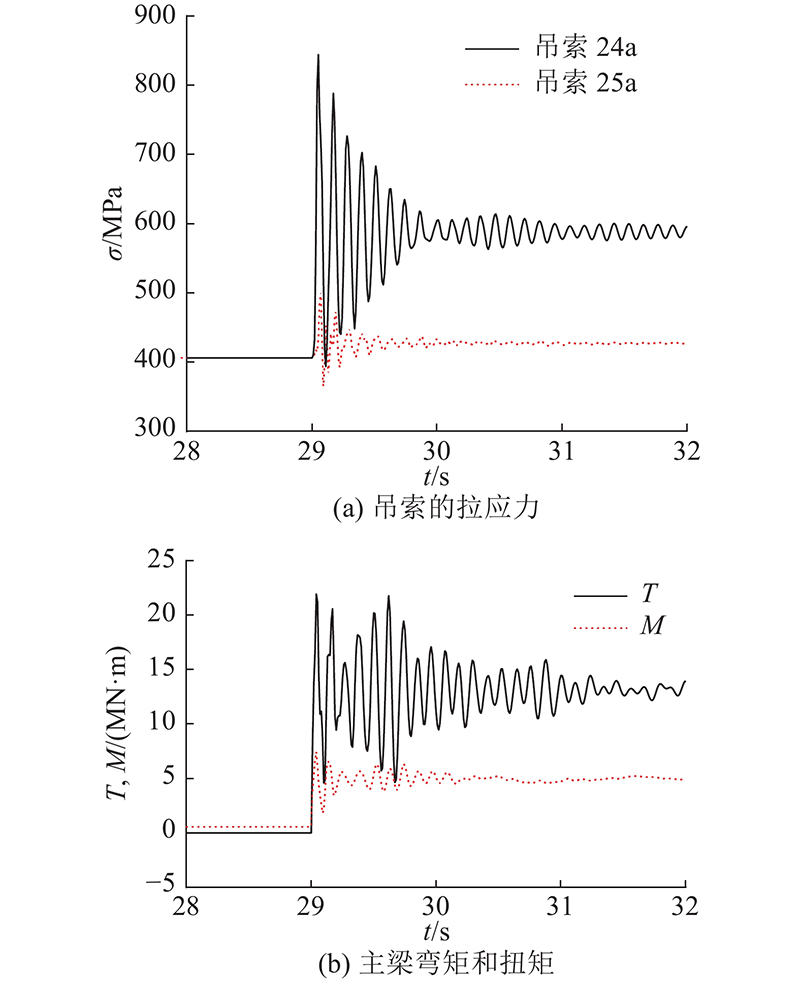
以中跨吊索23a为例,不考虑主缆物理抗弯刚度,采用瞬时刚度退化法将失效吊索单元移除. 如图5所示为单根吊索瞬间断裂后的结构动力响应时程曲线. 结果表明,吊索突然断裂引发与断裂吊索相邻的吊索剧烈动力响应,使断索位置主梁扭矩发生显著变化. 图5(a)中,吊索24a的拉应力σ动力响应最终和最大值分别为591、845 MPa,分别为初始值的1.5倍、2.1倍. 吊索25a的拉应力σ动力响应最终和最大值分别为427、501 MPa,分别为初始值的1.1倍、1.2倍. 图5(b)中,单根吊索突然断裂后,断索位置主梁弯矩M最终和最大值分别为4.9 、7.5 MN·m,主梁扭矩T最终和最大值分别为13.1 、21.9 MN·m.
图 5
图 5 吊索断裂引起的结构动力响应时程曲线
Fig.5 Time-history curves of structural dynamic response caused by hanger-breakage event
为了定量描述断索后结构动力响应,定义动力放大系数(dynamical amplification factor)
式中:
2.2. 影响主缆局部振动的模型参数分析
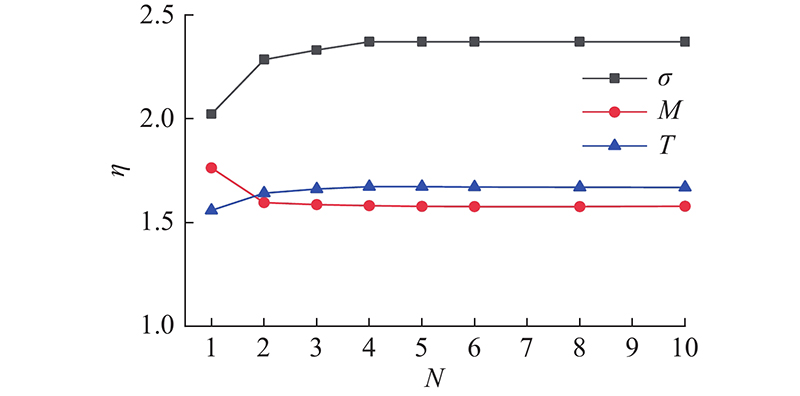
分析主缆局部振动对断索动力响应的影响程度时,将吊索间主缆单元数N由1增加至10,如图6所示. 当N=1时,主缆仅能在与吊索连接的节点位置产生振动,即不考虑吊索间主缆的局部振动. 此状况下的吊索应力放大系数为2.02,主梁弯矩放大系数为1.76,扭矩放大系数为1.56. 当N=4时,主缆局部振动效应得以体现,此时吊索拉应力放大系数增加至2.37,主梁弯矩放大系数减小至1.58,主梁扭矩放大系数增加至1.67. 当N>4时,节点数量已经足够描述实际主缆的局部振动效应,η随主缆划分单元数目的增长不再变化. 因此,分析悬索桥断索动力响应时,只有保证主缆足够的单元数目,才能充分体现主缆局部振动效应.
图 6
图 6 主缆网格密度对动力放大系数的影响
Fig.6 Effect of main cable ’s grid density on dynamical amplification factor
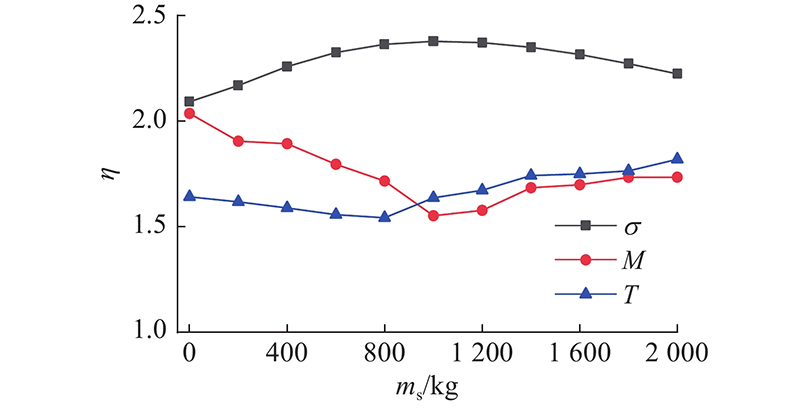
在进行悬索桥断索分析时,索夹质量ms产生惯性力对主缆局部振动的影响不可忽视. 算例中吊索索夹质量在1 000~1 600 kg,参数分析时将索夹质量取值范围扩展为0~2 000 kg. 随着索夹质量的增加,吊索拉应力动力放大系数呈现先增大后减小的变化趋势,主梁弯矩和扭矩动力放大系数呈现先减小后增大的变化趋势. 如图7所示,当ms从0增加到2 000 kg时,吊索拉应力放大系数在 2.09~2.38变化,变化幅度为13.9%. 主梁弯矩放大系数在1.55~2.04变化,变化幅度为31.6%. 主梁扭矩放大系数在1.54~1.82变化,变化幅度为18.2%.
图 7
图 7 索夹质量对动力放大系数的影响
Fig.7 Effect of clamp mass on dynamical amplification factor
悬索桥主缆有效抗弯刚度包括几何刚度和物理刚度. 在悬索桥断索动力分析模型中,主缆几何刚度可以通过无应力长度和初始应力自动计算,主缆物理抗弯刚度是须设定的参数. 鉴于缆索结构的特点,现有的理论与测试技术很难准确评估或预判缆索结构的真实抗弯刚度,使主缆物理抗弯刚度取值没有统一的认识[14]. 假设索体内钢丝可以自由滑动,此时缆索物理抗弯刚度最小,近似为各根钢丝抗弯刚度之和,记作EImin. 缆索按照公称直径计算惯性矩确定的抗弯刚度,记作EImax,缆索实际物理抗弯刚度介于EImax和EImin之间.
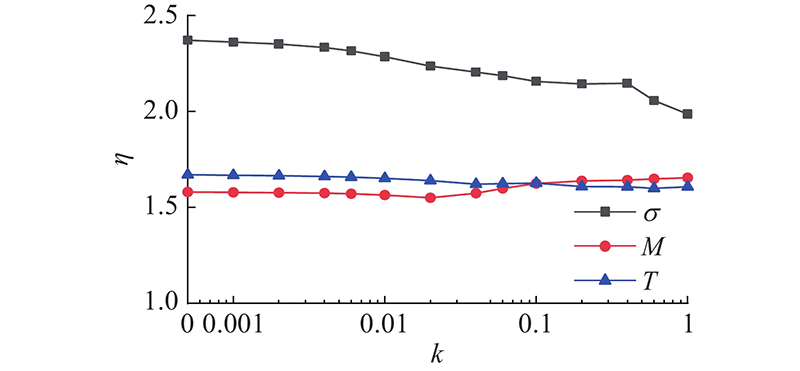
为了研究主缆物理抗弯刚度对结构断索动力响应的影响,假定主缆物理抗弯刚度在0~EImax(约为5 408EImin),以EImax为参考,引入取值倍率k,即主缆物理抗弯刚度取值为k倍的EImax. 如图8所示,主缆物理抗弯刚度对断索后吊索拉应力动力响应具有较大影响,对主梁弯矩和扭矩动力响应影响较小. 主缆物理弯曲刚度在0~0.01EImax时,吊索拉应力动力放大系数基本保持不变,主缆物理弯曲刚度从0.01EImax增长到EImax时,吊索拉应力放大系数呈现减小的趋势,变化幅度为15.8%.
图 8
图 8 主缆物理抗弯刚度对动力放大系数的影响
Fig.8 Effect of main cable ’s physical stiffness on dynamical amplification factor
2.3. 模型的阻尼设置
结构动力分析模型中,阻尼系数的设置对计算精度有很大影响. Rayleigh阻尼是全局性的结构阻尼,理论上基于结构固有频率设置的单元阻尼系数α、β可以很好地反映结构模态阻尼比. 除了结构整体模态阻尼比外,主缆的阻尼特性对断索后主缆局部振动的衰减速度也有重要影响. 基于结构固有频率设置的单元阻尼系数能否较好地反映断索后主缆的阻尼特性,需要对主缆阻尼比与结构整体模态阻尼比的差异程度进行模型验证. 计算结构模态阻尼比时,对有限元模型施加与模态振型相对应的荷载,突然释放提取自由振动时程曲线,通过振动衰减法得到结构整体模态阻尼比. 计算主缆阻尼比时,分为2种工况:1)不改变有限元模型的约束条件,完全删除失效吊索单元,提取断索点主缆竖向位移时程曲线计算主缆阻尼比,此时能够考虑主缆振动沿轴向传递以及剩余吊索做功引起的能量耗散;2)约束与断裂吊索相邻的吊索和主缆的连接点,完全删除失效吊索单元,提取断索点主缆竖向位移时程曲线计算主缆阻尼比,此时仅能考虑主缆自身阻尼引起的振动衰减.
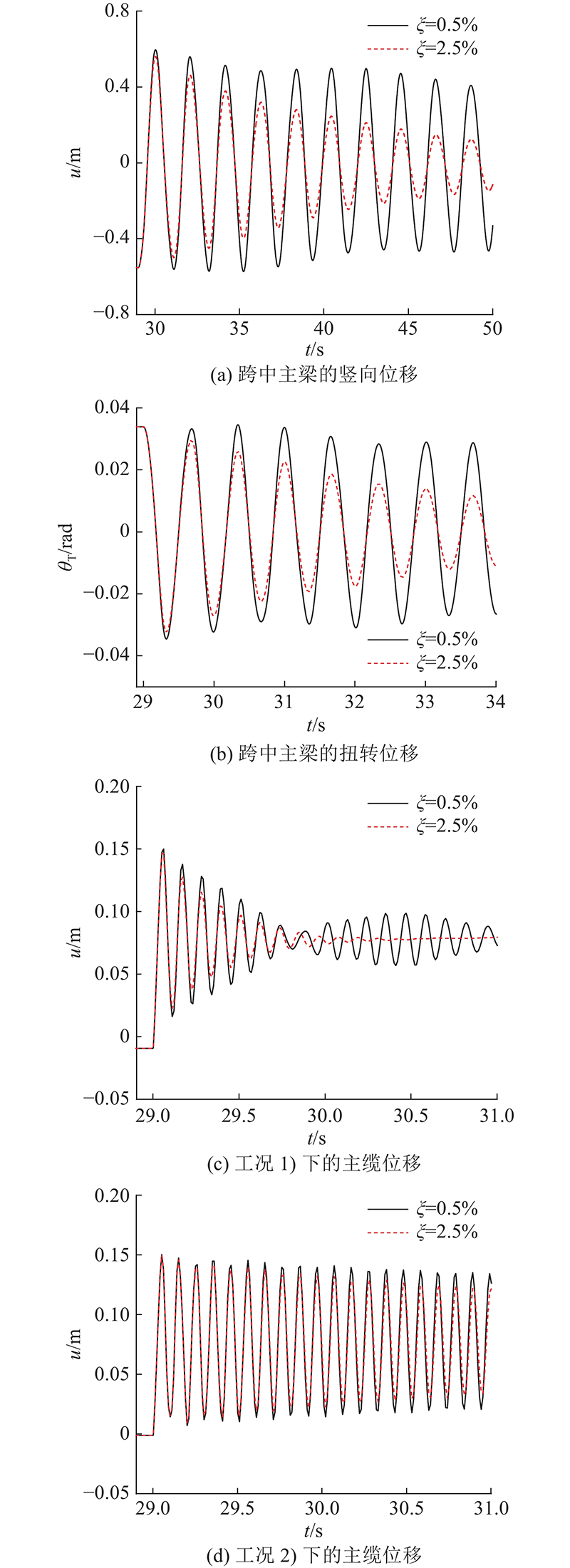
结构模态阻尼比ξ分别取0.5%和2.5%,选取主梁1阶竖弯和14阶扭转模态频率设置模型单元阻尼系数. 如图9所示为用于计算结构整体模态阻尼比和主缆局部振动阻尼比的自由振动时程曲线. 断索动力分析模型的结构整体模态阻尼比和预设值基本吻合,主缆局部振动阻尼比和结构整体模态阻尼差异较大. 图中,随着结构整体模态阻尼比增长,主梁振动衰减速度变快,提取的主梁竖向位移u曲线、扭转位移θT曲线的周期分别为2.108 s和0.666 s,与有限元模型动力特性计算结果吻合. 断索后主缆在工况1)下的振动快速衰减,在工况2)下的振动衰减较缓慢. 如表1所示为未修正模型的结构模态阻尼比和主缆局部振动阻尼比. 表中,ξB为主梁1阶竖弯模态阻尼比,ξT为主梁14阶扭转模态阻尼比,ξloc为主缆局部振动阻尼比. 可以看出,当ξ=2.5%时,在工况1)下得ξloc=5.94%,在工况2)下ξloc=0.32%.
图 9
图 9 计算模型阻尼比的自由振动时程曲线
Fig.9 Time-history curves of free vibration for calculating damping ratio of model
表 1 未修正模型的结构模态阻尼比与主缆局部振动阻尼比
Tab.1
| ξ | ξB | ξT | ξloc | |
| 工况1) | 工况2) | |||
| % | ||||
| 0.5 | 0.48 | 0.52 | 3.13 | 0.17 |
| 1.5 | 1.49 | 1.47 | 4.92 | 0.26 |
| 2.5 | 2.44 | 2.53 | 5.94 | 0.32 |
拉索阻尼可以耗散振动过程中的能量,依据耗能机理,拉索阻尼包含材料应变耗能和钢丝摩擦耗能. 拉索(单根钢丝)材料阻尼比一般不超过0.3%[15]. 谢旭等[16]按照能量损失计算得到的斜拉索整体阻尼比为2.5%,表明拉索振动耗能主要是钢丝间的摩擦. 对于悬索桥主缆,除了索夹局部强挤压效应外,缠丝也会对主缆产生较大挤压力,因此使用钢丝材料阻尼代替主缆整体阻尼并不合适,并且在主缆局部振动分析时,将主缆视为“细长索”不符合实际情况. 悬索桥断索后,主缆仅在断索附近相邻的两侧吊索间产生明显振动,层间滑移摩擦属于局部现象,其他范围的主缆振动幅度极小. 通过修改模型中吊索21a~25a间主缆单元阻尼系数α、β,将ξloc在工况2)下的值修正为2.5%、5%,模型修正后结构整体模态阻尼比和主缆局部振动阻尼比如表2所示.可以看出,有限元模型中局部主缆单元阻尼参数的修正对结构整体模态阻尼比基本没有影响,但对断索后主缆的局部振动衰减速度影响显著.
表 2 修正模型的结构模态阻尼比与主缆局部振动阻尼比
Tab.2
| ξ | ξB | ξT | ξloc | |
| 工况1) | 工况2) | |||
| % | ||||
| 0.5 | 0.52 | 0.53 | 5.31 | 2.5 |
| 1.5 | 1.51 | 1.51 | 6.27 | 2.5 |
| 2.5 | 2.51 | 2.55 | 7.17 | 2.5 |
| 0.5 | 0.54 | 0.53 | 6.73 | 5.0 |
| 1.5 | 1.55 | 1.57 | 8.04 | 5.0 |
| 2.5 | 2.57 | 2.59 | 9.03 | 5.0 |
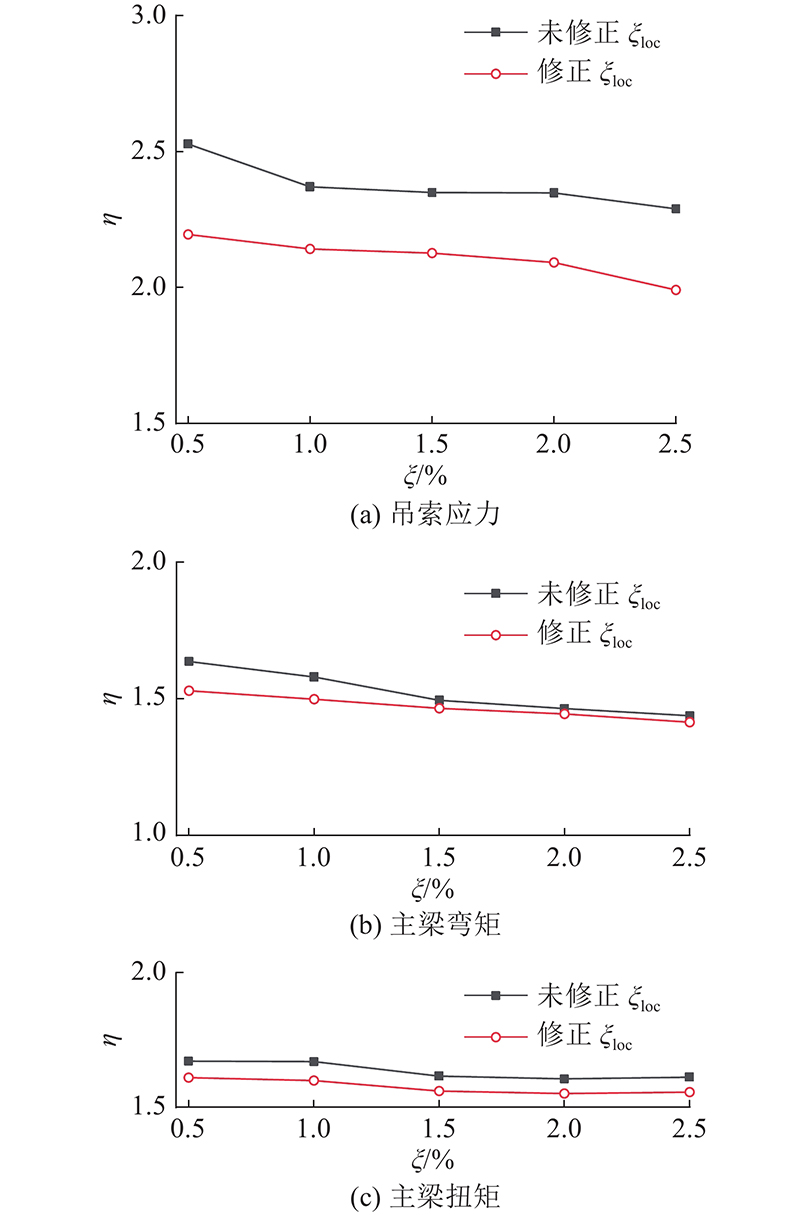
如图10所示为结构断索响应动力放大系数随主缆局部振动阻尼比ξloc和结构模态阻尼比ξ的变化曲线. 可以看出,ξ、ξloc的设置均对结构断索响应动力放大系数具有重大影响. 结构模态阻尼比从0.5%增加到2.5%,吊索应力动力放大系数从2.52减小到2.29,主梁弯矩动力放大系数从1.64减小到1.44,主梁扭矩动力放大系数从1.67减小到1.61,减小幅度分别为9.4%、12.1%、3.5%. 主缆阻尼系数修正后结构断索响应动力放大系数进一步减小,对吊索影响尤为明显. 当ξ=1%,局部主缆阻尼系数修正为2.5%后,模吊索应力动力放大系数从2.37减小到2.14,主梁弯矩动力放大系数从1.58减小到1.49,主梁扭矩动力放大系数从1.67减小到1.59.
图 10
图 10 结构模态阻尼比和主缆局部振动阻尼比对断索响应动力放大系数的影响
Fig.10 Effect of modal damping ratio of structure and local vibration damping ratio of main cable on dynamic amplification factor of hanger-breakage event induced responses
2.4. 吊索的初始状态
在理想成桥状态下,悬索桥各吊索初始拉力基本相等,主梁弯矩相对较小,主梁扭矩等于零. 在长期服役期间悬索桥缆索系统容易遭受腐蚀侵蚀,大面积吊索发生锈蚀不仅直接影响吊索拉力,还会影响主梁线形和内力. 如果吊索断裂是极端状况下车辆碰撞引发的,吊索断裂前拉力会显著增加. Hoang等[17]研究发现,拉索在撞击过程中由于横向变形导致内力增加,拉索断裂后释放的是拉力增长后的轴力. 在合理成桥状态下,算例中悬索桥的初始应力为407 MPa,弯矩为0.57 MN·m,扭矩为0.
为了分析断裂吊索初始状态对悬索桥断索动力响应的影响,断裂吊索初始应力变化与所关注构件初始状态和断索动力响应间的关系如表3所示. 表中,σ0,23a为吊索23a的应力初始值,σ0,24a、σmax,24a及ησ分别为吊索24a的应力初始值、最大值及对应的动力放大系数;M0、Mmax及ηM分别为主梁弯矩响应的初始值、最大值及对应的动力放大系数,T0、Tmax及ηT分别为主梁扭矩矩响应的初始值、最大值及对应的动力放大系数. 其中,主梁弯矩数据正负号代表方向,以截面上缘受压为正. 可以看出,结构断索动力响应最大值随着断裂吊索初始应力的增加而显著增大,由于关注构件的初始状态也发生变化,其断索响应动力放大系数几乎不发生变化.当断裂吊索初始应力σ0,23a偏离合理值407 MPa后,主梁的初始弯矩和扭矩逐渐增大,随着断裂吊索拉应力初始值的增加,其相邻吊索的初始应力σ0,24a逐步减小. 当断裂吊索的初始应力从204 Mpa增加至814 Mpa,吊索拉应力最大值从707 Mpa增加到1072 Mpa,对应的动力放大系数在2.34~2.45. 主梁弯矩最大值从5.63 MN·m增加到11.09 MN·m,对应的动力放大系数在1.56~1.60. 主梁扭矩最大值从16.27 MN·m增加到34.57 MN·m,对应的动力放大系数在1.67~1.71.
表 3 吊索初始状态对断索响应的影响
Tab.3
| σ0,23a/ Mpa | σ0,24a/MPa | σmax,24a/Mpa | ησ | M0/(MN·m) | Mmax/(MN·m) | ηM | T0/(MN·m) | Tmax/(MN·m) | ηT |
| 204 | 511 | 707 | 2.45 | 3.78 | 5.63 | 1.60 | 8.65 | 16.27 | 1.70 |
| 305 | 457 | 782 | 2.43 | 2.24 | 6.51 | 1.58 | 4.32 | 19.19 | 1.69 |
| 407 | 406 | 844 | 2.37 | 0.57 | 7.45 | 1.58 | 0.00 | 21.94 | 1.67 |
| 509 | 360 | 916 | 2.41 | −1.08 | 8.33 | 1.56 | 4.34 | 25.33 | 1.70 |
| 611 | 320 | 966 | 2.39 | −2.76 | 9.26 | 1.56 | 8.54 | 28.61 | 1.71 |
| 712 | 277 | 1020 | 2.37 | −4.41 | 10.19 | 1.56 | 12.81 | 31.63 | 1.71 |
| 814 | 231 | 1072 | 2.34 | −6.06 | 11.09 | 1.56 | 17.28 | 34.57 | 1.71 |
3. 结 论
(1)主缆网格密度和索夹质量是影响主缆局部振动的重要因素. 为了充分体现主缆局部振动效应, 模型吊索间主缆单元数目须大于5 (主缆单元长度与公称直径的比值小于2.5),悬索桥断索分析模型应该在索夹位置建立真实的质量单元.
(2)在悬索桥断索分析模型中,主缆物理刚度的设置对吊索动力响应具有较大影响. 主缆物理弯曲刚度在0.01EImax~EImax时,吊索动力响应随主缆物理弯曲刚度的增加而减小.
(3)结构整体模态阻尼和主缆阻尼系数的设置均影响断索响应动力放系数的取值,基于结构整体模态频率设置的单元阻尼系数不能较好地反映断索后主缆的局部振动阻尼特性. 在进行悬索桥断索动力分析时,有必要修正局部主缆单元阻尼系数,使悬索桥断索动力计算结果更符合实际情况.
(4)虽然断裂吊索初始应力对结构断索响应动力放大系数的影响不大,但结构断索响应最大值随着断裂吊索初始应力的增加而增加.在悬索桥断索安全评估时,如果吊索断裂的诱发原因是如车辆碰撞、爆炸的极端状况,须考虑吊索断裂前初始内力变化的影响.
(5)本研究在讨论模型参数对结构断索动力响应的影响程度时,基于理论分析假设了主缆的物理抗弯刚度和主缆局部振动过程中阻尼比的变化范围. 未来计划进一步研究主缆物理抗弯刚度和阻尼比的取值.
参考文献
Failure analysis of the hanger clamps of the Kutai-Kartanegara Bridge from the fracture mechanics viewpoint
[J].DOI:10.2208/journalofjsce.2.1_1 [本文引用: 1]
Dynamic response and robustness evaluation of cable-supported arch bridges subjected to cable breaking
[J].
单根吊索断裂时自锚式悬索桥强健性分析
[J].
Robustness analysis of self-anchored suspension bridge with loss of a single sling
[J].
下承式钢管混凝土刚架系杆拱桥吊杆断裂动力分析
[J].
Dynamic analysis for cable loss of a rigid-frame tied through concrete-filled steel tubular arch bridge
[J].
大跨混凝土斜拉桥施工过程中结构的断索动力响应
[J].
Broken cable- induced dynamic response of long-span concrete cable stayed bridge during construction
[J].
Response of under-deck cable-stayed bridges to the accidental breakage of stay cables
[J].DOI:10.1016/j.engstruct.2009.02.027 [本文引用: 1]
Numerical investigation of cable breakage events on long-span cable-stayed bridges under stochastic traffic and wind
[J].DOI:10.1016/j.engstruct.2015.07.009 [本文引用: 1]
悬索桥吊索断索动力响应分析的有限元模拟方法研究
[J].
Research on simulation method of dynamic response analysis of suspension bridges subjected to hanger-breakage events
[J].
高压输电塔的断线分析和断线张力计算
[J].
Broken wire analysis and broken wire load calculation of high voltage transmission tower
[J].
Mechanical behaviors and experimental study of submerged floating tunnel subjected to local anchor-cable failure
[J].DOI:10.1016/j.engstruct.2020.110521 [本文引用: 1]
基于细长梁单元的悬索桥主缆线形分析
[J].
Study on main cable shape of suspension bridge based on slender beam element
[J].
桥梁拉索用CFRP线材阻尼特性试验研究和理论分析
[J].
Experimental and theoretical studies on the damping properties of CFRP wire used in bridge cables
[J].
CFRP拉索阻尼特性实验研究和理论分析
[J].
Theoretical analysis and experimental test on damping characteristics of CFRP stay cables
[J].
Experimental and numerical study of lateral cable rupture in cable-stayed bridges: case study
[J].DOI:10.1061/(ASCE)BE.1943-5592.0001227 [本文引用: 1]