我国生活垃圾焚烧厂以炉排炉和流化床为主,焚烧处置过程主要包括垃圾给料、炉内焚烧、末端排放、灰渣转运等. 目前垃圾焚烧过程控制主要依赖运行人员通过分散控制系统(distributed control system, DCS)对焚烧炉进行手动调参,自动化程度低,在垃圾入厂计量、焚烧工况优化、环保监管、污染物排放反馈调控、预警及决策分析、日常生产及运营、数据驱动等过程的智能化控制方面亟待提升[4]. 由于垃圾焚烧炉以处置垃圾、控制污染、利用低品位热能为首要目的,构建焚烧优化和污染物排放的超前预测和闭环控制系统尤为重要.
在垃圾焚烧炉运行中,炉内烟气温度低、缺氧燃烧、垃圾混合不均等,易使焚烧工况恶化,易使焚烧过程中多氯代二苯并-对-二噁英及多氯代二苯并呋喃(polychlorinated dibenzo-p-dioxins and dibenzofurans)增量,并可能导致常规污染物浓度如NOx、CO、SO2等超标[7-9]. 目前焚烧过程优化和控制二噁英排放的主要方法为“3T+E”,即控制炉膛出口温度高于850 ℃,烟气停留时间大于2 s,且具有较大的湍流度和合适的过量空气系数[10-12]. GB18485-2014[13]生活垃圾焚烧污染控制标准中规定,生活垃圾焚烧炉炉膛温度(取DCS温度)应高于850 ℃,如在低于850 ℃情况下焚烧垃圾,依据《大气污染防治法》(
1. 研究方法
1.1. 研究对象
所研究的某生活垃圾焚烧锅炉为异重循环流化床、单锅筒结构,自然循环. 额定参数如下:日垃圾处理量400 t/d,额定锅炉蒸发量40 t/h,蒸汽压力3.82 MPa,过热蒸汽温度450 ℃,锅炉排污率2%,一次风温度237.5 ℃,二次风温度219.8 ℃,排烟温度148.7 ℃,锅炉焚烧系统热效率78.9%. 在正常运行中,该锅炉通常掺有质量分数为5%的煤炭,混合燃料的低位发热量为6019.3 kJ/kg.
1.2. 850 ℃-2 s烟气停留时间计算
垃圾焚烧炉中生活垃圾焚烧所需的O2直接来源于空气,为了保证充分燃烧,进入炉膛的空气都是过剩的. 烟气的主要成分有N2、O2、SO2、CO2、H2O,还有少量的CO、SO3、H2、CH4和其他CnHn.
N2主要来自于空气,垃圾中也含有少量的N,O2来源于过剩空气,CO2、SO2和SO3主要是垃圾中的C、S与O反应的生成物.
1.2.1. 理论空气量的计算
单位质量收到基垃圾中可燃组分为碳、氢、硫,故1 kg收到基垃圾中C、H、O完全燃烧所需理论氧气体积(m3)分别为
式中:
为了抵消收到基垃圾内所含O的影响,其对应理论氧气体积可以折算为
式中:
假定1 kg干空气中水蒸汽质量d为10 g,单位质量垃圾燃烧所需理论空气体积(
由此,单位质量垃圾燃烧所需理论空气体积V0(0 ℃,101 kPa)为
由于流量计测得的一、二次风流量是在20 ℃、101 kPa的条件下,故须进行温度换算. 同时,为了保证垃圾充分燃烧,在设计时会根据电厂的过量空气系数a计算实际空气体积流量q,表达式如下:
式中:q1、q2依次为流量计测得的一次风量、二次风量,
由此,可以根据理论CO2、SO2、N2、H2O量计算得到单位质量垃圾燃烧产生的理论烟气量:
式中:w(mois)为垃圾中水的质量分数.
式(8)中的入炉垃圾各收到基元素分析值、水分质量分数分析、热值分析如表1所示. 表中,Qnet为低位发热量. 表中在不同运行时间采集的样本在组分和热性质上存在空间和时间的非均一性,因此在未来预测模型工程应用过程中,可基于实时物料分组进行修正.
表 1 入炉垃圾元素分析及水的质量分数、热值分析
Tab.1
| 样本 | w(C) / % | w(H) / % | w(O) / % | w(N) / % | w(S) / % | w(Ash) / % | w(mois) / % | Qnet/ (kJ·kg−1) |
| 样本1 | 32.3 | 4.1 | 27.1 | 0.4 | 0.1 | 18.7 | 17.3 | 11 912.2 |
| 样本2 | 35.3 | 4.9 | 27.4 | 0.5 | 0.1 | 11.5 | 20.4 | 14 031.2 |
| 样本3 | 31.4 | 5.0 | 19.0 | 0.7 | 0.1 | 10.8 | 34.0 | 12 250.0 |
在垃圾完全燃烧且忽略CO产生的情况下,在一定的垃圾投料速率
1.2.2. 烟气停留时间计算
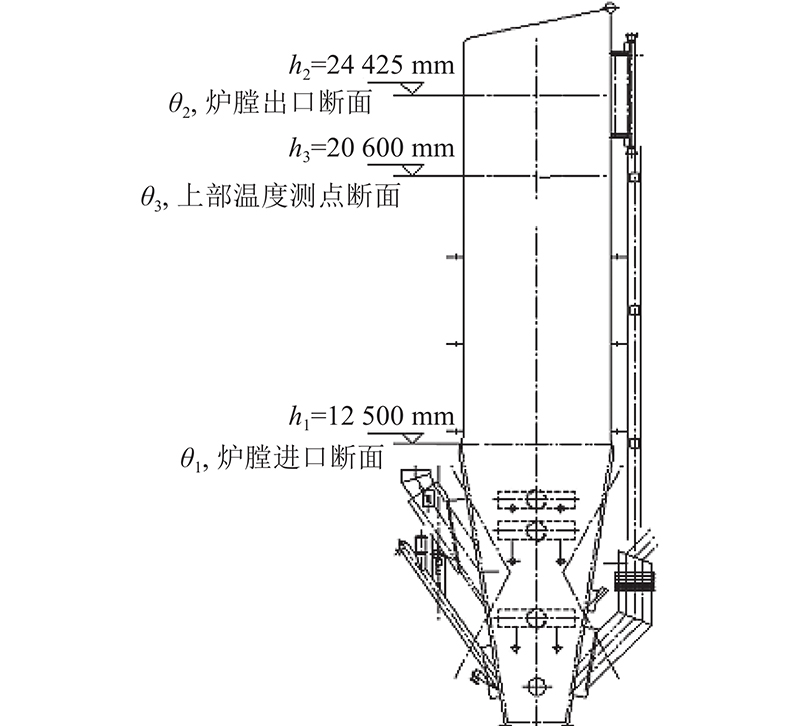
图 1
图 1 流化床炉膛内“850 ℃-2 s”烟气停留区域示意图
Fig.1 Schematic diagram of flue gas staying area of “850 ℃-2 s” in fluidized bed MSW incinerator
当炉膛出口断面烟气温度θ2≥850 ℃时,烟气停留区域为炉膛进口断面至炉膛出口断面,二次风断面处折算烟气量表达式为
炉膛出口断面折算烟气量表达式为
则在烟气850 ℃要求炉膛范围内,烟气平均体积流量可以由下式计算得到:
由此,可以计算得到烟气流速:
式中:S为烟道截面积.
进而可以计算得到烟气停留时间:
式中:H为停流区域高程.停留区域高程
当炉膛出口断面烟气温度θ2≤850 ℃时,烟气的停留区域为炉膛进口断面至靠近炉膛出口的850 ℃断面,此时靠近炉膛出口的850 ℃断面标高为
由此,炉膛进口断面烟气量可以由式(9)计算得到,靠近炉膛出口850 ℃断面的烟气量表达式为
则在烟气850 ℃要求炉膛范围内,烟气平均流量表达式为
由此,可以计算得到烟气流速:
最后,当炉膛出口断面烟气温度θ2≤850 ℃时,与式(14)计算过程一致,烟气停留时间T可以由上文计算的烟气停留区域高程H和烟气流速v相除获得.
1.3. 数据分析
基于烟气在“850 ℃-2 s”区域停留时间的机理和垃圾焚烧过程,通过控制软件AutoThink增加“850 ℃/2 s认证”点位,编入上述计算过程,每周定期对垃圾特性进行核准修正,将相关参数数据输入系统,可以获取炉膛内高温烟气停留时间并显示. 同时在炉膛出口预留的2处竖直管道处(DN80)安装体积流量计,采用法兰连接取压管通过预留管道插入烟道,并通过取压管上部的法兰与管道法兰连接. 采集到的体积流量信号由变送器经屏蔽线传输到控制机柜,由DCS系统进行信号转换. 通过实测体积流量和理论计算体积流量进行对比,验证计算结果准确性. 当两者出现偏差较大情况时,及时对一、二次风进风管进行检漏、校准一、二次风流量计、排查炉膛内温度测点等,做出整改,以达成数据修正. 经较长周期验证后,发现计算得到理论体积流量和所安装的威力巴均速管流量传感器的体积流量基本一致(误差<12%),验证了计算得到烟气停留时间的有效性.
经周期运行后导出运行数据,基于皮尔逊相关系数计算:
同时,对多组运行数据与烟气停留时间进行关联性分析(见表2),筛选机理上无关的参数并将其除外. 最终选取关联系数较大(0.8<ρ<1.0)的参数,具体包括:上部断面均温、中部断面均温、二次风喷入温度、旋风筒下部均温、补偿后一次风流量、一次风机出口压力、补偿后二次风流量、二次风机出口压力、炉膛出口温度和空预器出口一次热风均温等,舍弃其余无关系数,构建炉内关键运行数据和炉膛内烟气停留时间的关联模型.
表 2 运行参数与“850 ℃-2 s”烟气停留时间关联系数表
Tab.2
| 运行参数 | 相关系数 | 运行参数 | 相关系数 | 运行参数 | 相关系数 | ||
| 烟气DUST | 0.112 29 | 一次风机出口压力 | 0.912 32 | 空预器出口二次热风温度右 | 0.969 49 | ||
| 烟气HCl | 0.212 85 | 补偿后一次风流量 | 0.984 51 | 旋风筒出口烟气温度(左) | 0.106 55 | ||
| 烟气O2 | 0.525 43 | 二次风机出口压力 | 0.862 13 | 旋风筒出口烟气温度(右) | 0.205 64 | ||
| 烟气H2O | 0.100 78 | 补偿后二次风流量 | 0.978 78 | 喷水减温器进口蒸汽温度 | 0.196 71 | ||
| 烟气SO2 | −0.335 51 | 密相区出口压力(左) | −0.131 56 | 喷水减温器出口蒸汽温度 | −0.505 82 | ||
| 烟气NOx | 0.392 01 | 密相区出口压力(右) | −0.002 35 | 省煤器出口水温 | −0.220 36 | ||
| 烟气CO | −0.470 88 | 中部断面均温 | 0.919 32 | 补偿后给水体积流量 | 0.156 56 | ||
| 烟气流速 | 0.413 88 | 上部断面均温 | 0.928 84 | 炉膛出口温度 | 0.871 81 | ||
| 吸收塔前温度 | 0.047 27 | 炉膛出口压力(左) | 0.000 41 | 排烟温度 | −0.613 82 | ||
| 反应塔后压力变送器 | 0.030 15 | 炉膛出口压力(右) | −0.107 32 | 烟气处理设备出口烟气温度 | 0.593 85 | ||
| 布袋除尘空气压力 | 0.231 38 | 炉膛出口右温度 | −0.406 13 | 烟气处理设备入口烟气压力 | −0.314 86 | ||
| 布袋除尘器差压 | −0.309 85 | 炉膛出口左温度 | −0.504 52 | 烟气处理设备入口烟温 | 0.280 06 | ||
| 布袋除尘器后温度 | 0.402 67 | 旋风筒下部温度(左) | 0.851 88 | 给水温度 | 0.263 19 | ||
| 除尘器烟气体积流量 | 0.368 66 | 旋风筒下部温度(右) | 0.963 31 | 给水压力 | 0.437 10 | ||
| 除尘器后差压(体积流量计) | 0.272 06 | 返料物料温度(左) | −0.409 56 | 主汽集箱出口蒸汽压力 | −0.140 27 | ||
| 风室温度(左) | 0.621 17 | 返料物料温度(右) | −0.327 49 | 主汽集箱出口蒸汽温度 | −0.145 79 | ||
| 风室温度(右) | 0.620 30 | 左侧返料流化风压 | −0.162 98 | 主汽集箱蒸汽压力 | 0.387 53 | ||
| 炉膛下部压力(右) | −0.062 88 | 右侧返料流化风压 | −0.183 75 | 主汽集箱蒸汽温度 | −0.300 52 | ||
| 沸下温度(前左) | 0.229 23 | 一次风喷入温度 | 0.901 22 | 主蒸汽体积流量 | 0.407 25 | ||
| 沸中温度(右) | −0.585 89 | 空预器出口二次热风温度左 | 0.927 511 | 汽包水位 | −0.151 18 |
1.4. 关联预测模型构建
本研究构建多种拟合模型对850 ℃以上的烟气停留时间进行预测,包括:基于Matlab平台中的Neutral Fitting工具箱对反向(back propagation, BP)神经网络预测模型进行构建;基于Python编程并对sklearn库中基准模型调参和机器学习,构建循环神经(recurrent neural network, RNN)网络预测模型和随机森林(random forest regression, RFR)预测模型,对应进行拟合计算. 具体过程如下.
1.4.1. 反向传播神经网络构建关联模型
反向传播神经网络信号进行前向传播,而误差通过逆向传播. 在进行数据处理前无需明确关系方程,即可自主训练,逼近期望因变量数值. 训练后的神经网络可以自行处理类似样本的自变量数据,并输出最理想因变量预测数值,预测炉膛内850 ℃烟气停留时间.
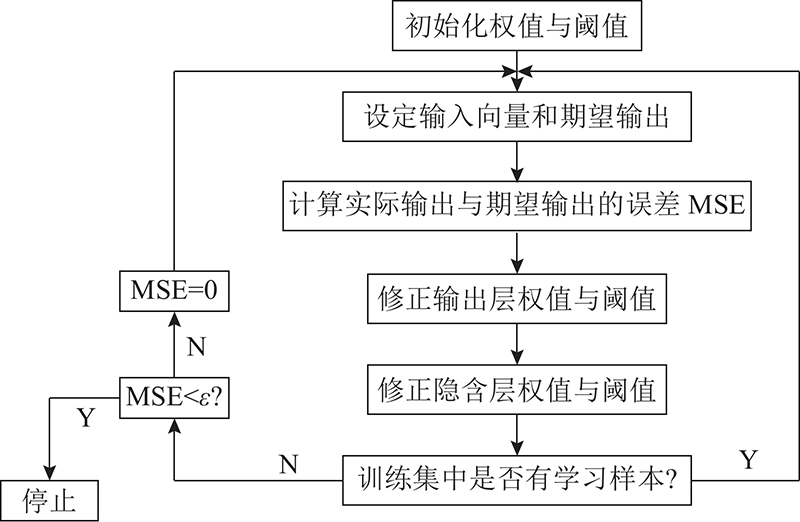
算法流程如图2所示,包括:1)导入输入和输出数据,归一化处理输入和输出数据;2)神经网络训练,初始化网络、网络训练;3)神经网络预测,预测数据归一化处理、输出数据的反归一化;4)输出结果绘图,预测输出、预测误差、预测误差百分比.
图 2
1.4.2. 循环神经网络构建关联模型
循环神经网络(recurrent neural network, RNN)以序列数据为输入,将所有节点按链式连接,随演进方向递归. 其神经元在某时刻的输出可以再次输入神经元,适合处理时间序列数据,可以保持数据中的依赖关系. 使用循环神经网络可以通过其较强的计算能力和联想记忆功能处理关键烟气运行参数数据集,并输出理想的850 ℃以上的烟气停留时间预测值.
循环神经网络由输入层、隐藏层和输出层组成,如图3所示. 图中,x表示输入层的向量值,s表示隐藏层的向量值,U表示输入层至隐藏层的权重矩阵,o表示输出层的向量值,V表示 隐藏层到输出层的权重矩阵. 循环神经网络隐藏层的值s不仅仅取决于当前输入x,还取决于上一次隐藏层的值s. 权重矩阵W以隐藏层前馈值作为本次输入的权重. 该网络在t时刻接收到输入xt之后,隐藏层的值为st,输出值为ot.
图 3
1.4.3. 随机森林算法构建关联模型
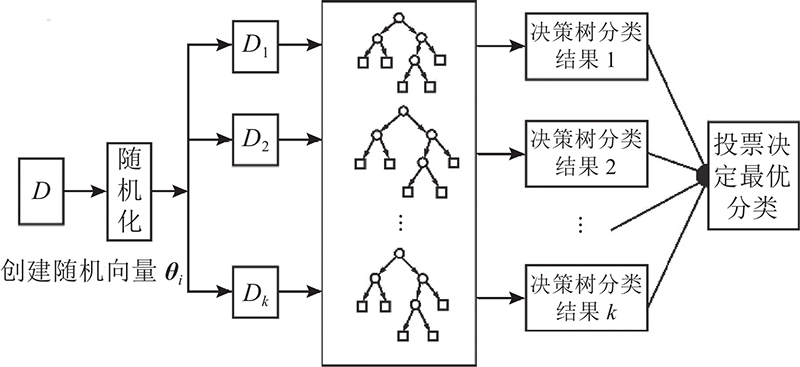
随机森林算法基于决策树思想,通过训练样本生成多棵决策子树形成森林,最后将子树结果汇总作为最终结果. 如图4所示,随机森林是一组由决策子树
图 4
式中:h(x, θt)表示基于x和θ的输出.
随机森林引入Bagging思想和随机子空间思想,随机抽取f个特征,并从中选择出最优特征进行节点分裂并构建单棵决策子树,基于均方误差建立回归树,通过实现样本选取随机性和特征选取随机性,重复上述过程建立T棵决策子树,形成森林. 最终综合决策子树的预测情况,结合集成学习思想将各决策子树结果汇总作为输出.
本研究选用回归模型,通过取平均方式,获得最终的结果,从而实现通过各炉膛内运行参数预测炉膛内850 ℃烟气停留时间的目的.
2. 结果与讨论
2.1. 反向传播神经网络
2.1.1. 反向传播神经网络构建
反向传播神经网络中程序编码主要分为以下几部分.
1)设计输入输出层. 以每组数据的各项自变量xi (i=1~10)为输入,以焚烧炉内烟气在850 ℃以上温度段停留时间作为输出;本模型的输入层节点数为10,输出层节点数为1.
借助式(21)计算得到l=4~13. 给定l初始值为7,经测试发现当l=10时,整体预测效果较好.
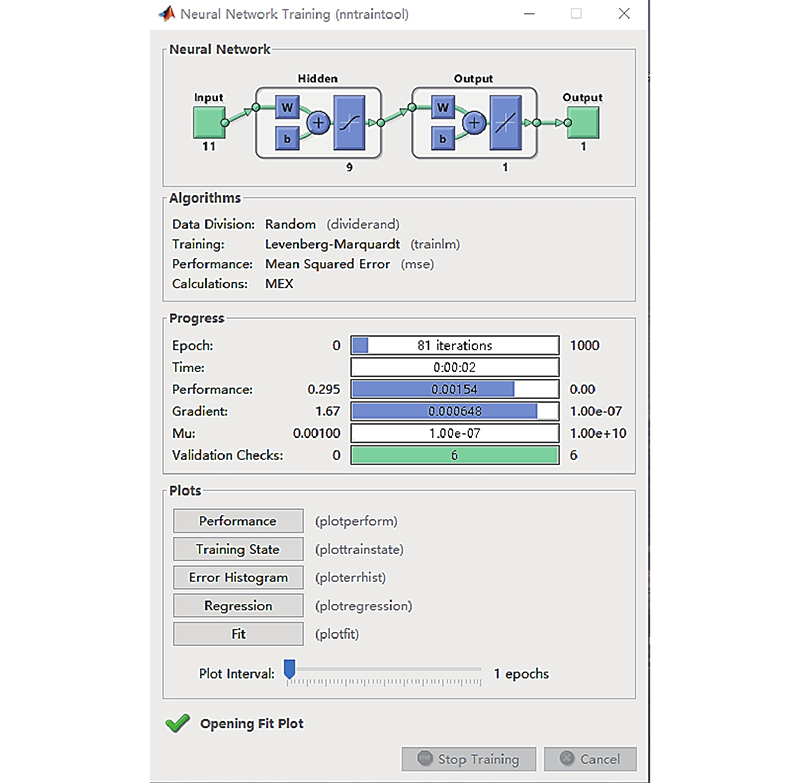
3)选择和设定激励函数. 反向传播神经网络模型网络在Matlab中的具体参数如下:设定Trainlm函数作为网络训练函数,Levenberg函数作为权值/阈值的学习函数,MSE函数作为网络性能函数,隐层神经元数目初设值为10;设定网络迭代次数Epochs为1000次,目标期望误差Goal为0.00002,学习速率LR为0.1;随机选择80%的数据进行网络训练,20%的数据进行验证和测试.
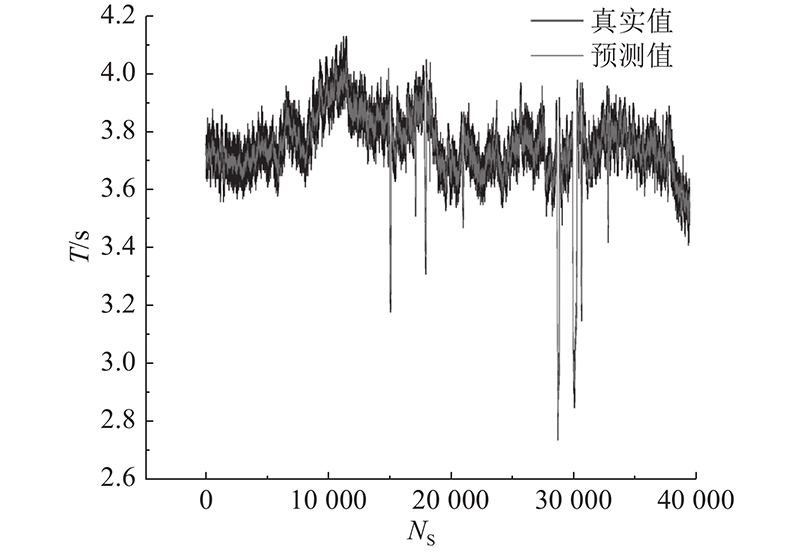
2.1.2. 反向传播神经网络拟合结果
在输入全过程参数和部分强关联性的关键运行参数的网络训练过程中,对训练数据、测试数据、样本数据以及整体数据进行回归分析,R值均高于0.95. 说明网络训练效果优秀,特别是测试数据的R值接近训练和验证数据的R值,证明了模型具有较高的预测置信度.
图 5
图 6
图 7
图 8
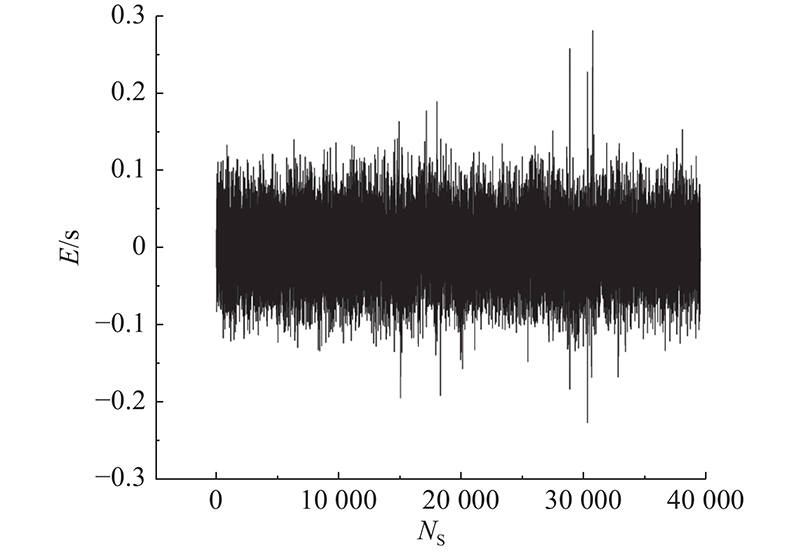
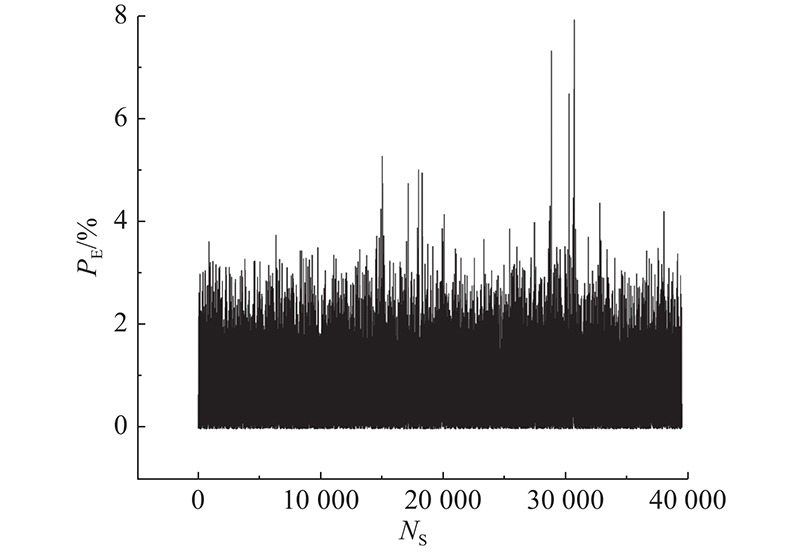
经过上述模型建立、测试以及结果分析发现,利用反向传播神经网络建立的模型的预测结果虽然存在一定误差,但整体来看其预测性能表现良好,具有一定稳定性和可靠性,通过优化反向传播神经网络模型进行训练可以取得更好的预测性能.
本研究所构建的反向传播神经网络模型的预测输出存在不可忽略的误差,分析原因如下:反向传播神经网络模型收敛速度慢,隐藏层未能耦合输出前一时刻的输出数据,且只能以经验选定神经网络结构,难以准确映射焚烧炉运行参数间的复杂时间关系,因此还须进一步优化,如使用循环神经网络模型之类的结构更复杂的模型以优化输入.
图 9
2.2. 循环神经网络
2.2.1. 循环神经网络构建
循环神经网络的设计过程包含4个部分:数据预处理、模型建立、结果预测和模型优化.
1)数据预处理. DCS系统导出实时运行数据并选取关联性较高的部分数据作为输入样本,包括上部断面均温、中部断面均温、二次风喷入温度、旋风筒下部均温、补偿后一次风体积流量、一次风机出口压力、补偿后二次风体积流量、二次风机出口压力、炉膛出口温度和空预器出口一次热风均温. 以总样本的80%作为训练集,其余20%作为测试集.
2)模型建立. 首先,采用分位数均匀分布映射Quantile Transformer对10维输入参数进行归一化,并使用均值标准差法Standard Scaler对目标参数(炉内停留时间)进行归一化. 其次,对神经网络权重W进行初始化,设置隐藏层为10层,采用Adam优化器并设置学习率为0.01,设置均方误差为损失函数.
3)模型训练与预测. 模型通过前5 s的数据预测后1 s的数据,在模型训练完成后,将测试集中的自变量参数输入模型中,最终得到输出预测值. 另外,计算各样本预测值与标签值的误差绝对值的均值作为模型训练情况的标准.
4)模型优化. 采取训练步数(Epoch)和学习率(LR)寻优的方式,对模型训练过程进行优化. 通过改变Epoch寻找预测效果最好的模型,另外,使用学习率降低的方法,在训练误差停止下降时,降低学习率提升模型预测精度,避免模型局部回归.
2.2.2. 循环神经网络拟合结果
图 10
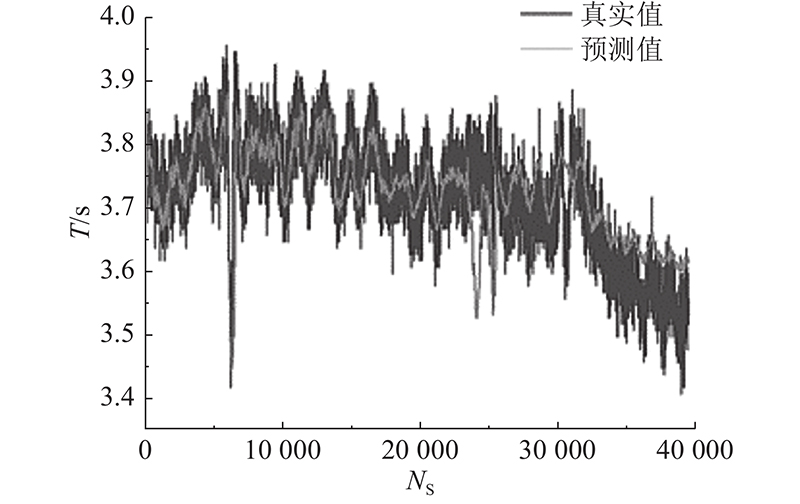
图 10 循环神经网络真实值与预测值对比图
Fig.10 Comparison of true values and predicted values of RNN
图 11
图 12
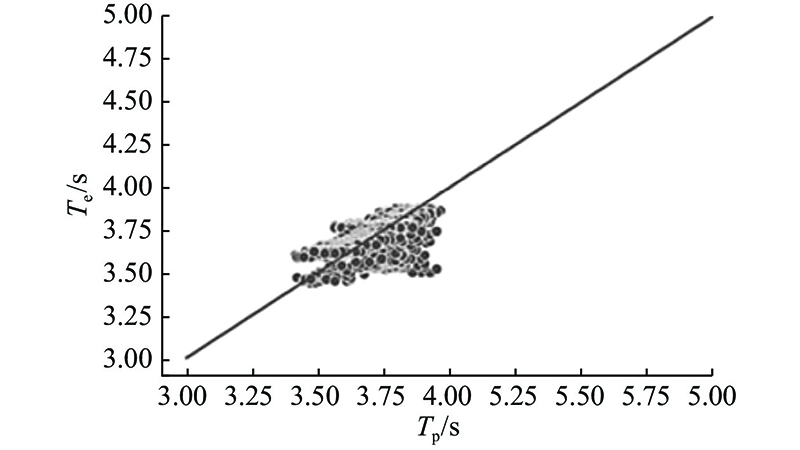
如图13所示为850 ℃烟气停留时间预测输出Tp、期望输出Te散点图. 可以看出,预测散点基本在标准线附近,说明拟合效果较好,但是仍然存在有一些预测点离标准线有一定的偏移. 这是训练样本容量限制导致的训练误差. 由于训练样本中目标数据大范围波动的情况的样本存在较少,神经网络未能更好地耦合处理实际运行中数据大范围波动的情况.
图 13
图 13 循环神经网络预测值与真实值散点图
Fig.13 Scatter plot of RNN predicted value and true value
结果表明,焚烧炉基本运行数据与高温烟气停留时间之间存在强非线性相关性,循环神经网络模型较反向传播神经网络对实际垃圾焚烧炉的泛化性能更好,能更准确地映射变量间的时间关系,其构建的数学模型为优化垃圾焚烧排放提供理论基础和借鉴价值.
2.3. 随机森林算法
2.3.1. 随机森林模型构建
随机森林回归总体设计主要包括:数据准备、模型建立、结果预测和参数寻优.
1)数据准备. 根据1.3节的数据分析,选取以下数据作为特征数据:炉上部断面均温、炉中部断面均温、二次风喷入温度、炉旋风筒下部均温、补偿后一次风体积流量、炉一次风机出口压力、补偿后二次风体积流量、炉二次风机出口压力、炉膛出口温度、炉空预器出口一次热风均温.
2)模型建立. Bootstrap设置为Ture,使用MSE评估模型参数的准确度,子树数量设置为10,最小样本叶片设置为1,内部节点再划分所需最小样本数设置为2,其他参数设置为默认值,进行模型的训练.
3)结果预测. 将各样本预测值与标签值的误差的绝对值的均值作为评判模型准确度的标准.
4)模型寻优. 主要对Bootstrap、子树数量、最大特征数、决策树最大深度、内部节点再划分所需最小样本数、叶子节点最小样本数等超参数进行寻优.
2.3.2. 随机森林模型拟合结果
根据数据集数量,随机取80%作为训练集,20%作为数据集,将子树数量在10~200进行寻优,步长为10,由于数据集庞大,所得结果表明无关子树数量,其平均绝对百分比误差为0.84%,准确度均为99.16%,因此仅须选择子树数量为10的随机森林模型即可实现精准快速预测.
图 14
图 15
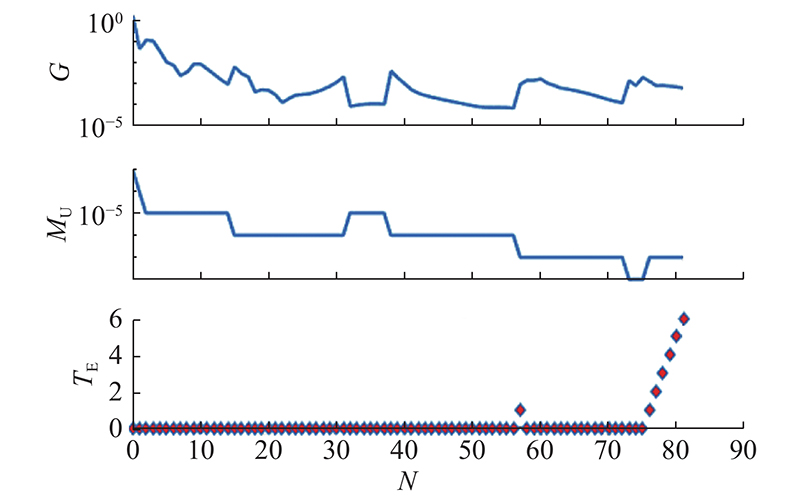
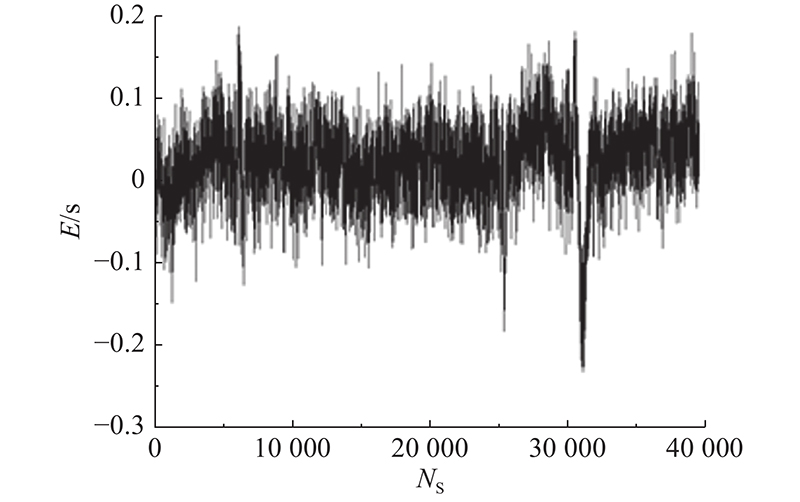
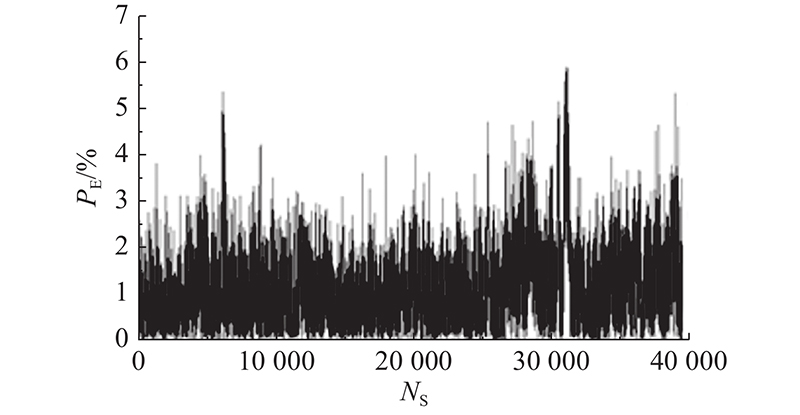
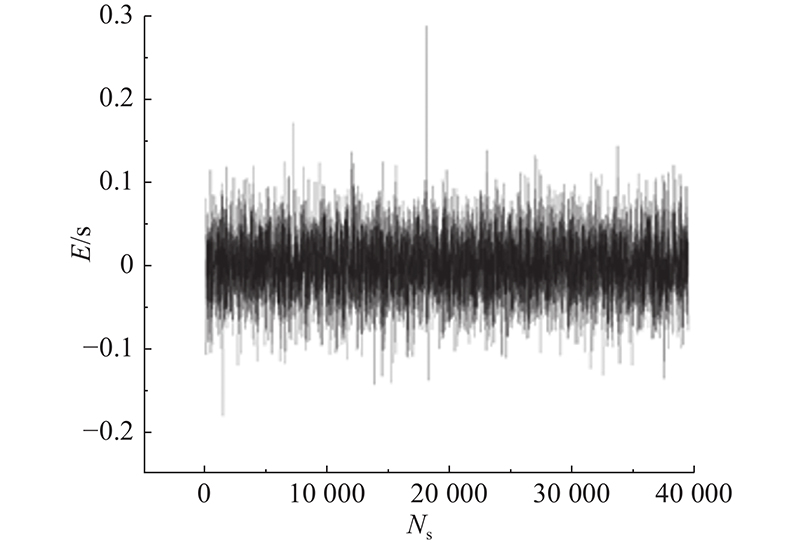
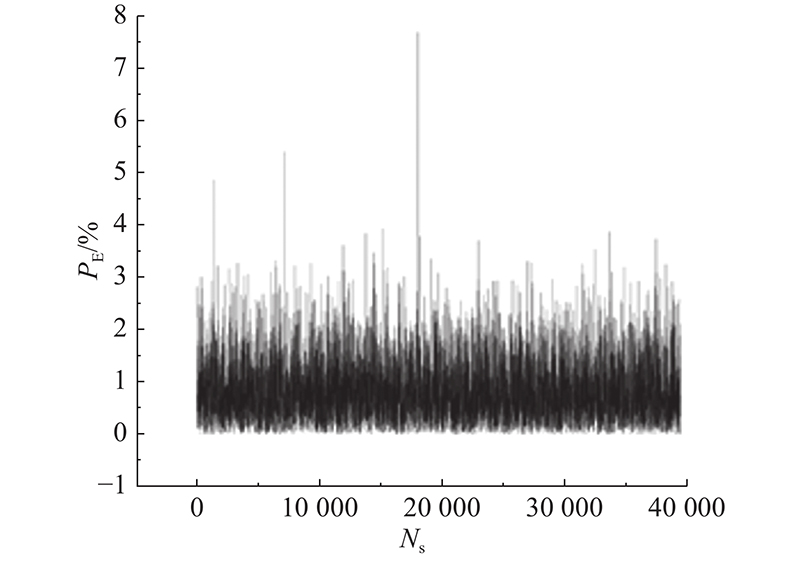
通过反向传播神经网络、循环神经网络和随机森林算法构建焚烧炉内关键烟气运行参数和高温烟气停留时间的关联预测模型,结果表明:1)反向传播神经网络建立的模型具有一定的可靠性,样片经第75次迭代后处于最好结果,其模型训练过程的MSE为0.015 672,经参数优化后拟合度为95.33%;反向传播神经网络模型难以解决垃圾焚烧炉的实例规模和网络规模间的矛盾问题. 2)循环神经网络可以利用内部记忆来处理任意时序的输入运行数据,将隐层输出延迟一个时间单元后与隐层输入一同再次输入隐层进行拟合,其模型训练过程的MSE为0.116 26,最终预测值与真实值的平均绝对误差为0.026 s,预测值与真实值的平均绝对误差百分比为1.17%. 整体来看,该预测模型能使预测绝对误差百分比低于4%,具有较好拟合效果. 3)随机森林算法构建的关联模型可以处理高维度数据,对运行数据集的适应能力强,且在模型生成过程中取得真实误差的无偏估计;该模型训练结果的平均绝对百分比误差为0.84%,准确度均为99.16%;但在存在一定噪音的运行数据样本集上,随机森林模型易陷入过拟合.
3. 结 语
本研究以某典型生活垃圾焚烧流化床锅炉为研究对象,构建了高温区域烟气停留时间的热力学计算模型,并对焚烧炉系统各运行参数与烟气停留时间进行了皮尔逊关联性分析,筛选获得了10个与烟气停留时间强关联的运行参数,如炉膛断面均温、一二次风温度及压力和炉膛出口温度等.
在此基础上,通过反向传播神经网络、循环神经网络和随机森林算法构建焚烧炉关键运行参数和高温烟气停留时间的关联预测模型,结果表明3种模型中循环神经网络预测模型预测效果最好,相对最适于循环流化床垃圾焚烧炉.
本研究可以为运行工况优化、污染物排放超前控制和智慧焚烧管理提供支撑,但由于数据集容量的限制,模型在普适性上仍有欠缺. 未来可以采集不同生活垃圾流化床焚烧炉上的运行数据集,进行数据清洗、特征衍生、特征筛选等数据预处理和模型自适应优化,从而提升“850 ℃-2 s”预测模型的准确性和泛化能力.
参考文献
Development and prospects of municipal solid waste (MSW) incineration in China
[J].DOI:10.1007/s11783-008-0028-6 [本文引用: 1]
生活垃圾智慧焚烧的研究现状及展望
[J].
Review and outlook on municipal solid waste smart incineration
[J].
Reduction of polychlorinated dibenzo-p-dioxins and dibenzofurans by chemical inhibition and physisorption from a municipal solid waste incineration system
[J].DOI:10.1021/acs.energyfuels.0c01918 [本文引用: 1]
Influences of PN-containing inhibitor and memory effect on PCDD/F emissions during the full-scale municipal solid waste incineration
[J].DOI:10.1016/j.chemosphere.2019.04.161 [本文引用: 1]
Potential role of chlorination pathways in PCDD/F formation in a municipal waste incinerator
[J].DOI:10.1021/es0497227 [本文引用: 1]
Modeling the formation of PCDD/F in solid waste incinerators
[J].DOI:10.1016/S0045-6535(02)00005-X
垃圾焚烧飞灰中主要元素的深度分布及形态
[J].
Distribution and chemical forms of major elements in MSWI fly ash
[J].
Sources and fate of PCDDs and PCDFs: an overview
[J].
Effect of different air pollution control devices on the gas/solid-phase distribution of PCDD/F in a full-scale municipal solid waste incinerator
[J].DOI:10.1016/j.envpol.2020.114888
Influence factors and mass balance of memory effect on PCDD/F emissions from the full-scale municipal solid waste incineration in China
[J].DOI:10.1016/j.chemosphere.2019.124614 [本文引用: 1]
Simultaneous suppression of PCDD/F and NOx during municipal solid waste incineration
[J].DOI:10.1016/j.chemosphere.2015.02.005 [本文引用: 1]
垃圾焚烧炉膛烟气温度计算模型的探讨: 满足烟气850 ℃以上停留2 s的监管要求
[J].
Discussion on the calculation model of flue gas temperature in waste incineration furnace: meet the supervision requirements that the flue gas Stays Above 850 ℃ for 2 s
[J].
层燃型垃圾焚烧锅炉的炉膛与炉膛温度简析
[J].DOI:10.19841/j.cnki.hjwsgc.2021.01.009 [本文引用: 1]
Brief analysis of furnace and furnace temperature of layer burning waste incineration boiler
[J].DOI:10.19841/j.cnki.hjwsgc.2021.01.009 [本文引用: 1]
Influence of start-up on PCDD/F emission of incinerators
[J].DOI:10.1016/j.chemosphere.2006.10.081 [本文引用: 1]
循环流化床锅炉炉膛横向 温度非均匀性模型研究
[J].
Modeling study on lateral temperature non-uniformity in CFB boiler furnace
[J].
An optimizing BP neural network algorithm based on genetic algorithm
[J].DOI:10.1007/s10462-011-9208-z [本文引用: 1]