车辆跟驰模型是一种微观交通流模型,是连接驾驶人微观驾驶行为和宏观交通流的桥梁,描述了在限制超车的单车道上行驶车队中相邻两车之间的相互作用. 对跟驰模型深入研究,有利于加深对交通流特性的认识,了解交通流的运行规律,提高交通仿真的真实性.
针对车辆之间的纵向静态作用关系的研究有很多. Newell[1]将速度与车头间距的函数关系引入跟驰模型. Bando等[2]提出优化速度(optimal velocity, OV)模型描述跟驰车与前导车之间的车头间距、速度差与跟驰车加速度的关系. Helbing等[3]根据实测数据对OV模型中出现的过高加、减速度问题进行改进,考虑相对速度对减速及加速过程的不同影响,提出广义力(generalized force, GF)模型. 姜锐等[4]在GF模型的基础上考虑到正速度差的影响,提出全速度差(full velocity difference, FVD)模型. 随后,基于FVD模型的改进不断涌现[5-7],其中王涛等[5]利用多前车的速度差信息建立多速度差(multiple velocity difference,MVD)模型. 杨龙海等[7]基于FVD模型中优化速度函数拟合精度不高的特点,提出改进优化速度函数的跟驰(modified full velocity difference,M-FVD)模型. 这些车辆跟驰模型参数值固定,加速度变化规律单一,无法体现交通流异质性对加速度的影响.
针对车辆间的纵向动态作用关系也进行了研究,Zhang等[8]考虑了安全车头间距和驾驶员敏感性的异质性因素,对OV模型进行了改进,提出动态安全距离模型(dynamic safety distance model,DSDM),模型在改善交通流稳定性和抑制交通拥堵方面具有显著效果,并且能够提高交通流的平均速度. Jin等[9]考虑了车道宽度的异质性条件对FVD模型进行了改进,提出基于非车道的全速度差(non-lane-based full velocity difference car following model,NLBCF)模型. Wang等[10]用双边界最优速度函数(dual boundary optimal velocity function,DBOVF)代替OV函数,提出了双边界最优速度模型(dual boundary optimal velocity model,DBOVM). 这些模型都对优化速度函数进行了改进,体现了交通流异质性对跟驰模型的影响,但没有考虑到交通流中不同类型驾驶员的异质性,忽略了在相同车头间距下速度的分布特征.
针对以上问题,本研究基于速度-车头间距的随机分位数回归函数,建立随机优化速度跟驰模型. 通过选择0到1.0之间的不同分位点值,用于表征不同的驾驶风格,可以反映在给定车头间距下不同分位点速度的变化情况,有利于提供仿真的维度,使仿真场景更加符合混合交通流异质性的特点. 分位数回归在计量经济学中已经获得了广泛的应用[11],能够反映数据整体的分布特征,增加了改进跟驰模型适用的数据集范围,对车队整体跟驰情况的描述更加准确,这是本研究的出发点. 基于分位数回归建立随机优化速度跟驰模型;利用分位数回归获取不同分位点优化速度函数的参数值,并对随机优化速度函数进行稳定性分析;搭建仿真场景对建立的随机优化速度跟驰模型进行数值模拟,获取不同情景下的速度变化特征.
1. 问题描述与建模
1.1. 典型的优化速度函数
Bando以反正切函数为基础,经过推导分析,得到了实用性较强的优化速度函数(optimal velocity function)[2]:
式中:
1.2. 基于分位数回归改进的随机优化速度函数
1.2.1. 分位数回归模型
作为均值回归的补充模型,分位数回归已经获得了广泛的应用,分位数回归模型强调条件分位数的变化,放宽了假设条件(残差项无须服从正态性、方差齐性),可以根据不同分位点得到对应的回归方程,可以直观地描述非中心位置自变量对因变量的变化. 分位数回归模型的目标函数为最小化加权误差绝对值之和,采用带简单边界约束的拟牛顿算法进行求解[12]. 分位数回归模型的基本定义为
式中:
1.2.2. 随机优化速度函数
基于分位数回归构建随机优化速度函数模型,充分挖掘数据中隐含的信息,改进后的优化速度函数为
式中:
将建立的随机优化速度函数应用于FVD跟驰模型,可以得到
式中:
2. 数据来源与稳定性分析
2.1. 数据来源
TransGuide交通管理系统基于环形探测器和摄像机检测每20 s所有车辆的信息,包括车辆的速度、20 s的交通量以及每辆车通过检测器的时间[13]. 通过TransGuide系统选取单向三车道I-10公路(中间车道)的交通流数据进行分析.
式中:
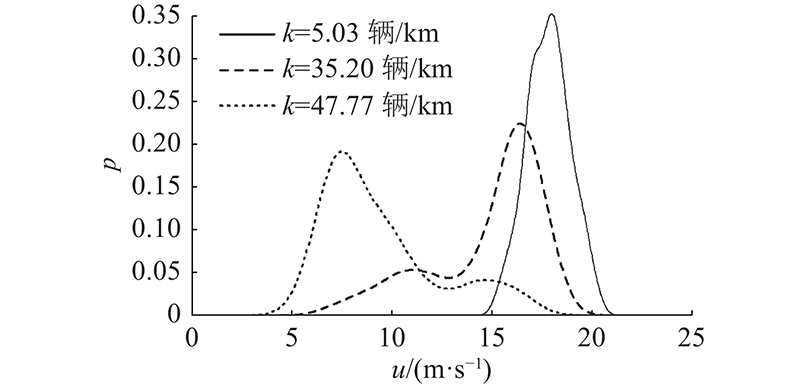
图 1
图 1 不同交通流密度下的速度概率分布
Fig.1 Speed distribution under different traffic flow densities
表 1 分位数回归模型拟合结果
Tab.1
| | | | | | | | | | | |
| 0.1 | 10.028 | 6.396 | 0.081 | 2.071 | 0.6 | 11.040 | 6.737 | 0.121 | 2.304 | |
| 0.2 | 10.423 | 6.476 | 0.095 | 2.226 | 0.7 | 10.990 | 7.051 | 0.115 | 2.059 | |
| 0.3 | 10.608 | 6.615 | 0.101 | 2.230 | 0.8 | 11.195 | 7.139 | 0.120 | 2.085 | |
| 0.4 | 10.840 | 6.408 | 0.125 | 2.619 | 0.9 | 11.512 | 7.327 | 0.129 | 2.071 | |
| 0.5 | 10.908 | 6.608 | 0.119 | 2.358 | − | − | − | − | − |
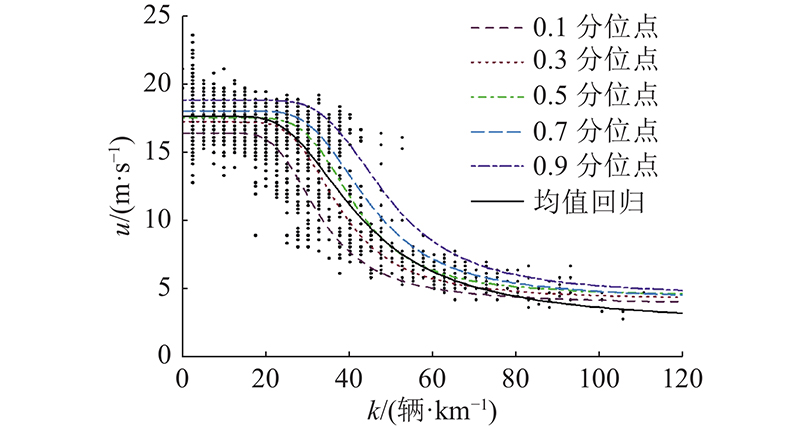
图 2
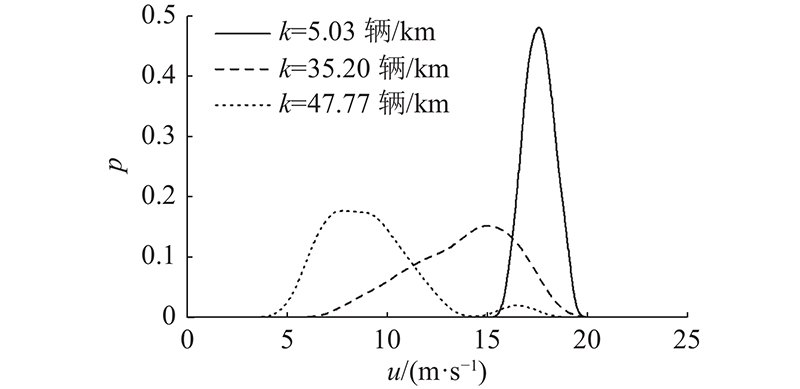
如图3所示为基于分位数回归在不同密度下得到的速度概率分布图,概率密度由
图 3
图 3 基于分位数回归在不同密度下的速度概率分布
Fig.3 Speed distribution under different densities based on quantile regression
表 2 原始数据-分位数回归拟合值的速度分布
Tab.2
| k (辆/km) | 原始数据速度分布 | 分位数回归速度拟合值分布 | |||||
| SK | N/ (km·h−1) | M/ (km·h−1) | SK | N/ (km·h−1) | M/ (km·h−1) | ||
| 5.03 | 0.003 | 17.780 | 17.963(0.352) | −0.086 | 17.230 | 17.564(0.447) | |
| 35.20 | −1.098 | 12.500 | 16.381(0.224) | −0.480 | 12.694 | 15.068(0.140) | |
| 47.77 | 1.049 | 11.250 | 7.510(0.191) | 1.435 | 11.775 | 7.581(0.164) | |
2.2. 稳定性分析
对基于分位数回归建立的随机优化速度跟驰模型采用傅里叶变换进行稳定性分析,得到的稳定条件为
式中:
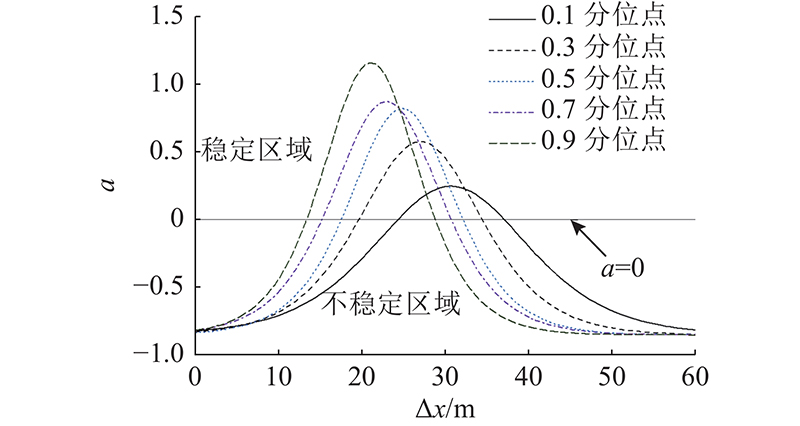
图 4
图 4
FVD模型稳定临界曲线(
Fig.4
Stability critical curve of FVD model(
3. 数值试验
3.1. 跟驰场景
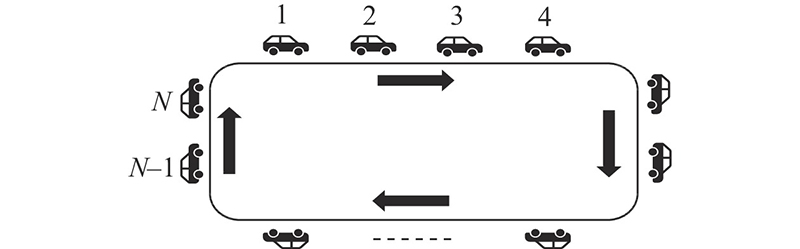
利用R语言对跟驰场景进行搭建和数值模拟,如图5所示为跟驰场景搭建的示意图. 仿真初始场景设置如下:80辆完全相同的车均匀分布在长度为2000 m的环形单车道道路上;每辆车初始时刻的车头间距为25 m,根据建立的随机优化速度函数计算该车头间距下的期望速度,以期望速度作为当前车辆的初始速度;所有车辆沿环路跟车行驶,考虑车辆行驶的平稳性,规定所有车辆的最大加速度为0.6 m/s2,最大减速度为3.0 m/s2.
图 5
3.2. 数值模拟
进行了2种类型的数值模拟实验:单一分位点车队行驶跟驰模型稳定性研究,仿真场景所有车辆速度变化特征一致;多分位点混合车队行驶跟驰模型稳定性研究,仿真场景不同车辆分配不同分位点速度变化特征.
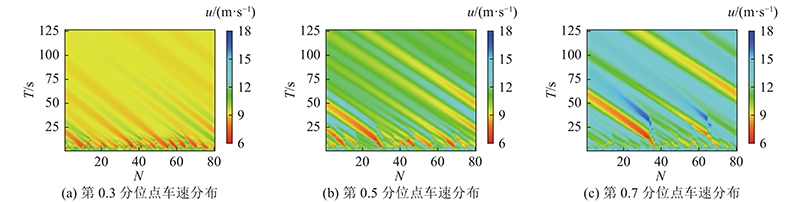
如图6所示为不同分位点跟驰模型的速度变化趋势图. 图中,T为仿真时间,N为车辆数. 时间长度为2000 s,时间精度为1 s,车头间距为25 m,反应系数为0.4,敏感系数为1.1(0.3、0.5和0.7分位点在车头间距为25 m时,车辆受到扰动后达到稳定状态的最小敏感系数为0.487、0.771和0.731),在t=1时,对所有车辆的速度添加扰动
图 6
式中:μ为初始振幅1 m/s,
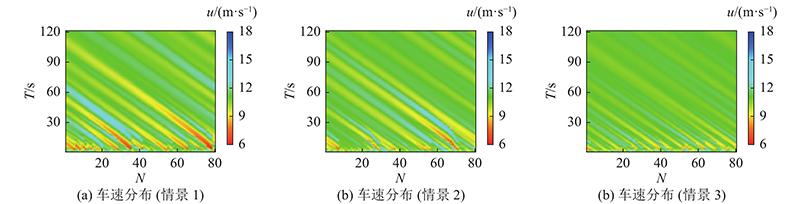
图 7
图 7 多分位点混合行驶车速分布
Fig.7 Speed distribution of mixed driving at multiple quantiles
图 8
图 9
3.3. 结果分析
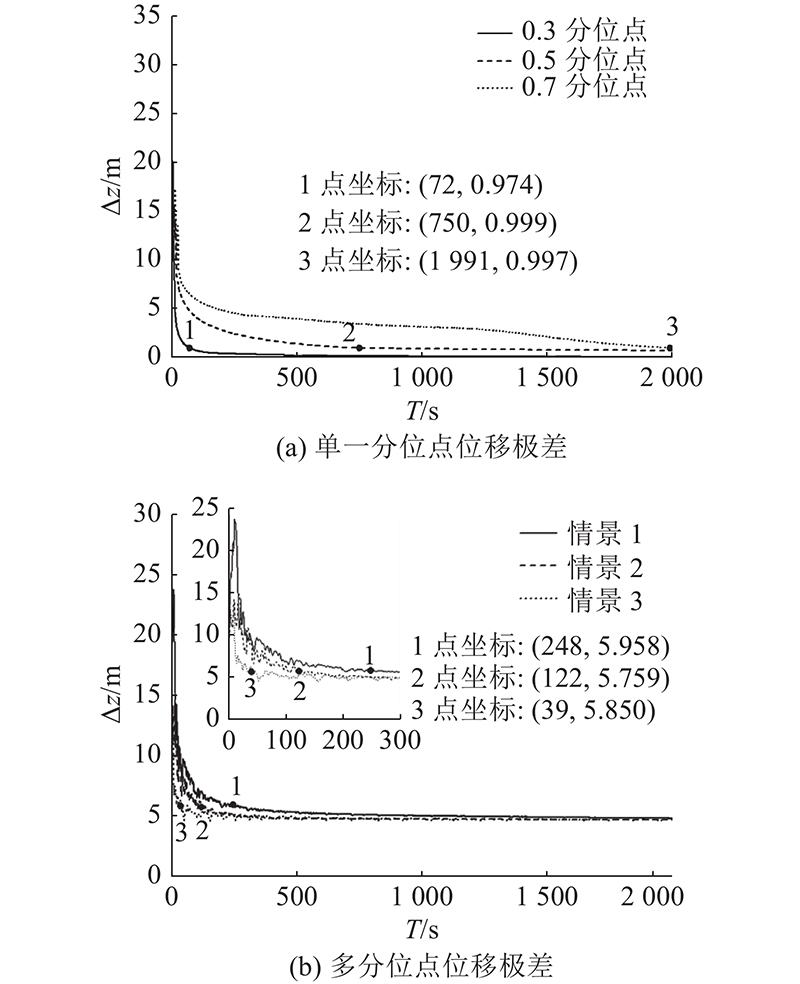
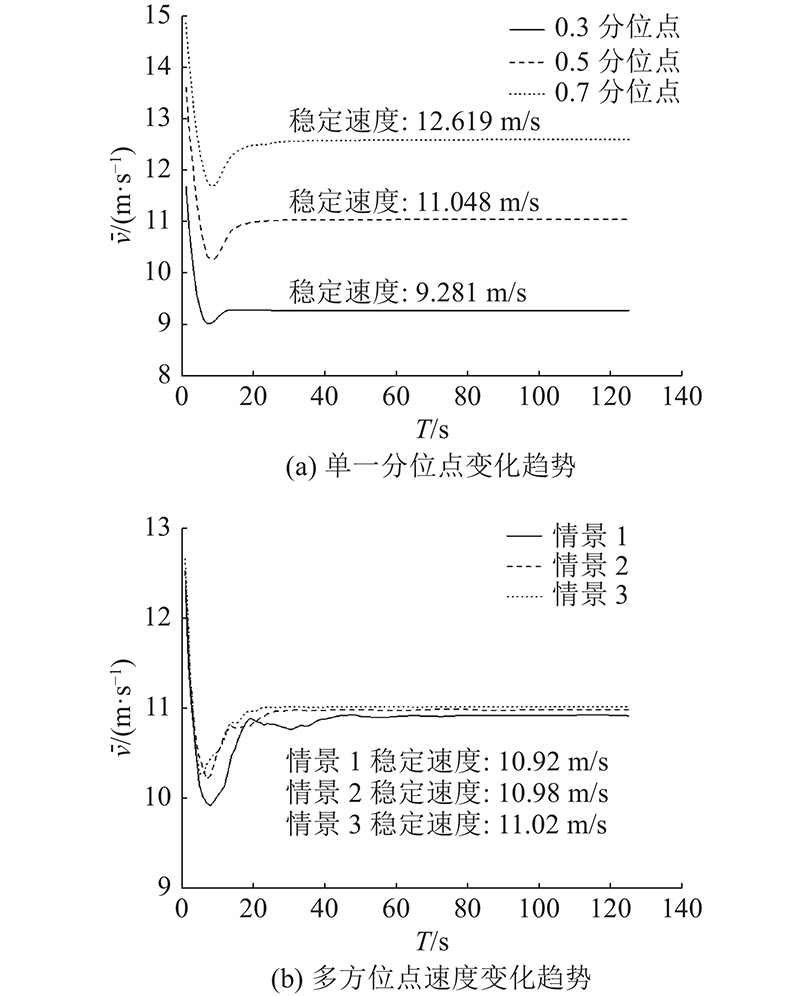
对单一分位点车队行驶得到的数值结果进行分析. 由图6可以看出,在车队行驶的过程中,当前车的速度发生变化时,后车的速度也会做出相应的变化,随着时间的增长,速度变化呈现出向后传播的带状区域;在相同的仿真设置条件下,3个分位点的速度变化呈现不同的趋势,图6(a)中驾驶员的期望速度(在车头间距为25 m时,期望速度为9.281 m/s)较低,且敏感系数较大(仿真场景设置的敏感系数为1.1,而0.3分位点所需的敏感系数为0.487),因此图6(a)中的车辆速度在受到扰动后能够在较短的时间恢复稳定. 结合图8(a)可以看出,0.3分位点车队达到稳定状态(位移极差小于1 m)所需时间为72 s,而0.5和0.7分位点车队达到稳定状态所需时间分别为750、1991 s. 由图9(a)也可以看出,0.3、0.5和0.7分位点车队达到稳定状态时的平均速度为9.281、11.048、12.619 m/s,与三者在车头间距为25 m时的期望速度(9.281、11.049、12.628 m/s)近似,反映出不同分位点的异质性.
对2种不同的仿真方式进行比较. 由图8可以看出,单一分位点达到稳定状态时的位移极差近似为0 m;多分位点达到稳定状态时的位移极差近似为5 m(其中情景3在1500仿真秒时车队中0.7、0.5、0.3分位点车辆平均车头间距分别为22.936、24.958、27.654 m). 由图9可以看出,单一分位点车队在不同的分位点车队的平均速度不同,且随着的分位点的增加,平均速度也会相应增加;多分位点车队3个情景中的平均速度较为接近,与0.5单一分位点车队的速度近似. 对比2种仿真方式,由于多分位点车队中存在0.3分位点车辆,相较于单分位点车队达到稳定状态的时间更短,且为了达到稳定的车队行驶速度,多分位点车队中不同分位点车辆的车头间距也不同.
4. 结 论
(1)所提出的分位数回归方法相较于均值回归能够反映交通流数据的整体分布特征,体现出交通流不同分位点驾驶员的异质性对速度分布的影响,能够有效提高仿真模型的维度,且基于分位数回归建立的随机优化速度跟驰模型在敏感系数为1.1、反应系数为0.4时均可达到稳定.
(2)单一分位点车队仿真结果表明,随着分位点的增加,车队达到稳定状态的时间也会增加,达到稳定状态的平均速度也会增加,能够反映理想状态下车队受到扰动后恢复稳定的运行特征.
(3)多分位点组合车队仿真结果表明,随着车队中0.5分位点车辆数的增多,车队达到稳定状态的时间会减少,而达到稳定状态的平均速度较为接近,且达到稳定状态时不同分位点车辆的车头间距不同,车头间距随着分位点的增加而减小.
本研究提出的随机优化速度函数对不同分位点的速度-车头间距进行了研究,但是对不同分位点跟驰模型的敏感系数和反应系数的选取仅停留在经验层面,因此下一步工作要收集数据对不同分位点的敏感系数和反应系数进行研究.
参考文献
Nonlinear effects in the dynamics of car following
[J].DOI:10.1287/opre.9.2.209 [本文引用: 1]
Dynamical model of traffic congestion and numerical simulation
[J].DOI:10.1103/PhysRevE.51.1035 [本文引用: 2]
Generalized force model of traffic dynamics
[J].DOI:10.1103/PhysRevE.58.133 [本文引用: 1]
交通流复杂动态特性的微观和宏观模式研究
[J].
Study on the complex dynamic properties of traffic flow from the micro and macro modelling
[J].
多速度差模型及稳定性分析
[J].DOI:10.3321/j.issn:1000-3290.2006.02.028 [本文引用: 2]
Multiple velocity difference model and its stability analysis
[J].DOI:10.3321/j.issn:1000-3290.2006.02.028 [本文引用: 2]
考虑前后车效应的反馈控制跟驰模型
[J].
A car-following model with considering control signals from front and rear
[J].
基于改进优化速度函数的跟驰模型研究
[J].DOI:10.16097/j.cnki.1009-6744.2017.02.007 [本文引用: 2]
Car-following model based on the modified optimal velocity function
[J].DOI:10.16097/j.cnki.1009-6744.2017.02.007 [本文引用: 2]
An improved car-following model considering desired safety distance and heterogeneity of driver’s sensitivity
[J].
Non-lane-based full velocity difference car following model
[J].DOI:10.1016/j.physa.2010.06.014 [本文引用: 1]
Optimal velocity model with dual boundary optimal velocity function
[J].
Random coefficient models for work zone headway distribution
[J].
Quantile regression methods for left-truncated and right-censored data
[J].DOI:10.1080/00949655.2015.1016433 [本文引用: 1]
基于随机参数线性回归的交通流速度-密度关系模型研究
[J].DOI:10.3969/j.issn.1006-8023.2021.05.012 [本文引用: 1]
Research on traffic flow speed-density model based on random-parameter linear regression
[J].DOI:10.3969/j.issn.1006-8023.2021.05.012 [本文引用: 1]
Traffic experiment reveals the nature of car-following
[J].DOI:10.1371/journal.pone.0094351 [本文引用: 1]