为了解决极小降压空间下管网的分区问题,本研究首先将谱聚类算法和MATLAB中的函数gamultiobj结合,确定了理想的分区BPs.然后通过设置一系列不同的最小服务水压,并将它们分别作为约束条件,运用函数gamultiobj得到BPs上设备的最优布置方案. 最后运用模拟退火算法找出需要更换管段的管径,使得分区后管网中所有节点的压力均可以满足最小服务压力.
1. 确定供水管网DMA分区的BPs
1.1. 谱聚类算法
将供水管网看作无向加权图,管网中的节点就是图中的顶点,节点和节点相连构成管段即为2个顶点的边,通过谱聚类算法将管网中的节点分区.分区的核心在于两节点间相似度(即管段权重)的确定,根据分区后不同分区间BPs的权重小,同一分区中管段权重之和高的特点,获得理想的分区结果.
1.2. 定义管网的相似度公式
若在体积流量较大的BPs上关闭阀门,会造成极大的水头损失,从而引起管网中其他节点水压大幅度的降低,极易使得管网末梢节点的水压不满足规定的最小服务水压.另一方面,若BPs的管径过大,会在无形之中增加分区改造的成本,因为无论是阀门或是体积流量计,其价格都随着管径的增加而成倍增大.此外,大管径往往对应着高体积流量,因此应尽量避免BPs的管径过大. 在BPs上安装关闭阀门,水质变差的风险会随着DMA截断管长度的增加而变大[9].综上所述,应选择体积流量较小、管径较小、长度较短的管段作为分区的BPs.故定义管网中两节点间的相似度为
式中:ωij、qV,ij、Dij、Lij分别为节点i、j之间管段的相似度、体积流量、管径、长度,N为管网中所有节点的集合,α、β、γ为相似度计算公式中的参数. 其中α、β、γ的选择会直接影响到分区BPs的结果,通过优化这3个参数的取值,达到选择出最优BPs的目的.
1.3. 确定α、β、γ的目标函数建立
为了减小分区后节点压力的波动,要求BPs的体积流量较小;为了减少分区成本,要求BPs管径较小;为了保证分区后截断管附近的水质安全,要求BPs的长度较短.此外,BPs数量越少,分区成本及后续运行管理难度也会越低.因此α、β、γ这3个参数的优化目标设为最小化BPs的数量nb、BPs的平均体积流量
式中:
1.4. 基于gamultiobj的优化方法
借助MATLAB中自带的求解多目标优化问题的函数gamultiobj确定3个参数的值.gamultiobj使用的算法是基于带精英策略的快速非支配排序遗传算法(NSGA-Ⅱ)改进的多目标优化算法[10]. 初始种群一般由随机产生的多个个体组成,每个个体由决策变量组成. 算法首先判断初始种群是否满足设置的终止条件,若满足则得到Pareto解集;否则种群进化一代,再一次进行判断,循环直至满足终止条件为止.种群进化一代由选择、交叉、变异、产生子种群、父子种群合并和修剪种群组成.选择是基于个体的序值和拥挤距离,从父种群中选择一定数量的个体,其中序值小的个体先被选中;当序值相同时,拥挤距离大的个体优先被选中. 对选择得到的个体进行交叉、变异,产生一个新个体的集合即子种群.将子种群和父种群合并成新种群,新种群的大小是父种群的2倍. 通过修剪算法从合并种群中选择出新种群,其规模与父种群相同,修剪算法是基于序值和拥挤距离进行的,序值高、拥挤距离小的个体被剔除[11]. 本研究中编码方式采用实数编码,决策变量即为相似度计算公式中的3个参数,在优化的过程中将它们的范围限制在区间(0,c),其中c可以通过多次试验确定,具体是使得α、β、γ在该区间,由此得到的规范化Laplacian矩阵在MATLAB中计算特征值和特征向量时不出现虚数.管网不同,c的选取也不相同,但对于同一管网的不同用水状态,c的确定可以参考上一用水状态,两者的差别较小或者无差别.
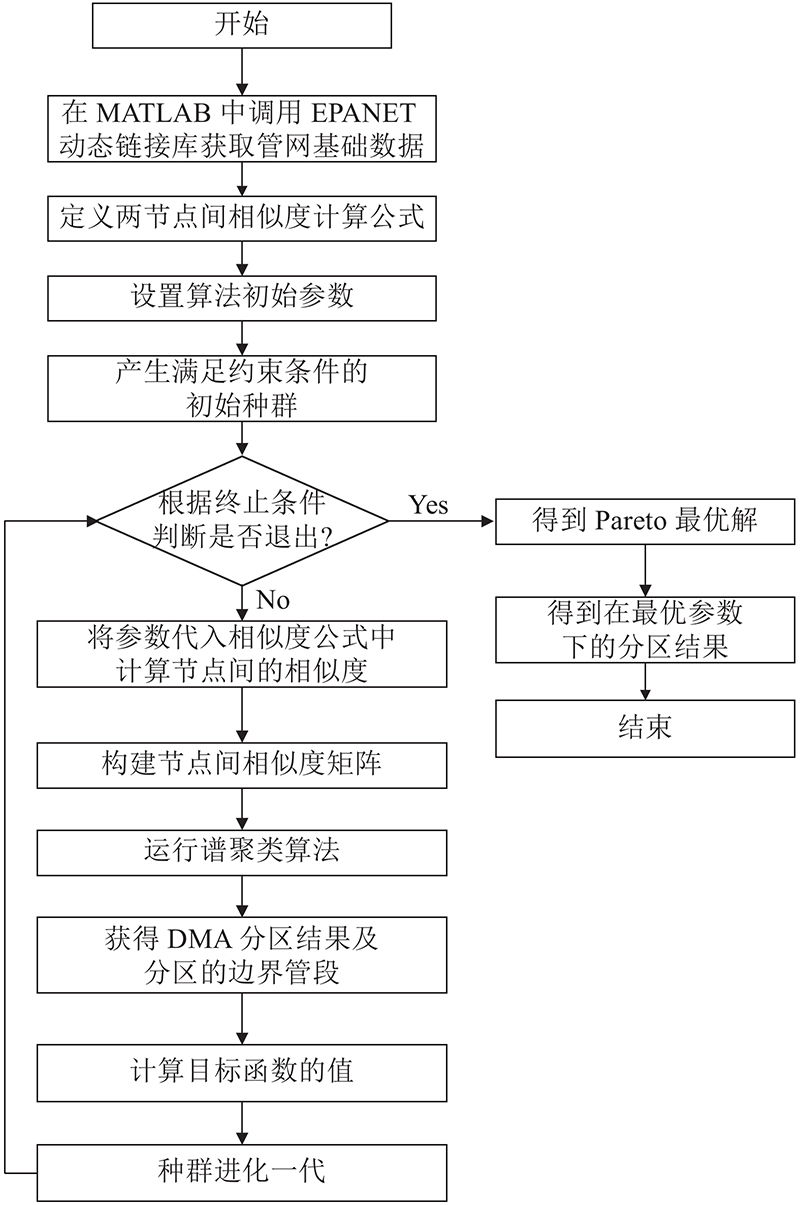
在MATLAB中调用EPANET动态链接库进行管网水力模拟,获取管网的基础数据.随机生成初始参数α、β、γ的值,在得到相似度之后构建管网的相似度矩阵,运行谱聚类算法得到分区结果和BPs,根据管网基础数据计算目标函数的值,然后种群进化一代,直到算法达到终止代数时输出得到的Pareto最优解,从中选出理想的参数值.将参数值代入相似度计算的公式中,计算后获得最终的分区结果和BPs,优化过程如图1所示.
图 1
图 1 分区边界管段确定的流程图
Fig.1 Flow chart for determination of partition boundary pipes
2. 优化BPs设备布置方案
2.1. 设置不同的最小服务水压
对于管网末梢降压空间极小的节点来说,一旦管网中新关闭阀门,其节点压力就会很容易低于规定的最小服务水压,因此在优化BPs上设备布置时,若是将规定的最小服务水压作为约束,很有可能会出现无解或解的质量很差的情况. 因此设置一系列不同的最小服务水压作为优化设备布置的约束条件,观察各个压力约束下解的情况,确定最优布置方案. 原则上每个DMA的入口最多为2个[12],否则容易造成监测误差过大,影响DMA分区效果甚至使得分区失效. 此外为了确保分区后管网水质安全,布置设备后的节点平均水龄不应高于分区前的水龄.在满足每个DMA入口数量要求和节点平均水龄限制的基础上,选择运行后能使低于管网规定最小服务水压的节点数量达到最少的设备布置方案. 这样在后续工作中只需要更换较少管段的管径便可以使管网中全部节点均满足规定的最小服务水压,从而能够节省DMA分区的投资成本. 另外,更换管径的管段数量越少,对管网水龄的影响就越小,能有效避免管网中水质的恶化.
2.2. BPs上布置设备的目标函数及约束条件
在定义DMA区域边界时,由于关闭了BPs上的阀门,从而引入了新的“死胡同”,可能会导致管段中水流出现停滞,使得管网水质受到影响.水龄作为常用的水质代替指标,水龄的变化可以较好地反映出水中温度、pH、氯浓度等指标的变化[13],简单的说,随着水龄的增大水质逐渐变差,故在BPs上布置设备后不应使管网的节点平均水龄增大,而应该尽可能减小水龄.另外,为了节省投资节约成本,设备的费用也应考虑进来.此外,在进行设备优化布置的计算中,必须满足节点连续性方程,能量守恒方程以及节点的水压约束,其中2大基本方程在EPANET2.2水力模拟中已经自动满足[14].指定BPs上设备布置的优化目标为最小化节点平均水龄
式中:M为管网中除水源外节点的总数目,ti为管网中节点i的节点水龄,Tv为BPs上安装阀门的数量,Cvalve,v为BPs上第v个阀门的价格,Tm为BPs上安装体积流量计的数量,Cmeter,m为BPs上第m台体积流量计的价格,A为管网的衔接矩阵,q为管段体积流量的列向量,Q为节点体积流量的列向量,L为管网的回路矩阵,h为管段水头损失的列向量,Hi为管网中节点i的实际水压,Hs,min为设置的管网最小水压,Hi,max为管网中节点i允许的最大水压.
2.3. 优化算法
仍借助函数gamultiobj求解设备的布置方案.决策变量为在BPs上安装阀门或者是安装体积流量计,其维度等于BPs的数量,编码方式采用二进制编码,其中“0”表示在BPs上安装体积流量计,“1”表示在BPs上安装阀门.因此最终得到的优化方案就是一串长度和BPs数量相等的由0和1构成的数字.依照先前指定的节点平均水龄、单个DMA入口数量和运行后低于管网规定最小服务水压的节点数量这3个分区原则,从Pareto最优解集中选择出符合条件的解即为布置方案.
3. 更换局部管网管径
3.1. 目标函数及约束条件的建立
对于不满足管网规定的最小服务水压的节点,可以放大流向该节点管段的管径以减少水流在转输过程中的能量损失,从而增大该节点的节点压力,使节点压力满足管网规定的最小服务压力. 但是在更换过程中须控制更换管段的数量、长度和管径以节省成本,更换后仍须满足管网的2大基本方程,且在更换完成后管网的节点平均压力不应大于更换前的平均压力,因为压力增大会导致管网中漏损量的增大. 目标函数设为管段的造价h[16],目标函数和约束条件的数学表达式为
式中:Di、Li分别为管段
3.2. 基于模拟退火算法的优化方法
本研究中模拟退火算法采用整数编码,决策变量是管段可更换的管径规格,其维度是拟更换管径的管段数量.为了编码和解码方便,用自然数1~9表示可以更换的管径规格,0表示该条管段的管径不变.例如某个解为x=[0, 3, 5, 8]表示共有4条拟更换管径的管段,第1条管段管径不变,第2、3、4条管段管径分别更换为150、250、400 mm.
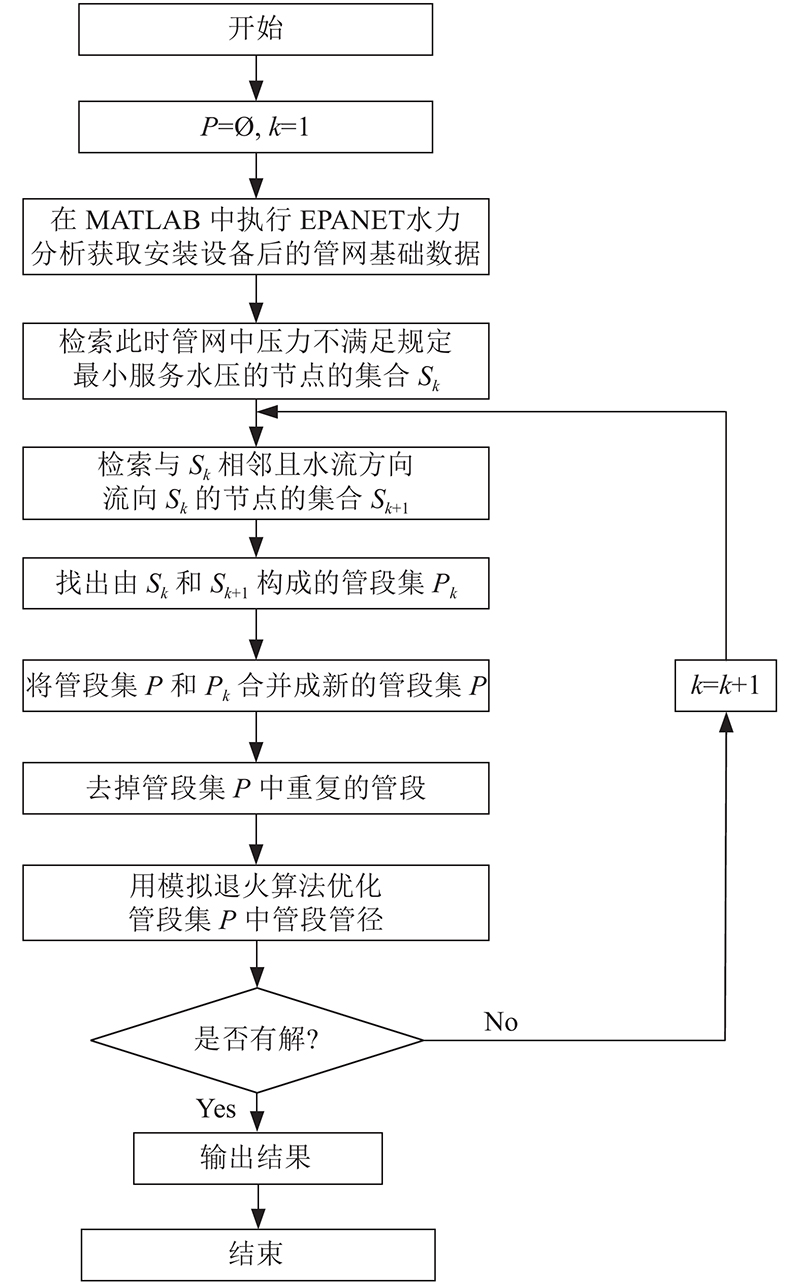
首先找到安装设备后管网中节点压力不满足规定最小服务压力的节点的集合S1,然后找到和它们相邻且水流流向它们的节点的集合S2,这些节点构成的管段集P就是拟更换管径的第1批管段. 采用模拟退火算法寻找使得目标函数最小且满足约束条件的管径更换方案.若优化完成后有解,此时就得到了较为经济的管径更换方案,若无解,则继续寻找与S2相邻且水流流向它们的节点的集合S3,然后更新管段集P得到拟更换管径的第2批管段. 继续用模拟退火算法寻找最优解,直至可以找到管径更换方案时算法停止. 此时可以认为已经得到了全局最优解,因为每一次继续向下检索都意味着集合P中的元素会逐渐增多,使得算法的搜索空间急剧扩大,找到可行解难度大大增加,进而增大了算法陷入局部最优的概率,使算法难以收敛到全局最优解.优化过程如图2所示.
图 2
图 2 管径更换方案优化流程图
Fig.2 Flow chart for optimization of pipe diameter replacement scheme
4. 案例分析
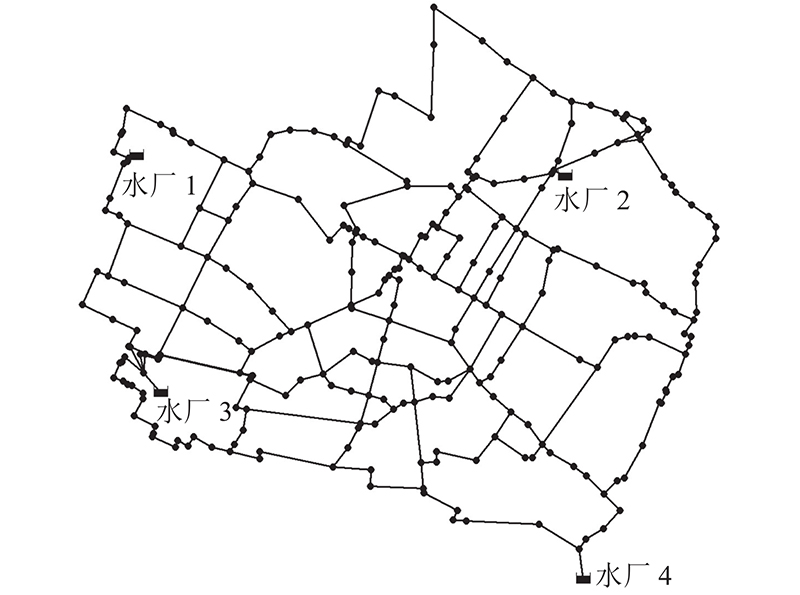
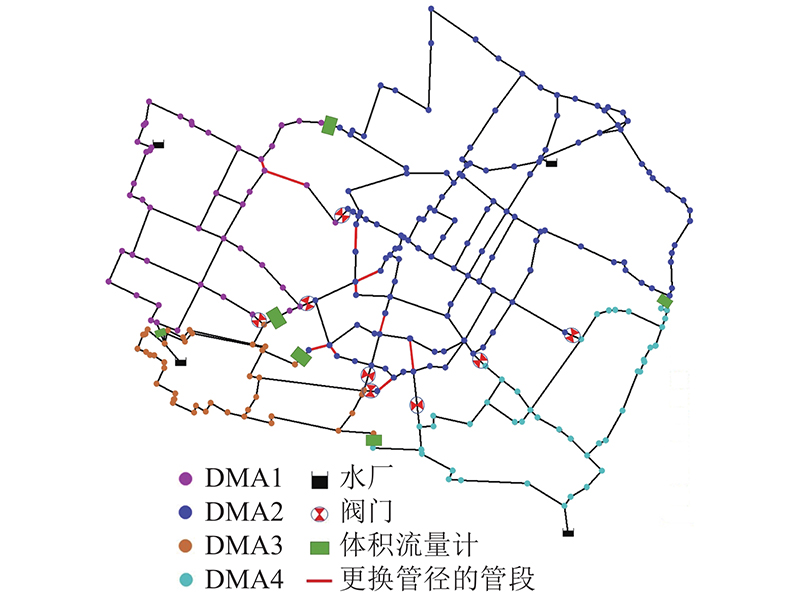
4.1. 案例概况
图 3
4.2. 分区BPs选择结果
采用函数gamultiobj确定分区BPs,参数设置如下:最优前端个体系数为0.3,种群大小为100,最大进化代数为600,停止代数也为600,适应度函数值偏差为0.01,其他参数为默认值. 经试验得到c的取值可以是3.5,因此3个参数的取值限定为(0, 3.5). 经MATLAB计算后得到Pareto最优解集,在此基础上确定了相似度计算公式中3个参数的值分别为α=0.198、β=2.41、γ=0.674,并以此得到了BPs和分区结果,将其记为方案A. 采用单台处理器为Intel®Core™i5-1135G7、16 GB运行内存的笔记本电脑确定了Modena管网的分区BPs,最终计算耗时为651.9 s. 通过进一步的试验得出本方法的计算耗时(以s计)约为管网节点数量的3倍(从数值上说),因此本方法适用于中大型管网. 如图4所示,对3种分区方案的相关指标进行对比. 图中,fs为分区尺寸均匀性[23],是评价DMA分区质量高低的一个重要指标. 分区尺寸均匀性反映了与具有平均规模的假设DMA相比,实际所有DMA分区偏离平均规模的累积大小偏差,值越小意味着分区越均匀. 分区尺寸均匀性的表达式为
图 4
图 4 3种分区方案下边界管段的相关指标对比
Fig.4 Comparison of related parameters of boundary pipes under three partition schemes
式中:k为DMA分区的数目,Di为第i个DMA中的总需水量,Dav为管网中每个DMA的平均需水量.
由图4可知,方案A中BPs的平均体积流量小于其余2种方案的50%,而平均管径和平均长度均为另外2种方案的53%~86%,BPs的数量也是最低的.因此,本研究确定的分区BPs相对于其他2种方案具有体积流量小、管径小、长度短和数量少的特点,利用优化后的相似度计算公式进行DMA分区,能够有效降低BPs的体积流量、管径、长度和数量,可以在减少分区成本、保障分区水质和保证管网分区后正常运行等方面起到极为重要的作用.
方案A的分区尺寸均匀性相较于方案B和方案C来说较差. 原因如下:如图3所示,Modena管网共有4个水源,总供水量为406.93 L/s,水厂1~4供水量分别:56.34、222.25、65.84、62.50 L/s. 由于本方法的主要目标之一是寻找体积流量较小的管段作为BPs,并尽量减小BPs的数量以保证用较小成本完成极小降压空间下管网的DMA分区工作,但该管网中水厂2与水厂1、3、4的供水规模严重不均衡,使得体积流量较小的一连串管段出现在距离水厂2较远的位置,由此导致包含水厂2的分区不得不涵盖大量的需水节点,致使该区域的尺寸相较于其他3个区域的尺寸明显偏大,故方案A的分区尺寸均匀性相对较差. 由此推断若管网中各水厂规模较为一致或相差不是很悬殊时,运用本方法得到的分区方案在保证高质量分区BPs的同时其分区尺寸均匀性会有明显好转.
4.3. 分区BPs设备优化布置
设置不同的最小服务水压为20、19、18、17 m,将它们分别作为约束条件,通过gamultiobj函数优化分区BPs上设备的布置方案. 参数设置如下:最优前端个体系数为0.1,种群大小为100,最大进化代数为50,停止代数也为50,适应度函数值偏差为0.01,其他参数为默认值. 如表1所示为分区所需设备的费用,数据来源于造价通,根据管段直径列出了每个设备的成本. 表中,D为管径,gval、gvol分别为阀门、体积流量计价格.
表 1 阀门和体积流量计价格
Tab.1
| D/mm | gval/(元·个−1) | gvol/(元·台−1) |
| 100 | 2300 | 11810 |
| 125 | 2450 | 13366 |
| 150 | 2700 | 15958 |
| 200 | 3150 | 17289 |
| 250 | 3700 | 20566 |
| 300 | 5000 | 25359 |
| 350 | 6700 | 28834 |
| 400 | 7800 | 31143 |
经MATLAB计算后,在不同压力约束下得到的Pareto最优解个数分别为3、4、3、5,其中在压力约束为17、18 m时有2个解重合. 如表2所示为15个Pareto最优解的2个目标函数值以及分区所需的体积流量计台数、布置设备后水压低于20 m的节点个数np和分区后各区域进水口数量nin. 可以看出,随着压力约束的降低,体积流量计的台数总体也呈现下降趋势,与之对应的阀门个数会增多,这是因为压力约束的降低给管网留出了一定的降压空间,可以接受更多由于关闭阀门而造成的水头损失;另一方面,在相同压力约束下,设备的安装成本越低(即安装阀门数量越多),节点的平均水龄就会升高,原因是安装阀门后,管网中可供流动的路径减少,水需要更长的时间才能到达需水节点,从而导致更高的水龄值[24];此外,在不同的压力约束下,当安装的阀门个数相同时,压力约束低的方案的节点平均水龄通常会低于压力约束高的方案的节点平均水龄,这是因为压力约束低的方案会在体积流量相对较大的BPs上安装阀门,导致该部分体积流量分散到其他管段上,从而使得这些管段流速增大,节点平均水龄有所降低.
表 2 不同压力约束下的Pareto前沿及其他相关信息
Tab.2
| 解编号 | Hs,min/ m | h | gc/ 万元 | Tm/ 台 | np | nin | |||
| DMA1 | DMA2 | DMA3 | DMA4 | ||||||
| 注:*表示该解在最小服务水压约束为17 m时重复出现 | |||||||||
| 原管网 | 20 | 0.72 | − | − | 0 | − | − | − | − |
| s-1 | 20 | 0.72 | 14.15 | 11 | 0 | 3 | 5 | 1 | 2 |
| s-2 | 20 | 0.72 | 13.2 | 10 | 0 | 3 | 4 | 1 | 2 |
| s-3 | 20 | 0.83 | 12.25 | 9 | 0 | 3 | 3 | 1 | 2 |
| s-4 | 19 | 0.70 | 11.29 | 8 | 5 | 3 | 3 | 1 | 1 |
| s-5 | 19 | 0.71 | 11.15 | 8 | 20 | 3 | 3 | 1 | 1 |
| s-6 | 19 | 0.81 | 10.34 | 7 | 5 | 3 | 2 | 1 | 1 |
| s-7 | 19 | 0.83 | 10.20 | 7 | 17 | 3 | 2 | 1 | 1 |
| s-8* | 18 | 0.70 | 10.34 | 7 | 13 | 3 | 2 | 1 | 1 |
| s-9 | 18 | 0.81 | 9.39 | 6 | 13 | 3 | 1 | 1 | 1 |
| s-10* | 18 | 0.81 | 8.44 | 5 | 14 | 2 | 1 | 1 | 1 |
| s-11 | 17 | 0.70 | 9.39 | 6 | 13 | 2 | 2 | 1 | 1 |
| s-12 | 17 | 0.72 | 9.25 | 6 | 27 | 2 | 2 | 1 | 1 |
| s-13 | 17 | 0.83 | 8.30 | 5 | 25 | 2 | 1 | 1 | 1 |
将不同压力约束下求得的Pareto最优解集按照以下3个原则进行筛选:1)单个DMA的进水口数量不得超过2个;2)管网的节点平均水龄不得高于0.72 h;3)运行后水压低于20 m的节点数目最少. 解s-11符合上述原则,其所对应的方案即为最优BPs上设备布置方案.因此Modena 管网安装阀门8个,体积流量计6台,设备安装成本93928元,安装设备后节点的平均水龄为0.70 h,单工况条件下运行后管网节点压力最低为17.61 m,共有13个节点的压力低于20 m.
4.4. 更换管网局部管段
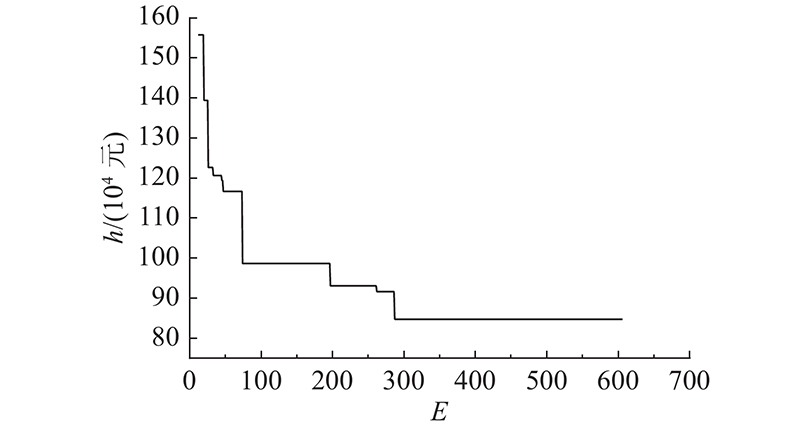
Modena管网规定的节点最小服务水压为20 m,分区后13个节点不满足要求,因此须对管网中部分管段加大管径,减少管网水头损失,使所有节点的压力均可满足要求. 在执行水力模拟后,找到拟更换管径的管段集,并对更换管段的管径大小进行优化,通过模拟退火算法得出最优解. 算法参数设置初始温度200 ℃,结束温度0.001 ℃,降温速率0.98,Mapkob链长50. 编码的数字是0~9的连续自然数,0代表该管段管径不变,1~9分别对应管径变化为100~450 mm. 在拟更换的管段集合更新2次后,计算停止. 模拟退火算法运算过程如图5所示,在降温次数E=290次时算法收敛,即得到了全局最优方案.管段更换情况如表3所示. 表中,BD和AD分别为更换前和更换后的管径规格.
图 5
图 5 模拟退火算法降温次数与最优值趋势
Fig.5 Trend of simulated annealing algorithm cooling number and optimal value
表 3 管段更换情况
Tab.3
| 管段编号 | BD | AD | 管段编号 | BD | AD | |
| 16 | DN100 | DN200 | 122 | DN100 | DN200 | |
| 123 | DN125 | DN200 | 145 | DN100 | DN150 | |
| 152 | DN100 | DN125 | 167 | DN100 | DN125 | |
| 204 | DN100 | DN125 | 248 | DN100 | DN125 | |
| 258 | DN100 | DN200 | 271 | DN100 | DN250 |
图 6
4.5. 分区结果分析
表 4 DMA分区前、后管网运行性能指标
Tab.4
| 管网状态 | | gw/h | Hav/m | Hlow/m | Qloss/(L·s−1) |
| 分区前 | 0.72 | 3.76 | 25.13 | 20.09 | 63.8 |
| 分区后 | 0.72 | 2.02 | 25.07 | 20.01 | 63.7 |
由表4可知,1)分区后的节点水龄相较于分区前没有发生变化,说明本次DMA分区未对管网的水质造成太大影响,但相较于在BPs上安装设备后水龄略微升高,这是因为放大部分管径使管网中这些管段的流速变慢,故节点平均水龄有所升高. 分区后管网的综合水龄指数下降,表明分区后管网的水质尤其是管网末梢和大体积流量用户的水质得到了明显改善. 2)在保证管网最小水压大于管网规定最小服务水压的前提下,分区后管网的平均水压降低,管网的漏损量也有所降低,尽管降低幅度很小,但在实施DMA分区后发现漏损、找到漏点的时间会大大缩短,能进一步降低管网漏损和供水公司的产销差.
5. 结 论
(1)结合水力模型首次提出针对极小降压空间下管网的DMA分区方法,分区流程如下:确定分区BPs,优化BPs上设备的布置,更换管网中部分管段的管径.运用相应算法依次完成,形成最终可行方案.
(2)为了确定分区的最佳BPs,首次对相似度公式进行优化并提出新的相似度计算方法.通过该方法选择出的BPs能有效降低BPs的体积流量、管径、长度和数量,从而降低分区成本,并为后续顺利进行分区奠定基础.
(3)首次通过人为预先降低管网规定的最小服务水压,找出符合DMA分区原则的设备布置方案. 为了使各节点水压满足规定的最小水压要求,通过模拟退火算法找到少量需要更换的管段及其对应的管径. 在更换后,管网水力水质特性并未发生太大变化,供水管网仍可正常运行.
(4)本研究未考虑多种工况条件共同作用下管网的DMA分区. 下一步将在多工况条件的基础上完成管网DMA分区,并在各个分区的入口处设置减压阀,优化减压阀的阀后设定压力,同时调节管网中变频泵的转速,实现减压阀和泵站的联调联控,最大限度减少管网的富余压力及漏损量,降低水泵能耗.
参考文献
Multiphase DMA design methodology based on graph theory and many-objective optimization
[J].
供水管网DMA分区优化方法及软件实现
[J].DOI:10.13789/j.cnki.wwe1964.2020.02.022 [本文引用: 1]
Optimization method and software implementation of the DMA zoning for water distribution network
[J].DOI:10.13789/j.cnki.wwe1964.2020.02.022 [本文引用: 1]
供水管网多目标分区方法
[J].DOI:10.15890/j.cnki.jsjs.2018.05.017 [本文引用: 1]
Multi-objective optimization of sectorization for water supply distribution network
[J].DOI:10.15890/j.cnki.jsjs.2018.05.017 [本文引用: 1]
基于节点自然邻的供水管网DMA分区方法研究
[J].DOI:10.13789/j.cnki.wwe1964.2019.07.023 [本文引用: 2]
Partition of DMAs within water distribution systems based on natural neighbors of nodes
[J].DOI:10.13789/j.cnki.wwe1964.2019.07.023 [本文引用: 2]
The latest research progress on spectral clustering
[J].
A tutorial on spectral clustering
[J].DOI:10.1007/s11222-007-9033-z [本文引用: 1]
独立计量分区截断管水质时空变化规律
[J].
Spatiotemporal change rules of water quality in cut-off water pipelines in district metering areas (DMA)
[J].
Composition control and temperature inferential control of dividing wall column based on model predictive control and PI strategies
[J].DOI:10.1016/j.cjche.2017.12.005 [本文引用: 1]
多目标优化算法在弹头侵彻明胶运动模拟中的应用
[J].
Application of multi-objective optimization algorithm to motional simulation of bullets penetrating ballistic gelatin
[J].
Geospatial and hydraulic simulation to design district metered areas for large water distribution networks
[J].DOI:10.1061/(ASCE)WR.1943-5452.0001243 [本文引用: 1]
Impact of network sectorisation on water quality management
[J].DOI:10.2166/hydro.2017.072 [本文引用: 1]
基于高维多目标优化的给水管网设计方法: 以意大利Fossolo小镇管网为例
[J].DOI:10.3969/j.issn.1002-8471.2018.05.028 [本文引用: 1]
Many-objective optimization based design of water distribution systems: a case study of Fossolo Town network in Italy
[J].DOI:10.3969/j.issn.1002-8471.2018.05.028 [本文引用: 1]
供水管网水龄的逐节点遍历简化算法
[J].DOI:10.3778/j.issn.1002-8331.2009.20.058 [本文引用: 1]
Simplified and junction by junction algorithm to calculate water age in urban water supply and distribution network
[J].DOI:10.3778/j.issn.1002-8331.2009.20.058 [本文引用: 1]
Optimization by simulated annealing
[J].
基于模拟退火算法的I/Q不平衡校正
[J].
I/Q imbalance calibration based on simulated annealing algorithm
[J].
On the optimal design of water distribution networks: a practical MINLP approach
[J].DOI:10.1007/s11081-011-9141-7 [本文引用: 1]
A practical multi-objective optimization sectorization method for water distribution network
[J].DOI:10.1016/j.scitotenv.2018.11.273 [本文引用: 1]
District metered area design through multicriteria and multiobjective optimization
[J].
Spectral clustering and multicriteria decision for design of district metered areas
[J].DOI:10.1061/(ASCE)WR.1943-5452.0000916 [本文引用: 1]
Design and performance of district metering areas in water distribution systems
[J].
供水管网漏失模型研究
[J].DOI:10.19853/j.zgjsps.1000-4602.2010.09.017 [本文引用: 1]
Study on leakage loss model for water distribution network
[J].DOI:10.19853/j.zgjsps.1000-4602.2010.09.017 [本文引用: 1]