Crushing of soil particles
1
1985
... 岩土、水利和交通工程中的颗粒材料在较高应力状态下会发生颗粒破碎[1-2],如堆石料在填筑碾压过程中以及地震或循环荷载作用下的破碎[3-4]. 大量试验研究表明颗粒破碎对岩土颗粒材料的应力变形特性有较大的影响,因此颗粒破碎的研究受到越来越多研究者的关注[5-12]. ...
Crushing a weak granular material: experimental numerical analyses
1
2005
... 岩土、水利和交通工程中的颗粒材料在较高应力状态下会发生颗粒破碎[1-2],如堆石料在填筑碾压过程中以及地震或循环荷载作用下的破碎[3-4]. 大量试验研究表明颗粒破碎对岩土颗粒材料的应力变形特性有较大的影响,因此颗粒破碎的研究受到越来越多研究者的关注[5-12]. ...
Effect of confining pressure on the degradation of ballast under cyclic loading
1
2005
... 岩土、水利和交通工程中的颗粒材料在较高应力状态下会发生颗粒破碎[1-2],如堆石料在填筑碾压过程中以及地震或循环荷载作用下的破碎[3-4]. 大量试验研究表明颗粒破碎对岩土颗粒材料的应力变形特性有较大的影响,因此颗粒破碎的研究受到越来越多研究者的关注[5-12]. ...
“5.12”汶川地震对紫坪铺混凝土面板坝的影响及原因分析
1
2008
... 岩土、水利和交通工程中的颗粒材料在较高应力状态下会发生颗粒破碎[1-2],如堆石料在填筑碾压过程中以及地震或循环荷载作用下的破碎[3-4]. 大量试验研究表明颗粒破碎对岩土颗粒材料的应力变形特性有较大的影响,因此颗粒破碎的研究受到越来越多研究者的关注[5-12]. ...
“5.12”汶川地震对紫坪铺混凝土面板坝的影响及原因分析
1
2008
... 岩土、水利和交通工程中的颗粒材料在较高应力状态下会发生颗粒破碎[1-2],如堆石料在填筑碾压过程中以及地震或循环荷载作用下的破碎[3-4]. 大量试验研究表明颗粒破碎对岩土颗粒材料的应力变形特性有较大的影响,因此颗粒破碎的研究受到越来越多研究者的关注[5-12]. ...
颗粒破碎对堆石料填充特性缩尺效应的影响研究
1
2020
... 岩土、水利和交通工程中的颗粒材料在较高应力状态下会发生颗粒破碎[1-2],如堆石料在填筑碾压过程中以及地震或循环荷载作用下的破碎[3-4]. 大量试验研究表明颗粒破碎对岩土颗粒材料的应力变形特性有较大的影响,因此颗粒破碎的研究受到越来越多研究者的关注[5-12]. ...
颗粒破碎对堆石料填充特性缩尺效应的影响研究
1
2020
... 岩土、水利和交通工程中的颗粒材料在较高应力状态下会发生颗粒破碎[1-2],如堆石料在填筑碾压过程中以及地震或循环荷载作用下的破碎[3-4]. 大量试验研究表明颗粒破碎对岩土颗粒材料的应力变形特性有较大的影响,因此颗粒破碎的研究受到越来越多研究者的关注[5-12]. ...
堆石料颗粒破碎对剪胀性及抗剪强度的影响
0
1997
堆石料颗粒破碎对剪胀性及抗剪强度的影响
0
1997
Macro-micro responses of crushable granular materials in simulated true triaxial tests
0
2015
On the effect of grain fragmentation on frictional instabilities in faults with granular gouge
0
2021
An experimental study on the influence of multiple contacts and size on contact behavior of marble sphere
0
2021
Machine learning reveals the influences of grain morphology on grain crushing strength
0
2021
遇水湿化对堆石体颗粒破碎和压缩特性的影响研究
0
2021
遇水湿化对堆石体颗粒破碎和压缩特性的影响研究
0
2021
On the micro mechanics of one-dimensional normal compression
1
2013
... 岩土、水利和交通工程中的颗粒材料在较高应力状态下会发生颗粒破碎[1-2],如堆石料在填筑碾压过程中以及地震或循环荷载作用下的破碎[3-4]. 大量试验研究表明颗粒破碎对岩土颗粒材料的应力变形特性有较大的影响,因此颗粒破碎的研究受到越来越多研究者的关注[5-12]. ...
Discrete element modelling of soil particle fracture
1
2002
... 目前,对单个颗粒的破碎研究常采用上下平板压缩颗粒直至破碎,得到荷载位移曲线和破碎强度,并对破碎后的碎片进行颗粒筛分以研究其破碎模式[13-14]. Huang等[14-16]采用室内试验和离散元数值模拟开展单颗粒压缩破碎研究,发现颗粒破碎强度服从Weibull分布. Turcotte[17]指出,颗粒的破碎可以用分形分布描述. 徐永福等[18]对岩石颗粒破碎进行系统研究,认为颗粒破碎的分形维数 $D$介于2.0~3.0. 王益栋等[19]进行大理岩颗粒的压缩破碎试验,测得其分形维数 $D$=2.48. 周海娟等[20]采用连续离散耦合分析方法(combined finite–discrete element method,FDEM)对5组不同粒径的堆石颗粒进行单颗粒破碎数值试验,结果表明颗粒破碎强度具有明显的尺寸效应,即颗粒特征强度随着颗粒尺寸的增大而逐渐减小. 孟敏强等[21]对3种不同粒径的泥岩和砂岩颗粒进行单颗粒破碎试验,也发现了相似的规律. 此外,众多国内外学者基于单颗粒压缩破碎试验,发现颗粒形状对颗粒破碎形式、破碎强度和Weibull模量等破碎特性有较大的影响[22-25]. ...
Size effect on the compression breakage strengths of glass particles
2
2014
... 目前,对单个颗粒的破碎研究常采用上下平板压缩颗粒直至破碎,得到荷载位移曲线和破碎强度,并对破碎后的碎片进行颗粒筛分以研究其破碎模式[13-14]. Huang等[14-16]采用室内试验和离散元数值模拟开展单颗粒压缩破碎研究,发现颗粒破碎强度服从Weibull分布. Turcotte[17]指出,颗粒的破碎可以用分形分布描述. 徐永福等[18]对岩石颗粒破碎进行系统研究,认为颗粒破碎的分形维数 $D$介于2.0~3.0. 王益栋等[19]进行大理岩颗粒的压缩破碎试验,测得其分形维数 $D$=2.48. 周海娟等[20]采用连续离散耦合分析方法(combined finite–discrete element method,FDEM)对5组不同粒径的堆石颗粒进行单颗粒破碎数值试验,结果表明颗粒破碎强度具有明显的尺寸效应,即颗粒特征强度随着颗粒尺寸的增大而逐渐减小. 孟敏强等[21]对3种不同粒径的泥岩和砂岩颗粒进行单颗粒破碎试验,也发现了相似的规律. 此外,众多国内外学者基于单颗粒压缩破碎试验,发现颗粒形状对颗粒破碎形式、破碎强度和Weibull模量等破碎特性有较大的影响[22-25]. ...
... [14-16]采用室内试验和离散元数值模拟开展单颗粒压缩破碎研究,发现颗粒破碎强度服从Weibull分布. Turcotte[17]指出,颗粒的破碎可以用分形分布描述. 徐永福等[18]对岩石颗粒破碎进行系统研究,认为颗粒破碎的分形维数 $D$介于2.0~3.0. 王益栋等[19]进行大理岩颗粒的压缩破碎试验,测得其分形维数 $D$=2.48. 周海娟等[20]采用连续离散耦合分析方法(combined finite–discrete element method,FDEM)对5组不同粒径的堆石颗粒进行单颗粒破碎数值试验,结果表明颗粒破碎强度具有明显的尺寸效应,即颗粒特征强度随着颗粒尺寸的增大而逐渐减小. 孟敏强等[21]对3种不同粒径的泥岩和砂岩颗粒进行单颗粒破碎试验,也发现了相似的规律. 此外,众多国内外学者基于单颗粒压缩破碎试验,发现颗粒形状对颗粒破碎形式、破碎强度和Weibull模量等破碎特性有较大的影响[22-25]. ...
On the yielding and plastic compression of sand
0
2002
Yielding of granular materials
1
2002
... 目前,对单个颗粒的破碎研究常采用上下平板压缩颗粒直至破碎,得到荷载位移曲线和破碎强度,并对破碎后的碎片进行颗粒筛分以研究其破碎模式[13-14]. Huang等[14-16]采用室内试验和离散元数值模拟开展单颗粒压缩破碎研究,发现颗粒破碎强度服从Weibull分布. Turcotte[17]指出,颗粒的破碎可以用分形分布描述. 徐永福等[18]对岩石颗粒破碎进行系统研究,认为颗粒破碎的分形维数 $D$介于2.0~3.0. 王益栋等[19]进行大理岩颗粒的压缩破碎试验,测得其分形维数 $D$=2.48. 周海娟等[20]采用连续离散耦合分析方法(combined finite–discrete element method,FDEM)对5组不同粒径的堆石颗粒进行单颗粒破碎数值试验,结果表明颗粒破碎强度具有明显的尺寸效应,即颗粒特征强度随着颗粒尺寸的增大而逐渐减小. 孟敏强等[21]对3种不同粒径的泥岩和砂岩颗粒进行单颗粒破碎试验,也发现了相似的规律. 此外,众多国内外学者基于单颗粒压缩破碎试验,发现颗粒形状对颗粒破碎形式、破碎强度和Weibull模量等破碎特性有较大的影响[22-25]. ...
Fractals and fragmentation
1
1986
... 目前,对单个颗粒的破碎研究常采用上下平板压缩颗粒直至破碎,得到荷载位移曲线和破碎强度,并对破碎后的碎片进行颗粒筛分以研究其破碎模式[13-14]. Huang等[14-16]采用室内试验和离散元数值模拟开展单颗粒压缩破碎研究,发现颗粒破碎强度服从Weibull分布. Turcotte[17]指出,颗粒的破碎可以用分形分布描述. 徐永福等[18]对岩石颗粒破碎进行系统研究,认为颗粒破碎的分形维数 $D$介于2.0~3.0. 王益栋等[19]进行大理岩颗粒的压缩破碎试验,测得其分形维数 $D$=2.48. 周海娟等[20]采用连续离散耦合分析方法(combined finite–discrete element method,FDEM)对5组不同粒径的堆石颗粒进行单颗粒破碎数值试验,结果表明颗粒破碎强度具有明显的尺寸效应,即颗粒特征强度随着颗粒尺寸的增大而逐渐减小. 孟敏强等[21]对3种不同粒径的泥岩和砂岩颗粒进行单颗粒破碎试验,也发现了相似的规律. 此外,众多国内外学者基于单颗粒压缩破碎试验,发现颗粒形状对颗粒破碎形式、破碎强度和Weibull模量等破碎特性有较大的影响[22-25]. ...
岩石颗粒破碎的尺寸效应
1
2014
... 目前,对单个颗粒的破碎研究常采用上下平板压缩颗粒直至破碎,得到荷载位移曲线和破碎强度,并对破碎后的碎片进行颗粒筛分以研究其破碎模式[13-14]. Huang等[14-16]采用室内试验和离散元数值模拟开展单颗粒压缩破碎研究,发现颗粒破碎强度服从Weibull分布. Turcotte[17]指出,颗粒的破碎可以用分形分布描述. 徐永福等[18]对岩石颗粒破碎进行系统研究,认为颗粒破碎的分形维数 $D$介于2.0~3.0. 王益栋等[19]进行大理岩颗粒的压缩破碎试验,测得其分形维数 $D$=2.48. 周海娟等[20]采用连续离散耦合分析方法(combined finite–discrete element method,FDEM)对5组不同粒径的堆石颗粒进行单颗粒破碎数值试验,结果表明颗粒破碎强度具有明显的尺寸效应,即颗粒特征强度随着颗粒尺寸的增大而逐渐减小. 孟敏强等[21]对3种不同粒径的泥岩和砂岩颗粒进行单颗粒破碎试验,也发现了相似的规律. 此外,众多国内外学者基于单颗粒压缩破碎试验,发现颗粒形状对颗粒破碎形式、破碎强度和Weibull模量等破碎特性有较大的影响[22-25]. ...
岩石颗粒破碎的尺寸效应
1
2014
... 目前,对单个颗粒的破碎研究常采用上下平板压缩颗粒直至破碎,得到荷载位移曲线和破碎强度,并对破碎后的碎片进行颗粒筛分以研究其破碎模式[13-14]. Huang等[14-16]采用室内试验和离散元数值模拟开展单颗粒压缩破碎研究,发现颗粒破碎强度服从Weibull分布. Turcotte[17]指出,颗粒的破碎可以用分形分布描述. 徐永福等[18]对岩石颗粒破碎进行系统研究,认为颗粒破碎的分形维数 $D$介于2.0~3.0. 王益栋等[19]进行大理岩颗粒的压缩破碎试验,测得其分形维数 $D$=2.48. 周海娟等[20]采用连续离散耦合分析方法(combined finite–discrete element method,FDEM)对5组不同粒径的堆石颗粒进行单颗粒破碎数值试验,结果表明颗粒破碎强度具有明显的尺寸效应,即颗粒特征强度随着颗粒尺寸的增大而逐渐减小. 孟敏强等[21]对3种不同粒径的泥岩和砂岩颗粒进行单颗粒破碎试验,也发现了相似的规律. 此外,众多国内外学者基于单颗粒压缩破碎试验,发现颗粒形状对颗粒破碎形式、破碎强度和Weibull模量等破碎特性有较大的影响[22-25]. ...
岩石单颗粒压缩破碎试验研究
1
2015
... 目前,对单个颗粒的破碎研究常采用上下平板压缩颗粒直至破碎,得到荷载位移曲线和破碎强度,并对破碎后的碎片进行颗粒筛分以研究其破碎模式[13-14]. Huang等[14-16]采用室内试验和离散元数值模拟开展单颗粒压缩破碎研究,发现颗粒破碎强度服从Weibull分布. Turcotte[17]指出,颗粒的破碎可以用分形分布描述. 徐永福等[18]对岩石颗粒破碎进行系统研究,认为颗粒破碎的分形维数 $D$介于2.0~3.0. 王益栋等[19]进行大理岩颗粒的压缩破碎试验,测得其分形维数 $D$=2.48. 周海娟等[20]采用连续离散耦合分析方法(combined finite–discrete element method,FDEM)对5组不同粒径的堆石颗粒进行单颗粒破碎数值试验,结果表明颗粒破碎强度具有明显的尺寸效应,即颗粒特征强度随着颗粒尺寸的增大而逐渐减小. 孟敏强等[21]对3种不同粒径的泥岩和砂岩颗粒进行单颗粒破碎试验,也发现了相似的规律. 此外,众多国内外学者基于单颗粒压缩破碎试验,发现颗粒形状对颗粒破碎形式、破碎强度和Weibull模量等破碎特性有较大的影响[22-25]. ...
岩石单颗粒压缩破碎试验研究
1
2015
... 目前,对单个颗粒的破碎研究常采用上下平板压缩颗粒直至破碎,得到荷载位移曲线和破碎强度,并对破碎后的碎片进行颗粒筛分以研究其破碎模式[13-14]. Huang等[14-16]采用室内试验和离散元数值模拟开展单颗粒压缩破碎研究,发现颗粒破碎强度服从Weibull分布. Turcotte[17]指出,颗粒的破碎可以用分形分布描述. 徐永福等[18]对岩石颗粒破碎进行系统研究,认为颗粒破碎的分形维数 $D$介于2.0~3.0. 王益栋等[19]进行大理岩颗粒的压缩破碎试验,测得其分形维数 $D$=2.48. 周海娟等[20]采用连续离散耦合分析方法(combined finite–discrete element method,FDEM)对5组不同粒径的堆石颗粒进行单颗粒破碎数值试验,结果表明颗粒破碎强度具有明显的尺寸效应,即颗粒特征强度随着颗粒尺寸的增大而逐渐减小. 孟敏强等[21]对3种不同粒径的泥岩和砂岩颗粒进行单颗粒破碎试验,也发现了相似的规律. 此外,众多国内外学者基于单颗粒压缩破碎试验,发现颗粒形状对颗粒破碎形式、破碎强度和Weibull模量等破碎特性有较大的影响[22-25]. ...
堆石颗粒压缩破碎强度的尺寸效应
1
2017
... 目前,对单个颗粒的破碎研究常采用上下平板压缩颗粒直至破碎,得到荷载位移曲线和破碎强度,并对破碎后的碎片进行颗粒筛分以研究其破碎模式[13-14]. Huang等[14-16]采用室内试验和离散元数值模拟开展单颗粒压缩破碎研究,发现颗粒破碎强度服从Weibull分布. Turcotte[17]指出,颗粒的破碎可以用分形分布描述. 徐永福等[18]对岩石颗粒破碎进行系统研究,认为颗粒破碎的分形维数 $D$介于2.0~3.0. 王益栋等[19]进行大理岩颗粒的压缩破碎试验,测得其分形维数 $D$=2.48. 周海娟等[20]采用连续离散耦合分析方法(combined finite–discrete element method,FDEM)对5组不同粒径的堆石颗粒进行单颗粒破碎数值试验,结果表明颗粒破碎强度具有明显的尺寸效应,即颗粒特征强度随着颗粒尺寸的增大而逐渐减小. 孟敏强等[21]对3种不同粒径的泥岩和砂岩颗粒进行单颗粒破碎试验,也发现了相似的规律. 此外,众多国内外学者基于单颗粒压缩破碎试验,发现颗粒形状对颗粒破碎形式、破碎强度和Weibull模量等破碎特性有较大的影响[22-25]. ...
堆石颗粒压缩破碎强度的尺寸效应
1
2017
... 目前,对单个颗粒的破碎研究常采用上下平板压缩颗粒直至破碎,得到荷载位移曲线和破碎强度,并对破碎后的碎片进行颗粒筛分以研究其破碎模式[13-14]. Huang等[14-16]采用室内试验和离散元数值模拟开展单颗粒压缩破碎研究,发现颗粒破碎强度服从Weibull分布. Turcotte[17]指出,颗粒的破碎可以用分形分布描述. 徐永福等[18]对岩石颗粒破碎进行系统研究,认为颗粒破碎的分形维数 $D$介于2.0~3.0. 王益栋等[19]进行大理岩颗粒的压缩破碎试验,测得其分形维数 $D$=2.48. 周海娟等[20]采用连续离散耦合分析方法(combined finite–discrete element method,FDEM)对5组不同粒径的堆石颗粒进行单颗粒破碎数值试验,结果表明颗粒破碎强度具有明显的尺寸效应,即颗粒特征强度随着颗粒尺寸的增大而逐渐减小. 孟敏强等[21]对3种不同粒径的泥岩和砂岩颗粒进行单颗粒破碎试验,也发现了相似的规律. 此外,众多国内外学者基于单颗粒压缩破碎试验,发现颗粒形状对颗粒破碎形式、破碎强度和Weibull模量等破碎特性有较大的影响[22-25]. ...
基于尺寸效应的粗粒土单颗粒破碎试验及数值模拟
1
2020
... 目前,对单个颗粒的破碎研究常采用上下平板压缩颗粒直至破碎,得到荷载位移曲线和破碎强度,并对破碎后的碎片进行颗粒筛分以研究其破碎模式[13-14]. Huang等[14-16]采用室内试验和离散元数值模拟开展单颗粒压缩破碎研究,发现颗粒破碎强度服从Weibull分布. Turcotte[17]指出,颗粒的破碎可以用分形分布描述. 徐永福等[18]对岩石颗粒破碎进行系统研究,认为颗粒破碎的分形维数 $D$介于2.0~3.0. 王益栋等[19]进行大理岩颗粒的压缩破碎试验,测得其分形维数 $D$=2.48. 周海娟等[20]采用连续离散耦合分析方法(combined finite–discrete element method,FDEM)对5组不同粒径的堆石颗粒进行单颗粒破碎数值试验,结果表明颗粒破碎强度具有明显的尺寸效应,即颗粒特征强度随着颗粒尺寸的增大而逐渐减小. 孟敏强等[21]对3种不同粒径的泥岩和砂岩颗粒进行单颗粒破碎试验,也发现了相似的规律. 此外,众多国内外学者基于单颗粒压缩破碎试验,发现颗粒形状对颗粒破碎形式、破碎强度和Weibull模量等破碎特性有较大的影响[22-25]. ...
基于尺寸效应的粗粒土单颗粒破碎试验及数值模拟
1
2020
... 目前,对单个颗粒的破碎研究常采用上下平板压缩颗粒直至破碎,得到荷载位移曲线和破碎强度,并对破碎后的碎片进行颗粒筛分以研究其破碎模式[13-14]. Huang等[14-16]采用室内试验和离散元数值模拟开展单颗粒压缩破碎研究,发现颗粒破碎强度服从Weibull分布. Turcotte[17]指出,颗粒的破碎可以用分形分布描述. 徐永福等[18]对岩石颗粒破碎进行系统研究,认为颗粒破碎的分形维数 $D$介于2.0~3.0. 王益栋等[19]进行大理岩颗粒的压缩破碎试验,测得其分形维数 $D$=2.48. 周海娟等[20]采用连续离散耦合分析方法(combined finite–discrete element method,FDEM)对5组不同粒径的堆石颗粒进行单颗粒破碎数值试验,结果表明颗粒破碎强度具有明显的尺寸效应,即颗粒特征强度随着颗粒尺寸的增大而逐渐减小. 孟敏强等[21]对3种不同粒径的泥岩和砂岩颗粒进行单颗粒破碎试验,也发现了相似的规律. 此外,众多国内外学者基于单颗粒压缩破碎试验,发现颗粒形状对颗粒破碎形式、破碎强度和Weibull模量等破碎特性有较大的影响[22-25]. ...
An investigation of breakage behaviour of single sand particles using a high-speed microscope camera
1
2016
... 目前,对单个颗粒的破碎研究常采用上下平板压缩颗粒直至破碎,得到荷载位移曲线和破碎强度,并对破碎后的碎片进行颗粒筛分以研究其破碎模式[13-14]. Huang等[14-16]采用室内试验和离散元数值模拟开展单颗粒压缩破碎研究,发现颗粒破碎强度服从Weibull分布. Turcotte[17]指出,颗粒的破碎可以用分形分布描述. 徐永福等[18]对岩石颗粒破碎进行系统研究,认为颗粒破碎的分形维数 $D$介于2.0~3.0. 王益栋等[19]进行大理岩颗粒的压缩破碎试验,测得其分形维数 $D$=2.48. 周海娟等[20]采用连续离散耦合分析方法(combined finite–discrete element method,FDEM)对5组不同粒径的堆石颗粒进行单颗粒破碎数值试验,结果表明颗粒破碎强度具有明显的尺寸效应,即颗粒特征强度随着颗粒尺寸的增大而逐渐减小. 孟敏强等[21]对3种不同粒径的泥岩和砂岩颗粒进行单颗粒破碎试验,也发现了相似的规律. 此外,众多国内外学者基于单颗粒压缩破碎试验,发现颗粒形状对颗粒破碎形式、破碎强度和Weibull模量等破碎特性有较大的影响[22-25]. ...
Modeling the fragmentation of rock grains using computed tomography and combined FDEM
0
2016
Study on the effect of particle morphology on single particle breakage using a combined finite-discrete element method
0
2020
颗粒形状对堆石颗粒破碎强度尺寸效应的影响
1
2021
... 目前,对单个颗粒的破碎研究常采用上下平板压缩颗粒直至破碎,得到荷载位移曲线和破碎强度,并对破碎后的碎片进行颗粒筛分以研究其破碎模式[13-14]. Huang等[14-16]采用室内试验和离散元数值模拟开展单颗粒压缩破碎研究,发现颗粒破碎强度服从Weibull分布. Turcotte[17]指出,颗粒的破碎可以用分形分布描述. 徐永福等[18]对岩石颗粒破碎进行系统研究,认为颗粒破碎的分形维数 $D$介于2.0~3.0. 王益栋等[19]进行大理岩颗粒的压缩破碎试验,测得其分形维数 $D$=2.48. 周海娟等[20]采用连续离散耦合分析方法(combined finite–discrete element method,FDEM)对5组不同粒径的堆石颗粒进行单颗粒破碎数值试验,结果表明颗粒破碎强度具有明显的尺寸效应,即颗粒特征强度随着颗粒尺寸的增大而逐渐减小. 孟敏强等[21]对3种不同粒径的泥岩和砂岩颗粒进行单颗粒破碎试验,也发现了相似的规律. 此外,众多国内外学者基于单颗粒压缩破碎试验,发现颗粒形状对颗粒破碎形式、破碎强度和Weibull模量等破碎特性有较大的影响[22-25]. ...
颗粒形状对堆石颗粒破碎强度尺寸效应的影响
1
2021
... 目前,对单个颗粒的破碎研究常采用上下平板压缩颗粒直至破碎,得到荷载位移曲线和破碎强度,并对破碎后的碎片进行颗粒筛分以研究其破碎模式[13-14]. Huang等[14-16]采用室内试验和离散元数值模拟开展单颗粒压缩破碎研究,发现颗粒破碎强度服从Weibull分布. Turcotte[17]指出,颗粒的破碎可以用分形分布描述. 徐永福等[18]对岩石颗粒破碎进行系统研究,认为颗粒破碎的分形维数 $D$介于2.0~3.0. 王益栋等[19]进行大理岩颗粒的压缩破碎试验,测得其分形维数 $D$=2.48. 周海娟等[20]采用连续离散耦合分析方法(combined finite–discrete element method,FDEM)对5组不同粒径的堆石颗粒进行单颗粒破碎数值试验,结果表明颗粒破碎强度具有明显的尺寸效应,即颗粒特征强度随着颗粒尺寸的增大而逐渐减小. 孟敏强等[21]对3种不同粒径的泥岩和砂岩颗粒进行单颗粒破碎试验,也发现了相似的规律. 此外,众多国内外学者基于单颗粒压缩破碎试验,发现颗粒形状对颗粒破碎形式、破碎强度和Weibull模量等破碎特性有较大的影响[22-25]. ...
2
... 上述研究均是采用上下平板压缩单个颗粒以研究其破碎特性,而实际颗粒集合体中颗粒受邻近颗粒的约束形式各异,导致颗粒受力情况复杂,其破碎特性与平板压缩下的情况可能存在较大差异. Salami等[26-27]在MTS试验机上加装了一个含多个夹具的夹持装置,通过调整夹具的数目和位置进行多点约束情况下的颗粒径向压缩试验,试验结果表明不同的约束模式会产生特定的破碎形式,但受限于装置刚度,试验过程中夹具易失稳脱落,因此相关试验数据较少. 邓璇璇等[28]采用FDEM模拟了Salami等[26-27]的室内试验,研究二维情况下颗粒在不同约束模式下的破碎特性,并引入奇异值分解的思想来量化颗粒约束模式,发现颗粒破碎强度与平均奇异值有关. Zhu等[29]采用近场动力学模拟颗粒在多约束情况下的破碎,分析现有颗粒破碎准则的适用性,发现多点接触情况下最大接触力准则适用性最好. Kuang等[30]采用离散元方法研究配位数对单颗粒破碎行为的影响,结果表明配位数的增加会导致更大的破碎强度和更具延性的破碎模式. ...
... [26-27]的室内试验,研究二维情况下颗粒在不同约束模式下的破碎特性,并引入奇异值分解的思想来量化颗粒约束模式,发现颗粒破碎强度与平均奇异值有关. Zhu等[29]采用近场动力学模拟颗粒在多约束情况下的破碎,分析现有颗粒破碎准则的适用性,发现多点接触情况下最大接触力准则适用性最好. Kuang等[30]采用离散元方法研究配位数对单颗粒破碎行为的影响,结果表明配位数的增加会导致更大的破碎强度和更具延性的破碎模式. ...
An experimental study on the influence of the coordination number on grain crushing
2
2017
... 上述研究均是采用上下平板压缩单个颗粒以研究其破碎特性,而实际颗粒集合体中颗粒受邻近颗粒的约束形式各异,导致颗粒受力情况复杂,其破碎特性与平板压缩下的情况可能存在较大差异. Salami等[26-27]在MTS试验机上加装了一个含多个夹具的夹持装置,通过调整夹具的数目和位置进行多点约束情况下的颗粒径向压缩试验,试验结果表明不同的约束模式会产生特定的破碎形式,但受限于装置刚度,试验过程中夹具易失稳脱落,因此相关试验数据较少. 邓璇璇等[28]采用FDEM模拟了Salami等[26-27]的室内试验,研究二维情况下颗粒在不同约束模式下的破碎特性,并引入奇异值分解的思想来量化颗粒约束模式,发现颗粒破碎强度与平均奇异值有关. Zhu等[29]采用近场动力学模拟颗粒在多约束情况下的破碎,分析现有颗粒破碎准则的适用性,发现多点接触情况下最大接触力准则适用性最好. Kuang等[30]采用离散元方法研究配位数对单颗粒破碎行为的影响,结果表明配位数的增加会导致更大的破碎强度和更具延性的破碎模式. ...
... -27]的室内试验,研究二维情况下颗粒在不同约束模式下的破碎特性,并引入奇异值分解的思想来量化颗粒约束模式,发现颗粒破碎强度与平均奇异值有关. Zhu等[29]采用近场动力学模拟颗粒在多约束情况下的破碎,分析现有颗粒破碎准则的适用性,发现多点接触情况下最大接触力准则适用性最好. Kuang等[30]采用离散元方法研究配位数对单颗粒破碎行为的影响,结果表明配位数的增加会导致更大的破碎强度和更具延性的破碎模式. ...
局部约束模式对单颗粒破碎强度的影响
1
2018
... 上述研究均是采用上下平板压缩单个颗粒以研究其破碎特性,而实际颗粒集合体中颗粒受邻近颗粒的约束形式各异,导致颗粒受力情况复杂,其破碎特性与平板压缩下的情况可能存在较大差异. Salami等[26-27]在MTS试验机上加装了一个含多个夹具的夹持装置,通过调整夹具的数目和位置进行多点约束情况下的颗粒径向压缩试验,试验结果表明不同的约束模式会产生特定的破碎形式,但受限于装置刚度,试验过程中夹具易失稳脱落,因此相关试验数据较少. 邓璇璇等[28]采用FDEM模拟了Salami等[26-27]的室内试验,研究二维情况下颗粒在不同约束模式下的破碎特性,并引入奇异值分解的思想来量化颗粒约束模式,发现颗粒破碎强度与平均奇异值有关. Zhu等[29]采用近场动力学模拟颗粒在多约束情况下的破碎,分析现有颗粒破碎准则的适用性,发现多点接触情况下最大接触力准则适用性最好. Kuang等[30]采用离散元方法研究配位数对单颗粒破碎行为的影响,结果表明配位数的增加会导致更大的破碎强度和更具延性的破碎模式. ...
局部约束模式对单颗粒破碎强度的影响
1
2018
... 上述研究均是采用上下平板压缩单个颗粒以研究其破碎特性,而实际颗粒集合体中颗粒受邻近颗粒的约束形式各异,导致颗粒受力情况复杂,其破碎特性与平板压缩下的情况可能存在较大差异. Salami等[26-27]在MTS试验机上加装了一个含多个夹具的夹持装置,通过调整夹具的数目和位置进行多点约束情况下的颗粒径向压缩试验,试验结果表明不同的约束模式会产生特定的破碎形式,但受限于装置刚度,试验过程中夹具易失稳脱落,因此相关试验数据较少. 邓璇璇等[28]采用FDEM模拟了Salami等[26-27]的室内试验,研究二维情况下颗粒在不同约束模式下的破碎特性,并引入奇异值分解的思想来量化颗粒约束模式,发现颗粒破碎强度与平均奇异值有关. Zhu等[29]采用近场动力学模拟颗粒在多约束情况下的破碎,分析现有颗粒破碎准则的适用性,发现多点接触情况下最大接触力准则适用性最好. Kuang等[30]采用离散元方法研究配位数对单颗粒破碎行为的影响,结果表明配位数的增加会导致更大的破碎强度和更具延性的破碎模式. ...
A peridynamic investigation on crushing of sand particles
1
2019
... 上述研究均是采用上下平板压缩单个颗粒以研究其破碎特性,而实际颗粒集合体中颗粒受邻近颗粒的约束形式各异,导致颗粒受力情况复杂,其破碎特性与平板压缩下的情况可能存在较大差异. Salami等[26-27]在MTS试验机上加装了一个含多个夹具的夹持装置,通过调整夹具的数目和位置进行多点约束情况下的颗粒径向压缩试验,试验结果表明不同的约束模式会产生特定的破碎形式,但受限于装置刚度,试验过程中夹具易失稳脱落,因此相关试验数据较少. 邓璇璇等[28]采用FDEM模拟了Salami等[26-27]的室内试验,研究二维情况下颗粒在不同约束模式下的破碎特性,并引入奇异值分解的思想来量化颗粒约束模式,发现颗粒破碎强度与平均奇异值有关. Zhu等[29]采用近场动力学模拟颗粒在多约束情况下的破碎,分析现有颗粒破碎准则的适用性,发现多点接触情况下最大接触力准则适用性最好. Kuang等[30]采用离散元方法研究配位数对单颗粒破碎行为的影响,结果表明配位数的增加会导致更大的破碎强度和更具延性的破碎模式. ...
Numerical investigation of the cushion and size effects during single-particle crushing via DEM
1
2020
... 上述研究均是采用上下平板压缩单个颗粒以研究其破碎特性,而实际颗粒集合体中颗粒受邻近颗粒的约束形式各异,导致颗粒受力情况复杂,其破碎特性与平板压缩下的情况可能存在较大差异. Salami等[26-27]在MTS试验机上加装了一个含多个夹具的夹持装置,通过调整夹具的数目和位置进行多点约束情况下的颗粒径向压缩试验,试验结果表明不同的约束模式会产生特定的破碎形式,但受限于装置刚度,试验过程中夹具易失稳脱落,因此相关试验数据较少. 邓璇璇等[28]采用FDEM模拟了Salami等[26-27]的室内试验,研究二维情况下颗粒在不同约束模式下的破碎特性,并引入奇异值分解的思想来量化颗粒约束模式,发现颗粒破碎强度与平均奇异值有关. Zhu等[29]采用近场动力学模拟颗粒在多约束情况下的破碎,分析现有颗粒破碎准则的适用性,发现多点接触情况下最大接触力准则适用性最好. Kuang等[30]采用离散元方法研究配位数对单颗粒破碎行为的影响,结果表明配位数的增加会导致更大的破碎强度和更具延性的破碎模式. ...
基于离散元法的颗粒破碎模拟研究进展
1
2018
... 为了进一步研究三维情况下单个颗粒在不同约束模式下的破碎特性,本研究开展了物理试验和FDEM数值试验研究. 通过改变颗粒周边约束板的个数和位置,设定了不同的约束模式. 并采用奇异值分解(singular value decomposition,SVD)对各约束模式下颗粒接触力平衡方程的系数矩阵进行转换,提出了颗粒约束模式的量化指标. 系统研究了约束模式对颗粒破碎模式、碎片尺寸分布和破碎强度的影响. 研究成果有助于帮助人们发展更合理的颗粒材料模拟方法[31-32]. ...
基于离散元法的颗粒破碎模拟研究进展
1
2018
... 为了进一步研究三维情况下单个颗粒在不同约束模式下的破碎特性,本研究开展了物理试验和FDEM数值试验研究. 通过改变颗粒周边约束板的个数和位置,设定了不同的约束模式. 并采用奇异值分解(singular value decomposition,SVD)对各约束模式下颗粒接触力平衡方程的系数矩阵进行转换,提出了颗粒约束模式的量化指标. 系统研究了约束模式对颗粒破碎模式、碎片尺寸分布和破碎强度的影响. 研究成果有助于帮助人们发展更合理的颗粒材料模拟方法[31-32]. ...
Discrete element modeling of particle breakage considering different fragment replacement modes
1
2020
... 为了进一步研究三维情况下单个颗粒在不同约束模式下的破碎特性,本研究开展了物理试验和FDEM数值试验研究. 通过改变颗粒周边约束板的个数和位置,设定了不同的约束模式. 并采用奇异值分解(singular value decomposition,SVD)对各约束模式下颗粒接触力平衡方程的系数矩阵进行转换,提出了颗粒约束模式的量化指标. 系统研究了约束模式对颗粒破碎模式、碎片尺寸分布和破碎强度的影响. 研究成果有助于帮助人们发展更合理的颗粒材料模拟方法[31-32]. ...
颗粒形状对人工模拟堆石料强度和变形特性影响的试验研究
1
2017
... 考虑到天然颗粒的大小、形状和材质均不同,难以进行重复试验,众多学者采用水泥、石膏、玻璃、钢铁等材料制作人工模拟颗粒开展相关试验研究[33-36]. 基于此,本研究采用粉煤灰-石膏净浆统一浇筑制作粒径为40 mm的球形人工模拟颗粒,制备材料包括:抗折强度为7 MPa的高强度石膏粉、粉煤灰和水. 制备过程主要如下:配置粉煤灰-石膏净浆、模具定型、成型养护,如图1所示. ...
颗粒形状对人工模拟堆石料强度和变形特性影响的试验研究
1
2017
... 考虑到天然颗粒的大小、形状和材质均不同,难以进行重复试验,众多学者采用水泥、石膏、玻璃、钢铁等材料制作人工模拟颗粒开展相关试验研究[33-36]. 基于此,本研究采用粉煤灰-石膏净浆统一浇筑制作粒径为40 mm的球形人工模拟颗粒,制备材料包括:抗折强度为7 MPa的高强度石膏粉、粉煤灰和水. 制备过程主要如下:配置粉煤灰-石膏净浆、模具定型、成型养护,如图1所示. ...
A unified fractional breakage model for granular materials inspired by the crushing tests of dyed gypsum particles
0
2021
冲击荷载下颗粒物质缓冲性能的试验研究
1
2012
... 考虑到天然颗粒的大小、形状和材质均不同,难以进行重复试验,众多学者采用水泥、石膏、玻璃、钢铁等材料制作人工模拟颗粒开展相关试验研究[33-36]. 基于此,本研究采用粉煤灰-石膏净浆统一浇筑制作粒径为40 mm的球形人工模拟颗粒,制备材料包括:抗折强度为7 MPa的高强度石膏粉、粉煤灰和水. 制备过程主要如下:配置粉煤灰-石膏净浆、模具定型、成型养护,如图1所示. ...
冲击荷载下颗粒物质缓冲性能的试验研究
1
2012
... 考虑到天然颗粒的大小、形状和材质均不同,难以进行重复试验,众多学者采用水泥、石膏、玻璃、钢铁等材料制作人工模拟颗粒开展相关试验研究[33-36]. 基于此,本研究采用粉煤灰-石膏净浆统一浇筑制作粒径为40 mm的球形人工模拟颗粒,制备材料包括:抗折强度为7 MPa的高强度石膏粉、粉煤灰和水. 制备过程主要如下:配置粉煤灰-石膏净浆、模具定型、成型养护,如图1所示. ...
Y-Geo: new combined finite-discrete element numerical code for geomechanical applications
1
2012
... FDEM方法采用有限单元法计算颗粒内部的应力变形,基于断裂力学的内聚力模型模拟颗粒的破碎,对离散块体进行接触检索和接触判断,然后采用接触力模型模拟块体之间的非弹性接触和摩擦耗散. 该方法能够准确合理地模拟颗粒材料中颗粒由于高接触力导致裂纹产生、扩展到破碎的全过程,是研究颗粒破碎的一种有效手段[37-41]. ...
Modeling the particle breakage of rockfill materials with the cohesive crack model
0
2014
Modeling the fragmentation of rock grains using computed tomography and combined FDEM
0
2017
模拟岩体失效全过程的连续-非连续变形体离散元方法及应用
0
2011
模拟岩体失效全过程的连续-非连续变形体离散元方法及应用
0
2011
用非连续变形分析方法模拟岩石裂纹扩展
1
2007
... FDEM方法采用有限单元法计算颗粒内部的应力变形,基于断裂力学的内聚力模型模拟颗粒的破碎,对离散块体进行接触检索和接触判断,然后采用接触力模型模拟块体之间的非弹性接触和摩擦耗散. 该方法能够准确合理地模拟颗粒材料中颗粒由于高接触力导致裂纹产生、扩展到破碎的全过程,是研究颗粒破碎的一种有效手段[37-41]. ...
用非连续变形分析方法模拟岩石裂纹扩展
1
2007
... FDEM方法采用有限单元法计算颗粒内部的应力变形,基于断裂力学的内聚力模型模拟颗粒的破碎,对离散块体进行接触检索和接触判断,然后采用接触力模型模拟块体之间的非弹性接触和摩擦耗散. 该方法能够准确合理地模拟颗粒材料中颗粒由于高接触力导致裂纹产生、扩展到破碎的全过程,是研究颗粒破碎的一种有效手段[37-41]. ...
An irreversible cohesive zone model for interface fatigue crack growth simulation
1
2003
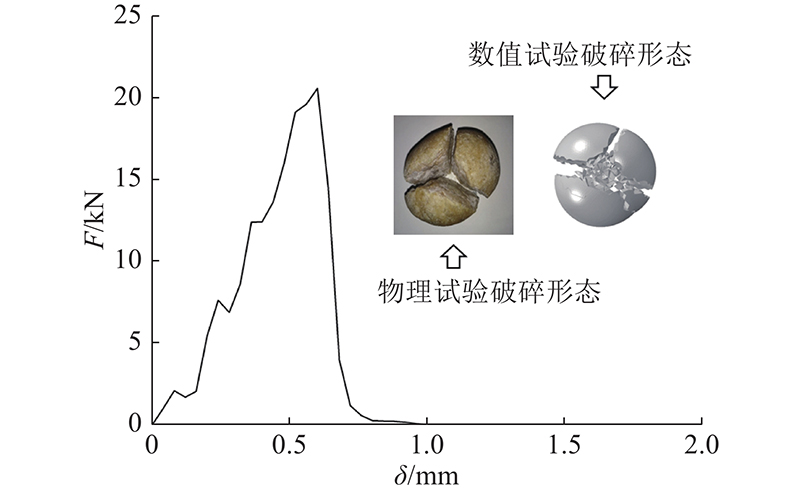
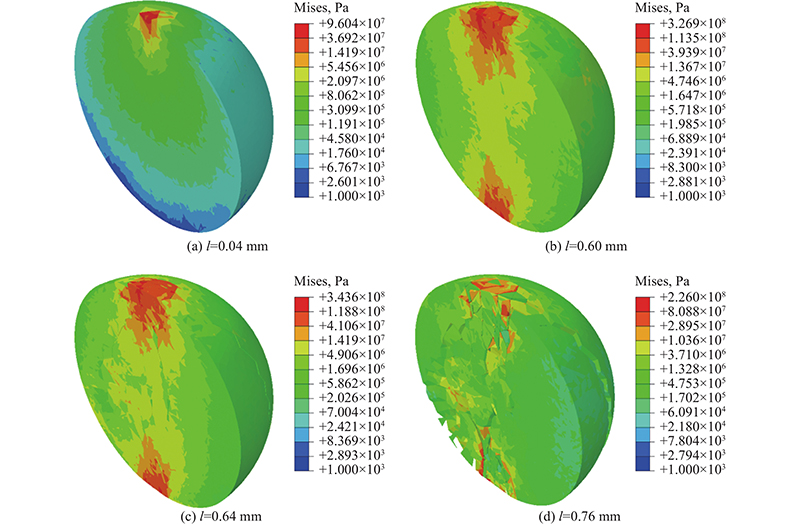
... 采用内聚力模型模拟颗粒破碎,通过无厚度界面单元的损伤和失效来模拟开裂过程[42-44]. 如图7所示为FDEM模拟的圆球颗粒. 为了便于形象展示,图中界面单元按一定厚度显示. 在界面单元发生开裂前,对外荷载的变形响应为线弹性,界面单元始终与实体单元保持变形协调,其力-位移关系满足如下公式: ...
Yielding of steel sheets containing slits
0
1960
The Mechanical theory of equilibrium cracks in brittle fracture
1
1962
... 采用内聚力模型模拟颗粒破碎,通过无厚度界面单元的损伤和失效来模拟开裂过程[42-44]. 如图7所示为FDEM模拟的圆球颗粒. 为了便于形象展示,图中界面单元按一定厚度显示. 在界面单元发生开裂前,对外荷载的变形响应为线弹性,界面单元始终与实体单元保持变形协调,其力-位移关系满足如下公式: ...
Principal component analysis
1
2002
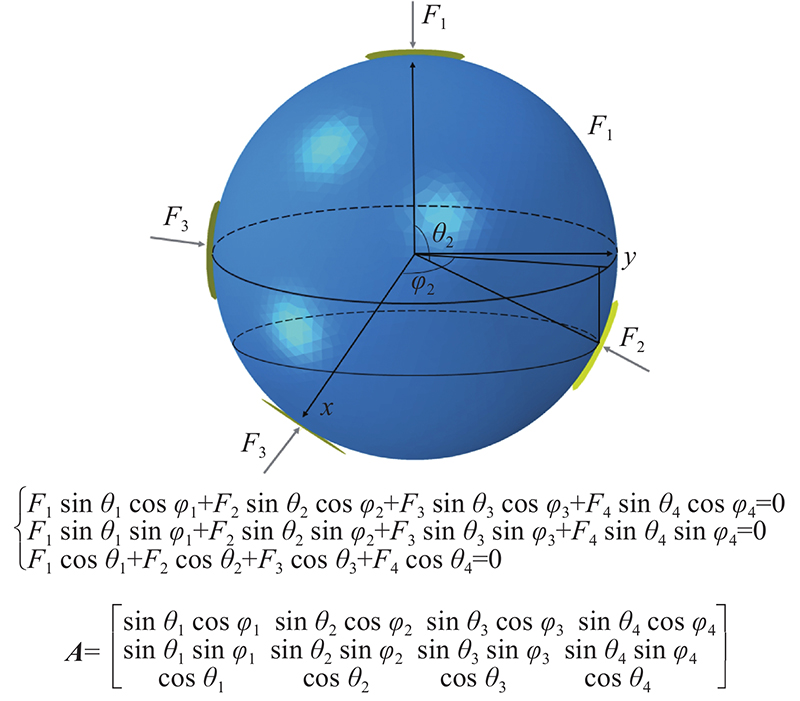
... 矩阵的奇异值分解常用于主成分分析[45],其作用可以理解为,通过正交变换将其分量相关的原随机向量转化成其分量不相关的新随机向量. 将n维空间 ${{\bf{R}}^n}$的标准正交基 $ \left\{ {{{\boldsymbol{\nu }}_{\boldsymbol{1}}},{{\boldsymbol{\nu }}_{\boldsymbol{2}}}, \cdots ,{{\boldsymbol{\nu }}_{\boldsymbol{n}}}} \right\} $映射到m维空间 ${{\bf{R}}^m}$的标准正交基 $ \left\{ {{{\boldsymbol{u}}_{\boldsymbol{1}}},{{\boldsymbol{u}}_{\boldsymbol{2}}}, \cdots ,{{\boldsymbol{u}}_{\boldsymbol{m}}}} \right\} $上,即 $ {\boldsymbol{AV}} = {\boldsymbol{U\varSigma }} $,其中, $ {\boldsymbol{V}} $表示原始域的标准正交基, $ {\boldsymbol{U}} $表示经过 $ {\boldsymbol{A}} $变换后的标准正交基, $ {\boldsymbol{\varSigma }} $表示 $ {\boldsymbol{V}} $中的向量与 $ {\boldsymbol{U}} $中相对应向量之间的关系,在几何上表现为将原坐标系变换成新的正交坐标系,即实现了对多维变量系统保留原数据重要信息的降维处理,使之能以一个较高的精度转换成低维变量系统. 本研究采用奇异值分解获取颗粒约束模式的简化指标,通过构建适当的价值函数,定量描述颗粒不同的约束状态. ...
The application of Weibull statistics to the fracture of soil particles
1
2000
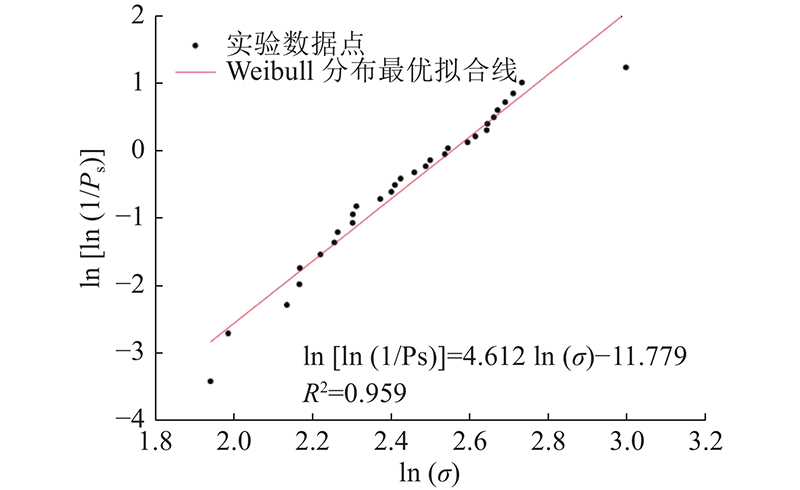
... 本研究不考虑颗粒形状的影响,选择直径为40 mm的圆球颗粒作为研究对象. 为了确定FDEM模拟所需参数,对30个直径为33.08~45.78 mm的类圆球岩石颗粒进行单颗粒压缩试验,对颗粒破碎强度进行Weibull拟合分析[46-47],如图9所示. 图中,Ps为颗粒的生存概率,σ为应力. 其特征破碎强度和Weibull模量分别为12.86 MPa和4.612. ...
The application of Weibull statistics to the strength of railway ballast
1
2004
... 本研究不考虑颗粒形状的影响,选择直径为40 mm的圆球颗粒作为研究对象. 为了确定FDEM模拟所需参数,对30个直径为33.08~45.78 mm的类圆球岩石颗粒进行单颗粒压缩试验,对颗粒破碎强度进行Weibull拟合分析[46-47],如图9所示. 图中,Ps为颗粒的生存概率,σ为应力. 其特征破碎强度和Weibull模量分别为12.86 MPa和4.612. ...
基于FDEM的岩石颗粒破碎后碎片形状的统计分析
1
2021
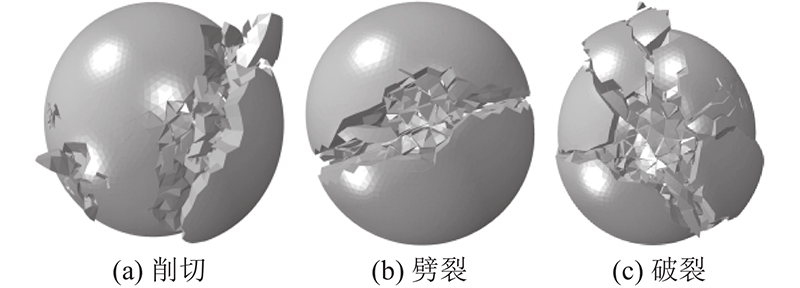
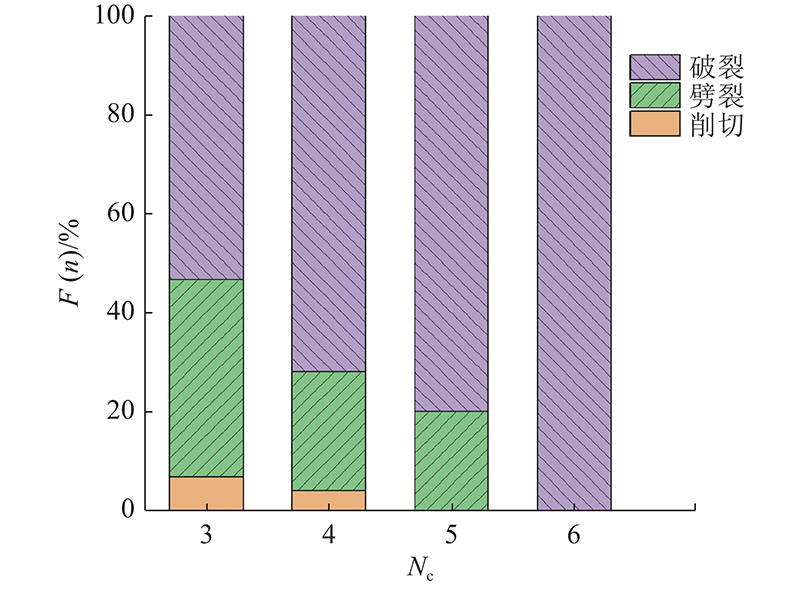
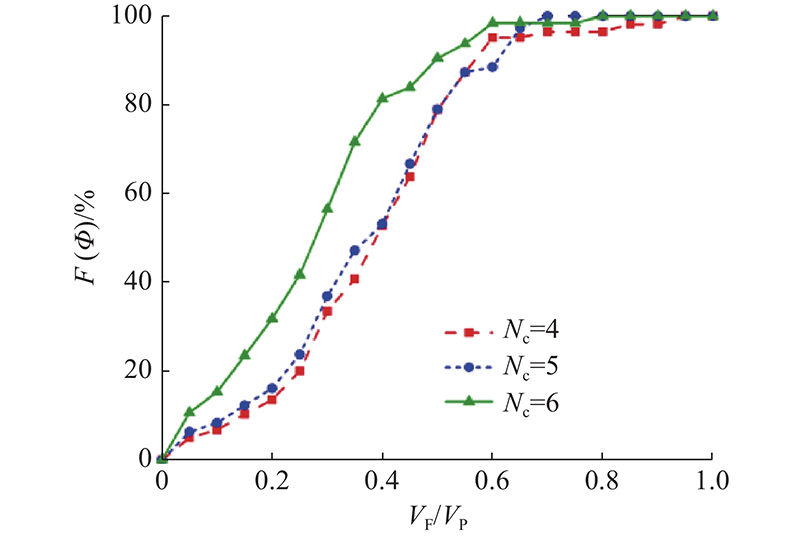
... 为了探究约束个数与颗粒破碎碎片分布的关系,根据数值计算结果统计各约束个数情况下颗粒破碎碎片的累积分布 $ F(\varPhi ) $,如图17所示[48]. 图中,VF为碎片体积,VP为初始颗粒体积. 对于脆性圆球颗粒,当约束个数为4时,最常见的碎片形式是1个颗粒破碎成2~4个体积大致相等的主碎片,故大部分碎片(>80%)的体积为初始颗粒的20%~60%,同时,在约束个数为4的情况下颗粒会出现削切破碎形式,故有少量碎片(约5%)的体积大于初始颗粒的60%. 随着约束个数的增长,颗粒破碎形式愈发复杂,颗粒破碎后碎片尺寸差异较大的情况更加普遍. 当约束个数为6时,小碎片数目显著增多,碎片体积集中在初始颗粒的0~40%,碎片尺寸分布较约束个数为4、5时的情况有明显差异. 因此,随着约束个数的增加,颗粒破碎后的碎片体积表现出减少趋势. ...
基于FDEM的岩石颗粒破碎后碎片形状的统计分析
1
2021
... 为了探究约束个数与颗粒破碎碎片分布的关系,根据数值计算结果统计各约束个数情况下颗粒破碎碎片的累积分布 $ F(\varPhi ) $,如图17所示[48]. 图中,VF为碎片体积,VP为初始颗粒体积. 对于脆性圆球颗粒,当约束个数为4时,最常见的碎片形式是1个颗粒破碎成2~4个体积大致相等的主碎片,故大部分碎片(>80%)的体积为初始颗粒的20%~60%,同时,在约束个数为4的情况下颗粒会出现削切破碎形式,故有少量碎片(约5%)的体积大于初始颗粒的60%. 随着约束个数的增长,颗粒破碎形式愈发复杂,颗粒破碎后碎片尺寸差异较大的情况更加普遍. 当约束个数为6时,小碎片数目显著增多,碎片体积集中在初始颗粒的0~40%,碎片尺寸分布较约束个数为4、5时的情况有明显差异. 因此,随着约束个数的增加,颗粒破碎后的碎片体积表现出减少趋势. ...
Macroscopic and microscopic behaviors of granular materials under proportional strain path: a DEM study
1
2016
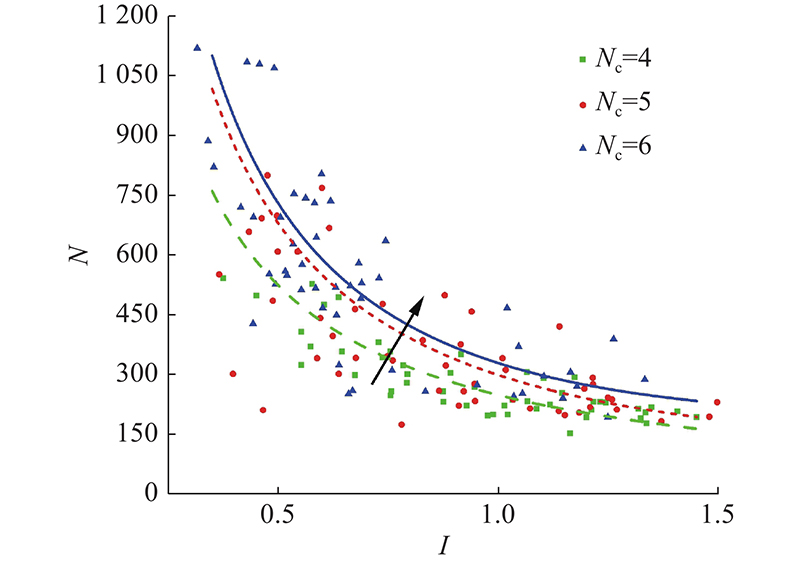
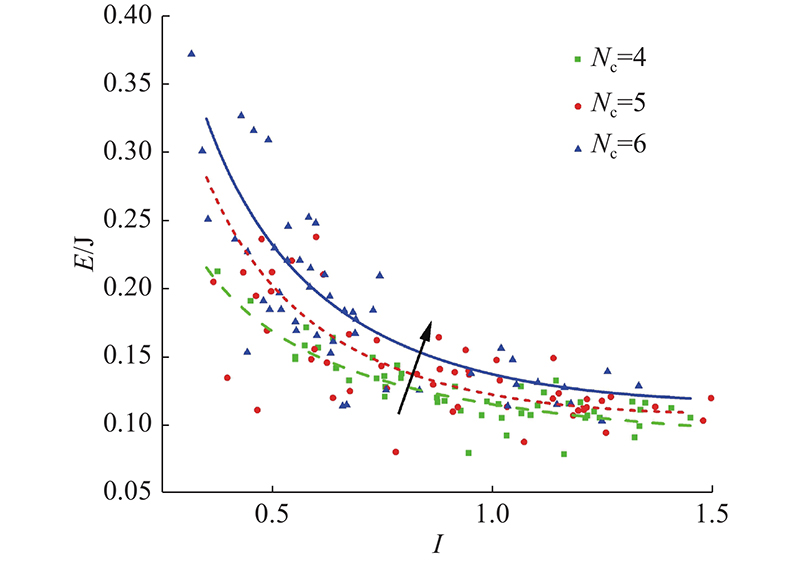
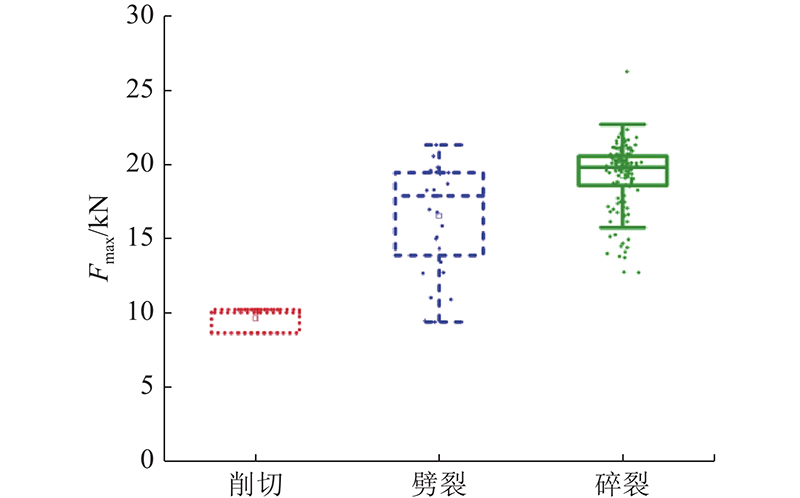
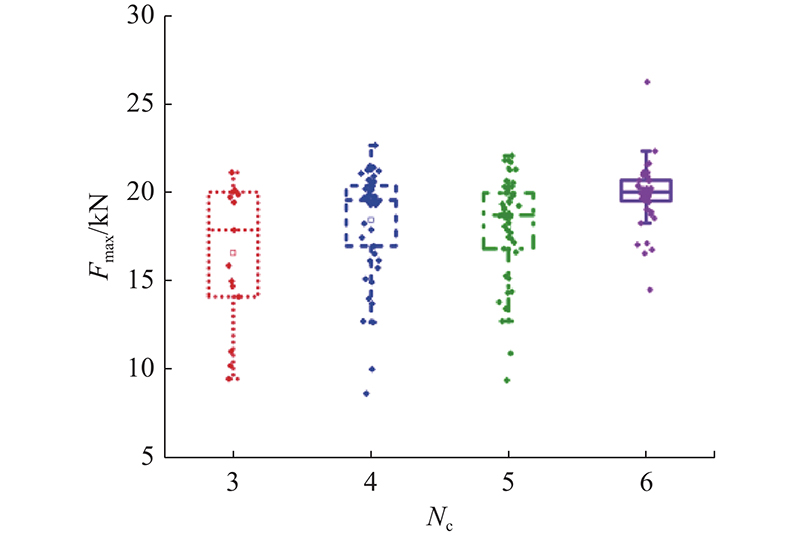
... 约束模式对颗粒破碎强度有显著的影响,研究对不同约束个数情况下的颗粒破碎强度进行了统计分析. 如图18所示为不同破碎形式下颗粒破碎峰值荷载 ${F_{\max }}$箱型图. 当颗粒发生削切破碎时,由于主要是剪切应力导致开裂,颗粒破碎并不完全,其破碎时的峰值荷载最低. 当发生劈裂破碎时,颗粒以劈拉开裂为主,破碎时峰值荷载的离散性较大. 如图19所示为不同约束个数下颗粒破碎峰值荷载箱型图. 总体来看,在不同约束个数情况下,颗粒破碎峰值荷载表现出随约束个数略微增大的趋势,但这种趋势在约束个数为4~6时并不明显,可以忽略. 在颗粒材料中,约束个数为4~6的颗粒占绝大多数[49]. 因此,使用最大接触力来判断颗粒破碎是一种简单且有效的方式. ...