三端口DC-DC变换器(three-port DC-DC converter, TPC)因功率器件少、集成度高,获得了广泛的研究与应用[1-7]. 本文以双Buck-Boost集成双有源桥(dual- active-bridge, DAB)型TPC作为研究对象. 王荣闯等[8]提出Buck-Boost与LCL谐振型DAB集成型TPC. Wang等[9]提出应用于混合储能的TPC的分布式充电状态平衡控制方法. Wang等[10]提出在TPC的副边采用内移相控制,以实现减小功率回流的目的. Wang等[11]提出应用于光储联合供电系统的TPC控制方法. Lu等[12]提出应用分布式光伏 (PV) 发电设备并网的TPC混合连接架构及该架构下的TPC控制方法. 该类TPC存在与DAB相同的问题,当原边DC Bus与负载端口电压不匹配时,高频变压器的漏感电流应力会急剧增加,导致效率降低、电压/电流变化率增大的问题. 为了优化电流应力,针对DAB拓扑,各种各样的优化移相控制方法被相继提出,包括双重移相控制[13-14]、扩展移相控制[15]及三重移相控制[16]. 安峰等[17]在DAB双重移相控制的基础上,提出基于模型前馈的电流应力优化方法. 胡燕等[18]提出自然软开关模式下的DAB电流应力优化算法,能够最大程度地降低电流应力. 涂春鸣等[19]给出三端口隔离 DC-DC 变换器(triple active bridge,TAB)高频链电流应力、有效值的计算方法,为后续的优化问题提供基础. 在电流应力的优化过程中,双Buck-Boost集成DAB型TPC电流应力最优值的求解与DAB、TAB具有差异性,目前对于该类TPC的高频链电流优化问题鲜有深入的研究.
为了实现双Buck-Boost集成DAB型TPC高频链应力优化,本文将副边桥臂间的内移相角作为控制自由度,分析该类TPC高频链的工作模式,给出各个模式下高频链传输功率与电流应力的表达式. 由各模式的运行边界给出优化求解过程的约束条件,分析TPC原副边电压匹配度大于等于1以及小于1这2种情况,建立TPC高频链电流应力优化的数学模型. TPC高频链电流应力优化问题转化为约束条件下的极值求解问题,给出各模式下的电流应力实现条件. 通过实验,验证了电流应力优化控制方法的有效性.
1. TPC拓扑与控制方法
1.1. TPC拓扑
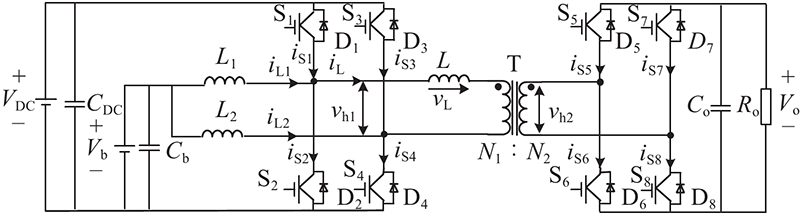
TPC变换器拓扑结构如图1所示. 图中,VDC、Vb、Vo 3个端口分别接直流母线、蓄电池与负荷,S1 ~ S4为高频变压器原边的主开关管,S5 ~ S8为高频变压器副边的主开关管,L1与L2为蓄电池端口的滤波电感,N1与N2为高频变压器原、副边绕组匝数,变比n =N1/N2,L为高频变压器等效漏感,CDC、Cb、Co为直流母线端口、蓄电池端口与负荷端口的滤波电容.
图 1
高频变压器原边2个端口均为双向端口,副边为隔离双向端口,端口之间均为单级功率变换,系统的整体变换效率高. 原边两路双向Buck-Boost电路采用180°交错并联工作方式,可以大大地减小输入电流纹波.
1.2. TPC控制方法
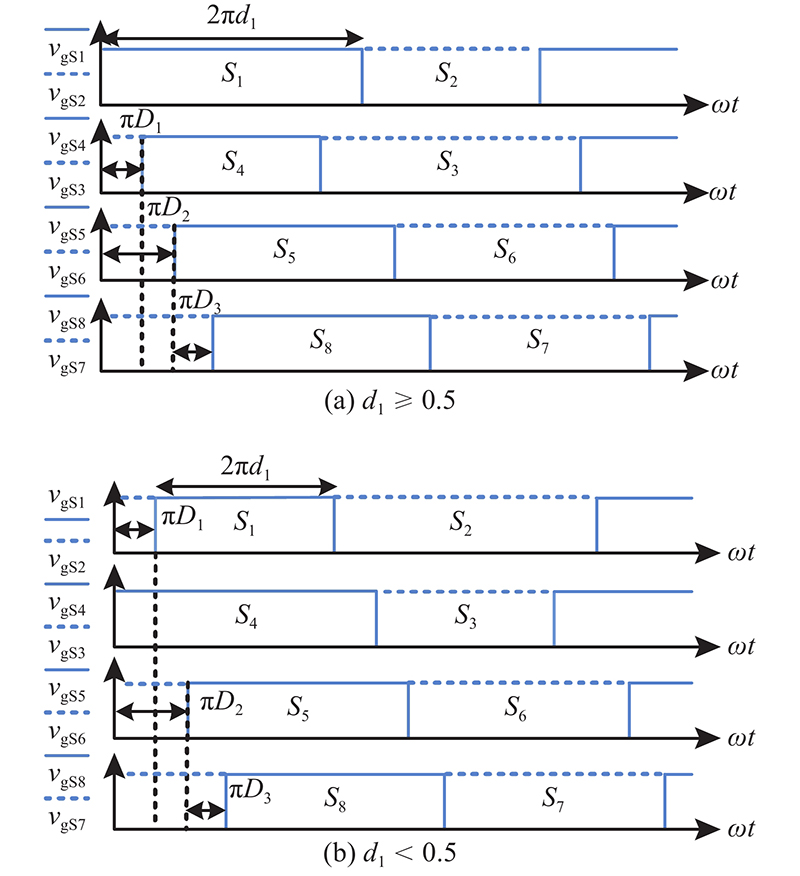
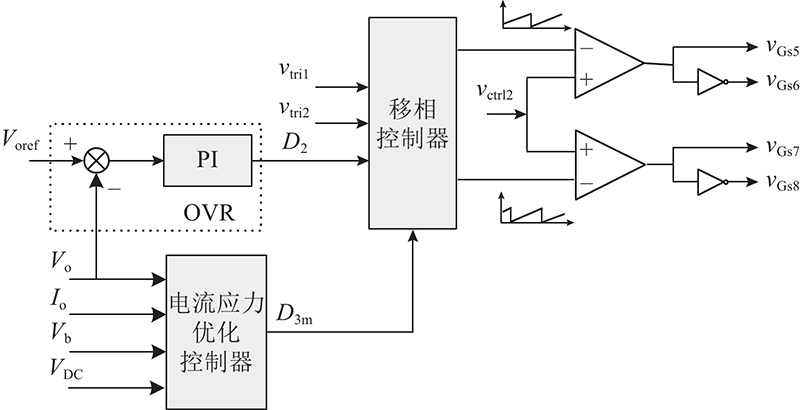
对于双Buck-Boost集成DAB型TPC,采用2个独立的控制变量来实现3个端口之间的功率控制. 如图2(a)所示,VDCref为直流母线端口电压VDC的参考值,Ibchamax为蓄电池的最大充电电流,Vbmax为蓄电池的最大充电电压. 对于直流母线端和蓄电池端,在任意时刻只有一个端口处于受控状态,可以通过调节原边桥臂的占空比d1实现对这2个端口之间的电压或功率控制. 在不同端口进行能量路由时,涉及到多工况运行,控制环路采用最小值竞争模式,当前时刻在直流母线端电压调节器、蓄电池端电流调节器、蓄电池端电压调节器中,输出值最小的调节器参与原边占空比d1的调节,实现了无缝工况切换.
图 2
2. TPC高频链运行分析
当直流并网端口VDC与负载端口电压Vo不匹配时,高频变压器的漏感电流应力会急剧增加,导致效率降低,电压/电流变化率增大的问题. 为了解决该问题,提出在移相控制方法上引入优化电流控制. 双Buck-Boost集成DAB型TPC在控制方式上存在第3个自由度D3,高频变压器原边占空比d1可以对原边两输入端口的电压、功率进行调节,原、副边之间的移相占空比D2可以对输出电压、功率进行调节,副边桥臂间的移相占空比D3可以用来优化高频变压器的漏感电流,减小器件的电流应力.
2.1. TPC高频链工作模式的分析
原边可以等效为交错并联Buck-Boost电路,占空比为
令
图 3
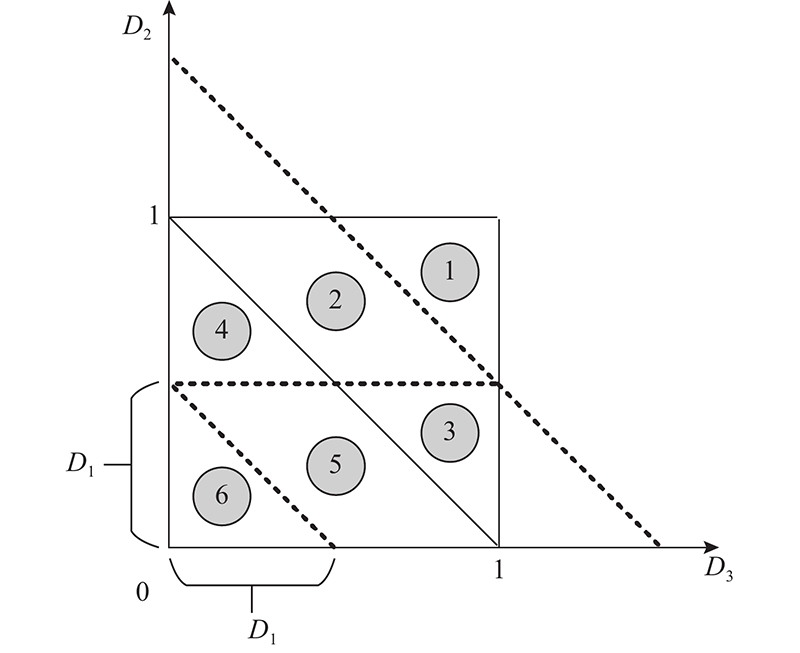
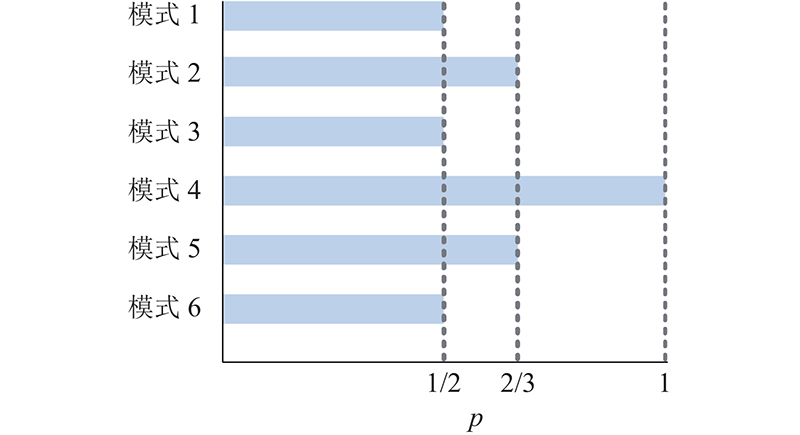
副边驱动采用占空比为0.5的方波,2个桥臂之间的移相占空比为D3. 根据D1、D2、D3的大小关系可知,TPC高频链可以分为6种工作模式,每种工作模式由3个不等式方程组成,这几个方程是“与”的关系. 各模式的工作范围如图4所示.
在各模式下,高频变压器原边电压vh1、副边电压vh2的波形如图5所示.
图 4
图 5
图 5 高频变压器的原、副边电压波形
Fig.5 Voltage waveforms of high-frequency transformer on primary and secondary sides
2.2. TPC高频链功率分析
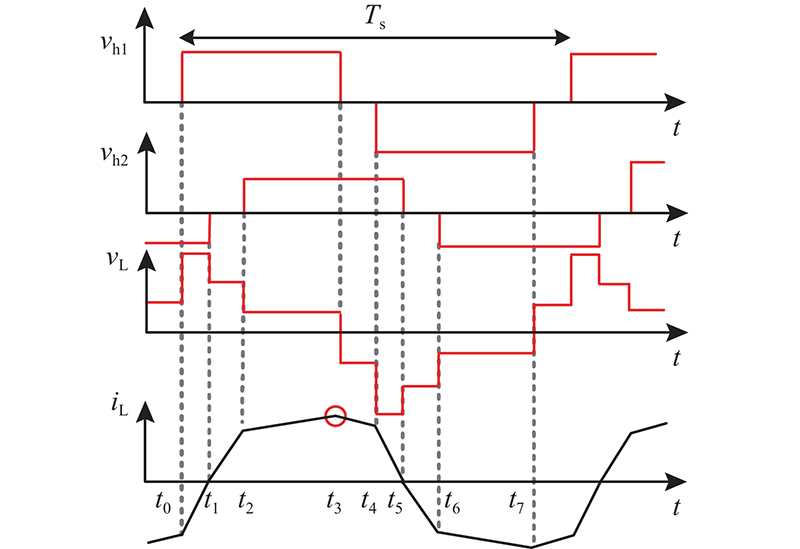
当k = VDC/(nVo) > 1时,以模式4为例,对高频链的传输功率进行分析,其他模式下的传输功率分析方法与模式4一致. 模式4下的高频变压器漏感电流、电压如 图6所示.
图 6
高频变压器原、副边之间传输的功率为
令功率基准值为
式中:p为功率标幺值.
在t3时刻,高频链电流iL达到峰值,这一时刻的电流表达式为
令电流基准值为
计算模式1~6下的传输功率标幺值,分别如下.
模式4的工作范围为:0≤D1≤D2,0≤D2≤1−D3,0≤D3≤1.0;模式5的工作范围为:D2≤D1≤D2 + D3,0≤D2≤1−D3,0≤D3≤1.0. 模式4与模式5之间的过渡状态为:D2=D1. 将D2=D1代入
3. TPC高频链电流应力优化控制方法
3.1. TPC高频链电流应力优化数学模型
优化控制方法的根本原理是调整高频变压器原边、副边电压波形以及两者之间的移相角进而调整高频变压器等效漏感上电压波形以实现对漏感电流应力的优化,而与DAB、TAB不同的是,双Buck-Boost集成DAB型TPC原边每个桥臂的占空比取决于直流母线与储能设备的电压,即其高频变压器原边电压与原边桥臂的占空比是相关的,也就是说,在TPC电流应力优化问题的求解过程中,原边桥臂的占空比是作为约束条件存在的.
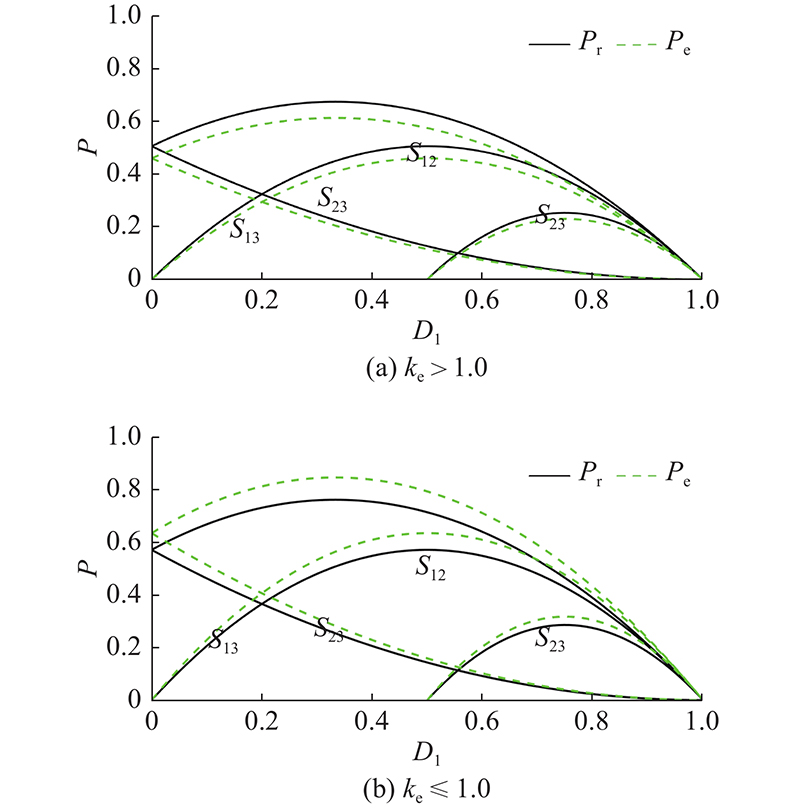
模式1~3在功率传输过程中需要高频变压器的等效漏电感来储存能量,这会造成较大的电流应力,因此将TPC的工作范围限制在模式4~6下. 根据各个模式中D1、D2、D3的取值范围,可以计算出对应各个模式下传输功率标幺值的取值范围,如图7所示. 可以看出,不同模式具有不同的功率传输能力,模式4、5、6的功率传输范围包含了模式1、2、3,因此这3种模式在全功率范围调节过程中可以替代模式1、2、3.
图 7
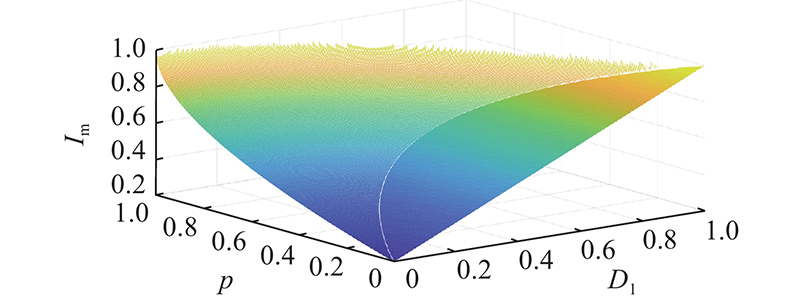
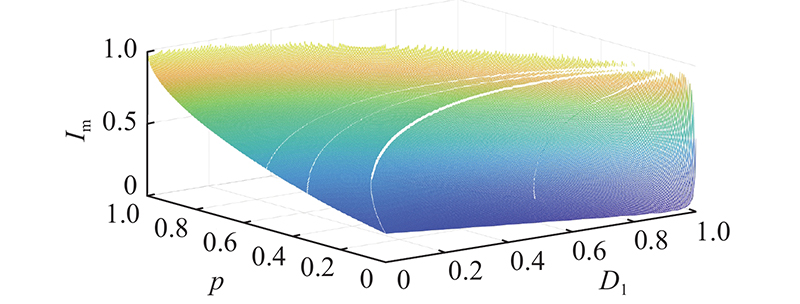
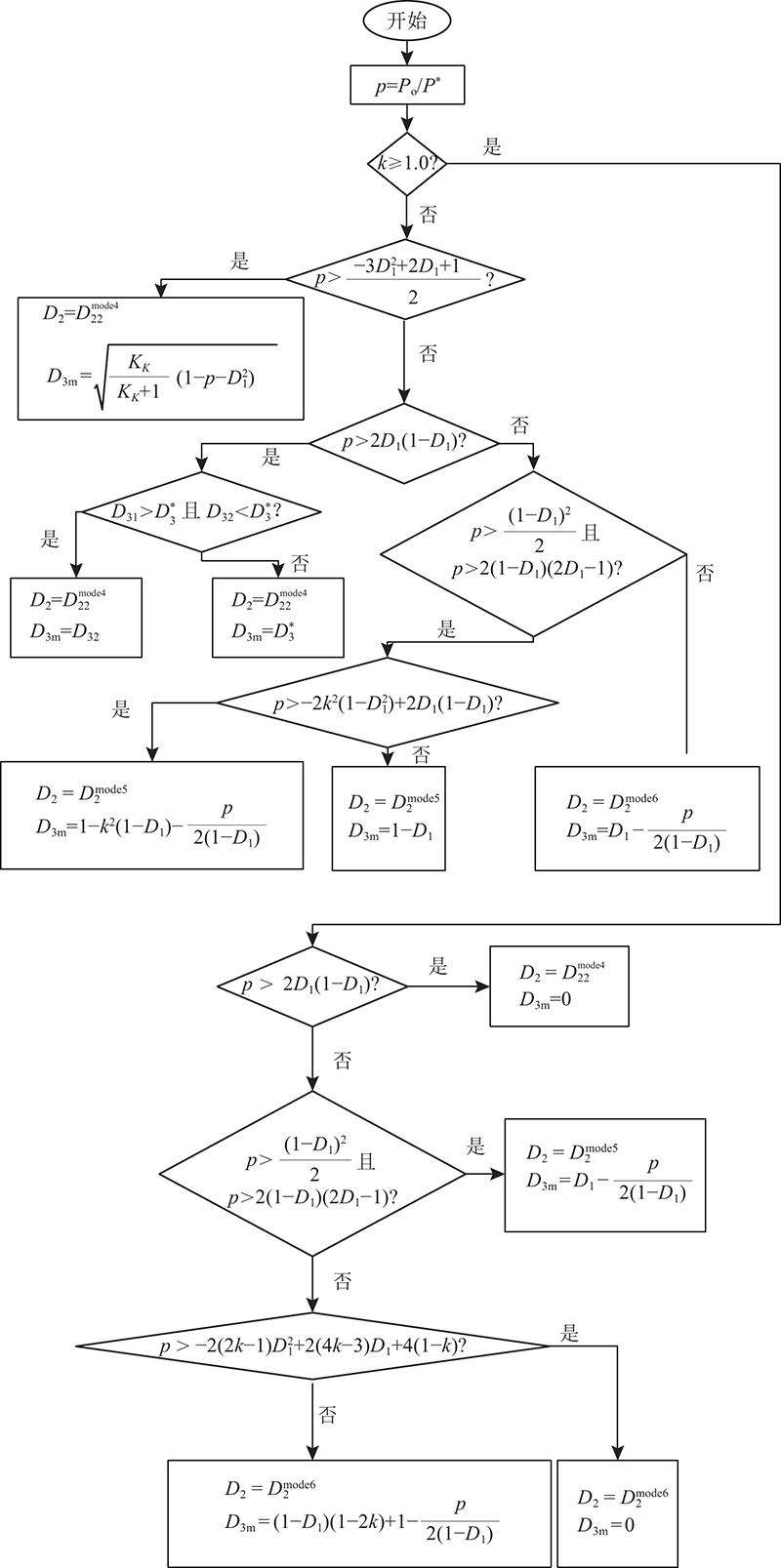
原边占空比d1取决于VDC与Vb,在直流母线稳定运行的情况下,VDC与Vb的波动范围较小,d1在一个开关周期内近似为常量,即D1在一个开关周期内为常量. 引入D3后,在一定的D1下,根据2.2节的功率表达式,可以求解出D2. 求解得到电流应力标幺值Im的表达式. 将电流应力优化问题转化为Im的极值求解问题,优化控制量D3可以根据传输功率p与D1确定. 优化过程中的约束条件为各工作模式的边界条件及令D2有解的条件. 由于k与1.0会对iL达到最大值的时刻造成影响,应分为0 < k < 1.0与 k≥1.0这 2种情况分别进行分析.
3.1.1. 模式4下的电流应力优化数学模型
引入副边内移相占空比D3后,根据模式4的功率表达式,在一定的D1下,原、副边的移相占空比D2存在2个稳定运行点,分别为
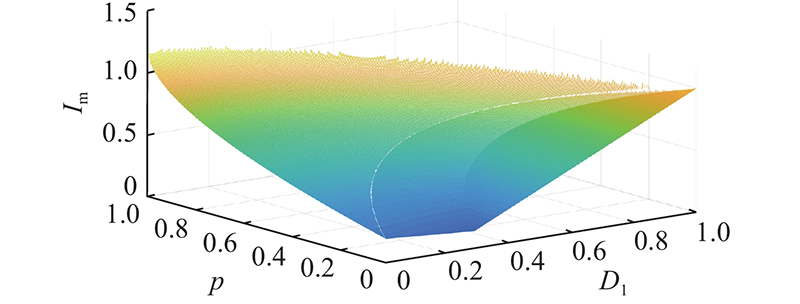
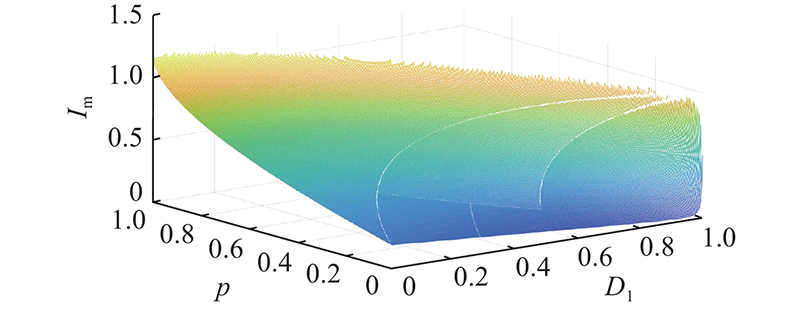
在0 < k < 1.0、 k≥1.0这 2种情况下,电流应力标幺值分别为
根据k与1.0的大小关系,模式4下系统的稳定运行点分为以下4种情况. 1)情况1: 0 < k < 1.0, D2 =
3.1.2. 模式5下的电流应力优化数学模型
在引入副边内移相占空比D3后,根据模式5的功率表达式,在一定的D1下,原、副边的移相占空比D2的稳定运行点为
在0 < k < 1.0、 k ≥ 1.0这 2种情况下,电流应力标幺值分别为
根据k与1.0的大小关系,模式5下系统的稳定运行点分为以下2种情况. 1)情况1:0 < k < 1.0. 2)情况2: k ≥ 1.0. 由模式5的边界条件及式(9)有解的条件,可得优化问题的约束条件为
3.1.3. 模式6下的电流应力优化数学模型
在引入副边内移相占空比D3后,根据模式6的功率表达式可知,在一定的D1下,原、副边的移相占空比D2的稳定运行点为
在0 < k < 1.0、 k ≥ 1.0这 2种情况下,电流应力标幺值分别为
根据模式6的边界条件,可得优化问题的约束条件为
3.2. TPC高频链电流应力优化控制方法
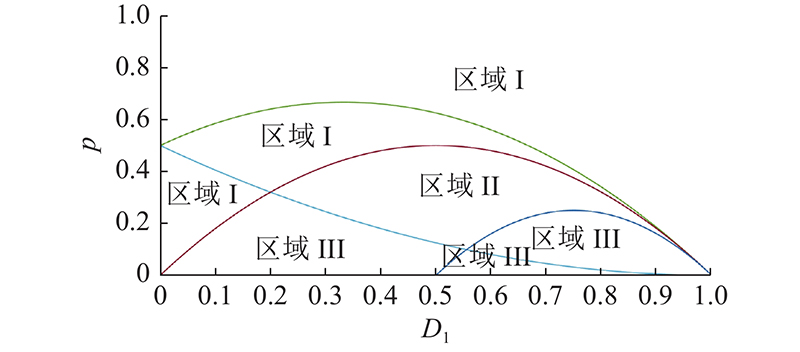
TPC高频链电流应力优化问题转化为约束条件下的最优值求解问题,在求解过程中将传输功率p与D1的运行区域划分为I、II、III 3个区域,如图8所示.
图 8
3.2.1. 运行区域I
在运行区域I内,优化量D3的取值如下.
1)当0 < k < 1.0,
式中:
2)当0 < k < 1.0,
式中:
3)当k ≥ 1.0,p > 2D1(1 − D1)时,
在运行区域I内,引入内移相D3后,优化后的电流应力标幺值为
3.2.2. 运行区域II
在运行区域II内,优化量D3的取值如下.
1)当0 < k < 1.0,
a)若
b)若
2)当k ≥ 1.0,
在运行区域II内,引入内移相D3后,优化后的电流应力标幺值为
3.2.3. 运行区域III
在运行区域III内,优化量D3的取值如下.
1)当0 < k < 1.0,
2)当k ≥ 1.0,
a)若
b)若
在运行区域III内,引入内移相D3后,优化后的电流应力标幺值为
图 9
图 10
图 11
图 12
图 13
图 14
由于高频变压器漏感参数的变化,计算所得的基准值具有一定的误差,令实际基准值为
实际功率标幺值为
计算所得的功率标幺值为
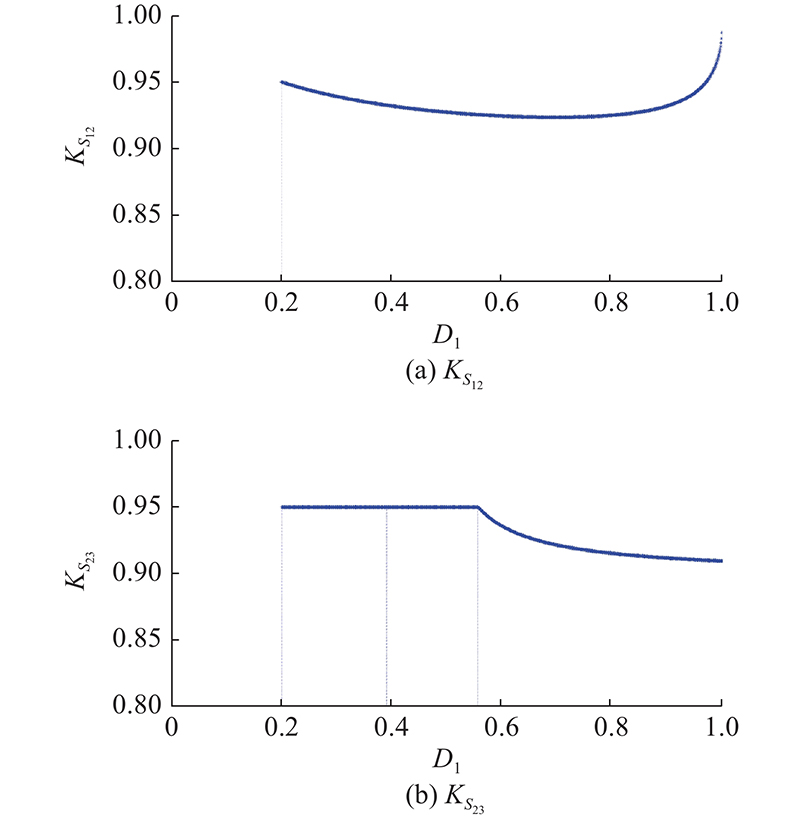
由于计算所得的标幺值与实际标幺值存在误差,会对区域范围的判断产生一定的影响. 当ke > 1.0时, pe < p < pr下的S12、S13、S23为因误差而产生误判的区域,如图15(a)所示,ke≤1.0的情况如图15(b)所示. D3mr为D3m的精准控制值,D3me为误差影响下的D3m计算值. 以k > 1.0, ke > 1.0为例,原本属于区域II的 S12区域被误判为区域I. 从表1、2可知,D3mr = D1 − pr/(2 − 2 D1),D3me= 0,即在S12区域内会失去电流应力优化的作用. 原本属于区域III的S13区域被误判为区域I,D3mr= 0,D3me= 0,即在S13区域内,标幺值误差的存在不会对电流应力优化作用产生影响. 原本属于区域III的S23区域被误判为区域II,当pe<−2(2k−1)×D12 + 2(4k − 3) D1 + 4(1−k)时,D3mr=D1 − pr/(2 − 2 D1)+2(1 − k)(1−D1),D3me=D1−pe/(2−2D1);当pe≥−2(2k − 1) D12 + 2(4k − 3) D1 + 4(1−k)时,D3mr = 0,D3me = D1 − pe/(2 − 2 D1). 定义参数K= Ime/ Imr,以此反映在一定误差下的控制精度. 区域S12、S13、S23的
表 1 电流应力优化前、后的参数对比
Tab.1
| 实验 编号 | k | iS1RMS/A | iS2RMS/A | iS5RMS/A | iLRMS/A | |||||||
| 优化 前 | 优化 后 | 优化 前 | 优化 后 | 优化 前 | 优化 后 | 优化 前 | 优化 后 | |||||
| 1 | 0.6 | 12.4 | 12.0 | 12.4 | 12.0 | 4.2 | 4.0 | 17.6 | 17.2 | |||
| 2 | 0.6 | 12.2 | 10.9 | 8.7 | 8.3 | 3.6 | 3.2 | 15.1 | 13.5 | |||
| 3 | 0.6 | 11.7 | 8.8 | 5.4 | 5.1 | 3.1 | 2.4 | 13.0 | 10.5 | |||
| 4 | 1.1 | 6.5 | 5.5 | 4.5 | 4.4 | 1.9 | 1.2 | 7.9 | 7.0 | |||
| 5 | 1.1 | 5.2 | 3.9 | 3.1 | 2.9 | 1.5 | 1.1 | 6.0 | 4.7 | |||
表 2 电流应力优化前、后S1-S8开关管损耗的对比
Tab.2
| 实验编号 | k | Pon/W | Pswitch/W | Ploss/W | |||||
| 优化前 | 优化后 | 优化前 | 优化后 | 优化前 | 优化后 | ||||
| 1 | 0.6 | 28.2 | 27.2 | 4.5 | 2.5 | 32.7 | 29.7 | ||
| 2 | 0.6 | 20.5 | 17.5 | 4.4 | 3.0 | 24.9 | 20.5 | ||
| 3 | 0.6 | 15.3 | 9.9 | 4.1 | 2.5 | 19.4 | 12.4 | ||
| 4 | 1.1 | 5.6 | 4.5 | 2.8 | 2.4 | 8.4 | 6.9 | ||
| 5 | 1.1 | 3.3 | 2.1 | 2.4 | 1.7 | 5.7 | 3.8 | ||
图 15
图 16
4. 实验验证
为了验证所提的电流应力优化的实际效果与可行性,搭建如图17所示的TPC实验平台.以TI公司的TMS320F28377SPTPT为控制器,开关频率fs为50 kHz,蓄电池端滤波电感L1、L2为230 μH,高频变压器漏感L为6 μH,高频变压器变比n为1∶3,滤波电容CDC、Cb、Co为1000 μF. 考虑高频变压器原、副边之间的传输效率问题,实验过程中的原边两端口之间无功率传输.
图 17
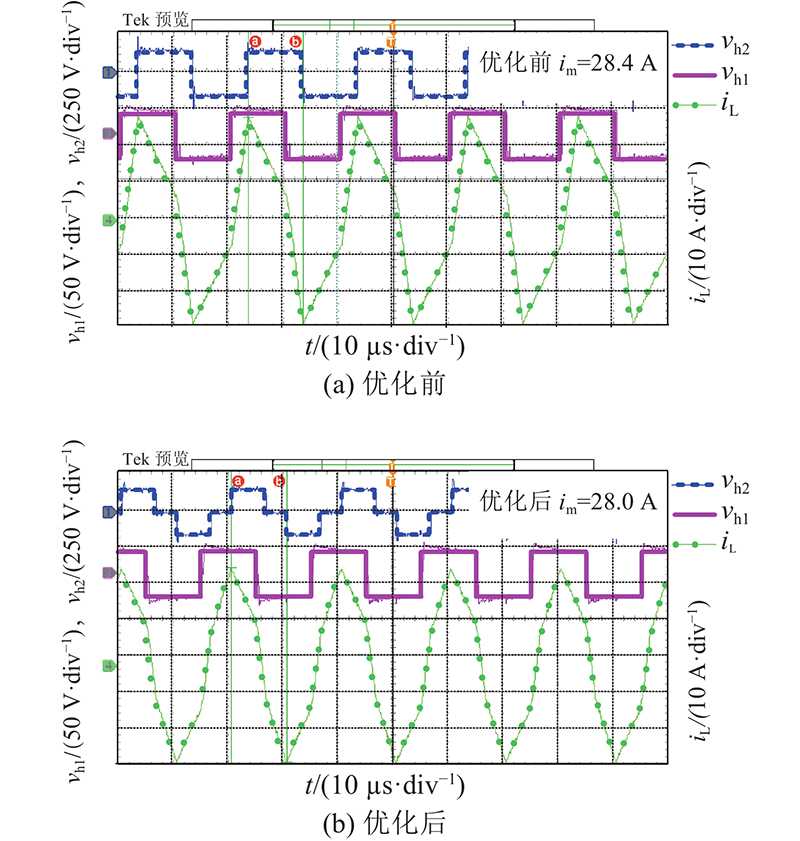
实验1的运行区域I内k = 0.6时优化前、后的变压器原边电压vh1、副边电压vh2与漏感电流iL波形如图18所示. 原边侧高压端口VDC与低压端口电压Vb分别为30、15 V,副边侧端口电压Vo与负载分别为150 V、50 Ω,优化前与优化后的电流应力分别为28.4与26.6 A,漏感电流应力的减小量ΔiL=1.8 A.
图 18
图 18 k = 0.6下优化前、后的对比波形(运行区域I)
Fig.18 Comparison waveforms before and after optimization in first operating area when k = 0.6
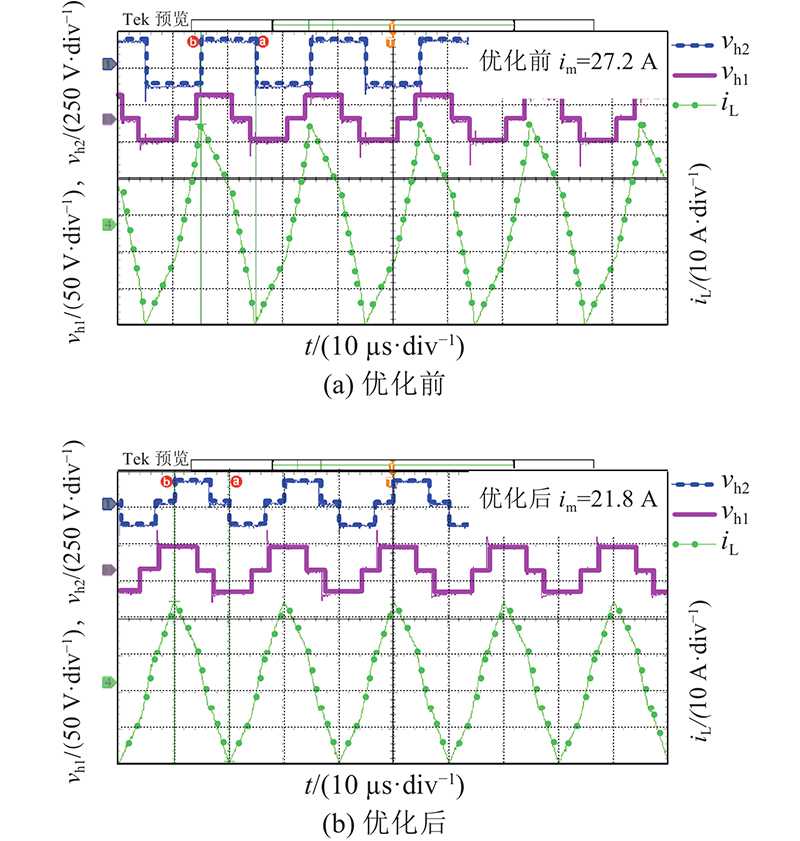
实验2的运行区域II内k = 0.6时优化前、后的变压器vh1、vh2与iL波形如图19所示. VDC与Vb分别为30、20 V,Vo与负载分别为150 V、85 Ω,优化前与优化后的电流应力分别为27.2与21.8 A,ΔiL= 5.4 A.
图 19
图 19 k = 0.6下优化前、后的对比波形(运行区域II)
Fig.19 Comparison waveforms before and after optimization in second operating area when k = 0.6
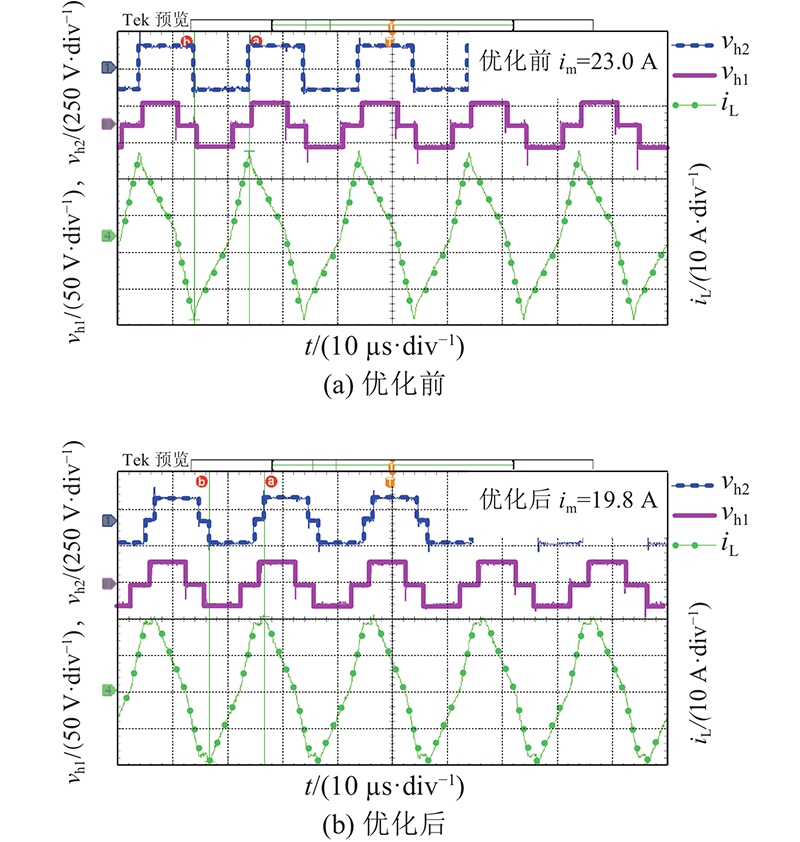
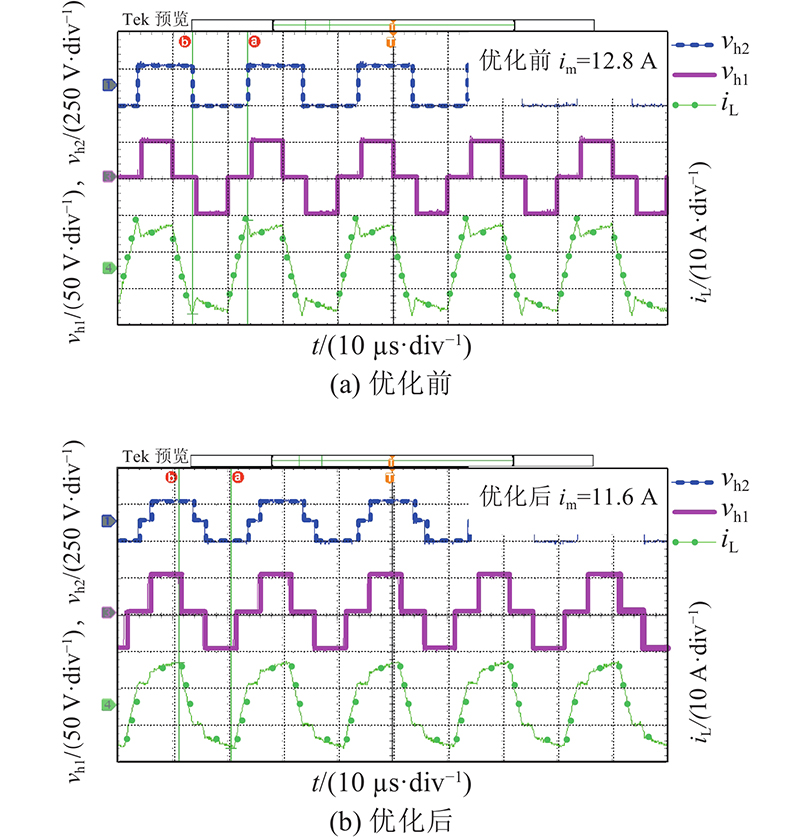
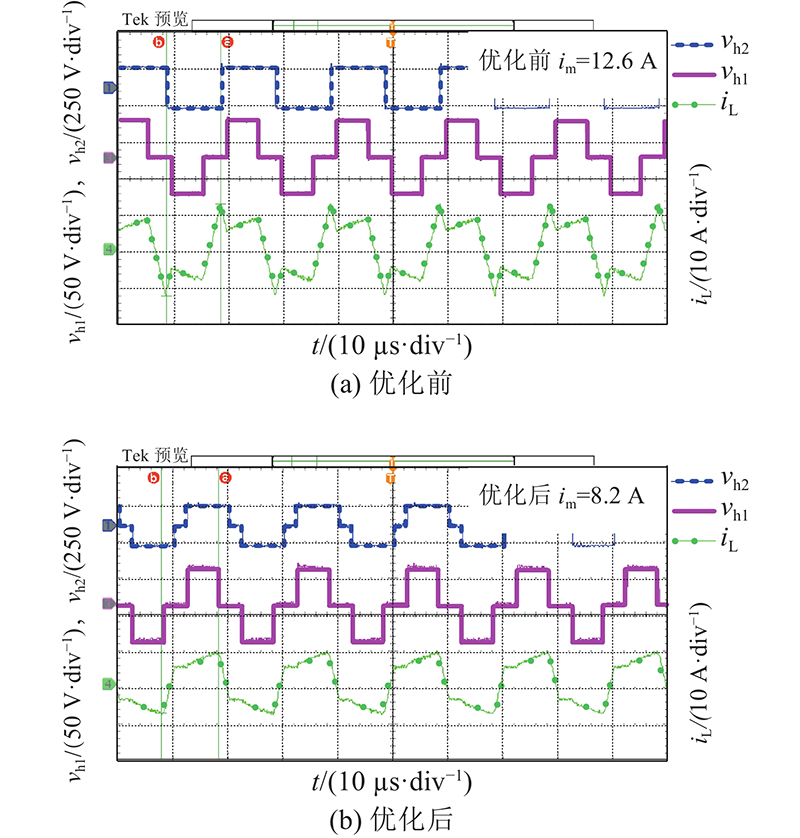
实验3的运行区域III内k = 0.6优化时前、后的变压器vh1、vh2与iL波形如图20所示. VDC与Vb分别为30、20 V,Vo与负载分别为150 V、170 Ω,优化前、后的电流应力分别为23.0、19.8 A,ΔiL=3.2 A. 实验4的运行区域II内k=1.1时优化前、后的变压器vh1、vh2与iL波形如图21所示. VDC与Vb分别为50、35 V,Vo与负载分别为130 V、70 Ω,优化前、后的电流应力分别为12.8、11.6 A,ΔiL=1.2 A. 实验5的运行区域III内k = 1.1时优化前、后的变压器vh1、vh2与iL波形如图22所示. VDC与Vb分别为50、35 V,Vo与负载分别为130 V、105 Ω,优化前、后的电流应力分别为12.6、8.2 A,ΔiL = 4.4 A.
图 20
图 20 k= 0.6下优化前、后的对比波形(运行区域III)
Fig.20 Comparison waveforms before and after optimization in third operating area when k= 0.6
图 21
图 21 运行区域II,k= 1.1下优化前、后的对比波形
Fig.21 Comparison waveforms before and after optimization in second operating area when k= 1.1
图 22
图 22 运行区域III,k = 1.1下优化前、后的对比波形
Fig.22 Comparison waveform before and after optimization in third operating area when k = 1.1
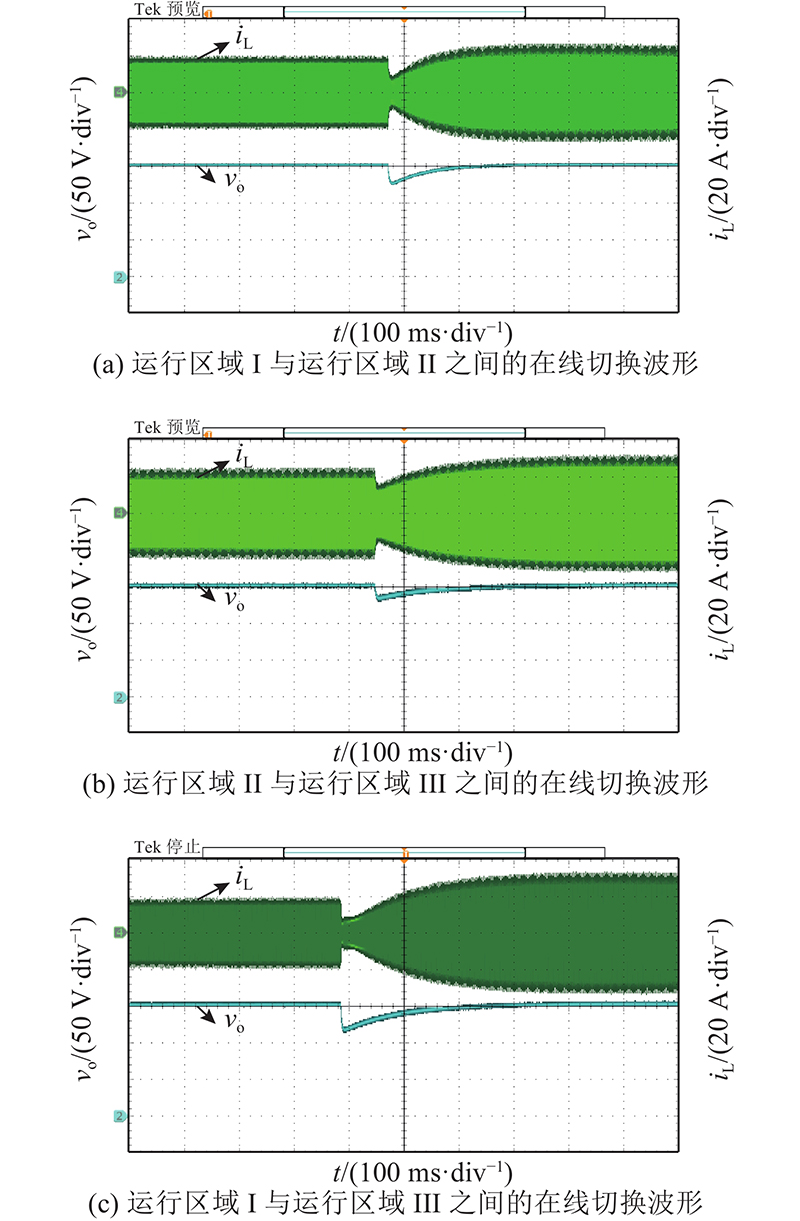
图 23
图 23 k = 0.6下不同运行区域的在线切换实验波形
Fig.23 Experimental waveforms of online switching between different working areas under k = 0.6
从图18~22可以看出,当k < 1.0时,即使在轻载的情况下,高频链电流具有较大的峰-峰值,使得流经原、副边开关管的电流及高频变压器线圈的电流具有较大的有效值,原、副边之间的传输效率较低. 引入电流应力优化控制,减小了高频链电流的峰-峰值,减小了流经原、副边开关管的电流及高频变压器线圈的电流有效值,提升了系统的传输效率. 当 k > 1.0时,电流应力优化控制在轻载情况下,具有更明显的效果. 在优化前、后,流经原、副边开关管的有效值及高频链电流有效值如 表1所示. 开关管损耗Ploss包括开关损耗Pswitch与通态损耗Pon,优化前、后的开关管损耗对比如表2所示. 高频变压器原边2个桥臂相同位置的电流有效值相同,副边4个开关管的电流有效值相同,给出如图1所示开关管1、2、5这3个开关管的电流有效值iS1RMS、iS2RMS、iS5RMS以及高频链iL的有效值iLRMS.
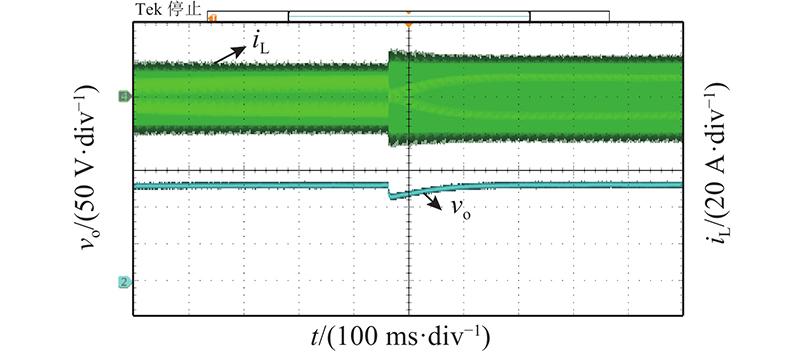
如图24所示为当k = 1.1时不同运行区域切换的vo与iL波形,VDC、Vb分别为50、35 V,切换前、后的负载分别为105、70 Ω,切换前、后的运行区域分别为区域III与区域II. 实验结果表明,不同运行区间在线切换过程中未出现电压、电流尖峰或畸变等问题.
图 24
图 24 k = 1.1下不同运行区域的在线切换实验波形
Fig.24 Experimental waveforms of online switching between different working areas under k = 1.1
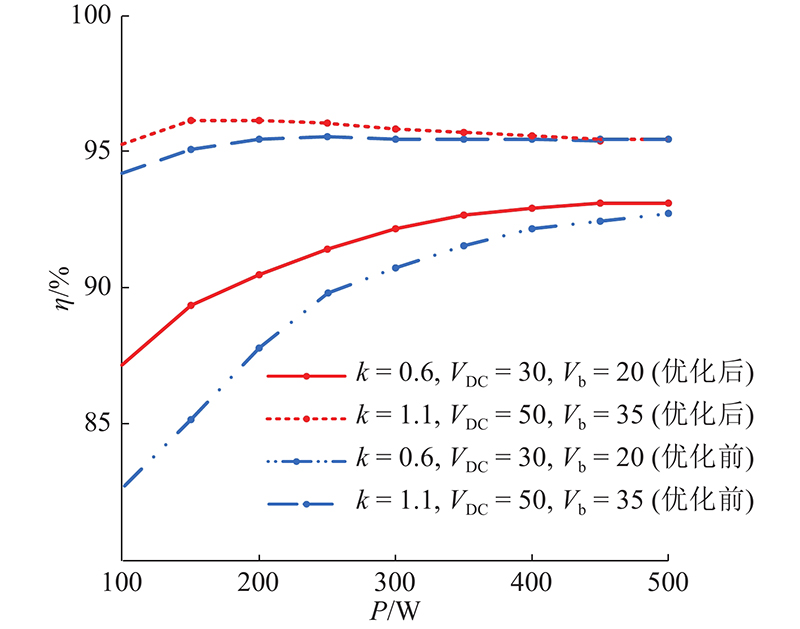
如图25所示为在电流应力优化前、后,系统的效率曲线随负载的变化图. 可以看出,在轻载的情况下,尤其是当k < 1.0时,系统效率的提升较明显.
图 25
5. 结 论
(1)本文以传统的双Buck-Boost集成DAB型TPC为研究对象,将副边桥臂间的内移相角作为第3个控制量,以实现高频链电流应力优化的控制目标.
(2)利用本文的电流应力优化控制方法可以有效降低高频链的电流应力,减小原、副边开关管与磁性元件的损耗,提升系统的效率.
(3)在负载端口轻载的情况下,电流应力优化控制方法具有更加明显的效果.
参考文献
An integrated three-port bidirectional DC-DC converter for PV application on a DC distribution system
[J].DOI:10.1109/TPEL.2012.2236580 [本文引用: 1]
Multiport converters based on integration of full-bridge and bidirectional DC-DC topologies for renewable generation systems
[J].
双Buck/Boost 集成双有源桥三端口DC-DC变换器
[J].DOI:10.3969/j.issn.1000-6753.2016.22.010
Double Buck/Boost integrated dual active bridge three-port DC-DC converter
[J].DOI:10.3969/j.issn.1000-6753.2016.22.010
交错并联双向Buck/ Boost集成LLC谐振型三端口直流变换器
[J].DOI:10.3969/j.issn.1000-6753.2016.14.019
Interleaved bidirectional Buck/Boost integrated LLC resonant three port DC/DC converter
[J].DOI:10.3969/j.issn.1000-6753.2016.14.019
一种基于三端口变换器的航天器分布式供电系统
[J].
A distributed power system with modular three-port converters for spacecraft
[J].
副边调整式三端口半桥 DC-DC变换器
[J].
Three-port half-bridge DC-DC converters with post regulation scheme
[J].
半桥式三端口变换器建模与解耦控制
[J].
Modeling and decoupling control of three-port half-bridge converters
[J].
基于LCL谐振型双有源桥的三端口DC-DC变换器及其解耦控制
[J].
Three-port DC-DC converter based on LCL resonant dual active bridge and its decoupling control
[J].
A distributed state-of-charge balancing control scheme for three-port output-series converters in DC hybrid energy storage systems
[J].
A three-port converter based distributed DC grid connected PV system with autonomous output voltage sharing control
[J].DOI:10.1109/TPEL.2018.2822726 [本文引用: 1]
Current stress optimized switching strategy of isolated bidirectional DC-DC converter with dual-phase-shift control
[J].DOI:10.1109/TIE.2012.2210374 [本文引用: 1]
双重移相控制的双主动全桥变换器全局电流应力分析及优化控制策略
[J].
Global current stress analysis and optimal control strategy of DAB converter based on dual-phase-shift control
[J].
基于扩展相移的双有源全桥DC-DC变换器多目标优化控制方法
[J].
Multi-objective optimization control scheme based on extended phase-shift of dual-active-bridge DC-DC converters
[J].
Unified triple-phase-shift control to minimize current stress and achieve full soft-switching of isolated bidirectional DC-DC converter
[J].DOI:10.1109/TIE.2016.2543182 [本文引用: 1]
基于模型前馈的双有源全桥DC-DC变换器电流应力优化方法
[J].
Current stress optimized scheme with model-based feedforward for dual-active-bridge DC-DC converters
[J].
考虑不同软开关模式的双有源桥变换器电流应力优化方法
[J].DOI:10.7500/AEPS20190429004 [本文引用: 1]
Optimization method of current stress for dual active bridge converter considering different soft switching modes
[J].DOI:10.7500/AEPS20190429004 [本文引用: 1]