基于次加载面摩擦模型的接触面剪切特性研究

doi:10.3785/j.issn.1008-973X.2022.07.008

基于次加载面摩擦模型的接触面剪切特性研究

龚涛^,, 刘开富, 谢新宇^,, 许纯泰, 娄扬, 郑凌逶

1. 浙江大学滨海和城市岩土工程研究中心，浙江杭州 310058

2. 浙江理工大学建筑工程学院，浙江杭州 310018

3. 浙江大学温州研究院，浙江温州 325035

4. 浙大宁波理工学院土木建筑工程学院，浙江宁波 315100

Shear characteristics of interface based on subloading-friction model

GONG Tao^,, LIU Kai-fu, XIE Xin-yu^,, XU Chun-tai, LOU Yang, ZHENG Ling-wei

1. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China

2. School of Civil Engineering and Architecture, Zhejiang Sci-Tech University, Hangzhou 310018, China

3. Institute of Wenzhou, Zhejiang University, Wenzhou 325035, China

4. School of Civil Engineering and Architecture, Ningbo Tech University, Ningbo 315100, China

通讯作者: 谢新宇，男，教授，博导. orcid.org/0000-0001-8582-0857. E-mail： xiexinyu@zju.edu.cn

收稿日期: 2021-07-7

基金资助:

国家自然科学基金资助项目（51878619, 52078465）

Received: 2021-07-7

Fund supported:

国家自然科学基金资助项目（51878619,52078465）

作者简介 About authors

龚涛（1996—），男，博士生，从事桩土相互作用的研究.orcid.org/0000-0002-7461-7471.E-mail：11812029@zju.edu.cn , E-mail：11812029@zju.edu.cn

摘要

为了反映土与结构接触面的应变软化特性以及剪切速率对土与结构接触面力学特性的影响，基于ABAQUS软件提供的FRIC子程序，采用显式积分算法，对能够表现接触面上应变软化的次加载面摩擦模型进行二次开发. 利用该模型模拟土与结构接触面的直剪试验，研究直剪试验过程中次加载面摩擦模型接触面上的应力演变过程. 研究结果表明，利用次加载面摩擦本构模型，能够较好地模拟土-结构接触面直剪试验中的应变软化和密实状态的类砂土残余切应力随剪切速率的增大而下降的现象. 在剪切位移的发展过程中，次加载面摩擦模型接触面上的切应力先增加后减小，接触面远离加载端一侧到另一侧的应力发挥水平先后达到最大值. 该研究表明，次加载面摩擦模型可以用于土与结构接触面的应变软化特性和速率相关性的模拟.

关键词： 土-结构接触面 ; 直剪试验 ; 应变软化 ; 次加载面摩擦模型

Abstract

A secondary development of the subloading-friction model that can describe the strain softening phenomenon of contact surface was realized based on subroutine FRIC provided by ABAQUS by using explicit integration algorithm in order to reflect the strain softening characteristics of soil-structure surface and the effect of shear rate on the mechanical properties of soil-structure interface. The developed model was used to simulate the direct shear tests of soil-structure interface, and the evolution process of the stress on the contact surface during direct shear test was analyzed. The numerical calculation results indicate that the subloading-friction model can simulate the strain softening phenomenon of soil-structure interface well, and simulate the decrease of residual shear stress of dense quasi-sands with the increase of shear rate in the direct shear test. The shear stress on the contact surface of subloading-friction model increases at first and then decreases with the development of shear displacement, and the stress exertion level of the contact surface reaches the maximum successively from one side away from the loaded end to the other side. Results show that the subloading-friction model can be used to simulate the strain softening characteristics and rate dependence of the mechanical properties of soil-structure interface.

Keywords： soil-structure interface ; direct shear test ; strain softening ; subloading-friction model

PDF (1547KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

龚涛, 刘开富, 谢新宇, 许纯泰, 娄扬, 郑凌逶. 基于次加载面摩擦模型的接触面剪切特性研究. 浙江大学学报(工学版)[J], 2022, 56(7): 1328-1335, 1352 doi:10.3785/j.issn.1008-973X.2022.07.008

GONG Tao, LIU Kai-fu, XIE Xin-yu, XU Chun-tai, LOU Yang, ZHENG Ling-wei. Shear characteristics of interface based on subloading-friction model. Journal of Zhejiang University(Engineering Science)[J], 2022, 56(7): 1328-1335, 1352 doi:10.3785/j.issn.1008-973X.2022.07.008

岩土工程领域中广泛存在着土与结构间的相互作用问题，通过合理的接触面本构模型模拟土与结构之间的接触，对岩土工程中的土与结构相互作用问题进行数值模拟分析，成为主要的技术手段^[1-3].

对于土与结构间的接触力学特性，学者们进行了大量的试验研究. Yoshimi等^[4]通过砂与钢之间的环剪试验发现，钢与砂摩擦之间的峰值摩擦系数与残余摩擦系数主要由钢表面的粗糙度决定. Yin等^[5]通过土与混凝土大尺寸接触面的直剪试验发现，直剪试验中接触面的破坏是由边缘向内部逐步发展的过程. 胡黎明等^[6-7]通过土与结构接触面的直剪试验，研究剪切过程中的应变软化现象. 钟世英^[8]开展模拟月壤与足垫材料之间的直剪试验，试验结果表明，密实状态下模拟月壤的残余强度随着剪切速率的增大而降低. 夏红春等^[9]开展的高应力条件下砂-结构接触面直剪试验结果表明，一定范围内的剪切速率（0.02~1.25 mm/min）对接触本构关系基本无影响. 刘希亮等^[10]开展的高应力下土与结构界面的直剪试验结果表明，剪切速率对土与结构切应力-剪切位移曲线的残余强度和初始切线斜率的影响与法向应力、土体性质、界面基底性质等因素相比较小.

基于土与结构间的接触面剪切试验，国内外学者提出多种土-结构接触面本构模型，如Yin等^[5]提出的接触面刚塑性本构模型、张冬霁等^[11]提出的“剪切错动带”双曲线关系模型、Clough等^[12]提出的双曲线接触本构模型. 对于土与结构接触剪切中表现出的应变软化特性，Boulon等^[13]建立可以描述接触面硬化与软化特性的双塑性势面模型. Hu等^[14]提出能够描述接触面应变软化的10参数损伤模型. 张嘎等^[15]建立能够统一描述应变软化、剪胀与剪缩规律、接触面异向性的17参数损伤模型. 凌道盛等^[16]基于黏聚区域模型，提出接触面多折线黏聚区域模型. 路德春等^[17]基于超固结土的β模型，建立能够统一描述硬化和软化特性的接触面本构模型. 考虑剪切速率对土与结构接触面力学特性影响的接触面本构模型较少.

在土与结构接触面剪切的数值研究方面，学者们研究数值实现不同接触面本构模型及使用不同接触面本构模型模拟土与结构间的接触力学特性^[5,11,15-17]，也有不同的学者采用数值模拟的手段，研究剪切作用下土与结构接触面的变形发展特性，如胡黎明等^[18]对粗粒土与结构接触面直剪试验进行数值模拟，研究和探讨接触面的剪切渐进破坏过程. 夏红春等^[19]用颗粒流软件PFC研究砂与结构接触面力学接触特性的内在机理，研究表明，在一定的法向应力条件下，不考虑颗粒破碎时，颗粒的“剪胀”是引起接触面剪切强度变化的主要原因之一. 殷殷等^[20]开展直剪试验数值分析，得到接触面变形中的相对位移和土体变形在有限元计算中可以分别用刚塑性接触模型和土体本构模型来模拟和分析的结论. 郑立宁等^[21]用FLAC研究含应变软化接触单元的数值直剪试验的渐进性破坏特征. 相关的数值研究深化了对土与结构接触剪切过程中接触面破坏发展的认识，但基于能考虑接触面应变软化的接触本构模型和能考虑接触面切应力速率相关的接触本构模型对土与结构间的接触力学特性和接触面变形发展特性进行的数值研究较少.

综上所述，对土与结构接触剪切中存在的应变软化特性，进行了一定的探索与研究，但部分能够考虑软化特性的接触模型参数多，计算难度大，同时考虑应变软化的接触面本构模型的数值应用较少，与速率相关的接触面本构模型数值实现的研究较少. 本文在ABAQUS中实现了接触面切应力速率相关的次加载面摩擦模型，建立土-结构接触面直剪试验三维数值模型，在土-结构接触面剪切模拟中采用次加载面摩擦模型，模拟土-结构剪切过程中的应变软化特性. 为了验证接触面本构模型的有效性与合理性，拟合试验数据，得到适用于土-结构物接触面的模型参数. 利用数值直剪试验，研究直剪试验过程中土与结构接触面上的应力变化特性.

1. 次加载面摩擦模型

次加载面摩擦模型（subloading-friction model）是由Hashiguchi等^[22-23]考虑变化的界面摩擦系数，提出的用来描述界面摩擦力学行为的与速率相关的摩擦模型. 次加载面摩擦模型主要包括正常滑动屈服面与滑动次加载面、正常滑动屈服比演化、滑动硬化函数演化、接触应力变化速率-滑动速度关系4个部分.

1.1. 滑动屈服面与滑动次加载面

次加载面摩擦模型在摩擦接触中引入弹塑性滑动的概念. 对于接触面上的应力向量 $ {\boldsymbol{f}} $，假定用于描述滑动屈服条件的各向同性硬化/软化的正常滑动屈服面为

$ f\left( {\boldsymbol{f}} \right) = \mu . $

(1)

当物体接触面之间发生摩擦滑动时，引入通过接触面当前接触应力状态的滑动次加载面，假定滑动次加载面与正常滑动屈服面形状相似，表达式为

$ f\left({\boldsymbol{f}}\right)=r\mu . $

(2)

式中： $f\left( {\boldsymbol{f}} \right)$为关于 ${\boldsymbol{f}}$的函数，在库仑摩擦条件下， $f\left( {\boldsymbol{f}} \right){{ = {f_{\text{t}}}} \mathord{\left/ {\vphantom {{ = {f_{\text{t}}}} {{f_{\text{n}}}}}} \right. } {{f_{\text{n}}}}}$，其中 ${f_{\text{t}}}$为接触面的切应力， ${f_{\text{n}}}$为接触面法向应力； $\;\mu $为滑动硬化函数，在库仑摩擦条件下， $\;\mu $为接触面摩擦系数； $r$为正常滑动屈服比， $0 \leqslant r \leqslant 1$.0，为滑动次加载面与正常滑动屈服面大小的比值，表征了滑动次加载面与正常滑动屈服面之间的接近程度. 当滑动次加载面靠近正常滑动屈服面时，产生塑性滑动速度；当滑动次加载面远离正常滑动屈服面时，只产生弹性滑动速度.

1.2. 正常滑动屈服比演化法则

次加载面摩擦模型假定正常滑动屈服比 $r$的变化速率 $\dot r$随着接触面的塑性滑动速度而变化，正常滑动屈服比 $r$的演化法则如下：

$ \dot r = \bar U\left( r \right)\left\| {{{\bar {\boldsymbol{v}}}^{\text{p}}}} \right\|,\;{\bar {\boldsymbol{v}}^{\text{p}}} \ne {\boldsymbol{0}} ; $

(3)

$ r = {{f\left( {\boldsymbol{f}} \right)}}/{\mu },\;{\bar {\boldsymbol{v}}^{\text{p}}} = {\boldsymbol{0}} . $

(4)

式中： $\bar U\left( r \right)$为 $r$的单调递减函数，当 $r = 0$ 时， $\bar U\left( r \right) \to + \infty$；当 $r = 1$时， $\bar U\left( r \right) = 0$，常取的函数有 $\bar U\left( r \right) = - \tilde u\ln \; r$（其中 $\tilde u$为常数）； $ {\bar {\boldsymbol{v}}^{\text{p}}} $为接触面塑性滑动速度.

1.3. 滑动硬化函数演化法则

物体接触之间的摩擦系数不是常数，在摩擦滑动过程中，摩擦系数先达到最大静摩擦系数，然后减小到动摩擦系数. 次加载面摩擦模型假定界面之间的摩擦系数由衰减和恢复2种竞争机制影响，随着接触面间的塑性滑动速度变化. 假定接触面摩擦系数的演化速率 $\;\dot \mu $为

$ \dot \mu = - \kappa \left( {\frac{\mu }{{{\mu _{\text{k}}}}} - 1} \right)\left\| {{{\bar {\boldsymbol{v}}}^{\text{p}}}} \right\| + \xi \left( {1 - \frac{\mu }{{{\mu _{\text{s}}}}}} \right). $

(5)

式中： $\kappa $为影响摩擦系数衰减速率的材料参数， $\xi $为影响摩擦系数恢复速率的材料参数， ${\mu _{\text{s}}}$为接触面峰值摩擦系数——静摩擦系数， ${\mu _{\text{k}}}$为接触面最小摩擦系数——动摩擦系数，上标“^·”表示摩擦系数的时间导数.

1.4. 切向接触牵引力与滑动速度之间的关系

次加载面摩擦模型假定接触面应力与弹性滑动速度之间满足超弹性本构关系：

$ \left. {\begin{array}{*{20}{c}} {{{\bar {\boldsymbol{v}}}^{\text{e}}} = \dfrac{1}{{{\alpha _{\text{n}}}}}{{\dot {\boldsymbol{f}}}_{\text{n}}} + \dfrac{1}{{{\alpha _{\text{t}}}}}{{\dot {\boldsymbol{f}}}_{\text{t}}}}, \\ {\dot {\boldsymbol{f}} = {\alpha _{\text{n}}}{{\bar {\boldsymbol{v}}}^{\text{e}}}_{\text{n}} + {\alpha _{\rm{t}}}{{\bar {\boldsymbol{v}}}^{\text{e}}}_{\text{t}}} . \end{array}} \right\} $

(6)

式中： ${\bar {\boldsymbol{v}}^{\text{e}}}$为接触面弹性相对速度向量， ${\bar {\boldsymbol{v}}^{\text{e}}}_{\text{n}}$和 ${\bar {\boldsymbol{v}}^{\text{e}}}_{\text{t}}$分别为接触面法向弹性相对速度向量和切向弹性相对速度向量， $\dot {\boldsymbol{f}}$为接触面应力向量变化速率， ${\dot {\boldsymbol{f}}_{\text{n}}}$和 ${\dot {\boldsymbol{f}}_{\text{t}}}$分别为接触面法向应力向量的变化速率和切应力向量的变化速率， ${\alpha _{\text{t}}}$和 ${\alpha _{\text{n}}}$分别为接触面切向刚度和法向刚度.

次加载面摩擦模型假定接触面塑性滑动速度满足切向相关联流动法则，即假定法向塑性滑动速度为零，接触面塑性滑动速度与切向塑性滑动速度同向，

$ {\bar {\boldsymbol{v}}^{\text{p}}} = \dot {\bar \lambda} {\boldsymbol{t}}_{\rm{t}}^{\text{p}} . $

(7)

式中： $ \dot {\bar \lambda} $为表征塑性滑动速度大小的塑性乘子； ${\boldsymbol{t}}_{\text{t}}^{\text{p}}$为切向塑性滑动速度的单位方向向量，在各向同性的滑动屈服面条件下，切向塑性滑动速度与接触面切应力的方向相同， ${\boldsymbol{t}}_{\text{t}}^{\text{p}} = {{\boldsymbol{t}}_{\text{f}}}$，其中 ${{\boldsymbol{t}}_{\text{f}}}$为接触面切应力的单位方向向量.

在各向同性库仑摩擦条件下，结合上述各假设，得到加/卸载判断准则以及弹塑性滑动状态下接触面切应力变化速率 ${\dot {\boldsymbol{f}}_{\text{t}}}$的表达式：

$ \dot{\overline{\varLambda }} = \dfrac{\dfrac{1}{{f}_{\text{n}}}\left({\alpha }_{\text{t}}{{\boldsymbol{t}}}_{\text{f}}+{\alpha }_{\text{n}}\dfrac{{f}_{\text{t}}}{{f}_{\text{n}}}{\boldsymbol{n}}\right)\overline{{\boldsymbol{v}}}-{m}^{{\rm{c}}}}{{m}^{{\rm{p}}}+\dfrac{{\alpha }_{\text{t}}}{{f}_{\text{n}}}} \left\{ {\begin{array}{l}\leqslant \text{0}\text{，}卸载\text{，}{\overline{{\boldsymbol{v}}}}^{\text{p}}=\boldsymbol{0};\\ > 0\text{，}加载\text{，}{\overline{{\boldsymbol{v}}}}^{\text{p}}=\dot{\overline{\varLambda }}{{\boldsymbol{t}}}_{\text{f}}.\end{array}} \right. $

(8)

$ {\dot {\boldsymbol{f}}_{\text{t}}} = {\alpha _{\text{t}}}{\bar {\boldsymbol{v}}_{\text{t}}} - {\alpha _{\text{t}}}{{\boldsymbol{t}}_{\text{f}}}\dfrac{{\dfrac{1}{{{f_{\text{n}}}}}\left( {{\alpha _{\text{t}}}{{\boldsymbol{t}}_{\text{f}}} + {\alpha _{\text{n}}}\dfrac{{{f_{\text{t}}}}}{{{f_{\text{n}}}}}{\boldsymbol{n}}} \right){\bar {\boldsymbol{v}}} - {m^{\rm{c}}}}}{{{m^{\rm{p}}} + \dfrac{{{\alpha _{\text{t}}}}}{{{f_{\text{n}}}}}}} . $

(9)

式中： ${\bar {\boldsymbol{v}}_{\text{t}}}$为接触面切向相对速度向量； $\bar{\boldsymbol{ v}}$为接触面相对速度向量； ${{\boldsymbol{t}}_{\text{f}}}$为接触面切应力的单位方向向量； ${\boldsymbol{n}}$为接触面单位外法向量； ${m^{\rm{c}}}$和 ${m^{\rm{p}}}$为中间参数，

$ {m^{\rm{c}}} = \xi \left( {1 - \frac{\mu }{{{\mu _{\text{s}}}}}} \right)r, $

(10)

$ {m^{\rm{p}}} = - \kappa \left( {\frac{\mu }{{{\mu _{\text{k}}}}} - 1} \right)r + \bar U\left( r \right)\mu . $

(11)

2. 次加载面摩擦模型在ABAQUS中的实现

ABAQUS中使用动力隐式分析步或动力显示分析步，开展与速率相关的接触相互作用问题的计算. 本文利用ABAQUS提供的适用于动力隐式分析步的FRIC相互作用子程序接口，使用Fortran语言开发了次加载面摩擦FRIC子程序. 使用动力隐式分析步和开发的FRIC子程序，对受剪切速率影响的接触问题进行联合分析.

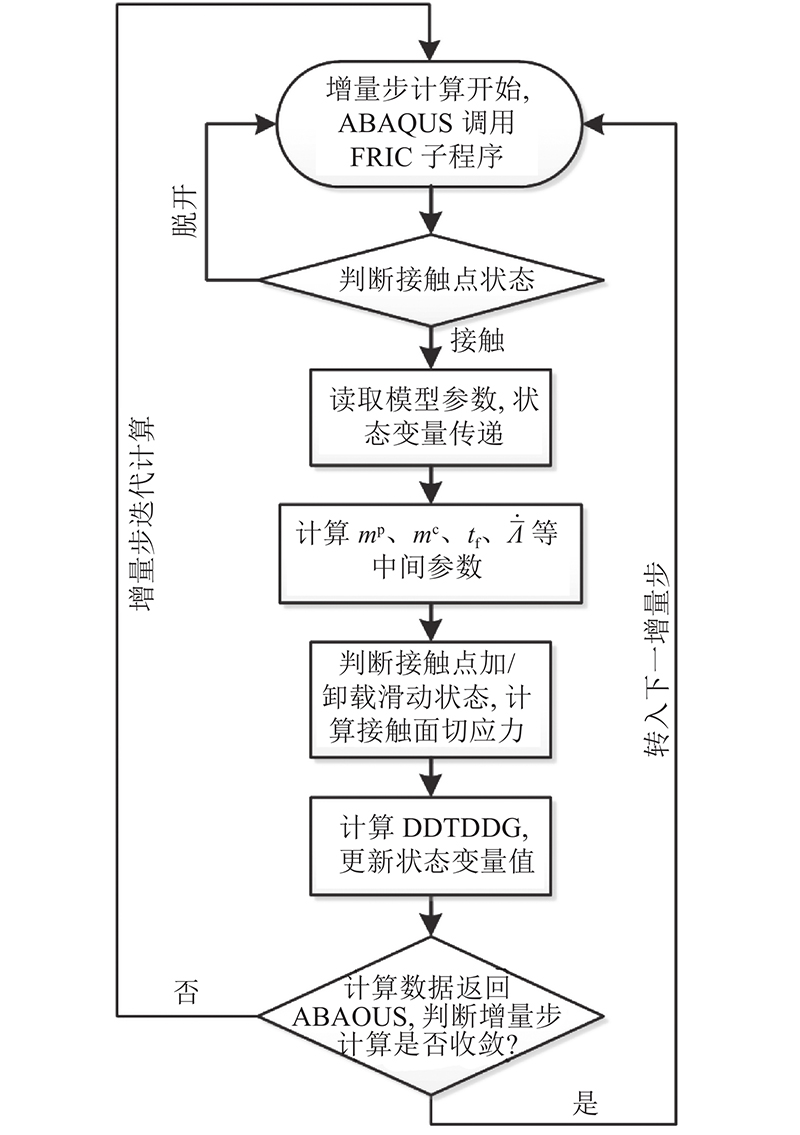
FRIC子程序需要提供接触面切向相互作用的完整定义，更新得到增量步结束时接触面的切应力. 选择向前欧拉积分法的应力更新方法，在次加载面摩擦模型理论中，参数正常滑动屈服比 $r$表征了滑动次加载面与正常滑动屈服面之间的靠近程度. 在假设的正常滑动屈服比演化法则中，当加载过程中 $r > 1$时， $\bar U\left( r \right) < 0$， $\dot r = \bar U\left( r \right)\left\| {{{\bar {\boldsymbol{v}}}^{\rm{p}}}} \right\| < 0$，接触面的应力状态能够自动控制回到滑动屈服面，因此使用显式应力积分方法，不用很小的时间增量步长也可以使计算收敛并得到较精确的结果. 基于向前欧拉积分方法，在应力更新的计算中不进行迭代，编制FRIC子程序，FRIC子程序的计算流程如图1所示. 运算步骤如下.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1 FRIC子程序计算流程图

Fig.1 Flow chart of FRIC subroutine

1)增量步开始，判断接触对的接触状态，对处于接触的点调用FRIC子程序，未处于接触的点则直接返回. FRIC子程序定义了表明接触节点之间相对运动状态的变量LM. 在增量步开始时，LM根据前一增量步中的接触状态传入FRIC子程序内：当接触点滑移时LM = 0, 当接触点刚性黏结时LM = 1,当接触点互相脱离时LM = 2. 对于未处于接触的点，增量步开始时传入的LM=2，设置RETURN语句自动退出子程序. 子程序在计算增量步的迭代步中根据接触节点间的接触状态更新LM：若接触点之间允许相对滑移，则令LM = 0；若接触点之间不允许相对滑移，则令LM = 1；若接触点之间忽略摩擦（无摩擦滑动），则令LM = 2；在该子程序中，接触节点之间允许相对滑移，将LM设为0.

2)设置 ${\mu _{\text{s}}}$、 ${\mu _{\text{k}}}$、 $ {\alpha _{\text{t}}} $、 $ {\alpha _{\text{n}}} $、 $\xi $、 $\kappa $、 $\tilde u$ 7个次加载面摩擦模型参量，读取主程序中相应的设定值，接收主程序传入的计算所需的接触面法向应力、切应力、剪切位移增量等计算参数. 次加载面摩擦模型中的正常滑动屈服比和摩擦系数为体现接触面状态变化的参量，在FRIC中设置2个状态变量STAVE(1)和STAVE(2)并赋初值，将2个状态变量分别赋给正常滑动屈服比和摩擦系数.

3)利用状态变量正常滑动屈服比和摩擦系数以及接触面法向应力、切应力等计算参数，计算判断接触点加卸载状态，计算接触面塑性滑动速度，更新接触面切应力所需的 ${m^{\rm{c}}}$、 ${m^{\rm{p}}}$、 $ {t_{\text{f}}} $和 $\dot {\bar \varLambda}$等中间参数.

4)根据式（8）判断接触点的加/卸载滑动状态，计算接触面塑性滑动速度，采用向前欧拉积分法更新接触点的切应力. 对处于卸载/弹性滑动状态的接触点，接触面塑性滑动速度为零，使用式（6）计算接触面切应力增量. 对处于加载/弹塑性滑动状态的接触点， ${\bar {\boldsymbol{v}}^{\text{p}}} = \dot {\bar \varLambda} {{\boldsymbol{t}}_{\text{f}}}$，使用式（9）计算接触面切应力增量.

5)计算接触面摩擦应力对相对滑移的偏导数矩阵DDTDDG. 计算正常滑动屈服比和摩擦系数的增量，更新正常滑动屈服比和摩擦系数：对处于卸载/弹性滑动状态的接触点，分别根据式（4）、（5）计算增量；对处于卸载/弹性滑动状态的接触点，分别根据式（3）、（5）计算. 将新的正常滑动屈服比和摩擦系数值赋给STAVE(1)和STAVE(2).

6）增量步结束，将子程序的计算数据返回主程序.

3. 模型的算例验证

3.1. 接触面切应力-剪切位移关系的验证

算例1采用文献[14]中的砂土与结构物接触面直剪试验，该试验的剪切盒内部尺寸为60 mm×53 mm×45 mm，建立三维数值模型. 用编写的次加载面摩擦模型子程序对该直剪试验进行模拟，与试验得到的应力-应变关系进行对比，以验证模型的合理性. 数值计算的有限元模型如图2所示，模型包括剪切盒、结构面板、土样3个部分，其中土样尺寸为60 mm×53 mm×30 mm，结构面板尺寸为120 mm×110 mm×10 mm，剪切盒的外部尺寸为93 mm×90 mm ×35 mm，内部尺寸为60 mm ×53 mm×35 mm. 试验采用应变控制，沿Y方向对下部结构面板施加剪切速率，剪切速率为0.01 mm/s. 接触面左端远离加载端，Y坐标设为0 mm，右侧靠近加载端，Y坐标为60 mm，X方向正交于Y方向. 计算中，土样与剪切盒、剪切盒底面与结构剪切板之间的接触均设置为光滑接触，土样底部与结构剪切板之间的接触采用次加载面摩擦模型，模型参数如表1所示. 为了便于分析，土样采用线弹性模型，根据文献[24]分别取弹性模量和泊松比为70 MPa和0.3. 计算采用动力隐式分析步，正式计算前进行了0.25 s、0.5 s、1 s和10 s增量步长方案的试算，计算的相对误差小于6%. 综合考虑计算精度及计算时间的代价后，前10 s的增量步长设为0.01 ~0.1 s，之后的增量步长设为0.5 s.

表 1 算例1的模型参数

Tab.1 Model parameter of numerical example 1

参数	数值	参数	数值
$\;{\mu _{\rm{s}}}$	1.05	$\kappa /{{\text{m}}^{ - 1}}$	215
$\;{\mu _{\rm{k}}}$	0.57	$\xi /{{\text{s}}^{ - 1}}$	0.00004
$ {\alpha _{\rm{t}}}/\left( {{{\text{kN}}} \cdot{{{\text{m}}^{-3}}}}\right) $	2×10⁶	$\tilde u/{{\text{m}}^{ - 1}}$	8500
${\alpha _{\rm{n} } }/\left( { {\text{kN} }\cdot{ {\text{m} }^{-3} } } \right)$	2×10⁶	−	−

新窗口打开| 下载CSV

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2 接触面直剪试验的三维模型

Fig.2 Three-dimensional model for direct shear test of interfaces

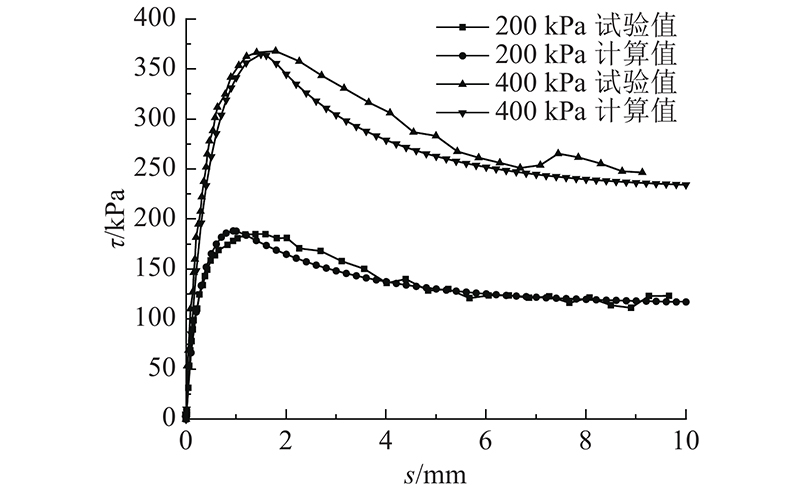
如图3所示为当法向应力分别为200和400 kPa时，切应力τ-剪切位移s的试验值曲线与模拟计算值的拟合曲线. 可知，数值模拟计算的结果与试验实测值吻合较好，利用次加载面摩擦模型能够较好地描述土与结构接触面剪切过程中的应变软化特性，表明次加载面摩擦模型用于土-结构接触面相互作用问题分析的可行性.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3 切应力-剪切位移关系的模拟曲线与试验结果比较

Fig.3 Comparison between simulated curves and experimental results of shear stress-displacement relationship

3.2. 剪切速率影响接触特性的验证

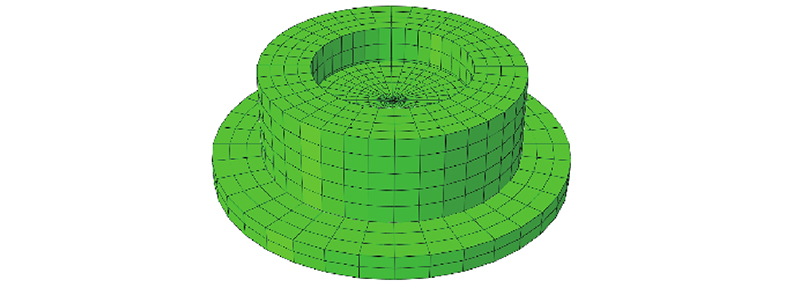
为了检验次加载面摩擦模型对速率影响力学剪切特性模拟的能力，算例2采用模拟月壤与足垫材料间的剪切试验^[8]. 模拟月壤是颗粒内部气孔发育、表面棱角丰富的类砂土材料，试验所用的模拟月壤试样直径为61.8 mm，高20 mm，建立三维数值模型对该试验进行模拟. 有限元模型如图4所示，模型包括剪切盒、结构面板、土样3个部分，其中土样尺寸为Φ(61.8) mm×20 mm（试样面积为30 cm²），结构面板尺寸为Φ(140) mm×10 mm，剪切盒的外部尺寸为Φ(101.8) mm×35 mm，内部尺寸为Φ(61.8) mm×35 mm. 试验采用应变控制，沿Y方向对下部结构面板施加剪切速率，剪切速率分别为0.2、1 和2 mm/min.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4 接触面直剪试验的三维模型

Fig.4 Three-dimensional model for direct shear test of interface

计算中，土样与剪切盒、剪切盒底面与结构剪切板之间的接触均设置为光滑接触，土样底部与结构剪切板之间的接触采用次加载面摩擦模型，模型参数如表2所示. 为了便于分析，土样采用线弹性模型，分别取弹性模量和泊松比为50 MPa和0.31. 计算采用动力隐式分析步.

表 2 算例2的模型参数

Tab.2 Model parameter of numerical example 2

参数	数值	参数	数值
$\;{\mu _{\rm{s}}}$	0.74	$\kappa /{{\text{m}}^{ - 1}}$	1500
$\;{\mu _{\rm{k}}}$	0.48	$\xi /{{\text{s}}^{ - 1}}$	0.005
$ {\alpha _{\rm{t}}}/\left( {{{\text{kN}}} \cdot{{{\text{m}}^{-3}}}}\right) $	10⁵	$\tilde u/{{\text{m}}^{ - 1}}$	15000
${\alpha _{\rm{n}}}/\left( {{\text{kN}}\cdot{{\text{m}}^{-3}}} \right)$	2×10⁶	−	−

新窗口打开| 下载CSV

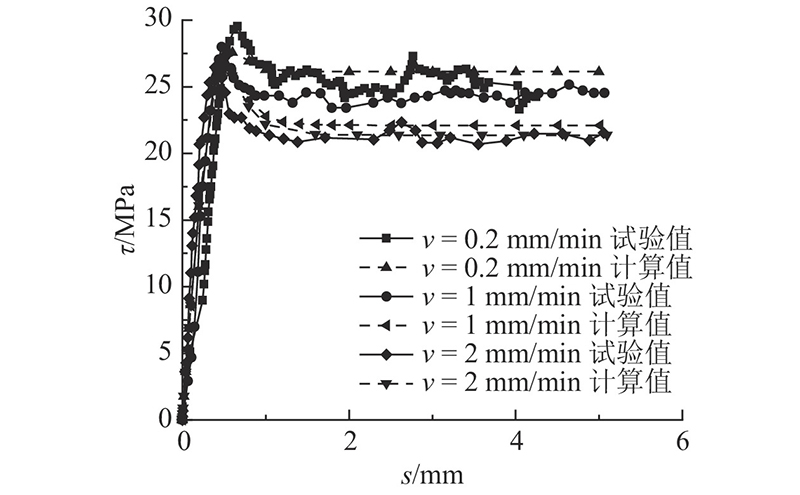
如图5所示为当法向应力为50 kPa，剪切速率v分别为0.2、1、2 mm/min时的τ-s试验值曲线与模拟计算值的拟合曲线. 可知，在50 kPa的法向应力作用下，模拟切应力-剪切位移曲线能够表现出剪切过程中应变软化的特征及残余切应力随剪切速率的增大而下降的现象，模型计算的结果与试验实测值吻合较好.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5 不同剪切速率下切应力-剪切位移关系的模拟曲线与试验结果比较

Fig.5 Comparison between simulated curves and experimental results of shear stress-displacement relationship under different shear rates

4. 接触面应力变化特性及直剪渐进破坏分析

利用本文编写的子程序，对文献[14]中200 kPa法向应力下的直剪试验进行模拟，分析接触面采用次加载面摩擦模型时，直剪过程中接触面应力的变化特征及直剪的渐进性破坏过程.

4.1. 接触面应力的分布

如图6所示为当剪切位移达到10 mm时，采用次加载面摩擦模型时接触面上的应力分布图. 可知，在直剪试验中，随着剪切过程的开展，接触面出现应力集中的现象. 当剪切位移达到10 mm时，次加载面摩擦模型会在靠近剪切加载端处产生较大的法向应力σ. 接触面上的Y方向切应力τ_Y在靠近剪切加载端处达到最大值，正交于剪切方向的X方向切应力τ_X可以忽略不计. 从图6可知，接触面上的法向应力和Y方向切应力沿剪切方向Y的分布在不同的X位置处基本一致，仅在剪切盒X方向两侧的边界附近有所减小，这是边界条件的设置导致的. 在数值计算中，可以将直剪试验的数值模拟简化为平面应变问题，降低计算的代价.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

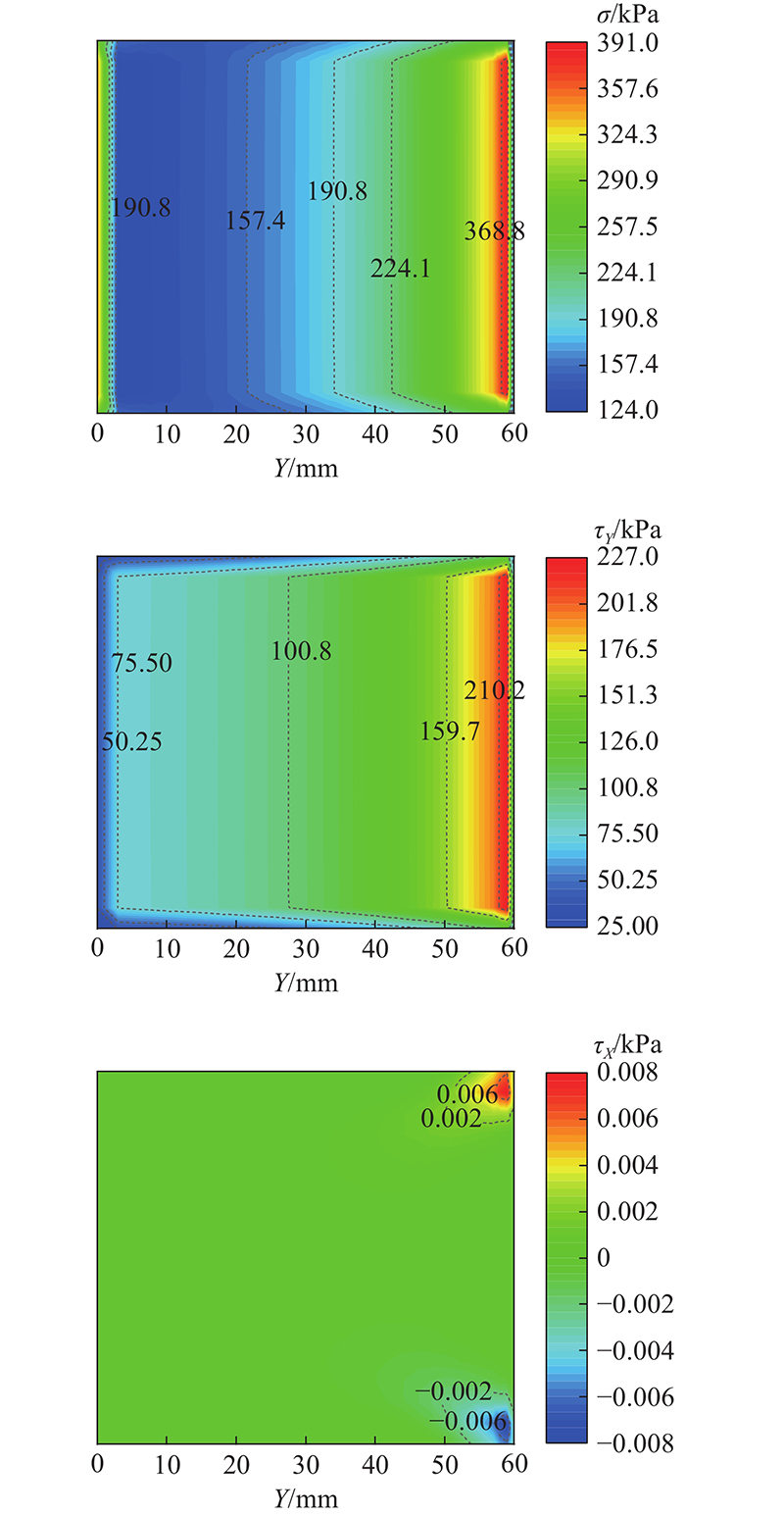
图 6 剪切位移达到10 mm时接触面上的应力分布

Fig.6 Distribution of stress on contact surface at 10 mm shear displacement

4.2. 接触面应力随相对位移的变化

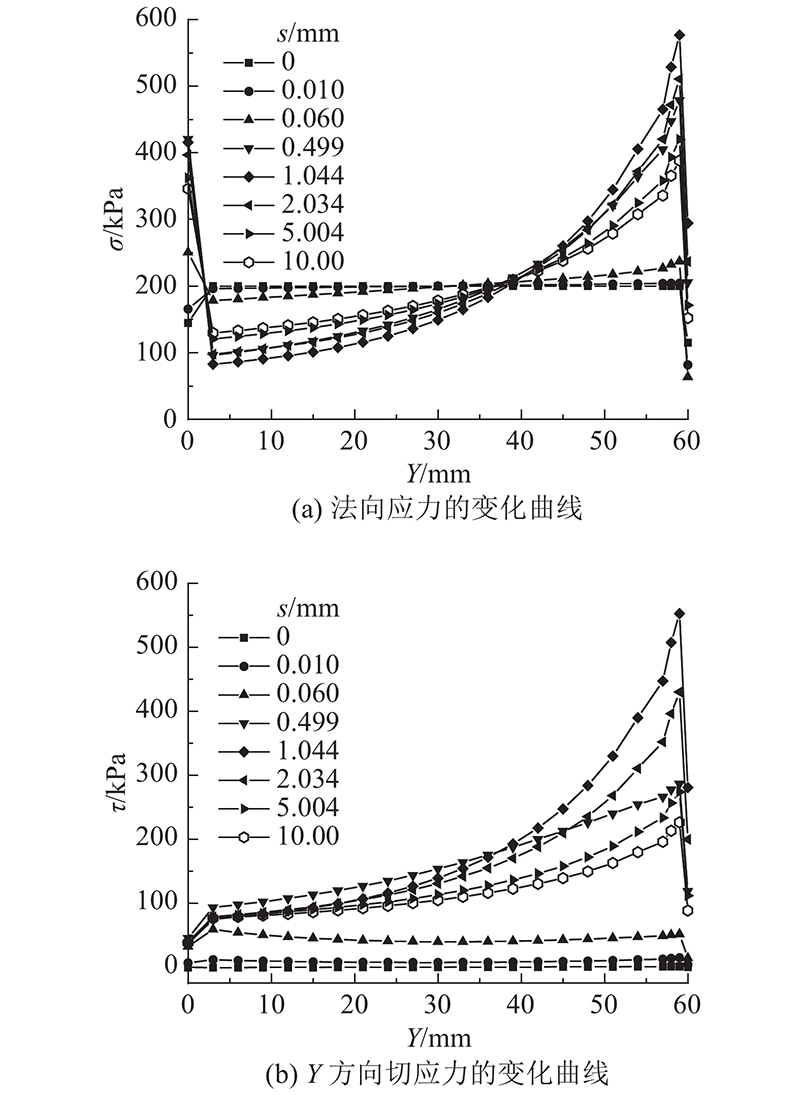
如图7所示为当采用次加载面摩擦模型时，接触面中轴线上沿Y方向切应力和法向应力随剪切位移发展的变化曲线.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7 接触面应力随剪切位移的发展变化曲线

Fig.7 Development curve of stress on contact surface with shear displacement

从图7可知，随着剪切位移的发展，次加载面摩擦模型的接触面法向应力向加载端集中，在Y = 5~40 mm处的法向应力不断减小，在Y = 45~60 mm处的法向压力不断增加. 次加载面摩擦模型接触面的切应力随着相对位移的发展表现出先增加、然后减小的趋势. 其中左侧的接触面单元的切应力在剪切位移达到0.499 mm附近开始下降，右侧的接触面单元的切应力峰值出现在1.044 mm左右，表明左侧接触面单元先于右侧接触面单元达到峰值切应力. 次加载面摩擦模型数值计算的结果表明：左侧接触面单元在接触面达到峰值切应力前已进入应力下降的阶段，右侧接触面单元在接触面达到峰值切应力时才进入应力下降的阶段. 应变软化过程中接触面上应力的变化常常较难通过试验手段检测得到，本文的方法提供了一个很好的技术手段.

4.3. 直剪试验的接触面渐进破坏分析

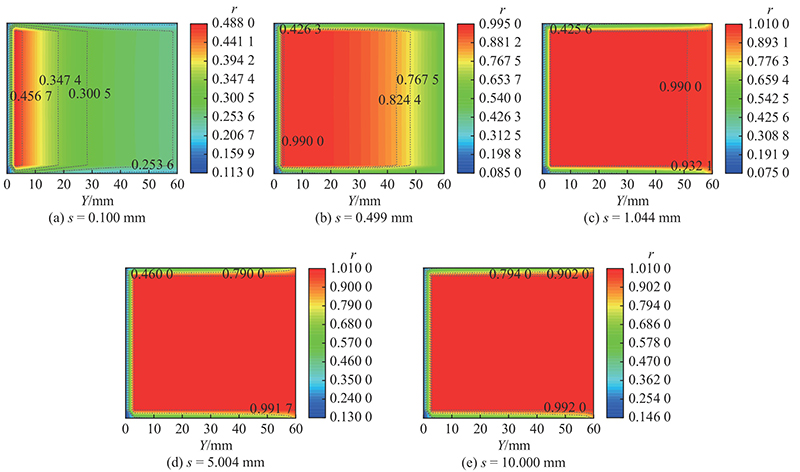
利用数值计算的结果，研究次加载面摩擦模型接触面的直剪渐进破坏过程. 利用正常滑动屈服比r，度量次加载面摩擦模型接触面上应力的发挥水平，r越接近1，接触面应力发挥水平越大. 如图8所示为当使用次加载面摩擦模型时，不同剪切位移下接触面上的正常滑动屈服比分布图.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8 不同剪切位移下接触面正常滑动屈服比的分布图

Fig.8 Distribution of normal sliding-yield ratio on contact surface at different shear displacement

从图8可以看出，剪切启动时，次加载面摩擦模型下的接触面应力发挥水平在远离加载端时较大. 随着剪切位移的发展，接触面应力发挥水平在远离加载端侧先达到最大，从远离加载端一侧到另一侧先后达到最大值，直到整个接触面完全屈服破坏. 次加载面摩擦模型的接触面具有明显的渐进破坏特性.

5. 结　论

（1）利用次加载面摩擦模型，能够较好地反映直剪试验中应力达到峰值后的应变软化行为，表现出密实状态的类砂土残余切应力随着剪切速率的增大而下降的现象.

（2）在相对位移的发展过程中，次加载面摩擦模型接触面不同位置处的切应力随剪切位移的发展先增加后下降. 远离剪切加载端的接触面单元在接触面达到峰值切应力前已经进入应力下降的阶段，靠近剪切加载端的接触面单元在接触面达到峰值切应力时进入应力下降的阶段.

（3）在次加载面摩擦模型情况下，接触面初始的应力发挥水平在远离加载端较大，并逐渐向接触面另一侧发展.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

齐良锋, 简浩, 唐丽云

引入接触单元模拟桩土共同作用

[J]. 岩土力学, 2005, 26 (1): 127- 130

DOI:10.3969/j.issn.1000-7598.2005.01.027 [本文引用: 1]

QI Liang-feng, JIAN Hao, TANG Li-yun

The computing model of adopting contact element to simulate the pile-soil’s reciprocity

[J]. Rock and Soil Mechanics, 2005, 26 (1): 127- 130

DOI:10.3969/j.issn.1000-7598.2005.01.027 [本文引用: 1]

[2]

LOUKIDIS D, SALGADO R

Analysis of the shaft resistance of non-displacement piles in sand

[J]. Géotechnique, 2008, 58 (4): 283- 296

[3]

LASHKARI A

Prediction of the shaft resistance of nondisplacement piles in sand

[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37 (8): 904- 931

DOI:10.1002/nag.1129 [本文引用: 1]

[4]

YOSHIMI Y, KISHIDA T

A ring torsion apparatus for evaluating friction between soil and metal surfaces

[J]. Geotechnical Testing Journal, 1981, 4 (4): 145- 152

DOI:10.1520/GTJ10783J [本文引用: 1]

[5]

YIN Z Z, ZHU H, XU G H

A study of deformation in the interface between soil and concrete

[J]. Computers and Geotechnics, 1995, 17 (1): 75- 92

DOI:10.1016/0266-352X(95)91303-L [本文引用: 3]

[6]

胡黎明, 濮家骝

土与结构物接触面物理力学特性试验研究

[J]. 岩土工程学报, 2001, 23 (4): 431- 435

DOI:10.3321/j.issn:1000-4548.2001.04.010 [本文引用: 1]

HU Li-ming, PU Jia-liu

Experimental study on mechanical characteristics of soil-structure interface

[J]. Chinese Journal of Geotechnical Engineering, 2001, 23 (4): 431- 435

DOI:10.3321/j.issn:1000-4548.2001.04.010 [本文引用: 1]

[7]

李登华, 郦能惠

土与混凝土结构接触面力学特性试验研究

[J]. 水电能源科学, 2009, 27 (5): 114- 118

DOI:10.3969/j.issn.1000-7709.2009.05.035 [本文引用: 1]

LI Deng-hua, LI Neng-hui

Experimental study on mechanical behavior of interface between soil and concrete slab

[J]. Water Resources and Power, 2009, 27 (5): 114- 118

DOI:10.3969/j.issn.1000-7709.2009.05.035 [本文引用: 1]

[8]

钟世英. 模拟月壤力学特性及软着陆足垫动力响应研究[D]. 杭州: 浙江大学, 2012.

[本文引用: 2]

ZHONG Shi-ying. Study on mechanical behaviors of lunar soil simulant and footpad dynamic response in soft landing [D]. Hangzhou: Zhejiang University, 2012.

[本文引用: 2]

[9]

夏红春, 周国庆

土-结构接触面剪切力学特性及其影响因素试验

[J]. 中国矿业大学学报, 2010, 39 (6): 831- 836