[2]
GEROLYMOS N, GIANNAKOU A, ANASTASOPOULOS L, et al Evidence of beneficial role of inclined piles: observations and summary of numerical analyses
[J]. Bulletin of Earthquake Engineering , 2008 , 6 (4 ): 705 - 722
DOI:10.1007/s10518-008-9085-2
[本文引用: 1]
[3]
ZHANG L, MCVAY M C, LAI P W Centrifuge modelling of laterally loaded single battered piles in sands
[J]. Canadian Geotechnical Journal , 1999 , 36 (6 ): 1074 - 1084
DOI:10.1139/t99-072
[本文引用: 5]
[4]
RAJASHREE S S, SITHARAM T G Nonlinear finite-element modeling of batter piles under lateral load
[J]. Journal of Geotechnical and Geoenvironmental Engineering , 2001 , 127 (7 ): 604 - 612
DOI:10.1061/(ASCE)1090-0241(2001)127:7(604)
[本文引用: 1]
[5]
MANOPPO F J Behaviour of the ultimate bearing capacity of single flexible batter pile under horizontal loads in homogeneous sand
[J]. Dinamika Teknik Sipil , 2010 , 10 (2 ): 116 - 119
[6]
BAJAJ P, YADU L, CHOUKSEY S K Study on vertical and batter piles subjected to lateral loads in different non-cohesive sub-soil conditions
[J]. International Journal of Geotechnical Engineering , 2019 , 14 (6 ): 601 - 613
[本文引用: 1]
[8]
吕凡任. 倾斜荷载作用下斜桩基础工作性状研究[D]. 杭州: 浙江大学, 2004.
LV Fan-ren. Study on behavior of batter piles under inclined load [D]. Hangzhou: Zhejiang University, 2004.
[10]
ASHOUR M, ALAAELDIN A, ARAB M G Laterally loaded battered piles in sandy soils
[J]. Journal of Geotechnical and Geoenvironmental Engineering , 2020 , 146 (1 ): 06019017
DOI:10.1061/(ASCE)GT.1943-5606.0002186
[11]
凌道盛, 任涛, 王云岗 砂土地基斜桩水平承载特性p-y曲线法
[J]. 岩土力学 , 2013 , 34 (1 ): 155 - 162
LING Dao-sheng, REN Tao, WANG Yun-gang A p-y curves method for horizontal bearing characteristics of single batter pile in sands
[J]. Rock and Soil Mechanics , 2013 , 34 (1 ): 155 - 162
[12]
曹卫平, 夏冰, 赵敏, 等 砂土中水平受荷斜桩的p-y曲线及其应用
[J]. 岩石力学与工程学报 , 2018 , 37 (3 ): 743 - 753
[本文引用: 1]
CAO Wei-ping, XIA Bing, ZHAO min, et al p-y curves of laterally loaded batter piles in sand and its application
[J]. Chinese Journal of Rock Mechanics and Engineering , 2018 , 37 (3 ): 743 - 753
[本文引用: 1]
[13]
曹卫平, 陶鹏, 赵敏, 等 砂土中循环荷载与单调荷载组合作用下斜桩水平承载变形特性
[J]. 长安大学学报:自然科学版 , 2020 , 40 (3 ): 11 - 21
[本文引用: 1]
CAO Wei-ping, TAO Peng, ZHAO Min, et al Model test on bearing deformation behavior of batter piles under combined horizontal loads and monotonic loads in sand
[J]. Journal of Chang’an University: Natural Science Edition , 2020 , 40 (3 ): 11 - 21
[本文引用: 1]
[16]
ROSQUOET F, THOREL L, GAENIER J, et al Lateral cyclic loading of sand-installed piles
[J]. Soils and Foundations , 2007 , 47 (5 ): 821 - 832
DOI:10.3208/sandf.47.821
[本文引用: 1]
[17]
ZHANG C R, WHITE D, RANDOLPH M Centrifuge modeling of the cyclic lateral response of a rigid pile in soft clay
[J]. Journal of Geotechnical and Geoenvironmental Engineering , 2011 , 137 : 717 - 729
DOI:10.1061/(ASCE)GT.1943-5606.0000482
[18]
朱斌, 熊根, 刘晋超, 等 砂土中大直径单桩水平受荷离心模型试验
[J]. 岩土工程学报 , 2013 , 35 (10 ): 1807 - 1815
[本文引用: 1]
ZHU Bin, XIONG Gen, LIU Jin-chao, et al Centrifuge modelling of a large-diameter single pile under lateral loads in sand
[J]. Chinese Journal of Geotechnical Engineering , 2013 , 35 (10 ): 1807 - 1815
[本文引用: 1]
[19]
LEBLANC C, HOULSBY G T, BYRNE B W Response of stiff piles in sand to long-term cyclic lateral loading
[J]. Géotechnique , 2010 , 60 (2 ): 79 - 90
[本文引用: 1]
[20]
张勋, 黄茂松, 胡志平 砂土中单桩水平循环累积变形特性模型试验
[J]. 岩土力学 , 2019 , 40 (3 ): 933 - 941
[本文引用: 1]
ZHANG Xun, HUANG Mao-song, HU Zhi-ping Model tests on cumulative deformation characteristics of a single pile subjected to lateral cyclic loading in sand
[J]. Rock and Soil Mechanics , 2019 , 40 (3 ): 933 - 941
[本文引用: 1]
[21]
GIANNAKOS S, GEROLYMOS N, GAZETAS G Cyclic lateral response of piles in dry sand: finite element modeling and validation
[J]. Computers and Geotechnics , 2012 , 44 : 116 - 131
DOI:10.1016/j.compgeo.2012.03.013
[本文引用: 1]
[22]
ACHMUS M, KUO Y S, ABDEL-RAHMAN K Behavior of monopile foundations under cyclic lateral load
[J]. Computer and Geotechnics , 2009 , 36 : 725 - 735
DOI:10.1016/j.compgeo.2008.12.003
[本文引用: 4]
[23]
张陈蓉, 朱治齐, 于锋, 等 砂土中大直径单桩的长期水平循环加载累积变形
[J]. 岩土工程学报 , 2020 , 42 (6 ): 1076 - 1084
[本文引用: 1]
ZHANG Chen-rong, ZHU Zhi-qi, YU Feng, et al Accumulative displacement of long-term cyclic laterally loaded monopiles with large diameter sand
[J]. Chinese Journal of Geotechnical Engineering , 2020 , 42 (6 ): 1076 - 1084
[本文引用: 1]
[24]
HUURMAN M Development of traffic induced permanent strains in concrete block pavements
[J]. Heron , 1996 , 41 (1 ): 29 - 52
[本文引用: 1]
[26]
ABDEL-RAHMEN K, ACHMUS M. Finite element modelling of horizontally loaded monopile foundations for offshore wind energy converters in Germany [C]// Proceedings of the International Symposium on Frontiers in Offshore Geotechnics . Perth: [s. n.], 2005: 309-396.
[本文引用: 1]
[27]
KUO Y S. On the behavior of large diameter piles under cyclic lateral load [D]. Hannover: Leibniz University of Hannover, 2008.
[本文引用: 1]
[28]
刘晋超, 熊根, 朱斌, 等 砂土海床中大直径单桩水平承载与变形特性
[J]. 岩土力学 , 2015 , 36 (2 ): 591 - 599
[本文引用: 2]
LIU Jin-chao, XIONG Gen, ZHU Bin, et al Bearing capacity and deflection behaviors of large diameter monopile foundations in sand seabed
[J]. Rock and Soil Mechanics , 2015 , 36 (2 ): 591 - 599
[本文引用: 2]
[29]
ZHU B, LI T, XIONG G, et al Centrifuge model tests on laterally loaded piles in sand
[J]. International Journal of Physical Modelling in Geotechnics , 2016 , 16 (4 ): 160 - 172
DOI:10.1680/jphmg.15.00023
[本文引用: 2]
[30]
王磊, 朱斌, 来向华 砂土循环累积变形规律与显式计算模型研究
[J]. 岩土工程学报 , 2015 , 37 (11 ): 2024 - 2029
DOI:10.11779/CJGE201511012
[本文引用: 1]
WANG Lei, ZHU Bin, LAI Xiang-hua Cyclic accumulative deformation of sand and its explicit model
[J]. Chinese Journal of Geotechnical Engineering , 2015 , 37 (11 ): 2024 - 2029
DOI:10.11779/CJGE201511012
[本文引用: 1]
[31]
ZDRAVKOVIĆ L, TABORDA D M G, POTTS D M, et al. Numerical modelling of large diameter piles under lateral loading for offshore wind applications [C]// Proceeding of 3rd International Symposium on Frontiers in Offshore Geotechnics . Oslo: CRC Press, 2015: 759-764.
[本文引用: 1]
[32]
KYUNG D, LEE J Interpretative Analysis of lateral load-carrying behavior and design model for inclined single and group micropiles
[J]. Journal of Geotechnical and Geoenvironmental Engineering , 2018 , 144 (1 ): 04017105
DOI:10.1061/(ASCE)GT.1943-5606.0001810
[本文引用: 1]
[33]
LITTLE R L, BRIAUD J L. Full scale cyclic lateral load tests on six single piles in sand: TAMU-RR-5640 [R]. Texas: College Station, 1988.
[本文引用: 1]
[34]
LI W, IGOE D, GAVIN K Field tests to investigate the cyclic response of monopiles in sand
[J]. Proceedings of the Institution of Civil Engineers-Geotechnical Engineering , 2015 , 168 (5 ): 407 - 421
DOI:10.1680/jgeen.14.00104
[35]
张勋, 黄茂松 水平循环荷载下砂土中沉井加桩基础累积变形特性
[J]. 岩石力学与工程学报 , 2016 , 35 (6 ): 1256 - 1272
[本文引用: 2]
ZHANG Xun, HUANG Mao-song Cumulative deformation of a caisson-piles composite foundation in sand subjected to cyclic lateral loading
[J]. Chinese Journal of Rock Mechanics and Engineering , 2016 , 35 (6 ): 1256 - 1272
[本文引用: 2]
Raked piles: virtues and drawbacks
1
2006
... 斜桩被广泛用作桥梁、码头、海洋平台等近海工程的基础,主要用于抵抗水平荷载. 现有的研究普遍表明,如果应用得当,斜桩基础能够提供更大的水平静力承载力[1 -2 ] ,因此拥有较大的应用潜力. 在近海工程中,斜桩基础普遍遭受风、浪、洋流等循环荷载,研究斜桩基础的循环受荷特性,对于指导斜桩基础的设计而言具有重要的意义. ...
Evidence of beneficial role of inclined piles: observations and summary of numerical analyses
1
2008
... 斜桩被广泛用作桥梁、码头、海洋平台等近海工程的基础,主要用于抵抗水平荷载. 现有的研究普遍表明,如果应用得当,斜桩基础能够提供更大的水平静力承载力[1 -2 ] ,因此拥有较大的应用潜力. 在近海工程中,斜桩基础普遍遭受风、浪、洋流等循环荷载,研究斜桩基础的循环受荷特性,对于指导斜桩基础的设计而言具有重要的意义. ...
Centrifuge modelling of laterally loaded single battered piles in sands
5
1999
... 现有针对斜桩基础的研究普遍集中在斜单桩的静力承载特性. Zhang等[3 ] 开展离心机模型试验,发现在砂土地基中,相较于竖直桩而言,负斜桩的水平承载力会有所提升,正斜桩会降低,为了便于比较,本文所述的正斜桩与负斜桩均与Zhang等[3 ] 所定义的一致,当桩身与加载方向的夹角大于90°时为负斜桩,小于90°时为正斜桩. Rajashree等[4 -6 ] 分别开展探究斜单桩水平承载特性的模型试验,研究结果均表明,在各种长径比条件下,负斜桩的水平承载力均高于相应的竖直桩,正斜桩的水平承载力最低. 曹卫平等[7 -12 ] 分别基于数值分析方法、广义弹性理论法、Mindin弹性解、变形楔模型、桩侧被动区楔形体模型以及p -y 曲线法,分析斜桩水平承载特性,研究结果均表明,负斜桩的水平静力承载力高于相应的竖直桩,且在一定的倾斜角范围内,负斜桩的水平承载力随着倾斜程度的增加而提升. ...
... [3 ]所定义的一致,当桩身与加载方向的夹角大于90°时为负斜桩,小于90°时为正斜桩. Rajashree等[4 -6 ] 分别开展探究斜单桩水平承载特性的模型试验,研究结果均表明,在各种长径比条件下,负斜桩的水平承载力均高于相应的竖直桩,正斜桩的水平承载力最低. 曹卫平等[7 -12 ] 分别基于数值分析方法、广义弹性理论法、Mindin弹性解、变形楔模型、桩侧被动区楔形体模型以及p -y 曲线法,分析斜桩水平承载特性,研究结果均表明,负斜桩的水平静力承载力高于相应的竖直桩,且在一定的倾斜角范围内,负斜桩的水平承载力随着倾斜程度的增加而提升. ...
... 本文中斜桩的定义与Zhang 等[3 ] 一致,如图5 所示. 桩身轴向与加载方向的夹角θ 大于90°时为负斜桩,小于90°时为正斜桩,桩身轴向与竖直方向所夹的锐角为倾斜角γ . 为了便于区分,负斜桩桩身倾斜角取负值,正斜桩取正值. ...
... 图6 的结果表明,在相同的水平荷载作用下,倾斜角为−25°~25°,负斜桩桩顶位移随着桩身倾斜程度的增加而减小,正斜桩反之;较竖直桩而言,负斜桩桩顶位移更小,正斜桩更大,这与Zhang等[3 ] 的研究结果基本一致. 各桩的静载曲线均为缓变型,拐点不明显,因此本文均采用桩顶位移达到10%D 时对应的水平荷载为桩的水平极限承载力[31 -32 ] . 采用指数函数模型分析斜单桩水平承载力H u ,该模型的表达式为 ...
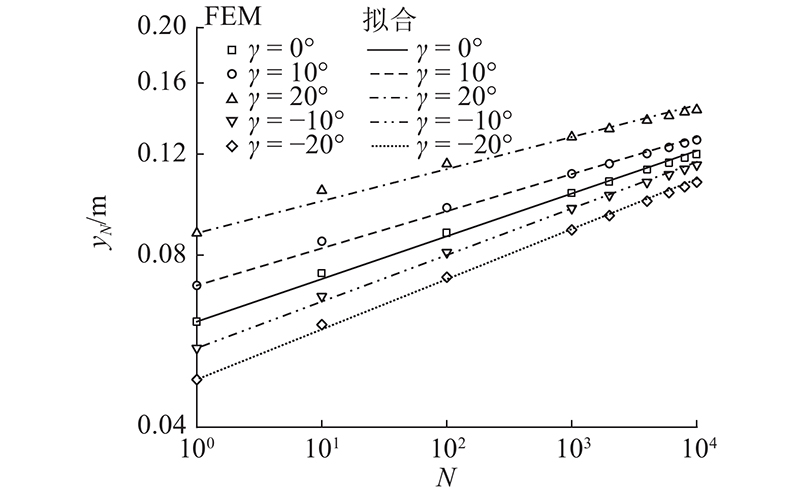
... 基于式(11)在双对数坐标系下对斜桩累积位移 ${y_N}$ 图11 所示. 可以看出,无论是斜桩还是竖直桩,利用幂指数模型都可以较好地用于预测桩顶累积位移. 各桩的β 取值如图12 所示. 结果表明,随着倾斜角从−25°逐渐过渡到25°,相应单桩的β 逐渐减小,说明虽然负斜桩较竖直桩和正斜桩在初次加载时桩顶位移较小,但是随着循环加卸载次数的增加,桩顶位移的累积速度较竖直桩和正斜桩更快. 当循环荷载幅值为28%H u0 时,随着循环次数的增加,负斜桩桩顶累积位移逐渐与竖直桩桩顶累积位移趋于一致,甚至略大于竖直桩. Zhang等[3 ] 指出,在强度更高的中密砂中,负斜桩的承载力较竖直桩提升幅度较大,在强度较低的松散砂中提升不明显. 在经历多次循环加卸载后,桩周土强度因循环弱化显著降低,导致负斜桩在承载力方面的优势较竖直桩逐渐减弱. ...
Nonlinear finite-element modeling of batter piles under lateral load
1
2001
... 现有针对斜桩基础的研究普遍集中在斜单桩的静力承载特性. Zhang等[3 ] 开展离心机模型试验,发现在砂土地基中,相较于竖直桩而言,负斜桩的水平承载力会有所提升,正斜桩会降低,为了便于比较,本文所述的正斜桩与负斜桩均与Zhang等[3 ] 所定义的一致,当桩身与加载方向的夹角大于90°时为负斜桩,小于90°时为正斜桩. Rajashree等[4 -6 ] 分别开展探究斜单桩水平承载特性的模型试验,研究结果均表明,在各种长径比条件下,负斜桩的水平承载力均高于相应的竖直桩,正斜桩的水平承载力最低. 曹卫平等[7 -12 ] 分别基于数值分析方法、广义弹性理论法、Mindin弹性解、变形楔模型、桩侧被动区楔形体模型以及p -y 曲线法,分析斜桩水平承载特性,研究结果均表明,负斜桩的水平静力承载力高于相应的竖直桩,且在一定的倾斜角范围内,负斜桩的水平承载力随着倾斜程度的增加而提升. ...
Behaviour of the ultimate bearing capacity of single flexible batter pile under horizontal loads in homogeneous sand
0
2010
Study on vertical and batter piles subjected to lateral loads in different non-cohesive sub-soil conditions
1
2019
... 现有针对斜桩基础的研究普遍集中在斜单桩的静力承载特性. Zhang等[3 ] 开展离心机模型试验,发现在砂土地基中,相较于竖直桩而言,负斜桩的水平承载力会有所提升,正斜桩会降低,为了便于比较,本文所述的正斜桩与负斜桩均与Zhang等[3 ] 所定义的一致,当桩身与加载方向的夹角大于90°时为负斜桩,小于90°时为正斜桩. Rajashree等[4 -6 ] 分别开展探究斜单桩水平承载特性的模型试验,研究结果均表明,在各种长径比条件下,负斜桩的水平承载力均高于相应的竖直桩,正斜桩的水平承载力最低. 曹卫平等[7 -12 ] 分别基于数值分析方法、广义弹性理论法、Mindin弹性解、变形楔模型、桩侧被动区楔形体模型以及p -y 曲线法,分析斜桩水平承载特性,研究结果均表明,负斜桩的水平静力承载力高于相应的竖直桩,且在一定的倾斜角范围内,负斜桩的水平承载力随着倾斜程度的增加而提升. ...
水平荷载作用下斜桩承载变形性状数值分析
1
2017
... 现有针对斜桩基础的研究普遍集中在斜单桩的静力承载特性. Zhang等[3 ] 开展离心机模型试验,发现在砂土地基中,相较于竖直桩而言,负斜桩的水平承载力会有所提升,正斜桩会降低,为了便于比较,本文所述的正斜桩与负斜桩均与Zhang等[3 ] 所定义的一致,当桩身与加载方向的夹角大于90°时为负斜桩,小于90°时为正斜桩. Rajashree等[4 -6 ] 分别开展探究斜单桩水平承载特性的模型试验,研究结果均表明,在各种长径比条件下,负斜桩的水平承载力均高于相应的竖直桩,正斜桩的水平承载力最低. 曹卫平等[7 -12 ] 分别基于数值分析方法、广义弹性理论法、Mindin弹性解、变形楔模型、桩侧被动区楔形体模型以及p -y 曲线法,分析斜桩水平承载特性,研究结果均表明,负斜桩的水平静力承载力高于相应的竖直桩,且在一定的倾斜角范围内,负斜桩的水平承载力随着倾斜程度的增加而提升. ...
水平荷载作用下斜桩承载变形性状数值分析
1
2017
... 现有针对斜桩基础的研究普遍集中在斜单桩的静力承载特性. Zhang等[3 ] 开展离心机模型试验,发现在砂土地基中,相较于竖直桩而言,负斜桩的水平承载力会有所提升,正斜桩会降低,为了便于比较,本文所述的正斜桩与负斜桩均与Zhang等[3 ] 所定义的一致,当桩身与加载方向的夹角大于90°时为负斜桩,小于90°时为正斜桩. Rajashree等[4 -6 ] 分别开展探究斜单桩水平承载特性的模型试验,研究结果均表明,在各种长径比条件下,负斜桩的水平承载力均高于相应的竖直桩,正斜桩的水平承载力最低. 曹卫平等[7 -12 ] 分别基于数值分析方法、广义弹性理论法、Mindin弹性解、变形楔模型、桩侧被动区楔形体模型以及p -y 曲线法,分析斜桩水平承载特性,研究结果均表明,负斜桩的水平静力承载力高于相应的竖直桩,且在一定的倾斜角范围内,负斜桩的水平承载力随着倾斜程度的增加而提升. ...
线载荷积分方程法分析桩顶受任意荷载的弹性斜桩
0
1999
线载荷积分方程法分析桩顶受任意荷载的弹性斜桩
0
1999
Laterally loaded battered piles in sandy soils
0
2020
砂土地基斜桩水平承载特性p-y曲线法
0
2013
砂土地基斜桩水平承载特性p-y曲线法
0
2013
砂土中水平受荷斜桩的p-y曲线及其应用
1
2018
... 现有针对斜桩基础的研究普遍集中在斜单桩的静力承载特性. Zhang等[3 ] 开展离心机模型试验,发现在砂土地基中,相较于竖直桩而言,负斜桩的水平承载力会有所提升,正斜桩会降低,为了便于比较,本文所述的正斜桩与负斜桩均与Zhang等[3 ] 所定义的一致,当桩身与加载方向的夹角大于90°时为负斜桩,小于90°时为正斜桩. Rajashree等[4 -6 ] 分别开展探究斜单桩水平承载特性的模型试验,研究结果均表明,在各种长径比条件下,负斜桩的水平承载力均高于相应的竖直桩,正斜桩的水平承载力最低. 曹卫平等[7 -12 ] 分别基于数值分析方法、广义弹性理论法、Mindin弹性解、变形楔模型、桩侧被动区楔形体模型以及p -y 曲线法,分析斜桩水平承载特性,研究结果均表明,负斜桩的水平静力承载力高于相应的竖直桩,且在一定的倾斜角范围内,负斜桩的水平承载力随着倾斜程度的增加而提升. ...
砂土中水平受荷斜桩的p-y曲线及其应用
1
2018
... 现有针对斜桩基础的研究普遍集中在斜单桩的静力承载特性. Zhang等[3 ] 开展离心机模型试验,发现在砂土地基中,相较于竖直桩而言,负斜桩的水平承载力会有所提升,正斜桩会降低,为了便于比较,本文所述的正斜桩与负斜桩均与Zhang等[3 ] 所定义的一致,当桩身与加载方向的夹角大于90°时为负斜桩,小于90°时为正斜桩. Rajashree等[4 -6 ] 分别开展探究斜单桩水平承载特性的模型试验,研究结果均表明,在各种长径比条件下,负斜桩的水平承载力均高于相应的竖直桩,正斜桩的水平承载力最低. 曹卫平等[7 -12 ] 分别基于数值分析方法、广义弹性理论法、Mindin弹性解、变形楔模型、桩侧被动区楔形体模型以及p -y 曲线法,分析斜桩水平承载特性,研究结果均表明,负斜桩的水平静力承载力高于相应的竖直桩,且在一定的倾斜角范围内,负斜桩的水平承载力随着倾斜程度的增加而提升. ...
砂土中循环荷载与单调荷载组合作用下斜桩水平承载变形特性
1
2020
... 近海环境中的斜桩基础主要承受风、浪、洋流等循环荷载,在长期循环加卸载的作用下,斜桩基础会产生循环累积变形,使得静力荷载作用下斜桩基础的设计方法不再适用. 曹卫平等[13 ] 通过室内1g模型试验发现,在经历20次循环加卸载后,负斜桩桩顶残余水平位移小于正斜桩. 现有研究普遍集中于竖直单桩的水平循环受荷特性探究. Long等[14 -15 ] 基于现场试验,提出用于预测水平循环荷载作用下竖直单桩位移累积的对数函数和幂函数显式模型. Rosquoet等[16 -18 ] 通过离心模型试验,探究水平循环荷载作用下单桩变形的累积规律. Leblanc等[19 -20 ] 开展不同循环加载路径下的单桩循环加载模型试验,循环加载次数达到上万次. Giannakos等[21 -23 ] 分别基于摩尔-库仑准则的运动硬化土体模型、砂土刚度循环衰减模型及砂土加卸载刚度演化模型,构建单桩循环受荷特性的数值分析方法,取得了较好的模拟效果. 目前针对斜单桩在水平循环荷载作用下受荷特性的研究较竖直桩而言较少,斜单桩的循环受荷设计方法远滞后于斜单桩的实际工程应用. ...
砂土中循环荷载与单调荷载组合作用下斜桩水平承载变形特性
1
2020
... 近海环境中的斜桩基础主要承受风、浪、洋流等循环荷载,在长期循环加卸载的作用下,斜桩基础会产生循环累积变形,使得静力荷载作用下斜桩基础的设计方法不再适用. 曹卫平等[13 ] 通过室内1g模型试验发现,在经历20次循环加卸载后,负斜桩桩顶残余水平位移小于正斜桩. 现有研究普遍集中于竖直单桩的水平循环受荷特性探究. Long等[14 -15 ] 基于现场试验,提出用于预测水平循环荷载作用下竖直单桩位移累积的对数函数和幂函数显式模型. Rosquoet等[16 -18 ] 通过离心模型试验,探究水平循环荷载作用下单桩变形的累积规律. Leblanc等[19 -20 ] 开展不同循环加载路径下的单桩循环加载模型试验,循环加载次数达到上万次. Giannakos等[21 -23 ] 分别基于摩尔-库仑准则的运动硬化土体模型、砂土刚度循环衰减模型及砂土加卸载刚度演化模型,构建单桩循环受荷特性的数值分析方法,取得了较好的模拟效果. 目前针对斜单桩在水平循环荷载作用下受荷特性的研究较竖直桩而言较少,斜单桩的循环受荷设计方法远滞后于斜单桩的实际工程应用. ...
Effects of cyclic lateral loads on piles in sand
1
1994
... 近海环境中的斜桩基础主要承受风、浪、洋流等循环荷载,在长期循环加卸载的作用下,斜桩基础会产生循环累积变形,使得静力荷载作用下斜桩基础的设计方法不再适用. 曹卫平等[13 ] 通过室内1g模型试验发现,在经历20次循环加卸载后,负斜桩桩顶残余水平位移小于正斜桩. 现有研究普遍集中于竖直单桩的水平循环受荷特性探究. Long等[14 -15 ] 基于现场试验,提出用于预测水平循环荷载作用下竖直单桩位移累积的对数函数和幂函数显式模型. Rosquoet等[16 -18 ] 通过离心模型试验,探究水平循环荷载作用下单桩变形的累积规律. Leblanc等[19 -20 ] 开展不同循环加载路径下的单桩循环加载模型试验,循环加载次数达到上万次. Giannakos等[21 -23 ] 分别基于摩尔-库仑准则的运动硬化土体模型、砂土刚度循环衰减模型及砂土加卸载刚度演化模型,构建单桩循环受荷特性的数值分析方法,取得了较好的模拟效果. 目前针对斜单桩在水平循环荷载作用下受荷特性的研究较竖直桩而言较少,斜单桩的循环受荷设计方法远滞后于斜单桩的实际工程应用. ...
Permanent strains of piles in sand due to cyclic lateral loads
1
1999
... 近海环境中的斜桩基础主要承受风、浪、洋流等循环荷载,在长期循环加卸载的作用下,斜桩基础会产生循环累积变形,使得静力荷载作用下斜桩基础的设计方法不再适用. 曹卫平等[13 ] 通过室内1g模型试验发现,在经历20次循环加卸载后,负斜桩桩顶残余水平位移小于正斜桩. 现有研究普遍集中于竖直单桩的水平循环受荷特性探究. Long等[14 -15 ] 基于现场试验,提出用于预测水平循环荷载作用下竖直单桩位移累积的对数函数和幂函数显式模型. Rosquoet等[16 -18 ] 通过离心模型试验,探究水平循环荷载作用下单桩变形的累积规律. Leblanc等[19 -20 ] 开展不同循环加载路径下的单桩循环加载模型试验,循环加载次数达到上万次. Giannakos等[21 -23 ] 分别基于摩尔-库仑准则的运动硬化土体模型、砂土刚度循环衰减模型及砂土加卸载刚度演化模型,构建单桩循环受荷特性的数值分析方法,取得了较好的模拟效果. 目前针对斜单桩在水平循环荷载作用下受荷特性的研究较竖直桩而言较少,斜单桩的循环受荷设计方法远滞后于斜单桩的实际工程应用. ...
Lateral cyclic loading of sand-installed piles
1
2007
... 近海环境中的斜桩基础主要承受风、浪、洋流等循环荷载,在长期循环加卸载的作用下,斜桩基础会产生循环累积变形,使得静力荷载作用下斜桩基础的设计方法不再适用. 曹卫平等[13 ] 通过室内1g模型试验发现,在经历20次循环加卸载后,负斜桩桩顶残余水平位移小于正斜桩. 现有研究普遍集中于竖直单桩的水平循环受荷特性探究. Long等[14 -15 ] 基于现场试验,提出用于预测水平循环荷载作用下竖直单桩位移累积的对数函数和幂函数显式模型. Rosquoet等[16 -18 ] 通过离心模型试验,探究水平循环荷载作用下单桩变形的累积规律. Leblanc等[19 -20 ] 开展不同循环加载路径下的单桩循环加载模型试验,循环加载次数达到上万次. Giannakos等[21 -23 ] 分别基于摩尔-库仑准则的运动硬化土体模型、砂土刚度循环衰减模型及砂土加卸载刚度演化模型,构建单桩循环受荷特性的数值分析方法,取得了较好的模拟效果. 目前针对斜单桩在水平循环荷载作用下受荷特性的研究较竖直桩而言较少,斜单桩的循环受荷设计方法远滞后于斜单桩的实际工程应用. ...
Centrifuge modeling of the cyclic lateral response of a rigid pile in soft clay
0
2011
砂土中大直径单桩水平受荷离心模型试验
1
2013
... 近海环境中的斜桩基础主要承受风、浪、洋流等循环荷载,在长期循环加卸载的作用下,斜桩基础会产生循环累积变形,使得静力荷载作用下斜桩基础的设计方法不再适用. 曹卫平等[13 ] 通过室内1g模型试验发现,在经历20次循环加卸载后,负斜桩桩顶残余水平位移小于正斜桩. 现有研究普遍集中于竖直单桩的水平循环受荷特性探究. Long等[14 -15 ] 基于现场试验,提出用于预测水平循环荷载作用下竖直单桩位移累积的对数函数和幂函数显式模型. Rosquoet等[16 -18 ] 通过离心模型试验,探究水平循环荷载作用下单桩变形的累积规律. Leblanc等[19 -20 ] 开展不同循环加载路径下的单桩循环加载模型试验,循环加载次数达到上万次. Giannakos等[21 -23 ] 分别基于摩尔-库仑准则的运动硬化土体模型、砂土刚度循环衰减模型及砂土加卸载刚度演化模型,构建单桩循环受荷特性的数值分析方法,取得了较好的模拟效果. 目前针对斜单桩在水平循环荷载作用下受荷特性的研究较竖直桩而言较少,斜单桩的循环受荷设计方法远滞后于斜单桩的实际工程应用. ...
砂土中大直径单桩水平受荷离心模型试验
1
2013
... 近海环境中的斜桩基础主要承受风、浪、洋流等循环荷载,在长期循环加卸载的作用下,斜桩基础会产生循环累积变形,使得静力荷载作用下斜桩基础的设计方法不再适用. 曹卫平等[13 ] 通过室内1g模型试验发现,在经历20次循环加卸载后,负斜桩桩顶残余水平位移小于正斜桩. 现有研究普遍集中于竖直单桩的水平循环受荷特性探究. Long等[14 -15 ] 基于现场试验,提出用于预测水平循环荷载作用下竖直单桩位移累积的对数函数和幂函数显式模型. Rosquoet等[16 -18 ] 通过离心模型试验,探究水平循环荷载作用下单桩变形的累积规律. Leblanc等[19 -20 ] 开展不同循环加载路径下的单桩循环加载模型试验,循环加载次数达到上万次. Giannakos等[21 -23 ] 分别基于摩尔-库仑准则的运动硬化土体模型、砂土刚度循环衰减模型及砂土加卸载刚度演化模型,构建单桩循环受荷特性的数值分析方法,取得了较好的模拟效果. 目前针对斜单桩在水平循环荷载作用下受荷特性的研究较竖直桩而言较少,斜单桩的循环受荷设计方法远滞后于斜单桩的实际工程应用. ...
Response of stiff piles in sand to long-term cyclic lateral loading
1
2010
... 近海环境中的斜桩基础主要承受风、浪、洋流等循环荷载,在长期循环加卸载的作用下,斜桩基础会产生循环累积变形,使得静力荷载作用下斜桩基础的设计方法不再适用. 曹卫平等[13 ] 通过室内1g模型试验发现,在经历20次循环加卸载后,负斜桩桩顶残余水平位移小于正斜桩. 现有研究普遍集中于竖直单桩的水平循环受荷特性探究. Long等[14 -15 ] 基于现场试验,提出用于预测水平循环荷载作用下竖直单桩位移累积的对数函数和幂函数显式模型. Rosquoet等[16 -18 ] 通过离心模型试验,探究水平循环荷载作用下单桩变形的累积规律. Leblanc等[19 -20 ] 开展不同循环加载路径下的单桩循环加载模型试验,循环加载次数达到上万次. Giannakos等[21 -23 ] 分别基于摩尔-库仑准则的运动硬化土体模型、砂土刚度循环衰减模型及砂土加卸载刚度演化模型,构建单桩循环受荷特性的数值分析方法,取得了较好的模拟效果. 目前针对斜单桩在水平循环荷载作用下受荷特性的研究较竖直桩而言较少,斜单桩的循环受荷设计方法远滞后于斜单桩的实际工程应用. ...
砂土中单桩水平循环累积变形特性模型试验
1
2019
... 近海环境中的斜桩基础主要承受风、浪、洋流等循环荷载,在长期循环加卸载的作用下,斜桩基础会产生循环累积变形,使得静力荷载作用下斜桩基础的设计方法不再适用. 曹卫平等[13 ] 通过室内1g模型试验发现,在经历20次循环加卸载后,负斜桩桩顶残余水平位移小于正斜桩. 现有研究普遍集中于竖直单桩的水平循环受荷特性探究. Long等[14 -15 ] 基于现场试验,提出用于预测水平循环荷载作用下竖直单桩位移累积的对数函数和幂函数显式模型. Rosquoet等[16 -18 ] 通过离心模型试验,探究水平循环荷载作用下单桩变形的累积规律. Leblanc等[19 -20 ] 开展不同循环加载路径下的单桩循环加载模型试验,循环加载次数达到上万次. Giannakos等[21 -23 ] 分别基于摩尔-库仑准则的运动硬化土体模型、砂土刚度循环衰减模型及砂土加卸载刚度演化模型,构建单桩循环受荷特性的数值分析方法,取得了较好的模拟效果. 目前针对斜单桩在水平循环荷载作用下受荷特性的研究较竖直桩而言较少,斜单桩的循环受荷设计方法远滞后于斜单桩的实际工程应用. ...
砂土中单桩水平循环累积变形特性模型试验
1
2019
... 近海环境中的斜桩基础主要承受风、浪、洋流等循环荷载,在长期循环加卸载的作用下,斜桩基础会产生循环累积变形,使得静力荷载作用下斜桩基础的设计方法不再适用. 曹卫平等[13 ] 通过室内1g模型试验发现,在经历20次循环加卸载后,负斜桩桩顶残余水平位移小于正斜桩. 现有研究普遍集中于竖直单桩的水平循环受荷特性探究. Long等[14 -15 ] 基于现场试验,提出用于预测水平循环荷载作用下竖直单桩位移累积的对数函数和幂函数显式模型. Rosquoet等[16 -18 ] 通过离心模型试验,探究水平循环荷载作用下单桩变形的累积规律. Leblanc等[19 -20 ] 开展不同循环加载路径下的单桩循环加载模型试验,循环加载次数达到上万次. Giannakos等[21 -23 ] 分别基于摩尔-库仑准则的运动硬化土体模型、砂土刚度循环衰减模型及砂土加卸载刚度演化模型,构建单桩循环受荷特性的数值分析方法,取得了较好的模拟效果. 目前针对斜单桩在水平循环荷载作用下受荷特性的研究较竖直桩而言较少,斜单桩的循环受荷设计方法远滞后于斜单桩的实际工程应用. ...
Cyclic lateral response of piles in dry sand: finite element modeling and validation
1
2012
... 近海环境中的斜桩基础主要承受风、浪、洋流等循环荷载,在长期循环加卸载的作用下,斜桩基础会产生循环累积变形,使得静力荷载作用下斜桩基础的设计方法不再适用. 曹卫平等[13 ] 通过室内1g模型试验发现,在经历20次循环加卸载后,负斜桩桩顶残余水平位移小于正斜桩. 现有研究普遍集中于竖直单桩的水平循环受荷特性探究. Long等[14 -15 ] 基于现场试验,提出用于预测水平循环荷载作用下竖直单桩位移累积的对数函数和幂函数显式模型. Rosquoet等[16 -18 ] 通过离心模型试验,探究水平循环荷载作用下单桩变形的累积规律. Leblanc等[19 -20 ] 开展不同循环加载路径下的单桩循环加载模型试验,循环加载次数达到上万次. Giannakos等[21 -23 ] 分别基于摩尔-库仑准则的运动硬化土体模型、砂土刚度循环衰减模型及砂土加卸载刚度演化模型,构建单桩循环受荷特性的数值分析方法,取得了较好的模拟效果. 目前针对斜单桩在水平循环荷载作用下受荷特性的研究较竖直桩而言较少,斜单桩的循环受荷设计方法远滞后于斜单桩的实际工程应用. ...
Behavior of monopile foundations under cyclic lateral load
4
2009
... 针对斜单桩循环受荷特性研究的不足,本文基于Achmus等[22 ] 结合砂土刚度衰减模型提出的单桩循环受荷特性数值分析方法,探究斜单桩的循环受荷特性,为近海工程中斜桩基础的设计提供参考. ...
... 由于桩-土体系中土单元存在初始应力,当受循环荷载时,桩周各位置的土单元应力状态均不同. 为了使式(1)能够用于砂土中单桩循环受荷特性的分析,Achmus等[22 ] 引入特征循环应力比X c 替换式(1)的循环应力比X : ...
... Achmus等[22 , 25 ] 基于引入的特征循环应力比X c ,提出通过砂土动三轴试验结果分析砂土中单桩水平循环受荷特性的数值方法. 采取的数值分析流程如图2 所示,相应的步骤具体如下. ...
... 桩采用线弹性模型模拟,在码头和桥梁工程中,桩材一般选用混凝土,因此采用C30混凝土强度参数作为桩的力学参数输入,弹性模量E p 取30 GPa,泊松比υ p 为0.15. 桩周土选为中密砂,根据郭玉樹等[25 ] 的推荐取值,土的刚度系数(λ 和κ )、泊松比υ s 、φ 、剪胀角ψ 及c 的取值如表1 所示,桩周土单元刚度衰减回归系数b 1 、b 2 根据Kuo[27 ] 的推荐取值,分别取0.16和0.38. 采用的有限元计算模型如图3 所示,桩和土单元均采用6面体8节点线性缩减积分单元(C3D8R)模拟. 图中,U Y Y 轴方向的位移,R X R Z X 轴和Z 轴的转角. ABAQUS中,根据桩-土表面定义接触属性,以模拟桩-土之间的相互作用,桩侧及桩底均采用主-从接触算法. 选择刚度较大的桩面作为主控面,刚度较小的土体表面作为从属面,桩-土接触采用摩尔-库仑摩擦罚函数的形式,界面摩擦系数选取u = tan (0.67φ )[22 ,25 ] . 为了保证计算结果的收敛性,桩-土弹性滑移变形设置为单位典型长度的5%. 为了消除场地边界对计算结果的影响,桩周土径向计算范围为25倍的桩径,底面边界距离桩端10倍桩径,以上模型尺寸可以忽略边界条件对计算结果的影响[28 ] . ...
砂土中大直径单桩的长期水平循环加载累积变形
1
2020
... 近海环境中的斜桩基础主要承受风、浪、洋流等循环荷载,在长期循环加卸载的作用下,斜桩基础会产生循环累积变形,使得静力荷载作用下斜桩基础的设计方法不再适用. 曹卫平等[13 ] 通过室内1g模型试验发现,在经历20次循环加卸载后,负斜桩桩顶残余水平位移小于正斜桩. 现有研究普遍集中于竖直单桩的水平循环受荷特性探究. Long等[14 -15 ] 基于现场试验,提出用于预测水平循环荷载作用下竖直单桩位移累积的对数函数和幂函数显式模型. Rosquoet等[16 -18 ] 通过离心模型试验,探究水平循环荷载作用下单桩变形的累积规律. Leblanc等[19 -20 ] 开展不同循环加载路径下的单桩循环加载模型试验,循环加载次数达到上万次. Giannakos等[21 -23 ] 分别基于摩尔-库仑准则的运动硬化土体模型、砂土刚度循环衰减模型及砂土加卸载刚度演化模型,构建单桩循环受荷特性的数值分析方法,取得了较好的模拟效果. 目前针对斜单桩在水平循环荷载作用下受荷特性的研究较竖直桩而言较少,斜单桩的循环受荷设计方法远滞后于斜单桩的实际工程应用. ...
砂土中大直径单桩的长期水平循环加载累积变形
1
2020
... 近海环境中的斜桩基础主要承受风、浪、洋流等循环荷载,在长期循环加卸载的作用下,斜桩基础会产生循环累积变形,使得静力荷载作用下斜桩基础的设计方法不再适用. 曹卫平等[13 ] 通过室内1g模型试验发现,在经历20次循环加卸载后,负斜桩桩顶残余水平位移小于正斜桩. 现有研究普遍集中于竖直单桩的水平循环受荷特性探究. Long等[14 -15 ] 基于现场试验,提出用于预测水平循环荷载作用下竖直单桩位移累积的对数函数和幂函数显式模型. Rosquoet等[16 -18 ] 通过离心模型试验,探究水平循环荷载作用下单桩变形的累积规律. Leblanc等[19 -20 ] 开展不同循环加载路径下的单桩循环加载模型试验,循环加载次数达到上万次. Giannakos等[21 -23 ] 分别基于摩尔-库仑准则的运动硬化土体模型、砂土刚度循环衰减模型及砂土加卸载刚度演化模型,构建单桩循环受荷特性的数值分析方法,取得了较好的模拟效果. 目前针对斜单桩在水平循环荷载作用下受荷特性的研究较竖直桩而言较少,斜单桩的循环受荷设计方法远滞后于斜单桩的实际工程应用. ...
Development of traffic induced permanent strains in concrete block pavements
1
1996
... 在循环荷载作用下,桩周砂土塑性变形的不断累积导致砂土中的单桩桩身位移逐渐增大. 砂土在循环荷载作用下的应力-应变关系如图1 所示. 当忽略弹性应变时,砂土在N 次循环荷载作用下的割线模量E sN 与初次循环荷载作用下的塑性应变 $\varepsilon _{{\text{p}},1}^{\text{a}}$ E s1 及N 次循环荷载作用下的塑性应变 $\varepsilon _{{\text{p}},N}^{\text{a}}$ [24 ] : ...
用循环三轴试验分析海上风力发电机单桩基础侧向位移
3
2009
... Achmus等[22 , 25 ] 基于引入的特征循环应力比X c ,提出通过砂土动三轴试验结果分析砂土中单桩水平循环受荷特性的数值方法. 采取的数值分析流程如图2 所示,相应的步骤具体如下. ...
... 桩采用线弹性模型模拟,在码头和桥梁工程中,桩材一般选用混凝土,因此采用C30混凝土强度参数作为桩的力学参数输入,弹性模量E p 取30 GPa,泊松比υ p 为0.15. 桩周土选为中密砂,根据郭玉樹等[25 ] 的推荐取值,土的刚度系数(λ 和κ )、泊松比υ s 、φ 、剪胀角ψ 及c 的取值如表1 所示,桩周土单元刚度衰减回归系数b 1 、b 2 根据Kuo[27 ] 的推荐取值,分别取0.16和0.38. 采用的有限元计算模型如图3 所示,桩和土单元均采用6面体8节点线性缩减积分单元(C3D8R)模拟. 图中,U Y Y 轴方向的位移,R X R Z X 轴和Z 轴的转角. ABAQUS中,根据桩-土表面定义接触属性,以模拟桩-土之间的相互作用,桩侧及桩底均采用主-从接触算法. 选择刚度较大的桩面作为主控面,刚度较小的土体表面作为从属面,桩-土接触采用摩尔-库仑摩擦罚函数的形式,界面摩擦系数选取u = tan (0.67φ )[22 ,25 ] . 为了保证计算结果的收敛性,桩-土弹性滑移变形设置为单位典型长度的5%. 为了消除场地边界对计算结果的影响,桩周土径向计算范围为25倍的桩径,底面边界距离桩端10倍桩径,以上模型尺寸可以忽略边界条件对计算结果的影响[28 ] . ...
... ,25 ]. 为了保证计算结果的收敛性,桩-土弹性滑移变形设置为单位典型长度的5%. 为了消除场地边界对计算结果的影响,桩周土径向计算范围为25倍的桩径,底面边界距离桩端10倍桩径,以上模型尺寸可以忽略边界条件对计算结果的影响[28 ] . ...
用循环三轴试验分析海上风力发电机单桩基础侧向位移
3
2009
... Achmus等[22 , 25 ] 基于引入的特征循环应力比X c ,提出通过砂土动三轴试验结果分析砂土中单桩水平循环受荷特性的数值方法. 采取的数值分析流程如图2 所示,相应的步骤具体如下. ...
... 桩采用线弹性模型模拟,在码头和桥梁工程中,桩材一般选用混凝土,因此采用C30混凝土强度参数作为桩的力学参数输入,弹性模量E p 取30 GPa,泊松比υ p 为0.15. 桩周土选为中密砂,根据郭玉樹等[25 ] 的推荐取值,土的刚度系数(λ 和κ )、泊松比υ s 、φ 、剪胀角ψ 及c 的取值如表1 所示,桩周土单元刚度衰减回归系数b 1 、b 2 根据Kuo[27 ] 的推荐取值,分别取0.16和0.38. 采用的有限元计算模型如图3 所示,桩和土单元均采用6面体8节点线性缩减积分单元(C3D8R)模拟. 图中,U Y Y 轴方向的位移,R X R Z X 轴和Z 轴的转角. ABAQUS中,根据桩-土表面定义接触属性,以模拟桩-土之间的相互作用,桩侧及桩底均采用主-从接触算法. 选择刚度较大的桩面作为主控面,刚度较小的土体表面作为从属面,桩-土接触采用摩尔-库仑摩擦罚函数的形式,界面摩擦系数选取u = tan (0.67φ )[22 ,25 ] . 为了保证计算结果的收敛性,桩-土弹性滑移变形设置为单位典型长度的5%. 为了消除场地边界对计算结果的影响,桩周土径向计算范围为25倍的桩径,底面边界距离桩端10倍桩径,以上模型尺寸可以忽略边界条件对计算结果的影响[28 ] . ...
... ,25 ]. 为了保证计算结果的收敛性,桩-土弹性滑移变形设置为单位典型长度的5%. 为了消除场地边界对计算结果的影响,桩周土径向计算范围为25倍的桩径,底面边界距离桩端10倍桩径,以上模型尺寸可以忽略边界条件对计算结果的影响[28 ] . ...
1
... 在数值模型中,采用摩尔-库仑模型模拟桩周砂土力学性质的非线性,土的非线性弹性模量随土中瞬时应力的变化而实时改变[26 ] : ...
1
... 桩采用线弹性模型模拟,在码头和桥梁工程中,桩材一般选用混凝土,因此采用C30混凝土强度参数作为桩的力学参数输入,弹性模量E p 取30 GPa,泊松比υ p 为0.15. 桩周土选为中密砂,根据郭玉樹等[25 ] 的推荐取值,土的刚度系数(λ 和κ )、泊松比υ s 、φ 、剪胀角ψ 及c 的取值如表1 所示,桩周土单元刚度衰减回归系数b 1 、b 2 根据Kuo[27 ] 的推荐取值,分别取0.16和0.38. 采用的有限元计算模型如图3 所示,桩和土单元均采用6面体8节点线性缩减积分单元(C3D8R)模拟. 图中,U Y Y 轴方向的位移,R X R Z X 轴和Z 轴的转角. ABAQUS中,根据桩-土表面定义接触属性,以模拟桩-土之间的相互作用,桩侧及桩底均采用主-从接触算法. 选择刚度较大的桩面作为主控面,刚度较小的土体表面作为从属面,桩-土接触采用摩尔-库仑摩擦罚函数的形式,界面摩擦系数选取u = tan (0.67φ )[22 ,25 ] . 为了保证计算结果的收敛性,桩-土弹性滑移变形设置为单位典型长度的5%. 为了消除场地边界对计算结果的影响,桩周土径向计算范围为25倍的桩径,底面边界距离桩端10倍桩径,以上模型尺寸可以忽略边界条件对计算结果的影响[28 ] . ...
砂土海床中大直径单桩水平承载与变形特性
2
2015
... 桩采用线弹性模型模拟,在码头和桥梁工程中,桩材一般选用混凝土,因此采用C30混凝土强度参数作为桩的力学参数输入,弹性模量E p 取30 GPa,泊松比υ p 为0.15. 桩周土选为中密砂,根据郭玉樹等[25 ] 的推荐取值,土的刚度系数(λ 和κ )、泊松比υ s 、φ 、剪胀角ψ 及c 的取值如表1 所示,桩周土单元刚度衰减回归系数b 1 、b 2 根据Kuo[27 ] 的推荐取值,分别取0.16和0.38. 采用的有限元计算模型如图3 所示,桩和土单元均采用6面体8节点线性缩减积分单元(C3D8R)模拟. 图中,U Y Y 轴方向的位移,R X R Z X 轴和Z 轴的转角. ABAQUS中,根据桩-土表面定义接触属性,以模拟桩-土之间的相互作用,桩侧及桩底均采用主-从接触算法. 选择刚度较大的桩面作为主控面,刚度较小的土体表面作为从属面,桩-土接触采用摩尔-库仑摩擦罚函数的形式,界面摩擦系数选取u = tan (0.67φ )[22 ,25 ] . 为了保证计算结果的收敛性,桩-土弹性滑移变形设置为单位典型长度的5%. 为了消除场地边界对计算结果的影响,桩周土径向计算范围为25倍的桩径,底面边界距离桩端10倍桩径,以上模型尺寸可以忽略边界条件对计算结果的影响[28 ] . ...
... Zhu等[29 ] 基于离心机模型试验开展单桩的水平受荷特性分析,分别进行竖直单桩的单向和循环加载试验. 离心机模型试验对应的原型桩身参数如下:桩为管桩,桩径为2.5 m,桩长为65 m,壁厚为45 mm,埋深为50 m. 刘晋超等[28 ,30 ] 分别对Zhu等[29 ] 离心机模型试验中所采用的60%密实度福建砂,开展静力和循环剪切三轴试验. 基于单元试验结果,本文中砂土的相关计算参数取值如表2 所示. ...
砂土海床中大直径单桩水平承载与变形特性
2
2015
... 桩采用线弹性模型模拟,在码头和桥梁工程中,桩材一般选用混凝土,因此采用C30混凝土强度参数作为桩的力学参数输入,弹性模量E p 取30 GPa,泊松比υ p 为0.15. 桩周土选为中密砂,根据郭玉樹等[25 ] 的推荐取值,土的刚度系数(λ 和κ )、泊松比υ s 、φ 、剪胀角ψ 及c 的取值如表1 所示,桩周土单元刚度衰减回归系数b 1 、b 2 根据Kuo[27 ] 的推荐取值,分别取0.16和0.38. 采用的有限元计算模型如图3 所示,桩和土单元均采用6面体8节点线性缩减积分单元(C3D8R)模拟. 图中,U Y Y 轴方向的位移,R X R Z X 轴和Z 轴的转角. ABAQUS中,根据桩-土表面定义接触属性,以模拟桩-土之间的相互作用,桩侧及桩底均采用主-从接触算法. 选择刚度较大的桩面作为主控面,刚度较小的土体表面作为从属面,桩-土接触采用摩尔-库仑摩擦罚函数的形式,界面摩擦系数选取u = tan (0.67φ )[22 ,25 ] . 为了保证计算结果的收敛性,桩-土弹性滑移变形设置为单位典型长度的5%. 为了消除场地边界对计算结果的影响,桩周土径向计算范围为25倍的桩径,底面边界距离桩端10倍桩径,以上模型尺寸可以忽略边界条件对计算结果的影响[28 ] . ...
... Zhu等[29 ] 基于离心机模型试验开展单桩的水平受荷特性分析,分别进行竖直单桩的单向和循环加载试验. 离心机模型试验对应的原型桩身参数如下:桩为管桩,桩径为2.5 m,桩长为65 m,壁厚为45 mm,埋深为50 m. 刘晋超等[28 ,30 ] 分别对Zhu等[29 ] 离心机模型试验中所采用的60%密实度福建砂,开展静力和循环剪切三轴试验. 基于单元试验结果,本文中砂土的相关计算参数取值如表2 所示. ...
Centrifuge model tests on laterally loaded piles in sand
2
2016
... Zhu等[29 ] 基于离心机模型试验开展单桩的水平受荷特性分析,分别进行竖直单桩的单向和循环加载试验. 离心机模型试验对应的原型桩身参数如下:桩为管桩,桩径为2.5 m,桩长为65 m,壁厚为45 mm,埋深为50 m. 刘晋超等[28 ,30 ] 分别对Zhu等[29 ] 离心机模型试验中所采用的60%密实度福建砂,开展静力和循环剪切三轴试验. 基于单元试验结果,本文中砂土的相关计算参数取值如表2 所示. ...
... [29 ]离心机模型试验中所采用的60%密实度福建砂,开展静力和循环剪切三轴试验. 基于单元试验结果,本文中砂土的相关计算参数取值如表2 所示. ...
砂土循环累积变形规律与显式计算模型研究
1
2015
... Zhu等[29 ] 基于离心机模型试验开展单桩的水平受荷特性分析,分别进行竖直单桩的单向和循环加载试验. 离心机模型试验对应的原型桩身参数如下:桩为管桩,桩径为2.5 m,桩长为65 m,壁厚为45 mm,埋深为50 m. 刘晋超等[28 ,30 ] 分别对Zhu等[29 ] 离心机模型试验中所采用的60%密实度福建砂,开展静力和循环剪切三轴试验. 基于单元试验结果,本文中砂土的相关计算参数取值如表2 所示. ...
砂土循环累积变形规律与显式计算模型研究
1
2015
... Zhu等[29 ] 基于离心机模型试验开展单桩的水平受荷特性分析,分别进行竖直单桩的单向和循环加载试验. 离心机模型试验对应的原型桩身参数如下:桩为管桩,桩径为2.5 m,桩长为65 m,壁厚为45 mm,埋深为50 m. 刘晋超等[28 ,30 ] 分别对Zhu等[29 ] 离心机模型试验中所采用的60%密实度福建砂,开展静力和循环剪切三轴试验. 基于单元试验结果,本文中砂土的相关计算参数取值如表2 所示. ...
1
... 图6 的结果表明,在相同的水平荷载作用下,倾斜角为−25°~25°,负斜桩桩顶位移随着桩身倾斜程度的增加而减小,正斜桩反之;较竖直桩而言,负斜桩桩顶位移更小,正斜桩更大,这与Zhang等[3 ] 的研究结果基本一致. 各桩的静载曲线均为缓变型,拐点不明显,因此本文均采用桩顶位移达到10%D 时对应的水平荷载为桩的水平极限承载力[31 -32 ] . 采用指数函数模型分析斜单桩水平承载力H u ,该模型的表达式为 ...
Interpretative Analysis of lateral load-carrying behavior and design model for inclined single and group micropiles
1
2018
... 图6 的结果表明,在相同的水平荷载作用下,倾斜角为−25°~25°,负斜桩桩顶位移随着桩身倾斜程度的增加而减小,正斜桩反之;较竖直桩而言,负斜桩桩顶位移更小,正斜桩更大,这与Zhang等[3 ] 的研究结果基本一致. 各桩的静载曲线均为缓变型,拐点不明显,因此本文均采用桩顶位移达到10%D 时对应的水平荷载为桩的水平极限承载力[31 -32 ] . 采用指数函数模型分析斜单桩水平承载力H u ,该模型的表达式为 ...
1
... Little等[33 -35 ] 均指出在长期循环荷载下, ${y_N}$ ${y_1}$ N 呈幂函数关系. 本文采用张勋等[35 ] 提出的沉井加桩复合基础水平循环累积位移预测模型分析桩顶累积位移,当水平受荷桩受单向循环荷载时,该模型的表达式为 ...
Field tests to investigate the cyclic response of monopiles in sand
0
2015
水平循环荷载下砂土中沉井加桩基础累积变形特性
2
2016
... Little等[33 -35 ] 均指出在长期循环荷载下, ${y_N}$ ${y_1}$ N 呈幂函数关系. 本文采用张勋等[35 ] 提出的沉井加桩复合基础水平循环累积位移预测模型分析桩顶累积位移,当水平受荷桩受单向循环荷载时,该模型的表达式为 ...
... [35 ]提出的沉井加桩复合基础水平循环累积位移预测模型分析桩顶累积位移,当水平受荷桩受单向循环荷载时,该模型的表达式为 ...
水平循环荷载下砂土中沉井加桩基础累积变形特性
2
2016
... Little等[33 -35 ] 均指出在长期循环荷载下, ${y_N}$ ${y_1}$ N 呈幂函数关系. 本文采用张勋等[35 ] 提出的沉井加桩复合基础水平循环累积位移预测模型分析桩顶累积位移,当水平受荷桩受单向循环荷载时,该模型的表达式为 ...
... [35 ]提出的沉井加桩复合基础水平循环累积位移预测模型分析桩顶累积位移,当水平受荷桩受单向循环荷载时,该模型的表达式为 ...