不同于红外图像和多光谱图像,高光谱图像 (hyperspectral image,HSI) 具有数百个窄带,包含一段连续光谱范围内地物的辐射值,光谱分辨率可达nm级. 基于这一特性,高光谱图像在目标检测方面具有强大优势,被广泛应用于智能农业、矿产勘探和大气科学等多个领域[1]. 作为高光谱图像处理的重要组成部分,异常检测旨在以无监督的方式检测出高维数据中的异常信息. 其中,异常是指在空间上稀疏分布的少量像素或者混合像元,具有和背景像素不同的光谱特征.
目前,Molero等[2]提出各种用于高光谱异常检测的方法. 最经典的是RX算法(Reed-Xiaoli,RX),它假设背景像素遵循正态分布统计模型,通过计算测试像素与相邻背景像素之间的马氏距离来检测异常. 在实际应用中,由于场景地物类型复杂,以整幅图像的协方差矩阵估计背景统计特征不准确.
根据高光谱数据的异常稀疏性、背景低秩性的特点,一些基于非高斯分布的检测模型[3-5]被提出. 鲁棒主成分分析(robust principal component analysis,RPCA)[6]将图像分解为低秩的背景矩阵和稀疏的异常矩阵,通过矩阵分解重构残差. 低秩表示模型(low-rank representation,LRR)[7]改进RPCA方法中单一子空间表示模型,将复杂背景用多个子空间线性混合表示. Xu等[8]对低秩系数添加局部约束的稀疏项,提出低秩稀疏表示模型(low rank and sparse representation,LRASR). 低秩稀疏表示的检测模型忽略了噪声和异常对构建背景字典过程中的污染问题. 只关注高光谱图像的光谱维信息,忽略图像的空间维信息. 这两点在一定程度上限制了最终的检测精度.
针对上述问题,本文提出基于FrFT(fractional Fourier transform,FrFT)变换与全变分正则化的异常检测模型. 通过FrFT变换提取光谱维的时频域特征,在每个子空间内构造FrFT-RX算子,剔除潜在的异常原子,得到纯净的背景字典. 在低秩稀疏模型中引入全变分正则化项,表示经过变换后中间域内背景部分的空间平滑性,综合利用图像的空谱信息. 采用交替方向乘子法(alternating direction method of multipliers,ADMM)[9]将模型求解转换成多个子问题的求解问题,得到异常部分. 计算异常部分的
1. 基于低秩稀疏表示的异常检测模型
基于背景的低秩特性和异常的稀疏特性,低秩稀疏表示模型把图像分为背景部分和异常部分. 对于任意高光谱图像
式中:
式中:‖·‖*为矩阵的核范数,表示矩阵奇异值的和,用于约束矩阵的低秩性;‖·‖1和‖·‖2,1分别为矩阵的
2. 基于FrFT变换的全变分正则化模型
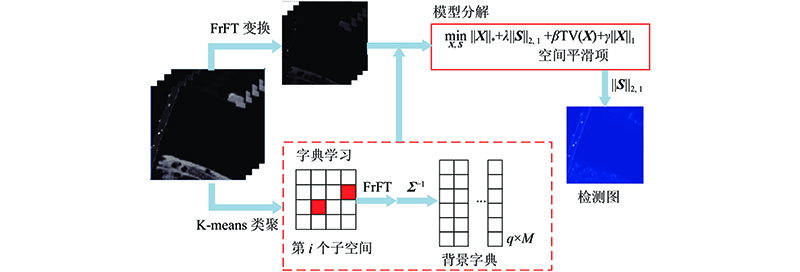
针对低秩稀疏模型中背景字典易被污染、空间信息利用不足的问题,提出基于FrFT变换的全变分正则化模型,整体流程的示意图如图1所示. 通过k-means聚类映射至
图 1
图 1 基于FrFT变换和全变分正则化的异常检测算法的流程
Fig.1 Flowchart of anomaly detection algorithm based on FrFT transform and total variation regularization
2.1. 分数阶傅里叶变换(FrFT)
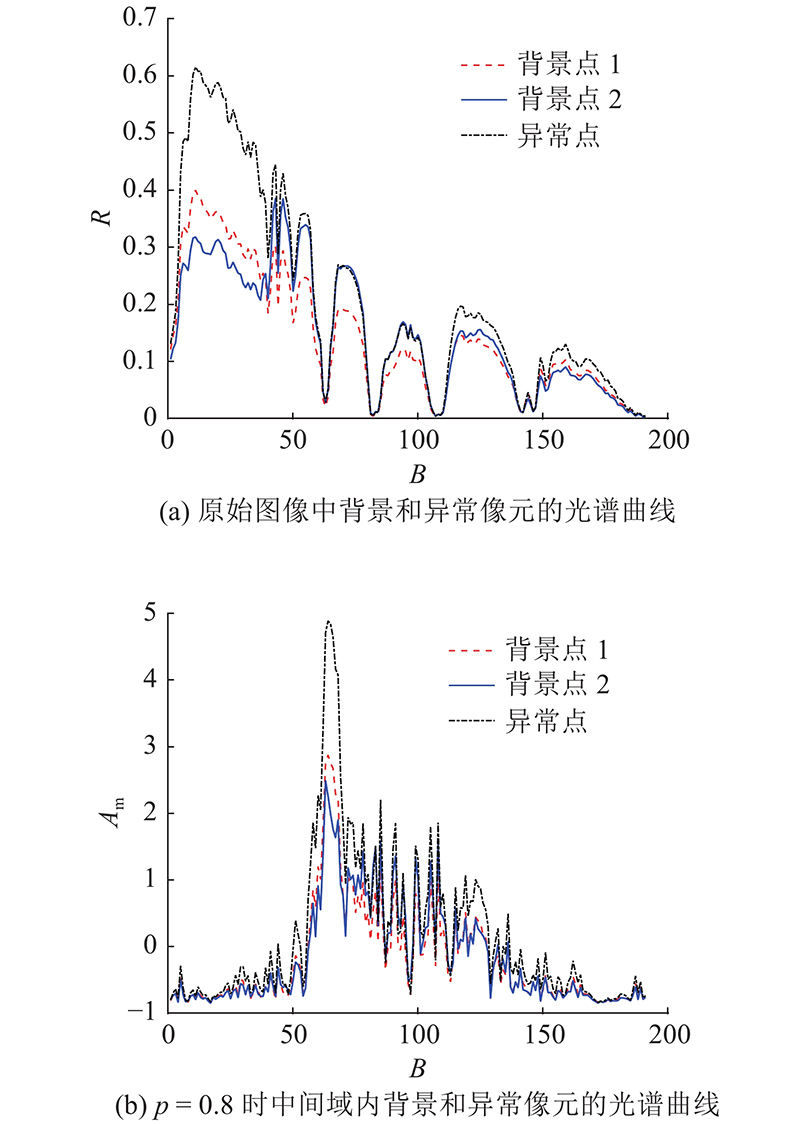
FrFT变换对高光谱图像中异常像元和背景像元的光谱曲线的变换效果如图2所示. 图中,R为反射值,Am为光谱幅值.
图 2
FrFT变换的本质是对光谱曲线进行特征提取. 实验表明,当选择合适的
2.2. 字典学习
背景字典的构建在异常检测中非常重要. 纯净的背景字典将进一步提高异常检测的精度,降低虚警率. 传统的基于表示的检测方法[7]常用整个高光谱图像或者部分图像构建背景字典,这样会引入异常像元的污染,影响后续检测的精度. 尽管LRR模型引入多个子空间概念,每个子空间代表相似地物类型的像元,但可能包含异常混合像元. 考虑上述因素,在采用多个子空间的基础上,结合FrFT变换剔除异常像元的干扰. 采用k-means聚类算法,将光谱信息相似的像元映射到一个子空间中. FrFT变换的表达式如下:
式中:
式中:
在字典学习中,当
2.3. 全变分正则化
空间特征是指当高光谱图像中的2个像素在空间维度上相邻时,它们对应的表示系数相似. 全变分正则化器(total variation,TV)[13]在保留边缘信息和促进分段平滑性方面非常强大. 高光谱图像通过FrFT变换后,背景像元与异常像元的空间差异性增强,即图像在背景区域是趋于平滑,在异常点邻域内存在梯度变化. 引入全变分正则化描述中间域内高光谱图像的空间信息,改进背景部分的估计.
由于空间相邻像素
式中:
式中:
2.4. 建模与优化
经过FrFT变换后,在中间域上引入全变分正则化项约束,模型表示为
式中:
构造增广拉格朗日函数如下:
式中:
1)固定变量(
式中:
2)固定变量(
上述问题为核范数和
3)固定变量(
对式(18)中的目标函数求导,等式右边取零,得到
式(19)可以通过离散傅里叶变换对角化[15] ,进行有效计算.
4)固定变量(
引入软阈值收缩运算符
5)固定变量(
6)固定变量(
引入
式中:
7)迭代拉格朗日乘子
当迭代条件满足
或最大迭代次数达到要求时,迭代结束,得到低秩矩阵和稀疏矩阵. 由于FrFT变换具有噪声抑制的效果,图像经过FrFT变换后,在中间域上引入全变分正则化约束进行迭代,得到的稀疏矩阵剔除噪声干扰,可以表示为异常部分.
当目标函数达到最优解时,异常部分可以求解如下:
式中:
式(33)表示
2.5. 算法流程
通过论述和公式推导,得到基于FrFT变换和全变分正则化的异常检测算法流程如下.
算法1:基于FrFT变换和全变分正则化异常检测算法
输入:高光谱图像
1)利用2.2节的内容,构建背景字典
2) 利用FrFT变换,将高光谱数据映射至中间域,得到
3)初始化变量:
4)模型求解. 当模型不收敛或未达到迭代次数时,执行以下步骤.
a)根据式(15)更新
b) 根据式(17)、(19)、(21)、(23),分别更新
c)根据式(25)更新
d) 根据式(26)~(31),分别更新
e) 计算是否满足收敛要求或达到最大迭代次数.
输出:稀疏矩阵
3. 实验与结果分析
为了验证所提算法的有效性,在3组真实高光谱数据集上进行实验.
3.1. 实验数据
第1组数据由机载成像光谱仪(hyperspectral digital image collection experiment,HYDICE)采集. 它的光谱分辨率是10 nm,空间分辨率是1.5 m,共有224个光谱波段,波长为400~2 500 nm. 去除水汽吸收和低信噪比波段(1~4、76、87、101~111、136~153和198~210),剩下162个波段作为实验数据. 实验中使用尺寸为80×120像素的场景,包含21个异常目标,假彩色图像和目标真值图如图3所示.
图 3
第2组数据覆盖意大利北部帕维亚市中心区域(Pavia),几何分辨率为1.3 m. 原始数据的空间大小为1 096×715像素,102个波段,波长为430~860 nm,用于实验的场景覆盖面积为108×120像素,总共有61个异常像元. 数据集的假彩色图像和目标真值图如图4所示.
第3组数据由EO-1(earth observing-1,EO-1)上的Hyperion传感器在奥卡万戈三角洲上空收集. 光谱分辨率为10 nm,空间分辨率为30 m. 去除水汽吸收和低信噪比波段(10~55、82~97、102~119、134~164和187~220),使用其中145个波段. 该场景的空间大小为1 476×256像素,采用100×100像素的区域,共有32个异常像素. 假彩色图像和目标真值图如图5所示.
图 4
图 5
3.2. 参数分析
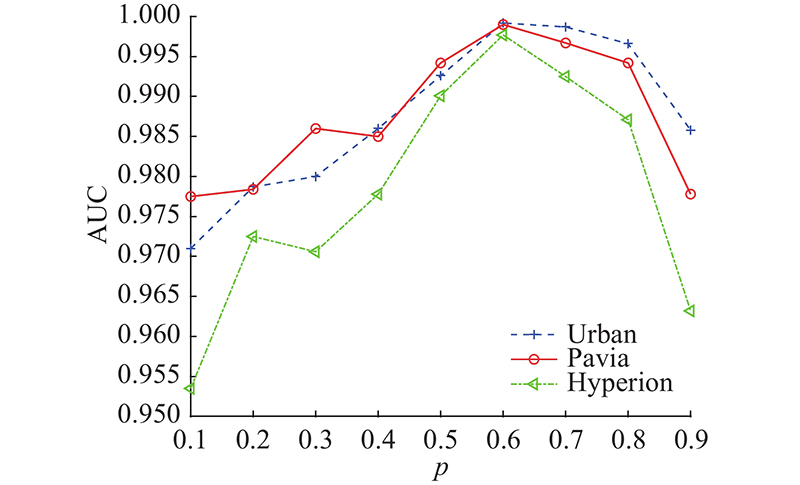
本文方法的参数主要有FrFT变换参数
图 6
当
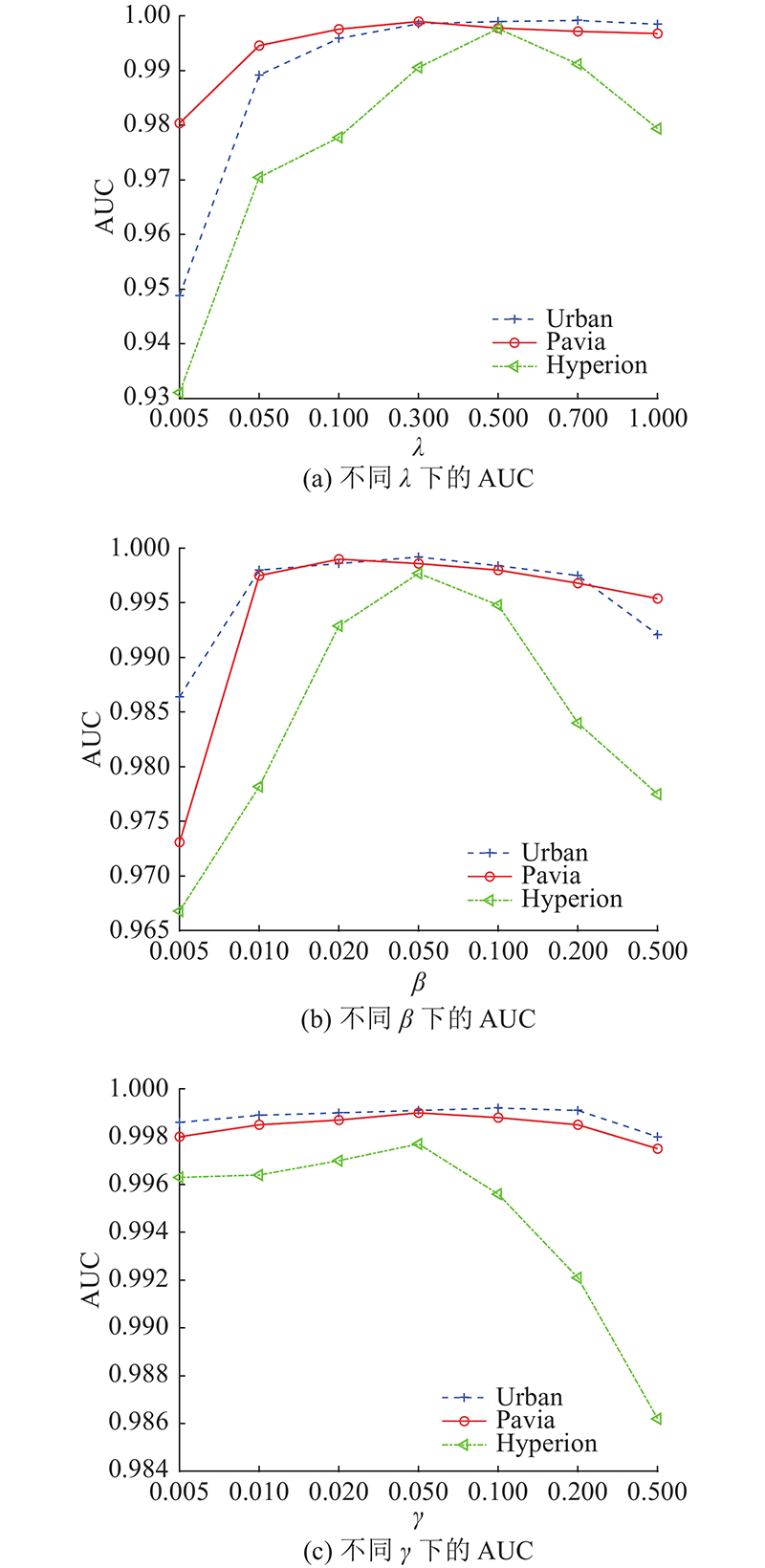
模型参数包括
图 7
3.3. 对比分析
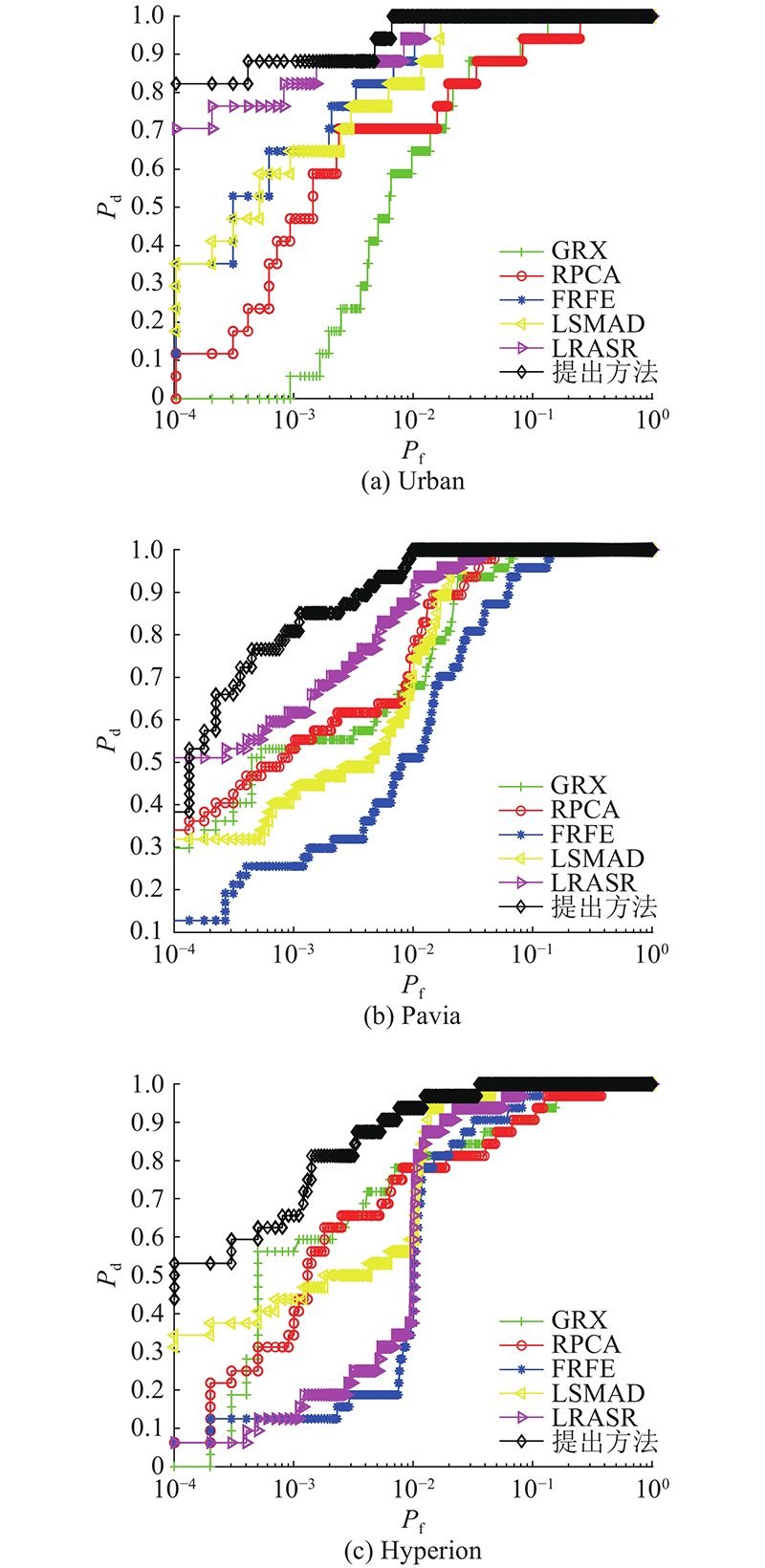
为了验证本文方法的异常检测效果,与5种经典算法GRX、RPCA、FRFE、LSMAD、LRASR进行对比. 其中,基于分数傅里叶熵的高光谱异常检测算法(fractional Fourier transform,FRFE)[19]在RX算法中引入FrFT变换,GRX是经典的RX系列算法,RPCA、LSMAD和LRASR属于稀疏表示类算法,具有较好的检测效果. 不同算法的定量评价指标采用ROC曲线(receiver operating characterstic,ROC)和ROC曲线下的面积AUC. 其中,ROC曲线越靠近左上方,表示检测效果越好. AUC越高,表示检测效果越好.
图 8
图 8 Urban数据集不同算法的异常检测图
Fig.8 Anomaly detection results of various detection algorithms in Urban dataset
图 9
图 9 Pavia数据集不同算法的异常检测图
Fig.9 Anomaly detection results of various detection algorithms in Pavia dataset
图 10
图 10 Hyperion数据集不同算法的异常检测图
Fig.10 Anomaly detection results of various detection algorithms in Hyperion dataset
表 1 不同算法在3个数据集上的AUC
Tab.1
| 数据集 | AUC | |||||
| GRX | RPCA | FRFE | LSMAD | LRASR | 提出方法 | |
| Urban | 0.9757 | 0.9798 | 0.9977 | 0.9955 | 0.9968 | 0.9992 |
| Pavia | 0.9907 | 0.9933 | 0.9775 | 0.9935 | 0.9966 | 0.9990 |
| Hyperion | 0.9741 | 0.9768 | 0.9828 | 0.9921 | 0.9880 | 0.9977 |
图 11
在3个数据集中,本文方法的AUC最高,分别是0.999 2、0.999 0和0.997 7. 对于Urban数据集和Hyperion数据集,ROC曲线处于左上角的位置,这表明本文方法在抑制背景与检测精度上均优于其他算法. 对于Pavia数据集,当虚警率约为
为了进一步表示算法的背景抑制效果和目标检测能力,引入
表 2
不同算法在3个数据集上的
Tab.2
| 数据集 | (Pf, η) | |||||
| GRX | RPCA | FRFE | LSMAD | LRASR | 本文方法 | |
| Urban | 0.0490 | 0.0219 | 0.0306 | 0.024 2 | 0.060 2 | 0.015 1 |
| Pavia | 0.0232 | 0.0061 | 0.0625 | 0.005 0 | 0.064 7 | 0.010 2 |
| Hyperion | 0.0402 | 0.0189 | 0.0141 | 0.010 7 | 0.066 1 | 0.012 3 |
表 3
不同算法在3个数据集上的
Tab.3
| 数据集 | (Pd, η) | |||||
| GRX | RPCA | FRFE | LSMAD | LRASR | 本文方法 | |
| Urban | 0.2949 | 0.2609 | 0.4432 | 0.3672 | 0.5072 | 0.5423 |
| Pavia | 0.1632 | 0.1081 | 0.1302 | 0.1292 | 0.2634 | 0.2937 |
| Hyperion | 0.1817 | 0.1408 | 0.1090 | 0.1828 | 0.3139 | 0.3305 |
综合而言,本文方法融合了FrFT变换和全变分正则化两者的优势,具有较高的检测率和较低的虚警率. 如表4所示为不同算法的运行时间tr. 由于利用图像的空间信息,算法的运行时间较长.
表 4 不同算法在3个数据集上的运行时间
Tab.4
| s | ||||||
| 数据集 | tr | |||||
| GRX | RPCA | FRFE | LSMAD | LRASR | 本文方法 | |
| Urban | 0.0627 | 3.6739 | 18.3643 | 9.3211 | 37.0203 | 148.9941 |
| Pavia | 0.0699 | 4.5899 | 17.6630 | 15.9884 | 150.7036 | 298.8545 |
| Hyperion | 0.0623 | 2.7474 | 16.4124 | 9.5605 | 37.5466 | 153.2101 |
4. 结 语
针对传统异常检测算法背景字典污染和空间信息利用不足而导致检测精度低的问题,本文提出基于FrFT变换和全变分正则化的异常检测算法. 利用FrFT变换能够有效地提取光谱维的时频域特征,在构造背景字典时有利于剔除潜在的异常原子,得到较纯净的背景字典. 将高光谱数据通过FrFT变换映射至中间域,在低秩稀疏模型中引入全变分正则化约束,以表示中间域内背景部分的空间平滑性,综合利用了图像的空谱信息. 通过交替方向乘子法,将模型求解转换成求解多个子问题的最优解,得到稀疏部分. 计算稀疏部分的范数,得到最终的检测结果. 通过定性和定量分析,本文算法在提高检测率和降低虚警率方面均取得了一定的效果. 由于联合空谱信息,算法的运行时间较长,在未来工作中,将进一步优化算法,在更多数据集上进行测试,提高算法的鲁棒性.
参考文献
Hyperspectral image restoration using low-rank representation on spectral difference image
[J].DOI:10.1109/LGRS.2017.2701805 [本文引用: 1]
Analysis and optimizations of global and local versions of the rx algorithm for anomaly detection in hyperspectral data
[J].DOI:10.1109/JSTARS.2013.2238609 [本文引用: 1]
Hyperspectral anomaly detection via background estimation and adaptive weighted sparse representation
[J].DOI:10.3390/rs10020272 [本文引用: 1]
Collaborative representation for hyperspectral anomaly detection
[J].
Joint reconstruction and anomaly detection from compressive hyperspectral images using mahalanobis distance-regularized tensor RPCA
[J].DOI:10.1109/TGRS.2017.2786718 [本文引用: 1]
Robust principal component analysis
[J].
Robust recovery of subspace structures by low-rank representation
[J].
Anomaly detection in hyperspectral images based on low-rank and sparse representation
[J].DOI:10.1109/TGRS.2016.2537152 [本文引用: 1]
Distributed optimization and statistical learning via the alternating direction method of multipliers
[J].DOI:10.1561/2200000016 [本文引用: 1]
Linearized alternating direction method with adaptive penalty for low-rank representation
[J].
Gaussian short-time fractional Fourier transform based detection algorithm of target with micro-motion at sea
[J].
An iterative regularization method for total variation-based image restoration
[J].DOI:10.1137/040605412 [本文引用: 1]
Hyperspectral anomaly detection based on low rank representation and learned dictionary
[J].DOI:10.3390/rs8040289 [本文引用: 1]
Total variation spatial regularization for sparse hyperspectral unmixing
[J].DOI:10.1109/TGRS.2012.2191590 [本文引用: 2]
基于低秩全变差正则化的高光谱异常检测方法
[J].DOI:10.3778/j.issn.1673-9418.2002003 [本文引用: 1]
Hyperspectral anomaly detection method based on low rank total variation regularization
[J].DOI:10.3778/j.issn.1673-9418.2002003 [本文引用: 1]
A singular value thresholding algorithm for matrix completion
[J].DOI:10.1137/080738970 [本文引用: 1]
Hyperspectral anomaly detection by fractional Fourier entropy
[J].DOI:10.1109/JSTARS.2019.2940278 [本文引用: 1]
3-D receiver operating characteristic analysis for hyperspectral image classification
[J].DOI:10.1109/TGRS.2020.2987137 [本文引用: 1]