路段自由流行程时间,指车辆以自由流速度从驶入路段上游到驶离下游交叉口所需的时间,期间不受其他车辆或交叉口信号的影响 [ 1] . 路段自由流行程时间是城市道路状态的基准参数,在服务水平、交通控制、交通状态评价等方面具有重要的作用. 为了获得估计路段自由流行程时间所需的车辆行程时间数据,传统的方法是在流量小、无信号灯影响的路段两侧架设检测器并进行人工校对 [ 1- 3] . 该方法的缺点在于设备架设成本高,数据采集耗时长. 为了更好地进行车辆监控、城市管理,中国许多城市布设了如车牌自动识别系统(automatic number plate recognition, ANPR)、蓝牙标签识别系统 [ 4- 6] 的新型检测系统,这为路段自由流行程时间估计提供了数据来源. 这些检测器通常安装在交叉口处,当车辆通过检测断面时,车辆ID、检测时刻、检测器定位等信息将被记录.
路段自由流行程时间估计方法可以分为3类:统计法、参数法和模型法. 在工程上统计法最常用. 例如,文献[ 7]将平均行程时间最小的前1/9平均值作为路段自由流行程时间. 分位值法 [ 8] 取足够长的行程时间数据由小到大排序,取其 k百分位数作为自由流行程时间(常取 k=5~20). 统计法基于经验,计算简便,但是没有理论基础,难以证明结果的准确性或科学性. 参数法假设行程时间服从包括正态分布 [ 9- 10] 、对数正态分布 [ 11] 、Weibull分布 [ 12] 、Γ分布 [ 13] 、广义Pareto分布、Halphen分布 [ 14] 、Burr分布 [ 10, 15] 、t-location分布 [ 10] 等在内的特定分布,利用数据拟合分布的参数,认为其中部分参数组成的分布为自由流行程时间分布以计算自由流行程时间 [ 16] . 参数法的假设来自经验观察,原理简单、算法成熟,但缺少对行程时间分布机理的深入分析. 同时,城市道路的行程时间分布与上下游信号控制策略相关,没有哪个分布能够符合所有交通情况,也就很难统一进行参数法的应用. 模型法结合交通流理论分析行程时间分布机理,得到行程时间分布的表达形式,以获得自由流行程时间. 例如,Olszewki [ 17] 假设交叉口服务率为常数、车流到达率服从确定分布,推导交叉口平均延误在每个周期的概率分布函数;Horváth等 [ 18] 基于交通波理论,用单个检测器数据推导实时排队长度和行程时间;Gao等 [ 19] 基于运动学理论和时空轨迹数据推导出信号配时、排队长度和车辆速度间的关系. 模型法有充足理论支撑,但通常基于严格的假设 [ 20] ,很难直接与实际交通数据结合,在不满足假设的城市道路间断流数据下难以应用. 城市道路车流受上游各进口道和下游出口道的相位与相位差因素影响,表现出随机性和脉冲性,若不进行前提假设,尚无方法能够获取符合实际、统一的行程时间分布解析表达式.
本研究结合参数法和模型法,提出数据重采样方法,该方法由车牌识别数据估计自由流行程时间,无需额外架设检测器或现场测算. 基于交通波理论和车辆均匀到达的假设,建立路段行程时间分布模型,将实际车牌识别数据转换为符合均匀流假设的行程时间数据,进行模型拟合. 从拟合得到的行程时间分布函数中提取相关参数,计算自由流行程时间. 验证实际数据,表明方法的准确性、科学性和实用性.
1. 城市路段行程时间分布模型
非饱和状态下城市道路的行程时间 y由自由流行程时间 y f和由信号引起的延误 d组成,记为
设 y的概率密度函数为 g( y), y f的概率密度函数为 φ( y f), d的概率密度函数为 h(d). 根据概率论知识,有如下关系:
分别对自由流行程时间和延误的概率分布建模,以获得路段行程时间分布函数.
1.1. 自由流行程时间分布
式中: α为形状参数, β为逆尺度参数. 根据Γ分布的性质,自由流行程时间的期望为
1.2. 延误分布
图 1
记受阻流在车流中占比为 η,则自由流占比为1– η. 有
受阻流的延误 d b服从均匀分布, d b~ U (0, R),有
自由流的延误 d f=0. 引入狄拉克 δ函数,函数
结合式(6)、(7),延误 d的概率密度函数为二者的加权和:
1.3. 行程时间分布
结合式(2)、(3)、(8),计算并化简 [ 23] ,得行程时间概率密度函数:
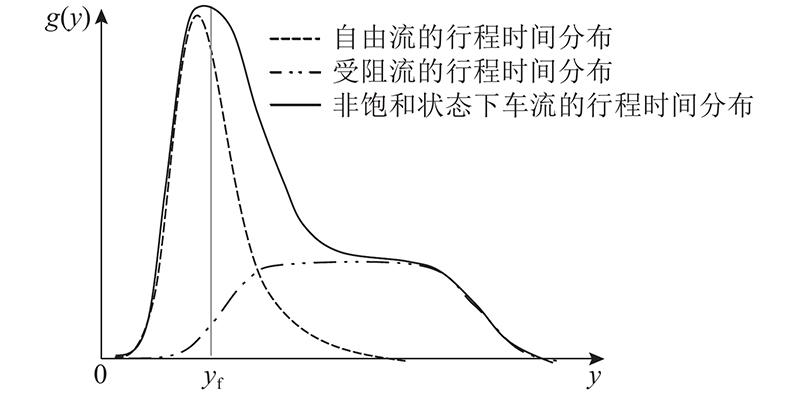
该函数的示意图如 图2所示.
图 2
图 2 非饱和状态下的行程时间概率密度函数
Fig.2 Probability density function of travel time in unsaturated condition
1.4. 自由流行程时间估计
对于下游信号配时已知的交叉口,推导得到的概率密度函数 g( y)包含3个待定参数:Γ分布参数的 α、 β,受阻流占比 η. 只要获得这3个参数的值,就可以根据式(4)计算出路段自由流行程时间. 本研究采用最小二乘法求解函数参数. 最小二乘法的目标是最小化误差的平方和:
式中: f( y j )为行程时间的真实分布, g( y j )为行程时间的理论分布, J为行程时间样本数.
由于待估参数较少且可行域很小,参数具备物理意义,可以使用网格搜索法进行拟合求解. 解得行程时间概率密度函数后,根据式(4)计算出对应自由流行程时间.
2. 均匀流行程时间数据生成
在行程时间分布模型中,均匀流假设体现为受阻流的延误服从均匀分布. 当车流满足均匀流假设时,只要取足够多个周期的车辆行程时间数据,就可以稳定地拟合参数. 现实车流受交叉口信号的影响,表现出随机性和脉冲性,因此均匀流假设失效. 本研究从数据的角度入手,采样小流量时段的数据,得到符合均匀流假设的车辆行程时间数据.
2.1. 行程时间数据
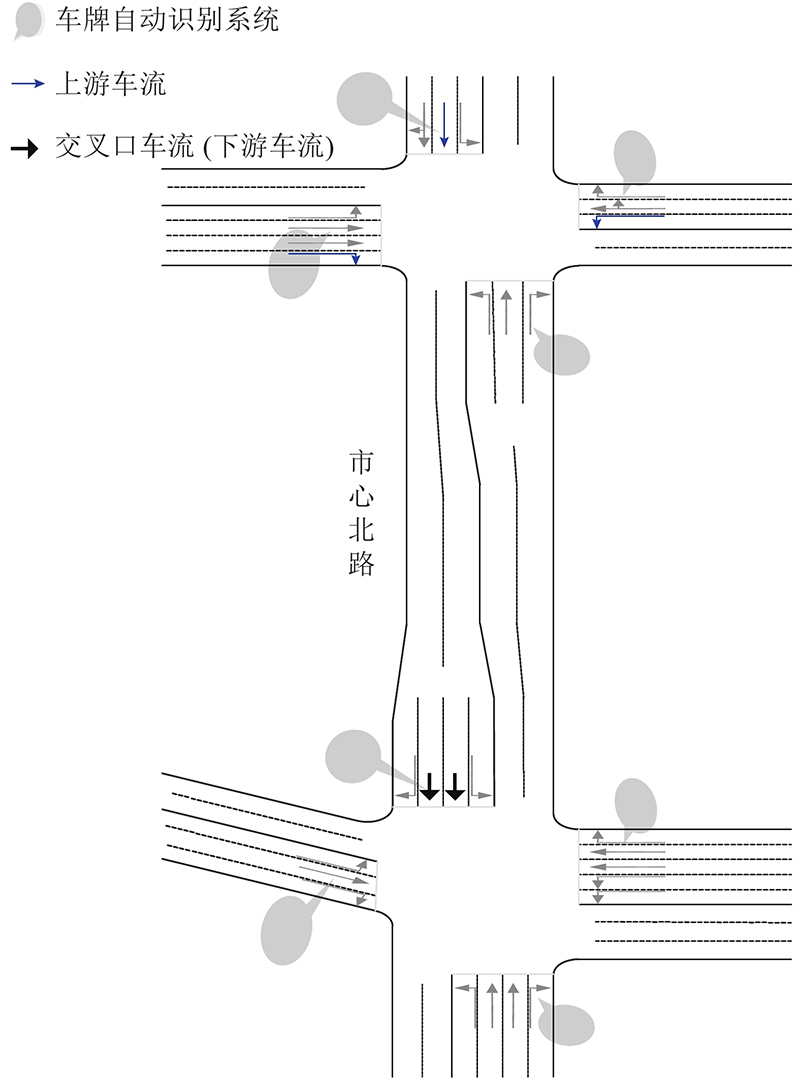
利用ANPR系统获得车辆行程时间信息. ANPR设备通常安装在交叉口或关键断面上,记录经过车辆的车牌ID、时间戳信息. 如 图3所示,当上、下游交叉口均安装ANPR设备时,即可获得通过该路段的车辆对应的行程时间数据集合
图 3
路段的行程时间主要受到下游交叉口信号的影响,以下游任意红灯开始时刻为0时刻,向后取整数倍周期时长作为研究时长 T,筛选0 ≤ t d ≤ T的行程时间数据.
2.2. 数据采样
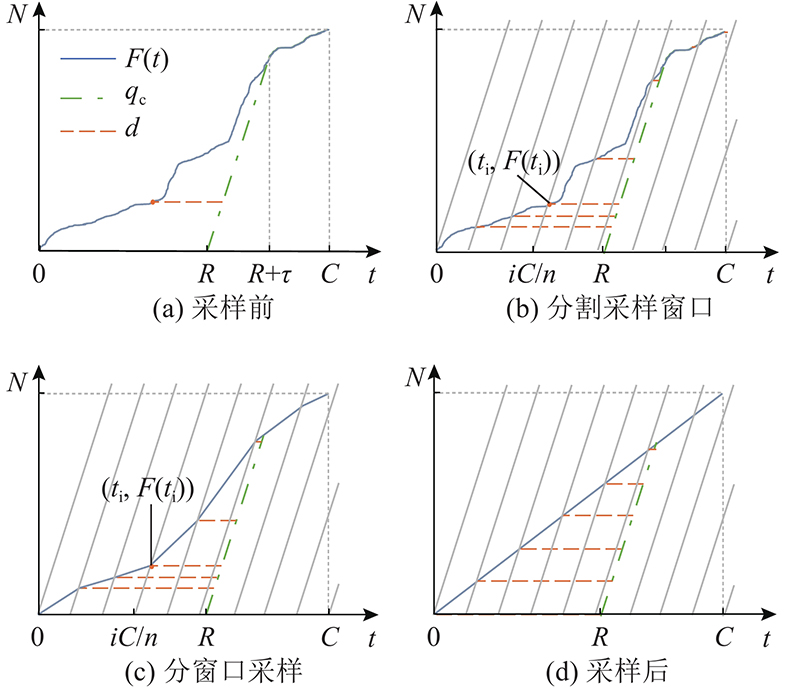
图 4
图 4 数据采样过程中车辆累积到达和释放情况
Fig.4 Accumulated arrival and release of vehicles in data sampling process
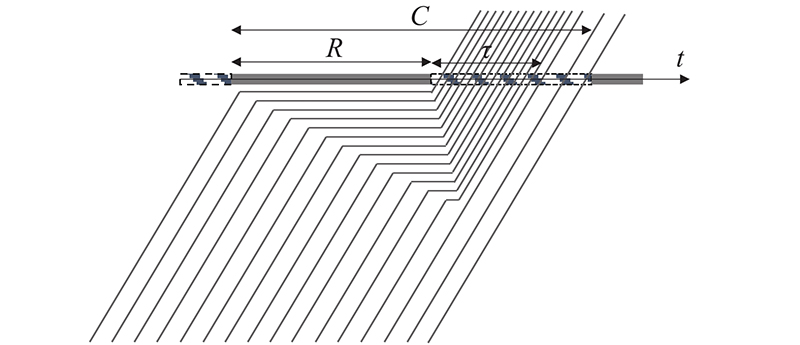
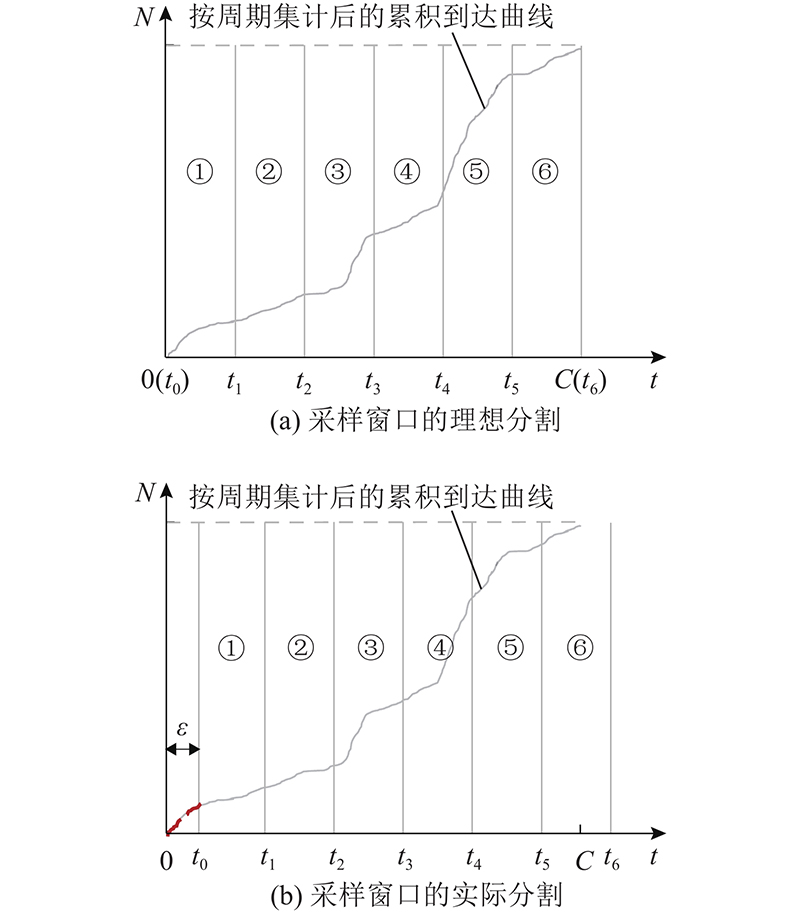
1)确定采样窗口. 将车流累积到达区间切分为 n个采样窗口,窗口的分割时刻由序列{ t 0, t 1, t 2,··· t k ,···, t n }表示,其中 t 0 = 0 < t k –1 < R+ τ ≤ t k (即受阻车辆在 t k 前全部通过停车线),该序列要满足特征: t 0, t 1, t 2,··· t k–1 时刻到达下游的车辆延误等差递减, t k 及其后时刻的车辆延误为0. 为此,将周期 C等分为 n个窗口. 在车辆累积到达和释放的 图4(b)中,第 i个分割点的坐标为( iC/ n,0), i=0,1,···, n. 在每个分割点处以 q c为斜率作下游饱和释放曲线的平行线,过分割点 i的斜线与到达曲线相交于点( t i , F( t i )),如 图4(b)所示. 当 iC< R时, t i 时刻对应的延误为 R– iC/ n;当 iC/ n ≥ R时, t i 时刻对应的延误为0. 序列{ t i | i=0,1,···, n}符合上述要求.
2.3. 小流量时段数据
计算窗口分割时刻序列是数据采样的重要步骤. 对于交点( t i , F( t i )),根据 图4(b)的几何关系,有
移项得
求解式(13)需要 F( t)的表达式. 常用做法是将上游交叉口释放曲线向右平移 y f,作为下游累积到达曲线. 本研究不适用该方法,为此,使用小流量时段的数据,实现在 y f未知的情况下求得 t i . 由于
为了满足小流量的要求,本研究提出使用夜间数据进行自由流行程时间估计. 夜间数据的优势在于,当车流密度接近于0,车辆的行驶速度几乎不受其他车辆的影响,路段上的非受阻流即为自由流. 相反地,日间车流量较大,车辆受到车流的影响难以达到自由流速度,非受阻流并非自由流.
2.4. 行程时间数据集计
夜间流量数据存在缺点:由于交通量过小,大多数采样窗口内没有车辆经过,给采样造成困难. 本研究提出行程时间数据集计方法,将多个周期同一采样窗口内的数据集计入1个窗口内进行采样.
用采样窗口分割车辆到达曲线,需要知道车辆veh i 到达下游停车线的时刻,
式中:
图 5
图 5 自由流行程时间取值对采样的影响分析
Fig.5 Influence of free flow travel time value on resampling
2.5. 行程时间数据采样步骤小结
行程时间采样方法的步骤可以归纳如下. 1)已知信号周期时长 C和红灯开始时刻,筛选行程时间数据;2)设置足够大的采样窗口个数 n,计算窗口分割时刻序列;3)取自由流行程时间 y f = 0,将行程时间数据集计到时间窗内;4)完成数据采样.
3. 案例分析
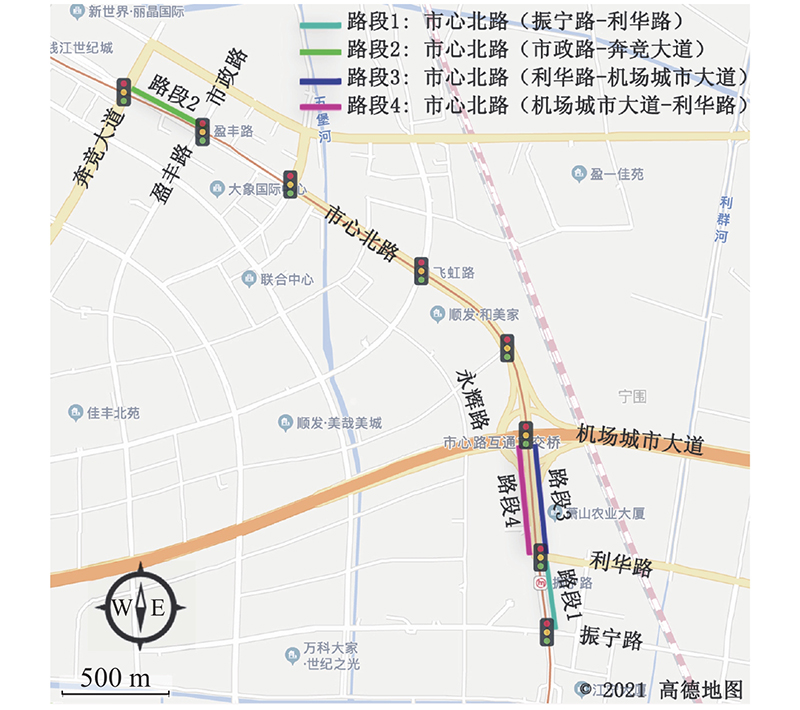
3.1. 数据描述
图 6
表 1 案例路段的信号控制参数及车牌识别数据量描述
Tab.1
| 路段编号 | L/m | C up/s | C/s | R/s | N |
| 1 | 353 | 120 | 120 | 70 | 2886 |
| 2 | 382 | 100 | 100 | 60 | 2470 |
| 3 | 539 | 120 | 100 | 60 | 2056 |
| 4 | 542 | 100 | 120 | 70 | 176 |
3.2. 行程时间数据采样
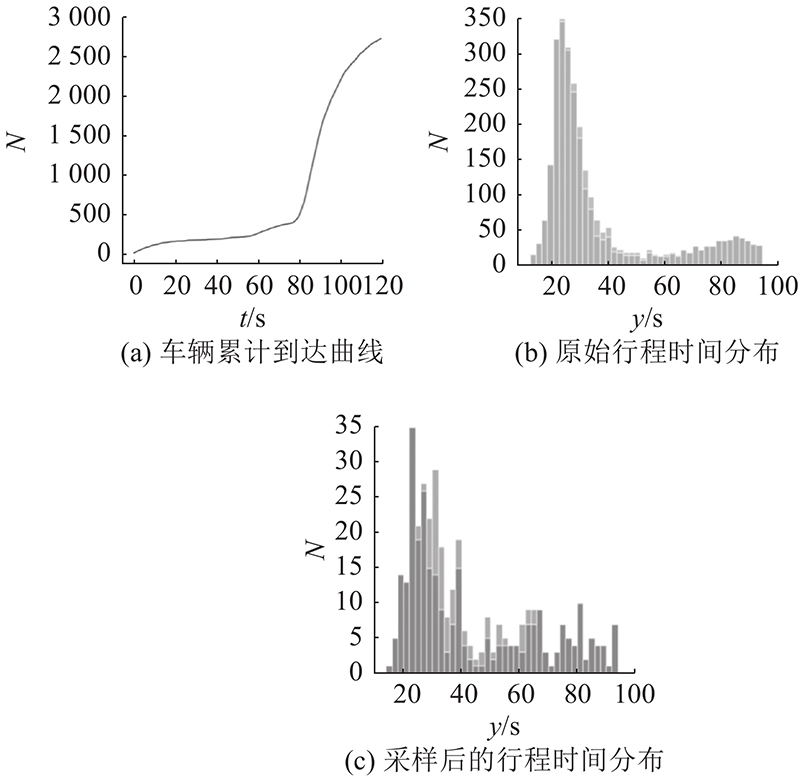
每个周期内的采样窗口越多,采样后的行程时间分布与理论分布越接近,但采样窗口过小会导致窗口内样本量过少. 经过多次试验,本研究取10 s作为窗口宽度. 对于每个集计后的窗口,随机抽取30个数据样本.
图 7
图 7 路段1行程时间数据重采样过程与结果展示
Fig.7 Resampling process and results of travel time data in link 1
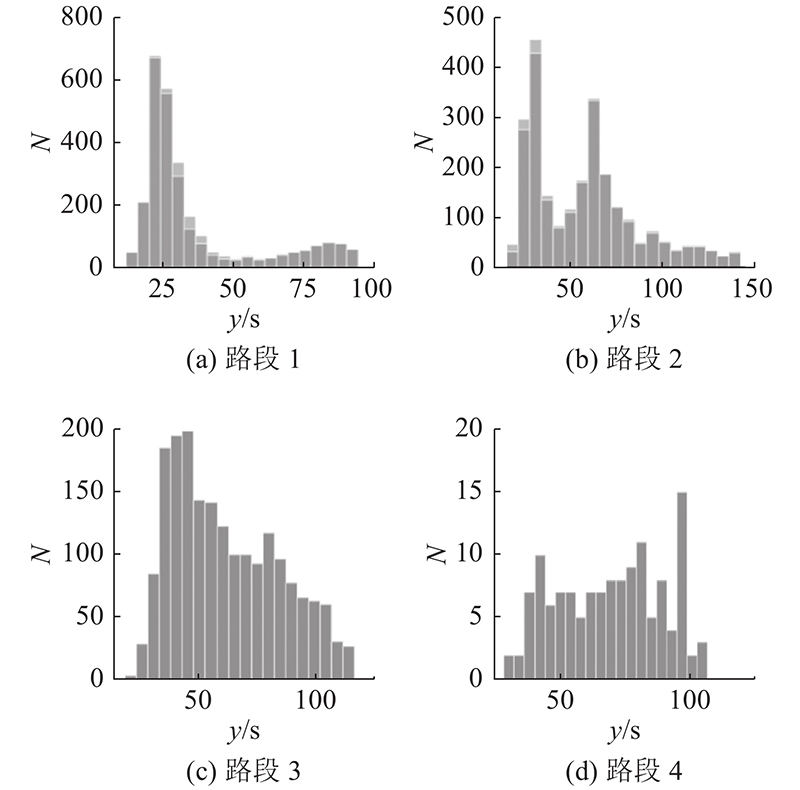
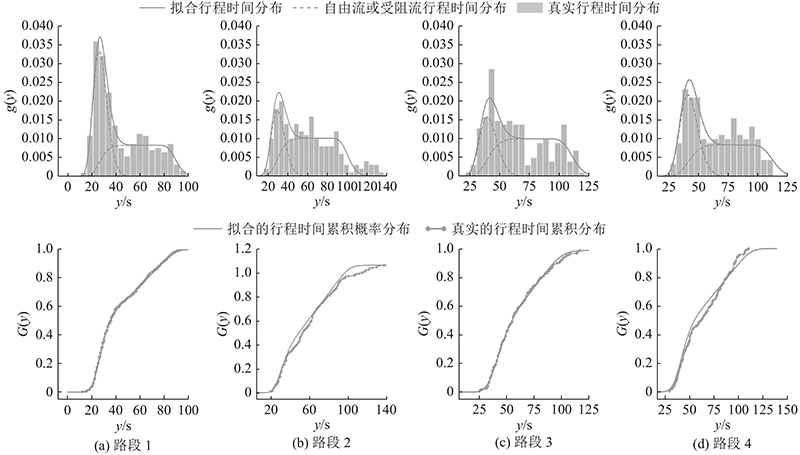
3.3. 自由流行程时间估计
共有3个参数须拟合:Γ分布参数的 α、 β,受阻流占比 η. 对于小流量时段的数据,受阻流全部通过停车线所需时长 τ近似为0, η用 R / C近似. 当信号参数已知时,待拟合参数简化为2个.
表 2 自由流行程时间拟合值
Tab.2
| 路段编号 | y/s | K-S p | 路段编号 | y/s | K-S p | |
| 1 | 26.0 | 0.84 | 3 | 40.5 | 0.83 | |
| 2 | 27.6 | 0.06 | 4 | 40.3 | 0.33 |
图 8
图 9
3.4. 方法对比
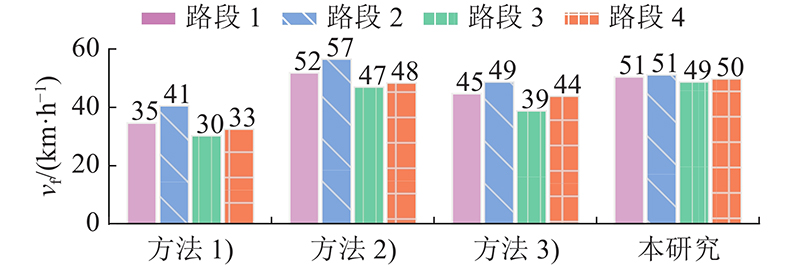
除适用性外,为了验证方法获得自由流行程时间的准确性,选用4个路段30 d(2019年6月1~30日)01:00~05:00的车牌识别数据,对比本研究提出的自由流行程时间估计方法与3种常用方法. 3种常用方法的步骤及参数设置如下. 1)局部均值法 [ 7] :(a)将6:00~24:00按照15 min时间窗等分;(b)计算每个时间窗平均行程速度的算术平均值,总样本天数应不少于30 d;(c)将计算出的平均值降序排序,取结果前1/9的平均值为路段自由流速度;(d)若获得的自由流速度大于路段限速,取限速为自由流速度. 2)分位值法 [ 8] :(a)取多日路段行程时间数据,按行程时间从小至大排序;(b)将 k百分位对应的行程时间作为自由流行程时间,本研究取 k=10. 3)参数法 [ 16] :(a)收集日间平峰期(11:00~16:00)行程时间数据;(b)使用混合分布拟合行程时间数据;(c)期望值较小的子分布作为自由流,取其期望值作为自由流行程时间. 本研究使用高斯混合分布,子分布数取2.
分别用方法1)~3)与本研究方法估计自由流行程时间,结果如 表3所示. 可以看出,方法1)的行程时间远大于其他方法. 这是因为该方法不加筛选地使用时间窗内的所有样本,其中必然包含部分受阻车辆,使得估计结果偏大. 方法2)、3)和本研究方法的自由流行程时间没有固定的顺序. 这是因为车流的行程时间分布受到信号的影响:当上、下游协调相位车流较大时,方法2)、3)得到的结果偏小;当协调效果较差或缺乏协调时,受阻车流比例增大,方法2)、3)得到的结果偏大.
表 3 自由流行程时间结果对比
Tab.3
| 路段 编号 | y f | |||
| 方法1) | 方法2) | 方法3) | 本研究 | |
| 1 | 36.71 | 24.5 | 28.41 | 26.59 |
| 2 | 33.93 | 24.33 | 28.29 | 28.54 |
| 3 | 64.34 | 41.29 | 50.15 | 41.70 |
| 4 | 59.97 | 40.29 | 44.59 | 40.12 |
为了进一步验证本研究方法的优势,对比各方法获得的路段自由流速度 v f. 方法2)的自由流速度等于路段长度除以自由流行程时间;方法1)的自由流速度由平均所取样本的速度得到;在方法3)中,根据各个子分布的相对大小筛选出属于自由流的车辆,计算各样本的速度并取平均 [ 16] ;本研究方法的自由流行程时间服从Γ分布 y f~Ga( α, β),自由流速度服从逆Γ分布 v f ~ invGa( α, L/ β),其期望为 L/( β( α–1)). 自由流速度对比如 图10所示. 本研究方法得到的自由流速度集中在50 km/h附近,方法1)的结果普遍偏小. 方法2)、3)的结果受信号策略影响,自由流速在39~57 km/h波动. 4条路段位于同一主干道路上,路况接近,应当具有相似的自由流速度,分析结果说明,相比于3种常用方法,本研究方法可以消除信号对车流的影响,估计的结果更加合理.
图 10
与3种常用方法相比,本研究提出用行程时间建模来估计自由流行程时间的方法:1)可以准确估计自由流行程时间,结果具备理论支撑;2)能够抵抗信号控制的影响,所获自由流速度为路段本身属性,与信号策略无关;3)拟合效果较好,证明本研究方法适用于不同数据条件的多个城市路段. 在实际工程中,可以根据不同应用场景选择不同的城市道路自由流行程时间计算方法. 如果需要较准确、可解释性强的自由流行程时间,可以采用本研究提出的方法.
4. 结 语
自由流行程时间作为交通状态、服务水平、信号控制等评价模型的基准参数,在城市交通管理中尤为重要. 本研究基于交通波理论和车辆均匀到达的假设,建立信号影响下的路段行程时间分布模型. 针对城市路网交通流的脉冲性和随机性,提出数据采样方法,从城市间断流数据中得到符合均匀流假设的行程时间数据. 使用最小二乘法拟合行程时间概率密度函数,分离出自由流和受阻流,估计路段自由流行程时间. 利用实际数据进行验证,并与3种常用方法对比. 结果表明,本研究的采样方法可以消除信号对车流的影响,在多个路段上都能得到稳定、合理的结果. 未来拟进一步扩大研究范围,在不同城市更多路段上进行拟合试验.
参考文献
城市快速路互通立交环形匝道自由流速度研究
[J].
Study on free speed of ring ramp on interchange of urban expressway
[J].
al. Queue length estimation for signalized intersections using license plate recognition data
[J].DOI:10.1109/MITS.2019.2919541 [本文引用: 1]
al. Lane-based saturation degree estimation for signalized intersections using travel time data
[J].
al. A novel vision-based framework for identifying dynamic vehicle loads on long-span bridges: a case study of Jiangyin bridge, China
[J].
网络行程时间可靠性评价方法与影响因素
[J].DOI:10.3969/j.issn.1671-1637.2018.04.014 [本文引用: 2]
al. Evaluation method and influence factors of network travel time reliability
[J].DOI:10.3969/j.issn.1671-1637.2018.04.014 [本文引用: 2]
al. Modeling distributions of travel time variability for bus operations
[J].DOI:10.1002/atr.1314 [本文引用: 1]
Finding most reliable paths on networks with correlated and shifted log–normal travel times
[J].DOI:10.1016/j.trb.2013.10.011 [本文引用: 1]
Using GPS data to gain insight into public transport travel time variability
[J].DOI:10.1061/(ASCE)TE.1943-5436.0000126 [本文引用: 1]
Arterial travel time forecast with streaming data: a hybrid approach of flow modeling and machine learning
[J].DOI:10.1016/j.trb.2012.03.006 [本文引用: 2]
Travel time statistical modeling with the Halphen distribution family
[J].DOI:10.1080/15472450.2017.1326115 [本文引用: 1]
al. A novel arterial travel time distribution estimation model and its application to energy/emissions estimation
[J].DOI:10.1080/15472450.2017.1365606 [本文引用: 3]
Modeling probability distribution of delay at signalized intersections
[J].DOI:10.1002/atr.5670280306 [本文引用: 1]
Real-time queue length estimation applying shockwave theory at urban signalized intersections
[J].
al. A novel relationship model between signal timing, queue length and travel speed
[J].DOI:10.1016/j.physa.2021.126331 [本文引用: 1]
al. Analysis of delay variability at isolated signalized intersections
[J].DOI:10.1631/jzus.A1300208 [本文引用: 1]
al. Estimating travel time distribution under different traffic conditions
[J].DOI:10.1016/j.trpro.2014.10.014 [本文引用: 1]