仿生计算算法是近年来兴起的一种智能技术，通过模拟动物群体的行为，为解决高维、非线性、多极值的复杂全局优化问题提供了有效的解决方案. 近些年来涌现了许多新兴的仿生计算算法,如蚁群算法^[1]、布谷鸟算法^[2]、蝙蝠算法^[3]、磷虾算法^[4]、蚁狮优化算法^[5]等. 蜻蜓算法（dragonfly algorithm, DA）是Seyedali^[6]提出的一种新型仿生计算算法. 其思想源于对蜻蜓群体生活的模拟，具有参数少、实现简单的优点，在彩色图像分割^[7]、特征提取^[8]、工程设计^[9]等方面取得了较好的效果. 同大多数仿生计算算法一样，蜻蜓算法存在收敛速度慢、收敛精度低的不足. 为了改进蜻蜓算法收敛精度低的不足，赵齐辉等^[10]提出基于差分进化的蜻蜓算法，在迭代后期通过对个体进行差分进化来增强种群的多样性，进而提高算法的收敛精度. 为了改进蜻蜓算法收敛速度的不足，林涛等^[11]提出基于精英策略与正弦余弦机制的蜻蜓算法，该算法通过精英机制来增强重权的初始化，使用正余弦机制加强蜻蜓之间的信息交流，在保证全局搜索的同时，加快蜻蜓算法的收敛速度. 为了解决蜻蜓算法容易陷入局部最优以及收敛精度低的不足，张水平等^[12]提出基于随机替换和混合变异的蜻蜓算法，该算法通过随机替换，来提高初始解的质量，通过混合变异来跳出局部最优，最终提高算法精度. 为了解决蜻蜓算法收敛速度慢，易陷入局部最优的不足，Zhong等^[13]提出风驱蜻蜓算法，将收敛速度快、全局搜索能力强的风力驱动优化算法与蜻蜓算法结合，以提高蜻蜓算法的收敛速度和收敛精度. 以上算法均在一定程度上提升了蜻蜓算法的收敛速度和收敛精度，但与其他仿生计算算法相比仍然存在收敛精度低、容易陷入局部收敛的不足.

本研究提出基于聚类和探测精英引导的蜻蜓算法（dragonfly algorithm based on clustering and detection elite guidance，CEDA）. 通过tent混沌映射^[14]生成初始种群，成功地解决了随机生成种群覆盖区域小的问题，使用K-means++^[15]聚类算法对种群质量进行分类，对不同质量的种类执行不同的学习策略，在增强种群多样性的同时，提升了种群初始解的质量；引入非线性因子来拟合蜻蜓觅食的飞行步长，加快蜻蜓向食物源聚集的速度；使用探测精英引导策略给予种群一个更好的移动方向，克服了蜻蜓算法易陷入局部最优陷阱的缺点；平方散列探测充分利用了每一维度信息，进一步提高算法的收敛精度.

蜻蜓算法受到理想状态下蜻蜓的狩猎和迁徙的启发. 蜻蜓的狩猎行为是指一小群蜻蜓在小范围内寻找食物源，对应于仿生计算算法的开发阶段. 蜻蜓的迁徙行为是指大量的蜻蜓在一个方向上长时间大跨度的飞行，对应于仿生计算算法的探索阶段. 蜻蜓的行为遵循分离、对齐、聚集、觅食和避敌的原则，因此蜻蜓群体中的个体位置更新主要依靠这5个因素.

分离（避免碰撞）表达式如下：

(1) $ {{\boldsymbol{S}}_i} = - \sum\limits_{j = 1}^N {\left( {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right)} . $

式中： ${{\boldsymbol{x}}_i}$表示当前个体位置， ${{\boldsymbol{x}}_j}$表示第j个相邻个体的位置，N为相邻个体的数量.

对齐（列队飞行）表达式如下：

(2) $ {{\boldsymbol{A}}_i} = \sum\nolimits_{j = 1}^N {{{\boldsymbol{V}}_j}} /N. $

式中： ${{\boldsymbol{V}}_j}$表示第j个相邻个体的飞行速度.

聚集行为表达式如下：

(3) $ {{\boldsymbol{C}}_i} = {{\displaystyle \sum\nolimits_{j = 1}^N {{{\boldsymbol{x}}_j}} }}/{N} - {{\boldsymbol{x}}_i}. $

觅食行为表达式如下：

(4) $ {{\boldsymbol{F}}_i} = {{\boldsymbol{x}}^{\text{ + }}} - {{\boldsymbol{x}}_i} . $

式中： $ {{\boldsymbol{x}}^{\text{ + }}} $表示食物源.

躲避天敌的表达式如下：

(5) $ {{\boldsymbol{E}}_i} = {{\boldsymbol{x}}^ - } + {{\boldsymbol{x}}_i} . $

式中： $ {{\boldsymbol{x}}^ - } $表示天敌位置.

蜻蜓算法认为蜻蜓的行为是这5种因素的结合，为了模拟蜻蜓的运动，蜻蜓个体步长更新公式如下：

(6) $ \Delta {{\boldsymbol{x}}_{t + 1}} = (s{{\boldsymbol{S}}_i} + a{{\boldsymbol{A}}_i} + c{{\boldsymbol{C}}_i} + f{{\boldsymbol{F}}_i} + e{{\boldsymbol{E}}_i}) + w\Delta {{\boldsymbol{x}}_t}. $

式中： $s$为分离权重， $a$为对齐权重， $c$为聚集权重， $f$为食物因子， $e$为天敌因子， $w$为惯性权重，t为迭代次数.

为了提高蜻蜓算法的全局搜索能力和收敛精度，蜻蜓的位置更新有2种方式.

当该个体周围存在邻近个体时，采用如下方式进行位置更新：

(7) $ {{\boldsymbol{x}}_{t + 1}} = {{\boldsymbol{x}}_t} + \Delta {{\boldsymbol{x}}_{t + 1}} . $

否则，采用如下方式：

(8) $ {{\boldsymbol{x}}_{t + 1}} = {{\boldsymbol{x}}_t} + {\text{Levy}}\;(d) \otimes {{\boldsymbol{x}}_t} . $

式中：d为位置向量的维数. ${\text{Levy}}$的表达式如下：

(9) $ {\text{Levy}}\;(x) = 0.01{{\boldsymbol{r}}_1}\sigma |{{\boldsymbol{r}}_2}{|^{ - {1 \mathord{\left/ {\vphantom {1 \beta }} \right. } \beta }}} . $

式中： $ {{\boldsymbol{r}}_1} $、 $ {{\boldsymbol{r}}_2} $为d维随机数， $ {{\boldsymbol{r}}_1} $、 $ {{\boldsymbol{r}}_2} $各维度的元素均为0~1.0； $\;\beta = 1.5$； $\sigma $为莱维飞行控制参数. $\sigma $的表达式如下：

(10) $ \left.\begin{aligned} &\sigma = {\left( {\frac{{\varGamma (1 + \beta ) \times \sin\; \left({{\pi \beta }}/{2}\right)}}{{\varGamma \left(\dfrac{{1 + \beta }}{2}\right) \times \beta \times {2^{({{\beta - 1}})/{2}}}}}} \right)^{{1}/{\beta }}}\text{，}\\ &\varGamma (1 + \beta ) = (\beta )!\varGamma \left(\frac{{1 + \beta }}{2}\right) = \left(\frac{{\beta - 1}}{2}\right)!. \end{aligned}\right\} $

根据上述分析，蜻蜓算法的伪代码如下.

算法1 蜻蜓算法伪代码

输入：目标函数 $f$

输出： ${{\boldsymbol{x}}^{\text{ + }}}$

//阶段1：初始化

1.初始化蜻蜓种群 $ {\boldsymbol{X}} = [{{\boldsymbol{x}}_1},{{\boldsymbol{x}}_2},{{\boldsymbol{x}}_3}, \cdots ,{{\boldsymbol{x}}_n}] $;

2.初始化步长 $\Delta {{\boldsymbol{x}}_i}(i = 1,2, \cdots ,n)$ ;

3.while$(t < T)\;{\bf{do}}$

//阶段2：更新参数

4.计算全部蜻蜓适应度;

5.更新食物源 ${{\boldsymbol{x}}^ + }$和敌人 ${{\boldsymbol{x}}^{{ - }}}$位置;

6.更新参数 $w、s、a、c、f、e$;

7.根据式(1)~(5)计算 ${\boldsymbol{S}}、{\boldsymbol{A}}、{\boldsymbol{C}}、{\boldsymbol{F}}、{\boldsymbol{E}}$;

8.更新相邻半径 $r = \left( {{{l_{\rm{u}} - l_{\rm{b}}}}} \right) /4+ ({{l_{\rm{u}} - l_{\rm{b}}}}){t}/{T}$ ;

// ${l_{\rm{u}}}、{l_{\rm{b}}}$分别为某一维度变化的上下界

//阶段3：更新蜻蜓个体位置

9. if （neighboring dragonfly $\geqslant $1）

10. $\Delta {{\boldsymbol{x}}_{t + 1}} = (s{{\boldsymbol{S}}_i} + a{{\boldsymbol{A}}_i} + c{{\boldsymbol{C}}_i} + f{{\boldsymbol{F}}_i} + e{{\boldsymbol{E}}_i}) + w\Delta {{\boldsymbol{x}}_t}$;

11. $ {{\boldsymbol{x}}_{t + 1}} = {{\boldsymbol{x}}_t} + \Delta {{\boldsymbol{x}}_{t + 1}} $;

12.else

13. ${{\boldsymbol{x}}_{t + 1}} = {{\boldsymbol{x}}_t} + {\text{Levy}}\;(d) \otimes {{\boldsymbol{x}}_t}$;

14. end if

15.对${{\boldsymbol{x}}_i}(i = 1,2, \cdots ,n)$进行越界检测;

16. end while

17.return ${{\boldsymbol{x}}^{\text{ + }}}$;

针对基本蜻蜓算法存在的收敛速度慢、收敛精度低、易陷入局部最优解等现象，提出基于聚类和探测精英引导的蜻蜓优化算法，该算法从4个不同方面对基本蜻蜓算法进行改进. 1）通过tent混沌映射，使种群初始化分布均匀，之后对种群进行聚类，对不同的类别分别进行反向学习和变异处理，丰富种群的多样性. 2）改进非线性自适应因子，加快收敛速度，提高收敛精度. 3）采用探测精英引导的机制，帮助个体跳出局部最优. 4）引入平方散列探测来充分利用每一维度信息，提高收敛精度. 通过这4种改进方式从整体上提高算法的寻优性能.

对仿生计算来说，初始种群的质量直接影响收敛速度和收敛精度^[16]，然而基本的蜻蜓算法使用随机生成的方式生成初始化种群，存在生成种群随机性大、覆盖区域小、算法初期收敛速度慢的问题. 混沌运动具有遍历性和随机性的特点^[17]，目前已经广泛应用于各种仿生计算. 常见的混沌映射主要有Logistics映射^[18]和Tent混沌映射，而相关研究^[19]表明Tent混沌映射相比Logistics映射有更加均匀的概率密度以及更快的收敛速度.

因此，本研究使用Tent混沌映射生成初始种群 ${\boldsymbol{X}}$. 聚类算法^[20]不关心所划分的每一类是什么，只是将相似的个体聚为一类，聚类算法通过迭代更新质心 ${{\boldsymbol{C}}_l}$，将不同个体划分到不同的类别，使类内的每一个体间相似度最大，使不同类别的类间相似度最小. 相似度由平方误差 $E$衡量， $E$越小表示类内个体的相似度越大.

(11) $ {{\boldsymbol{x}}_{n + 1}} = \left\{ \begin{gathered} 2{{\boldsymbol{x}}_n},\quad\quad{{0}} \leqslant |{{{{\boldsymbol{x}}}}_n}| \leqslant {{\alpha }}, \;{{\alpha}} \in [{{0}},{{1.0}}];\hfill \\ 2({\boldsymbol{1}} - {{\boldsymbol{x}}_n}),\;{{\alpha}} \leqslant |{{{{\boldsymbol{x}}}}_n}| \leqslant {{1.0}},\;{{\alpha}} \in [{{0}},{{1.0}}]. \hfill \\ \end{gathered} \right. $

(12) $ {{\boldsymbol{C}}_l} = \frac{1}{{\left| {{\rm{class}}\_l} \right|}}\sum\limits_{{\boldsymbol{x}} \in {{{\rm{class}}}}\_l} {\boldsymbol{x}} , $

(13) $ E = \sum\nolimits_{{{l}} = 1}^k {\sum\limits_{{\boldsymbol{x}} \in {\rm{class}}\_l} {{{\left\| {{\boldsymbol{x}} - {{\boldsymbol{C}}_l}} \right\|}_2}} } . $

由于K-means聚类方法须人工选取初始质心，而质心的好坏又会影响到聚类的效果，本研究使用可以按照概率 $ P(x) $来自主选择质心的K-means++聚类方法对种群进行聚类，并将种群分为3类. K-means++聚类方法使用启发式方法找到聚类的质心，减少了人工的干预，可以使聚类效果更接近真实分布情况. K-means++聚类方法的伪代码如下.

算法2 K-means++伪代码

输入：蜻蜓种群 ${\boldsymbol{X}}$，分类个数 $k$;

输出： ${\text{class\_1,class\_2,}} \cdots ,{\text{class\_}k}$

//阶段1：计算k个聚类质心

1. ${\boldsymbol{X}}$中随机选取一个蜻蜓的位置 ${{\boldsymbol{C}}_{{l}}}$ $(l = 1,2, \cdots ,k)$作为第1个初始聚类质心;

2. for l=1 to k do

3. ${{D}}({{\boldsymbol{x}}_i}) = {\left[ { \sum\nolimits_{j = 1}^{d} {{{({{{x}}_{i,j}} - {{{C}}_{l,j}})}^2}} } \right]^{1/2}}$ $(i = 1,2, \cdots ,n)$，x_i,j为第i只蜻蜓的第j维元素，C_l,j为第l个质心的第j维元素;

4. $P({{\boldsymbol{x}}_i}) = {{{{D}}{{({{\boldsymbol{x}}_i})}^2}}}/{{ \sum\nolimits_{i = 1}^n {{{D}}{{({{\boldsymbol{x}}_i})}^2}} }},$ $ P({{\boldsymbol{x}}_i}) $表示 $ {{\boldsymbol{x}}_i} $被选为下一个聚类质心的概率;

4. $P({{\boldsymbol{C}}_l}) = \max\;\left\{ {P({{\boldsymbol{x}}_1}),P({{\boldsymbol{x}}_2}), \cdots, P({{\boldsymbol{x}}_n})} \right\}$，对应的C_l为所选质心;

5. end for

//阶段2：使用K-means进行聚类

6. while (达到最大迭代次数)do

7. for $i = 1$to $n$do

8. for $l = 1$to $k$do

//计算 ${{\boldsymbol{x}}_i}$与 ${{\boldsymbol{C}}_l}$之间距离

9. $ {\text{distance}} = {\left\| {{{\boldsymbol{x}}_i} - {{\boldsymbol{C}}_l}} \right\|_2} $;

10. end for

11. 将样本 ${{\boldsymbol{x}}_i}$与它距离最近的质心 ${{\boldsymbol{C}}_l}$归为 ${{{\rm{class}}\_l}}$类;

12. end for

13. for $l = 1$to $k$do

14. ${{\boldsymbol{C}}_l} = \frac{1}{{\left| {{\text{class\_}}l} \right|}}\sum\limits_{{\boldsymbol{x}} \in {\text{class\_}}l} {\boldsymbol{x}}$ ;

15. end for

16. end while

17. return ${\text{class\_1,class\_2,}} \cdots ,{\text{class\_}}k$ ;

自然界存在优胜劣汰的制度，因此每一代的动物群体中都存在优秀群体、精英群体、劣质群体，本研究使用K-means++聚类算法将种群分为3类. 计算每一类群体的平均适应度，将适应度最低的一类作为精英群体，适应度最高的一类作为劣质群体，其余的为普通群体. 由于精英群体和劣质群体包含更多有效的生物信息，对精英群体和劣质群体使用反向学习机制^[21]. 普通群体含有的有用信息较少，为了增加种群的多样性获取更多的有用信息，对这一群体进行高斯变异处理^[22]，生成群体 ${{\boldsymbol{X}}_2}$，之后将 ${\boldsymbol{X}}$与 ${{\boldsymbol{X}}_2}$合并成为一个新的种群.

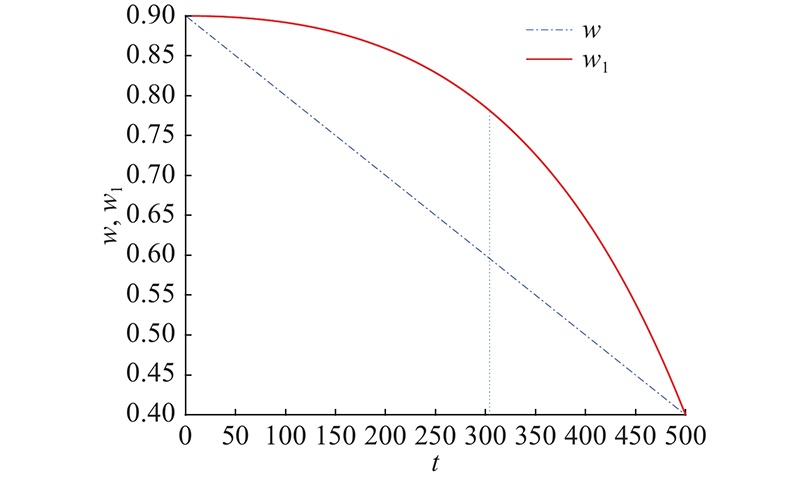
在初始DA中参数 $w$作为飞行步长的调节因子用于调控算法的全局搜索和局部开发能力， $W$在迭代过程中呈线性递减，不能较好地契合蜻蜓前期广泛探索食物、后期加速聚集在一起分享食物的这一自然特性. 因此，本研究提出改进的非线性自适应参数因子 ${w_1}$^[23]：

(14) $ {w_1} = 0.9 - \frac{1}{2}{\left( {\frac{{{{\rm{e}}^{{t}/{T}}} - 1}}{{{\rm{e}} - 1}}} \right)^2}. $

式中：T为最大迭代次数，t为当前迭代次数.

${w_1}$在迭代前期数值较大时能够有较强的跳出局部最优的能力，并且前期 ${w_1}$的下降速度慢，可以增加算法的全局搜索能力，后期下降速度逐渐加快，提高收敛速度. 原始 $w$与改进后的 ${w_1}$的对比如图1所示. 可以看出， ${w_1}$前期数值较大且下降平缓，使得算法有较强的跳出局部最优的能力；后期下降速度快，有利于提高收敛速度.

在原始的蜻蜓算法中，蜻蜓种群的每一次迭代都没有使用上一代的信息. 本研究在精英引导机制^[24]的基础上引入探测精英引导机制，加强每一代种群的信息交流，引领蜻蜓个体快速找到食物，加快收敛速度，提高收敛精度，帮助个体跳出局部最优. 探测精英引导机制分为2个阶段，第1阶段为探测精英阶段，探测精英 ${{{\boldsymbol{x}}}}'$可能存在的地方，并且利用贪心选择策略选择最优的探测精英 ${{{\boldsymbol{x}}}}'$，精英探测算法伪代码如下.

算法3 探测精英算法伪代码

输入：上代最佳个体 ${{\boldsymbol{x}}^{{{\text{1}}}{{*}}}}$，当代最佳个体 ${{\boldsymbol{x}}^{{{\text{2}}}{{*}}}}$

输出：精英引导下的步长 $\Delta {\boldsymbol{x}}_{t + 1}^{{\rm{PE}}}$

//阶段1：探测精英位置

1. 半径 $r = {{\left| {{{\boldsymbol{x}}^{{{\text{2}}}{{*}}}}{{ - }}{{\boldsymbol{x}}^{{{\text{1}}}{{*}}}}} \right|}}/{2} \;$ // $ r $为预测 ${\boldsymbol{x}}'$的半径

2. ${\bf{temp = }}{{\boldsymbol{x}}^{{{\text{2}}}{{*}}}}$

3. for $i = 1$ to $L$do //$L$用来调控预测层数

4. ${\text{p\_r}} ={i}/{L}$

5. ${\boldsymbol{x}}{{' = }}{{\boldsymbol{x}}^{{\text{2}}*}} + {\text{p\_r}}\times r\times {\bf{rand}}$

6. if ${\text{fobj(}}{\boldsymbol{x}}{{') < {\rm{fobj}}({\bf{temp}})}}$do

7. ${\bf{temp = }}{\boldsymbol{x}}{{'}}$

8. end if

9. end for

10. if ${{{\rm{fobj}}({\bf{temp}}) < {\rm{fobj}}(}}{{\boldsymbol{x}}^{{\text{2}}*}})$

11. ${\boldsymbol{x}}{{' = {\bf{temp}}}}$

12. end if

//阶段2：计算精英引导的步长

13. $\Delta {\boldsymbol{x}}^{\rm{PE}} = a({\boldsymbol{x}}{{'}} - {{\boldsymbol{x}}_i}){\left[ {\sum\nolimits_{j = 1}^{d} {{{({\boldsymbol{x}}{'_j} - {{\boldsymbol{x}}_{ij}})}^2}} } \right]^{ - 1/2}}$

14. return $\Delta {\boldsymbol{x}}^{{\rm{PE}}}$

第2阶段为引导机制，即在探测得到精英后，由探测精英来引导其他个体的步长更新方向. 每个蜻蜓个体的步长更新过程的表达式如下：

(15) $ \Delta {\boldsymbol{x}}^{\rm{PE}} = a \times \frac{{({\boldsymbol{x}}{{'}} - {{\boldsymbol{x}}_i})}}{{\sqrt {\displaystyle \sum\nolimits_{j = 1}^{d} {{{({\boldsymbol{x}}{'_j} - {{\boldsymbol{x}}_{ij}})}^2}} } }}, $

(16) $ {{\boldsymbol{x}}_{t + 1}} = {{\boldsymbol{x}}_t} + \Delta {{\boldsymbol{x}}_{t + 1}} + {{\Delta}}{{{{\boldsymbol{x}}}}_{{{t + 1}}}^{\rm{PE}}} . $

式中： $ {{\boldsymbol{x}}_t} $为当前个体位置，a∈(0，1.0).

探测精英引导机制的示意图如图2所示. 图中， ${{\boldsymbol{x}}^{{{\text{1}}}{{*}}}}$为上一代最佳个体， ${{\boldsymbol{x}}^{{{\text{2}}}{{*}}}}$为当前最佳个体， ${\boldsymbol{x}}{{'}}$为全局最佳个体预测位置， ${\boldsymbol{x}}{{'}}$在以 ${{\boldsymbol{x}}^{{{\text{2}}}{{*}}}}$为形心，半径 $r = {{\left| {{{\boldsymbol{x}}^{{{\text{2}}}{{*}}}} - {{\boldsymbol{x}}^{{{\text{1}}}{{*}}}}} \right|}}/{2}$的范围内逐层随机产生. 在预测出精英个体 ${\boldsymbol{x}}{{'}}$之后用式（15）计算 ${{\Delta}}{{{\boldsymbol{x}}}_{{{t + 1}}}^{\rm{PE}}}$. $a $用于调节引导步长的变化， $ a $前期数值较大，有利于全局搜索，中期快速下降有利于收敛，后期下降缓慢可以加强局部搜索的能力.

在蜻蜓算法的搜索过程中，原始蜻蜓算法在个体全部维度都更新后，才对个体进行适应度评估. 由于个体的每一维度都包含不同的信息，每一维度的改变都会影响个体的适应度. 因此该适应度评估的更新方式忽略了某一维度对个体的影响. 为了使算法充分地利用每一维度的信息. 本研究结合逐维更新策略^[25]和纵横交叉算法^[26]来对蜻蜓个体位置进行位置更新：

(17) $ {{{x}}}_{ij}=\left\{\begin{array}{l}{{{x}}}_{iK},\quad 适应度提升\text{；}\\ {{{x}}}_{ij},\quad 其他.\end{array}\right. $

式中： $ {{{x}}_{iK}} $表示第i个个体的第K维的元素， $K = j + {2^n}\times $ $ \boldsymbolod (d)-1$且 ${2^n} \leqslant d $. 当某一维度更新后没有使整体适应度更优时，使用平方散列探测替换方式（式（17））对当前更新维度进行修正. 当某一维度的改变使该个体适应度有所提升时即停止探测. 平方散列探测替换策略示意图如图3所示.

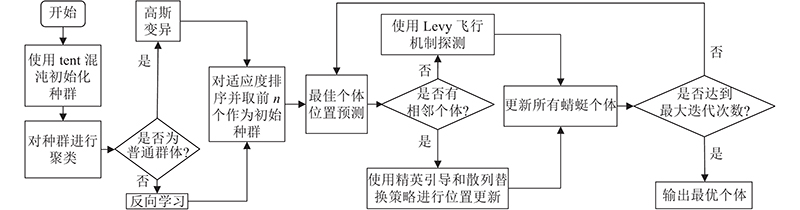
对标准的DA算法进行上述改进后，得到的CEDA算法伪代码如下. 其流程图如图4所示.

算法4 CEDA算法伪代码

输入：目标函数 $f$

输出： ${{\boldsymbol{x}}^{\text{ + }}}$

//阶段1：初始化

1. 基于聚类的初始化蜻蜓种群 ${\boldsymbol{X}}$;

2. 初始化步长 $\Delta {{\boldsymbol{x}}_i}(i = 1,2, \cdots ,n)$ ;

3. while $(t < T)$ do

//阶段2：更新参数

4. 计算全部蜻蜓适应度;

5. 更新食物源 ${{\boldsymbol{x}}^{\text{ + }}}$和敌人 ${{\boldsymbol{x}}^{{ - }}}$位置;

6. 更新参数 $w、s、a、c、f、e$;

7. 根据式(1)~(5)计算 ${\boldsymbol{S}}、{\boldsymbol{A}}、{\boldsymbol{C}}、{\boldsymbol{F}}、{\boldsymbol{E}}$;

8. 更新相邻半径 $r =({{{{l_{\rm{u}} - l_{\rm{b}}}}}})/{4} + ({{l_{\rm{u}} - l_{\rm{b}}}})\;{t}/{T}$ ;

//阶段3：更新蜻蜓个体位置

9. if （neighboring dragonfly $\geqslant $1）

//引入改进的 ${w_1}$

10. $\Delta {{\boldsymbol{x}}_{t + 1}} = (s{{\boldsymbol{S}}_i} + a{{\boldsymbol{A}}_i} + c{{\boldsymbol{C}}_i} + f{{\boldsymbol{F}}_i} + e{{\boldsymbol{E}}_i}) + {w_1}\Delta {{\boldsymbol{x}}_t}$

//引入探测精英引导的步长 $\Delta {{\boldsymbol{x}}_{t + 1}^{\rm{PE}}}$

11. ${{\boldsymbol{x}}_{t + 1}} = {{\boldsymbol{x}}_t} + \Delta {{\boldsymbol{x}}_{t + 1}} + \Delta {{\boldsymbol{x}}_{t + 1}^{\rm{PE}}}$;

12. if $ {\text{fobj}}({{\boldsymbol{x}}_{t + 1}}) > {\text{fobj}}({{\boldsymbol{x}}_t}) $

13. 使用平方散列探测替换策略对 $ {{\boldsymbol{x}}_{t + 1}} $进行更新;

14. end if

15. else

16. ${{\boldsymbol{x}}_{t + 1}} = {{\boldsymbol{x}}_t} + {\text{Levy}}\;(d) \otimes {{\boldsymbol{x}}_t}$;

17. end if

18. 越界检测;

19. end while

20. return ${{\boldsymbol{x}}^{\text{ + }}}$;

本仿真实验在intel(R)Core(TM)i5-8400CPU@2.80 GHz 16 GB内存Matlab2019a条件下实现. 为了检测算法的有效性，从文献[6]中挑选了8个典型的复杂函数进行仿真实验，8个典型的复杂函数如表1所示，其中f₁~f₃为单峰函数可以测试算法的局部搜索能力，f₄~f₈为多峰值函数可以测试算法跳出局部收敛，寻找全局最优的能力. 对CEDA、DA、灰狼优化算法^[27] （grey wolf algorithm, GWO）、果蝇优化算法^[28]（fruit fly optimization algorithm, FOA）、差分进化算法^[29]（differential evolution，DE）、人工蜂群算法^[30]（artificial bee colony，ABC）、粒子群算法^[31]、（particle swarm optimization，PSO）进行对比. 为了确保对比实验的准确性，算法参数统一设置如下：最大迭代次数Max_iter=500，种群规模N=40. 为了避免实验的偶然性，每一种算法都进行了2 000次独立实验，并计算其最优值、平均值、标准差，结果如表2所示. 最优值 ${X_{{\rm{best}}}} = \min\; \left\{ {{X_{{\rm{best}}\_1}},{X_{{\rm{best}}\_2}},\cdots,{X_{{\rm{best}}\_i}}} \right\}$, ${X_{{\rm{best}}\_i}}$为第i次独立运行时算法达到的最优解；平均值 ${X_{{\rm{mean}}}} = \dfrac{1}{n}\displaystyle \sum\nolimits_{i = 1}^n {{X_{{\rm{best}}\_i}}}$，其中n=2 000，是多次运行的平均情况，值越小越好；标准差 $\sigma =\bigg[ \dfrac{1}{n}\displaystyle\sum\nolimits_{i=1}^{n}{\left( {{X}_{{\rm{best}}\_i}}- \right.} \bigg.$ ${{\bigg. \Big. {{X}_{{\rm{mean}}}} \Big)^2 \bigg]}^{1/2}}$则用来衡量数据的离散程度，可以度量算法的稳定性.

由表2可知，对于f₁~f₃单峰函数，CEDA算法均优于其他算法，并且在f₃函数中收敛到了理论最优值0，表明CEDA算法与其他算法相比有更好的全局搜索能力. 由表3可知，对于多峰函数f₄~f₈，CEDA算法不仅在f₄、f₆的函数中收敛到了理论最优值，而且在其他函数中的收敛精度也优于其他算法的. 除此之外，在f₁~f₄、f₆~f₈这7个测试函数中，CEDA算法的标准差与DA算法、GWO算法、FOA算法、DE算法、ABC算法、PSO算法相比均是最小的，表明CEDA算法比其他算法具有更好的稳定性.

为了更加直观地对比7种算法之间的优劣性，进一步证明CEDA在收敛性上的提升，对比7种算法在8个测试函数上的收敛曲线，如图5所示. 图中，t表示算法的迭代次数；F为适应度，代表算法每次迭代得到的最佳值. 可以看出，对于单峰函数f_１，DA算法和FOA算法均陷入局部最优即收敛曲线平缓不能够继续探索函数的理论最优值，GWO算法没有陷入局部最优，但是与CEDA算法相比，GWO后期收敛缓慢无法获得更优的收敛精度，DE算法虽未陷入局部最优但是收敛速度缓慢远低于CEDA算法. CEDA算法改进了线性收敛因子，加快了收敛的速度，引入了平方散列探测替换，充分利用了每一维度所包含的信息提高了收敛的精度. 对于多峰函数f₄~f₈，DA、FOA、ABC算法在收敛时均陷入了局部最优无法跳出，而CEDA曲线有多次大幅波动的情况，说明在精英探测引导策略下的CEDA算法，能更好地跳出布局收敛. 由函数f₂、f₆~f₈可知，由于CEDA算法在初始化种群时使用了K-means++算法，并根据不同类别进行了反向学习和高斯变异方法获得了高质量的初始化种群，相比DA算法，在迭代初始时就有更好的起点.

原始的蜻蜓算法所有个体都使用相同的搜索模式，导致种群多样性差和过早收敛. 本研究使用无监督学习的聚类分析，将蜻蜓个体划分为不同的类别，根据所划分类别的质量，分别执行不同的学习策略丰富种群的多样性. 同时提出探测精英引导策略，使用2代的最佳个体来预测下一代最佳个体可能出现的位置，并以此位置来引导其余蜻蜓个体，使得群体快速迁移至最佳位置，加快算法的收敛速度. 最后提出了平方散列探测替换策略，对蜻蜓个体每一维度的变化进行贪心选择，充分利用蜻蜓个体每一维度所包含的信息，以此来提升算法的收敛精度.

本研究提出的基于聚类和探测精英引导的蜻蜓优化算法(CEDA)，在8个典型的复杂函数中进行测试，结果表明与DA、FOA、GWO、DE、ABC、PSO算法相比，本研究提出的CEDA算法具有强大的全局搜索能力、良好的收敛精度以及更高的稳定性. 在未来的研究中，应考虑能更好地提高收敛速度和收敛精度的算法，并将其运用到工程设计优化问题，如焊接梁、压力容器、三杆桁架等设计问题.