以上降雨入渗研究,未考虑地表径流作用. 为了反映这一作用,目前已经有不少学者在理论和数值上进行地表径流与土壤水流的模拟,且大致分为2种假设,一种是假设当土体饱和时,地表产生积水,另一种是假设当土体的入渗强度小于降雨强度时,地表将产生积水. 张培文等[4]考虑了地表积水的现象,但简化了模型,未考虑坡面水流的动量守恒;Zhao[5]采用第1种假设计算坡面流;Wang等[6]用有限元法将Navier-Stokes方程同Richards方程耦合,假设饱和积水的条件,考虑复杂地面的积水情况;Zhang等[7]同样采用有限元法耦合Navier-Stokes方程和Richards方程,也设置了饱和积水的条件,计算边坡的降雨入渗;刘育田等[8-9]对地表径流方程采用有限差分法求解,土壤水流方程采用有限元法求解,假设饱和积水条件,对比考虑与不考虑地表径流条件下的坡体入渗. Tan等[10]根据第2种假设,在理论上计算地表径流的质量守恒式,并采用Green-Ampt模型模拟土壤水流,用有限差分法考虑坡面流对无限长边坡造成的影响,该模型并未考虑地表水的动量守恒;Jahnson等[11]使用Richards方程推导一维、半无限土层的理论解,并依据土壤水流场和地表径流场之间的质量交换将地表径流与土壤水流模型耦合,用有限差分法求解该模型,此模型同样忽略了地表水在坡面的流动;Zhu等[12]采用假设2,将地表径流方程简化成扩散波方程,并通过有限元法计算边坡降雨入渗的问题;Pato等[13]采用有限体积法模拟地表径流条件下饱和土体的入渗;Pato等[14-15]采用有限体积法模拟两者耦合作用,土壤水流模型采用Green-Ampt模型.
分析已有研究成果可知,许多学者在模拟雨水入渗过程中采用Green-Ampt模型,数值方法采用有限元法. G-A模型要求入渗土体中水的初始体积分数是均匀分布的,且在入渗过程中将湿润锋简化为一条线,将入渗土体分为湿润锋上部饱和区域和下部初始体积分数区域2个部分,即湿润锋由初始体积分数变为饱和体积分数的土层厚度被忽略. Green-Apmt入渗模型是对复杂的水入渗过程的简化. Richards方程是在达西定律和质量守恒的基础上,应用数学物理方法推导出的非饱和土壤水分流动方程,其初始条件和边界条件的选择更加灵活,且各单元的水头值,以及各单元表面的通量大小都可以计算得出,只是求解较困难. 在数值方法的选取上,本研究采用有限体积法求解耦合方程,相比于有限单元法,有限体积法要求因变量的积分守恒对任意一组控制体积都得到满足,对整个计算区域,自然也得到满足,而有限元法则是满足了整体的质量守恒,局部守恒无法保证,且有限体积法在计算方面也更为简单.
本研究采用有限体积法耦合求解地表径流和土壤水流方程,用Navier-Stokes方程模拟地表径流,用Richards方程模拟土壤水流,通过对比数值耦合解与SEEP/W计算的解,验证耦合模型的有效性,通过计算土坡降雨入渗的案例,对比分析坡顶和坡底的入渗深度情况.
1. 理论模型
1.1. 地表径流模型理论
地表径流模型采用不可压缩流体的Navier-Stokes[15]方程,其中有2个前提假设:1)相对于水平面的尺寸而言,水头高度是微小的,因此土体表面水流的流速在水的深度范围内是定值,且以水流在深度方向的平均流速作为该定值;2)水流所产生的压力是静水压力,因此方程在积分时采用的竖向的压力场为
式中:
图 1
一般将式(1)化简成向量形式的欧拉方程组:
式中:
进一步化简得到
式中:
可以根据
图 2
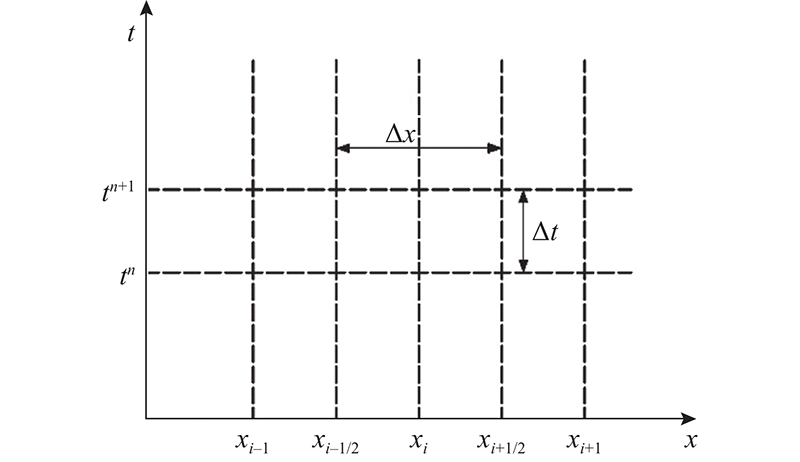
图 2 地表径流方程时间空间离散分布图
Fig.2 Space and time discretization of surface runoff equation
式(1)在求解时被划分为了2部分,第1部分为去除源项后的方程即式(2),第2部分为源项即式(1)等号右边项,因此在求解方程组时须进行2步计算.
第1步须用有限体积法化简式(2):
式中:
可以使用heun法(也被称为改进的欧拉法)保证时间项具有二阶精度,该方法须对时间项进行3步计算以修正式(5). 修正计算公式如下:
式中:
式中:
第2步对源项进行处理,源项包括
1.2. 流体在变饱和孔隙介质中的流动模型理论
变饱和孔隙介质流动模型来用古典的非线性Richards方程[22]描述,该方程由质量守恒和达西定律推导出来,并且可以被表示成3种不同的形式,如下所示.
1)以
式中:
2)以
式中:
3)混合形式的方程:
在确保每一时间步中
1.2.1. 空间项的离散
以式(8)为例,通过有限体积法,将控制方程离散成如下形式:
式中:
通过假定在
式中:
图 3
图 4
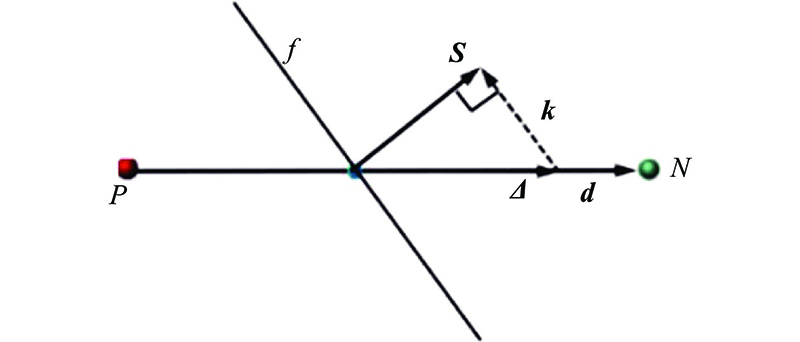
图 4 相邻控制单元非正交网格向量图
Fig.4 Non-orthogonality mesh vector of adjacent control units
式中:表面的
1.2.2. 时间项的离散
与时间相关的积分控制方程如下:
式中:
式(14)的2种隐式离散方式表达式如下.
1)一阶精度的欧拉法:
2)二阶精度的向后欧拉法:
对于瞬态问题,由于须处理空间项的倒数以及确定时间项精度,对式(14)进行时间上的积分:
式中:
1)隐式欧拉法:
2)显式法:
3)Crank Nicolson法:
方法1)和2)在时间上都是一阶精度,方法1)保证了
1.2.3. 迭代操作
由于材料本构关系的非线性,对控制方程的直接求解是不可能的,使用古典的Celia等[27]提出的迭代法,并结合式(10)可以得到:
式中:上标
将式(22)代入到式(21),可以得到
式中:
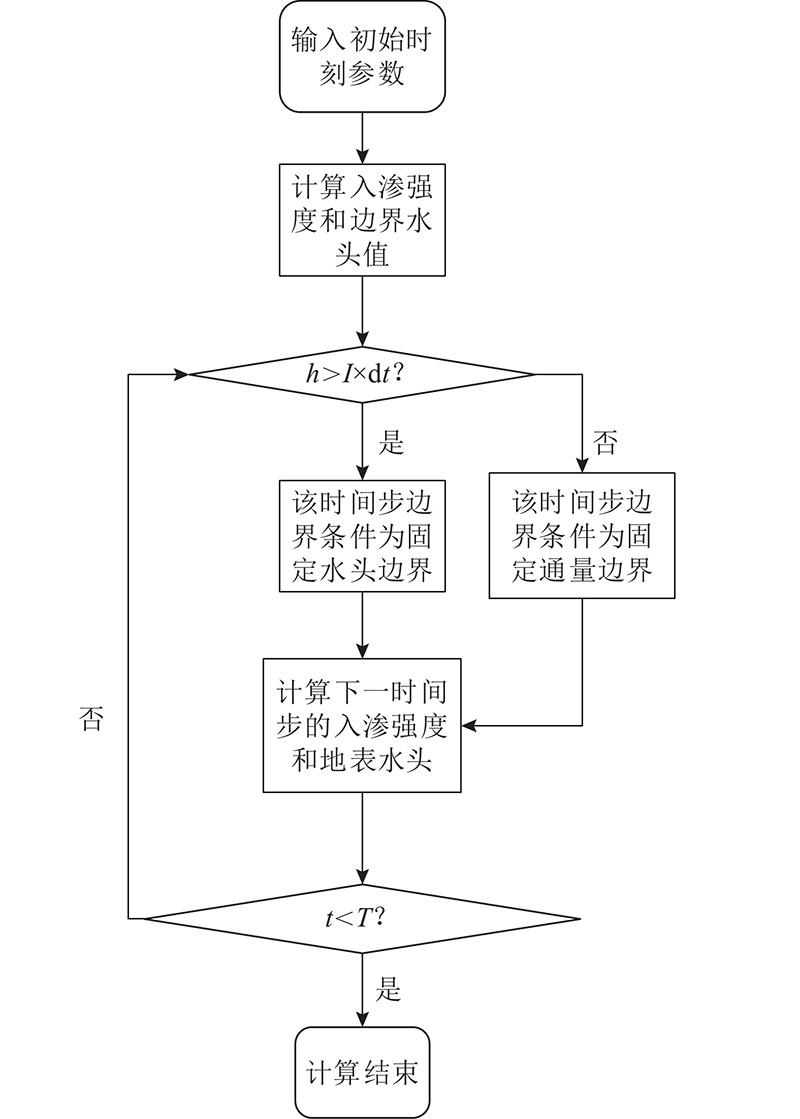
1.3. 耦合方法
通过将Navier-Stokes方程中的入渗项用Richards方程中计算的边界流通量表示以实现2个方程的耦合. 具体方法如图5所示. 图中,
图 5
图 5 地表径流与土壤水流耦合流程图
Fig.5 Couple steps of surface runoff and soil water movement
偏微分方程有3类边界条件,分别为Dirichlet边界、Neumann边界、Cauchy边界. 计算土壤水流的程序中有4种类型的边界,分别为常水头边界、常总水头边界、特定通量边界、内部位置固定值边界. 它们都可以是时间的函数. 其他边界的模拟都可以用这4种边界组合来实现. 常水头边界和常总水头边界可以分别表示为
式中:
若有
2. 算法验证
2.1. 一维固定水头算例验证
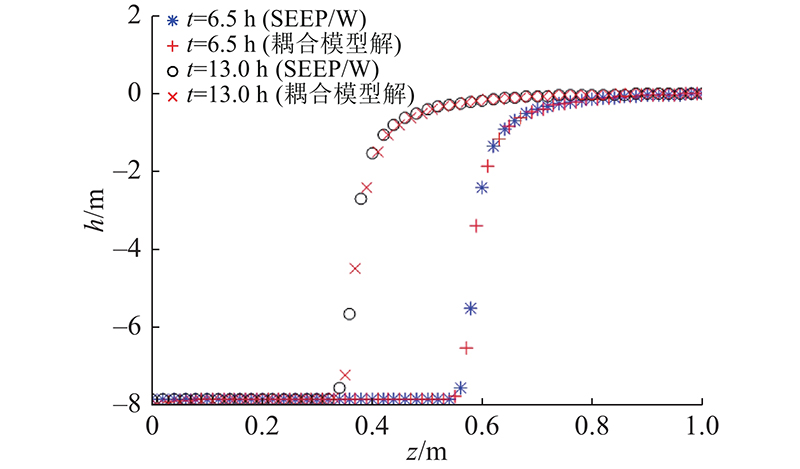
采用一维土柱入渗试验来验证耦合模型的算法,土柱的高度为1 m,在土柱顶部的固定水头为0 m,土柱底部的固定水头为−8 m,水的饱和体积分数为0.363,残余水的体积分数为0.186,饱和渗透系数为1×10−6 m/s,土柱的初始水头均匀分布,设置为−7.848 m,VG模型参数
分别采用SEEP/W和本研究耦合模型计算t=6.5、13.0 h时刻土柱的水头分布情况,如图6所示,由结果可以看出,两者差别较小.
图 6
图 6 相同固定水头条件下耦合模型与SEEP/W实例结果比较
Fig.6 Case result comparison of coupled model and SEEP/W under same fixed head condition
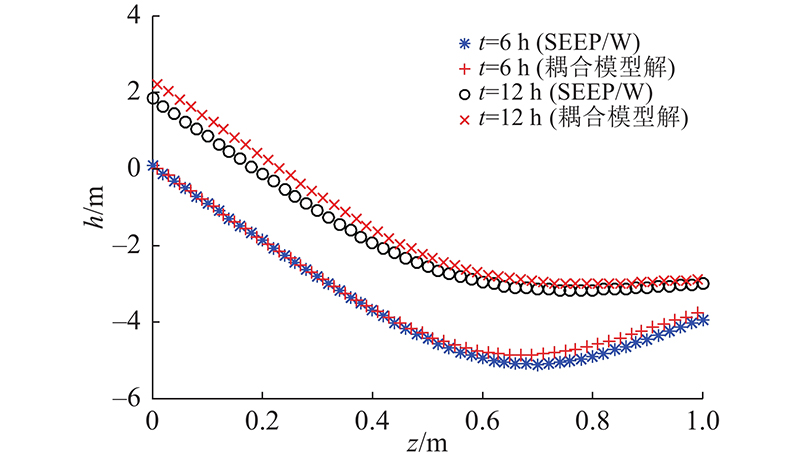
2.2. 一维固定通量算例验证
图 8
图 8 相同固定通量条件下耦合模型与SEEP/W实例结果对比
Fig.8 Case result comparison of coupled model and SEEP/W under same fixed flux condition
计算结果表明,土壤水流和地表径流耦合模型在固定水头边界和通量边界条件下计算的结果是有效的.
图 7
图 7 土柱初始水头数值模拟分布图
Fig.7 Numerical simulation distribution diagram of soil column initial water head
3. 案例分析
3.1. 土体水力特性模型
非饱和土渗透模型采用Van Genuchten[28]提出的模型,该模型下体积分数
相对渗透系数
式中:
3.2. 模型参数
模型所采用的裂隙土为火山碎屑土[29],其VanGenuchten模型参数如下:α=1.8 m−1,n=1.34,
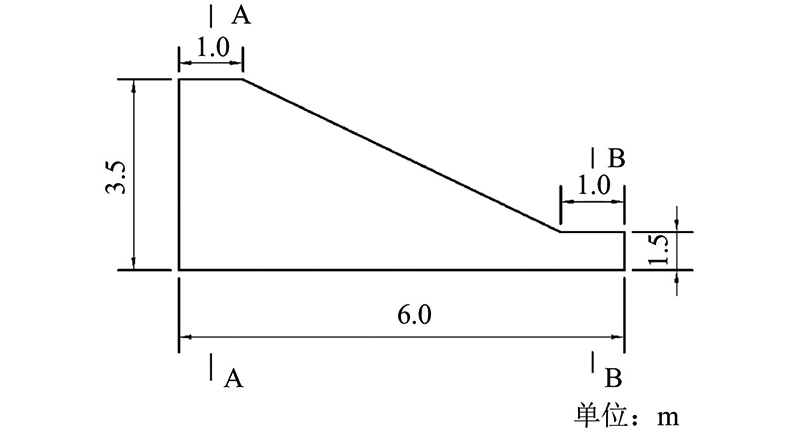
模型将模拟3.5 m高、坡度为26°的边坡,模型几何尺寸如图9所示.
图 9
3.3. 模型假设
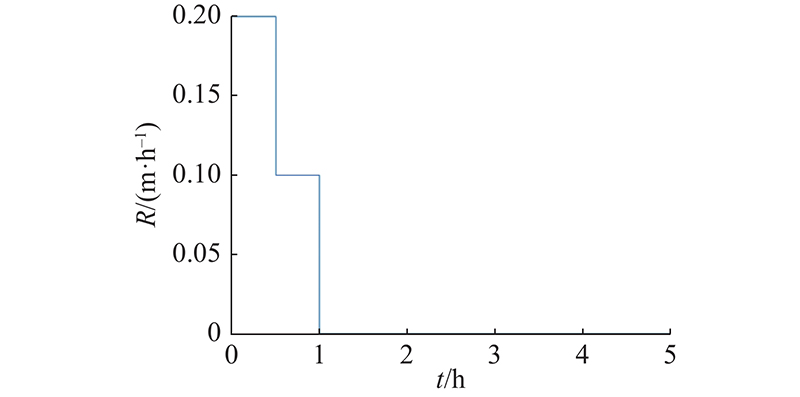
模型假定坡体是均质的且入渗是各向同性的,初始时刻地表径流场的初始水头为零,时间步长和空间步长分别为0.05 h和0.5 m,对土坡的地表径流场的左边界采用不透水边界条件,对土坡的地表径流场的右边界采用自由排水边界. 土壤水流场中水的初始体积分数为0.4,侧面边界和底面边界则采用与初始水头值相同的水头边界,其值为−3.9 m,每0.05 h记录一次运算结果. 初始降雨强度为0.2 m/h,在半小时后降至0.1 m/h,持续2.5 h后降雨停止,直至5.0 h结束计算,降雨强度随时间的变化如图10所示.
图 10
图 10 数值模拟中降雨强度随时间变化图
Fig.10 Variation of numerical rainfall intensity over time
3.4. 结果分析
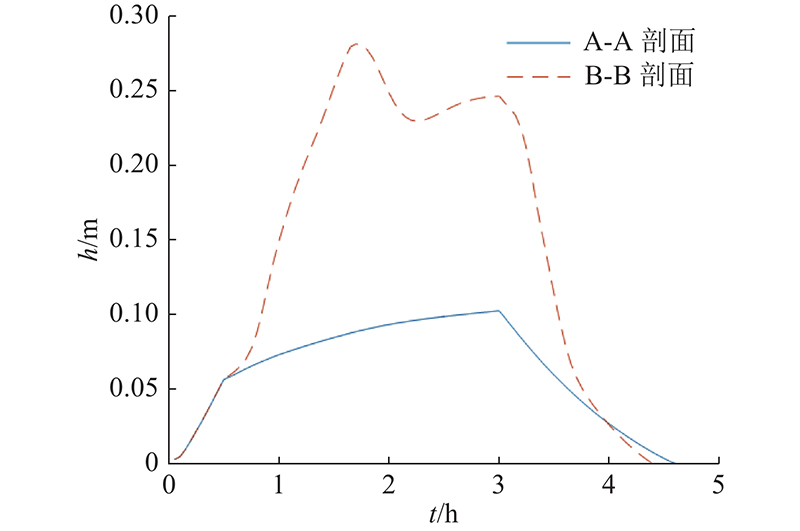
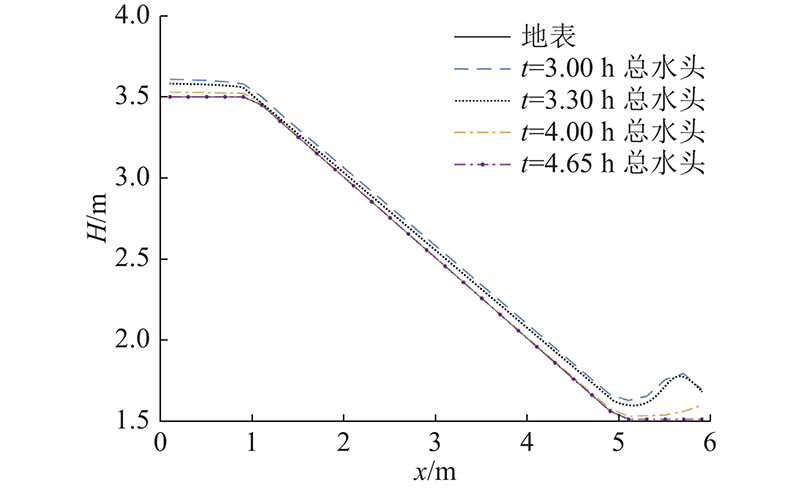
如图9所示的A-A剖面处和B-B剖面处的水头随时间的变化如图11所示. 可以看出,在初始时刻,土的入渗能力较强,坡面积水较小,坡顶和坡底的水头较接近,坡面水的流动较小;随着地表入渗强度的降低,坡体表面积水深度开始增加,由于坡顶水的流动,坡底水出现从亚临界流到超临界流再到亚临界流的变化,坡底水出现先增大再减小又增大又减小的波动特征,坡顶水头变化较为单一;到降雨结束时,由于入渗和重力作用,坡顶和坡底积水开始迅速减少,坡顶水头和坡底水头大约在t=4.65 h时刻减小为零. 如图12所示为降雨结束后坡体表面水头的分布情况. 图中,H为总水头. 可以看出,在降雨结束时坡底部分位置水头并没有很快降低,这主要是由坡面水的流动对坡底水头的补充所导致的,且在降雨结束后地表径流大约持续了1.65 h.
图 11
图 11 A-A剖面坡顶和B-B剖面坡顶水头随时间变化图
Fig.11 Water head of slope top at profile A-A and B-B over time
图 12
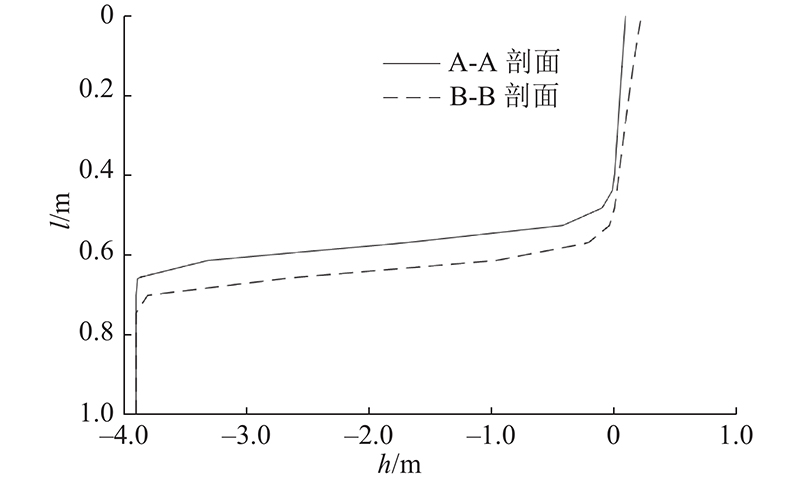
为了表示坡面径流对土壤入渗水流的影响,如图13所示为坡顶处(A-A剖面)和坡脚处(B-B剖面)在时间t=3 h时的入渗雨水分布情况. 图中,l为入渗深度. 可以看出,坡脚处入渗深度大于坡顶的入渗深度,说明水的流动导致的坡面水头分布的不均对土体入渗的影响是存在的.
图 13
图 13 t=3 h时刻A-A剖面和B-B剖面入渗深度情况
Fig.13 Infiltration at profile A-A and B-B at time of 3 h
4. 结 论
(1) 以边界水头作为自变量将地表径流和土壤水流方程耦合后,可以模拟地表水在坡面的流动和确定坡面水头的动态变化,以及相应的土壤中水分流动.
(2) 根据计算结果,在降雨停止后,由于地表水的径流,坡底水头仍会在一段时间内维持在一定高度.
(3) 对比2种工况下坡底的水头分布可知,地表径流引起地表水流动,造成地表水头在坡面上分布的不均匀性,对坡底和坡顶入渗的影响是不同,坡底的入渗量相对较高,说明考虑地表径流对边坡入渗的影响是有必要的.
须指出的是,本研究只考虑了均质各向同性坡体,对于坡体渗透各向异性、入渗土体分层情况还须进一步研究.
参考文献
Influence of rainfall on transient seepage field of deep landslides: a case study of area II of Jinpingzi landslide
[J].DOI:10.1088/1755-1315/570/2/022056 [本文引用: 1]
Unsaturated slope stability around the Three Gorges Reservoir under various combinations of rainfall and water level fluctuation
[J].DOI:10.1016/j.enggeo.2019.105231 [本文引用: 1]
考虑裂隙非饱和膨胀土边坡入渗模型与数值模拟
[J].DOI:10.3969/j.issn.1000-7598.2004.10.014 [本文引用: 1]
Numerical model and simulation of expensive soils slope infiltration considered fissures
[J].DOI:10.3969/j.issn.1000-7598.2004.10.014 [本文引用: 1]
饱和-非饱和非稳定渗流的数值模拟
[J].DOI:10.3969/j.issn.1000-7598.2003.06.011 [本文引用: 1]
Saturated and unsaturated unsteady seepage flow numerical simulation
[J].DOI:10.3969/j.issn.1000-7598.2003.06.011 [本文引用: 1]
The Xinanjiang model applied in China
[J].DOI:10.1016/0022-1694(92)90096-E [本文引用: 1]
Coupled model of surface runoff and surface-subsurface water movement
[J].DOI:10.1016/j.advwatres.2019.103499 [本文引用: 1]
A surface and subsurface model for the simulation of rainfall infiltration in slopes
[J].
地表径流与地下渗流耦合的斜坡降雨入渗研究
[J].DOI:10.3969/j.issn.1003-8825.2010.03.031 [本文引用: 1]
The study of the slope rainfall infiltration considered the couple of surface runoff and subsurface water movement
[J].DOI:10.3969/j.issn.1003-8825.2010.03.031 [本文引用: 1]
考虑地表径流与地下渗流耦合的斜坡降雨入渗研究
[J].
the study of slope rainfall infiltration considered surface surface and subsurface water movement
[J].
Numerical investigation on infiltration and runoff in unsaturated soils with unsteady rainfall intensity
[J].DOI:10.3390/w10070914 [本文引用: 1]
Coupled infiltration and kinematic-wave runoff simulation in slopes: implications for slope stability
[J].DOI:10.3390/w9050327 [本文引用: 1]
Simultaneous analysis of slope instabilities on a small catchment-scale using coupled surface and subsurface flows
[J].DOI:10.1016/j.enggeo.2020.105750 [本文引用: 1]
A 2D finite volume simulation tool to enable the assessment of combined hydrological and morphodynamical processes in mountain catchments
[J].DOI:10.1016/j.advwatres.2020.103617 [本文引用: 1]
Rainfall/runoff simulation with 2D full shallow water equations: sensitivity analysis and calibration of infiltration parameters
[J].DOI:10.1016/j.jhydrol.2016.03.021 [本文引用: 1]
FullSWOF: a free software package for the simulation of shallow water flows
[J].
A well-balanced scheme for the numerical processing of source terms in hyperbolic equations
[J].
A fast and stable well-balanced scheme with hydrostatic reconstruction for shallow water flows
[J].DOI:10.1137/S1064827503431090 [本文引用: 1]
A numerical method for simulating discontinuous shallow flow over an infiltrating surface
[J].DOI:10.1002/(SICI)1097-0363(20000130)32:2<219::AID-FLD936>3.0.CO;2-J [本文引用: 1]
Capillary conduction of liquids through porous mediums
[J].DOI:10.1063/1.1745010 [本文引用: 1]
Computational modelling of variably saturated flow in porous media with complex three-dimensional geometries
[J].DOI:10.1002/fld.1087 [本文引用: 1]
Modeling one-dimensional infiltration into very dry soils: 1. model development and evaluation
[J].DOI:10.1029/WR025i006p01259 [本文引用: 1]
A mass-conservative switching method for simulating saturated-unsaturated flow
[J].DOI:10.1016/j.jhydrol.2005.01.019 [本文引用: 2]
A general mass-conservative numerical solution for the unsaturated flow equation
[J].DOI:10.1029/WR026i007p01483 [本文引用: 1]
A closed-form equation for predicting the hydraulic conductivity of unsaturated soils
[J].DOI:10.2136/sssaj1980.03615995004400050002x [本文引用: 1]
Geotechnical characterization of pyroclastic soils involved in huge flowslides
[J].