浙江大学学报(工学版)

浙江大学学报(工学版), 2022, 56(5): 890-900, 908 doi: 10.3785/j.issn.1008-973X.2022.05.006

土木工程

碳纤维布约束型钢混凝土矩形柱轴压承载力

高鹏,, 曾学波, 吴宜龙, 彭飞

1. 合肥工业大学 土木与水利学院，安徽合肥 230009

2. 同济大学 工程结构性能演化与控制教育部重点实验室，上海 200092

3. 国网安徽省电力有限公司，安徽合肥 230009

Axial compression bearing capacity of steel reinforced concrete rectangular columns confined by carbon fiber reinforced polymer

GAO Peng,, ZENG Xue-bo, WU Yi-long, PENG Fei

1. School of Civil Engineering, Hefei University of Technology, Hefei 230009, China

2. Key Laboratory of Performance Evolution and Control for Engineering Structures of Ministry of Education, Tongji University, Shanghai 200092, China

3. State Grid Anhui Electric Power Limited Company, Hefei 230009, China

收稿日期: 2021-06-7  

基金资助: 国家自然科学基金资助项目 (51208166); 工程结构性能演化与控制教育部重点实验室开放基金资助项目 (2018KF-1)

Received: 2021-06-7  

Fund supported: 国家自然科学基金资助项目(51208166);工程结构性能演化与控制教育部重点实验室开放基金资助项目(2018KF-1)

作者简介 About authors

高鹏（1978—），男，副教授，从事混凝土结构研究.orcid.org/0000-0002-5327-9821.E-mail：penggao@hfut.edu.cn , E-mail：penggao@hfut.edu.cn

摘要

为了研究碳纤维布(CFRP)约束型钢混凝土矩形柱的轴压性能，对29个构件进行静力加载试验，考虑配筋率、预载水平、截面圆角半径和高宽比、纤维布加固率和加固方式共6个参数. 结果表明：所有约束柱均以核心区混凝土压碎和纤维布断裂为破坏标志；随着预载水平提高，布的有效拉应变不断减小，柱承载力降低；随着圆角半径增大和高宽比减小，纤维布环向应变更高且分布趋于均匀；随着加固率增加，柱破坏模式由弱约束转成强约束，纤维布加固效率降低；在同等用量布的加固下，当条带宽度和间距减小时，构件承载力增幅增加. 基于各因素对约束应力的影响，确定了区分大尺寸柱强弱约束模式的界限值；采用叠加法建立了多参数的约束型钢柱轴压承载力计算式.

关键词： 纤维增强复合材料 ; 约束型钢混凝土柱 ; 轴压试验 ; 承载力 ; 强弱约束

Abstract

Twenty-nine specimens were conducted to the axial compression experiment, in order to study the axial compression performance of steel reinforced concrete rectangular columns confined by carbon fiber reinforced polymer (CFRP). Six parameters were considered, which included reinforcement ratio, preload level, corner radius and aspect ratio of cross sections, as well as amount and scheme of CFRP. Results indicated that the confined columns all failed in the fracture of CFRP when the core concrete crushed. With the increasing preload level, both the effective tensile strain of CFRP and the bearing capacity of confined columns decreased gradually. With the increasing corner radius and decreasing aspect ratio, the circumferential strain of CFRP got higher value and more uniform distribution. As increasing amount of CFRP, the constraint mode of the column changed from weak constraint to strong constraint, and the utilization of CFRP decreased. When the width and spacing of the strips decreased, the increment of bearing capacity increased with the same amount of CFRP. Finally, considering various parameters, the boundary value for determining the strong and weak modes was proposed. The formulation of the axial bearing capacity of confined steel reinforced rectangular columns was set up by superposition method.

Keywords： fiber reinforced polymer ; confined steel reinforced concrete column ; axial compression experiment ; bearing capacity ; strong and weak confinement

PDF (3086KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

高鹏, 曾学波, 吴宜龙, 彭飞. 碳纤维布约束型钢混凝土矩形柱轴压承载力. 浙江大学学报(工学版)[J], 2022, 56(5): 890-900, 908 doi:10.3785/j.issn.1008-973X.2022.05.006

GAO Peng, ZENG Xue-bo, WU Yi-long, PENG Fei. Axial compression bearing capacity of steel reinforced concrete rectangular columns confined by carbon fiber reinforced polymer. Journal of Zhejiang University(Engineering Science)[J], 2022, 56(5): 890-900, 908 doi:10.3785/j.issn.1008-973X.2022.05.006

型钢混凝土组合结构具有承载力高、刚度大和延性好等特点. 我国解放前的租界建筑和建国初期从苏联引进的重型工业厂房多采用组合结构. 随着时间推移，这些房屋已经进入维修期，组合结构加固问题也被提到日程. 碳纤维增强复合材料（carbon fiber reinforced polymer，CFRP）具有轻质高强、可设计性和高耐久性等优点，在基础设施领域逐步得到广泛应用[1-3]. 近年来国内外研究者就纤维增强复合材料约束混凝土柱的轴压性能进行了大量的试验和理论研究，潘毅等[4-5]进行了负载下CFRP约束混凝土方柱轴压试验研究，结果表明随着负载水平的提高，柱的约束效应下降；并采用增量迭代方法，建立了长期荷载作用下考虑初始应力的纤维增强复合材料（fiber reinforced polymer，FRP）约束混凝土应力-应变关系的分析模型. Wang等[6]进行不同圆角半径的约束方柱轴压试验，柱边长为150 mm，圆角半径从0变化至75 mm，发现约束后混凝土强度增长率与圆角半径呈正比. Mostofinejad等[7-8]通过试验研究发现，随着矩形柱截面高宽比增加，FRP布约束混凝土效应逐渐减弱，当试件截面为正方形时强度增幅最大，当截面长短边比值为2时，强度增长基本消失. Park等[9]对包裹FRP层数不同的约束混凝土柱进行轴压试验，结果表明混凝土柱的承载能力和变形能力随FRP加固量的增加而提高，但是提高的幅度并不与FRP包裹层数成正比. 周长东等[10]通过试验研究加固量大体相等但条带间距与宽度不等的FRP约束混凝土柱，结果表明约束效果随布条带间距增大而逐渐减弱，超过一定间距后布条带对核心混凝土无明显约束作用. 敬登虎等[11]根据FRP对于试验中方柱约束效应强弱不同的情况，提出约束混凝土两段式本构模型，并给出强弱约束临界点计算公式. 目前《纤维增强复合材料建设工程应用技术规范》（GB 50608—2010）[12]中的约束加固矩形柱设计方法还不够全面，未能概括相关细节参数对于构件承载力的影响，如纤维布的黏贴方式只限于连续全包，对于柱高宽比和圆角半径参数对纤维布应变的影响缺少定量描述，而预载水平对构件承载力的影响则没有涉及到.

现有研究成果多基于小尺寸的素混凝土试件试验建立，构件截面边长通常为100~200 mm，高度为150~500 mm，与实际柱尺寸有较大差别. 约束柱轴压受力性能提升幅度与构件大小有关，尺寸效应强弱受多参数影响[13-14]. 以圆角半径为例，小尺寸的混凝土矩形柱经过倒圆角处理后会接近圆柱，而大尺寸柱边长较长，倒圆角时不会得到和小尺寸柱占同样边长比例的圆角半径，所以尺寸效应会更加明显[15-16]. 另外如预载水平、截面形状和纤维布条带等因素的影响也在工程中的大尺寸配筋柱和组合柱中才凸显出来.

本研究进行29个碳纤维布约束大尺寸型钢混凝土矩形柱的轴压试验，考察不同参数下组合柱的被约束效果. 结合这些参数对侧向约束应力的影响，给出矩形柱的修正约束强度比计算式，利用收集的试验数据，提出大尺寸混凝土柱强弱约束界限判定值. 考虑型钢对柱混凝土截面约束区的划分影响，建立多参数下CFRP约束型混凝土矩形柱的承载力计算式.

1. 试验概况

1.1. 试件设计

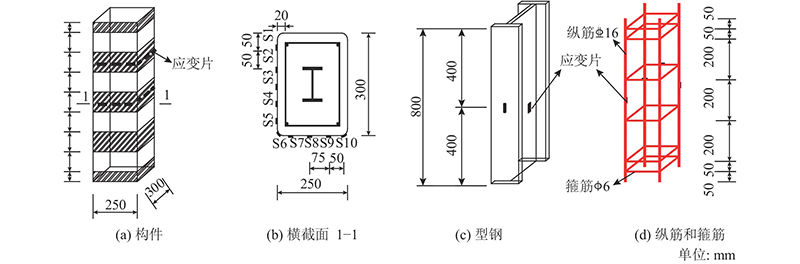
试验含有2个对比柱和27个不同参数的约束柱. 受场地条件限制分为2批浇筑构件，各组构件设计参数如表1所示. 表中，h、b为构件截面高度和宽度，d为纵筋直径，n为CFRP层数，w、s'为条带宽度和间距，r为圆角半径，m为预载水平，Pc为试件浇筑批次. 基本构件尺寸和配筋如图1所示，柱高度为800 mm，截面尺寸为300 mm×250 mm，截面中部设置10号工字钢，设置纵筋为4C16，混凝土保护层厚度为40 mm；构件中箍筋为A6@200，并且为了防止局压破坏，在柱两端加密至间距为50 mm. 采用条带式布约束，条带宽度为100 mm，间距为100 mm. 在贴布前对柱截面做倒角处理，圆角半径为20 mm. 在配筋率组(PJ)中，变化柱中纵向钢筋直径，14 ~22 mm. 在预载组(YZ)中，构件以0.5fcoA作为预载水平初始值（简记为0.5，其中fco为混凝土棱柱体抗压强度，A为柱截面积，预载水平初始值大于对比柱DB1的实测开裂荷载692 kN），之后逐渐增大至0.7. 在圆角半径组(YJ)中，构件采用预制钢模板进行浇筑，圆角半径为20~80 mm. 在高宽比组(GK)中，构件短边长b=250 mm，长边h变化. 在加固率组(JL)中，构件布条带宽度均为100 mm，通过改变布层数和条带间距来设定不同加固量. 在加固方式组(JF)中，各柱使用等量碳纤维布，1个采用完全包裹，其他4个采用纤维布的等条带宽度和等间距包裹.

表 1   CFRP约束型钢混凝土柱轴压试验的各试件参数

Tab.1  Parameters of CFRP-confined reinforced steel concrete columns in axial compression experiment

编号 h×b/mm×mm d/mm n w/mm s´/mm r/mm m Pc
1）注：以构件YZ2-0.50为例：“YZ”指预载组；“2”指包裹2层纤维布；“0.50”指对应的设计预载水平为0.50.
DB1 300×250 16 0 − − − − 1
DB2 300×250 16 0 − − − − 2

YZ2-0.501） 300×250 16 2 100 100 20 0.50 1
YZ2-0.60 300×250 16 2 100 100 20 0.60 1
YZ2-0.65 300×250 16 2 100 100 20 0.65 1
YZ2-0.70 300×250 16 2 100 100 20 0.70 1
YJ2-20 300×250 16 2 100 100 20 − 1
YJ2-40 300×250 16 2 100 100 40 − 1
YJ2-60 300×250 16 2 100 100 60 − 1
YJ2-80 300×250 16 2 100 100 80 − 1
JL2-100 300×250 16 2 100 100 20 − 1
JL3-100 300×250 16 3 100 100 20 − 1
JL3-75 300×250 16 3 100 75 20 − 1
JL3-50 300×250 16 3 100 50 20 − 1
JL4-50 300×250 16 4 100 50 20 − 1
JF1-0 300×250 16 1 800 0 20 − 2
JF2-50 300×250 16 2 50 50 20 − 2
JF2-80 300×250 16 2 80 80 20 − 2
JF2-100 300×250 16 2 100 100 20 − 2
JF2-200 300×250 16 2 200 200 20 − 2
GK2-1.0 250×250 16 2 100 100 20 − 2
GK2-1.2 300×250 16 2 100 100 20 − 2
GK2-1.4 350×250 16 2 100 100 20 − 2
GK2-1.6 400×250 16 2 100 100 20 − 2
PJ1-14 300×250 14 1 100 100 20 − 2
PJ1-16 300×250 16 1 100 100 20 − 2
PJ1-18 300×250 18 1 100 100 20 − 2
PJ1-20 300×250 20 1 100 100 20 − 2
PJ1-22 300×250 22 1 100 100 20 − 2

新窗口打开| 下载CSV


图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   CFRP约束型钢混凝土柱的轴压试验构件设计

Fig.1   Specimen design for axial compression experiment of CFRP-confined reinforced steel concrete columns


1.2. 材料力学性能

采用强度等级为C30的商品混凝土，受场地限制分2批浇筑试件. 每批预留边长为150 mm的立方体和150 mm×150 mm×300 mm的棱柱体试块，采用标准试验方法测得2次浇筑的混凝土立方体抗压强度分别为32.11、39.13 MPa，棱柱体抗压强度fco分别为21.95、20.26 MPa，以及弹性模量ES分别为2.64×104、2.31×104 MPa. 纵筋等级为HRB400，箍筋等级为HPB300，型钢为Q235号工字钢，采用《金属材料室温拉伸试验标准》（GB/T 228—2002）[17]测得钢材屈服强度分别为465、227 、210 MPa. 采用HM-20型CFRP布，面密度为200 g/m2，单层厚度为0.111 mm，抗拉强度为3506 MPa，弹性模量为242 GPa；黏结剂采用HM-180型底胶和HM-180C3P型浸渍胶.

1.3. 加载与量测

试验采用安徽省土木工程结构与材料重点试验室的5000 kN长柱压力机，装置如图2所示. 试验采用逐级单调加载，加载速率为1 kN/s. 起初荷载步长为150 kN，采用力控制，在每级荷载保持稳定时采集数据；当接近开裂荷载时，荷载步长为100 kN；当接近极限荷载时，荷载步长为50 kN，并改为位移控制和连续采集数据，直至试件破坏. 对于预载水平组构件，在设定好预载水平后，对构件反复加卸载5次，加载速率为2 kN/s；在预载水平上保持受力1 h；卸载后在混凝土残余应变达到稳定后，再实施包裹 CFRP布.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   CFRP约束型钢混凝土柱轴压试验加载装置

Fig.2   Axial compressive test setup of CFRP-confined reinforced steel concrete column


在试验中采用荷载传感器和位移计量测柱轴向承载力及变形；位移计布置在压力机底板上的构件两侧；构件底部与承压板之间有荷载传感器来量测轴力. 采用应变片量测各种材料的应变，如图1(a)、(b)所示的CFRP布环向拉应变，如图1(c)、(d)所示的柱中部混凝土、型钢和纵筋的压应变.

2. 试验现象

对比构件呈现典型的组合柱轴压破坏，如图3(a)所示. 随着荷载增加，混凝土出现纵向裂缝并不断延伸；型钢和纵筋先后屈服；之后柱进入不稳定状态，混凝土保护层剥落；纵筋压屈并向外鼓出，柱达到峰值承载力；在极限状态时型钢腹板两侧与翼缘间的混凝土被压碎. 各约束柱破坏过程相似. 随着荷载增大，表面混凝土裂缝数量逐渐增多，纤维布条带边混凝土碎屑脱落；在接近峰值荷载时纵筋屈服，纤维布断裂声密集,混凝土剥落速度加快；在峰值荷载后核心区混凝土被压碎，纵筋压屈外鼓，纤维布断裂，构件失去承载力. 各组柱由于参数不同，其破坏存在一定差异.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   构件DB1和YZ组中典型柱的破坏形态对比

Fig.3   Comparison of failure modes of DB1 and typical columns in YZ Group


如图3所示，在预载后试件混凝土表面出现受压裂缝，方向与高度方向一致，最大宽度为0.10~0.25 mm. 由于预载使试件开裂，在正式加载初期各加固构件的变形发展较快；随着荷载增加，预裂缝处胶水劈裂的声响较普遍. 在各约束柱达到极限状态后拨去表面纤维条带和混凝土层，对比构件YZ2-0.5和YZ2-0.7破坏形态可知，随着预载水平增大，柱纵筋压屈现象越明显；初始损伤越大的构件，核心区混凝土被压碎的越充分.

圆角组典型构件破坏形态如图4(a)、(b)所示. 对于圆角半径较小的构件YJ2-20，在加载过程中有连续不断的纤维滑移和撕裂声；但随着圆角半径增大，YJ2-80在加载过程中的声响越来越少,纤维布最终破坏形态也逐渐由撕裂向整条拉断转变，且断口齐整. 这是因为随着圆角半径增大，纤维布产生更均匀的拉应力，减缓截面角部的混凝土应力集中，实现更高的核心区约束混凝土应力. 从长边观察高宽比组典型柱破坏形态如图4(c)、(d)所示,构件高宽比从1.0增加到1.6，在加载过程中混凝土裂缝延展越迅速，分布越稀疏；混凝土块体越大，破坏越不充分；纤维布也呈现从整条断裂向逐渐撕裂变化. 说明高宽比较小的柱内部混凝土应力分布较均匀，实现了更高的约束混凝土应力.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   YJ组和GK组中典型柱和CFRP布的破坏形态

Fig.4   Failure modes of columns and CFRP in YJ and GK group


如图5(a)、(b)所示为加固量组典型构件破坏形态. 随着纤维布条带间距变小和层数增多，混凝土裂缝开展越缓慢而密集，纤维条带断裂位置越集中，破坏时纤维布爆裂声越显著，压坏的混凝土碎粒更加细小. 加固方式组各柱破坏形态如图5(c)~(e)所示，纤维布条带间距越小，裂缝开展越缓慢和密集，混凝土破坏越充分. 较宽的布条带能给纤维一定应力重分布空间，但撕裂现象明显；当条带较窄时布纤维应变趋于一致，易呈现瞬时迸裂. 对于加固率相同的全包加固柱JF1-0，一层纤维布易出现撕裂，且实现约束应力较小，其混凝土破坏范围和程度没有其他条带式约束构件的大.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   JL组和JF组中典型柱破坏形态

Fig.5   Failure modes of columns in JL and JF group


3. 试验结果及分析

3.1. 荷载位移曲线

如图6所示为各组试件的荷载-位移(P-Δ)曲线，在加载初期，各试件曲线基本呈线性增长，变形发展较小，材料基本处于弹性状态；随着荷载增加，试件表面混凝土出现裂缝，混凝土有横向变形，纤维布逐渐发挥出约束作用，构件曲线斜率逐渐减小；当加载至峰值荷载后，混凝土开始出现剥落和压碎现象，纤维布之间呈现滑移和撕裂；直至最终条带断裂，构件失去承载力. 结合图6对不同参数构件曲线进行分析，屈服荷载取试件达到纵筋屈服时的，峰值荷载指加载过程中柱承载力最大值，极限荷载指柱丧失承载能力时的荷载.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

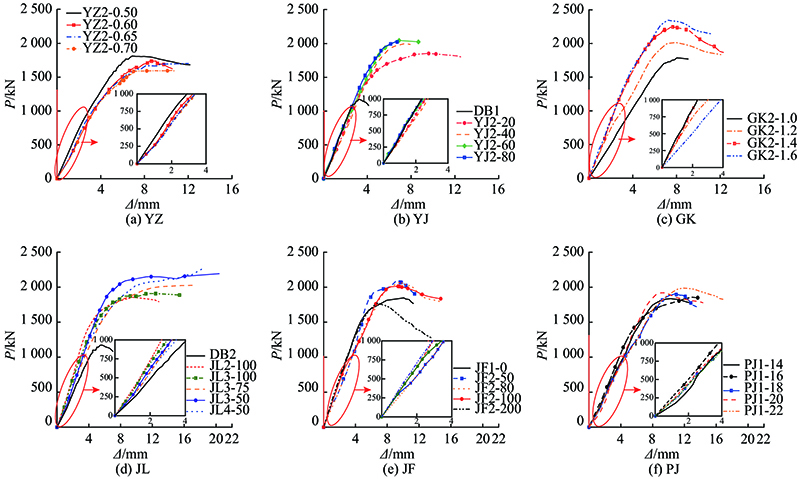
图 6   CFRP约束型钢混凝土试验中各组柱的轴向荷载-变形曲线

Fig.6   Axial load-deformation curves of CFRP-confined reinforced steel concrete test columns in each group


预载组试件荷载-位移曲线如图6(a)所示，由曲线放大图可以看出，随着预载水平增大，柱中混凝土发生了一定的软化，曲线初始斜率逐渐降低，构件屈服荷载呈降低趋势. 在加载至峰值荷载段时，试件YZ2-0.5~YZ2-0.7对应的峰值荷载分别为1813、1740、1704、1601 kN，与DB1的1172 kN相比，分别提高了54.7%、48.5%、45.4%、36.6%，整体上说，随着预载水平增大，构件承载力不断减小. 屈服荷载后的构件轴向变形随预载水平升高而逐渐减少.

如图6(b)所示为圆角半径YJ组试件，在加载初期变形基本一致；在接近峰值荷载段时，曲线斜率逐渐减小，试件YJ2-20、YJ2-40、YJ2-60以及YJ2-80的峰值荷载分别为1856、1997 、2047 、2027 kN，与构件DB1的峰值荷载1172 kN相比，分别提高了58.4%、70.4%、74.7%、73.0%，显示大圆角半径对于混凝土有较强约束作用. 在越过峰值荷载后，YJ2-20、YJ2-40及YJ2-60变形急剧增大，直至纤维布断裂和构件破坏，荷载位移曲线斜率随圆角半径增大而增大；YJ2-80的曲线后半段近水平.

如图6(c)所示为高宽比GK组试件，当截面长边增大时，截面积增大造成轴向初始刚度和峰值承载力上升；高宽比为1的柱在达到峰值荷载后曲线并无明显下降段，但加固柱的荷载位移曲线下降段随着高宽比持续增大而越来越明显，构件破坏变为弱约束模式，说明在截面边长接近时，纤维布能实现更好的约束作用.

如图6(d)所示为加固量JL组试件. 体积加固率分别为0.163%、0.245%、0.306%、0.337%、0.449%的JL2-100、JL3-100、JL3-75、JL3-50、JL4-50，峰值荷载比DB1的分别提高了58.4%、63.0%、72.9%、87.0%、92.4%，极限变形分别增加了82.34%、137.04%、144.30%、190.31%、158.83%. 可以看出，随着加固率增加，约束柱峰值荷载和极限变形越大；但荷载增加幅度并不与加固率成正比. 曲线第2阶段的斜率也随加固率增加而增加.

如图6(e)所示为加固方式JF组试件. 随条带宽度和间距减小，JF2-200、JF2-100、JF2-80和JF2-50构件承载力增幅不断增加；采用同等加固布用量，但全包式的JF1-0在布的层数降低后，其承载力增幅降低. 条带式包裹对相邻条带布间隙处裸露的混凝土约束相对较弱，使得条带间距大的构件在约束后的轴压承载力提高幅度有限；且条带布宽度较窄有利于提高布的工作应变.

如图6(f)所示为配筋率PJ组试件，其纵筋配筋率为0.82%~2.00%，随着配筋率增大，约束后构件的承载力和变形能力也不断增加.

3.2. CFRP布应变

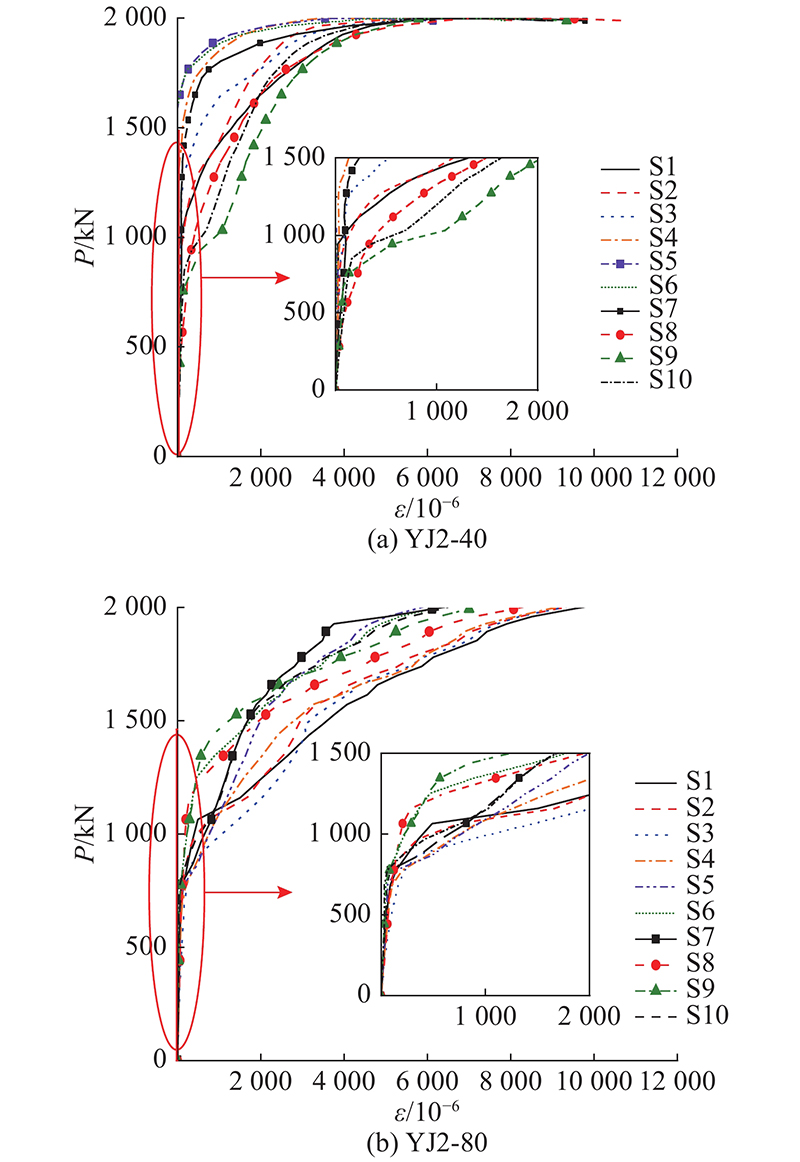
圆角组典型构件YJ2-40和YJ2-80的荷载和布应变ε如图7所示. 图中，S1~S10为图1(b)中沿截面周边各布应变测点. 可以看出，在加载初期各曲线基本呈线性增长，混凝土侧向变形不明显，布应变较小；随着荷载增加，混凝土裂缝发展，布应变逐渐增大，不同位置处应变差距大，各曲线斜率不断减小，并且在构件纵筋屈服后尤其明显；在峰值荷载处，曲线斜率逐渐减小直至近似呈水平；在峰值荷载后布应变仍继续增加. 对比图7(a)、(b)可以看出，YJ2-80中曲线斜率较小，且在柱的混凝土进入不稳定阶段后梯度明显；各测点应变总体高于YJ2-40的；且在相同荷载下，YJ2-80相应位置测点的应变大于YJ2-40的，如YJ2-80在极限荷载下的布平均拉应变为8754×10−6，大于YJ2-40相应的8388×10−6. 说明圆角半径增大使得布在截面上的应变分布趋于均匀并发挥更充分.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   YJ2-40和YJ2-80的荷载-CFRP应变曲线

Fig.7   Load-CFRP strain curves of YJ2-40 and YJ2-80


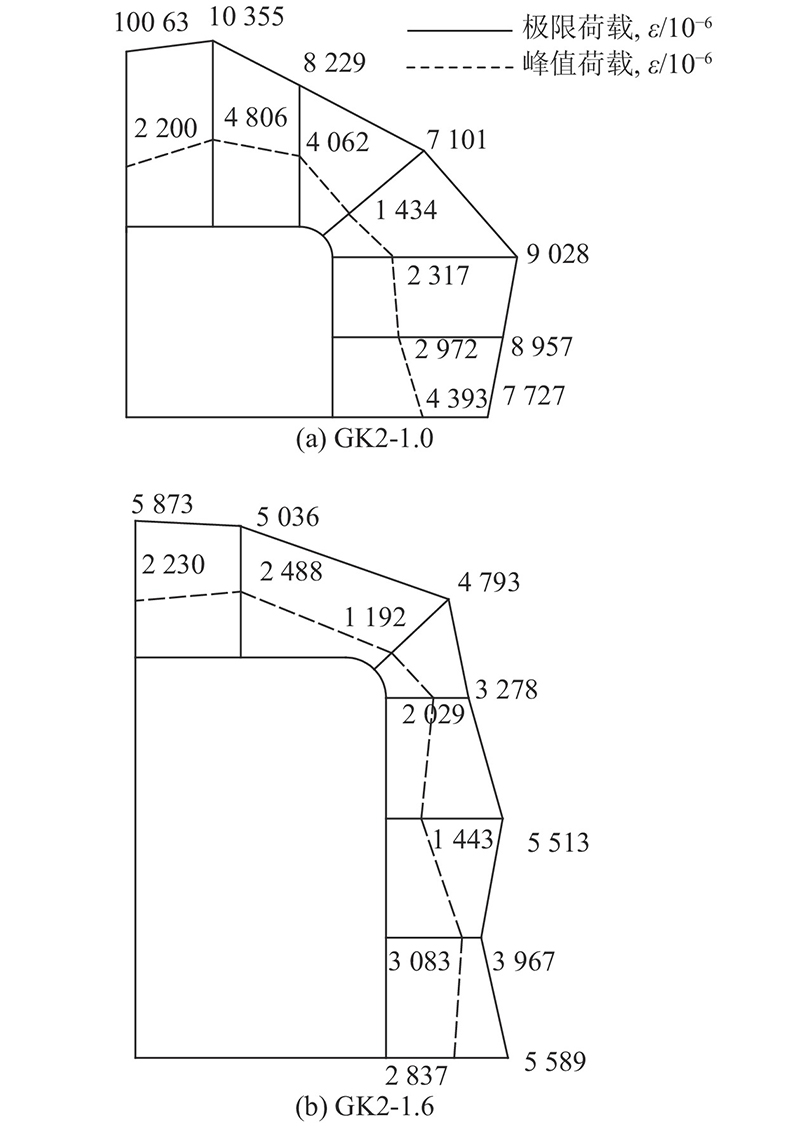
选取高宽比组中典型构件GK2-1.0和GK2-1.6，峰值和极限荷载时CFRP布应变分布如图8所示. 可以看出，各构件边长中部布应变均大于角部，且短边布应变较长边的大，差异随荷载增加而增大. GK2-1.0在峰值和极限荷载下布平均拉应变为3459×10−6、9060×10−6，分别大于GK2-1.6相应荷载下的对应值2354×10−6、5021×10−6. 说明随截面高宽比增大，CFRP布应变减小，等截面边长有利于实现约束作用.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   GK2-1.0和GK2-1.6的CFRP应变分布

Fig.8   CFRP strain distribution of GK2-1.0 and GK2-1.6


随着预载水平提高，在极限荷载时构件上布应变逐渐降低，由7962×10−6逐渐降低到6949×10−6. 因为预载引起构件中混凝土塑性残余应变，正式加载后布应变滞后现象明显. 在极限荷载时JL2-100、JL3-100、JL3-75和 JL3-50的布应变也随层数增加而减小.

4. 计算理论

4.1. 预载水平

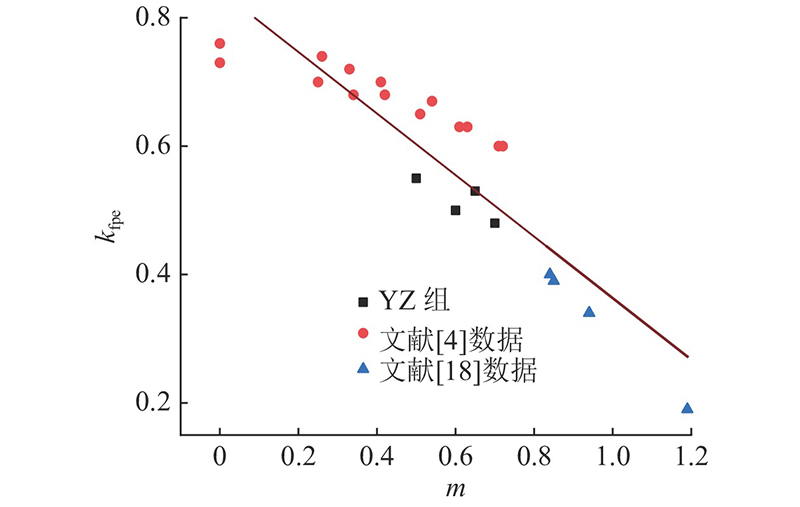
柱在轴力N预压作用下会形成混凝土开裂和塑性损伤，FRP布在约束柱时会有应变滞后现象，且应变滞后值与预载水平m=N/(fcoA)相关. 因此，定义布有效拉应变系数kfpe=εfpe/εfu，其中εfpe为CFRP布平均拉应变，εfu为布在材料试验中极限拉应变. 由试验纤维布应变数据可以计算出预载组各试件在极限状态下的布有效拉应变系数. 引用潘毅等[4]和熊学玉等[18]的构件试验数据，通过拟合得到有效拉应变系数kfpe和预载水平m的关系式：

$ {k_{{\rm{fpe}}}} = - 0.476m + 0.842\;1 . $

可见CFRP布有效拉应变系数随着预载水平的增大而降低，如图9所示.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   CFRP布有效拉应变系数和预载水平关系

Fig.9   Relationship between efficiency factor of CFRP strain and preload level


4.2. 圆角半径

采用Nistico等[19]通过试验数据回归分析得到的圆角半径与FRP布有效应变系数kε的关系式：

$ k_{\varepsilon }=f\left(r^{\prime}\right)=\left\{\begin{array}{l} 0.31+2 r^{\prime}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 \leqslant r^{\prime} \leqslant 02; \\ 0.71+0.087\;5\left(r^{\prime}- 02\right), \;0.2 < r \leqslant 1.0. \end{array}\right .$

式中：r′为等效圆角半径r/R，r为截面圆角半径，R=b/2. YJ2-20、YJ2-40、YJ2-60、YJ2-80对应的kε计算值为0.63、0.72、0.73、0.75，试验中CFRP布断裂应变分别为8139×10−6、8388×10−6、8675×10−6、8784×10−6，与计算值趋势一致.

4.3. 截面高宽比

在计算矩形柱的侧向约束应力f1时应考虑高宽比变化造成的不均匀性. 如图10(a)所示，Karam等[20]通过静力平衡分析计算出长短边方向的约束应力flx和fly 与布抗拉强度ffrp关系：

图 10

新窗口打开| 下载原图ZIP| 生成PPT

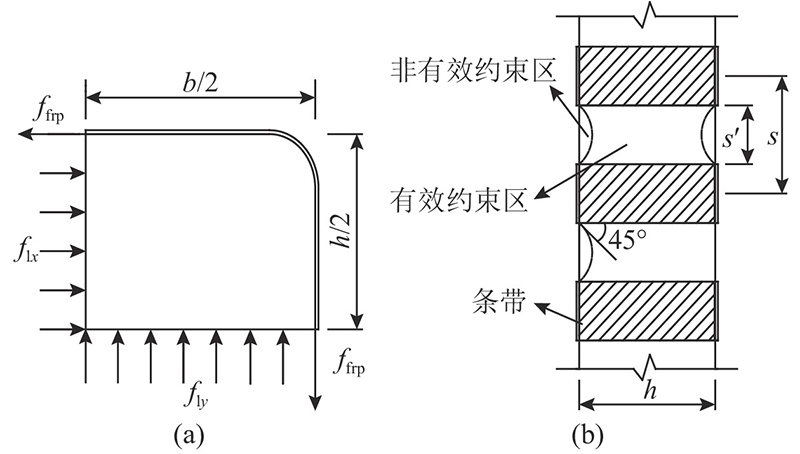
图 10   等效应力隔离体和条带式约束示意图

Fig.10   Illustration of free-body of equivalent stress and striped confinement


$ t{f_{{\rm{frp}}}} = h{f_{{{\rm{l}}x}}} = b{f_{{{\rm{l}}y}}}. $

式中：t为布厚度.

Saatcioglu等[21]指出f1与flx和fly，以及对应边长成比例关系：

$ {f_1} = \frac{{{f_{{{\rm{l}}x}}}b + {f_{{{\rm{l}}y}}}h}}{{b + h}}. $

综上，给出改进侧向约束应力表达式：

$ {f_{\rm{l}}} = \frac{{b/h + h/b}}{{b + h}}{f_{{\rm{frp}}}}t. $

当试验柱高宽比h/b由1.0变化至1.6时，fly计算值逐渐减小，对应f1分别为3.11、2.88、2.74、2.66，与试验中显示的约束效果趋势一致.

4.4. 条带间距

条带式布置会造成布对混凝土的约束在沿柱纵向长度各位置上分布不均匀，在考虑约束效应时须对f1进行折减. 参考Mander的研究[22]，定义条带间距影响系数kf，其为在条带间隙中间的约束最薄弱面处，柱混凝土的有效约束面积和全面积在各自减去配筋和配钢面积后的比值. 如图10(b)所示，设相邻条带之间有效约束与非有效约束区域采用二次抛物线划分，抛物线端部切线与柱边成45°，得到条带间距影响系数kf：

$ {k_{\rm{f}}} = \frac{{{S_{\rm{e}}}}}{{{S_{\rm{c}}}}} = \frac{{\left( {b - s'/2} \right)\left( {h - s'/2} \right) - {A_{\rm{y}}} - {A_{\rm{s}}}}}{{bh - {A_{\rm{y}}} - {A_{\rm{s}}}}} . $

式中：Se为最薄弱处的柱混凝土有效约束截面面积，Sc为柱全面积， $ {s'} $为相邻条带净间距,Ay和As分别为纵筋和型钢截面积. 试验中构件JF2-200、JF2-100、JF2-80、JF2-50的kf计算值分别为0.382、0.656、0.720、0.820.

5. 轴压承载力

5.1. 强弱约束界限

如前试验结果的 JL3-50和JL4-50构件，强约束柱外围纤维布断裂发生在荷载上升过程中，构件的峰值承载力发生在极限破坏状态；而其他弱约束柱的极限破坏状态发生在峰值承载力之后，这有利于加固柱的正常使用和破坏前预警. 现有研究中多使用约束比f1/fco来判定构件破坏模式. Mirmiran等[23]对约束比f1/fco乘以2r/D的圆角半径修正系数，h为矩形柱长边；当约束比(2r/h)f1/fco<0.15时，构件判定为弱约束. 而敬登虎等[11]在考虑矩形柱截面形状和圆角半径影响后将这个约束比限值降低到0.075. 工程柱截面尺寸较试验构件大，FRP布约束刚度比较小尺寸试验试件的偏小，更易形成弱约束状态. 基于考虑矩形截面高宽比的侧向约束应力fl（式(5)），结合影响FRP应变的其他参数，包含预载水平、圆角半径和条带间距等（代入式(1)、(2)、(6)），给出修正约束比的定义：

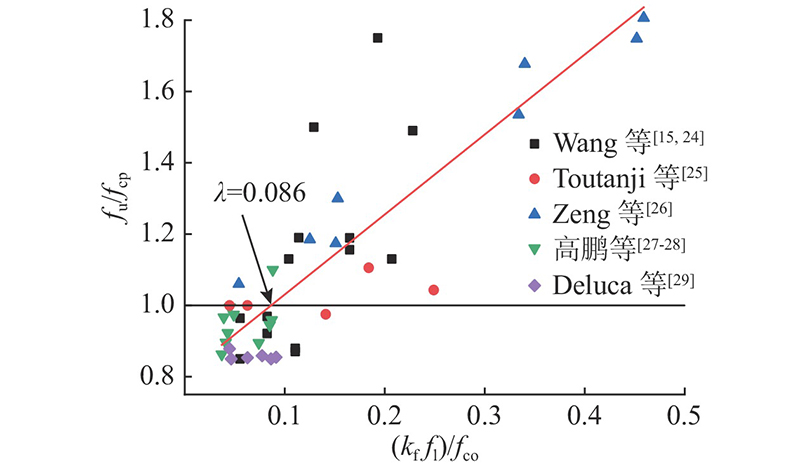
$ \lambda = \left.{\frac{{{f_{\rm{l}}}}}{{{f_{{\rm{co}}}}}} = \left({k_{\rm{f}}}{k_\varepsilon }{k_{{\rm{fpe}}}}\frac{{b/h + h/b}}{{b + h}}{f_{{\rm{frp}}}}t\right)}\right/{f_{{\rm{co}}}}. $

收集现有纤维布约束柱轴压性能试验数据，包含7篇文献中41个约束大矩形柱[15，24-29]. 柱边长为200~400 mm，高度为600~2000 mm；预载水平为0~0.75，对应有效拉应变系数kfpe为0.5089~0.8421；圆角半径为0~80 mm，有效应变系数kε为0.310~0.749；截面高宽比为1~2，由改进侧向约束应力公式（式（5））得到的fl计算值为3.62~23.92；条带间距分别为0、100 mm. 构件试验结果数据如图11所示. 图中，横坐标为约束比(kf fl)/ fco计算值，由式(7)计算得到；纵坐标为约束混凝土矩形柱极限应力fu与转折点或峰值点应力fcp的比值fu/ fcp，当fu/ fcp>1.0时构件表现为强约束，反之则表现为弱约束. 通过对图11数据的线性回归分析发现，当应力应变关系曲线处于强弱约束临界状态，即fu/ fcp=1.0时，与拟合直线交点得到对应修正约束比(kf fl)/ fco界限值λ=0.086. 在设计约束柱时，可以通过式(7)来调整参数，将破坏模式控制为弱约束.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   侧向约束比的强弱模式界限值

Fig.11   Boundary value of lateral confinement ratio for strong and weak modes


5.2. 约束区划分

根据ACI规范[30]将FRP约束矩形柱定义为有效约束区和非有效约束区，其中由4条抛物线所围成的部分为有效约束区，且这些抛物线与柱四边的夹角均为45°. 采用Chen等[31]对组合柱核心约束区的定义，以翼缘和腹板为边界，和由2条在型钢翼缘端点的初始正切角为45°的二次抛物线组成高强约束区. 因此，将FRP约束型钢混凝土柱截面划分为：高强约束区、部分约束区和未约束区，如图12所示.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

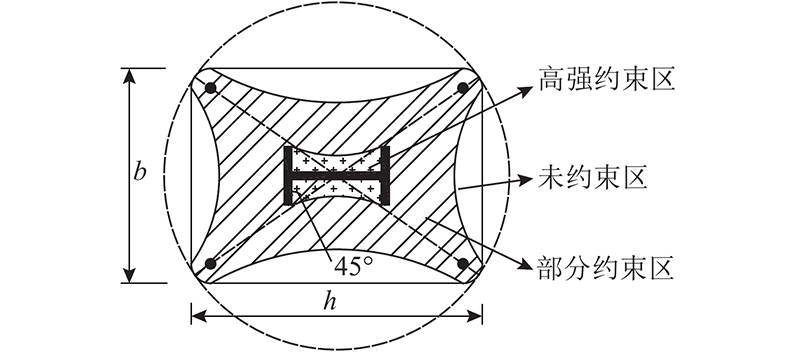
图 12   约束混凝土组合柱截面中混凝土约束区划分

Fig.12   Regionalization of confined concrete in cross sections of strengthened composite column


5.3. 承载力计算式

基于Razvi等[32]得到的混凝土在约束作用下的强度模型： $f_{{\rm{c c}}} / f_{{\rm{c o}}}=1+k_{1} f_{1} / f_{{\rm{c o}}}$，其中fcc为部分约束区混凝土抗压强度，k1为有效约束系数，可以引入不同参数考虑约束的不均匀性，进而修正k1. 因此，结合上文修正约束比λ，提出包含圆角半径、高宽比、预载水平、布条带加固方式等多参数影响的强度表达式：

$ \frac{{f}_{{\rm{cc}}}}{{f}_{{\rm{co}}}}=1+\lambda \text{=1+}\left({k}_{{\rm{f}}}{k}_{\varepsilon }{k}_{{\rm{fpe}}}\frac{b/h+h/b}{b+h}{f}_{{\rm{frp}}}t\right)/{f}_{{\rm{co}}} . $

高强约束区混凝土抗压强度fch可以定义为fch=kh fcc，其中kh为强度提高因子. 参考文献[28]约束柱构件数值分析的高强区混凝土应力结果，在考虑安全可靠性的基础上，kh取1.1.

采用静力叠加法[33]，建立多参数影响下约束组合柱的轴压承载力表达式：

$ {N_{\rm{c}}} = 0.85\left( {{f_{\rm{y}}}{A_{\rm{y}}} + {f_{\rm{s}}}{A_{\rm{s}}} + {f_{{\rm{co}}}}{A_{{\rm{co}}}} + {f_{{\rm{cc}}}}{A_{{\rm{cc}}}} + {f_{{\rm{ch}}}}{A_{{\rm{ch}}}}} \right) . $

式中：fy、fs分别为纵筋和型钢的屈服强度设计值，Aco、Acc、Ach分别为未约束混凝土、部分约束混凝土和高强约束混凝土的截面积，0.85为柱承载力可靠系数.

6. 计算验证

采用式（9）对文中试验构件进行计算验证，材料强度均取试验值，其中型钢和纵筋强度分别为227、465 MPa，第1批混凝土强度为21.95 MPa，第2批混凝土为20.26 MPa. CFRP布强度为3506 MPa，单层厚度为0.111 mm. 由5.1节可知，修正约束比界限值为0.084，本研究中仅有试件JL3-50和JL4-50对应的λ不小于界限值0.086，分别为0.086和0.114，这与图6试验结果中显示的荷载位移曲线结果一致. 各个构件的承载力试验值Ne与计算值Nc对比结果如表2所示. 其中弱约束构件的Nc/Ne的平均值为1.015，标准差为0.082；2个强约束构件的Nc/Ne的平均值为0.908，标准差为0.012. 表明根据（9）式得到的弱约束构件计算值与试验结果更吻合.

表 2   碳纤维布约束型钢混凝土柱轴压承载力的试验值与计算值对比

Tab.2  Comparison between experimental results and calculation value of compressive bearing capacities for CFRP-confined reinforced steel concrete columns

编号 A/mm2 Aco/mm2 Acc/mm2 Ach/mm2 λ fcc/MPa Nc/kN Ne/kN Nc/Ne
YZ2-0.50 74656 36418 33031 2968 0.033 22.67 1973 1813 1.088
YZ2-0.60 74656 36418 33031 2968 0.030 22.61 1972 1740 1.133
YZ2-0.65 74656 36418 33031 2968 0.029 22.58 1971 1704 1.157
YZ2-0.70 74656 36418 33031 2968 0.028 22.55 1970 1601 1.230
YJ2-20 74656 36418 33031 2968 0.046 22.95 1982 1856 1.068
YJ2-40 73624 25004 43413 2968 0.052 23.10 1977 1997 0.990
YJ2-60 71904 15760 50937 2968 0.053 23.12 1954 2047 0.954
YJ2-80 69496 8684 55605 2968 0.054 23.14 1915 2027 0.945
JL2-100 74656 36418 33031 2968 0.046 22.95 1982 1856 1.068
JL3-100 74656 36418 33031 2968 0.068 23.45 1998 1928 1.036
JL3-75 74656 36418 33031 2968 0.077 23.64 2003 2026 0.989
JL3-50 74656 36418 33031 2968 0.086 23.83 2009 2192 0.917
JL4-50 74656 36418 33031 2968 0.114 24.45 2028 2255 0.900
JF1-0 74656 36418 33031 2968 0.038 21.02 1870 1848 1.012
JF2-50 74656 36418 33031 2968 0.062 21.51 1885 2082 0.906
JF2-80 74656 36418 33031 2968 0.054 21.36 1881 2070 0.909
JF2-100 74656 36418 33031 2968 0.049 21.26 1878 2014 0.932
JF2-200 74656 36418 33031 2968 0.029 20.84 1865 1772 1.052
GK2-1.0 62156 29400 27549 2968 0.051 21.30 1659 1786 0.929
GK2-1.2 74656 36418 33031 2968 0.049 21.26 1878 2014 0.932
GK2-1.4 87156 43461 38488 2968 0.049 21.25 2097 2246 0.934
GK2-1.6 99656 50520 43929 2968 0.048 21.24 2317 2346 0.987
PJ1-14 74656 36418 33220 2968 0.025 20.76 1791 1838 0.974
PJ1-16 74656 36418 33031 2968 0.025 20.76 1862 1856 1.003
PJ1-18 74656 36418 32818 2968 0.025 20.76 1943 1906 1.019
PJ1-20 74656 36418 32579 2968 0.025 20.76 2033 1923 1.057
PJ1-22 74656 36418 32315 2968 0.025 20.76 2133 1988 1.073

新窗口打开| 下载CSV


7. 结　论

本研究通过试验和理论研究圆角半径、截面高宽比、预载水平、加固方式和加固量等参数对CFRP约束型钢混凝土矩形柱承载力的影响，得到结论如下：

（1）随着预载水平提高，纤维布有效拉应变不断减小，约束柱承载力降低；随着圆角半径增大，布环向应变分布趋于均匀，约束柱轴压荷载-变形曲线在峰值荷载后由平缓下降段向上升段转化；截面高宽比越大，布工作应变越小；在布用量相同的前提下，构件承载力随条带间距减小而增大.

（2）由收集文献的试验数据结果确定出FRP布约束大尺寸混凝土柱强弱约束界限值0.086. 考虑圆角半径、高宽比、预载水平和布条带加固方式对侧向约束应力fl的影响，根据叠加法建立FRP约束矩形型钢混凝土组合柱的轴压承载力计算公式.

本研究结果对FRP约束加固组合柱的轴压性能具有指导作用，但此次试验柱尺寸受设备的加载吨位限制，后续可以进行更大尺寸的约束加固柱轴压试验和数值模拟研究.

参考文献

刘伟庆, 方海, 方园

纤维增强复合材料及其结构研究进展

[J]. 建筑结构学报, 2019, 40 (4): 1- 16

[本文引用: 1]

LIU Wei-qing, FANG Hai, FANG Yuan

Research progress of fiber-reinforced composite and structure

[J]. Journal of Building Structures, 2019, 40 (4): 1- 16

[本文引用: 1]

吴智深, 汪昕, 史健喆

玄武岩纤维复合材料性能提升及其新型结构

[J]. 工程力学, 2020, 37 (5): 1- 14

WU Zhi-shen, WANG Xin, SHI Jian-zhe

Advancement of basalt fiber-reinforced polymers (BFRPS) and the novel structures reinforced with BFRPS

[J]. Engineering Mechanics, 2020, 37 (5): 1- 14

史庆轩, 戎翀, 陈云枭

FRP-钢-混凝土组合柱的研究现状

[J]. 建筑材料学报, 2019, 22 (3): 431- 439

DOI:10.3969/j.issn.1007-9629.2019.03.015      [本文引用: 1]

SHI Qing-xuan, RONG Chong, CHEN Yun-xiao

Research status of FRP-steel-concrete composite column

[J]. Journal of Building Materials, 2019, 22 (3): 431- 439

DOI:10.3969/j.issn.1007-9629.2019.03.015      [本文引用: 1]

潘毅, 曹双寅, 敬登虎

负载下碳纤维布约束混凝土方柱轴压应力-应变关系的试验研究与分析

[J]. 土木工程学报, 2009, 42 (1): 23- 29

DOI:10.3321/j.issn:1000-131X.2009.01.004      [本文引用: 2]

PAN Yi, CAO Shuang-yin, JING Deng-hu

Test and analysis of the axial stress-strain relationship of square section concrete columns confined by CFRP under preload

[J]. Journal of Civil Engineering, 2009, 42 (1): 23- 29

DOI:10.3321/j.issn:1000-131X.2009.01.004      [本文引用: 2]

潘毅, 吴晓飞, 郭瑞, 等

长期荷载作用下FRP约束混凝土应力-应变关系分析模型

[J]. 建筑结构学报, 2017, 38 (10): 139- 148

[本文引用: 1]

PAN Yi, WU Xiao-fei, GUO Rui, et al

Analysis-oriented stress-strain model of FRP-confined concrete under long-term sustained load

[J]. Journal of Building Structures, 2017, 38 (10): 139- 148

[本文引用: 1]

WANG L M, WU Y F

Effect of corner radius on the performance of CFRP-confined square concrete columns: test

[J]. Engineering Structures, 2008, 30: 493- 505

DOI:10.1016/j.engstruct.2007.04.016      [本文引用: 1]

MOSTOFINEJAD D, MOSHIRI N, MORTAZAVI N

Effect of corner radius and aspect ratio on compressive behavior of rectangular concrete columns confined with CFRP

[J]. Materials and Structures, 2015, 48 (1/2): 107- 122

[本文引用: 1]

WU Y F, WEI Y Y

Effect of cross-sectional aspect ratio on the strength of CFRP confined rectangular concrete columns

[J]. Engineering Structures, 2010, 32 (1): 32- 45

DOI:10.1016/j.engstruct.2009.08.012      [本文引用: 1]

PARK T W, NA U J, CHUNG L, et al

Compressive behavior of concrete cylinders confined by narrow strips of CFRP with spacing

[J]. Composites Part B: Engineering, 2008, 39 (7/8): 1093- 1103

[本文引用: 1]

周长东, 黄承逵

玻璃纤维聚合物约束混凝土方柱简化分析模型

[J]. 哈尔滨工业大学学报, 2004, 36 (5): 637- 641,651

DOI:10.3321/j.issn:0367-6234.2004.05.021      [本文引用: 1]

ZHOU Chang-dong, HUANG Cheng-kui

Simplified analytic models for GFRP confined concrete square columns

[J]. Journal of Harbin Institute of Technology, 2004, 36 (5): 637- 641,651

DOI:10.3321/j.issn:0367-6234.2004.05.021      [本文引用: 1]

敬登虎, 曹双寅

方形截面混凝土柱FRP约束下的轴向应力-应变曲线计算模型

[J]. 土木工程学报, 2005, 38 (12): 32- 37

DOI:10.3321/j.issn:1000-131X.2005.12.006      [本文引用: 2]

JING Deng-hu, CAO Shuang-yin

A model for calculating the axial stress-strain curve of square-section concrete column confined by FRP

[J]. China Civil Engineering Journal, 2005, 38 (12): 32- 37

DOI:10.3321/j.issn:1000-131X.2005.12.006      [本文引用: 2]

中国冶金建设协会. 纤维增强复合材料建设工程应用技术规范: GB 50608—2010 [S]. 北京: 中国计划出版社, 2011.

[本文引用: 1]

王作虎, 申书洋, 崔宇强, 等

CFRP加固混凝土柱轴压性能尺寸效应试验分析

[J]. 哈尔滨工业大学学报, 2020, 52 (8): 112- 120

DOI:10.11918/201906169      [本文引用: 1]

WANG Zuo-hu, SHEN Shu-yang, CUI Yu-qiang, et al

Experimental analysis on size effect of axial compressive behavior for reinforced concrete columns with CFRP

[J]. Journal of Harbin Institute of Technology, 2020, 52 (8): 112- 120

DOI:10.11918/201906169      [本文引用: 1]

GUO Y C, GAO W Y, ZENG J J

Compressive behavior of FRP ring-confined concrete in circular columns: effects of specimen size and a new design-oriented stress-strain model

[J]. Construction and Building Materials, 2019, 201: 350- 368

DOI:10.1016/j.conbuildmat.2018.12.183      [本文引用: 1]

WANG D Y, WANG Z Y, SMITH S T, et al

Size effect on axial stress-strain behavior of CFRP-confined square concrete columns

[J]. Construction and Building Materials, 2016, 118: 116- 126

DOI:10.1016/j.conbuildmat.2016.04.158      [本文引用: 2]

MASIA M J, GALE T N, SHRIVE N G

Size effects in axially loaded square-section concrete prisms strengthened using carbon fibre reinforced polymer wrapping

[J]. Canadian Journal of Civil Engineering, 2004, 31 (1): 1- 13

DOI:10.1139/l03-064      [本文引用: 1]

中国国家标准化管理委员会. 金属材料室温拉伸试验方法: GB/T 228—2002 [S]. 北京: 中国标准出版社, 2002.

[本文引用: 1]

熊学玉, 徐海峰, 李亚明

负载下CFRP布约束钢筋混凝土矩形柱轴心受压性能分析

[J]. 土木工程学报, 2010, 43 (6): 26- 33

[本文引用: 1]

XIONG Xue-yu, XU Hai-feng, LI Ya-ming

The axial compressive behavior of CFRP-confined rectangular RC columns under service loading

[J]. China Civil Engineering Journal, 2010, 43 (6): 26- 33

[本文引用: 1]

NISTICO N, MONTI G

RC square sections confined by FRP: analytical prediction of peak strength

[J]. Composites Part B: Engineering, 2013, 45 (1): 127- 137

[本文引用: 1]

KARAM G, TABBARA M

Confinement effectiveness in rectangular concrete columns with fiber reinforced polymer wraps

[J]. Journal of Composites for Construction, 2005, 9 (5): 388- 396

DOI:10.1061/(ASCE)1090-0268(2005)9:5(388)      [本文引用: 1]

SAATCIOGLU M, RAZVI S R

Strength and ductility of confined concrete

[J]. Journal of Structural Engineering, 1992, 118 (6): 1590- 1607

DOI:10.1061/(ASCE)0733-9445(1992)118:6(1590)      [本文引用: 1]

MANDER J B, PRIESTLEY M J N, PARK R

Theoretical stress-strain model for confined concrete

[J]. Materials in Civil Engineering, 1988, 114 (8): 1804- 1826

[本文引用: 1]

MIRMIRAN A, SHAHAWY M, SAMAAN M, et al

Effect of column parameters on FRP-confined concrete

[J]. Journal of Composites for Construction, 1998, 2 (4): 175- 185

DOI:10.1061/(ASCE)1090-0268(1998)2:4(175)      [本文引用: 1]

王代玉, 王震宇, 乔鑫

CFRP中等约束钢筋混凝土方柱反复受压本构模型

[J]. 湖南大学学报:自然科学版, 2014, 41 (4): 39- 46

[本文引用: 1]

WANG Dai-yu, WANG Zhen-yu, QIAO Xin

Cyclic stress strain model for CFRP moderately confined reinforced concrete square columns

[J]. Journal of Hunan University: Natural Science Edition, 2014, 41 (4): 39- 46

[本文引用: 1]

TOUTANJI H, HAN M, GILBERT J, et al

Behavior of large-scale rectangular columns confined with FRP composites

[J]. Journal of Composites for Construction, 2010, 14 (1): 62- 71

DOI:10.1061/(ASCE)CC.1943-5614.0000051     

ZENG J J, LIN G, TENG J G, et al

Behavior of large-scale FRP-confined rectangular RC columns under axial compression

[J]. Engineering Structures, 2018, 174: 629- 645

DOI:10.1016/j.engstruct.2018.07.086     

高鹏, 殷强, 王健, 等

复材布约束有预压荷载的型钢混凝土矩形短柱轴压性能试验研究

[J]. 工业建筑, 2016, 46 (6): 170- 176

GAO Peng, YIN Qiang, WANG Jian, et al

Experimental study of the axial compressive performance of preloaded steel reinforced concrete rectangular short column confined by carbon fiber reinforced polymer laminates

[J]. Industrial Building, 2016, 46 (6): 170- 176

高鹏, 赵元鸿, 洪丽, 等

圆角半径对碳纤维增强聚合物复合材料布约束型钢混凝土矩形短柱轴压性能的影响

[J]. 复合材料学报, 2020, 37 (4): 775- 785

[本文引用: 1]

GAO Peng, ZHAO Yuan-hong, HONG Li, et al

Effect of corner radius on axial compressive performance of steel reinforced concrete rectangular short column confined by carbon fiber reinforced polymer composite

[J]. Acta Materiae Composite Sinica, 2020, 37 (4): 775- 785

[本文引用: 1]

DELUCA A, NARDONE F, MATTA F, et al

Structural evaluation of full-scale FRP-confined reinforced concrete columns

[J]. Journal of Composites for Construction, 2011, 15 (1): 112- 123

DOI:10.1061/(ASCE)CC.1943-5614.0000152      [本文引用: 1]

ACI 440 Committee. Guide for design and construction of externally bonded FRP systems for strengthening concrete structures: ACI 440.2R-08 [S]. Farmington Hills: American Concrete Institute, 2008.

[本文引用: 1]

CHEN C C, LIN N J

Analytical model for predicting axial capacity and behavior of concrete encased steel composite stub columns

[J]. Journal of Constructional Steel Research, 2006, 62 (5): 424- 433

DOI:10.1016/j.jcsr.2005.04.021      [本文引用: 1]

RAZVI S, SAATCIOGLU M

Confinement model for high-strength concrete

[J]. Journal of Structural Engineering, 1999, 125 (3): 281- 289

DOI:10.1061/(ASCE)0733-9445(1999)125:3(281)      [本文引用: 1]

王连广, 秦国鹏, 周乐

GFRP管钢骨高强混凝土组合柱轴心受压试验研究

[J]. 工程力学, 2009, 26 (9): 170- 175

[本文引用: 1]

WANG Lian-guang, QIN Guo-peng, ZHOU Le

Experimental research of GFRP tube columns filled with steel-reinforced high-strength concrete subjected to axial loading

[J]. Engineering Mechanics, 2009, 26 (9): 170- 175

[本文引用: 1]

/

〈 〉