随着风电渗透率的提高,风电对电网频率稳定性的影响愈加严重,将增加电网调频的需求. 风电参与电网的调频能力研究更加必要. 目前,风电机组参与调频的思路是让风电自行提供一部分调频容量. 设置合理的市场机制,确定风电参与调频市场的投标策略,将有助于缓解电网调频压力,提升风电场收益[1].
本文提出考虑风电不确定性的风电场参与电网调频的分析方法,求解得到风电机组参与能量和调频市场的投标功率. 在风电场收益机制方面,调频市场收益中引入调频性能指标,以有效地反映风电场真实的调频收益,提出调频性能指标的估值方法. 在风电功率预测方面,基于粒子群优化(particle swarm optimization,PSO)算法,结合核极限学习机(kernel extreme learning machine,KELM)和核密度非参数估计的特点,建立风电功率的概率密度预测模型. 基于该概率密度预测结果,建立以风电场收益最大为目标函数的优化模型. 利用蚁狮优化(ant lion optimization,ALO)算法求解模型,确定次日风电场参与能量与调频市场的最优投标功率. 利用风电场数据,开展仿真验证. 结果表明,本文提出的风电场参与能量和调频市场的投标策略更加灵活,可以提高风电场收益,具有优越性和普适性.
1. 基于PJM交易规则的风电场交易收益分析
1.1. 风电场在能量市场的收益
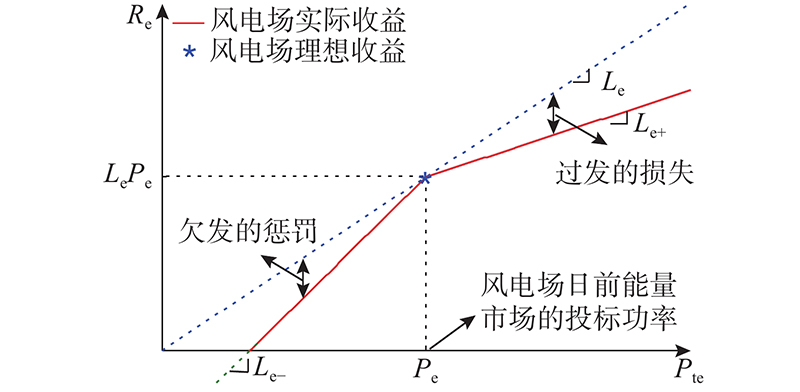
由于国内风电参与电力市场辅助服务的交易规则还需完善,以美国的宾夕法尼亚州-新泽西州-马里兰州电力联营体(PJM)能量交易市场的交易规则为依据,展开风电场的相关收益分析. 根据PJM的日前市场交易规则可知,风电场在能量市场的收益可以表示为
式中:
图1中,*表示风电场理想情况下的收益,即
图 1
1.2. 风电场在调频备用市场的收益
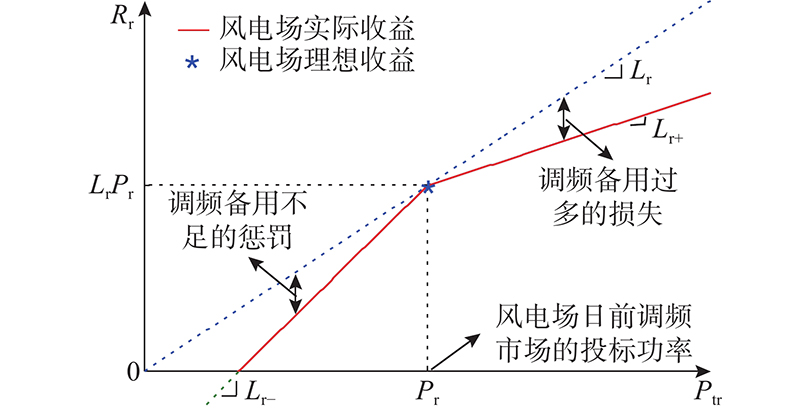
风电场在调频市场参与二次调频服务[1]. 根据PJM的日前市场交易规则可知,收益可以表示为
式中:
式中:
式中:
通过对具体数据的回归分析,可以得到K与多元变量的关系,实现在日前投标时精确考虑风电的动态调频性能,有效地反映风电场真实的调频收益.
图2中,*表示理想情况下风电场在调频市场中的收益,即风电场的实际调频功率与日前调频市场的投标功率一致时的收益;实线为风电场在调频市场中的收益随风电场实际提供的调频功率的变化情况.
图 2
2. 风电场同时参与能量市场与调频市场的投标策略
风电场单独参与能量市场时风电功率的波动会降低风电场的经济效益. 风电场同时参与能量市场与调频市场并进行最优投标时,能够利用风电功率的波动提供调频备用,在提供调频备用的同时提高风电场经济收益. 根据1章的描述可知,风电场同时参与2种市场的总收益为
风电场收益可以表示为
式中:
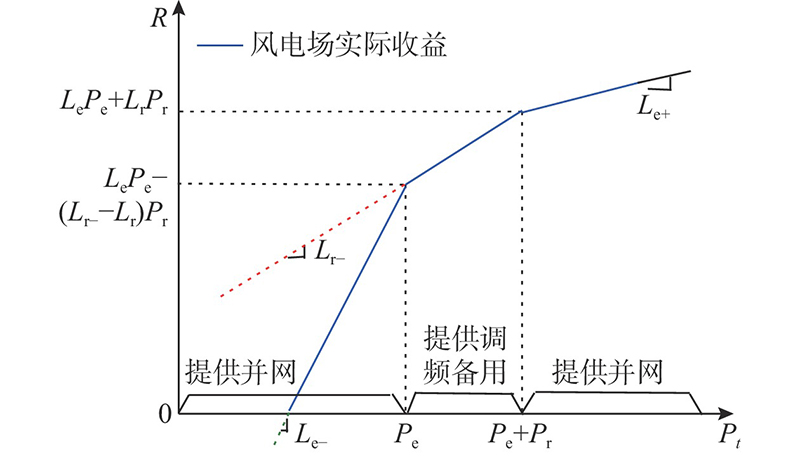
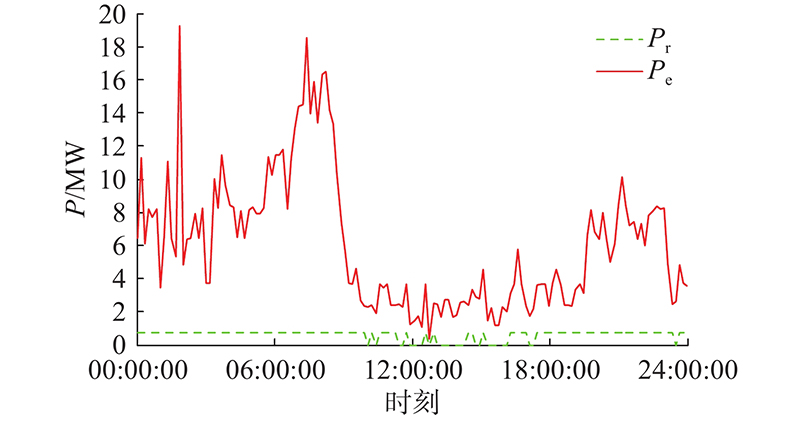
如图3所示为风电场同时参与能量市场和调频市场的投标策略及风电场收益随
图 3
图 3 风电场同时参与2种市场的投标策略及收益情况
Fig.3 Bidding strategy and revenue of wind farm participating in both markets
3. KELM-PSO-KDE风电功率概率密度预测模型
从图3可知,风电场在日前市场投标的并网功率和调频备用功率直接影响风电场收益. 风电场想要确定在日前能量市场和调频市场的投标功率,必须借助风电功率的预测. 若风电功率的单点预测是精确的,则风电场只需要依据单点预测结果在能量市场投标,即可获得最大收益. 由于风电功率的单点预测存在无法消除的误差,风电的概率预测能够更好地描述功率分布的情况,为风电场的投标策略提供参考. 提出结合核极限学习机(KELM)、粒子群优化(PSO)算法和核密度估计(kernel density estimation,KDE)的风电功率概率密度预测模型.
3.1. 基于PSO优化的KELM风电功率点预测模型
Huang等[10]提出极限学习机(extreme learning machine,ELM). KELM是改进ELM模型,具有更强的泛化能力和稳定性. KELM模型为
式中:xi为风速;
其中σ为核参数.
核矩阵为
式中:
3.2. 基于核密度估计(KDE)的概率密度函数估计
利用建立的风电功率点预测模型和获得的历史预测误差,可以得到风电功率在t时刻的独立同分布数据
式中:
核密度估计方法作为有效的非参数估计方法之一,无需先验分布假设,可以直接估计被求变量的概率密度函数. 使用KDE估计风电功率的概率密度,具有更强的适应性.
给定
式中:ht > 0为平滑参数,称为带宽(bandwidth); qt为通过ht和
3.3. KELM-PSO-KDE风电功率概率密度预测模型
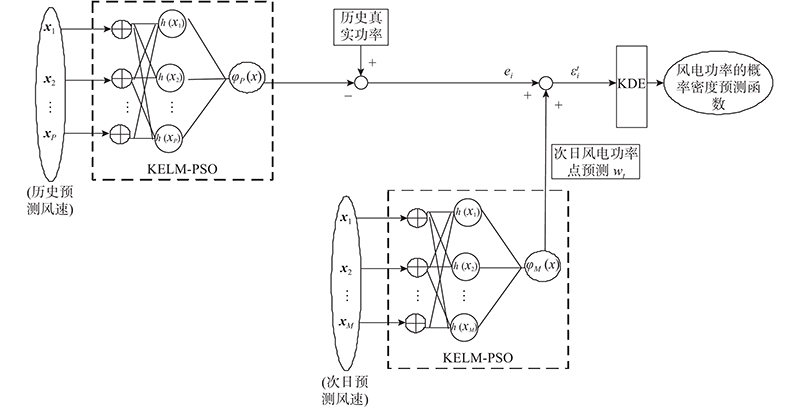
将KELM、PSO算法和KDE组合,提出基于PSO算法优化的核极限学习机核密度估计的风电功率概率密度预测模型KELM-PSO-KDE,示意图如图4所示. 具体步骤如下.
图 4
图 4 核极限学习机-粒子群-核密度估计预测模型
Fig.4 Wind power probability prediction model of KELM-PSO-KDE
1)结合PSO算法与KELM模型,通过PSO算法优化得到最优的核参数σ和C,代入KELM中,得到KELM-PSO模型.
2)将历史预测风速数据代入KELM-PSO模型中,通过式(11)得到历史风电功率点预测结果,并将此预测结果与真实风电功率数据比较后得到
3)将次日预测风速数据代入KELM-PSO模型中,通过式(11)得到次日风电功率的点预测结果,将此预测结果与
4)对
在提出的风电功率概率密度预测模型中,KELM模型较神经网络具有更快的学习速度和更好的非线性拟合能力,可以拟合风速与风电功率的非线性关系. KDE不给任何分布的假定,通过设置合适的带宽和核函数,可以完整地估计对象风电功率的概率密度. 在模型中,将两者结合,能够很好地把握风电功率预测中的不确定信息变化情况,生成风电功率的概率密度函数,避免传统功率概率预测方法中模型复杂、需要先验分布的假设、参数估计偏离等带来的预测误差问题,为后续得到能量和调频市场最优投标功率奠定基础.
4. 基于风电功率概率密度预测的最优投标功率确定
基于风电功率概率密度预测结果,构建风电场期望收益模型. 通过蚁狮优化(ALO)算法,求解得到风电场参与能量市场和调频市场的最优投标功率,获得风电场的最大收益.
利用式(16)得到次日t时刻的风电功率概率密度预测函数
式中:
构建风电场t时刻的期望收益模型:
式(18)中含有调频性能指标K,满足关系
提出的确定风电场最优投标功率的步骤如下.
1)根据市场交易规则,确定风电场同时参与能量市场和调频市场的投标策略,计算风电场收益随实际发电功率的变化情况.
2)利用风电功率概率密度预测模型KELM-PSO-KDE,求得次日每一时刻的风电功率概率密度预测函数.
3)根据风电功率概率密度预测结果,以风电场期望收益最大为目标,建立风电场同时参与能量市场和调频市场的优化模型. 利用ALO算法获得风电场在2种市场日前最优的投标计划,使风电场的收益最大化.
5. 算例分析
以内蒙古某风电场为例,该风场装机容量为50 MW,分辨率为10 min. 取该风场 2014 年的风电功率数据,包括实际功率数据和对应的数值天气预报数据中的风速信息.
5.1. 最优投标功率确定及对应的风电场收益
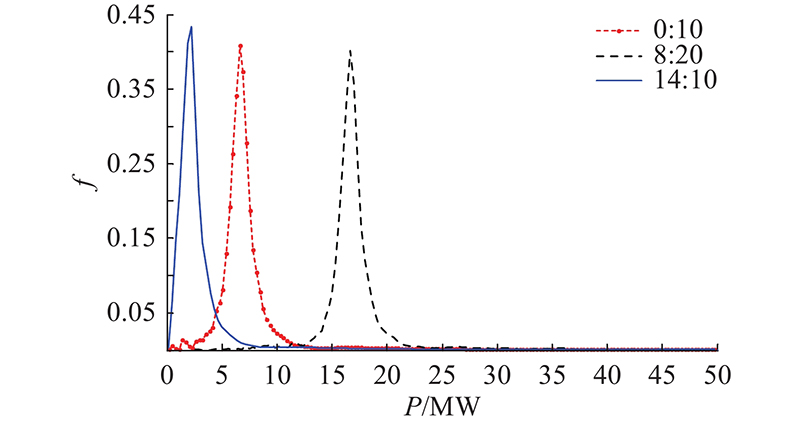
根据3.3节的具体步骤,利用KELM-PSO-KDE模型对次日所有时刻进行风电功率的概率密度函数预测. 该天一些时刻的风电功率概率密度预测曲线如图5所示. 图中,f为概率密度,P为风电功率.
图 5
图 5 某些时刻的风电功率概率密度预测曲线
Fig.5 Probability density prediction curves of wind power at some time
KEIM具有非线性拟合能力强的特点,因此利用KELM拟合
基于获得的一天所有时刻的功率概率密度预测曲线和调频性能指标估值模型,建立式(18)所示的所有时刻的优化模型. 风电上网电价
利用ALO算法对所有时刻的优化模型进行求解,ALO算法的初始参数如表1所示.
表 1 ALO算法的初始参数
Tab.1
| 蚁狮数目 | 迭代次数 | | |
| 50 | 100 | [0,50] | [0,50] |
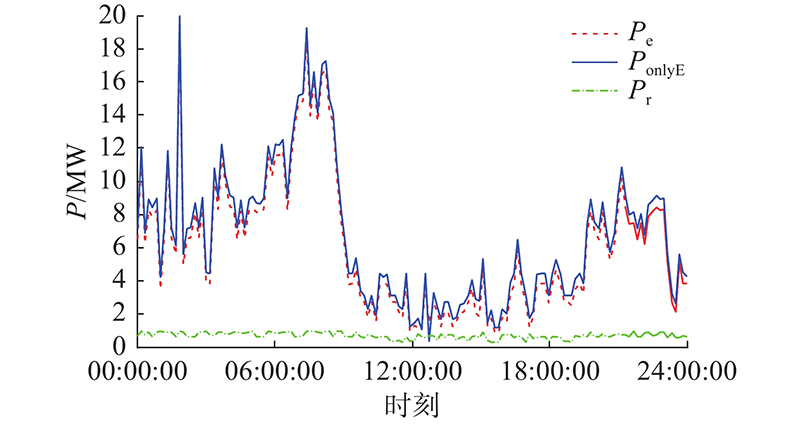
图 6
图 6 在2种市场同时投标与单独在能量市场投标的功率对比
Fig.6 Comparison of bidding power in both two markets versus only in energy market
如表2所示为2种参与方式下风电场在该天某些时刻的收益和一天的总收益. 可知,该天风电场参与2种市场并进行最优投标时的收益比风电场单独参与能量市场时的收益增加3 289元,原因如下. 当风电场单独参与能量市场时,实际的发电功率为并网功率,因投标功率与并网功率的误差较大,风电场收益减小.当风电场参与2种市场并进行最优投标时,风电场不仅向能量市场提供功率,而且可以将多余的功率放入调频市场,提供调频备用,缓解电网调频压力. 这种投标策略更加灵活,可以提高风电场收益.
表 2 风电场部分时刻的收益及一天总收益的对比
Tab.2
| 时刻 | 同时参与能量市场与调频市场 | 单独参与能量市场 | ||||
| | | R/元 | | Re /元 | ||
| | | | | | | |
| 0:30 | 6.274 8 | 0.725 5 | 478.836 1 | 6.864 1 | 439.943 7 | |
| 6:30 | 11.853 4 | 0.934 9 | 889.246 7 | 12.538 5 | 844.201 9 | |
| 21:00 | 8.505 3 | 0.821 7 | 635.723 0 | 9.198 8 | 589.714 7 | |
| | | | | | | |
| 一天 | − | − | 56803 | − | 53514 | |
5.2. 在能量市场的投标误差对比
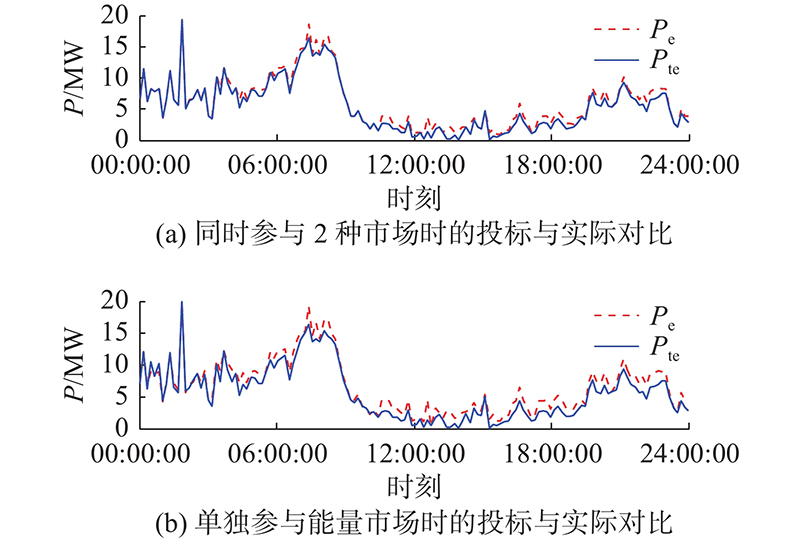
图7给出风电场参与电力市场的2种方式下,
图 7
图 7 能量市场投标功率与第2天在能量市场提供功率的对比图
Fig.7 Comparison of bidding power and actual power of next day in energy market
表3给出风电场参与电力市场的2种方式下,一天部分时刻
表 3 能量市场投标功率与实际提供功率的误差对比
Tab.3
| 时刻 | EE-FR/MW | EonlyE/MW |
| | | |
| 0:30 | 0.110 8 | 0.700 1 |
| 6:30 | 0.325 3 | 1.010 3 |
| 16:00 | 0.682 8 | 1.132 8 |
| | | |
| 一天平均值 | 0.616 4 | 1.088 1 |
5.3. 与参与2种市场的常量投标策略对比
为了验证提出的风电场同时参与能量和调频市场的最优投标策略的优越性,选用同时参与2种市场的常量投标策略进行对比分析.
根据文献[4],可以设定当风电功率点预测值大于装机容量的6%,即在本文中大于3 MW时,风电场参与能量市场和调频市场,此时2种市场的投标功率分别为
式中:
表 4 不同投标策略下的结果对比
Tab.4
| 投标策略 | R/元 | Eb/MW |
| 常量投标策略 | 50626 | 0.962 0 |
| 本文投标策略 | 56803 | 0.616 4 |
图 8
5.4. 不同风电功率概率密度预测模型的对比验证
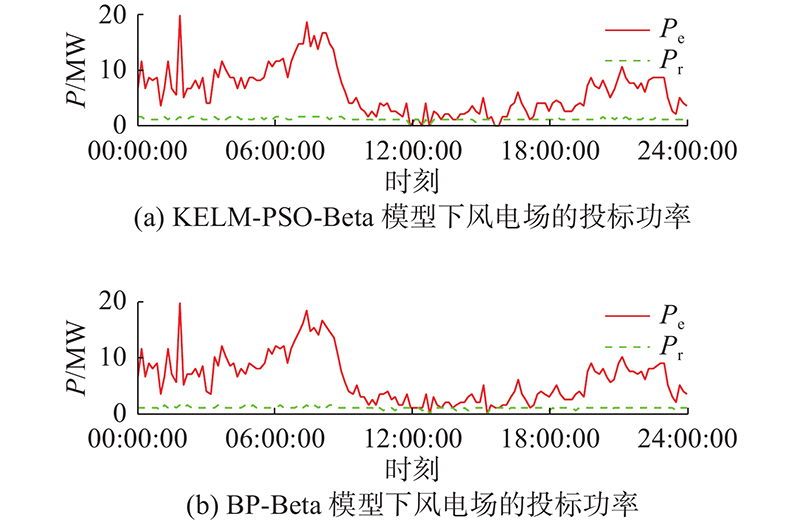
为了验证提出的KELM-PSO-KDE的优越性,基于相同的风电功率数据,选用风电概率密度预测模型KELM-PSO-Beta和BP-Beta进行对比分析.
从表5可知,与另外2种风电功率概率密度预测模型相比,在KELM-PSO-KDE模型下得到的风电场收益更高,能量市场日平均投标误差更小,说明该模型具有优越性,可以避免不准确的先验分布假设所造成的预测误差,更准确地描述风电不确定性,提高风电场收益.
图 9
图 9 3种风电功率概率密度预测模型下的风电场投标功率
Fig.9 Bidding power in E&FR markets obtained from three probability density prediction models of wind power
表 5 不同风电功率概率密度预测模型下的结果对比
Tab.5
| 风电功率概率密度预测模型 | R/元 | E/MW |
| BP-Beta | 56287 | 0.671 6 |
| KELM-PSO-Beta | 56305 | 0.637 3 |
| KELM-PSO-KDE | 56803 | 0.616 4 |
5.5. 不同求解方法的对比验证
为了验证所提的ALO算法的优越性,基于相同的风电功率数据,选用粒子群优化(PSO)算法求解模型,开展对比分析.
利用PSO算法和ALO算法分别求解该天所有时刻的优化模型,得到PSO算法的每一时刻平均求解时间为292.295 s,ALO算法的每一时刻平均求解时间为274.740 s. ALO算法的计算时间少于PSO算法,求解效率更高. 利用2种算法求解模型的结果如表6所示. 可知,在ALO算法下得到的风电场收益更高,能量市场的日平均投标误差更小,证明了ALO算法具有优越性.
表 6 不同求解方法下的结果对比
Tab.6
| 求解方法 | R/元 | E/MW |
| PSO | 56634 | 0.624 9 |
| ALO | 56803 | 0.616 4 |
5.6. 不同天的风电功率数据对比验证
表 7 另外一天的风电场收益及投标误差
Tab.7
| 投标策略 | R/元 | E/MW |
| 单独参与能量市场 | 158720 | 3.274 3 |
| 常量投标策略 | 153920 | 2.524 3 |
| 本文投标策略 | 161410 | 2.066 7 |
6. 结 语
本文提出考虑风电不确定性的风电场同时参与能量与调频市场的日前投标方法. 基于表征风电不确定性的KELM-PSO-KDE模型,利用ALO算法求解得到风电场在2种市场的日前最优投标功率. 该研究方法为风电机组同时参与2种市场及确定最优投标功率提供了新思路. 如何提高风电功率预测模型KELM-PSO-KDE的预测精度,使风电场参与2种市场的投标计划更加准确,是下一步的研究重点.
参考文献
风电参与能量—调频联合市场的优化策略
[J].DOI:10.7500/AEPS20151112004 [本文引用: 7]
Optimal strategy for wind power bidding in energy and frequency regulation markets
[J].DOI:10.7500/AEPS20151112004 [本文引用: 7]
Increased wind revenue and system security by trading wind power in energy and regulation reserve markets
[J].DOI:10.1109/TSTE.2011.2111468 [本文引用: 6]
Optimal offering strategies for wind power in energy and primary reserve markets
[J].DOI:10.1109/TSTE.2016.2516767 [本文引用: 11]
Evaluation de la performance des réglages de fréquence des Eoliennes à l'Echelle du système electrique: application à un cas insulaire
[J].
Methods for assessing available wind primary power reserve
[J].DOI:10.1109/TSTE.2014.2369235 [本文引用: 3]
风电功率预测的发展现状与展望
[J].
Wind power prediction achievement and prospect
[J].
电力市场中旋转备用的效益和成本分析
[J].DOI:10.3321/j.issn:1000-1026.2000.21.004 [本文引用: 2]
Study on benefits and costs of spinning reserve capacity in power market
[J].DOI:10.3321/j.issn:1000-1026.2000.21.004 [本文引用: 2]
Extreme learning machine: a new learning scheme of feedforward neural networks
[J].
Probabilistic wind power forecasting based on logarithmic transformation and boundary kernel
[J].
基于蚁狮算法的风电集群储能容量配置优化方法
[J].
Optimization of storage capacity allocation in wind farm cluster based on ant lion optimization algorithm
[J].
The ant lion optimizer
[J].DOI:10.1016/j.advengsoft.2015.01.010 [本文引用: 1]
自适应 Tent 混沌搜索的蚁狮优化算法
[J].DOI:10.11918/j.issn.0367-6234.201706044 [本文引用: 1]
Ant lion optimization algorithm based on self-adaptive tent chaos search
[J].DOI:10.11918/j.issn.0367-6234.201706044 [本文引用: 1]
美国调频辅助服务市场的调频补偿机制分析
[J].DOI:10.7500/AEPS20170406002 [本文引用: 1]
Analysis of frequency modulation compensation mechanism in frequency modulation ancillary service market of the United States
[J].DOI:10.7500/AEPS20170406002 [本文引用: 1]
Assessment of the cost associated with wind generation prediction errors in a liberalized electricity market
[J].DOI:10.1109/TPWRS.2005.852148 [本文引用: 2]