考虑到以上方法的不足,本文提出基于改进型相似性建模的积灰状态监测方法.相似性建模方法(similarity-based modeling, SBM)是数据驱动的非参数经验建模技术,通过部分具有代表性的历史数据估计各种状态下对应的正常情况. SBM基于参数的相关性,但不依赖于超参数和标签数据[15-16]. SBM方法多用于定性的故障检测[17-18].为了使该方法更加适合光伏系统的应用并提高诊断的准确性和响应速度,对算法中参数选择、状态矩阵构造、相似性算子设计、状态矩阵更新4个关键步骤进行改进.通过清洁–积灰对比实验,获取积灰对光伏发电影响的实验数据. 对改进型SBM方法的积灰程度监测效果进行验证,与其他5种方法进行对比.
1. 基于相似性的建模方法(SBM)
介绍SBM算法的基本原理. SBM是非参数经验建模技术,根据设备历史数据中具有代表性的正常运行的数据,通过插值运算估算设备当前正常运行应该呈现的数据. 这种方法是弱监督的,不需要历史数据具有积灰程度标签;不存在超参数设定的问题. 主要步骤如下所示.
1)为数据集选取参数,将参数个数标记为
2)从历史数据集中划定正常运行下的数据,称为“参考数据,
3)从参考数据
4)获取输入,即某一时刻的实际运行数据
比较与状态矩阵
其中
5)按照下式将相似性向量
式中:
6)结合
7)利用
式中:
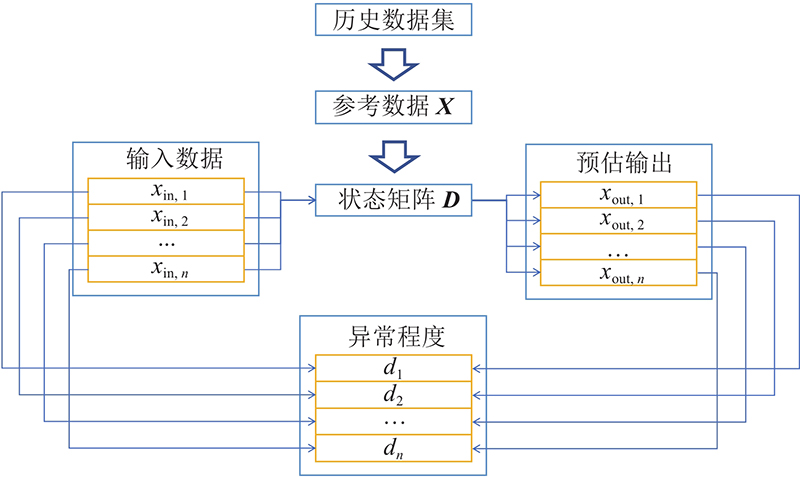
上述过程可以总结为如图1所示的流程图. 在将该方法应用到光伏系统积灰监测问题中时,“正常状态”对应系统在清洁无积灰时的工作状态,“异常程度”对应于组件的积灰程度.
图 1
在基于上述原理的原始型SBM方法的基础上,为了实现更好的积灰诊断效果,提出改进型SBM方法,在参数选取、状态矩阵构建、相似性算子设计、状态矩阵更新等方面进行研究与改进.
2. 改进型SBM方法
在原始SBM算法的基础上,针对光伏发电积灰问题提出对应的参数选择方法. 将单一状态矩阵的构建方式改进为分类状态矩阵. 提出新的相似性算子,改进对向量的相似性度量效果. 提出应用中的状态矩阵更新方法. 对以上诸点分别进行介绍,总结基于改进型SBM方法的光伏积灰诊断算法.
2.1. 参数选择
参数选择是SBM算法的第1个步骤.由于光伏发电依赖于环境状态,选用部分光伏系统运行参数以及与发电相关的气象参数. 关键参数的缺失和不必要参数的冗余都会影响预估结果的准确性. 在本文的改进型SBM算法中,选取4个参数:直流发电功率、斜面总辐射照度、温度和相对湿度. 依据有以下2个方面:1)对光伏发电原理的分析;2)对这些参数的相关性分析.
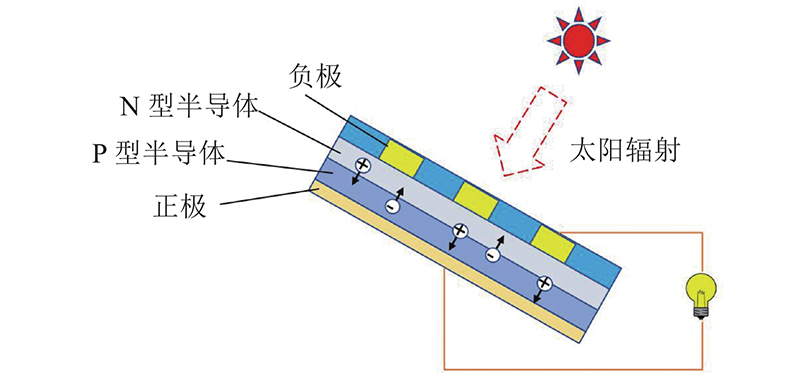
光伏电池板通过光生伏打效应,将太阳能转化为电能. 如图2所示为光伏发电的工作原理. 当太阳光照射到半导体上,一部分被吸收的光子与半导体中的价电子碰撞,形成电子-空穴对,光能以这种形式转化为电能.电池板产生的电能是直流电,经过逆变器后成为交流电.分析组件表面积灰对发电的影响,应尽量避免后续环节的干扰,因此在选择光伏运行参数时,选用组件输出的直流功率. 在环境参数中,太阳辐射照度是影响功率的最重要因素.衡量太阳辐射有很多参数,包括全局总辐射照度、直接计算辐射照度、漫射辐射照度、斜面总辐射照度等.选择斜面总辐射照度. 这一参数考虑了光伏电池板倾角及太阳入射角度来量化电池板实际可以接收到的辐射,是与能量转化最直接相关的辐射参数. 温度是与发电相关的气象条件. 更高的温度会加速电子和空穴的重组,降低发电的效率. 另一个相关气象参数是相对湿度. 相对湿度的影响主要体现在对光伏板表面灰尘积累的影响上. 在不同湿度下,积灰过程的快慢不同,积灰对发电造成的影响不同.
图 2
除了上述原理分析,根据历史数据开展参数的相关性分析,结果如表1所示. 在积灰程度监测中,光伏板直流发电效率、斜面总辐射、温度和相对湿度被确定为模型所包含的参数.
表 1 参数的相关性分析
Tab.1
| 参数 | 功率 | 斜面总辐射照度 | 温度 | 相对湿度 |
| 功率 | 1 | 0.973 | 0.333 | −0.481 |
| 斜面总辐射照度 | 0.973 | 1 | 0.252 | −0.437 |
| 温度 | 0.333 | 0.252 | 1 | −0.244 |
| 相对湿度 | −0.481 | −0.437 | −0.244 | 1 |
2.2. 状态矩阵构建
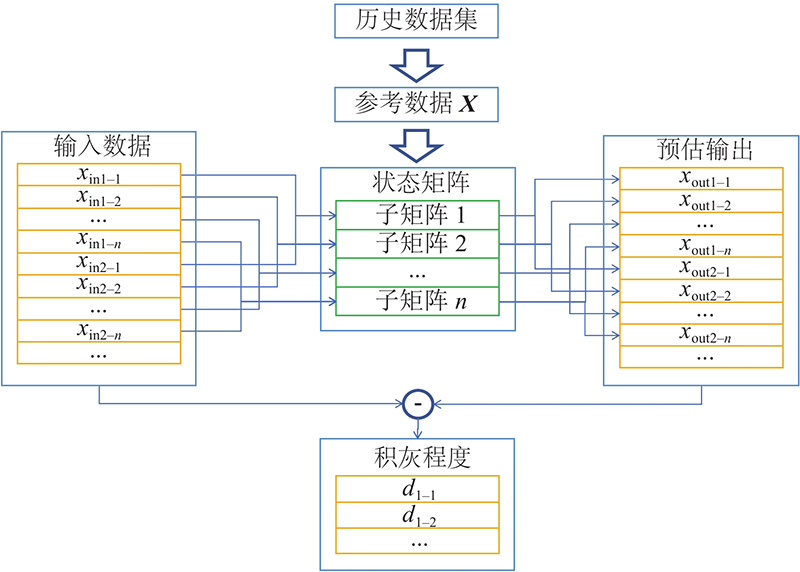
本文提出的分类状态矩阵是在基于相似性建模的方法中考虑数据的时间特性来构造状态矩阵. 在分类状态矩阵中,分类的标准是一天中的不同时刻,单位是h,每天从日出到日落的时间范围内,以每小时为单位各建立一个子矩阵. 于是,整体的状态矩阵成为由多个子矩阵组成的集合. 改进型状态矩阵对应的SBM算法的流程框图如图3所示. 输入矩阵的各个向量根据时刻,分别与对应的子矩阵进行相似性分析,得到正常状态的预估结果,例如子矩阵1对应xin1−1~xin n−1、xout1−1~xout n−1.于是,可以避免环境参数在一天中不同时刻隐含的一些内在规律,排除不同时刻的干扰,使得到的输入与输出的差距更加贴近积灰程度这个单一原因造成的影响.
图 3
2.3. 相似性算子
SBM算法中对向量之间进行相似性度量的算子称为相似性算子. 目前,大多数相关研究采用欧氏距离作为相似性算子. 由于欧氏距离没有考虑到不同参数之间的量纲差距,当模型中某个参数的取值过大时,该参数对应的相似性计算结果会很大,相应的权重也很大.受此影响,预估结果变得不够准确. 为了解决这一问题,在一些研究中对测量值进行归一化处理,将测量值投射到0~1.0. 这种处理方式有以下2个问题. 1)在归一化后的值中会有0值或近似0值. 在计算相对误差时,若除数为0,则无法得到结果;若除数为近似0值,则会计算得到很大的结果. 2)归一化处理后各个参数的值都失去了自身的物理意义,使得状态监测的结果不直观.
考虑到上述问题,提出使用标准化欧氏距离作为相似性算子. 向量
式中:
2.4. 状态矩阵的更新设计
在原始SBM方法中,状态矩阵构建完成并开始使用后保持不变. 考虑到光伏系统工作所处环境状态多变的问题,利用状态矩阵的组成数据相对独立的特点,提出改进型SBM方法中状态矩阵的在线更新设计.
状态矩阵中数据集的覆盖性和代表性在很大程度上决定了积灰诊断结果的准确性. 这意味着可以根据积灰诊断效果来反向判断状态矩阵的合理性并进行调整,在离线状态下,可以利用已知实际积灰程度的实验数据对状态矩阵进行调整. 在光伏系统的实际在线工作过程中,没有实时的真实积灰程度作为参照. 基于相似性建模方法的特点是利用理想情况下的工作状态预估得到实际运行时应有的理想状态. 对于本身是理想状态的数据,预估得到的输出值应与实际值相同或相近. 利用这一点,可以进行状态矩阵的在线更新.
在光伏系统的运行过程中,运维人员可以通过运行日志,获知组件何时进行了人工清洗;清洗完之后的较短时间段内可以认为组件是在清洁状态下工作的. 若积灰监测算法对清洁状态组件的诊断结果为积灰程度接近0,则说明此时的状态矩阵可以覆盖这段时间内出现的环境状态. 如果出现将清洁状态诊断为积灰程度较高的情况,说明这条输入数据没有被状态矩阵通过插值找到很好的相似结果,建议通过人工判断确认光伏板的清洁情况. 如果确实是清洁的,那么将该输入数据纳入状态矩阵中,实现状态矩阵覆盖性和代表性的提升.
2.5. 改进型SBM算法总结
将改进型SBM算法流程总结为算法1.
算法1 改进型SBM积灰诊断算法
1 初始化:由历史数据构建改进型状态矩阵
2 while 积灰诊断正在进行
3 输入:某一时刻的实际运行数据
4 比较
5 将相似性向量
6 结合
7 输出:积灰程度
8 if (输入对应时刻为清洁状态且
9 then 将
10 end if
11 end while
3. 实验分析
3.1. 实验系统
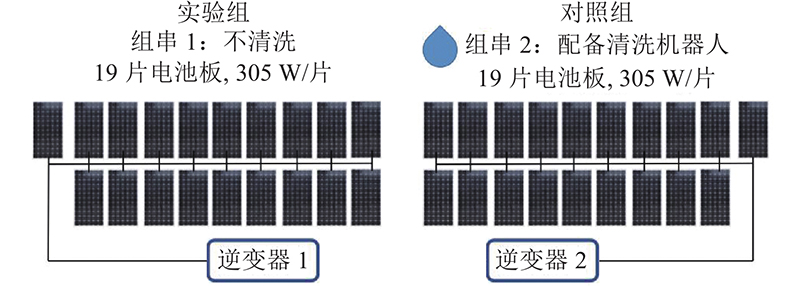
2组组串的相互距离很近,均没有被建筑物、树木及其他阴影遮挡. 一组作为实验组,保持自然积灰状态,不进行清洗. 另一组配备了自动清洗机器人作为对照组. 南德意志集团(TÜV SÜD)对清洗机器人进行实验测试. 测试对2组(2个品牌、每组5块)光伏组件进行机器人清扫,累计5 000次. 结果表明,机器人有良好的清洗效果,由于机器人清扫导致的2组光伏组件发电效率衰减分别约为0.04%/年和0.05%/年,可以认为清洗机器人不会造成组件效率明显衰减.
图 4
图 5
图 5 清洁–积灰对比实验系统的结构图
Fig.5 Diagram of clean-dusty comparative experiment system
表 2 光伏组件参数的标称值
Tab.2
| 参数 | 参数值 |
| 标准辐射照度/(W·m−2) | 1000 |
| 标准环境温度/(°) | 25 |
| 额定最大功率/W | 305 |
| 标准条件工作电流/A | 7.71 |
| 标准条件工作电压/V | 29.2 |
| 标准条件短路电流/A | 8.15 |
| 标准条件开路电压/V | 37.6 |
| 组件尺寸 | 1658 mm×992 mm×6 mm |
在对比实验中,机器人每天自动清洗对照组组串一次. 忽略2次清洗之间的积灰过程,可以将对照组的光伏组件视为在无积灰的清洁状态下工作. 机器人清洗会选择日落后的时间,每次清洗只需要耗时5 min. 清洗机器人有独立的供电系统,不需要消耗光伏组串生产的电力. 根据以上几点,可以忽略清洗工作对光伏发电带来的影响. 2组组串发电情况的差别可以用来衡量积灰带来的影响. 环境监测仪可以测量并记录包括太阳辐射、温度、湿度在内的气象参数. 光伏系统运行数据与环境监测数据的采样频率均为5 min/次.
3.2. 积灰影响
选取从2019年5月到9月的数据. 在进行数据分析之前,开展数据预处理,主要包括以下步骤.
1) 有些天清洗机器人由于故障没有工作,对应的数据为无效数据,进行去除.
2) 下雨天的数据进行去除. 在下雨的状态下,光伏系统的发电功率很低,对应的数据会有很大的噪声,计算相对值时会有较大的误差.
3) 由于光伏系统在没有光照的时候不工作,每天日出前和日落后的数据为无效数据,进行去除.
4) 为了避免噪声的干扰,对数据进行周期为1 h的重采样.
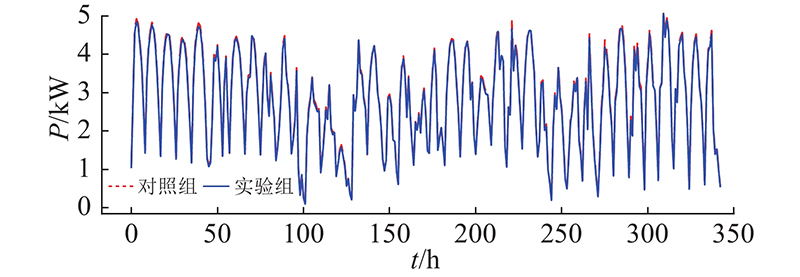
在实验时间范围内,对照组与实验组组串发电功率的平均相对差距为2.29%. 可知,在上海这样的沿海大城市,屋顶光伏系统因积灰而产生的平均发电量损失会超过2%. 根据光伏行业的现状可知,一个装机容量为1 mW的光伏系统每年可发电120万kW·h. 在不采取人工清洗的情况下,因积灰造成的功率损失约为27.48万kW·h. 到2020年,中国分布式光伏系统的装机容量将达到6万MW. 积灰造成的电力损失将超过16.2亿kW·h,每年经济损失将超过5.5亿美元. 考虑到积灰对光伏发电的影响,积灰状态监测是值得研究的问题.
图 6
图 7
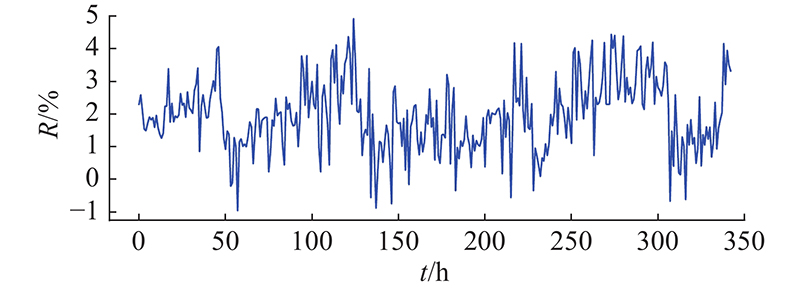
图 7 对照组与实验组发电功率的相对差距
Fig.7 Relative difference of power of control group and experimental group
3.3. 积灰程度诊断
3.3.1. 对比方法与评价指标
基于对比实验的数据结果,比较以下6种积灰诊断方法的性能:1)基于理论公式的方法;2)FNN;3)SVR;4)RF;5)原始SBM方法;6)本文提出的改进型SBM方法.
式中:
式中:
为了更直观地评价这些方法的诊断性能,选择6个误差指标对诊断结果的准确性进行评价,分别为:均方误差(mean square error,MSE)、平均相对误差(mean relative error,MRE)、均方根误差(root mean square error,RMSE)、归一化均方误差(normalized mean square error,NMSE)、归一化平均绝对误差(normalized mean absolute error,NMAE)和确定系数(R-Squared,R2). 这些误差指标的计算方法如下.
式中:
3.3.2. 结果分析
利用积灰监测结果进行应用的时间单位一般为1 d. 对预处理后的数据集以1 h为单位进行估计,每日的积灰程度取当天各小时结果的平均值. 各诊断方法的性能表现如表3所示. 在这些方法中,基于理论公式的方法的估计误差与其他方法的估计误差均在不同的数量级上. 该方法的准确性较低,且诊断结果中有许多负值. 一般来说,实验系统的积灰情况不算严重. 用标准情况下的公式计算系统的理想发电量是比较困难的,容易出现较大的误差.考虑到该方法的性能过差,不对相应结果进行对比分析.
表 3 积灰诊断结果评价
Tab.3
| 方法 | 训练数据占比/% | MSE/10−5 | MRE/10−4 | RMSE/10−2 | NMSE | NMAE | R2 |
| 理论公式法 | — | 79.241 | 4.812 | 8.902 | 84.112 | −83.112 | −83.112 |
| FNN | 40 | 1.237 | 0.653 | 1.112 | 1.313 | 0.242 | −0.313 |
| FNN | 60 | 1.102 | 0.683 | 1.050 | 1.170 | 0.240 | −0.170 |
| FNN | 80 | 0.992 | 0.658 | 0.996 | 1.053 | 0.217 | −0.053 |
| SVR | 40 | 0.992 | 0.617 | 0.996 | 1.053 | 0.215 | −0.053 |
| SVR | 60 | 0.911 | 0.549 | 0.954 | 0.966 | 0.200 | 0.034 |
| SVR | 80 | 0.839 | 0.568 | 0.916 | 0.890 | 0.197 | 0.110 |
| RF | 40 | 1.125 | 0.669 | 1.061 | 1.194 | 0.232 | −0.194 |
| RF | 60 | 1.102 | 0.577 | 1.050 | 1.170 | 0.236 | −0.170 |
| RF | 80 | 0.880 | 0.485 | 0.938 | 0.934 | 0.200 | 0.066 |
| 原始SBM | — | 1.735 | 0.550 | 1.324 | 1.861 | 0.266 | −0.861 |
| 改进型SBM | — | 0.412 | 0.339 | 0.642 | 0.437 | 0.130 | 0.053 |
图 8
图 9
图 10
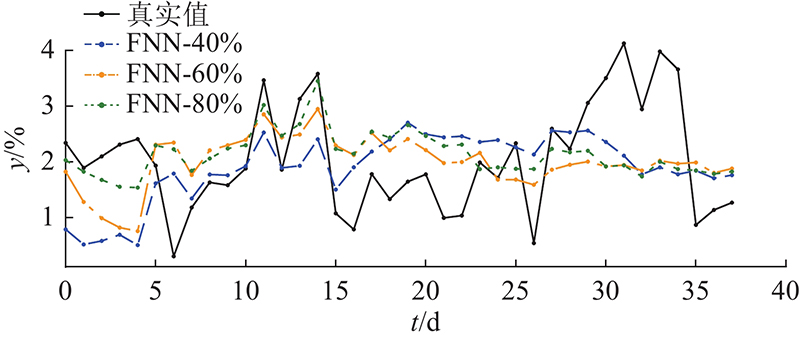
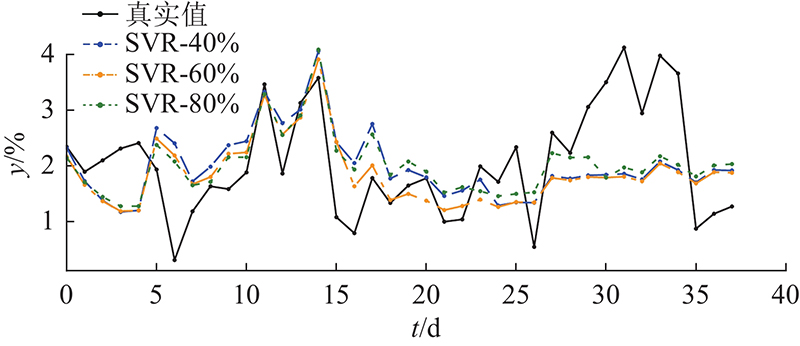
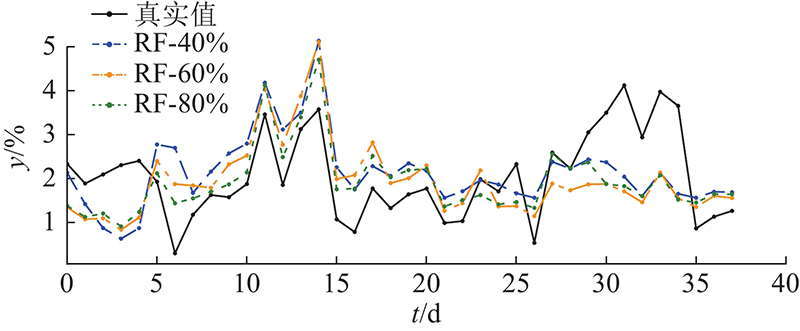
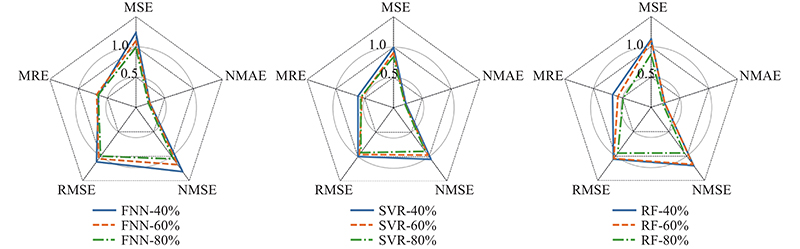
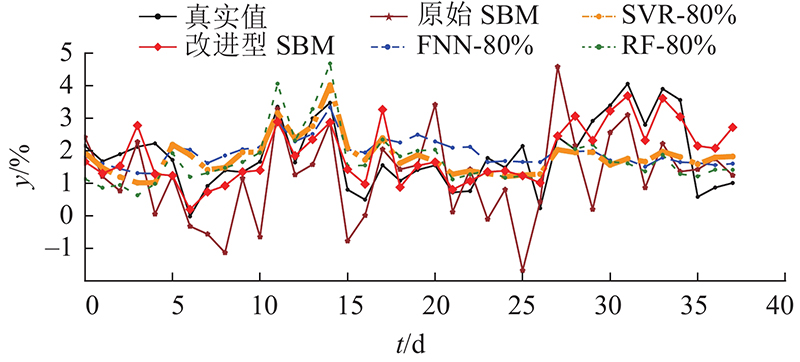
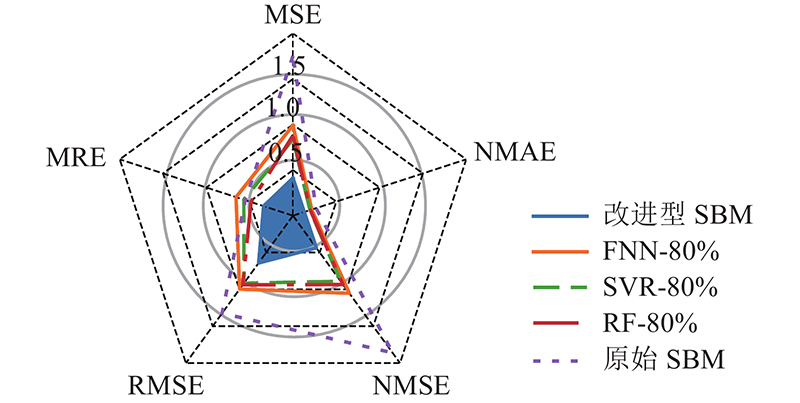
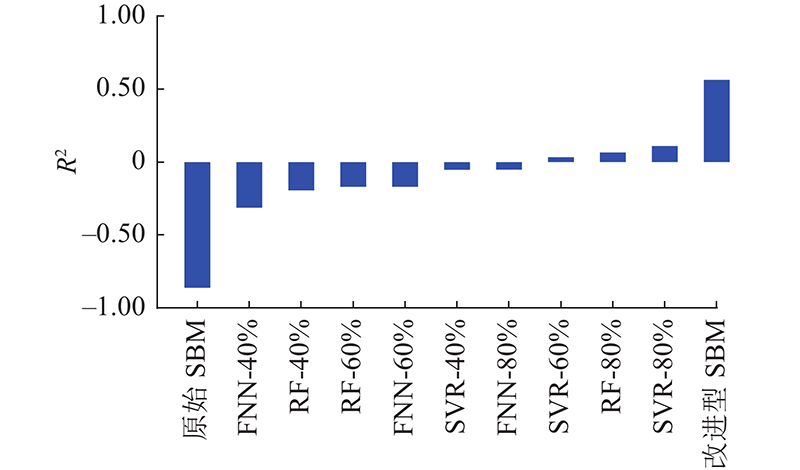
改进型SBM方法、原始SBM方法、FNN、SVR和RF的诊断结果如图12所示. 这些方法的评估指标结果如图13所示. 结果表明,FNN、SVR和RF的主要问题是对取值较大和较小样本的估计精度较低. 它们的估计值与实际情况相比过于稳定,无法很好地监测较大的波动. 原始的SBM方法具有匹配较大和较小值的能力. 波动过大,导致评价指标不理想. 利用提出的改进型SBM方法解决了波动大的问题,保持了对较大值和较小值的拟合能力. 实现效果提升的原因主要有以下几点. 1)由于分类状态矩阵的构造,每个子矩阵对正常工况的代表性更有针对性. 2)提出的标准化欧氏距离有助于对异常数据对应的正常情况进行估计. 从如图14所示的R2评价结果可以看出,原始SBM方法和FNN方法的拟合结果较差. 在训练数据充足的情况下,RF和SVR可以实现更好的性能,改进型SBM方法在所有测试方法中的表现最好. 根据使用的评价指标结果可知,在诊断准确性方面,这6种方法的效果排名为:改进型SBM、SVR、RF、FNN、原始SBM、理论公式方法.
图 11
图 11 FNN、SVR、RF积灰诊断结果的评价
Fig.11 Evaluation results for dust deposition of FNN, SVR, and RF
图 12
图 12 各方法积灰诊断结果的对比
Fig.12 Comparision of dust diagnostic results of all methods
图 13
图 13 各方法积灰诊断结果的评价指标
Fig.13 Evaluation results for dust deposition of all methods
图 14
图 14 各方法积灰诊断结果的评价指标:R2
Fig.14 Evaluation results for dust deposition of all methods: R2
表 4 各方法的响应时间
Tab.4
| 诊断方法 | tr/ms | 诊断方法 | tr/ms | |
| FNN | 8.45 | 原始SBM | 103 | |
| SVR | 2.38 | 改进型SBM | 10.75 | |
| RF | 3.79 | — | — |
从表4可以看出,原始SBM方法和改进型SBM方法均需要比3种机器学习方法更长的响应时间,这一点是此类依赖矩阵计算方法的弱项. 与原始SBM方法相比,改进型方法将反应时间降低了一个数量级,可以达到与机器学习方法相同的数量级. 响应时间得以明显缩短的原因主要是分类状态矩阵的构建,使得输入向量可以只与最相关的矩阵数据进行相似性计算,大幅减低计算量,以缩短算法响应时间. 虽然响应速度比几种机器学习方法慢一些,但在可接受的范围内,可以满足在线应用的需求.
4. 结 语
本文研究光伏系统的积灰状态监测问题,提出弱监督的数据驱动方法:改进型SBM方法. 在传统的SBM方法基础上改进参数选择、状态矩阵构造、相似性算子设计、状态矩阵更新等步骤,提高了诊断精度和响应速度.
基于清洁–积灰对比实验系统的真实运行数据,对比基于理论公式的方法、3种有监督的机器学习方法(FNN、SVR、RF)、原始SBM方法及改进型SBM方法等6种方法的积灰监测效果. 结果表明,改进型SBM方法可以以可接受的响应速度劣势,实现最佳的积灰程度监测准确性.
在未来的研究中,可以关注SBM算法计算效率的问题,考虑通过状态矩阵构建和相似性计算的进一步优化来提高算法响应速度. 考虑将积灰程度监测的问题扩展成积灰程度的预测问题,结合光伏发电功率预测对清洗计划进行优化决策.
参考文献
Optimal cleaning scheduling for photovoltaic systems in the field based on electricity generation and dust deposition forecasting
[J].DOI:10.1109/JPHOTOV.2020.2981810 [本文引用: 1]
Experimental analysis of the effect of dust’s physical properties on photovoltaic modules in Northern Oman
[J].DOI:10.1016/j.solener.2016.09.019 [本文引用: 1]
Impact of soiling on IV-curves and efficiency of PV-modules
[J].DOI:10.1016/j.solener.2014.12.003 [本文引用: 1]
基于状态监测的电池板积灰清洗周期确定与费用评估
[J].
Cleaning cycle determination and cost estimation for photovoltaic modules based on dust accumulating condition monitoring
[J].
Calculation of the polycrystalline PV module temperature using a simple method of energy balance
[J].DOI:10.1016/j.renene.2005.03.010 [本文引用: 2]
Design of a cleaning program for a pv plant based on analysis of energy losses
[J].DOI:10.1109/JPHOTOV.2015.2478069 [本文引用: 2]
Assessment of a practical model to estimate the cell temperature of a photovoltaic module
[J].
On the investigation of photovoltaic output power reduction due to dust accumulation and weather conditions
[J].DOI:10.1016/j.renene.2016.07.063 [本文引用: 1]
Soiling quantification using an image-based method: effects of imaging conditions
[J].DOI:10.1109/JPHOTOV.2020.3018257 [本文引用: 1]
Smart soiling sensor for PV modules
[J].DOI:10.1016/j.microrel.2020.113789 [本文引用: 1]
Modeling of soiled PV module with neural networks and regression using particle size composition
[J].DOI:10.1016/j.solener.2015.11.012 [本文引用: 1]
Power prediction of soiled PV module with neural networks using hybrid data clustering and division techniques
[J].DOI:10.1016/j.solener.2016.04.004
Detection of cleaning interventions on photovoltaic modules with machine learning
[J].DOI:10.1016/j.apenergy.2020.114642 [本文引用: 1]
Similarity-based modeling of vibration features for fault detection and identification
[J].DOI:10.1108/02602280510585691 [本文引用: 2]
Estimation of bearing remaining useful life based on multiscale convolutional neural network
[J].
Modeling daily reference evapotranspiration via a novel approach based on support vector regression coupled with whale optimization algorithm
[J].DOI:10.1016/j.agwat.2020.106145 [本文引用: 1]
Shallow landslide susceptibility mapping by random forest base classifier and its ensembles in a semi-arid region of Iran
[J].DOI:10.3390/f11040421 [本文引用: 1]