临近超载是导致软土地基变形显著的另一个主要因素. 不少学者围绕基坑开挖的超载问题和时间效应进行探讨. 包旭范[10]结合上海地区软土蠕变试验曲线,利用土体蠕变方程研究软土地基超大型基坑的变形特征,分析基坑超载位置及大小对土坡蠕变的影响规律,为超大型软土基坑的施工优化提供了依据. 张飞等[11]通过建立考虑土体蠕变-固结耦合效应的有限元模型,分析不同超载引起的深基坑工程变形特性,得出在超载作用下软土基坑支护结构的变形规律. 黄珏皓等[12]基于软土蠕变(soft soil creep,SSC)模型,分析时间效应对开挖工程中支护结构及基坑自身的变形影响. 朱江华等[13]研究坑边堆载对临江深基坑支护结构变形的影响,针对特定工程分析极限堆载,得出在深基坑开挖中控制堆载的重要性. 林志斌等[14]通过有限元数值模拟,研究软土深基坑开挖对围护结构及基坑周围地表沉降的影响,确定支护结构的变形形态,指出地表沉降最大值与时间的线性相关性. 王坤[15]使用有限元软件拟合土体蠕变实验数据,将所得的蠕变参数应用于软土基坑开挖分析,得出针对具有蠕变特性的工程,应进一步优化施工方案,以达到更好的变形控制,保证施工安全. 郭海柱等[16]通过室内三轴流变实验,拟合土体蠕变参数,将其应用于深基坑的施工模拟,指出蠕变模型在软土基坑变形分析中的可靠性,提出支护不及时或支护不当会放大软土蠕变的时空效应.
本文以太湖隧道某大型基坑工程为背景,提出 结合智能反演和蠕变实验的分析方法. 结合现场监测数据与大量的数值模拟结果,构建基于支持向量机算法的参数智能反演系统,确定土体的基本力学参数. 开展软土蠕变实验,确定软土蠕变模型的相关参数. 针对现场实际堆载作用下基坑的变形,验证了该方法在进行软土基坑超载作用下的长期稳定性分析及变形预测中的可适用性. 基于该方法针对本工程其他施工段不同超载作用的变形分析,开展了超载优化设计,取得了良好的效果.
1. 背景概况
图 1
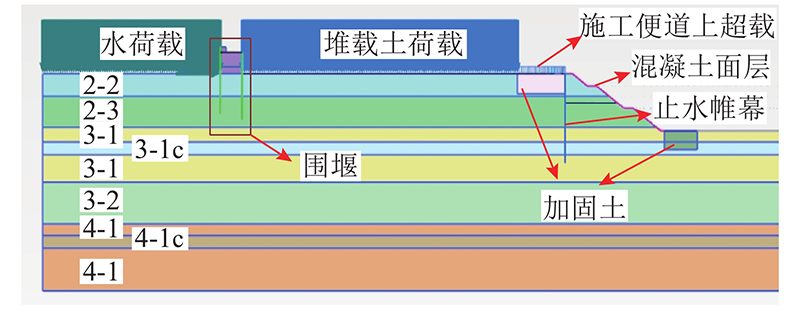
图 2
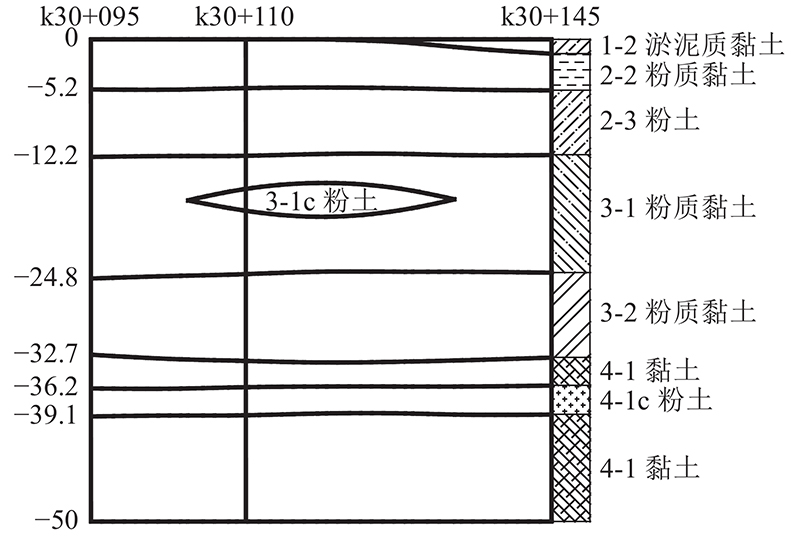
以k30+110断面为例,现场地质勘察剖面图如图3所示,勘探地层深度为50 m,共包括7个土层,土层分别为2-2粉质黏土、2-3粉土、3-1粉质黏土、3-1c粉土、3-2粉质黏土、4-1黏土、4-1c粉土. 其中2-2和2-3土层,压缩特性高,易受到施工荷载而产生扰动.
图 3
该区域的基坑施工主要包括以下2个阶段:第1阶段主要为土体的开挖,时间大约持续20 d,施工期较短;第2阶段为基坑顶部的堆载,预计堆载时间为4~12个月,具体的施工工况如表1所述. 长时间的超载作用加上软土的蠕变特性,会促使基坑的稳定性进一步降低. 如何科学地描述土体的蠕变行为,对于评价软土基坑的长期稳定性至关重要,科学地优化堆载的高度及堆载的时间对于现场的工程施工具有重要的工程指导意义.
表 1 基坑的施工工况
Tab.1
| 序号 | 工况 | 时间 | 阶段 |
| 1 | 第1层土开挖(含堆土) | 2020-09-24—2020-09-27 | 第1阶段 |
| 2 | 第1层喷锚 | 2020-09-28—2020-09-29 | |
| 3 | 第2层土开挖(含堆土) | 2020-09-30—2020-10-03 | |
| 4 | 第2层喷锚 | 2020-10-04—2020-10-05 | |
| 5 | 第3层土开挖(含堆土) | 2020-10-06—2020-10-09 | |
| 6 | 第3层喷锚及垫层施工 | 2020-10-10—2020-10-15 | |
| 7 | 稳定堆土(设计高度为7 m) | 2020-10-15以后 | 第2阶段 |
2. 模型构建
针对这种软土基坑长期稳定性的分析,常规的做法是通过室内试验确定土体变形的相关参数,包括土体强度参数及控制土体蠕变行为的次固结系数[17-20]. 由于土体受施工荷载的扰动影响,使得原位的力学性质与室内试验获得的结果会存在一定程度上的差异,基于室内试验获得的蠕变模型往往在土体的蠕变变形分析上会导致一定误差. 考虑到基坑第1阶段的开挖时间较短,大约持续20 d,土体应力状态持续变化,时效变形在第1阶段并非主要影响因素,该阶段土体参数受施工扰动的影响大,不同施工阶段的物理力学性质存在差异性,传统的实验方法仅能获得特定状态下土体的物理力学参数. 针对该阶段的土体参数,通过智能参数反演的方法确定. 在第2阶段,基坑土体主要承受较稳定的超载作用,变形主要由软土蠕变效应引起. 若采取反演的方法获得相应的参数,则需要基于现场长时间的数据监测;在实际工程中,会落后于现场进度,不利于研究的开展. 第2阶段由于没有施工扰动的影响,土体的应力状态较稳定,因此通过室内试验确定的参数能够较好地表征土体的蠕变特性,采用实验方法确定土体蠕变参数.
2.1. 土体力学参数智能反演
选取施工段典型剖面作为参数反演的计算截面,利用Plaxis有限元分析软件建立二维有限元模型,如图4所示. 模型的长为400 m,深度为50 m,模型有3 788个单元、31 869个节点. 该模型的剖面处于湖中深埋段,清除表层土后采用大放坡施工,该放坡为3级放坡,每级边坡的坡比为1∶1.5,坡间平台宽2.5 m. 第1次放坡深度为2.8 m,第2次放坡深度为5 m,第3次放坡深度为5 m.
图 4
小应变本构模型为针对软土计算引入的应用较广泛的土体本构模型,在研究不涉及时间问题的软土基坑变形分析中有很好的适用性[21-22],利用SSC本构模型可以考虑软土的蠕变效应所引起的土体变形[12]. 肖明清等[23]经敏感度分析之后,确定土体弹性模量E、内摩擦角
采用的反分析方法是最小二乘支持向量机(least squares support vector machine, LSSVM),是支持向量机(support vector machine, SVM)的拓展,避免了支持向量机二次规划的问题,使目标函数的约束从不等式变为等式,将二次规划问题转化为线性方程组进行求解,提高了计算精度和速度[24]. 假设训练样本集
式中:w为权向量,b为偏置量.
Suykens等[26]在正则化理论的基础上,采用最小二乘函数和等式约束,建立最小二乘支持向量机(LSSVM)问题的目标函数J为
式中:C为惩罚参数,
约束条件为
采用最小二乘支持向量机(LSSVM)的核函数为径向基核函数(radial basis function,RBF),公式为
式中:σ为核函数.
最小二乘支持向量机的输出函数为
根据现场典型截面处边坡深层水平位移监测数据,通过交叉验证与网格搜索法确定最小二乘支持向量机模型参数. 基于训练好的最小二乘支持向量机对典型截面处各土体进行参数反演,反演前、后的土体参数如表2所示. 表中,括号内为反演前的参数(基于现场取样与室内试验获得).
表 2 反演前、后的土体参数
Tab.2
| 土层 | φ/ (°) | c/kPa |
| 2-2粉质黏土 | 12.5(15.1) | 21.3(25.5) |
| 2-3粉土 | 28.3(33.5) | 16.2(19.2) |
| 3-1粉质黏土 | 13.2(17.4) | 41.1(47.0) |
| 3-1c粉土 | 26.2(27.5) | 12.6(13.8) |
| 3-2粉质黏土 | 10.4(10.4) | 20.0(20.0) |
| 4-1黏土 | 16.1(16.1) | 49.5(49.5) |
| 4-1c粉土 | 20.7(20.7) | 10.3(10.3) |
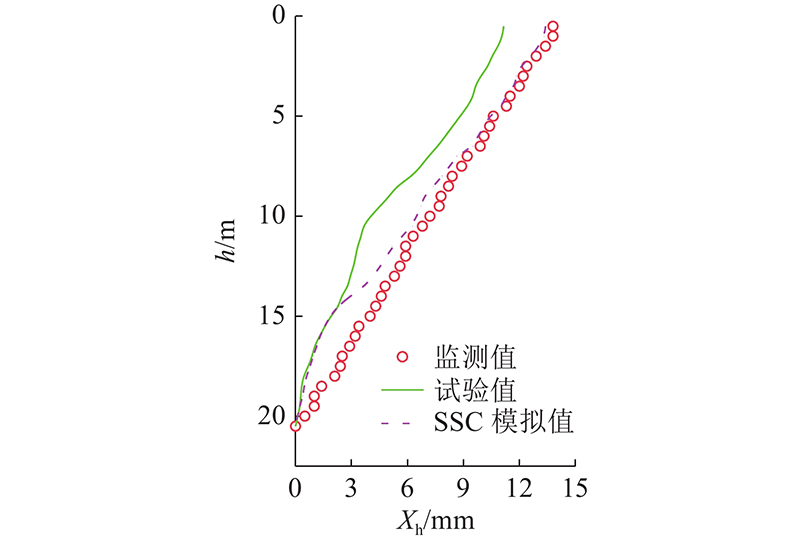
图 5
图 5 k30+110号桩水平位移随深度的分布
Fig.5 Distribution of horizontal displacement with depth of pile k30+110
通过反演系统获得的土体基本力学参数,在变形趋势及变形值的计算上,都取得了与实际情况很好的一致性,结果是可靠的.
2.2. 土体蠕变试验
根据地层图的分布和现场的实际挖方情况,选择南侧k30+100附近进行钻孔取土. 根据地层图中土层的分布,分别在深度为2、7、9、11、14、19、21 m位置处取得2-2土层、2-3土层及3-1土层不同深度处的土样.
在取得现场土样后,利用图6所示的三轴仪,开展固结试验,共开展2组试验. 一组试验在不同的加压等级下,开展回弹指数的测定;另一组试验与之对照,获得蠕变模型的压缩参数
图 6
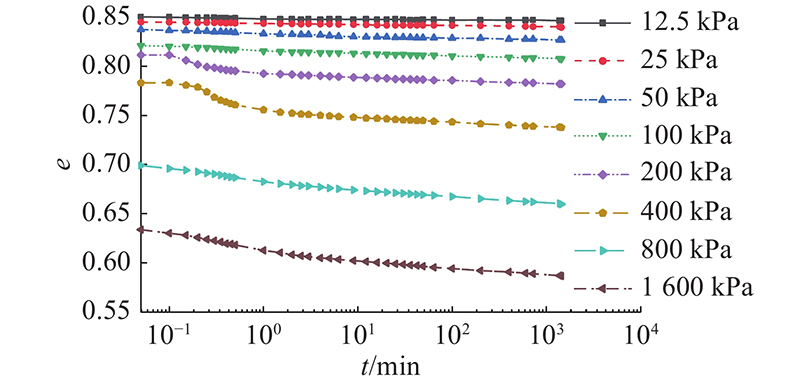
以2-2土层为例,根据高压固结试验所获得的在不同加压等级下试样随时间的变形值,试样孔隙比与时间的对数关系曲线图如图7所示.
图 7
从图7可以看出,在同一加载压力下,对试样的加载时间越长,试样孔隙比越小,最后趋于稳定. 在加载时间相同的情况下,对试样的加载压力越大,试样的孔隙比越小.
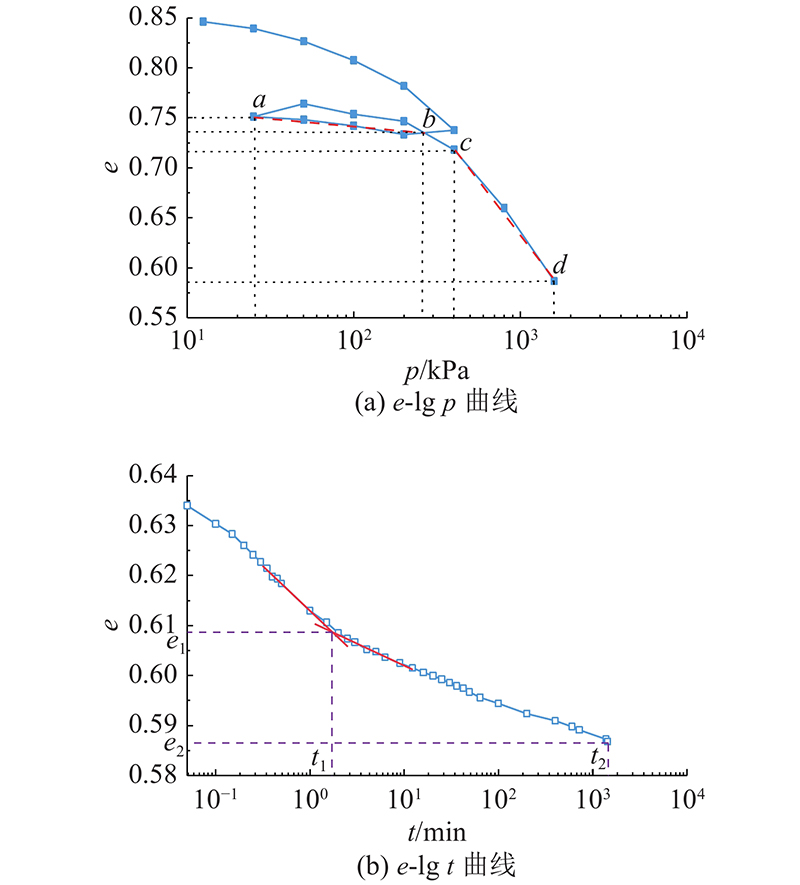
图 8
压缩指数和回弹指数采用下式[18]获得:
式中:
式中:t1为次固结开始时间,取主固结与次固结的相交位置;t2为试验结束时间. 基于曲线,可得2-2土层的
综合式(6)~(8),2-2土层所有的蠕变模型参数均可以确定,分别为
重复同样的试验步骤,其他各土层蠕变参数分别如表3所示.
表 3 各土层的蠕变参数
Tab.3
| 土层 | | | |
| 2-2 | 0.028 840 | 0.013 723 | 0.001 468 00 |
| 2-3 | 0.012 782 | 0.008 909 | 0.000 900 74 |
| 3-1 | 0.022 098 | 0.022 633 | 0.001 575 99 |
土体蠕变模型采用SSC本构模型,假设土壤是均质且各向同性的,土壤应变由弹性应变和蠕变应变组成,可以分别使用胡克定律和蠕变定律来分析. 屈服函数类似于修正剑桥模型,参数
式中:
3. 结果分析
3.1. 软土基坑时效变形机制分析
综合智能反演算法确定的土体物理力学基本参数,结合室内蠕变试验确定的相关蠕变模型参数,针对现场某区域内7 m高度的实际堆载,分别选择从基坑开挖到基坑开挖完成、基坑开挖完成后第15天、第30天、第60天、第90天、第120天以及第150天这几个关键时间点,探讨蠕变效应对基坑变形的影响.
如图9所示为基坑开挖完成后各时间节点的塑性区发展情况. 可见,在基坑开挖完成时,塑性点主要分布在2-2粉质黏土与加固土交界的位置和边坡底部3-1c粉土与加固土交界的位置. 在基坑开挖完成后150 d内,与基坑开挖完成时相比,塑性区范围主要向加固土下方的2-3粉土层内不断增大的趋势发展. 塑性点较密集的地方主要在2-2粉质黏土和3-1c粉土层中,因为2-2粉质黏土与3-1c粉土的强度较其他土层低,且现场施工荷载导致土层之间相互作用,该位置处塑性点分布较密集. 软土的蠕变效应会引起土体内部结构的逐步劣化,塑性区不断发展,最终导致形成潜在滑裂面.
图 9
图 9 k30+100断面处的基坑塑性区分布图
Fig.9 Plastic zone distribution at k30+100 profile of foundation pit
表 4 不同时间点基坑安全系数及塑性区
Tab.4
| 时间点 | F | 塑性区贯通 |
| 基坑开挖完成 | 1.559 | 否 |
| 基坑开挖完成后第15天 | 1.435 | 否 |
| 基坑开挖完成后第30天 | 1.407 | 否 |
| 基坑开挖完成后第60天 | 1.384 | 否 |
| 基坑开挖完成后第90天 | 1.365 | 否 |
| 基坑开挖完成后第120天 | 1.352 | 否 |
| 基坑开挖完成后第150天 | 1.335 | 是 |
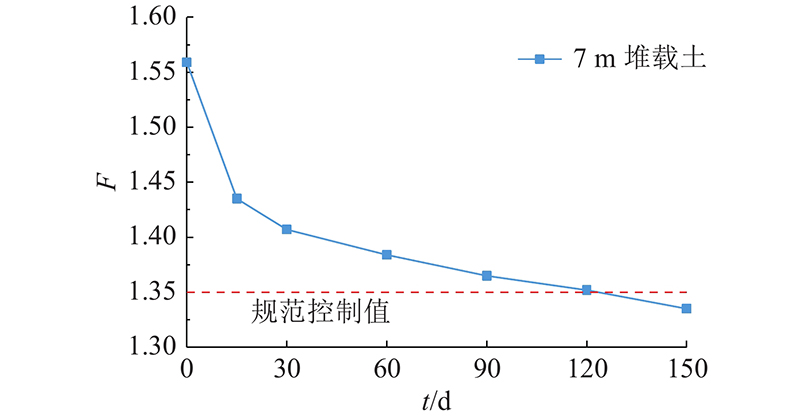
图 10
图 10 k30+100断面处基坑安全系数随时间变化曲线
Fig.10 Variation curve of safety factor of foundation pit with time at k30+100 profile
如图10所示为基坑安全系数随时间不断衰减的过程. 可见,从基坑开挖完成到基坑开挖完成后15 d期间内,基坑安全性系数较之后的时间衰减最快. 太湖隧道基坑安全等级为一级,基坑整体稳定性分析的安全系数不小于1.35,在基坑开挖完成后第120天时间点附近,基坑安全系数为1.352,接近规范限值,故在基坑围堰板与基坑之间的堆载土高度为7 m时,堆载时间不宜超过120 d.
3.2. 变荷载下的超载优化设计
为了验证提出方法的适用性,将该方法应用于不同堆载高度(7.0、7.5、8.0、8.5、9.0 m)下的长期稳定性分析. 基于分析结果,对太湖隧道的超载设计进行优化. 如表5所示为不同堆载高度下不同时间节点的基坑安全系数. 表中,F7.0、F7.5、F8.0、F8.5、F9.0分别为堆载高度为7.0、7.5、8.0、8.5、9.0 m时基坑的安全性系数.
表 5 不同堆载高度下不同时间点处的基坑安全系数
Tab.5
| 时间点 | F7.0 | F7.5 | F8.0 | F8.5 | F9.0 |
| 基坑开挖完成 | 1.559 | 1.488 | 1.431 | 1.373 | 1.282 |
| 基坑开挖完成后第15天 | 1.435 | 1.409 | 1.395 | 1.361 | − |
| 基坑开挖完成后第30天 | 1.407 | 1.386 | 1.376 | 1.354 | − |
| 基坑开挖完成后第60天 | 1.384 | 1.372 | 1.361 | 1.343 | − |
| 基坑开挖完成后第90天 | 1.365 | 1.356 | 1.347 | 1.329 | − |
| 基坑开挖完成后第120天 | 1.352 | 1.338 | 1.331 | 1.314 | − |
| 基坑开挖完成后第150天 | 1.335 | 1.321 | 1.311 | 1.297 | − |
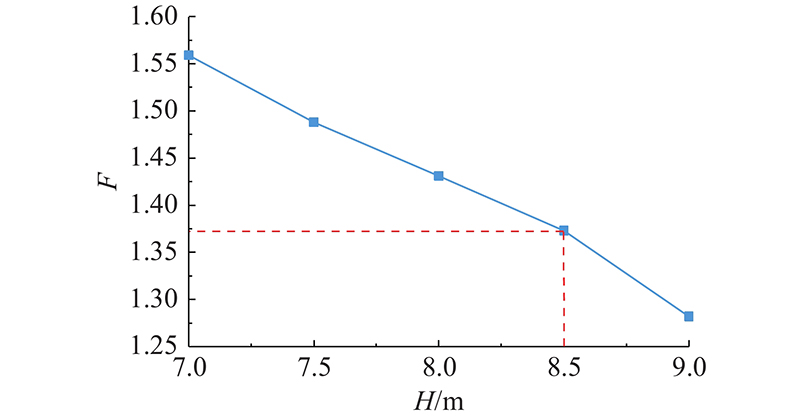
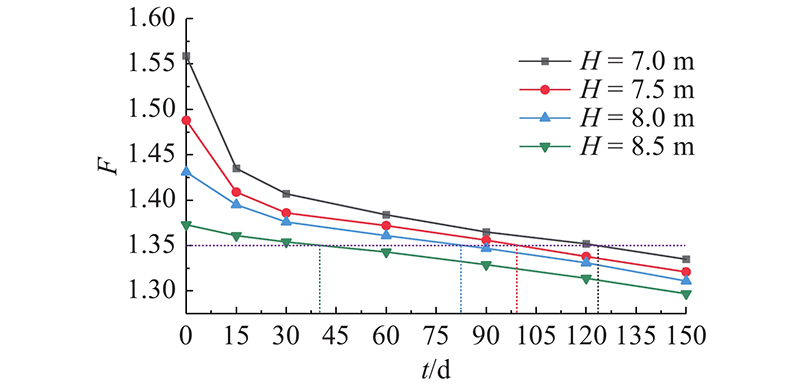
如图11所示为在基坑开挖完成后,不同高度堆载下的基坑安全系数变化趋势. 随着堆载土高度H的增加,基坑安全系数逐渐降低. 在堆土高度超过8.5 m后,安全系数有加速下滑的趋势,可以认为在基坑开挖期间,极限堆载高度约为8.5 m,堆载土的高度不宜超过8.5 m.
图 11
图 11 基坑开挖完成时基坑安全系数随堆载土高度的变化曲线
Fig.11 Curve of safety factor of foundation pit versus surcharge height when excavation is completed
图 12
图 12 不同堆载土高度下基坑安全系数随时间的变化曲线
Fig.12 Curve of safety factor of foundation pit versus time under different surcharge heights
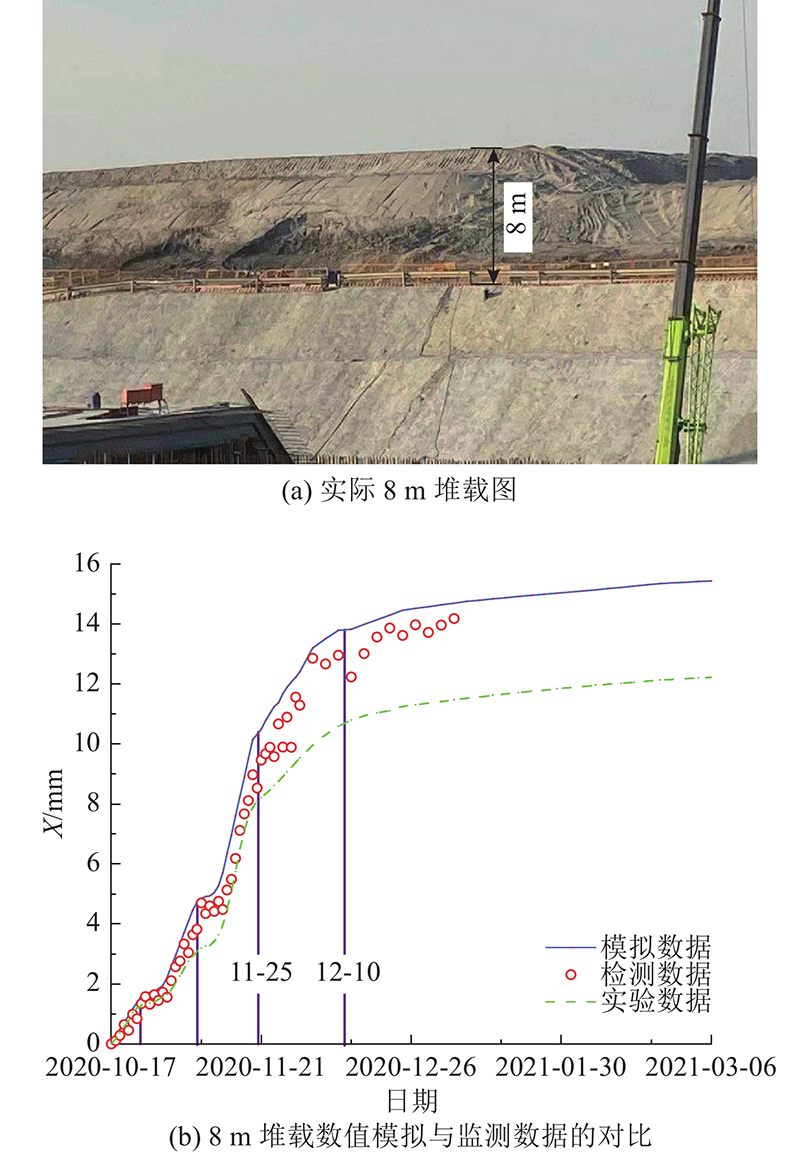
综合考虑基坑堆载时间及堆载高度,提出在必要情况下k29+310~k30+310区段可以将堆载高度增至8.0 m,堆载时间不宜超过80 d. 将该方案应用于实际工程,对比数值模拟预测结果与相应的断面实际监测数据,结果如图13所示. 图中, X为水平位移.
图 13
图 13 8 m堆载下坡顶水平位移随时间的变化曲线
Fig.13 Curve of horizontal displacement at slope top versus time under 8 m surcharge
从变形趋势上看,在基坑开挖过程中,实测变形与基于本文提出的“智能反演+蠕变实验”得到的数值模拟结果有很好的一致性. 在实际8 m堆载下,基坑开挖完成后的15 d内,边坡顶部水平位移持续增大,且增大速率较快,此后,边坡顶部水平位移的增长速率变缓,逐渐趋于稳定. 实际变形与数值模拟结果取得了很好的一致性.
从几个关键值来看,在基坑开挖结束(2020-11-25)时,边坡顶部的水平位移模拟值为11.38 mm,与现场的实际监测值10.67 mm相差0.71 mm. 在开挖完成后的稳定期内,堆载40 d时(2021-01-05)边坡顶部的水平位移模拟值为14.7 mm,与现场的实际监测值14.18 mm相差0.52 mm. 考虑到基于该方法数值模拟计算的安全系数在堆载80 d左右将接近1.35的规范限值,故未进行长期堆载.
仅根据试验确定的相关计算参数进行的数值模拟,由于不能反映软土的c、φ受开挖扰动降低这一情况,土体强度较模拟值偏大,导致通过数值模拟计算的开挖结束时边坡顶部水平位移为8.36 mm,较实际监测数据11.38 mm偏小26.5%,堆载40 d时,边坡顶部水平位移为11.47 mm,较实际监测数据14.18 mm偏小19.1%. 通过试验获得的土体参数进行数值模拟,基坑整体变形趋势虽然与实际情况一致,但变形模拟值偏小. 根据数值模拟计算得到的变形值进行验算,会对设计方案的评估过于乐观,在安全裕度不充足的情况下,可能导致工程事故的发生.
3.3. 常荷载(7 m)下的超载优化设计
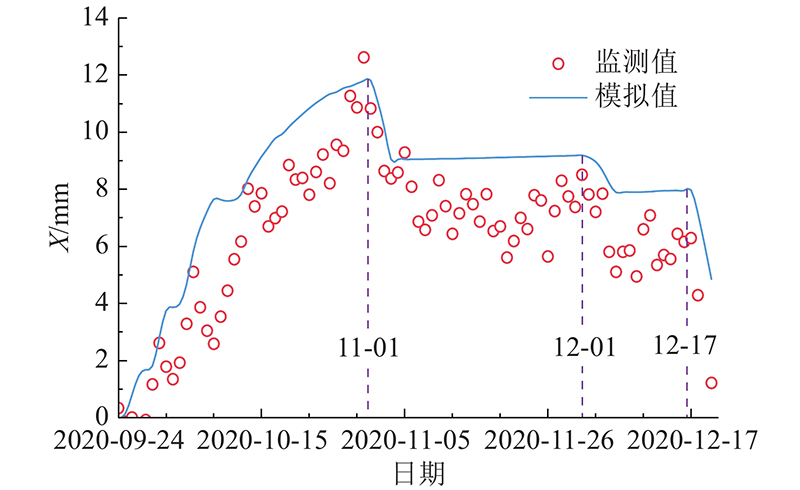
为了延长堆载时间,根据提出的方法,结合超载预压处理软土地基的思路,考虑在不同时间点进行卸载,降低软土时效变形带来的不利影响. 结合3.2节的分析,选择在开挖完成后第15天、第45天、第60天进行3次卸载,每次卸载1 m高度堆土,数值模拟及实际的监测结果如图14所示.
图 14
图 14 k30+100断面处边坡顶水平位移随时间的变化曲线图
Fig.14 Horizontal displacement at slope top of k30+100 profile versus time
实际的施工过程如下:2020年9月24日至2020年10月13日,基坑处于开挖阶段;10月13日至10月30日,基坑处于开挖后的稳定状态;后分别于11月1日、12月1日和12月17日进行3次卸载.
从整体趋势上看,模拟结果能够很好地预测实际施工过程中的变形. 在开挖阶段,基坑为3级放坡开挖,每层开挖结束后通过挂网喷砼进行边坡加固. 数值模拟分别在3次开挖后(9月27日~28日、10月1日~2日、10月8日~10日)出现一定时间内的变形基本稳定,由于全过程引入蠕变参数,该阶段变形略有增大,体现出软土的时效变形,数值模拟结果与土体的实际变形有很好的一致性. 在基坑开挖完成后(10月13日至10月30日),边坡顶部的水平位移持续增大,反映了软土的蠕变效应. 后续的3次卸荷,使得边坡顶部水平位移减小;卸荷后,基坑蠕变效应较卸载前显著降低. 这主要是因为超载使得土体的孔隙比大幅度降低,土体更加密实,改善了软土的性质,减小了蠕变效应.
从几个关键值来看,在基坑开挖结束时,边坡顶部水平位移模拟值为8.22 mm,与现场实际监测值8.02 mm相差0.2 mm. 在开挖完成后的稳定期内,边坡顶部水平位移模拟值为11.7 mm,与现场的实际监测值12.7 mm相差1.0 mm,说明基于本文提出方法确定的土体物理力学参数合理,能够较好地预测一定时间内超载作用下软土基坑的蠕变效应. 3次卸荷及卸荷后的变形值说明,基于“智能反演+蠕变实验”方法确定的土体参数在超载基坑优化设计中取得了良好的效果,能够降低软土的时效变形.
综合上述分析可知,基于该研究方法提出的优化堆载方案取得了较好的效果,较仅通过试验方法确定土体参数,模拟结果更能够反映土体的真实物理力学性质,验证了提出的结合智能反演和蠕变实验的分析方法的可靠性.
4. 结 论
(1)结合智能反演和蠕变实验的分析方法,对软土基坑的长期稳定性分析及变形预测具有很好的适用性.
(2)从基坑稳定性的发展趋势来看,在蠕变效应下,基坑开挖完成后的15 d,基坑安全性系数急剧衰减,随后衰减速率减缓,最终逐渐趋于稳定.
(3)通过逐级卸载的方式,可以减缓软土的时效变形,提高软土基坑的稳定性.
(4)针对软土基坑在超载作用下的稳定性分析,应充分考虑蠕变效应引起的土体时效变形,从而综合确定合理的超载堆载时间及堆载高度,以确保基坑的稳定性.
参考文献
软土基坑工程中时空效应理论与实践(上)
[J].
The theory and its practice by using the rule of time-space effect in soft soil excavation
[J].
大面积软土基坑放坡开挖引起蠕变的数值分析
[J].
Numerical analysis of creep induced by excavating slope in soft soil pit with larger area
[J].
Wall and ground movements due to deep excavations in Shanghai soft soils
[J].DOI:10.1061/(ASCE)GT.1943-5606.0000299
软土地区深基坑变形控制设计实践与分析
[J].
Design practice and analysis of deformation control of deep excavations in soft soil areas
[J].
软土地区深大基坑双环形支撑体系受力变形特性分析
[J].
Analysis on bearing and deforming behavior of a large-scale double annular arched girders structural system in deep excavation
[J].
Finite element analysis of time-dependent behavior in deep excavations
[J].DOI:10.1016/j.compgeo.2019.103300 [本文引用: 1]
地下工程建设安全面临的挑战与对策
[J].DOI:10.3969/j.issn.1000-6915.2012.10.001 [本文引用: 1]
Challenges faced by underground projects construction safety and countermeasures
[J].DOI:10.3969/j.issn.1000-6915.2012.10.001 [本文引用: 1]
南京软土地区基坑墙体变形性状研究
[J].
Characteristics of deformation of retaining wall due to deep excavation in Nanjing
[J].
软土地铁深基坑倒塌分析
[J].
Collapse of deep excavations for metro lines in soft clay
[J].
邻近超载状态下软土深基坑变形时间特性研究
[J].DOI:10.3969/j.issn.1009-0185.2019.05.002 [本文引用: 1]
Study on time characteristics of soft soil deep foundation pit deformation under the condition of overload
[J].DOI:10.3969/j.issn.1009-0185.2019.05.002 [本文引用: 1]
基于时间效应理论的软土深基坑变形分析
[J].DOI:10.11988/ckyyb.20151067 [本文引用: 2]
Analysis of deformation of deep excavation in soft clay based on time-effect theory
[J].DOI:10.11988/ckyyb.20151067 [本文引用: 2]
堆载下临江深基坑支护结构性状的ABAQUS数值分析
[J].
Numerical analysis of characteristics of retaining structures of deep foundation pit adjacent to river under heaped load by software ABAQUS
[J].
软土基坑变形时空演化规律研究
[J].
A study on the spatial-temporal evolution regularity of the deformation of a foundation pit in soft soil
[J].
深圳土体蠕变特性在深基坑工程中的应用
[J].DOI:10.3969/j.issn.1006-2106.2011.08.010 [本文引用: 1]
Application of soil creep characteristics in deep foundation pit project in Shenzhen
[J].DOI:10.3969/j.issn.1006-2106.2011.08.010 [本文引用: 1]
土体耦合蠕变模型在基坑数值模拟开挖中的应用
[J].DOI:10.3969/j.issn.1000-7598.2009.03.020 [本文引用: 1]
Application of soil coupled creep model to simulate foundation pit excavation
[J].DOI:10.3969/j.issn.1000-7598.2009.03.020 [本文引用: 1]
福州软土次固结变形特性试验研究
[J].
Experimental study on secondary consolidation properties of Fuzhou soft soils
[J].
考虑小应变下刚度衰减特征的软土本构模型
[J].
Constitutive model of soft soil after considering small strain stiffness decay characteristics
[J].
基于神经网络的深厚软土地层参数反演分析
[J].
Analysis of parameters in deep soft soil layer based on neural network
[J].
基于BA-LSSVM模型的黄土滑坡致灾范围预测
[J].
Prediction of the disaster area of loess landslide based on least square support vector machine optimized by bat algorithm
[J].
Least squares support vector machine classifiers
[J].