智能电网、交直流混合微电网、电力牵引等的发展,对中、大功率双向变流器的小型化、智能化提出了更高的要求,隔离型交−直流固态变压器(solid state transformer,SST)的研究也因此受到越来越多的关注[1-2]. 以交直流混合微电网的接口变流器为例,为了提高SST的运行范围与功率密度,实现原副边的隔离,拓扑通常采用前、后级级联结构:前级为双向全控整流级(rectifier stage,RS),连接交流电网与后级的原边,实现整流变换;后级为双向的中频DC/DC隔离级(isolated bidirectional DC/DC converter stage,IBDC),连接前级与直流电网,实现交、直流电网间的隔离与电压匹配[3].
SST的控制需要考虑前、后各级的独立控制,该方向的研究已较为深入,包括各级控制目标的设定、各类控制方法的设计、各级效率的优化等[4-6]. 由于前、后级通常被设计成不同的运行频率,导致两级的控制带宽与响应速度存在差异. (为了便于论述,以下将交流电网看作电网侧,直流电网作为负载侧,前后级间的电容电压简称为级间电压. )为了缩小各级变换器的响应差异,改善前、后级功率传递的一致性,郭力等[7-13]从加快RS响应的角度出发开展研究. 郭力等[7-8]将整流器直流侧的输出电流通过前馈系数,前馈到整流器的电流环中,以提高整流器对直流负载扰动的响应. 此方法原理简单,应对低纹波负载的变化效果明显. 王成山等[9]在以上方法的前馈量中增加微分环节,进一步提高系统的动态性能,但也给RS的电流环引入更多的噪声,使得系统的鲁棒性下降. Wang等[10-11]采用功率前馈的方法,将负载侧功率直接前馈到RS的电流环,以提高RS对负载侧变化的响应,由于前馈功率直接采用负载侧电流进行计算,导致RS对高纹波负载的控制性能较差;Ge等[12]的功率前馈避开对SST负载侧电流的直接检测,通过负载侧电压的变化间接获取前馈功率,由于负载侧电容对功率波动的滤波作用,系统对高纹波负载的暂态控制性能被提高. 孙玉巍等[13]在各级平均模型的基础上,提出前、后级交错前馈的协调策略,在一定程度上将系统整体的动态性能提升. 陆翔等[14]将状态反馈精确线性化方法成功应用于三相PWM整流器的电流环建模,实现非线性、强耦合整流器电流环的解耦,在此基础上设计的滑模控制器取得良好的控制效果. 但状态反馈精确线性化的实现较依赖于准确的系统数学模型. 刘海波等[15]针对SST多变量、非线性、强耦合的系统模型,忽略隔离级的动态特性,应用精确反馈线性化对整流级和逆变级进行非线性控制,孙玉巍等[16]将精确反馈线性化引入级联固态变压器的控制,加强变流器前后两级功率传递的一致性,其仅就单相系统进行探讨,该方法对三相系统不能完全适用.
本研究以前、后级级联的隔离型交−直流SST为研究对象,建立三相两级一体化的平均模型,引入输入-输出精确反馈线性化的方法,消除RS电流环,级间电压与负载侧电压的非线性耦合,实现SST的精确反馈线性化. 为各控制环路设计积分滑模控制器,改善前、后级传递功率的一致性,提高系统对参数摄动的鲁棒性.
1. SST拓扑及数学模型
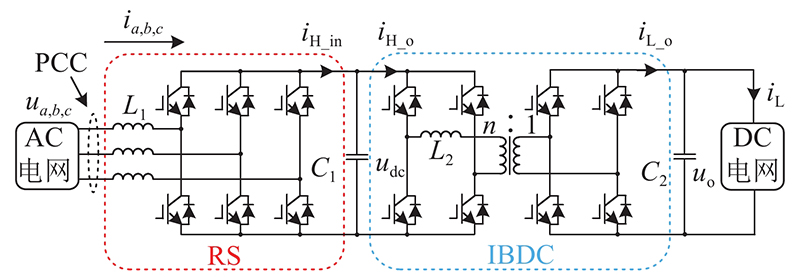
1.1. SST系统拓扑描述
SST拓扑如图1所示,前级RS采用三相两电平全控桥结构,后级IBDC采用隔离型对称全桥结构. 图中,ua、ub、uc为SST电网侧并网点电压(point of common coupling, PCC),ia、ib、ic为PCC流入SST的电流,udc为级间电压,uo为负载电压,iH_in为RS直流侧输出电流,iH_o为IBDC输入电流,iL_o为IBDC输出电流,iL为负载电流,L1为RS交流侧滤波电感,C1为级间电容,L2为IBDC的中频变压器等效漏感,n为IBDC变压器原副边的匝比,C2为IBDC的输出电容.
图 1
1.2. SST前后级一体化数学模型
假设电网侧电压平衡,忽略系统损耗. RS在两相同步旋转坐标系中的动态方程为
式中:ed、eq为电网电压在旋转坐标系中的d、q轴分量,id、iq为PCC流入SST电流的d、q轴分量,ω为PCC电压基波角频率,ud、uq为RS交流侧电压的d、q轴分量,串级控制系统中内环与外环设计的带宽相差较大,因此在涉及RS电压外环模型时,忽略RS电流内环的响应延迟[20],即为
式中:id,ref、iq,ref分别为RS电流环id、iq的指令值. 由能量守恒可得,RS交、直流侧的功率关系为
式中:PRS为RS交流侧输入的有功功率,Pout为RS直流侧输出的功率. 采用单移相控制IBDC的平均模型为[21]
式中:fs为IBDC的开关频率;Dm=d1(1-|d1|),其中d1为IBDC的移相比,d1∈[−0.5,0.5].
结合式(1)~(5),整理可得SST前后级的一体化数学模型为
2. SST多输入−多输出系统反馈线性化
由式(6)可知,RS并网电流id、iq存在非线性耦合,udc与uo也存在着非线性的强耦合关系. 因此,基于式(6)设计的传统线性控制器,暂态时的系统性能难以保障. 应用微分几何理论,引入输入−输出反馈线性化的方法,消除模型中的非线性耦合对控制的影响.
2.1. SST多输入-多输出系统仿射模型
由式(6),定义系统的状态向量x=[x1, x2, x3, x4]T=[id, iq, udc, uo]T;选取输入控制向量u=[u1, u2, u3, u4]T=[ud, uq, id,ref, Dm]T;将反馈值与指令值的误差量作为输出被控向量y=[y1, y2, y3, y4]T,其中y1=h1(x)=x1−id,ref、y2=h2(x)=x2−iq,ref、y3=h3(x)=x3−udc,ref、y4=h4(x)=x4−uo,ref,udc,ref、uo,ref分别为udc和uo的指令值. 系统模型可整理为[22]
由以上模型可知,系统的输出被控量y对状态量x是非线性的,但对控制量u是线性可达的. 因此,可将系统模型整理为标准4输入、4输出的仿射非线性模型.
2.2. SST系统反馈线性化
系统可满足精确反馈线性化的充要条件是:在x(0)=x0的领域内,总关系度r与系统状态变量的维数n相等,其中x0为系统的初始状态[23].
若系统在x0的领域内,有
式中:
是非奇异矩阵,则
由式(11)可知,系统各子关系度r1=r2=r3=r4=1,总关系度r=4,与系统状态变量的维数n相等. 因此,在x0的领域内,存在合适的坐标变换与状态反馈可实现系统的精确反馈线性化. 选取新的非线性坐标变换z为
式(7)可转化为
引入新的控制向量v=[v1, v2, v3, v4]T,令z、v满足线性关系,即为
将式(11)、(13)、(14)带入式(15),可求得系统非线性状态反馈的控制率为
经以上变换后,原输出被控向量
3. 多环积分滑模控制器设计
选取滑模面S为
式中:kij(i,j=1, 2, 3, 4)为积分滑模面参数,其中e1=id,ref − id、e2=iq,ref − iq、e3=udc,ref − udc、e4=uo,ref − uo.
为了消弱滑模的高频抖振,引入边界层控制,在边界层内部采用连续状态的反馈控制,外部采用正常的滑模控制,趋近率为
式中:−βs为指数趋近项;−ξsat(s)为变速趋近项,ξ为趋近项系数,sat(s)为
联立式(12) 、(15) 、(17) 、(18),整理可得
其中:A=1/k11,B=1/k21,C=1/k31,D=1/k41. 由式(15)~(23)可得系统的输出误差方程为
综上可得,系统精确反馈线性化后新的控制量为
反解求得IBDC的移向比d1为
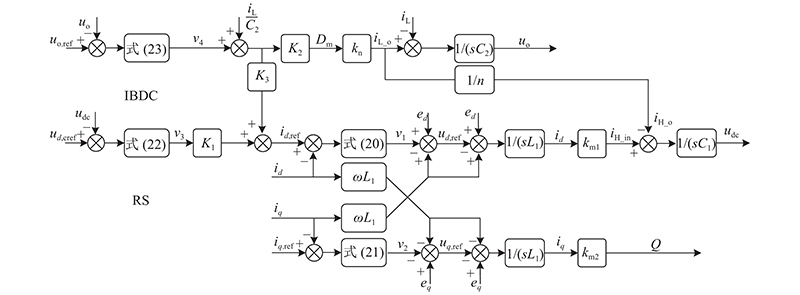
由式(16)~(28)可得SST前后级非线性一体化的控制框图,如图2所示. 图中,K1=2C1x3/3ed,K2=2fsC2L2/nx4,K3=2C2x4/3ed,kn=nudc/2fsL2,km1=3ed/2udc,km2=−3ed/2udc.
图 2
图 2 SST前后级一体化滑模控制框图
Fig.2 Control block diagram of integrated sliding mode controller for front and rear stages of SST
4. 仿真与实验验证
4.1. 仿真验证
表 1 SST仿真参数
Tab.1
| 子系统 | 参数 | 数值 |
| RS级 | 并网电压uab/V | 380 |
| 并网电感L1/mH | 2 | |
| 级间电容C1/µf | 2200 | |
| 开关频率f1/kHz | 5 | |
| 级间电压参考值udc,ref/V | 700 | |
| IBDC级 | IBDC级电感L2/µH | 20 |
| 直流侧电容C2/µF | 1 500 | |
| IBDC开关频率f2/kHz | 10 | |
| 变压器变比n | 1∶1 | |
| 直流侧电压参考值uo/V | 700 |
图 3
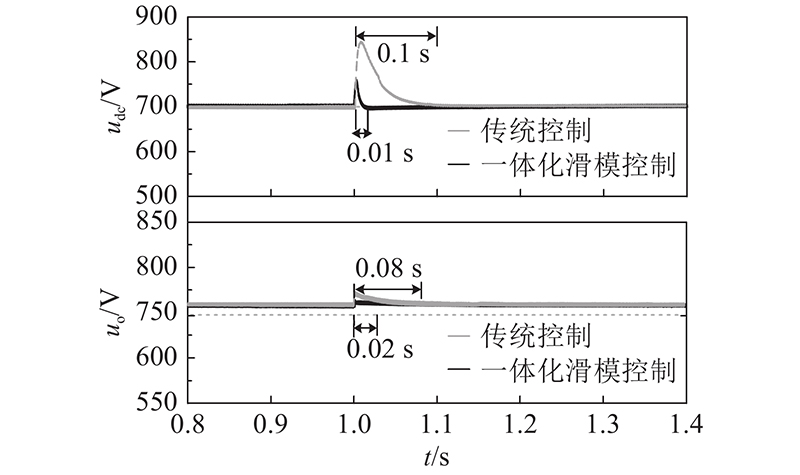
如图4所示为级间电压udc和负载侧电压uo的对比波形. 稳态时,传统方法与一体化滑模方法均能保持电压稳定、可控. 暂态时,传统方法级间电压波动峰值达150 V,暂态过程0.1 s. 负载侧电压波动15 V,暂态过程0.08 s;对一体化滑模方法,级间电压波动仅为50 V,暂态过程0.01 s. 负载侧电压波动5 V,暂态过程0.02 s,均优于传统方法.
图 4
为了验证一体化滑模方法对模型精度的鲁棒性,将L1的数值由2 mH提高到4 mH,重复上述仿真. 如图5所示,当L1数值增加后,稳态时,传统方法控制下的级间电压和负载侧电压均发生了局部震荡,稳定时间变长. 暂态时,电压的调节时间也由感量的增大而变长. 对比一体化滑模方法,级间电压和负载侧电压的控制性能几乎不受影响.
图 5
图 5 参数改变后级间电压和负载侧电压波形
Fig.5 Waveforms of inter stage voltage and load side voltage after parameter change
4.2. 实验验证
搭建如图6所示结构的实验平台. 平台由SST、PWM整流器、功率电阻、变压器、调压器构成. 实验平台采用组态屏控制,SST与PWM整流器采用2块独立的DSP控制板,PWM整流器模拟负载侧的分布式微源,以电流源形式恒功率并网;功率电阻模拟负载侧阻性负荷,通过控制其串接的MOSFET开关模拟负荷的投切,平台实物如图7所示. 受实验条件限制,SST运行功率为680 W,电源侧线电压有效值为110 V,级间电压、负载侧电压均设定为200 V,功率电阻40 Ω. 其他参数如表2所示,滑模控制参数为ξ1=ξ2=ξ3=ξ4=0.2,k11=k21=k31=k41=2,β1=β2=β3=β4=2,k12=k22=2000,k32=2200,k42=2500,φ=0.01.
图 6
图 7
表 2 SST实验参数
Tab.2
| 子系统 | 参数 | 数值 |
| RS级 | 并网电感L1/mH | 10 |
| 级间电容C1/µf | 2 200 | |
| 开关频率f1/kHz | 5 | |
| IBDC级 | IBDC级电感L2/µH | 255 |
| 直流侧电容C2/µF | 1 100 | |
| IBDC 开关频率f2/kHz | 10 | |
| 变压器变比n | 1∶1 |
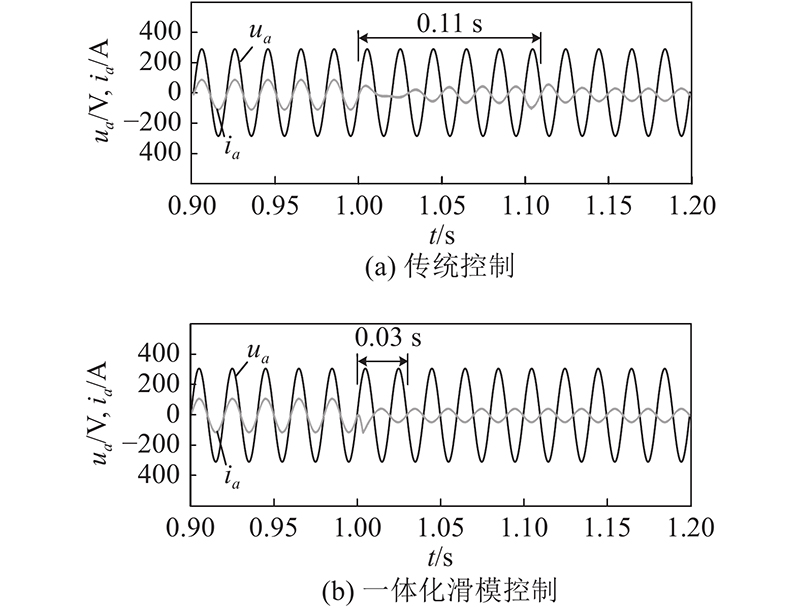
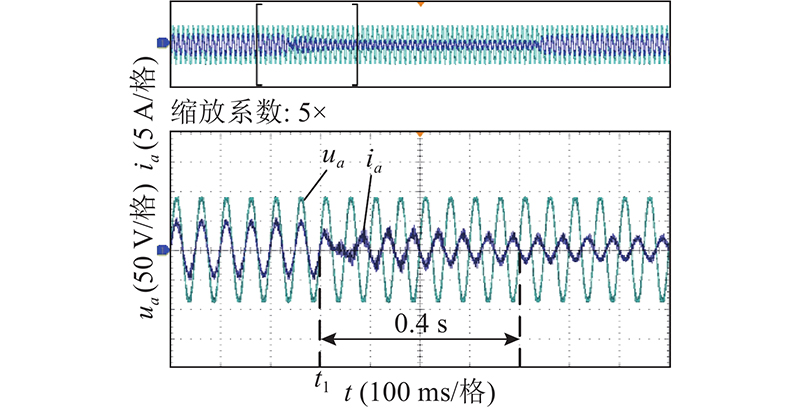
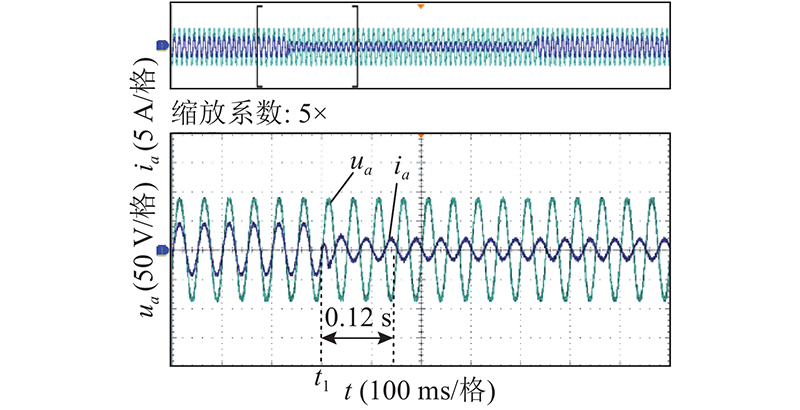
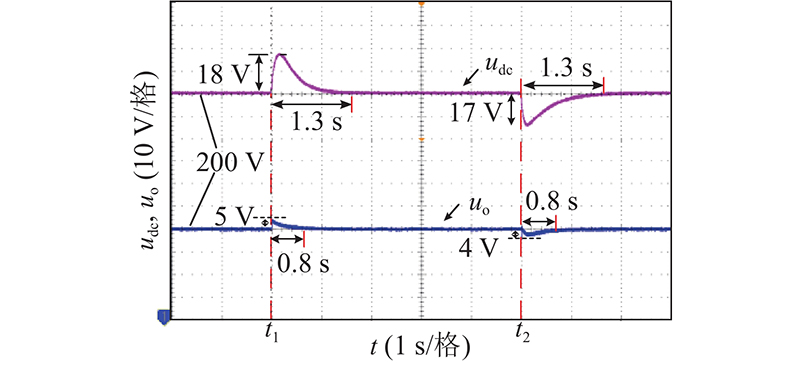
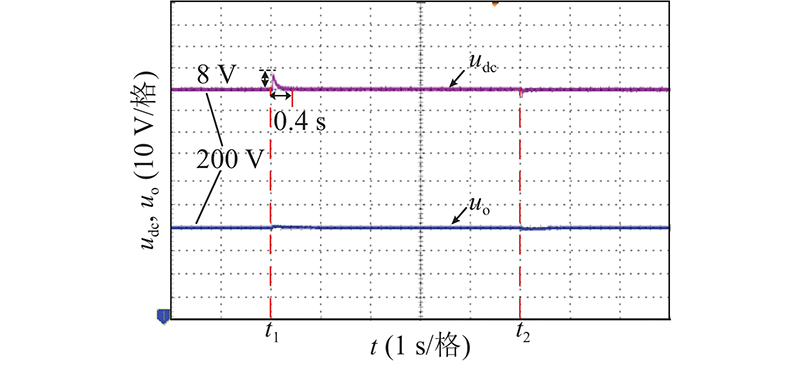
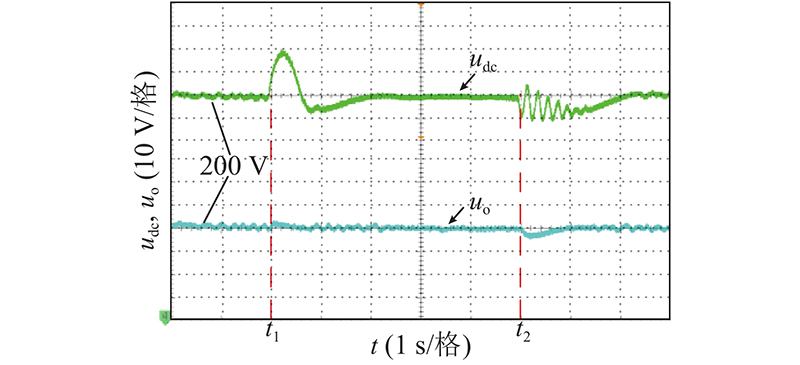
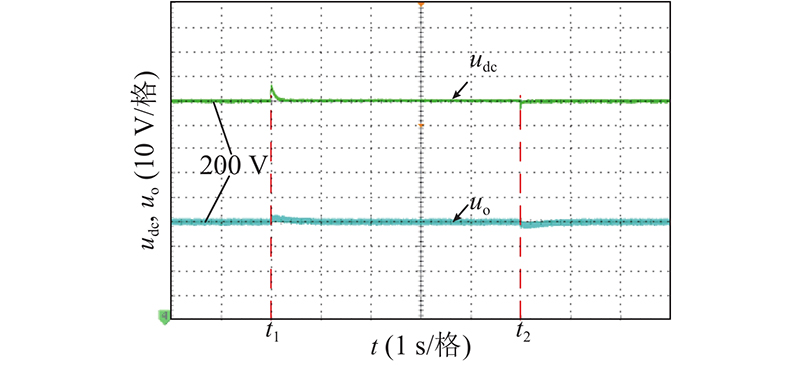
如图8、9所示分别为SST电源侧a相电压、电流波形变化图. 负载切除后,传统控制下SST电源侧电流暂态过程约为0.4 s,一体化滑模控制暂态过程约为0.12 s,缩短60%,与仿真效果基本一致.如图10、11所示分别为级间电压udc和负载侧电压uo波形变化图. 负载切除后,传统控制下,SST级间电压波动峰值约为18 V,暂态过程约1.3 s,SST负载侧电压波动峰值约为5 V,暂态过程约0.8 s. 负载再次投入后,SST级间电压波动峰值约为17 V,暂态过程约1.3 s,SST负载侧电压波动峰值约为4 V,暂态过程约0.8 s.一体化滑模控制下,SST级间电压波动峰值约为8 V,暂态过程约0.32 s,SST负载侧电压波动峰值约为1 V,暂态过程约0.18 s. 负载再次投入后,SST级间电压波动峰值约为7 V,暂态过程约0.28 s,SST负载侧电压波动峰值约为1V,暂态过程约0.18 s. 电压波动峰值与暂态过程均优于传统控制.
图 8
图 8 传统控制电源侧a相电压、电流波形
Fig.8 Waveforms of power side a phase voltage and current under traditional control
图 9
图 9 一体化滑模控制电源侧a相电压、电流波形
Fig.9 Waveforms of power side aphase voltage and current under integrated sliding mode control
图 10
图 10 传统控制级间电压和负载侧电压波形
Fig.10 Waveforms of inter stage and load side voltage under traditional control
图 11
图 11 一体化滑模控制级间电压和负载侧电压波形
Fig.11 Waveforms of inter stage and load side voltage under integrated sliding mode control
图 12
图 12 参数改变后传统控制级间电压、负载侧电压波形
Fig.12 Waveforms of inter stage and load side voltage with different parameters under traditional control
图 13
图 13 参数改变后一体化滑模控制级间电压、负载侧电压波形
Fig.13 Waveforms of inter stage and load side voltage with different parameters under integrated sliding mode control
5. 结 论
(1)一体化滑模控制方法能够实现SST级间电容电压与负载侧电压的高性能控制. 暂态过程中,该方法可明显提升前后两级功率传递的一致性.
(2)一体化滑模控制方法在提高SST控制性能的同时,降低了系统对参数变化的敏感度,控制方法的适用性更强.
(3)一体化滑模控制方法改善了控制系统的动态性能,加强了前后级之间的协调性,但并未考虑RS级网侧出现不平衡后对系统的影响,此外,该控制策略能否延伸到三级式固态变压器有待进一步深入研究.
参考文献
电能路由器的发展及其关键技术
[J].
The development and key technologies of electric energy router
[J].
Review of solid-state transformer technologies and their application in power distribution systems
[J].DOI:10.1109/JESTPE.2013.2277917 [本文引用: 1]
电力电子变压器技术研究综述
[J].
Research review of power electronic transformer technologies
[J].
Research on voltage and power balance control for cascaded modular solid-state transformer
[J].
双向全桥DC-DC变换器的负载电流前馈控制方法
[J].
A load current feedforward control scheme of dual active bridge DC/DC converters
[J].
计及非线性因素的混合供能系统协调控制
[J].
Coordinated control of hybrid power supply systems considering non-linear factors
[J].
基于优化负载电流前馈控制的400Hz三相PWM航空整流器
[J].
Three-phase 400 Hz PWM rectifier based on optimized feedforward control for aeronautical application
[J].
基于功率平衡及时滞补偿相结合的双级式变流器协调控制
[J].
Coordinated control of two-stage power converters based on power balancing and time-delay compensation
[J].
Energy feed-forward and direct feed-forward control for solid-state transformer
[J].DOI:10.1109/TPEL.2014.2382613 [本文引用: 1]
级联式电力电子变压器协调控制策略
[J].
Coordinative control strategy for cascaded power electronic transformer
[J].
基于多滑模变结构控制的三相PWM整流器非线性控制
[J].DOI:10.3969/j.issn.1000-6753.2016.04.012 [本文引用: 1]
Nonlinear control of three-phase PWM rectifier based on multi-sliding mode variable structure control
[J].DOI:10.3969/j.issn.1000-6753.2016.04.012 [本文引用: 1]
配电系统电子电力变压器非线性控制
[J].DOI:10.3321/j.issn:0258-8013.2009.27.001 [本文引用: 1]
Nonlinear control of electronic power transformer for distribution systems
[J].DOI:10.3321/j.issn:0258-8013.2009.27.001 [本文引用: 1]
级联式电力电子变压器非线性综合控制策略
[J].
Nonlinear integrated control strategy of cascaded power electronic transformer
[J].
级联式电力电子变压器混合脉宽调制谐波分析及均衡控制
[J].DOI:10.7500/AEPS20160624013 [本文引用: 3]
Harmonic analysis and balancing control of cascade power electronic transformer based on hybrid pulse width modulation
[J].DOI:10.7500/AEPS20160624013 [本文引用: 3]
Virtual direct power control scheme of dual active bridge DC–DC converters for fast dynamic response
[J].DOI:10.1109/TPEL.2017.2682982 [本文引用: 1]
三相PWM整流器混合非线性控制研究
[J].
Novel hybrid nonlinear control method for three-phase PWM rectifier
[J].
基于状态反馈精确线性化的MMC非线性解耦控制研究
[J].
Nonlinear decoupling control of MMC based on feedback linearization theory
[J].
LI X Y. Design of the static var compensator adaptive sliding mode controller considering model uncertainty and time-delay
[J].
基于反馈线性化滑模控制的直驱风电场经柔直并网系统次同步振荡抑制策略
[J].
Sub-synchronous oscillation mitigation strategy of direct-drive wind farms via VSC-HVDC system based on feedback linearization sliding mode control
[J].
基于振荡状态反馈的直流微网储能换流器的有源阻尼控制技术
[J].
Active damping control of energy storage converter in DC microgrid based on oscillatory state feedback
[J].
基于滑模控制的感应耦合电能传输系统输出电压控制研究
[J].
Investigation of output voltage control for the inductive power transfer system based on sliding mode control theory
[J].
储能型准Z源逆变器的积分滑模电流控制策略
[J].
Integrated sliding-mode current control strategy for energy-stored quasi-Z-source inverter
[J].