特高压输电相比于与传统的输电方式,具有明显的经济效益,而特高压电网已成为电力供应的主要模式. 输电塔作为输电线路中关键的一环,其安全性将直接影响整个系统的可靠性. 随着特高压直流输电方式的普及,T型输电塔得以广泛建设,相比于常规输电塔,T型输电塔的扭转效应更加显著,但输电塔设计规范中还没有扭转方面的规定.
扭转效应的研究主要集中在高层建筑领域. 扭转向风荷载主要由风湍流与尾流激励引起,当结构质心与空气动力中心不重合时还有可能产生偏心扭转振动[1-2],梁枢果等[3-4]在考虑风的紊流与尾流激励的影响下推导了扭转向风振力的计算方法;Marukawa等[5]利用高频天平研究宽厚比对高层建筑基底扭矩谱的影响;Tallin等[6]根据试验研究不同结构振型对高层建筑广义扭转风荷载谱的影响. 对于特高压T型输电塔,国内已有一些研究. 特高压T型输电塔由于横担较长,风振效应与常规输电塔有较大差异[7-12]. 在扭转效应方面,杨子烨等[13]对某±1 100 kV特高压输电塔进行时频域的响应分析,发现1阶扭转振型对塔身和横担的响应以及斜材轴力有较大影响;张骞等[14]通过有限元动力时程计算分析扭转效应对特高压输电塔结构内力的影响,发现结构会产生0.01 rad的扭转;张爽等[15]计算特高压输电塔的风振系数,发现输电塔的扭转效应随风速非线性增大;聂建波等[16]进行某特高压直流输电塔的风致响应分析,建议横担部分风振系数应高于同等高度塔身风振系数;杨子烨等[17]将长横担输电塔简化为弹簧−多质点模型,提出扭转向风荷载的计算公式,并建议提高斜材及横隔材的设计可靠度. 特高压T型输电塔的强扭转性使得其风致响应与一般输电塔差异较大,现行规范没有详细说明这种横向宽度突变结构的设计计算方法,对于其扭转效应的研究主要集中在数值模拟方面,对于扭转响应和等效风荷载的计算尚需进一步研究.
基于以上背景,本研究提出输电塔顺线路方向的扭转效应计算方法,分析扭转模态及相干函数对计算结果的影响,应用角度风分配系数获得角度风作用下的输电塔扭转效应计算公式,并设计气弹模型试验对计算方法进行验证,给出同时考虑扭转与平动的风振系数计算方法和计算公式.
1. 输电塔顺线路方向的扭转效应计算
结构各点沿扭心的扭转运动方程可以写为
式中:J为各点相对于转动中心的转动惯量矩阵,C为各点的转动阻尼矩阵,K为各点的转动刚度矩阵,θ为各点的扭转角向量,T为各点所受到的扭转荷载向量. 各点的扭转运动表示为各阶振型与广义位移函数:
式中:Θ为各点的各阶扭转振型矩阵,q为扭转振型的广义位移. 对运动方程进行解耦,可以得到i阶模态下的运动方程:
式中:ζi为第i阶扭转模态的阻尼比,ωi为第i阶扭转模态的自振圆频率,Ti*为第i阶扭转模态的广义力,Tk为k点所受扭矩,Θik、Qik为k点第i阶扭转模态,Ji为第i阶扭转模态的广义转动惯量,mk为k点的质量,rk为k点到扭转中心的距离,N为节点总数.
根据伯努利方程,在不可压缩的低速气流下,考虑无黏且忽略体力作用时,结构某位置所受扭矩T̃及扭矩标准差σT可以表示为
式中:Cd为某节点挡风系数,ρ为空气密度,
式中:Sf为风谱,coh为相干函数,下标k、n为点号,下标i、j为模态号. i、j阶扭转模态力的互功率谱STij可以表示为
根据结构动力学[18],i、j阶扭转模态作用下k点的扭转角互功率谱Sθkij和扭转角方差sqkij可以表示为
式中:H为传递函数,k点的扭转角标准差sqk可以表示为
式中:G为模态总数. 将响应分为背景和共振响应[19]:
式中:ni为第i阶模态的自振频率,ζi为i阶模态的阻尼比. 将式(9)~(11)、(13)代入式(12),扭转角标准差可以表达为
其中背景响应因子和共振响应因子计算式分别为
根据模态力计算方法,k点的等效扭矩Meqk可以表示为
式中:ωθ1为第1阶扭转模态的频率;Jzk为k点转动惯量;g为峰值因子,可取g=2.5. 利用力偶可以换算为扭转等效风荷载FTeqk:
2. 某T型塔的扭转响应
2.1. T型塔的扭转振型和频率
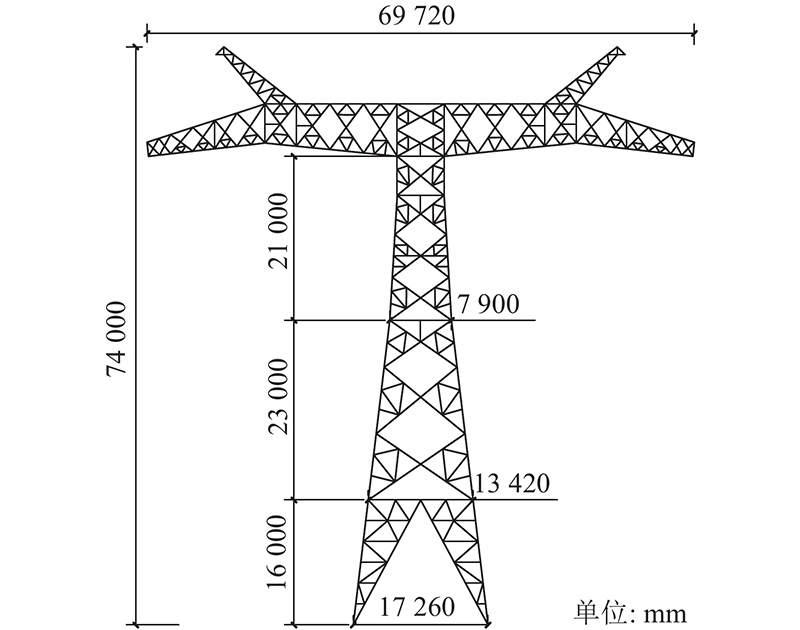
图 1
表 1 T型输电塔的角钢杆件截面
Tab.1
| 主材 | 斜材 | 辅材 |
| mm | ||
| L280×35 | L200×18 | L140×12 |
| L250×32 | L200×16 | L140×10 |
| L250×30 | L200×14 | L90×7 |
| L250×28 | L180×16 | L80×7 |
| L250×24 | L180×14 | L80×6 |
| L220×26 | L160×14 | L75×6 |
| L220×22 | L160×12 | L75×5 |
| - | L160×10 | L70×5 |
| - | - | L63×5 |
| - | - | L56×5 |
| - | - | L50×5 |
| - | - | L50×4 |
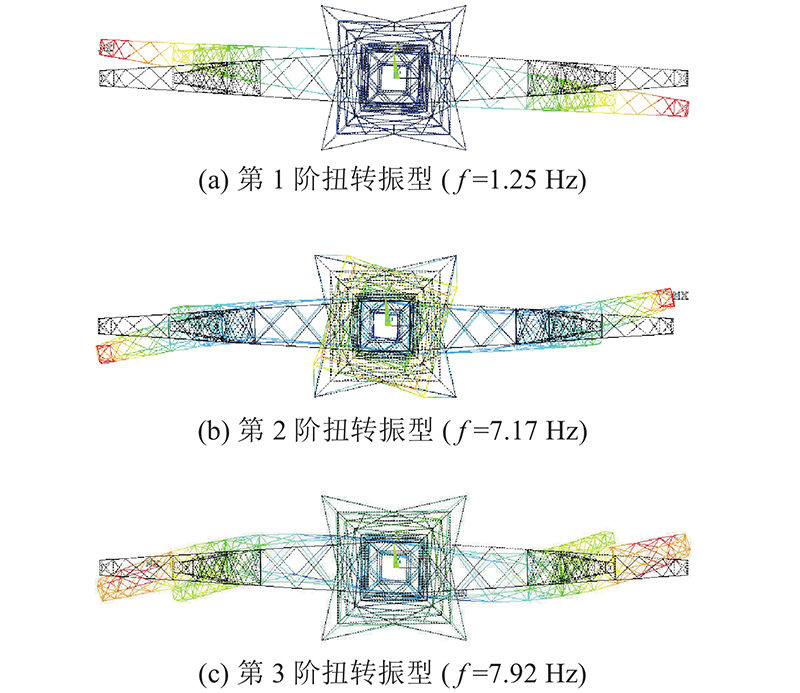
图 2
图 2 T型输电塔前3阶扭转模态
Fig.2 First three-order torsion mode of T-shaped transmission tower
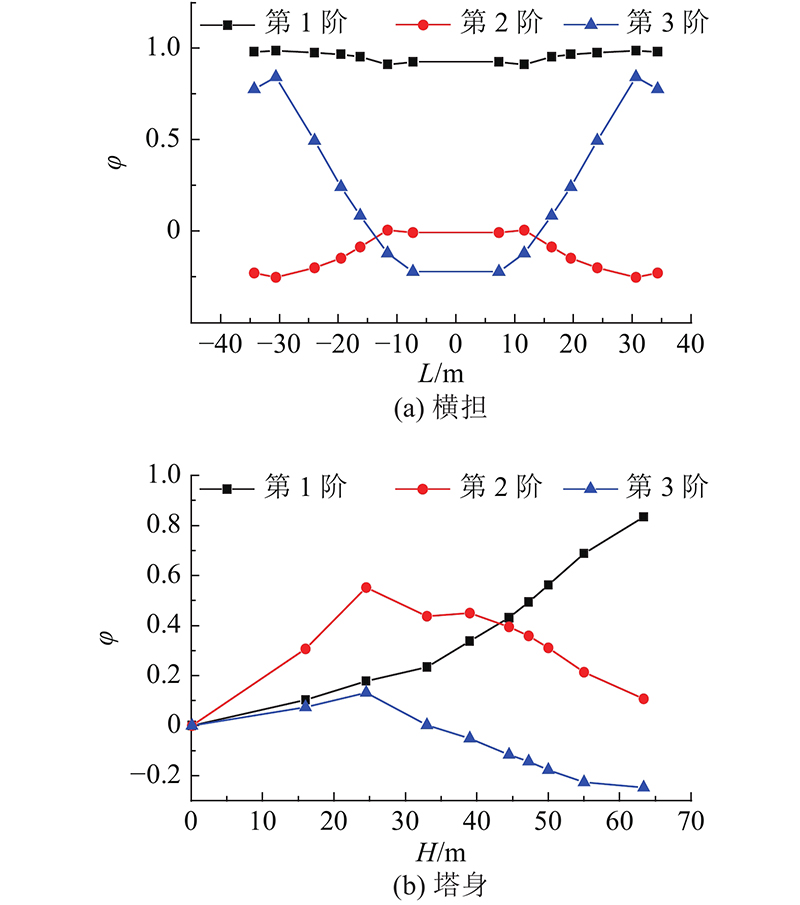
图 3
图 3 T型输电塔横担和塔身的前3阶扭转振型
Fig.3 First three-order torsion mode of T-shaped transmission tower cross arm and tower body
2.2. T型输电塔的扭转响应
计算时采用Davenport谱,表达式为
式中:kw为地面粗糙度修正系数,B类地貌下取1.0. 相干函数采用Shiotani提出的与频率无关的竖向和水平相干函数:
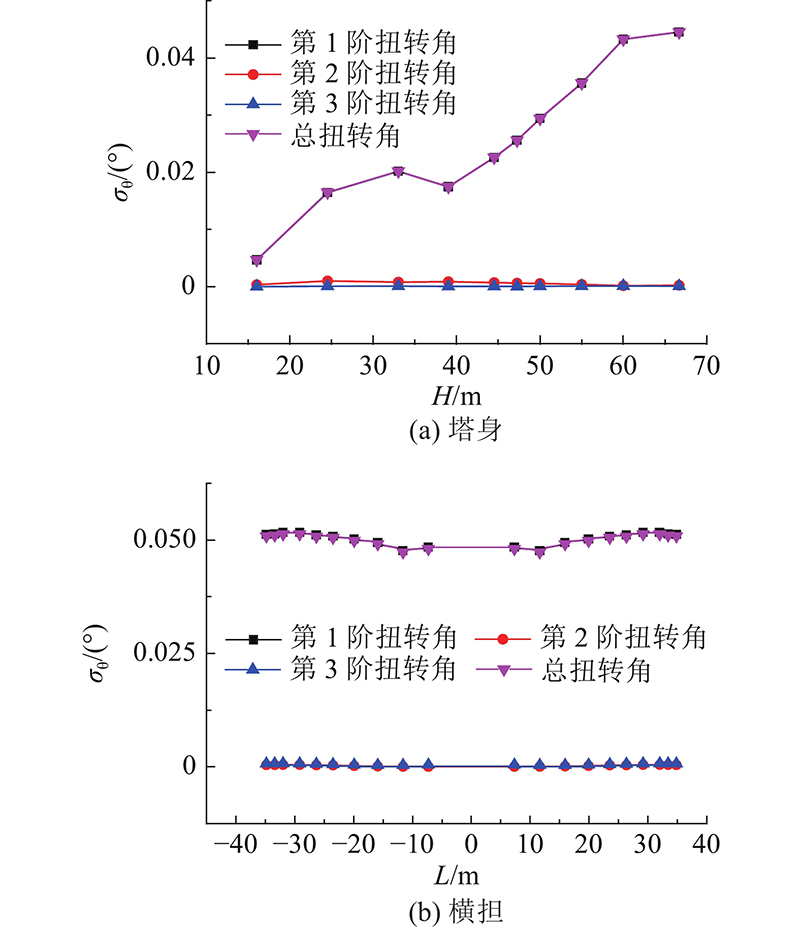
各阶模态扭转角θ标准差以及总扭转角标准差如图4所示,总扭转角为各阶模态扭转角的SRSS组合. 可以发现:1)第1阶扭转响应与总扭转响应相近,第2、3阶扭转响应很小,T型输电塔的扭转效应基本由第1阶模态控制,在实际应用中,仅考虑第1阶扭转模态已具备足够的精度;2)塔身的总扭转角标准差随高度增加而增加,且近似为线性变化;3)横担的扭转角标准差沿横担长度方向变化不大,靠近羊角位置的扭转角标准差会略微增大. 本研究后续计算中,均只考虑第1阶扭转模态.
图 4
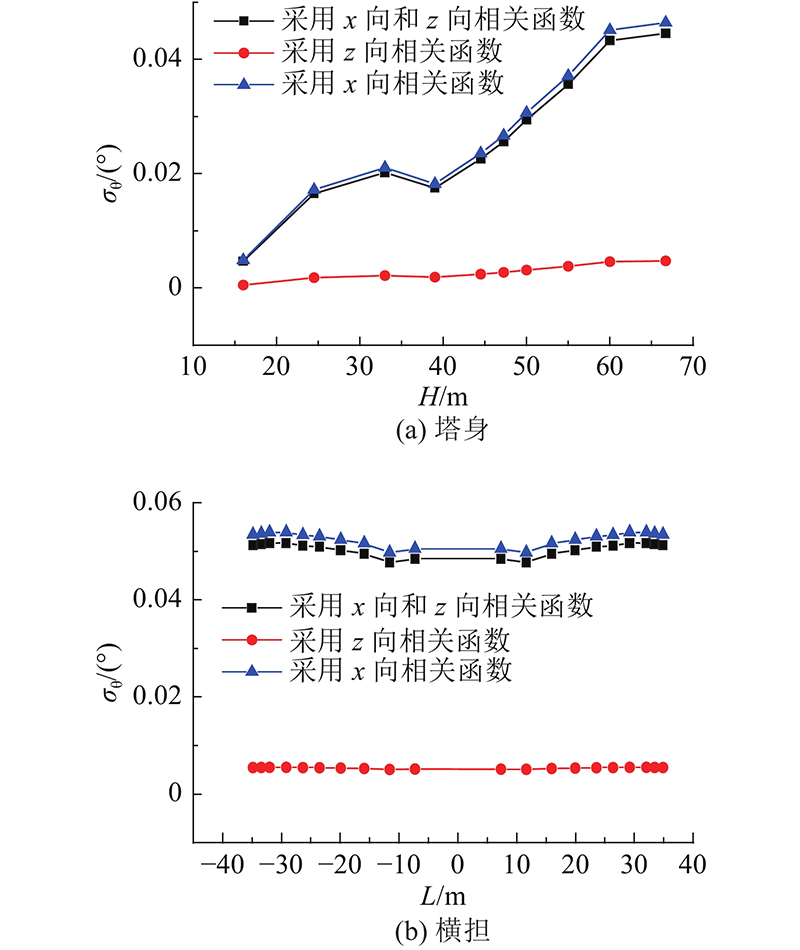
2.3. 相干函数对扭转效应的影响
图 5
图 5 不同相干函数的扭转角标准差
Fig.5 Standard deviation of torsion angle of different coherence functions
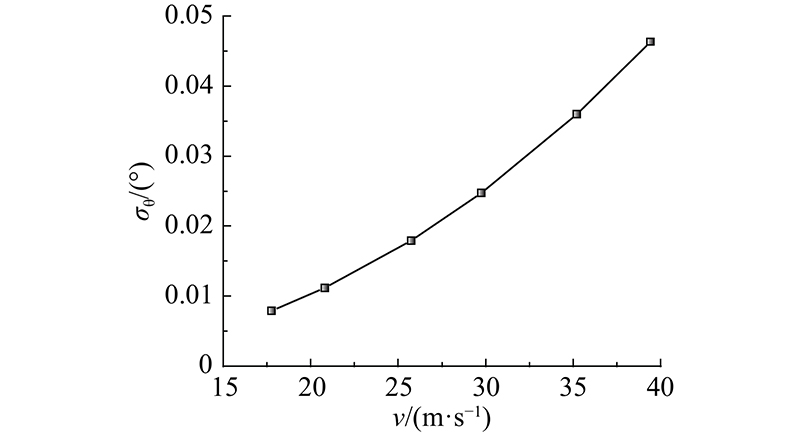
2.4. 不同风速作用下的扭转角
计算不同风速下T型输电塔的扭转响应,选取横担端点作为特征位置进行对比,结果如图6所示,可知,随着风速增大,横担端点的扭转角增大.
图 6
图 6 0°风向下横担端点扭转角标准差
Fig.6 Standard deviation of torsion angle at end of downward cross arm at 0°
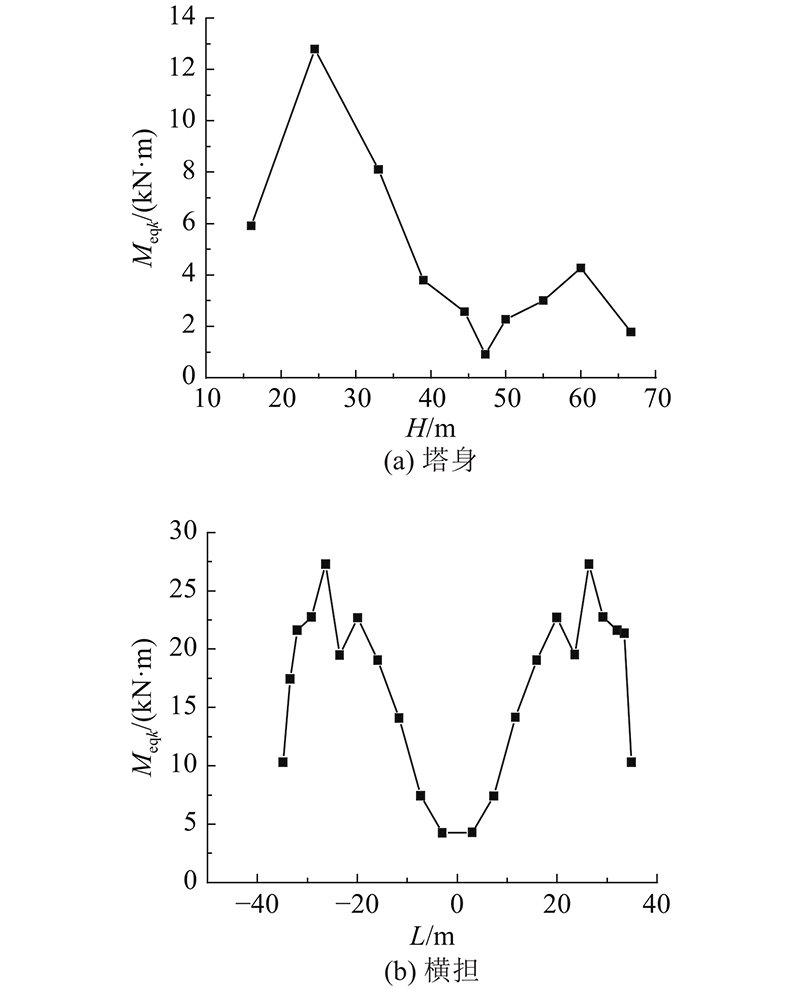
2.5. 扭转向等效风荷载
如图7所示为T型输电塔各节点的等效扭矩Meqk,可以发现:1)塔身下部等效扭矩较大,上部等效扭矩较小,主要由于下部结构尺寸大,导致转动惯量偏大;2)横担等效扭矩沿横担长度方向先增大后减小,最大值出现在羊角位置.
图 7
3. 扭转响应的气弹模型风洞试验验证
3.1. 气弹模型设计
通过量纲分析方法获得气弹试验所需要满足的各相似参数. 输电塔可以看作空间桁架结构体系,各杆件为二力杆,因此刚度的模拟只要做到拉伸刚度相似. 在模型设计时,对于有些对整塔模型刚度影响很小的杆件(如部分辅杆和横隔杆件),直接以外形要求选取模型材料,节点板的质量在配重时给予考虑. 确定模型几何缩尺比为1∶40,风速相似比为1∶3,如表2所示为各相似系数值.
表 2 气弹模型的相似系数
Tab.2
| 名称 | 数值 | 名称 | 数值 | |
| 尺寸相似系数CL | 1/40 | 拉伸刚度相似系数CEA | 1/14400 | |
| 面积相似系数CA | 1/1600 | 频率相似系数Cf | 13.33 | |
| 空气密度相似系数Cρf | 1 | 加速度相似系数Ca | 4.44 | |
| 结构密度相似系数Cρs | 1 | 风速相似系数Cv | 1/3 | |
| 质量相似系数Cm | 1/64000 | 位移相似系数Cy | 1/40 |
输电塔全塔质量为131 465.10 kg,实际质量比为1∶64 095. 模型采用厚0.10~0.45 mm的H62黄铜带为原材料,密度为7 800 kg/m3,弹性模量为100 GPa. 模型外观如图8所示.
图 8
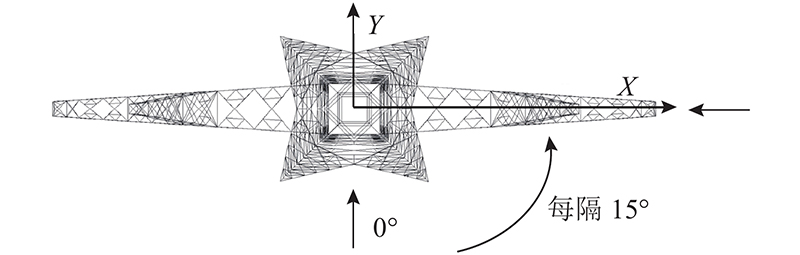
3.2. 风场模拟和试验工况
图 9
图 9 风向角和力系规定示意图
Fig.9 Schematic diagram of wind direction angle and force coordinate system
图 10
3.3. 测点布置和测试仪器
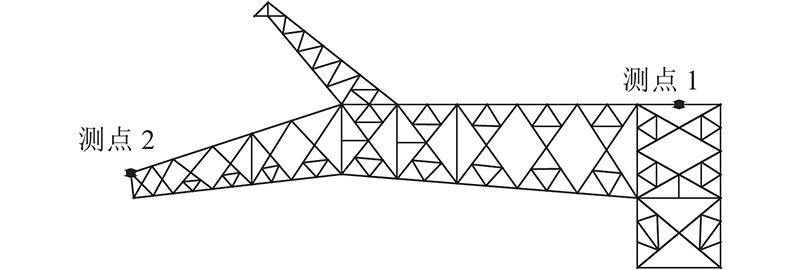
采用IMETRUM非接触式视频测量仪测试输电塔横担上的位移响应. 为了让非接触式视频测量仪更好捕捉测点位置,在模型上布置纸质标靶. 非接触式视频测量仪布置在风洞外,以减少风对测量仪器的干扰,测点布置如图11所示.
图 11
3.4. 气弹模型的动力标定
对输电塔模型进行动力特性标定试验,采用锤击法激振进行模态识别,获得该模型的模态参数. 通过各测量点上的响应,测得锤击点的自功率谱. 通过对模型主轴向的多次敲击,得到由外力激励下模型在不同主轴向的自由振动,分析得到模型的扭转前3阶自振频率和相应的阻尼比ζ. 识别结果如表3所示. 可知,基于IMETRUM位移计识别频率nt与期望频率nc符合较好.
表 3 模态参数识别结果
Tab.3
| 振型 | nc/Hz | nt/Hz | ζ |
| 1阶扭转 | 16.67 | 16.49 | 0.019 1 |
| x向一弯 | 20.40 | 18.89 | 0.008 2 |
| y向一弯 | 23.33 | 24.07 | 0.017 8 |
3.5. 扭转角的计算
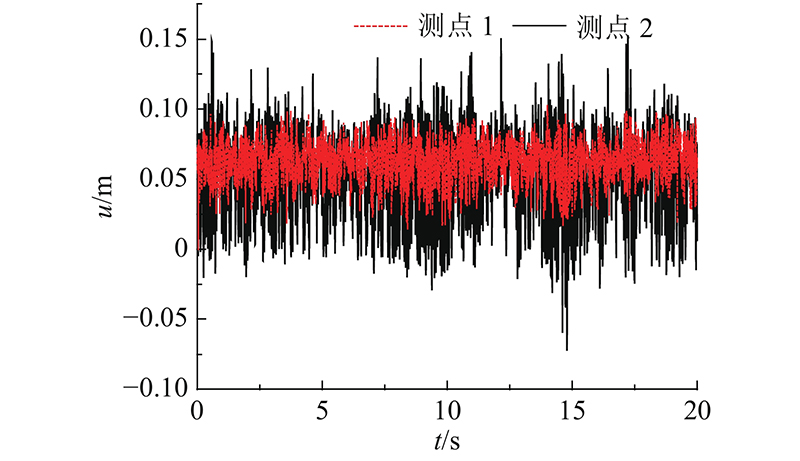
以17.95 m/s风速的测试结果为例进行分析,塔身测点(测点1)和横担测点(测点2)的位移u随时间t的变化如图12所示。图中数据已通过相似比换算为实际位移. 可知,与塔身相比,横担端点位移更加显著,横担存在扭转运动.
图 12
横担端点的扭转角位移时程θt可由下式计算:
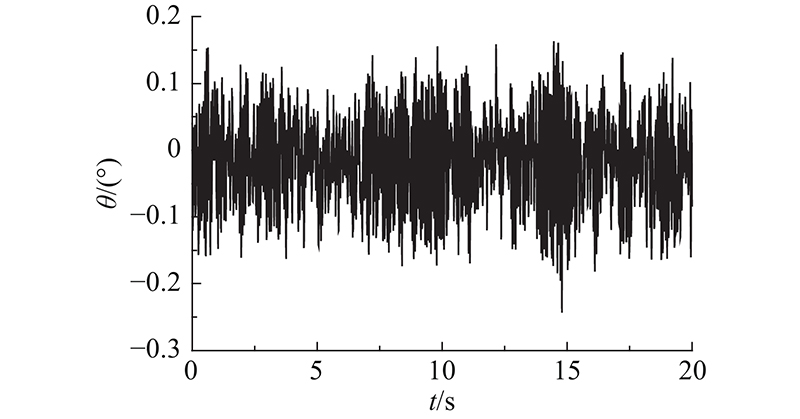
式中:u2、u1分别为横担测点和塔身测点的位移响应,L为半横担长度. 横担测点扭转角时程如图13所示.
图 13
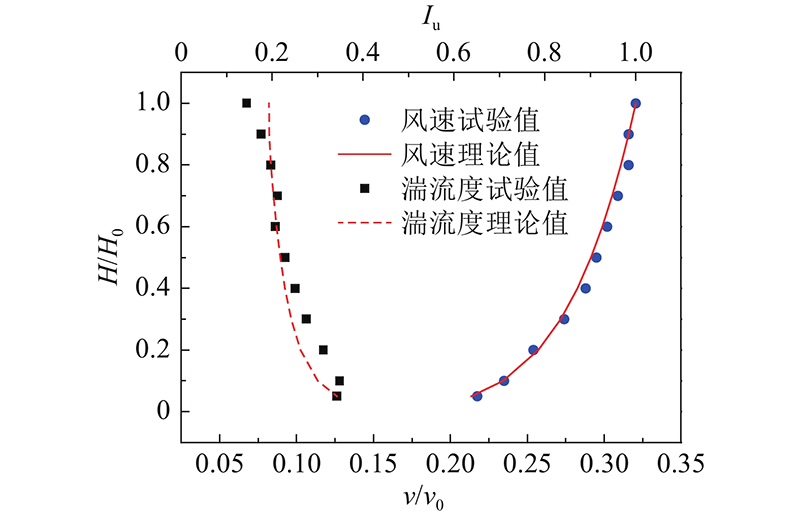
由时程可以得到模型横担端点的扭转角标准差。如图14所示为本研究所提算法的理论计算结果与风洞试验结果的对比. 可知:1)计算结果与试验结果吻合较好,本研究方法和气弹模型风洞试验方法的准确性得以验证;2)横担扭转角标准差随风速的增大而增大.
图 14
图 14 0°风向下横担端点扭转角标准差
Fig.14 Standard deviation of torsion angle at end of downward cross arm at 0°
4. 角度风作用下的扭转效应
4.1. 角度风作用下的分配系数
计算角度风作用下的扭转响应时,结构自身的扭转特性与风向角无关,因此只考虑风向角对结构扭转风荷载的影响. 根据文献[20],在角度风作用下,输电塔的荷载可以由线路方向和横担方向荷载组合而成. 在进行扭转荷载计算时,将总扭转荷载分为线路方向与横担方向,分别计算对应的扭矩再进行组合. 角度风分配系数可以表示为
表 4 角度风情况下的风荷载分配表
Tab.4
| η/(°) | Fsx | Fsy | Fbx | Fby |
| 0 | 0 | Wsb | 0 | Wsc |
| 45 | 0.424× (Wsa+Wsb) | 0.424× (Wsa+Wsb) | 0.35Wsc | 0.7Wsc |
| 60 | (0.747Wsa+ 0.249Wsb) | (0.431Wsa+ 0.144Wsb) | 0.40Wsc | 0.55Wsc |
| 90 | Wsa | 0 | 0.45Wsc | 0 |
式中:
4.2. 风洞试验结果的验证
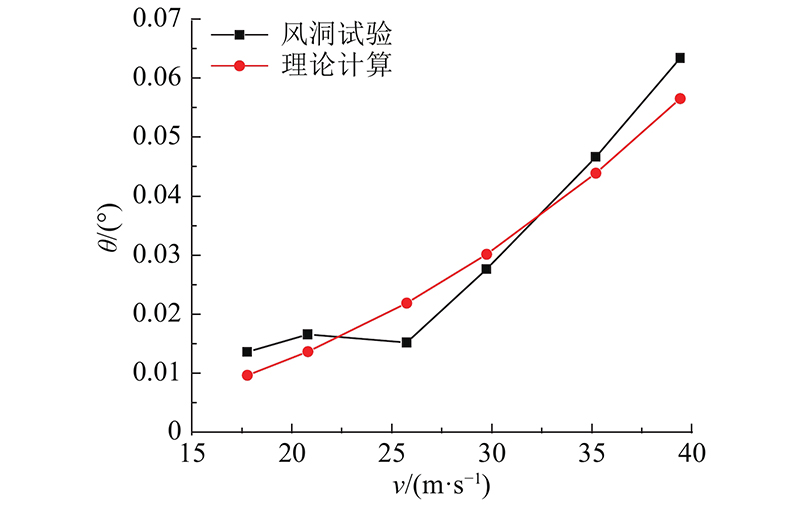
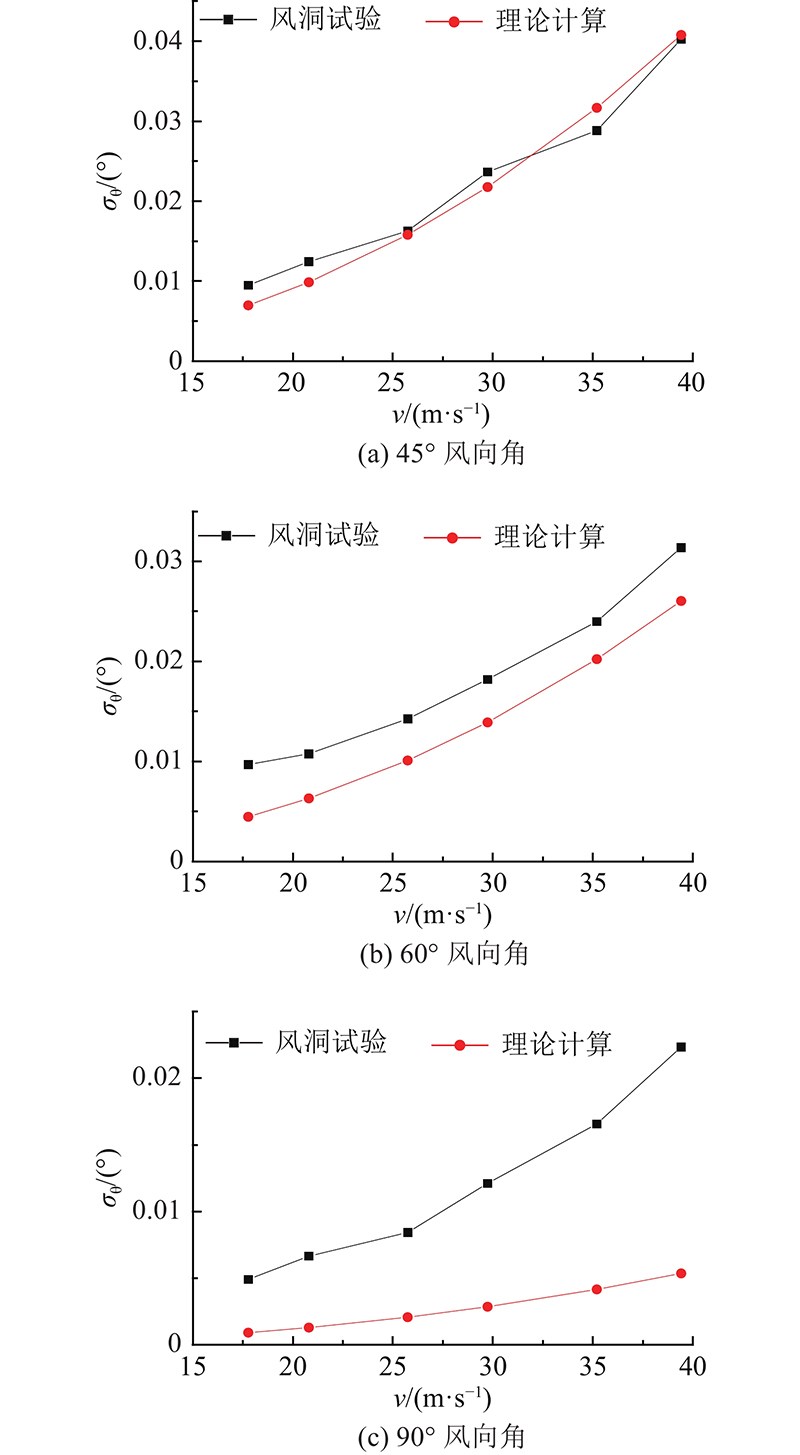
45°、60°和90°风向角下风洞试验和理论计算的扭转角对比如图15所示. 可知:1)输电塔扭转效应随角度增加而减小,2)45°风向角下,计算结果与气弹模型试验结果吻合较好;3)60°与90°风向下计算结果小于试验结果,且随着风速增大,差距逐渐加大,原因是此时杆件间遮挡效应严重,在风荷载作用下产生了较大的特征湍流,放大了整塔扭转响应,这种效应在本研究推导的基于准定常假定的扭转效应计算过程中无法考虑;4)本研究方法适用于输电塔顺线路的来流风向,对于输电塔横线路的来流风向的模拟效果较差.
图 15
图 15 倾斜风向下横担端点扭转角标准差
Fig.15 Standard deviation of torsion angle of inclined wind downward cross arm end point
5. 考虑平动和扭转的风振系数计算
5.1. 风振系数计算方法
设计中由于无法直接输入扭转风荷载,可以考虑将扭转荷载反推的扭转力与平动力进行对比,或者在平动风荷载基础上考虑一定的修正以考虑扭转效应.
输电塔k点的平均风荷载为
如果只考虑平动情况,其风振系数可采用文献[20]中推荐的算法如下。
式中:βPk为k点平动风振系数,FPeqk为k点平动的等效风荷载,ωx1为第1阶平动模态频率,ϕx1k为k点在第1阶平动模态的振型,σq1为顺风向1阶广义位移均方根.
如果只考虑扭转风荷载、平均风荷载和扭转风荷载,则k点扭转风振系数计算公式为
式中:Fck为k点平均风荷载.
如果同时考虑扭转和平动组合效应时,由于两者等效风荷载均为模态力,叠加采用SRSS方法,计算公式为
式中:αk为在平动风振系数基础上考虑扭转等效风荷载后的修正系数.
扭转转化为扭转等效风荷载时,在横担两侧呈现正负号相反的一对力,当该力与平动等效风荷载同号时,考虑扭转等效风荷载后的放大系数α1k采用的计算公式为
此时,横担另一侧的扭转等效风荷载与平动等效风荷载反号,考虑扭转等效风荷载后的折减系数α2k采用的计算公式为
由式(33)~(35),得到同时考虑平动和扭转的风振系数计算公式为
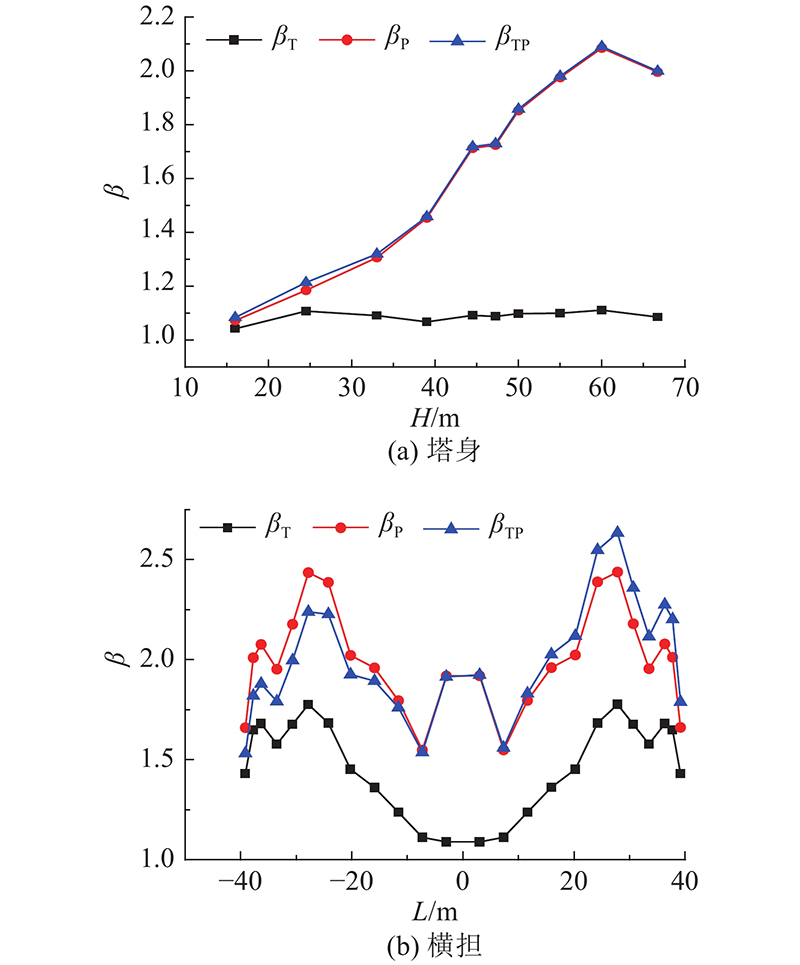
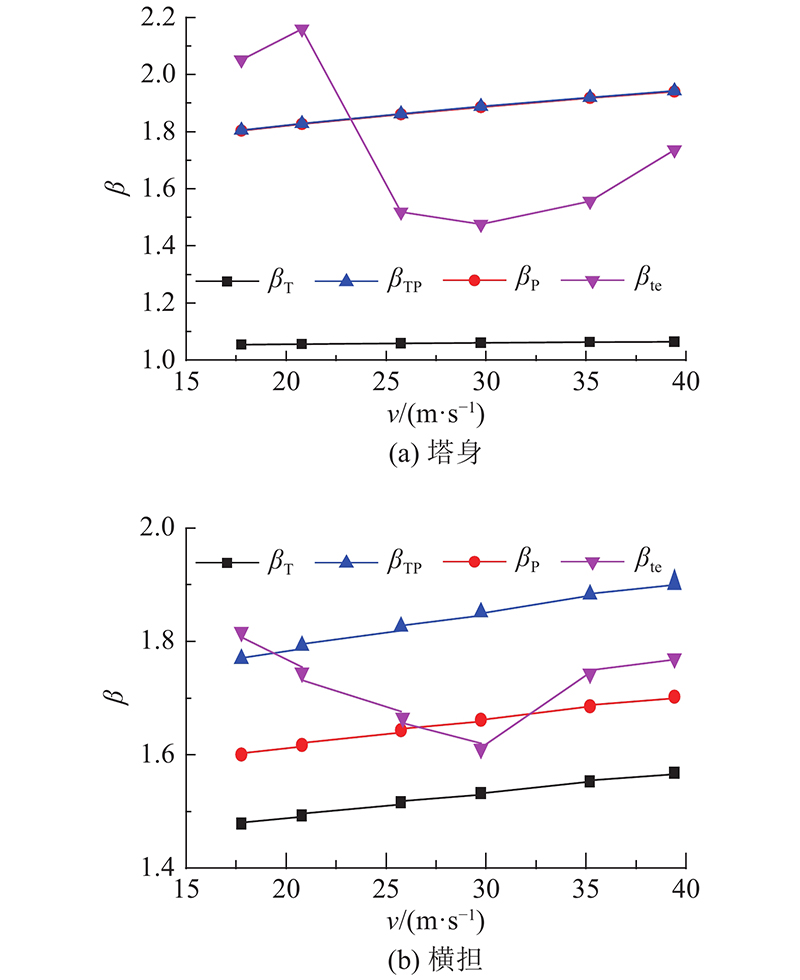
0°风向下,T型输电塔各位置的风振系数如图16所示,由于塔身对扭转效应不敏感,只给出扭转效应较大一侧的结果. 可以发现:1)塔身的扭−平组合风振系数沿高度增大而增大,与平动风振系数较为接近,扭转分量占比较小;2)横担的扭转风振系数与平动风振系数量级相近,平动风振系数沿横担长度方向几乎不变,扭转风振系数沿横担长度方向逐渐增大,在横担端点两者相近.
图 16
图 16 T型输电塔风振系数
Fig.16 Wind vibration coefficient of T-shaped transmission tower
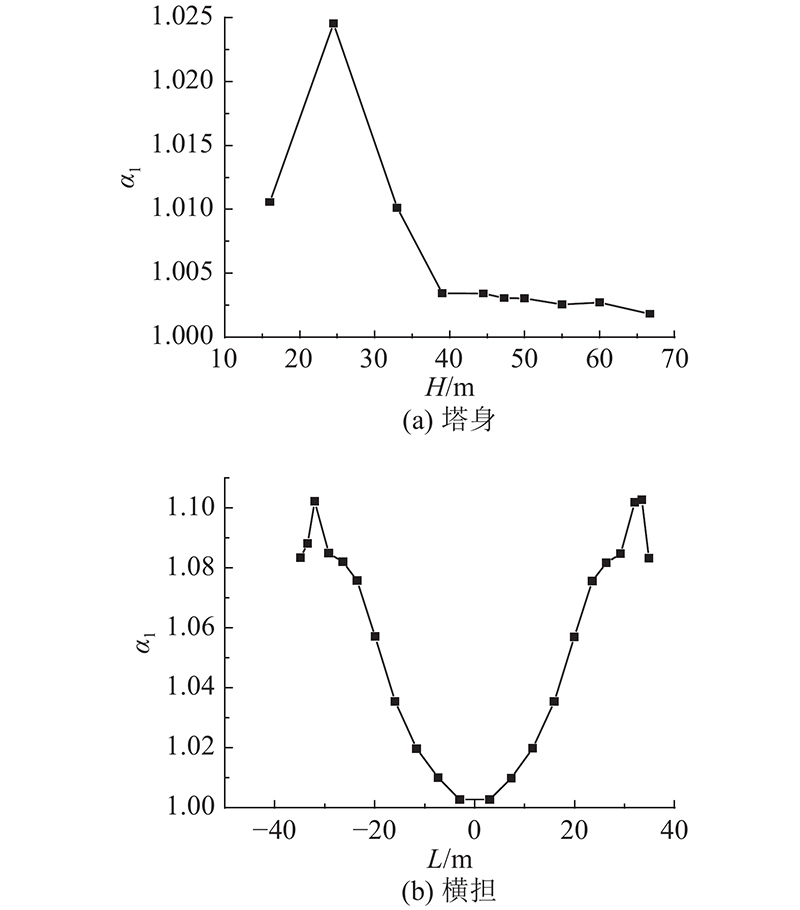
T型输电塔的扭转放大系数α1如图17所示,可知:1)塔身扭转放大系数量级较小,放大系数最大为1.036,出现在塔身下部;2)横担扭转放大系数沿横担长度方向增加,放大系数最大为1.1,出现在横担端部.
图 17
图 17 T型输电塔扭转放大系数
Fig.17 T-shaped transmission tower torsion amplification factor
5.2. 气弹模型的风洞试验结果验证
气弹模型试验的风振系数可以利用惯性力法获得:
式中,Fte为试验获得的等效风荷载,σte为试验获得的位移标准差. 在0 °风向下,不同风速塔身和横担端部截面风振系数的试验值与计算值对比结果如图18所示. 可知:1)3种风振系数随风速增大而略微增大;2)塔身扭转风振系数很小,组合风振系数与平动风振系数相近,且接近试验值;3)横担扭转风振系数与平动风振系数均小于试验值,仅考虑平动或扭转会低估输电塔的响应,组合风振系数与试验值较为接近,且基本大于试验值,较为准确,适于在工程上应用.
图 18
图 18 0°风向下T型输电塔的风振系数
Fig.18 Wind vibration coefficient of T-shaped transmission tower under 0°wind
6. 结 论
(1)提出输电塔顺线路方向扭转响应和扭转等效风荷载的计算方法,扭转响应结果得到气弹模型风洞试验的验证.
(2)长横担T型输电塔的扭转效应基本由第1阶模态控制,在实际应用中,仅考虑第1阶扭转模态已具备足够的精度;塔身的总扭转角标准差随高度增加而增加,且近似为线性变化;横担的扭转角标准差沿横担长度方向变化不大.
(3)仅采用竖直向相干函数无法体现T型输电塔的扭转特性;仅采用水平向相干函数方法会放大扭转响应,计算时应同时采用水平向与竖直向相干函数.
(4)提出角度风作用下输电塔扭转效应的计算方法,并与气弹模型试验的结果进行对比;气弹模型试验结果表明:0°与45°风向角下,理论计算值与气弹模型试验值吻合较好;60°与90°风向下理论计算值小于试验值,且随着风速增大,差距逐渐加大,这是由于输电塔杆件遮挡效应严重,在风荷载作用下产生较大的特征湍流,放大了整塔的扭转响应,这种效应在理论计算中无法考虑.
(5)提出同时考虑平动和扭转效应的风振系数计算方法. 计算结果表明,塔身的扭−平组合风振系数与平动风振系数较为接近,塔身扭转放大系数最大值为1.036,扭转占比较小;扭转风振系数沿横担长度方向逐渐增大,横担扭转放大系数最大值为1.1,出现在横担端部附近;扭−平组合风振系数随风速增大而略微增大,仅考虑平动或扭转会低估输电塔的响应;气弹模型试验结果的风振系数与理论计算值比较接近.
(6)本研究只考虑了输电塔顺线路方向的扭转响应和扭转等效风荷载,后续将研究不同来流方向下的扭转效应,以及扭转振动与平动振动的耦合情况.
参考文献
Mathematical model to predict 3-D wind loading on buildings
[J].DOI:10.1061/(ASCE)0733-9399(1985)111:2(254) [本文引用: 1]
Wind induced torque on square and rectangular building shapes
[J].
高层建筑横风向与扭转风振力计算
[J].
An evaluation of dynamic loads in across-wind direction and torsion on tall buildings
[J].
Torsional dynamic wind loads on rectangular tall buildings
[J].DOI:10.1016/j.engstruct.2003.09.004 [本文引用: 1]
Across-wind and torsional acceleration of prismatic high rise buildings
[J].
Wind induced lateral-torsional motion of buildings
[J].DOI:10.1061/(ASCE)0733-9445(1985)111:10(2197) [本文引用: 1]
基于风洞试验的对称截面高层建筑三维等效静力风荷载研究
[J].
Analysis of three dimensional equivalent static wind loads on symmetrical high-rise buildings based on wind tunnel tests
[J].
特高压直流输电塔风振响应参与模态分析
[J].
Participant mode analysis of wind-induced responses of HVDC power transmission tower
[J].
±1 100 kV特高压直流输电线铁塔风致响应及风振系数研究
[J].
Wind-induced dynamic response and vibration coefficient of ±1 100 kilovolt extra-high voltage direct current transmission line tower
[J].
风速水平空间相关性对长横担输电塔风效应的影响
[J].
Influence of turbulent transverse space correlation on wind induced responses of long cantilever transmission towers
[J].
±1 100 kV特高压长悬臂输电铁塔风振特性研究
[J].
Wind-induced dynamic response and vibration coefficient of ±1 100 kilovolt DC UHV transmission tower with long cantilever
[J].
±1 100 kV特高压输电塔风振响应频域分析
[J].
Frequency domain analysis of wind-induced response of ±1 100 kV ultra-high voltage (UHV) transmission tower
[J].
特高压长悬臂输电塔与输电塔-线耦合体系的风振特性
[J].
Wind-induced response of UHV long cantilever transmission tower and tower-line coupled system
[J].
±1 100 kV输电塔风振响应及风振系数研究
[J].DOI:10.3969/j.issn.1001-3598.2018.04.009 [本文引用: 1]
Research on wind-induced response analysis and vibration coefficient of ±1 100 kV transmission tower
[J].DOI:10.3969/j.issn.1001-3598.2018.04.009 [本文引用: 1]
±800 kV特高压T型长横担输电塔风振特性研究
[J].
Study on wind-induced vibration characteristics of ± 800 kV UHV T shaped long cross-arm transmission tower
[J].
长横担输电塔扭转向等效静力风荷载
[J].
Equivalent static wind load in torsional direction of long cross arm transmission tower
[J].
Random vibration of structures
[J].DOI:10.1115/1.3269806 [本文引用: 1]