对钢箱梁制造参数计算的研究可归纳为2类. 1)基于无应力状态控制理念[9],通过结构成桥时的有应力状态直接解算制造时的无应力状态. Yiu等[10]在单元级别采用线性理论或线性二阶理论由力反算变形,提出按单元“放松-组装-制造”过程求节段无应力构形的方法. 梁鹏等[5]利用单元随转坐标系法直接得到节段设计状态相对于制造状态的变形,可以方便地由设计构形直接得到无应力构形. 结构解体法[5]从成桥状态出发,通过解除主梁多余约束及所有荷载得到无应力构形. 董道福等[11]根据已知的结构部分构件的目标构形及外荷载,采用几何法及零作用法直接求解单元的无应力构形基本参数及构件完整无应力构形. Li等[12-14]用简便的一次落架法确定顶推钢箱梁相邻节段制造时的位置关系,提出“等高等邻边梯形法”获得节段的制造参数. 2)根据计算或测量获得的结构位移及转角信息对安装过程中相邻节段的位置关系进行分析,获得节段制造参数. 李乔等[6]通过引入切线位移概念及计算方法,得到用于制造参数计算的制造线形,对悬臂拼装施工桥梁具有很好的适用性. 赵雷等[15]从新起吊悬拼节段与相邻已安装节段间的位置关系着手,利用施工阶段分析结果计算节段制造参数. 陈太聪等[16]综合考虑结构整体变形和节段局部变形的影响,提出端截面转角补偿的方法确定节段制造参数. Kim等[17]利用地面激光扫描仪,精确测量施工现场两侧悬臂段的三维位置及相对位移,获得合龙段的制造参数. Wang等[18]推导大节段钢箱梁各状态下的几何状态方程和状态传递矩阵,根据状态方程中的状态向量准确计算钢箱梁制造参数.
分阶段桥梁施工中节段的几何形态和相对位置关系与具体的施工方法、步骤密切相关[19],工程中存在节段交接处两侧弹性曲线不光滑连续的情形,此时完全按照无应力状态控制理念得到的无应力构形进行安装会出现强迫合龙的情况[9]. 此外,桥梁施工过程中节段的转角不易量测,利用结构位移和转角计算节段制造参数略显烦琐. 本研究基于安装时节段间交界面实现平顺对接的思想,直接根据结构累计位移确定已安装节段和待安装节段桥位现场的相对位置关系,并以设计成桥状态下节段形心处梁长为基准,提出分阶段施工钢箱梁桥节段间制造夹角、顶底板长度制造参数的通用计算方法,以三跨变截面钢箱连续梁桥为背景验证该方法的实用性,并给出相应的计算结果.
1. 节段安装匹配关系分析
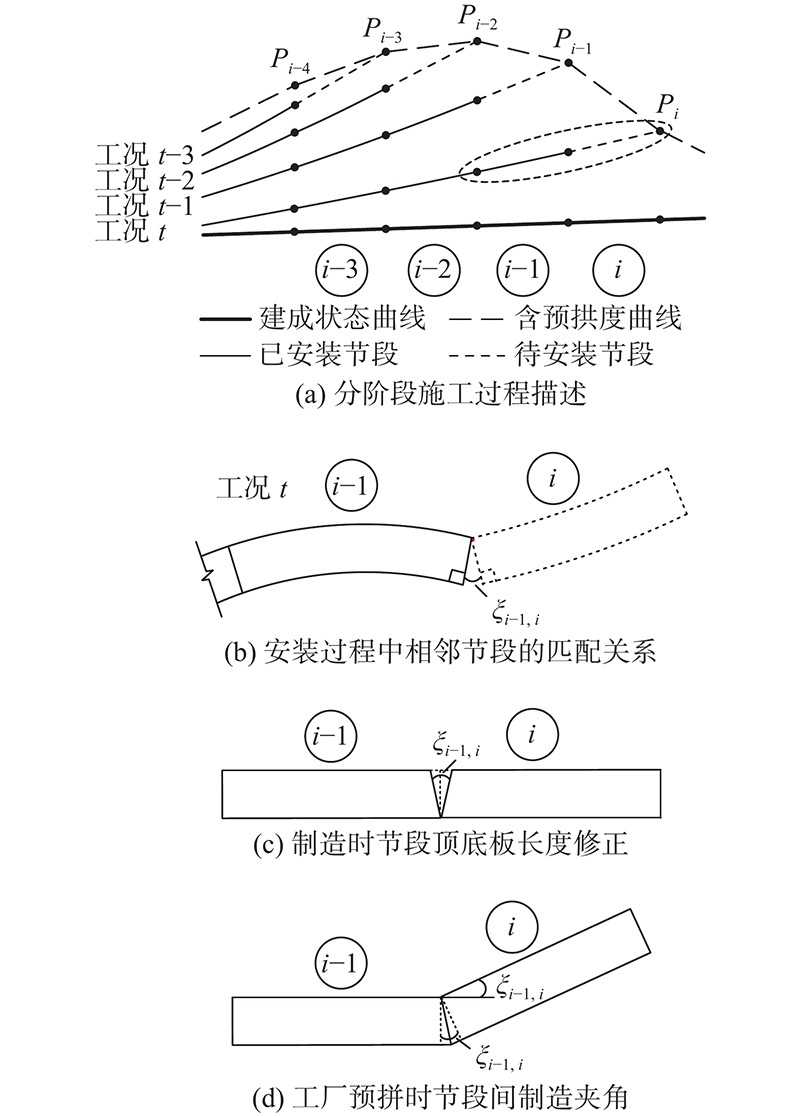
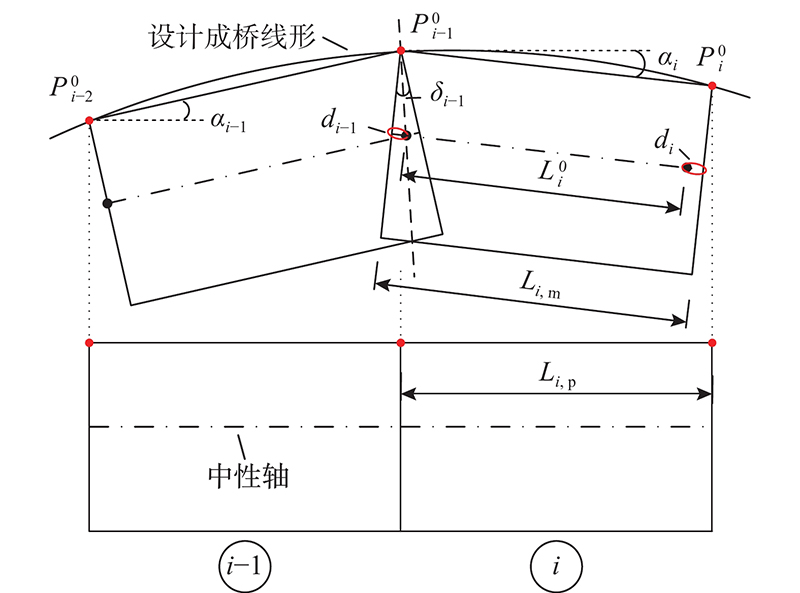
如图1 (a)所示,钢箱梁桥建造一般采用分阶段施工法,在工况
图 1
图 1 分阶段施工中节段制造状态的确定
Fig.1 Determination for manufacturing status of segments in staged construction
2. 钢箱梁制造参数的计算
从设计文件上能方便地获取设计成桥状态下节段中性轴的里程及高程信息,通过有限元进行施工过程仿真分析可准确地得到各施工工况下节段的累计位移,因此在理想施工情况下待安装节段与已安装节段桥位现场的相对位置关系可以根据节段的里程及高程信息进行描述,进而得到包括节段间制造夹角、顶底板长度的制造参数.
2.1. 节段间制造夹角确定
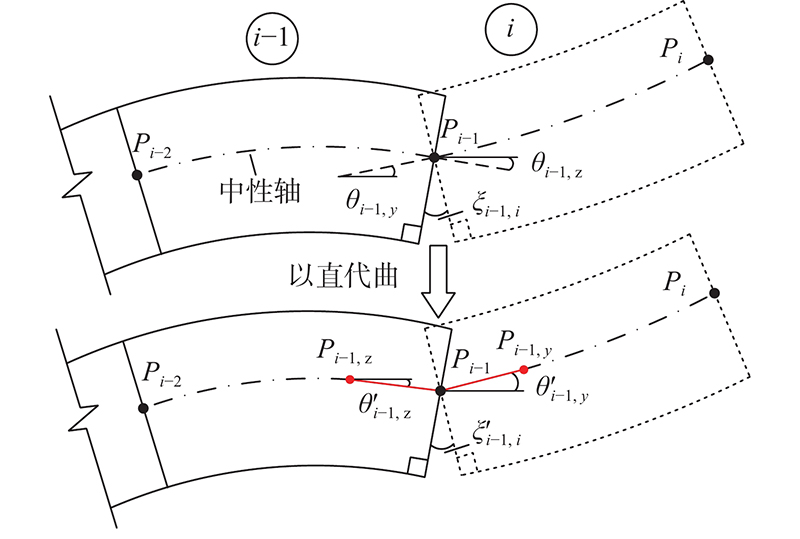
如图2所示,节段i-1、i的制造夹角
图 2
图 2 节段间制造夹角的计算
Fig.2 Calculation of manufacturing included angle between segments
式中:
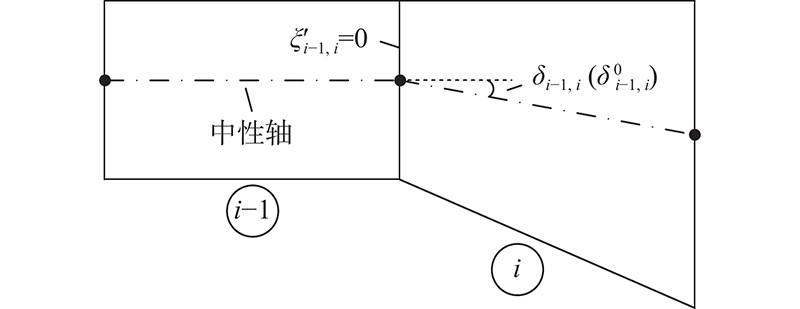
当钢箱梁为等截面时,节段中性轴均与节段端截面垂直,由几何关系可知
图 3
图 3 节段间制造夹角与中性轴夹角的关系
Fig.3 Relationship between manufacturing included angle between segments and neutral axis included angle
2.2. 顶底板制造长度计算
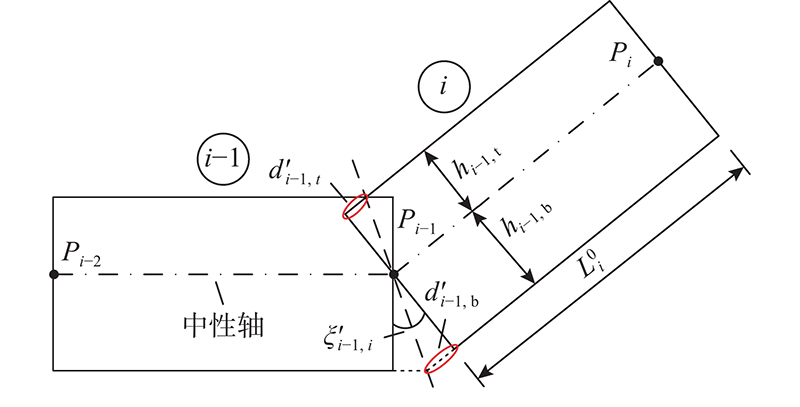
根据假定,当钢箱梁节段受力几何状态发生变化时,其中性轴长度保持不变,因此须保证制造状态与设计成桥状态节段形心处梁长一致. 如图4所示,以设计文件中获得的节段中性轴长度
图 4
式中:
在计算节段间制造夹角时,采用“以直代曲”的思想会使计算出的节段顶底板制造长度存在误差. 节段间制造夹角
将式(11)带入式(7) ~ (10),得到精确的顶底板制造长度,可以对误差进行评估. 对于已安装节段的转角
2.3. 节段形心处梁长计算
节段顶底板长度修正时要以形心处梁长为基准. 如图5所示,设计文件上一般给出的是节段在水平方向投影后的长度
图 5
图 5 设计成桥状态下形心处梁长计算
Fig.5 Calculation of girder length at centroid under design finished bridge state
3. 工程实例
3.1. 工程概况
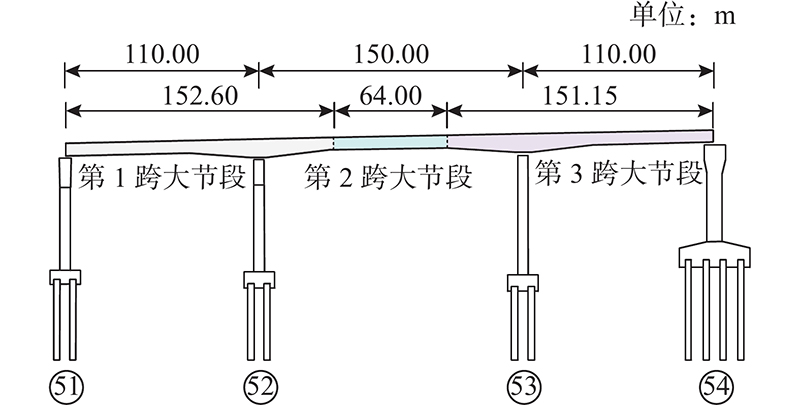
某三跨变截面钢箱连续梁桥,跨径布置为110 +150+110=370 m,如图6所示. 主梁采用整幅变截面钢箱梁,梁宽33.1 m,52、53号墩墩顶5 m区段钢箱梁梁高为6.5 m,墩顶等高梁段两侧各37.5 m区段梁高从6.5 m线性变化至4.5 m,其余区段梁高为4.5 m. 如图7所示,钢箱梁划分为3个大节段,细分为1#~33#共33个小节段,工厂制造时首先进行小节段的制作,然后组拼形成大节段. 该桥采用大节段吊装方案进行施工,先吊装第1跨大节段,再吊装第3跨大节段,最后吊装第2跨大节段,中跨与边跨大节段间通过牛腿进行匹配连接,调整至设计高程后,将第2跨与第1、3跨大节段连接,全桥合龙.
图 6
图 7
3.2. 钢箱梁制造参数计算
3.2.1. 结构分析模型
建立全桥杆系有限元模型进行施工过程正装分析计算,得出相应施工过程的累计位移. 如图8所示,主梁划分为55个单元,基本以每个钢箱梁小节段为1个单元,同时在截面变化位置、支座位置设置相应节点. 模型建立时考虑桥梁2%的纵坡,计算主梁位移时考虑剪切变形的影响. 依据实际施工过程,划分边跨吊装、大节段匹配、焊接合龙、吊点拆除及二期荷载施加共5个施工阶段. 在53号墩上设置固定支座,其余墩上均设置纵向活动支座.
图 8
3.2.2. 小节段钢箱梁制造参数计算
小节段钢箱梁制造及组拼形成大节段的过程均在工厂胎架上进行,相邻小节段进行拼接时自身均未发生变形,因此至拼接时刻节段前后控制点的累计位移均为零,且节段在前后控制点处的切线角均等于其中性轴的水平倾角,此时不存在以直代曲产生的误差.
可直接根据式(18)、(19)计算节段在控制点处的切线角,再根据式(11)准确求解节段间制造夹角.
为了减少制造时的工作量,该桥仅在小里程侧对节段的顶底板长度进行修正,大里程侧端面与顶板保持垂直. 限于篇幅,表1中仅列出第1跨大节段钢箱梁制造参数的计算结果,其中预拱度按照结构分析获得的成桥累计位移与0.5倍静活载挠度之和进行反向取值,表中0#一行为节段1#小里程侧控制点数据. 按计算的数据进行钢箱梁的工厂制造,各小节段端面实现平顺对接,交界面焊缝宽度均匀一致,没有出现由于节段间端面不匹配而通过焊缝宽度进行调整的情况.
表 1 小节段钢箱梁顶底板长度修正量(第1跨大节段)
Tab.1
| 节段 | | | | | | | | | | |
| 0# | 37.332 | −3.0 | — | — | — | — | — | — | — | — |
| 1# | 37.614 | 61.4 | 14.1 | 1.407 | — | — | — | — | — | — |
| 2# | 37.840 | 108.1 | 15.0 | 1.041 | −0.283 | −0.083 | 1573.1 | 2926.9 | 2.3 | −4.2 |
| 3# | 38.090 | 119.3 | 12.5 | 1.197 | 0.283 | -0.127 | 1647.2 | 2852.8 | 3.7 | −6.3 |
| 4# | 38.417 | 105.4 | 12.5 | 1.438 | 0.357 | −0.115 | 1647.2 | 2852.8 | 3.3 | -5.7 |
| 5# | 38.590 | 71.7 | 12.5 | 0.635 | −0.713 | −0.090 | 1569.4 | 2930.6 | 2.5 | −4.6 |
| 6# | 38.650 | 31.9 | 12.5 | 0.096 | −0.511 | −0.028 | 1647.2 | 2852.8 | 0.8 | −1.4 |
| 7# | 38.642 | 7.0 | 10.0 | −0.188 | −0.324 | 0.040 | 1836.4 | 3170.2 | −1.3 | 2.2 |
| 8# | 38.544 | −4.7 | 10.0 | −0.632 | −0.519 | 0.075 | 2044.4 | 3495.6 | −2.7 | 4.6 |
| 9# | 38.439 | −2.8 | 7.5 | −0.785 | −0.236 | 0.082 | 2343.0 | 3730.3 | −3.4 | 5.3 |
| 10# | 38.559 | 14.3 | 6.0 | 1.309 | 1.946 | 0.149 | 2597.8 | 3875.5 | −6.7 | 10.0 |
| 11# | 38.964 | 55.3 | 7.5 | 3.401 | 1.946 | 0.147 | 2597.8 | 3875.5 | -6.6 | 9.9 |
| 12# | 39.462 | 124.9 | 10.0 | 3.251 | −0.236 | 0.085 | 2343.0 | 3730.3 | −3.5 | 5.6 |
| 13# | 39.870 | 207.9 | 10.0 | 2.811 | −0.519 | 0.078 | 2044.4 | 3495.6 | −2.8 | 4.8 |
| 14# | 40.156 | 319.6 | 12.5 | 1.822 | −1.026 | 0.038 | 1836.4 | 3170.2 | −1.2 | 2.1 |
3.2.3. 大节段接缝处顶底板长度修正量计算
大节段进行匹配时边跨2个大节段钢箱梁支撑在主墩上,第2跨大节段两端通过牛腿支撑在已就位的边跨大节段上,该工况下3个大节段均已受力发生变形. “以直代曲”计算该工况下大节段接缝处的切线角时,点
表 2 大节段接缝处顶底板长度修正量
Tab.2
| 节段 | | | | | | | | | | | |
| 14# | 40.078 | 40.476 | −166.8 | −255.2 | 12.5 | — | — | — | — | — | — |
| 15# | 40.589 | 40.998 | −368.1 | −395.0 | 12.5 | 0.3507 | −0.0207 | 1800.4 | 2699.6 | 0.7 | −1.0 |
| 19# | 41.778 | 41.871 | −395.8 | −369.5 | 12.5 | — | — | — | — | — | — |
| 20# | 41.766 | 41.865 | −265.6 | −174.0 | 12.5 | 0.3507 | −0.0206 | 1800.4 | 2699.6 | 0.6 | −1.0 |
图 9
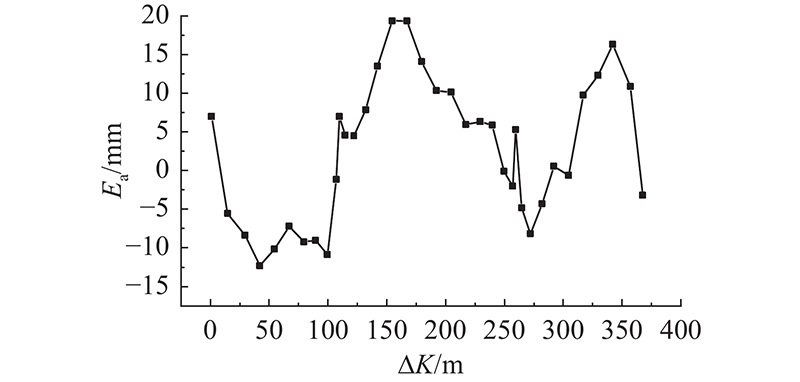
3.3. 成桥线形误差
成桥后主梁线形误差情况如图10所示. 图中,
图 10
3.4. 与常用方法比较
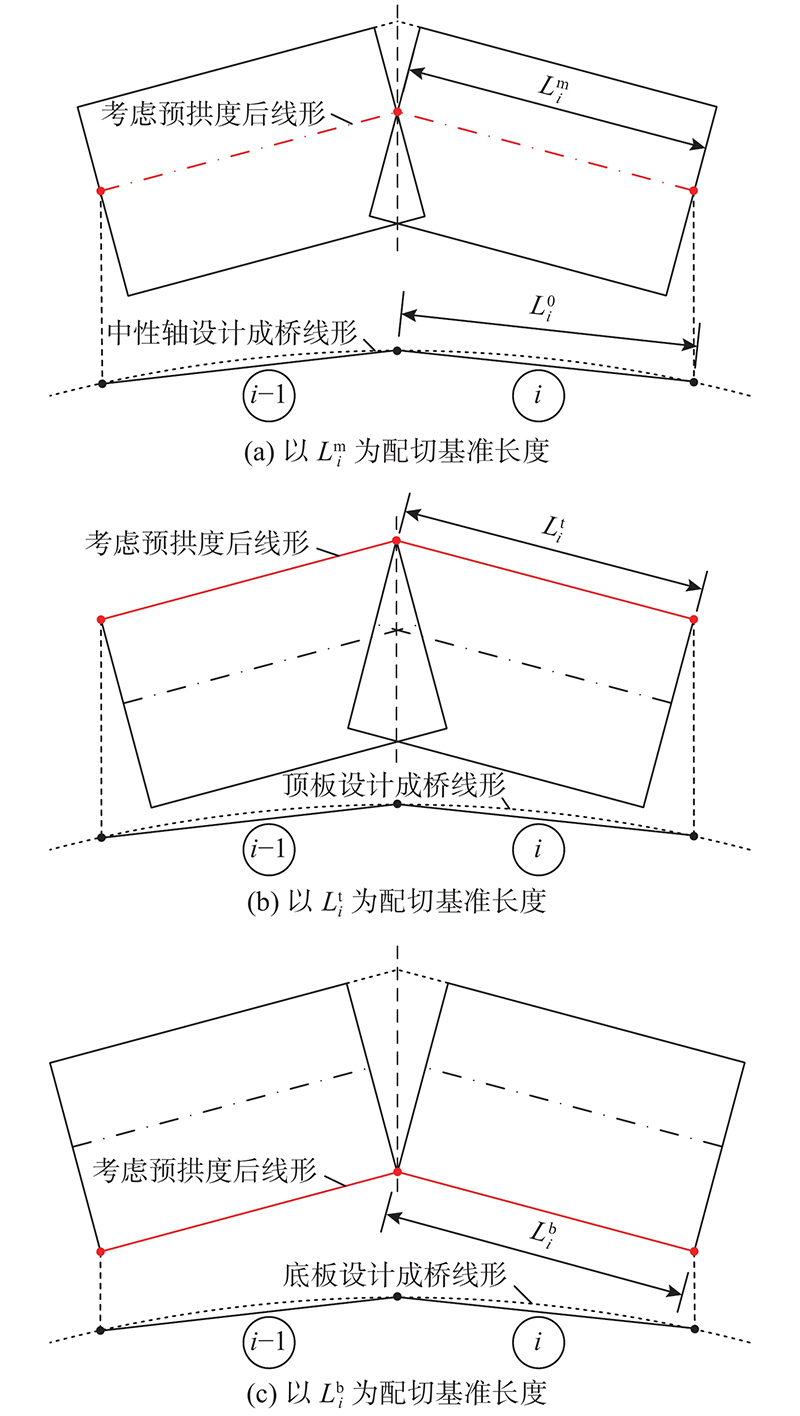
整跨吊装钢箱梁桥大节段内部各小节段钢箱梁制造参数常用的计算方法:由设计成桥线形考虑预拱度后,获得制造状态下相邻小节段的位置关系,对钢箱梁的顶底板长度进行修正后,获得节段制造参数. 如图11所示,在实际计算时,保证考虑预拱度后线形上节段控制点的里程不变,仅高程发生变化,并以该线形上节段控制点间的长度作为基准长度进行节段制造参数的计算. 控制点可位于节段中性轴、顶板或底板,相应地以
表 3 配切后主梁形心处长度
Tab.3
| mm | |||||
| 钢箱梁节段 | | | | | |
| 第1跨大节段 | 152 654.6 | 152 664.9 | 152 678.3 | 152 655.5 | 23.7 |
| 第2跨大节段 | 64 013.8 | 64 014.9 | 64 001.8 | 64 034.5 | 20.7 |
| 第3跨大节段 | 151 205.4 | 151 211.7 | 151 217.0 | 151 189.8 | 15.6 |
| 全桥钢箱梁节段 | 367 873.8 | 367 891.4 | 367 897.1 | 367 879.8 | 23.3 |
图 11
此外,对于大节段间的匹配,常用方法一般不对接缝处钢箱梁顶底板长度进行修正,而是保证钢箱梁端面与顶板保持垂直,并预留一定的配切量,最终根据施工对接情况对接缝处钢箱梁进行现场切割. 本研究方法通过对大节段接缝处钢箱梁顶底板长度修正量的准确计算,可以直接实现施工现场大节段端面间的精准匹配,避免现场切割,提高施工效率,实现桥梁结构的精细化施工.
4. 结 语
基于安装时节段间交界面实现平顺对接的思想,直接根据结构累计位移逐次确定每个拼装工况下已安装、待安装节段的相对位置关系,以设计成桥状态下节段形心处梁长为基准,提出桥梁分阶段施工中钢箱梁制造参数的通用计算方法. 将所提方法应用于三跨变截面钢箱连续梁桥大节段吊装施工,实现小节段钢箱梁的平顺对接、大节段钢箱梁的精准匹配及合龙后主梁高程误差满足精度要求. 验证了该方法的正确性及实用性,可以进一步推广应用于悬臂施工、顶推施工、逐跨施工等分阶段施工桥梁的工程实践. 所提方法计算钢箱梁制造参数时仅考虑结构纵桥向的变形,对于横桥向宽度较大的钢箱梁桥,其在自重及施工荷载作用下的横桥向变形同样需要关注,后续将对钢箱梁横桥向制造参数计算开展相应的研究.
参考文献
大跨度预应力混凝土桥梁施工控制技术
[J].
Control technique for construction of long span prestressed concrete bridge
[J].
Refined analysis and construction parameter calculation for full-span erection of the continuous steel box girder bridge with long cantilevers
[J].DOI:10.1631/jzus.A1900322 [本文引用: 1]
千米级斜拉桥施工过程中主梁的预转折角研究
[J].
Study on the prearranged angle of girders in construction state for a thousand-meter scale cable-stayed bridge
[J].
超大跨度斜拉桥的自适应无应力构形控制法
[J].
Construction control of self-adaptive zero-stress configure for super long-span cable-stayed bridge
[J].
超大跨度斜拉桥的安装构形与无应力构形
[J].
Assembled geometry and unstrained geometry of super long span cable-stayed bridges
[J].
千米级混合梁斜拉桥双目标控制施工监控体系
[J].
Construction control system for thousand-meter-scale hybrid girder cable-stayed bridge based on double target control
[J].
大跨径钢-混混合梁连续刚构桥施工控制关键技术
[J].
Key construction control techniques for long-span continuous rigid-frame bridge with steel-concrete hybrid girders
[J].
斜拉桥安装无应力状态控制法
[J].
Control method of stress-free status for erection of cable-stayed bridges
[J].
Computation of fabrication dimensions for cable-stayed bridges
[J].
单元解体法精确求解梁元无应力构形
[J].
Accurate solution for unstressed configuration of beam by element disintegration theory
[J].
Control of self-adaptive unstressed configuration for incrementally launched girder bridges
[J].DOI:10.1061/(ASCE)BE.1943-5592.0000709 [本文引用: 1]
基于相位变换的顶推曲梁桥自适应无应力构形控制
[J].
Control of self-adaptive unstressed configuration for incrementally launched curved girder bridge based on phase transformation
[J].
顶推钢箱梁的梁段制造构形与无应力线形实现
[J].
Fabrication configuration and unstressed geometry achievement of beam segment of incrementally launched steel box girder
[J].
悬拼施工中钢箱梁制造尺寸的确定
[J].
Determination of fabrication dimensions of steel box girders in cantilever construction
[J].
桥梁悬臂拼装施工中钢箱梁制造尺寸的确定
[J].
Determination of fabrication dimensions of steel box girders in cantilever erection construction of bridge
[J].
Accelerated cable-stayed bridge construction using terrestrial laser scanning
[J].DOI:10.1016/j.autcon.2020.103269 [本文引用: 1]
Geometric state transfer method for construction control of a large-segment steel box girder with hoisting installation
[J].
宽幅钢箱梁斜拉桥悬拼匹配技术研究
[J].
Research on matching technology in cantilever erection for wide steel box girder of cable-stayed bridge
[J].
Engineering the tower and main span construction of stonecutters bridge
[J].DOI:10.1061/(ASCE)BE.1943-5592.0000042 [本文引用: 1]