半导体的制造过程包含4个阶段：晶圆处理、晶圆针测、构装和测试. 其中，晶圆处理过程因其复杂性和高成本成为半导体制造过程中最为重要的阶段. 在晶圆处理过程中，离子注入工序的任务是晶圆掺杂，即将杂质引入到晶圆中，改变晶圆的电学性能. 离子注入机中的真空部件、控制单元以及元器件等会随着加工过程而发生老化，造成设备加工性能变化，导致晶圆卡的加工时间延长^[1]. 这种系统时变效应造成该道工序的加工效率降低，成为晶圆处理过程中的瓶颈环节. 实施预防性维护能改善设备状态，减少晶圆卡加工时间的延长，但是会带来额外的维护时间^[2-3]. 本研究关注离子注入工序的平行机调度问题，同时考虑系统时变效应和预防性维护.

在现有文献中，已有许多学者结合设备状态考虑生产调度问题，并通过引入各种维护手段提升设备性能. Pacheco等^[4]在研究单机调度问题时，考虑设备的状态并引入周期性维护来保证设备的正常运行. Najat等^[5]在研究平行机调度问题中，利用周期性维护来改善设备状态，以达到最小化延迟工件数量的目的. Xu等^[6]在平行机调度问题中考虑概周期维护，并把最小化最大完工时间作为优化目标. Li等^[7]则在模型中考虑周期性维护的时长与设备相关的问题. 在生产调度问题中考虑柔性维护的文献也有许多，预防性维护必须在规定的时间窗内完成^[8-11]. 但是，上述文献并未明确定义设备的状态. 此外，一些文献明确给定了设备状态的表达式. 其中，有文献以设备役龄定义设备状态^[12]. 另外，有文献指出以设备可靠性来描述设备状态相较于以设备役龄来描述设备状态更加符合实际生产. Lu等^[13]考虑设备失效模型，认为设备的可靠性服从威布尔分布. Duffuaa等^[14]同时将生产调度、维护和质量这3方面结合考虑，以达到最小化总成本的目标，其中设备的可靠性服从指数分布.

考虑到系统时变效应，许多研究都认为工件的实际加工时间将发生延长. 最常见的工件加工时间函数有3类：1）与加工位置相关；2）与加工时间相关；3）与累积加工时间相关. 与加工位置相关是指，工件的实际加工时间是其在加工序列中位置的函数^[15-17]. 与加工时间相关是指，工件的实际加工时间是加工开始时间的函数，其中最常见的是线性函数，即工件实际加工时间随着加工开始时间线性变化^[18-21]. 假设为线性变化虽然能在一定程度上简化计算，但是适用场景有限. 与累积加工时间相关是指，工件的实际加工时间是其前序所有工件的累积加工时间的函数^[22-23].

现有的大多数文献都假设设备具有相同的衰退效应. 但是，在晶圆制造这种复杂的加工环境中，时变效应更加复杂. 设备状态差异会造成不同设备具有不同的时变效应，此外，在利用同一设备加工不同晶圆卡时，晶圆卡的时变效应也会由于其敏感程度不同而存在显著差异. 因此，考虑设备状态衰退导致晶圆卡加工时间延长的系统时变效应对解决晶圆制造厂的调度问题具有现实意义.

研究考虑系统时变效应与预防性维护的平行机调度问题，建立以最小化最大完工时间为目标的数学规划模型. 设计开发求解大规模问题的学习型遗传算法. 利用算例实验证明该算法的有效性及效率.

采用指数型可靠度函数来描述设备的状态：

(1) $ r\left(L\right)=\mathrm{exp}\,\left(-\lambda L\right);\;L\geqslant 0 . $

式中： $ \lambda $为设备故障率， $ L $为设备役龄.

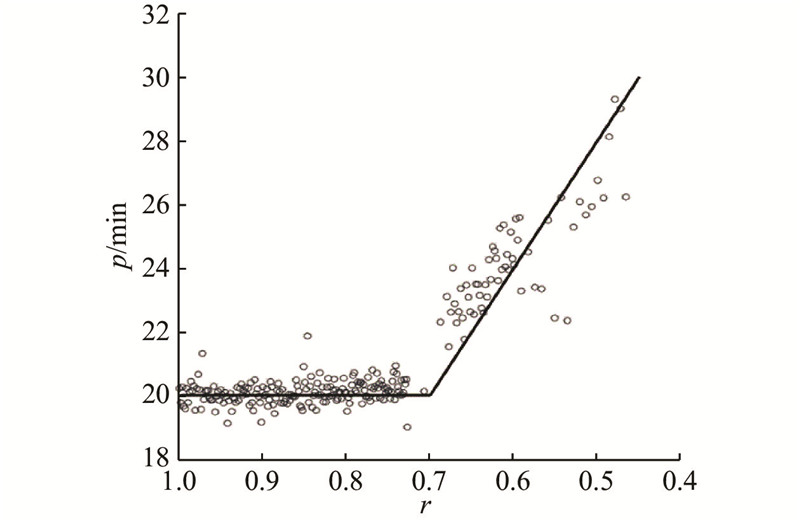
对从离子注入区获得的300个数据样点进行处理，得到晶圆卡的实际加工时间与设备可靠性的变化关系如图1所示. 图中，p为晶圆卡实际加工时间，r为设备可靠性.

如图1所示的曲线可以定义为

(2) $ {p_{i,j}} = \left\{ {\begin{array}{*{20}{l}} {{{\bar p}_{i,j}},}&{{r_{{\rm{th}}1}} < {r_i}\leqslant 1.0;}\\ {{{\bar p}_{i,j}} + w{\alpha _j}\left( {{r_{{\rm{th}}1}} - {r_i}} \right){{\bar p}_{i,j}},}&{{r_{{\rm{th}}2}}\leqslant{r_i}\leqslant{r_{{\rm{th}}1}};}\\ {\infty ,}&{0\leqslant r_i < {r_{{\rm{th}}2}}.} \end{array}} \right. $

式中： $ {p}_{i,j} $为工件j（晶圆卡j，一个晶圆卡可以视为一个工件）在设备i上的实际加工时间； $ {r}_{i} $为设备i的可靠性； $ {r}_{{\rm{th}}1} $、 $ {r}_{{\rm{th}}2} $为设定的阈值； $ {\bar{p}}_{i,j} $为工件j在设备i上的基本加工时间； $ w $为设备可靠性降低带来的工件额外加工时间的增长率； $ {\alpha }_{j}(0\leqslant {\alpha }_{j}\leqslant 1.0 $)为工件j的敏感性因子，表示工件j对设备状态衰退的敏感性. 当设备可靠性高于 $ {r}_{{\rm{th}}1} $时，工件的实际加工时间为基本加工时间. 当设备可靠性等于或低于 $ {r}_{{\rm{th}}1} $但不低于 $ {r}_{{\rm{th}}2} $时，工件的实际加工时间会随设备可靠性的降低而增加. 其增加的时间不仅与设备可靠性相关，还与工件自身的敏感性因子有关. 当设备可靠性低于 $ {r}_{{\rm{th}}2} $时，若继续在此设备上加工，会导致工件的实际加工时间过长，还可能面临工件发生质量损失、设备停机风险. 故此时必须停止此台设备的加工并进行预防性维护(preventive maintenance, PM). 因此，在模型中将工件的实际加工时间设为 $ \mathrm{\infty } $.

在离子注入工序中，有m台并行加工的设备组（设备集合 $ M $），准备加工进入该工序的n个工件（工件集合 $ N $）. 每台设备的初始状态各不相同，且随着加工时间的增长，设备可靠性降低. 实施一个具有恒定维护时长的预防性维护可以将设备恢复到更好的状态，定义 $ T $为维护时长， $ \theta $为维护因子， $ \theta \in \left(\mathrm{0,1.0}\right] $. 被加工工件根据其加工工艺的差异被分为不同种类，定义 $ {f}_{j} $为工件j所属的种类. 每个种类的工件都对应一个敏感性因子. 工件加工过程分为2个阶段，即准备加工阶段和实际加工阶段. 在准备加工阶段，同一设备加工不同种类的相邻工件需要准备时间，同一设备加工同一种类的相邻工件不需要准备时间，定义 $ {S}_{{f}_{h},{f}_{j}} $为从加工工件h切换到工件j所需的准备时间. 调度决策是将工件分配给各台设备，并确定每台设备上工件的加工顺序，以及进行PM的位置（PM可以多次被插入到调度序列中），使得这批工件在该工序的最大完工时间最小.

模型假设：1）所有工件在零时刻即可开始加工；2）设备的初始役龄可以在零时刻确定；3）每台设备在同一时刻只能加工一个工件且不允许抢占；4）每台设备加工的第1个工件不需要准备时间；5）在单个工件的加工过程中，设备的可靠性不会发生变化.

决策变量如下： $ {x}_{i,j,k} $为0/1变量，如果工件j在设备i的第k个位置上加工，则取1，否则取0； $ {y}_{i,k} $为0/1变量，如果PM在设备i加工第k个位置上的工件之前进行，则取1，否则取0.

辅助决策变量如下： $ {s}_{i,k} $为设备i加工第k个位置上的工件的开始时间； $ {C}_{j} $为工件j的完工时间； $ {L}_{i,k}^{0} $为设备i在加工第k个位置上的工件之前的役龄； $ {L}_{i,k}^{1} $为设备i加工完第k个位置上的工件之后的役龄； $ {r}_{i,k} $为设备i在加工第k个位置上的工件之前的可靠性.

最大完工时间的数学模型如下所示：

(3) $ \mathrm{min}\;\;{C}_{\mathrm{m}\mathrm{a}\mathrm{x}} . $

所须满足的条件如下：

(4) $ \sum\nolimits_{j\in N}{x}_{i,j,k}\leqslant 1 ; $

(5) $ \sum\nolimits_{i\in M}\sum\nolimits_{k\in V}{x}_{i,j,k}=1 ; $

(6) $ {x}_{i,j,k}\leqslant \sum\nolimits_{h\in N,\;h\ne j}{x}_{i,h,\left(k-1\right)},\;\mathrm{ }\forall k\in V\backslash \left\{1\right\} ; $

(7) $ {s}_{i,k}+H\left(1-{x}_{i,h,(k-1)}\right)\geqslant {C}_{h}+{y}_{i,k} T,\;\mathrm{ }\forall k\in V\backslash \left\{1\right\} ; $

(8) $\begin{split} {C}_{j}+&H\left(2-{x}_{i,j,k}-{x}_{i,h,(k-1)}\right)\geqslant {s}_{i,k}+{S}_{{f}_{h},{f}_{j}}+{p}_{i,j},\\ &\forall h\in N,\;h\ne j,\;k\in V\backslash \left\{1\right\} ; \end{split} $

(9) $ {C}_{j}+H\left(1-{x}_{i,j,1}\right)\geqslant {s}_{i,1}+{p}_{i,j} ; $

(10) $ {C}_{\mathrm{m}\mathrm{a}\mathrm{x}}\geqslant {C}_{j} ; $

(11) $ {L}_{i,k}^{0}={L}_{i,(k-1)}^{1} \left(1-{\theta y}_{i,k}\right),\;\mathrm{ }\forall k\in V\backslash \left\{1\right\} ; $

(12) $ {L}_{i,k}^{1}+H\left(1-{x}_{i,j,k}\right)\geqslant {L}_{i,k}^{0}+{p}_{i,j} ; $

(13) $ {r}_{i,k}={{\rm{exp}}}\;\left({-\lambda {L}_{i,k}^{0}}\right) ; $

(14) $ {r}_{i,k}\geqslant {r}_{{\rm{th}}2} ; $

(15) $ {x}_{i,j,k},\;{y}_{i,k}\in \left\{\mathrm{0,1}\right\} ; $

(16) $ {s}_{i,k},{C}_{j},{L}_{i,k}^{0}\geqslant 0,\;\mathrm{ }\forall i\in M,\;j\in N,\;k\in V . $

式中： $ H $为一个极大的正数； $ {s}_{i,1}=0 $； $ V $为位置集合， $ V=\left\{\mathrm{1,2},\cdots ,n\right\} $.

目标函数即式（3）为最小化最大完工时间. 式（4）、（5）保证每个工件只能在某台设备上的某个位置被加工一次. 式（6）确保如果某个工件在某台设备的某个位置上加工（除了每台设备的第1个位置），其前一个位置必然有工件被加工. 式（7）描述工件和其相邻前序工件的完工时间的关系. 式（8）、（9）描述工件的开始时间和完工时间的关系，即每台设备加工第1个工件的开始时间为0. 式（10）定义最大完工时间. 式（11）、（12）计算设备的役龄. 式（13）定义设备的可靠性. 式（14）保证设备的可靠性必须高于阈值 $ {r}_{{\rm{th}}2} $. 式（15）、（16）约束决策变量的取值范围.

由于非线性约束式（13）的存在，利用Lingo18求解模型. 考虑2台设备加工6个工件的调度问题，参数设置如下： $ {\bar{p}}_{1,j} $= $ \{ $200, 100, 200, 400, 280, 400 $ \} $ min, j=1, 2 $,\cdots, $ 6; $ {\bar{p}}_{2,j} $= $ \{ $300, 400, 200, 450, 200, 200 $ \} $ min, j=1, 2 $,\cdots, $ 6; $ {\alpha }_{j} $= $ \{ $1.0, 1.0, 1.0, 0.5, 0.5, 0.1 $ \} $, j =1, 2 $,\cdots, $ 6; $ {S}_{{f}_{h},{f}_{j}} $= $ \{ $0, 0, 0, 700, 700, 800 $ \} $ min, h=1, 2, 3，j=1, 2 $,\cdots, $ 6; $ {S}_{{f}_{h},{f}_{j}} $= $ \{ $400, 400, 400, 0, 0, 800 $ \} $ min,h=4, 5, j=1, 2 $,\cdots, $ 6; $ {S}_{{f}_{h},{f}_{j}} $= $ \{ $200, 200, 200, 500, 500, 0 $ \} $ min, h=6, j=1, 2 $,\cdots, $ 6; $ {r}_{{\rm{th}}1} $=0.7; $ {r}_{{\rm{th}}2} $=0.4; $ \lambda $=0.00035; $ w $=2；T=300 min； $ \theta $=0.58； $ {L}_{i,1}^{0} $= $ \{ $2400，200 $ \} $ min，i=1, 2. 其中，工件1、2、3属于同一种类，工件4、5属于同一种类.

如图2所示为利用Lingo求解得到的最优调度序列，在设备1上依次进行加工工件6、执行PM、加工工件1和加工工件2，在设备2上依次进行加工工件4、加工工件5和加工工件3. 最大完工时间C_max=1254.77 min. 然而，当设备数量为4，工件数量为8时，Lingo就无法在1 h内求得最优解. 因此，须设计开发学习型遗传算法来解决大规模生产调度问题.

遗传算法为解决复杂大规模生产调度问题提供了一种通用框架，并得到了有效的应用. 然而遗传算法容易出现收敛速度慢或者早熟收敛的问题，这是由于在算法中缺乏明确的导向因子. 考虑到实施PM能改善设备状态从而减弱系统的时变效应，PM策略对调度决策至关重要，提出一种学习型遗传算法(learnable genetic algorithm, LGA)，通过学习精英个体中的PM策略，并将学习到的PM知识对PM决策进行引导优化，使算法能快速收敛到质量更高的满意解.

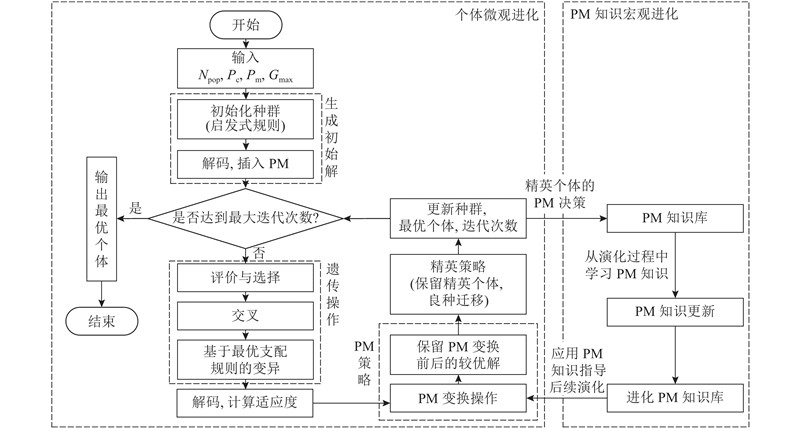
学习型遗传算法采用遗传算法优化模型和PM知识模型相结合的集成建模思路，构建个体微观进化和PM知识宏观进化的双层进化模型. 挖掘在种群进化过程中与PM决策信息有关的设备可靠性信息，以PM知识的形式存储，并随着算法的演化而不断更新，以指导在进化后期个体PM决策,加快算法收敛. 同时，基于问题特性的分析，引入2种最优支配规则用于变异操作，以确定工件的优先关系，提升解的质量. 学习型遗传算法框架如图3所示. 图中， $ {N}_{\mathrm{p}\mathrm{o}\mathrm{p}} $为种群规模， $ {P}_{\mathrm{c}} $为交叉概率， $ {P}_{\mathrm{m}} $为变异概率， $ {G}_{\mathrm{m}\mathrm{a}\mathrm{x}} $为最大迭代次数.

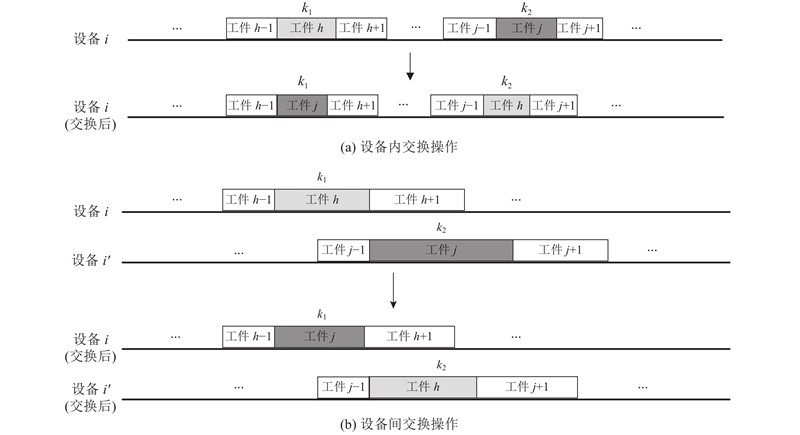
如图4所示，定义2种工件交换操作：设备内交换操作和设备间交换操作. 设备内交换操作IS( $ {k}_{1},{k}_{2},i $)：将设备i上的第k₁和第k₂个工件进行交换（假设在进行工件交换之前，工件h在设备i的第k₁个位置上加工，工件j在设备i的第k₂个位置上加工）. 设备间交换操作ID( $ {k}_{1},{k}_{2},i,i{{'}} $)：将设备i上的第k₁个工件和设备 $ i' $上的第k₂个工件进行交换（假设在进行工件交换之前，工件h在设备i的第k₁个位置上加工，工件j在设备 $ i{'} $的第k₂个位置上加工）.

定义 $ {\hat{p}}_{i,j} $为设备i上工件j的总加工时间，包括工件j的准备加工时间和实际加工时间. $ {\hat{p}}_{i,j}' $为进行工件交换操作后的总加工时间. $ {r}_{i,k}' $为进行工件交换操作后，设备i在加工第k个位置上的工件之前的可靠性. $ {G}_{\left[i\right]} $为设备i上最后一个工件的完工时间. $ {G}_{\left[i\right]}' $为进行工件交换操作后的设备i上最后一个工件的完工时间.

最优支配规则1  当满足下列条件之一时，进行操作IS( $ {k}_{1},{k}_{2},i $)会使得完工时间减小（假设k₁ < k₂）：

1）若 $ {k}_{2}={k}_{1}+1 $，则须满足

$ \left(\mathrm{a}\right){\hat{p}}_{i,j}'+{\hat{p}}_{i,h}'+{\hat{p}}_{i,j+1}' < {\hat{p}}_{i,h}+{\hat{p}}_{i,j}+{\hat{p}}_{i,j+1} \text{；} $

$ \left(\mathrm{b}\right){r}_{i,{k}_{2}+2}'\geqslant {r}_{i,{k}_{2}+2} . $

2）若 $ {k}_{2} > {k}_{1}+1 $，则须满足

$ \left(\mathrm{a}\right){\hat{p}}_{i,j}'+{\hat{p}}_{i,h+1}' < {\hat{p}}_{i,h}+{\hat{p}}_{i,h+1}\text{，}{\hat{p}}_{i,h}'+{\hat{p}}_{i,j+1}' < {\hat{p}}_{i,j}+{\hat{p}}_{i,j+1} \text{；} $

$ \left(\mathrm{b}\right){r}_{i,{k}_{1}+2}'\geqslant {r}_{i,{k}_{1}+2} \text{，} {r}_{i,{k}_{2}+2}'\geqslant {r}_{i,{k}_{2}+2} . $

条件(a)确保交换的工件和其后一个位置上的工件的总加工时间减少. 条件(b)确保从交换的工件其后第2个位置上的工件开始，其实际加工时间减少.

最优支配规则2  当满足下列条件时，进行操作ID( $ {k}_{1},{k}_{2},i,i' $)会使得完工时间变小（假设设备 $ i $上的完工时间大于设备 $ i' $）：

$ \left(\mathrm{a}\right){\hat{p}}_{i,j}'+{\hat{p}}_{i,h+1}' < {\hat{p}}_{i,h}+{\hat{p}}_{i,h+1} \text{；} $

$ \left(\mathrm{b}\right){r}_{i,{k}_{1}+2}'\geqslant {r}_{i,{k}_{1}+2} \text{；} $

$ \left(\mathrm{c}\right){G}_{\left[{i}'\right]}' < {G}_{\left[i\right]} . $

条件(c)确保进行工件交换操作后,设备 $ {i}' $上最后一个工件的完工时间小于进行工件交换操作前设备i上最后一个工件的完工时间.

上述2个最优支配规则可以用于学习型遗传算法的变异过程中，以提高算法的搜索性能.

每条染色体由m×n个基因组成. 染色体的m行代表m台设备，每行中的n个基因代表这台设备上可加工工件的n个位置. 每个基因中的数字代表这个位置上所加工工件的序号. 数字0表示此位置不加工任何工件. 如图5所示为在2台设备上加工6个工件的染色体示例. 在设备1上依次加工6、1、2号工件，在设备2上依次加工4、5、3号工件.

为了保证设备可靠性不低于阈值 $ {r}_{{\rm{th}}2} $，在解码阶段插入PM. 对每台设备上的每个加工位置，在加工工件前先计算设备的可靠性. 如若可靠性低于 $ {r}_{{\rm{th}}2} $，则在加工此工件前插入PM，重新计算设备可靠性.

80%的初始种群依照如下的启发式规则产生：按工件种类将n个待加工工件进行排序，其中属于同类的工件随机排序；按工件的排序顺序，将 $ ⌈n/m⌉ $（向上圆整）个工件分配给各台设备. 为了不丢失种群的多样性，剩下的20%初始种群随机生成.

个体 $ Y $的适应度函数定义为 $ {f}_{ Y}=1/{C}_{\mathrm{m}\mathrm{a}\mathrm{x}} $. 由轮盘赌法进行选择父代，即个体 $ Y $被选为父代的概率 $ {q}_{ Y}={f}_{ Y}/\displaystyle \sum\nolimits _{ Y=1}^{{N}_{\mathrm{p}\mathrm{o}\mathrm{p}}}{f}_{ Y} $. 交叉方式采用基于位置的交叉(position-based crossover).

将3.2节提出的2种最优支配规则应用于学习型遗传算法的变异步骤中，如算法1所示. 为了不丢失染色体的多样性，对不满足最优支配规则的2个工件，仍以变异概率 $ {P}_{\mathrm{m}} $进行随机交换.

算法1. 变异

1. 随机挑选2个工件h和j

2. If (工件h和j在同一台设备上且满足最优支配规则1)

3. 交换工件h和j

4. Elseif (工件h和j在不同设备上且满足最优支配规则2)

5. 交换工件h和j

6. Else

7. If (产生0~1.0的随机数 $ < {P}_{\mathrm{m}} $)

8. 交换工件h和j

9. Else

10. Return

11. End if

12. End if

考虑到实施PM可以提高设备可靠性，从而降低系统产生的时变效应对生产调度的影响，提出PM变换操作，用于前期的PM优化. 包括在加工序列中随机插入一个PM或者去除一个PM或者对PM进行随机位置移动.

为了提高算法对PM最佳决策的搜索效率，设计PM知识学习过程. 不同于进化前期PM的随机变换，在进化后期由PM知识库指导PM决策，加快算法收敛.

将每代精英个体中的PM序列以及实施PM前的设备可靠性信息存储到PM知识库中，并用统计方式对PM知识模型进行挖掘，利用学习得到的PM进化知识，指导优化进化后期每代个体的PM变换操作. 在种群进化的过程中，不断更新PM知识库.

设备可靠性区间[ $ {r}_{{\rm{th}}2},{r}_{{\rm{th}}1}] $被分为d等份，整个设备可靠性区间[ $ 0,1.0] $被分为 $ \left[0,{r}_{{\rm{th}}2}- ({r}_{{\rm{th}}1}-{r}_{{\rm{th}}2})/d\right] $， $ \left({r}_{{\rm{th}}2}-({r}_{{\rm{th}}1}-{r}_{{\rm{th}}2})/d,{r}_{{\rm{th}}2}\right] $ $，\cdots ，$ $ \left({r}_{{\rm{th}}1},{r}_{{\rm{th}}1}+({r}_{{\rm{th}}1}-{r}_{{\rm{th}}2})/d\right] $， $ \left({r}_{{\rm{th}}1}+({r}_{{\rm{th}}1}-{r}_{{\rm{th}}2})/d,1\right] $共(d+4)份区间. PM知识库中存储着(d+4)份区间中执行PM的次数 $ {Q}_{q} $（q=1, 2 $,\cdots, $ (d+4)）. 定义 $ {Q}_{\mathrm{m}\mathrm{a}\mathrm{x}}=\mathrm{m}\mathrm{a}\mathrm{x}\;\{{Q}_{1},{Q}_{2},\cdots ,{Q}_{(d+4)}\} $.

由于在进化初始阶段挖掘出的知识可信度不高，学习型优化算法一般在迭代至10%~15% $ {G}_{\mathrm{m}\mathrm{a}\mathrm{x}} $代时，开始进行知识存储. 在预实验中发现，当迭代至第10% $ {G}_{\mathrm{m}\mathrm{a}\mathrm{x}} $代时，解的质量已经可以接受，故设置在第10% $ {G}_{\mathrm{m}\mathrm{a}\mathrm{x}} $代时，开始进行PM知识存储.

在进化后期利用PM知识库指导PM决策过程如下. 定义 $ {P}_{{\rm{o}}} $为插入PM的概率， $ {P}_{{\rm{o}}}' $为去除PM的概率.

1）随机挑选一台设备 $ i $， $ i\in M $. 2）检查此台设备上是否有PM，如果没有，则随机将一个PM插入到该设备的任意位置上，结束. 否则，转到步骤3）. 3）产生一个0~1.0的随机数R. 如果 $ {R < P}_{{\rm{o}}} $，随机将一个PM插入到任意原来无PM的位置上. 如果 $ {P}_{{\rm{{\rm{o}}}}}\leqslant R < {P}_{{\rm{o}}}' $，随机从调度序列中移除任意一个PM. 如果 $ R\geqslant {P}_{{\rm{o}}}' $，根据PM知识库中的统计信息，以概率 $ {{P}}' $选择一个PM，并以概率 ${{P}}_{\varsigma }''$将其移动到可靠性区间 ${\varsigma }$中任意无PM的位置上，其中 $ {{P}}_{\varsigma }''={Q}_{\varsigma }/ $ $ \displaystyle \sum\nolimits_{q=1}^{d+4}{Q}_{q} $， ${Q}_{\varsigma }$为区间 ${\varsigma }$中执行PM的次数. 4）计算此台设备加工每个工件之前的可靠性. 如果可靠性低于阈值 $ {r}_{{\rm{th}}2} $，则在加工此工件前插入一个PM，结束.

在步骤3）中，对设备i第k₁个位置上实施的PM（ $ {y}_{i,{k}_{1}}=1 $），若其对应的设备可靠性在区间 $ \varsigma $内，则 $ {{P}}_{0,k_1}=({Q}_{\mathrm{m}\mathrm{a}\mathrm{x}}+1-{Q}_{\varsigma })\left/{\displaystyle\sum\nolimits_{q=1}^{d+4}({Q}_{\mathrm{m}\mathrm{a}\mathrm{x}}+1-{Q}_{q}) }\right.$. 假设集合A中包含设备i上所有的PM实施的位置，则第k₁个位置上的PM被选择的概率 $ {{P}}'= $ $ {{P}}_{0,k_1}\left/{\displaystyle \sum\nolimits_{a\in {A}}{{P}}_{0},a }\right. $.

以下将详细说明如何选择PM并进行位置移动. 假设如图6所示为当前PM知识库中储存的信息（取d=10，将设备可靠性区间分为14份）.

假设挑选的设备i分别在k₁和k₂位置实施PM，在实施PM前其设备可靠性分别在区间q和区间13内. 则 $ {{P}}_{0,k_1}=1/76 $， $ {{P}}_{0,k_2}=1/19 $，故k₁、k₂位置上的PM被选中的概率 $ {{P}}' $分别为 $ 1/5 $、 $ 4/5 $. 当选中某个PM后，将此PM以概率 $ {{P}}_{3}''=1/8 $移动到区间3中任意无PM的位置上；以概率 $ {{P}}_{q}''=5/8 $移动到区间q中任意无PM的位置上；以概率 $ {{P}}_{13}''=1/4 $移动到区间13中任意无PM的位置上.

当代PM知识库更新过程如下. 1）提取当代种群中前10%的个体，将其PM序列以及其对应的设备可靠性信息存储到PM知识库中；2）对每个个体中的每台设备，根据此台设备上执行PM前的设备可靠性，更新(d+4)份设备可靠性区间中执行PM的次数，直至更新完毕；3）统计设备可靠性区间中的PM的次数，结束.

为了评价学习型遗传算法的性能，进行若干实验. 采用Matlab R2020a对算法进行实现，所有的算例均在配置为Intel(R) Core(TM) i7-9750H(2.60 GHz)处理器、8 GB内存的个人电脑上运行.

以某晶圆制造厂离子注入工序的实际加工信息为依据，随机生成不同的算例. 该工序上有4台并行设备，待加工工件的基本处理时间服从N(20, 0.3²)的正态分布（单位：min）. 工件种类为9，每个种类的工件所对应的敏感性因子如表1所示. 其余参数设置如表2所示.

利用Lingo18对小规模问题进行求解. 待加工工件的数量为5~12. 求解时间上限设置为3600 s，如果Lingo不能在3600 s内获得全局最优解，则以当前局部最优解作为Lingo的最大完工时间的最终解. 将学习型遗传算法求得的解与Lingo求得的解进行比较，来评价算法的性能. 对每种规模的问题，随机生成10个算例，并取均值作为最终的目标函数值. 如表3所示为2种方法所获得的平均目标函数值和平均计算时间. 表中， $ C_{\max }^{{\rm{Lingo}}} $为Lingo解的平均值， $ C_{\max }^{{\rm{LGA}}} $为LGA解的平均值，t_CPU为获得解所需的CPU时间，Dev表示LGA解与Lingo解的偏差程度. Dev的表达式为

(17) $ \mathrm{D}\mathrm{e}\mathrm{v}=\frac{C_{\max }^{{\rm{Lingo}}}-C_{\max }^{{\rm{LGA}}}}{C_{\max }^{{\rm{Lingo}}}}\times 100\text{%} . $

小规模算例结果表明，当工件数量少于8时，Lingo可以在3600 s内获得全局最优解，而学习型遗传算法可以用更少的计算时间获得完全一致的最优解，学习型遗传算法的有效性得以验证. 随着工件数量的增加，Lingo无法在有限时间内获得全局最优解，学习型遗传算法却能在短时间内获得比Lingo更好的解.

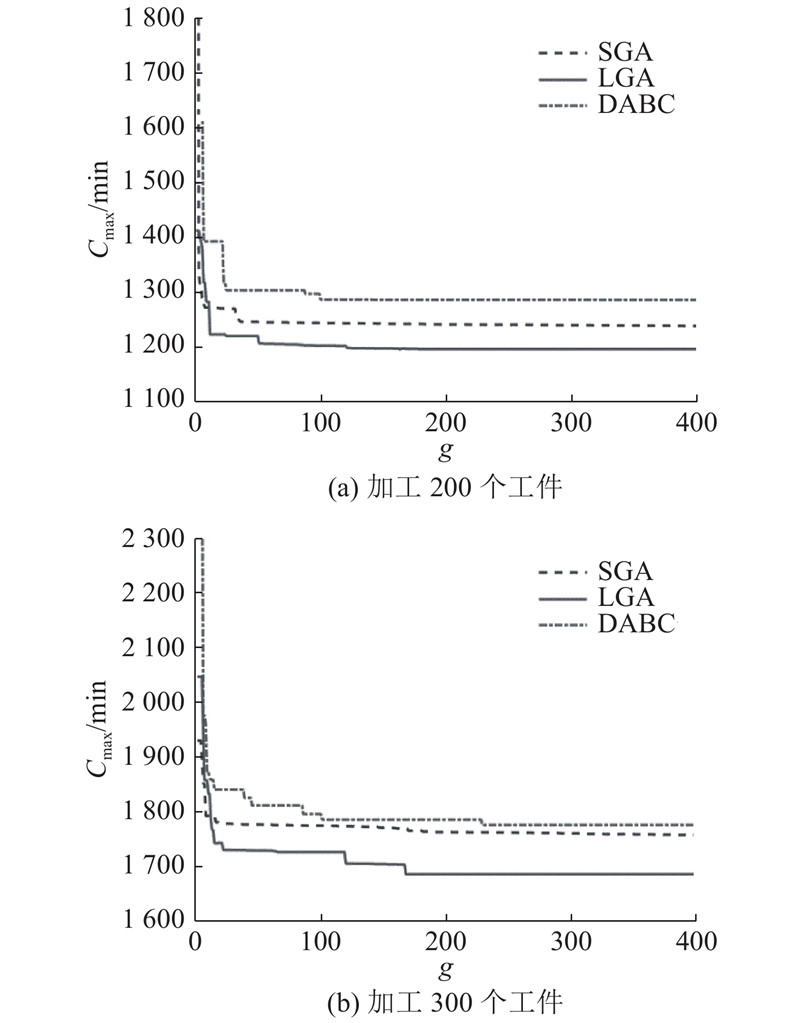
为了验证学习型遗传算法在求解中大型规模问题中的性能，对以下不同算法进行比较：1）学习型遗传算法(learnable genetic algorithm，LGA)；2）标准遗传算法(standard genetic algorithm，SGA)；3）改进的人工蜂群算法(artificial bee colony with division，DABC). 其中，SGA为仅仅不包含学习过程的LGA，其参数设置与LGA相同. DABC算法是Lei等^[10]提出的用于解决考虑预防性维护的并行机调度问题的算法. Lei等^[10]的研究表明，DABC算法的性能优于遗传算法（genetic algorithm，GA）和混合粒子群算法与遗传算法（hybrid particle swarm optimization and genetic algorithm，HPSOGA）. DABC算法中初始种群生成按3.4节中的方式生成，参数设置与文献[10]中相同，迭代次数设为400.

利用这3种算法对中大型规模问题进行求解. 待加工工件的数量为50~300. 对每种规模的问题，随机生成10个算例，并取均值作为最终的目标函数值. 如表4所示为3种算法所获得的平均目标函数值C_max和平均计算时间t_CPU. 如图7所示为3种算法在迭代过程中的收敛曲线. 图中，g为当前迭代代数.

中、大规模算例结果表明，在3种算法中，学习型遗传算法性能最好. 在加工300个工件时，LGA比SGA目标函数值降低了46.28，比DABC目标函数值降低了92.58. 相较于SGA，拥有PM学习机制的LGA所获得的目标函数值降低了1.48%~2.66%. 此外，LGA的收敛速度快于其他2种算法. 这说明学习型遗传算法能有效引导PM决策朝着PM最佳插入位置方向进化，使算法能快速收敛于质量更高的满意解.

待加工工件集合根据具有各种敏感性因子的工件的数量占比被分为3类：高敏感性工件集合、中敏感性工件集合和低敏感性工件集合，如表5所示. 其中， $ \phi $表示具有各种敏感性因子的工件的数量占比.

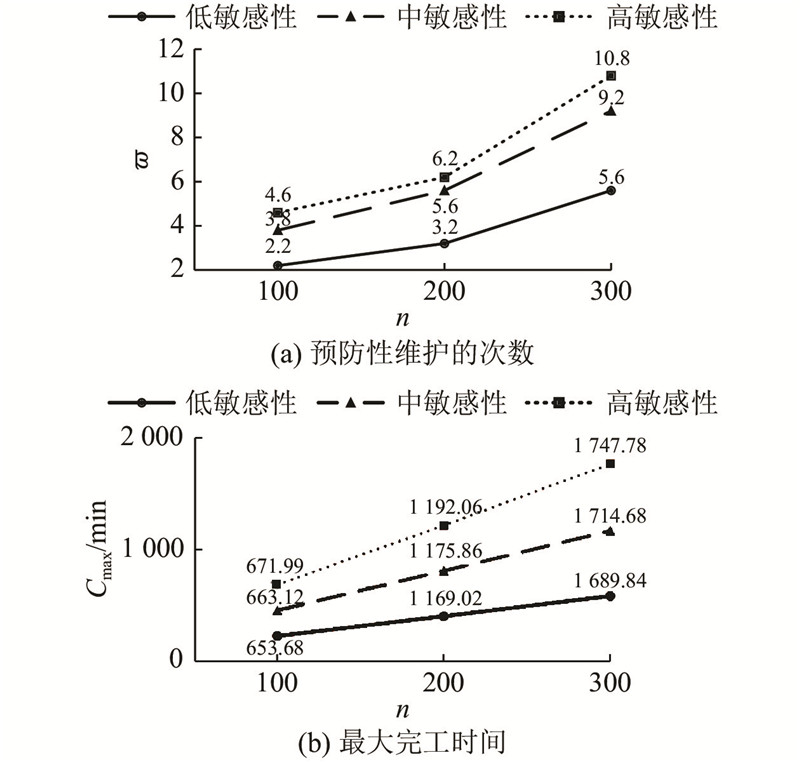
每种规模实验取10组不同算例，并取均值作为实验结果. 4台设备的初始役龄分别为0、1000、1500、2000 min. 如图8所示为不同特性的待加工工件集合所需的PM次数以及得到的最大完工时间. 图中， $ \varpi $为实施PM的次数. 可以看出，随着工件集合敏感性的升高，所需的PM次数增加. 当加工高敏感性工件集合时，会插入更多的PM以保证设备一直处于良好状态. 但是，其最大完工时间没有出现大幅增加. 即使是高敏感性工件集合，加工100、200、300个工件时，最大完工时间分别只增加了2.80%、1.97%、3.43%. 说明虽然PM的实施会带来额外的维护时间，但是由于设备状态的改善会减少工件加工时间的延长，最大完工时间并不会出现明显的增加. 学习型遗传算法能根据加工工件集合特性的不同，去选择不同的调度和维护策略，降低工件集合敏感性的升高对总完工时间的影响.

在之前的分析中，只考虑了能在一定程度上降低设备役龄的不完全PM. 但是，在实际生产中可以实施不同类型的PM（包括完全PM），它们具有不同的维护时长和维护效果. 依据离子注入区的实际维护情况，考虑短期PM(T=30 min， $ \theta $=0.58)、中期PM (T=40 min， $ \theta $=0.80)和长期PM (T=50 min， $ \theta $=1.00)对调度决策的影响. 此外，实验还考虑了3种不同类型的设备组，即新设备组（每台设备的初始役龄为0）、混合设备组（4台设备的初始役龄分别为0、1000、1500、2000 min）和老化设备组（每台设备的初始役龄为2000 min）. 待加工工件集合具有高敏感性.

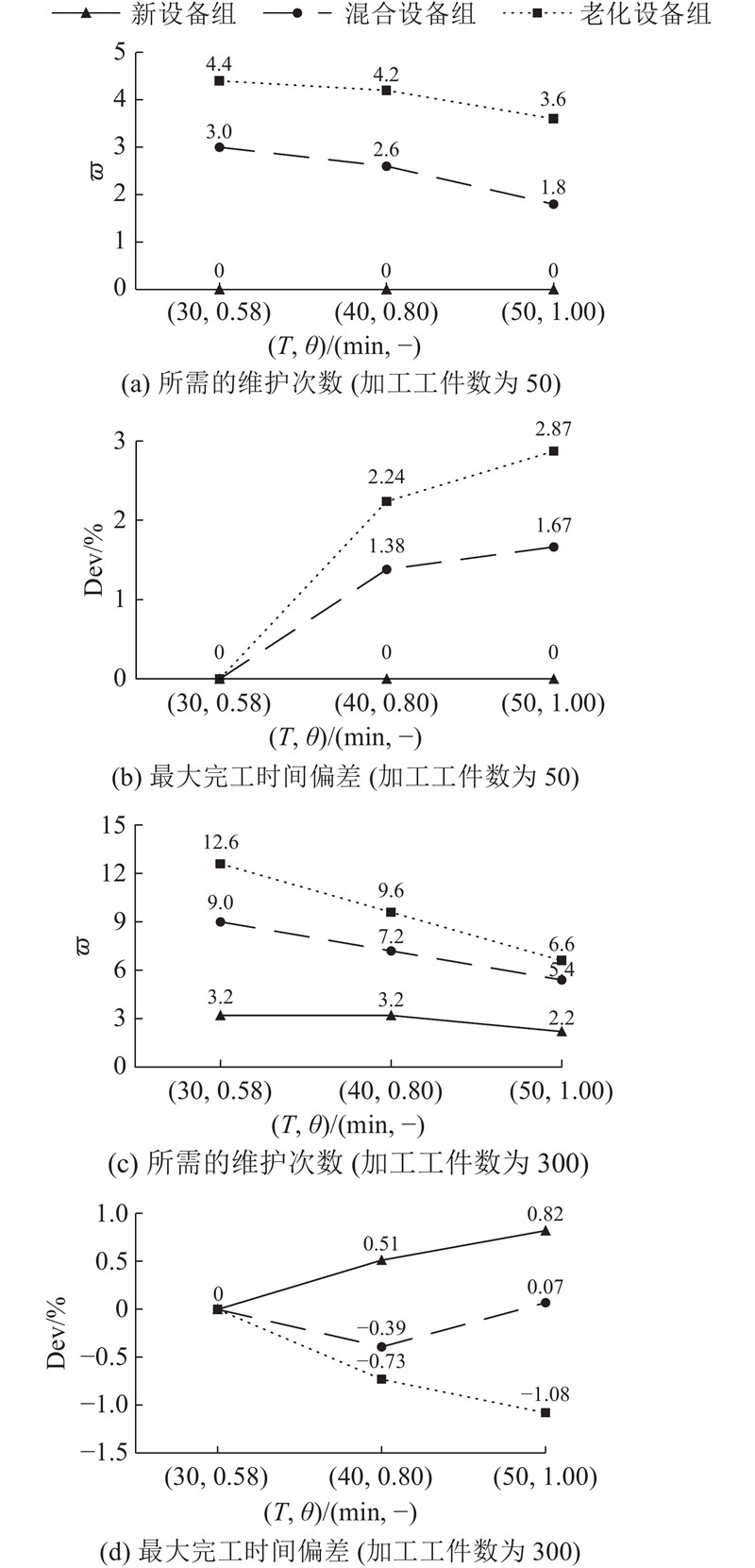
每种规模实验取10组不同算例，并取均值作为实验结果. 以考虑短期PM获得的最大完工时间（用 $ {C}_{\bar{{\rm{P}}}} $表示）作为基准，计算考虑其他类型PM获得的最大完工时间 $ {C}_{{\rm{P}}} $的偏差. 偏差表达式如下：

(18) $ \mathrm{D}\mathrm{e}\mathrm{v}=\frac{{C}_{{\rm{P}}}-{C}_{\bar{{\rm{P}}}}}{{C}_{\bar{{\rm{P}}}}}\times 100\text{%} . $

由图9可以看出，1）对于50个工件的加工实例，随着维护时长的增长和维护效果的增强，所需的维护次数减少（只有“新设备组”所需的插入PM的次数为0）. 此外，最大完工时间的偏差急剧增大. 这是因为，PM维护时长的增加对完工时间的影响大于维护效果增强所导致的后续工件加工时间的缩短. 而且，这种现象在实施长期PM时更加明显，长期PM将大幅增加完工时间. 并且，随着设备的老化，这种趋势更加明显. 2）对于300个工件的加工实例，PM次数的变化规律大致相同. 但是，最大完工时间的偏差规律不同. 若在新设备组上进行加工，则变化规律一致，选择短期PM更加合适. 若在混合设备组上进行加工，选择中期PM获得的效果最好. 若在老化设备组上进行加工，中期或者长期PM都优于短期PM. 进行长期PM所获得的最大完工时间比短期PM降低了1.08%.

不同类型的PM适用于不同加工场景. 对于小规模的问题，短期PM是最好的选择. 完全PM更适用于老旧设备的大型加工问题.

研究考虑系统时变效应和预防性维护的平行机调度问题. 建立最小化最大完工时间的数学规划模型，并设计求解该模型的学习型遗传算法，为解决实际车间调度问题提供了新思路.

本研究所提出的PM学习型机制不仅适用于遗传算法，也可以拓展到其他算法之中. 实验结果表明，所提出的算法对所研究的问题有效且求解质量较高. 此外，灵敏度分析实验表明，高敏感性的工件集合对设备状态的要求更高，PM的插入虽然会占据设备的加工时间，但是能在一定程度上改善设备状态，使得占据的加工时间得到一定补偿. 不同类型的PM适用于不同的加工场景. 对于小规模问题，短期PM是最好的选择. 长期PM更适用于老旧设备的大型加工问题. 这些结论为基于设备可靠性的实际车间调度提供了决策支持.

在后续的研究中，将考虑加工工件的质量，实现调度和质量的联合优化.