(4) $ \begin{gathered} {{{{\dot {\boldsymbol{x}}}}}}{\text{ = }}{\left[{\begin{array}{*{20}{c}} {{{\dot x}_1},}&{{{\dot x}_2},}&{{{\dot x}_3},}&{{{\dot x}_4},}&{\cdots}&{,{{\dot x}_n}}\end{array}}\right]^{\text{T}}} = \\ {\left[ {\begin{array}{*{20}{c}} {{x_2},}&{ - \dfrac{{\mu {x_2}^2}}{R} - g\sin \;\dfrac{{{x_1}}}{R} - \mu g\cos\; \dfrac{{{x_1}}}{R},}&{0,}&{0,}&{\cdots}&{,0} \end{array}} \right]^{\text{T}}}. \\ \end{gathered} $
[1]
陈云敏, 刘晓成, 徐文杰, 等 填埋生活垃圾稳定化特征与可开采性分析: 以我国第一代卫生填埋场为例
[J]. 中国科学:技术科学 , 2019 , 49 (2 ): 199 - 211
DOI:10.1360/N092018-00140
[本文引用: 1]
CHEN Yun-min, LIU Xiao-cheng, XU Wen-jie, et al Analysis on stabilization characteristics and exploitability of landfilled municipal solid waste: case of a typical landfill in China
[J]. Scientia Sinica: Technologica , 2019 , 49 (2 ): 199 - 211
DOI:10.1360/N092018-00140
[本文引用: 1]
[2]
中华人民共和国国家统计局. 国家数据: 年度数据[DB/OL]. [2020-12-13]. https://data.stats.gov.cn/easyquery.htm?cn=C01.
[本文引用: 1]
[3]
HOGLAND W Remediation of an old landsfill site
[J]. Environmental Science and Pollution Research , 2002 , 9 : 49 - 54
DOI:10.1007/BF02987426
[本文引用: 1]
[4]
KROOK J, BAAS L Getting serious about mining the technosphere: a review of recent landfill mining and urban mining research
[J]. Journal of Cleaner Production , 2013 , 55 (14 ): 1 - 9
URL
[5]
JAIN P, TOWNSEND T G, JOHNSON P Case study of landfill reclamation at a Florida landfill site
[J]. Waste Management , 2013 , 33 (1 ): 109 - 116
DOI:10.1016/j.wasman.2012.09.011
[本文引用: 1]
[6]
FORSTER G A. Assessment of landfill reclamation and the effects of age on the combustion of recovered municipal solid waste [M]. Lancaster: National Renewable Energy Laboratory, 1995: 1-125.
[本文引用: 1]
[7]
ASHKIKI A R, FELSKE C, MCCARTNEY D Impacts of seasonal variation and operating parameters on double-stage trommel performance
[J]. Waste Management , 2019 , 86 : 36 - 48
DOI:10.1016/j.wasman.2019.01.026
[8]
赵先. 陈垃圾开采回用工程的综合效益评价研究[D]. 武汉: 华中科技大学, 2008: 1-51.
[本文引用: 1]
ZHAO Xian. A study on integrate-benefit evaluation of landfill mining project [D]. Wuhan: Huazhong University of Science and Technology, 2008: 1-51.
[本文引用: 1]
[9]
李兵, 赵由才, 施庆燕, 等 上海市生活垃圾分选模式研究
[J]. 同济大学学报:自然科学版 , 2007 , (4 ): 507 - 510
DOI:10.3321/j.issn:0253-374X.2007.04.015
[本文引用: 1]
LI Bing, ZHAO You-cai, SHI Qing-yan, et al State-of-the-art separation mode for municipal solid wastes in Shanghai
[J]. Journal of Tongji University: Natural Science , 2007 , (4 ): 507 - 510
DOI:10.3321/j.issn:0253-374X.2007.04.015
[本文引用: 1]
[10]
WHEELER P A, BARTON J R, NEW R An empirical approach to the design of trommel screens for fine screening of domestic refuse
[J]. Resources, Conservation and Recycling , 1989 , 2 (4 ): 261 - 273
DOI:10.1016/0921-3449(89)90003-7
[11]
黄楚雨, 韩华, 康敏娟, 等 非正规垃圾堆放点垃圾质量及筛分产物比例精准勘测方法研究
[J]. 环境卫生工程 , 2020 , 28 (5 ): 33 - 37
URL
[本文引用: 1]
HUANG Chu-yu, HAN Hua, KANG Min-juan, et al Accurate survey method study of waste quality and screening product proportion in informal waste dump sites
[J]. Environmental Sanitation Engineering , 2020 , 28 (5 ): 33 - 37
URL
[本文引用: 1]
[12]
ALTER H, GAVIS J, RENARD M L Design models of trommels for resource recovery processing
[J]. Resources and Conservation , 1981 , 6 (3/4 ): 223 - 240
URL
[本文引用: 3]
[13]
GLAUB J C, JONES D B, SAVAGE G M. Design and use of trommel screens for processing municipal solid waste [C]// Proceedings of ASME National Waste Processing Conference . New York: [s. n.], 1982: 447-457.
[本文引用: 3]
[15]
MELLMANN J The transverse motion of solids in rotating cylinders: forms of motion and transition behavior
[J]. Powder Technology , 2001 , 118 (3 ): 251 - 270
DOI:10.1016/S0032-5910(00)00402-2
[本文引用: 1]
[17]
李兵. 生活垃圾深度分选及设备优化组合技术研究[D]. 上海: 同济大学, 2006: 1-155.
[本文引用: 3]
LI Bing. Integrated mechanical separation and parameter optimization for municipal solid wastes [D]. Shanghai: Tongji University, 2006: 1-155.
[本文引用: 3]
[18]
张大卫. 用于粗煤泥脱水脱泥滚筒筛的研制及其性能试验研究[D]. 太原: 太原理工大学, 2015: 1-89.
[本文引用: 3]
ZHANG Da-wei. The development and study on the trommel screen used for dewatering and desliming of coal slime [D]. Taiyuan: Taiyuan University of Technology, 2015: 1-89.
[本文引用: 3]
[19]
肖嘉. 基于EEP法的线法二阶常微分方程组有限元自适应分析[D]. 北京: 清华大学, 2009: 1-152.
[本文引用: 1]
XIAO Jia. Adaptive FEM analysis of second order ODEs of FEMOL based on EEP super-convergent method [D]. Beijing: Tsinghua University, 2009: 1-152.
[本文引用: 1]
[20]
夏敦行. 二阶变系数线性微分方程的解法[D]. 武汉: 武汉科技大学, 2009: 1-37.
[本文引用: 1]
XIA Dun-xing. Solution of second order variable coefficients linear differential equation [D]. Wuhan: Wuhan University of Science and Technology, 2009: 1-37.
[本文引用: 1]
[21]
王冠, 霍丽丽, 赵立欣, 等 秸秆类生物质原料筛分除杂试验及滚筒筛改进
[J]. 农业工程学报 , 2016 , 32 (13 ): 218 - 222
DOI:10.11975/j.issn.1002-6819.2016.13.031
[本文引用: 2]
WANG Guan, HUO Lili, ZHAO Lixin, et al Screening of biomass straw materials and improvement of feedstock equipment
[J]. Transactions of the Chinese Society of Agricultural Engineering , 2016 , 32 (13 ): 218 - 222
DOI:10.11975/j.issn.1002-6819.2016.13.031
[本文引用: 2]
[22]
TURES G L. A guide to implementing reclamation processes at department of defense municipal solid waste and construction debris landfills [D]. Montgomery: Air Force Institute of Technology, 2007: 1-81.
[本文引用: 1]
[23]
MÖNKÄRE T J, PALMROTH M R T, RINTALA J A Characterization of fine fraction mined from two Finnish landfills
[J]. Waste Management , 2016 , 47 : 34 - 39
DOI:10.1016/j.wasman.2015.02.034
[本文引用: 1]
[24]
张恩广. 筛分破碎及脱水设备 [M]. 北京: 煤炭工业出版社, 1989: 22-23.
[本文引用: 1]
[25]
煤炭部选煤设计研究院情报室. 选煤技术文集 分离效率[M]. 北京: 煤炭工业出版社, 1980: 27-111.
[本文引用: 1]
[26]
张钰. 煤泥脱水筛分滚筒筛性能试验研究与离散元模拟[D]. 太原: 太原理工大学, 2016: 1-68.
[本文引用: 1]
ZHANG Yu. Experimental study and discrete element simulation of coal slime dewatering sieving drum screen’s performance [D]. Taiyuan: Taiyuan University of Technology, 2016: 1-68.
[本文引用: 1]
[27]
KE H, HU J, XU X B, et al Evolution of saturated hydraulic conductivity with compression and degradation for municipal solid waste
[J]. Waste Management , 2017 , (65 ): 63 - 74
URL
[本文引用: 1]
填埋生活垃圾稳定化特征与可开采性分析: 以我国第一代卫生填埋场为例
1
2019
... 面对我国多地生活垃圾填埋场出现的库容紧张的难题,填埋场陈垃圾开采成为卫生填埋场库容循环再利用的有效措施[1 ] . 2019年底我国城市生活垃圾清运量已达2.42×108 t,近5a平均增速在6.27%左右,按此增长率推算,2030年我国城市固体废物(municipal solid waste,MSW)年处理需求将扩大至现有的195%,库容释放迫在眉睫[2 ] . 填埋垃圾开采是指对在役或封场填埋场内垃圾进行挖掘开采并处置的技术,Hogland等[3 -5 ] 在美国佛罗里达州开展的陈垃圾开采筛分工程使填埋场库容释放62.2%. 垃圾滚筒筛是陈垃圾开采与分选工艺中的常用设备[6 -8 ] .现有对滚筒筛内陈垃圾的运动分析都存在一定的局限性,无法准确描述滚筒筛各参数对运动模式的影响,导致滚筒筛中原料的运动原理不清晰,陈垃圾分选工艺、滚筒筛设计常常仅依赖工程经验[9 -11 ] . ...
填埋生活垃圾稳定化特征与可开采性分析: 以我国第一代卫生填埋场为例
1
2019
... 面对我国多地生活垃圾填埋场出现的库容紧张的难题,填埋场陈垃圾开采成为卫生填埋场库容循环再利用的有效措施[1 ] . 2019年底我国城市生活垃圾清运量已达2.42×108 t,近5a平均增速在6.27%左右,按此增长率推算,2030年我国城市固体废物(municipal solid waste,MSW)年处理需求将扩大至现有的195%,库容释放迫在眉睫[2 ] . 填埋垃圾开采是指对在役或封场填埋场内垃圾进行挖掘开采并处置的技术,Hogland等[3 -5 ] 在美国佛罗里达州开展的陈垃圾开采筛分工程使填埋场库容释放62.2%. 垃圾滚筒筛是陈垃圾开采与分选工艺中的常用设备[6 -8 ] .现有对滚筒筛内陈垃圾的运动分析都存在一定的局限性,无法准确描述滚筒筛各参数对运动模式的影响,导致滚筒筛中原料的运动原理不清晰,陈垃圾分选工艺、滚筒筛设计常常仅依赖工程经验[9 -11 ] . ...
1
... 面对我国多地生活垃圾填埋场出现的库容紧张的难题,填埋场陈垃圾开采成为卫生填埋场库容循环再利用的有效措施[1 ] . 2019年底我国城市生活垃圾清运量已达2.42×108 t,近5a平均增速在6.27%左右,按此增长率推算,2030年我国城市固体废物(municipal solid waste,MSW)年处理需求将扩大至现有的195%,库容释放迫在眉睫[2 ] . 填埋垃圾开采是指对在役或封场填埋场内垃圾进行挖掘开采并处置的技术,Hogland等[3 -5 ] 在美国佛罗里达州开展的陈垃圾开采筛分工程使填埋场库容释放62.2%. 垃圾滚筒筛是陈垃圾开采与分选工艺中的常用设备[6 -8 ] .现有对滚筒筛内陈垃圾的运动分析都存在一定的局限性,无法准确描述滚筒筛各参数对运动模式的影响,导致滚筒筛中原料的运动原理不清晰,陈垃圾分选工艺、滚筒筛设计常常仅依赖工程经验[9 -11 ] . ...
Remediation of an old landsfill site
1
2002
... 面对我国多地生活垃圾填埋场出现的库容紧张的难题,填埋场陈垃圾开采成为卫生填埋场库容循环再利用的有效措施[1 ] . 2019年底我国城市生活垃圾清运量已达2.42×108 t,近5a平均增速在6.27%左右,按此增长率推算,2030年我国城市固体废物(municipal solid waste,MSW)年处理需求将扩大至现有的195%,库容释放迫在眉睫[2 ] . 填埋垃圾开采是指对在役或封场填埋场内垃圾进行挖掘开采并处置的技术,Hogland等[3 -5 ] 在美国佛罗里达州开展的陈垃圾开采筛分工程使填埋场库容释放62.2%. 垃圾滚筒筛是陈垃圾开采与分选工艺中的常用设备[6 -8 ] .现有对滚筒筛内陈垃圾的运动分析都存在一定的局限性,无法准确描述滚筒筛各参数对运动模式的影响,导致滚筒筛中原料的运动原理不清晰,陈垃圾分选工艺、滚筒筛设计常常仅依赖工程经验[9 -11 ] . ...
Getting serious about mining the technosphere: a review of recent landfill mining and urban mining research
0
2013
Case study of landfill reclamation at a Florida landfill site
1
2013
... 面对我国多地生活垃圾填埋场出现的库容紧张的难题,填埋场陈垃圾开采成为卫生填埋场库容循环再利用的有效措施[1 ] . 2019年底我国城市生活垃圾清运量已达2.42×108 t,近5a平均增速在6.27%左右,按此增长率推算,2030年我国城市固体废物(municipal solid waste,MSW)年处理需求将扩大至现有的195%,库容释放迫在眉睫[2 ] . 填埋垃圾开采是指对在役或封场填埋场内垃圾进行挖掘开采并处置的技术,Hogland等[3 -5 ] 在美国佛罗里达州开展的陈垃圾开采筛分工程使填埋场库容释放62.2%. 垃圾滚筒筛是陈垃圾开采与分选工艺中的常用设备[6 -8 ] .现有对滚筒筛内陈垃圾的运动分析都存在一定的局限性,无法准确描述滚筒筛各参数对运动模式的影响,导致滚筒筛中原料的运动原理不清晰,陈垃圾分选工艺、滚筒筛设计常常仅依赖工程经验[9 -11 ] . ...
1
... 面对我国多地生活垃圾填埋场出现的库容紧张的难题,填埋场陈垃圾开采成为卫生填埋场库容循环再利用的有效措施[1 ] . 2019年底我国城市生活垃圾清运量已达2.42×108 t,近5a平均增速在6.27%左右,按此增长率推算,2030年我国城市固体废物(municipal solid waste,MSW)年处理需求将扩大至现有的195%,库容释放迫在眉睫[2 ] . 填埋垃圾开采是指对在役或封场填埋场内垃圾进行挖掘开采并处置的技术,Hogland等[3 -5 ] 在美国佛罗里达州开展的陈垃圾开采筛分工程使填埋场库容释放62.2%. 垃圾滚筒筛是陈垃圾开采与分选工艺中的常用设备[6 -8 ] .现有对滚筒筛内陈垃圾的运动分析都存在一定的局限性,无法准确描述滚筒筛各参数对运动模式的影响,导致滚筒筛中原料的运动原理不清晰,陈垃圾分选工艺、滚筒筛设计常常仅依赖工程经验[9 -11 ] . ...
Impacts of seasonal variation and operating parameters on double-stage trommel performance
0
2019
1
... 面对我国多地生活垃圾填埋场出现的库容紧张的难题,填埋场陈垃圾开采成为卫生填埋场库容循环再利用的有效措施[1 ] . 2019年底我国城市生活垃圾清运量已达2.42×108 t,近5a平均增速在6.27%左右,按此增长率推算,2030年我国城市固体废物(municipal solid waste,MSW)年处理需求将扩大至现有的195%,库容释放迫在眉睫[2 ] . 填埋垃圾开采是指对在役或封场填埋场内垃圾进行挖掘开采并处置的技术,Hogland等[3 -5 ] 在美国佛罗里达州开展的陈垃圾开采筛分工程使填埋场库容释放62.2%. 垃圾滚筒筛是陈垃圾开采与分选工艺中的常用设备[6 -8 ] .现有对滚筒筛内陈垃圾的运动分析都存在一定的局限性,无法准确描述滚筒筛各参数对运动模式的影响,导致滚筒筛中原料的运动原理不清晰,陈垃圾分选工艺、滚筒筛设计常常仅依赖工程经验[9 -11 ] . ...
1
... 面对我国多地生活垃圾填埋场出现的库容紧张的难题,填埋场陈垃圾开采成为卫生填埋场库容循环再利用的有效措施[1 ] . 2019年底我国城市生活垃圾清运量已达2.42×108 t,近5a平均增速在6.27%左右,按此增长率推算,2030年我国城市固体废物(municipal solid waste,MSW)年处理需求将扩大至现有的195%,库容释放迫在眉睫[2 ] . 填埋垃圾开采是指对在役或封场填埋场内垃圾进行挖掘开采并处置的技术,Hogland等[3 -5 ] 在美国佛罗里达州开展的陈垃圾开采筛分工程使填埋场库容释放62.2%. 垃圾滚筒筛是陈垃圾开采与分选工艺中的常用设备[6 -8 ] .现有对滚筒筛内陈垃圾的运动分析都存在一定的局限性,无法准确描述滚筒筛各参数对运动模式的影响,导致滚筒筛中原料的运动原理不清晰,陈垃圾分选工艺、滚筒筛设计常常仅依赖工程经验[9 -11 ] . ...
上海市生活垃圾分选模式研究
1
2007
... 面对我国多地生活垃圾填埋场出现的库容紧张的难题,填埋场陈垃圾开采成为卫生填埋场库容循环再利用的有效措施[1 ] . 2019年底我国城市生活垃圾清运量已达2.42×108 t,近5a平均增速在6.27%左右,按此增长率推算,2030年我国城市固体废物(municipal solid waste,MSW)年处理需求将扩大至现有的195%,库容释放迫在眉睫[2 ] . 填埋垃圾开采是指对在役或封场填埋场内垃圾进行挖掘开采并处置的技术,Hogland等[3 -5 ] 在美国佛罗里达州开展的陈垃圾开采筛分工程使填埋场库容释放62.2%. 垃圾滚筒筛是陈垃圾开采与分选工艺中的常用设备[6 -8 ] .现有对滚筒筛内陈垃圾的运动分析都存在一定的局限性,无法准确描述滚筒筛各参数对运动模式的影响,导致滚筒筛中原料的运动原理不清晰,陈垃圾分选工艺、滚筒筛设计常常仅依赖工程经验[9 -11 ] . ...
上海市生活垃圾分选模式研究
1
2007
... 面对我国多地生活垃圾填埋场出现的库容紧张的难题,填埋场陈垃圾开采成为卫生填埋场库容循环再利用的有效措施[1 ] . 2019年底我国城市生活垃圾清运量已达2.42×108 t,近5a平均增速在6.27%左右,按此增长率推算,2030年我国城市固体废物(municipal solid waste,MSW)年处理需求将扩大至现有的195%,库容释放迫在眉睫[2 ] . 填埋垃圾开采是指对在役或封场填埋场内垃圾进行挖掘开采并处置的技术,Hogland等[3 -5 ] 在美国佛罗里达州开展的陈垃圾开采筛分工程使填埋场库容释放62.2%. 垃圾滚筒筛是陈垃圾开采与分选工艺中的常用设备[6 -8 ] .现有对滚筒筛内陈垃圾的运动分析都存在一定的局限性,无法准确描述滚筒筛各参数对运动模式的影响,导致滚筒筛中原料的运动原理不清晰,陈垃圾分选工艺、滚筒筛设计常常仅依赖工程经验[9 -11 ] . ...
An empirical approach to the design of trommel screens for fine screening of domestic refuse
0
1989
非正规垃圾堆放点垃圾质量及筛分产物比例精准勘测方法研究
1
2020
... 面对我国多地生活垃圾填埋场出现的库容紧张的难题,填埋场陈垃圾开采成为卫生填埋场库容循环再利用的有效措施[1 ] . 2019年底我国城市生活垃圾清运量已达2.42×108 t,近5a平均增速在6.27%左右,按此增长率推算,2030年我国城市固体废物(municipal solid waste,MSW)年处理需求将扩大至现有的195%,库容释放迫在眉睫[2 ] . 填埋垃圾开采是指对在役或封场填埋场内垃圾进行挖掘开采并处置的技术,Hogland等[3 -5 ] 在美国佛罗里达州开展的陈垃圾开采筛分工程使填埋场库容释放62.2%. 垃圾滚筒筛是陈垃圾开采与分选工艺中的常用设备[6 -8 ] .现有对滚筒筛内陈垃圾的运动分析都存在一定的局限性,无法准确描述滚筒筛各参数对运动模式的影响,导致滚筒筛中原料的运动原理不清晰,陈垃圾分选工艺、滚筒筛设计常常仅依赖工程经验[9 -11 ] . ...
非正规垃圾堆放点垃圾质量及筛分产物比例精准勘测方法研究
1
2020
... 面对我国多地生活垃圾填埋场出现的库容紧张的难题,填埋场陈垃圾开采成为卫生填埋场库容循环再利用的有效措施[1 ] . 2019年底我国城市生活垃圾清运量已达2.42×108 t,近5a平均增速在6.27%左右,按此增长率推算,2030年我国城市固体废物(municipal solid waste,MSW)年处理需求将扩大至现有的195%,库容释放迫在眉睫[2 ] . 填埋垃圾开采是指对在役或封场填埋场内垃圾进行挖掘开采并处置的技术,Hogland等[3 -5 ] 在美国佛罗里达州开展的陈垃圾开采筛分工程使填埋场库容释放62.2%. 垃圾滚筒筛是陈垃圾开采与分选工艺中的常用设备[6 -8 ] .现有对滚筒筛内陈垃圾的运动分析都存在一定的局限性,无法准确描述滚筒筛各参数对运动模式的影响,导致滚筒筛中原料的运动原理不清晰,陈垃圾分选工艺、滚筒筛设计常常仅依赖工程经验[9 -11 ] . ...
Design models of trommels for resource recovery processing
3
1981
... 已有的陈垃圾滚筒筛运动理论主要基于几何导向,从假定的某几种特定参数出发进行推导. Alter等[12 ] 假定1个抛出曲线,并由此确定3个相关角度,描述物料运动状态,并反推摩擦因数.Glaub等[13 ] 添加与颗粒尺度相关的参数,研究粒度与筛分概率的关系.Stessel[14 ] 在前两者的基础上考虑了大直径滚筒筛中空气阻力对抛落的影响.Mellmann[15 ] 通过计算弗劳德数Fr 判断物料状态,把运动模式进一步细分为7个子类型.唐红侠等[16 ] 采用力学分析方法,指出物料最大提升角与滚筒摩擦角息息相关,且物料临界抛落转速与滚筒转速存在一定差异,但没有说明差异的具体量化指标. ...
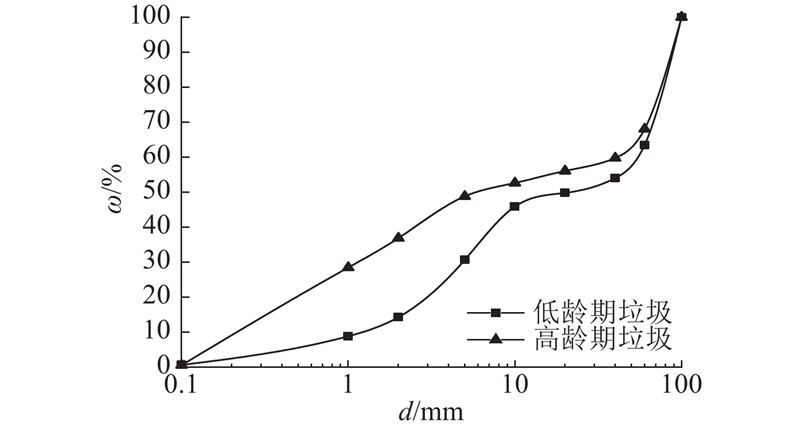
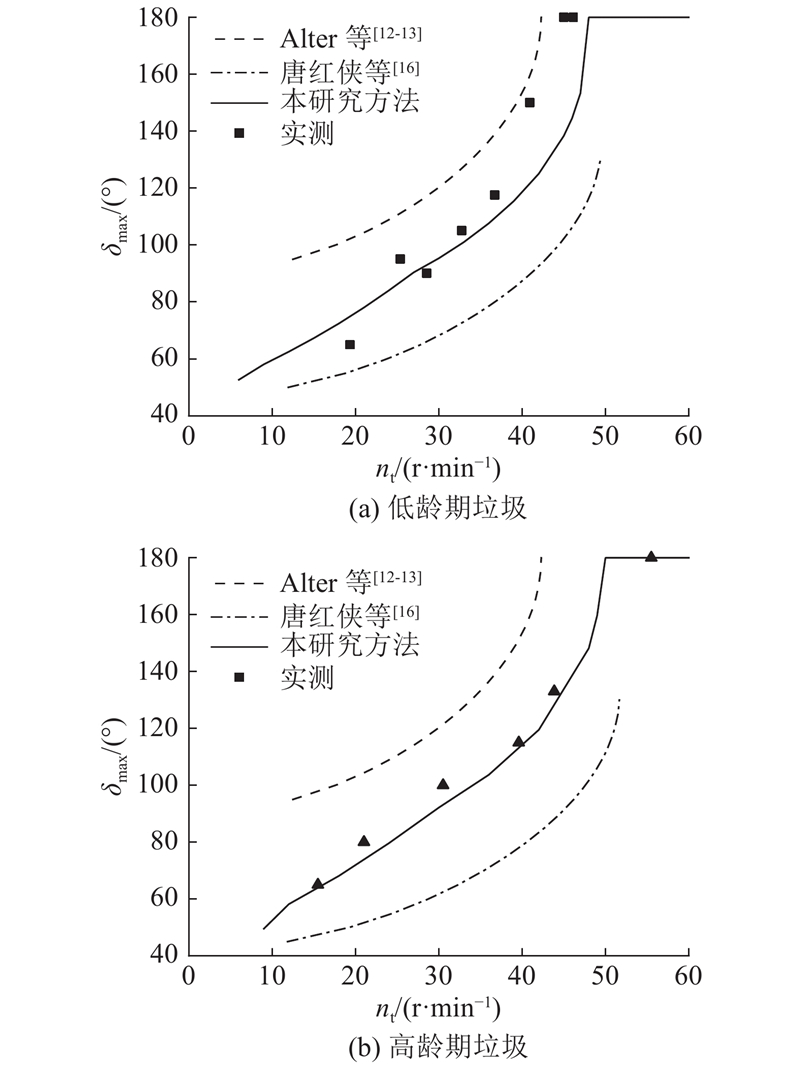
... 陈垃圾的最大角理论计算要用到动摩擦因数μ .通过等孔径平面筛板作斜坡进行多次自由下滑试验取均值,可以确定老港低龄期陈垃圾与筛筒壁的动摩擦因数约为1.06,最大静摩擦因数约为1.07;老港高龄期陈垃圾与筛筒壁的动摩擦因数约为0.90,最大静摩擦因数约为0.97. 如图11 所示,根据以上摩擦因数值,按本研究前述方法进行计算,并与老港陈垃圾室内试验实测值,文献[12 ]、[13 ]、[16 ]的计算方法进行对比. ...
... 本研究方法计算结果显示,随着转速的升高,陈垃圾运动的最大角先逐渐增大,在进入圆周运动后达到最大值180°并不再变化. 低龄期垃圾至48 r/min后进入圆周运动,高龄期垃圾至50 r/min后进入圆周运动. 由图11 可知,该方法计算结果与实测值吻合程度最高,其他2种计算方法所得最大角度δ max 与实测值相较均存在较大的偏离,Alter等[12 -13 ] 计算结果明显偏大,唐红侠等[16 ] 计算结果则偏小. 室内试验结果表明,本研究方法分析的滚筒筛陈垃圾运动理论与实际偏差最小、轨迹重合度高,且计算方式不复杂,能够验证该理论的合理性与实用性. 另外,高龄期垃圾室内试验最大角值相比本文理论线平均高出4.0°,低龄期垃圾平均高出11.4°,这说明高龄期垃圾对理论结果的吻合程度相比低龄期垃圾高,可能与低龄期垃圾组分内部差异度大、参数离散度高导致试验误差大有关系. ...
3
... 已有的陈垃圾滚筒筛运动理论主要基于几何导向,从假定的某几种特定参数出发进行推导. Alter等[12 ] 假定1个抛出曲线,并由此确定3个相关角度,描述物料运动状态,并反推摩擦因数.Glaub等[13 ] 添加与颗粒尺度相关的参数,研究粒度与筛分概率的关系.Stessel[14 ] 在前两者的基础上考虑了大直径滚筒筛中空气阻力对抛落的影响.Mellmann[15 ] 通过计算弗劳德数Fr 判断物料状态,把运动模式进一步细分为7个子类型.唐红侠等[16 ] 采用力学分析方法,指出物料最大提升角与滚筒摩擦角息息相关,且物料临界抛落转速与滚筒转速存在一定差异,但没有说明差异的具体量化指标. ...
... 陈垃圾的最大角理论计算要用到动摩擦因数μ .通过等孔径平面筛板作斜坡进行多次自由下滑试验取均值,可以确定老港低龄期陈垃圾与筛筒壁的动摩擦因数约为1.06,最大静摩擦因数约为1.07;老港高龄期陈垃圾与筛筒壁的动摩擦因数约为0.90,最大静摩擦因数约为0.97. 如图11 所示,根据以上摩擦因数值,按本研究前述方法进行计算,并与老港陈垃圾室内试验实测值,文献[12 ]、[13 ]、[16 ]的计算方法进行对比. ...
... 本研究方法计算结果显示,随着转速的升高,陈垃圾运动的最大角先逐渐增大,在进入圆周运动后达到最大值180°并不再变化. 低龄期垃圾至48 r/min后进入圆周运动,高龄期垃圾至50 r/min后进入圆周运动. 由图11 可知,该方法计算结果与实测值吻合程度最高,其他2种计算方法所得最大角度δ max 与实测值相较均存在较大的偏离,Alter等[12 -13 ] 计算结果明显偏大,唐红侠等[16 ] 计算结果则偏小. 室内试验结果表明,本研究方法分析的滚筒筛陈垃圾运动理论与实际偏差最小、轨迹重合度高,且计算方式不复杂,能够验证该理论的合理性与实用性. 另外,高龄期垃圾室内试验最大角值相比本文理论线平均高出4.0°,低龄期垃圾平均高出11.4°,这说明高龄期垃圾对理论结果的吻合程度相比低龄期垃圾高,可能与低龄期垃圾组分内部差异度大、参数离散度高导致试验误差大有关系. ...
A new trommel model
2
1991
... 已有的陈垃圾滚筒筛运动理论主要基于几何导向,从假定的某几种特定参数出发进行推导. Alter等[12 ] 假定1个抛出曲线,并由此确定3个相关角度,描述物料运动状态,并反推摩擦因数.Glaub等[13 ] 添加与颗粒尺度相关的参数,研究粒度与筛分概率的关系.Stessel[14 ] 在前两者的基础上考虑了大直径滚筒筛中空气阻力对抛落的影响.Mellmann[15 ] 通过计算弗劳德数Fr 判断物料状态,把运动模式进一步细分为7个子类型.唐红侠等[16 ] 采用力学分析方法,指出物料最大提升角与滚筒摩擦角息息相关,且物料临界抛落转速与滚筒转速存在一定差异,但没有说明差异的具体量化指标. ...
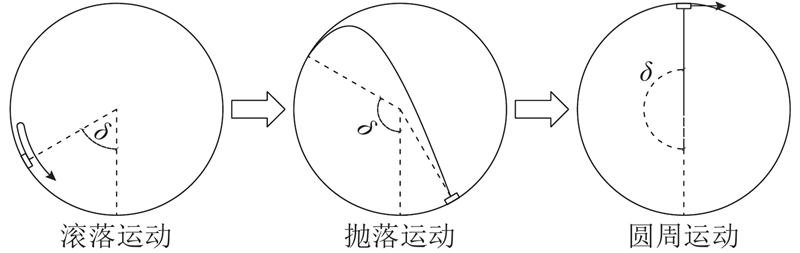
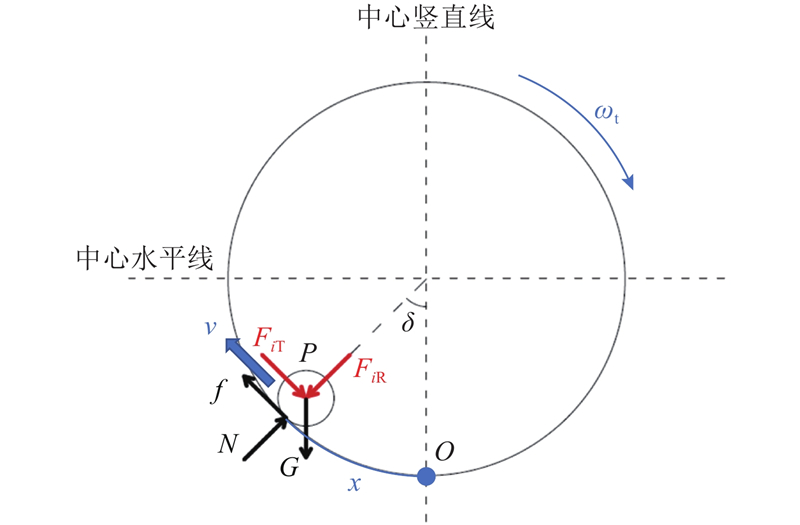
... 如图1 所示,陈垃圾物料在滚筒筛内的运动模式主要有3种,可以按转速由小到大分为滚落运动、抛落运动、圆周运动. 图中,δ 为物料位置角,即物料质心到滚筒筛中心轴的垂线与竖直方向所成夹角. 每个模式各自的运动特点如表1 所示[14 ,17 ] .表中,δ max 为物料最大位置角,n t 为滚筒筛转速,η 为筛分效率. ...
The transverse motion of solids in rotating cylinders: forms of motion and transition behavior
1
2001
... 已有的陈垃圾滚筒筛运动理论主要基于几何导向,从假定的某几种特定参数出发进行推导. Alter等[12 ] 假定1个抛出曲线,并由此确定3个相关角度,描述物料运动状态,并反推摩擦因数.Glaub等[13 ] 添加与颗粒尺度相关的参数,研究粒度与筛分概率的关系.Stessel[14 ] 在前两者的基础上考虑了大直径滚筒筛中空气阻力对抛落的影响.Mellmann[15 ] 通过计算弗劳德数Fr 判断物料状态,把运动模式进一步细分为7个子类型.唐红侠等[16 ] 采用力学分析方法,指出物料最大提升角与滚筒摩擦角息息相关,且物料临界抛落转速与滚筒转速存在一定差异,但没有说明差异的具体量化指标. ...
滚筒筛筛分生活垃圾的理论研究
3
2007
... 已有的陈垃圾滚筒筛运动理论主要基于几何导向,从假定的某几种特定参数出发进行推导. Alter等[12 ] 假定1个抛出曲线,并由此确定3个相关角度,描述物料运动状态,并反推摩擦因数.Glaub等[13 ] 添加与颗粒尺度相关的参数,研究粒度与筛分概率的关系.Stessel[14 ] 在前两者的基础上考虑了大直径滚筒筛中空气阻力对抛落的影响.Mellmann[15 ] 通过计算弗劳德数Fr 判断物料状态,把运动模式进一步细分为7个子类型.唐红侠等[16 ] 采用力学分析方法,指出物料最大提升角与滚筒摩擦角息息相关,且物料临界抛落转速与滚筒转速存在一定差异,但没有说明差异的具体量化指标. ...
... 陈垃圾的最大角理论计算要用到动摩擦因数μ .通过等孔径平面筛板作斜坡进行多次自由下滑试验取均值,可以确定老港低龄期陈垃圾与筛筒壁的动摩擦因数约为1.06,最大静摩擦因数约为1.07;老港高龄期陈垃圾与筛筒壁的动摩擦因数约为0.90,最大静摩擦因数约为0.97. 如图11 所示,根据以上摩擦因数值,按本研究前述方法进行计算,并与老港陈垃圾室内试验实测值,文献[12 ]、[13 ]、[16 ]的计算方法进行对比. ...
... 本研究方法计算结果显示,随着转速的升高,陈垃圾运动的最大角先逐渐增大,在进入圆周运动后达到最大值180°并不再变化. 低龄期垃圾至48 r/min后进入圆周运动,高龄期垃圾至50 r/min后进入圆周运动. 由图11 可知,该方法计算结果与实测值吻合程度最高,其他2种计算方法所得最大角度δ max 与实测值相较均存在较大的偏离,Alter等[12 -13 ] 计算结果明显偏大,唐红侠等[16 ] 计算结果则偏小. 室内试验结果表明,本研究方法分析的滚筒筛陈垃圾运动理论与实际偏差最小、轨迹重合度高,且计算方式不复杂,能够验证该理论的合理性与实用性. 另外,高龄期垃圾室内试验最大角值相比本文理论线平均高出4.0°,低龄期垃圾平均高出11.4°,这说明高龄期垃圾对理论结果的吻合程度相比低龄期垃圾高,可能与低龄期垃圾组分内部差异度大、参数离散度高导致试验误差大有关系. ...
滚筒筛筛分生活垃圾的理论研究
3
2007
... 已有的陈垃圾滚筒筛运动理论主要基于几何导向,从假定的某几种特定参数出发进行推导. Alter等[12 ] 假定1个抛出曲线,并由此确定3个相关角度,描述物料运动状态,并反推摩擦因数.Glaub等[13 ] 添加与颗粒尺度相关的参数,研究粒度与筛分概率的关系.Stessel[14 ] 在前两者的基础上考虑了大直径滚筒筛中空气阻力对抛落的影响.Mellmann[15 ] 通过计算弗劳德数Fr 判断物料状态,把运动模式进一步细分为7个子类型.唐红侠等[16 ] 采用力学分析方法,指出物料最大提升角与滚筒摩擦角息息相关,且物料临界抛落转速与滚筒转速存在一定差异,但没有说明差异的具体量化指标. ...
... 陈垃圾的最大角理论计算要用到动摩擦因数μ .通过等孔径平面筛板作斜坡进行多次自由下滑试验取均值,可以确定老港低龄期陈垃圾与筛筒壁的动摩擦因数约为1.06,最大静摩擦因数约为1.07;老港高龄期陈垃圾与筛筒壁的动摩擦因数约为0.90,最大静摩擦因数约为0.97. 如图11 所示,根据以上摩擦因数值,按本研究前述方法进行计算,并与老港陈垃圾室内试验实测值,文献[12 ]、[13 ]、[16 ]的计算方法进行对比. ...
... 本研究方法计算结果显示,随着转速的升高,陈垃圾运动的最大角先逐渐增大,在进入圆周运动后达到最大值180°并不再变化. 低龄期垃圾至48 r/min后进入圆周运动,高龄期垃圾至50 r/min后进入圆周运动. 由图11 可知,该方法计算结果与实测值吻合程度最高,其他2种计算方法所得最大角度δ max 与实测值相较均存在较大的偏离,Alter等[12 -13 ] 计算结果明显偏大,唐红侠等[16 ] 计算结果则偏小. 室内试验结果表明,本研究方法分析的滚筒筛陈垃圾运动理论与实际偏差最小、轨迹重合度高,且计算方式不复杂,能够验证该理论的合理性与实用性. 另外,高龄期垃圾室内试验最大角值相比本文理论线平均高出4.0°,低龄期垃圾平均高出11.4°,这说明高龄期垃圾对理论结果的吻合程度相比低龄期垃圾高,可能与低龄期垃圾组分内部差异度大、参数离散度高导致试验误差大有关系. ...
3
... 如图1 所示,陈垃圾物料在滚筒筛内的运动模式主要有3种,可以按转速由小到大分为滚落运动、抛落运动、圆周运动. 图中,δ 为物料位置角,即物料质心到滚筒筛中心轴的垂线与竖直方向所成夹角. 每个模式各自的运动特点如表1 所示[14 ,17 ] .表中,δ max 为物料最大位置角,n t 为滚筒筛转速,η 为筛分效率. ...
... 试验设备在参考李兵等[17 ,21 -22 ] 的设计基础上,结合本研究所于我国多地现场陈垃圾筛分工程经验改进的室内小型滚筒筛,如图7 所示. 滚筒筛驱动方式:利用380 V、2.2 kW电机驱动,通过变速比为1∶5的手轮变速器带动齿轮转动,齿轮通过链条传动至滚筒筛中轴上的齿轮带动筒体旋转,滚筒筛筒体再通过摩擦力带动陈垃圾原料筛分. 滚筒筛筒体尺寸参数:半径为0.5 m,筒体长为2.0 m,筒壁厚为5 mm,筒壁与中轴通过总计20根支撑轴形成稳定结构. 筒体两侧设置挡板,使得筛下物可汇聚至下端,减少细粒散落率,提升试验精度. 筒口为一端封闭一端开放,开放端设有导料板,开放端下部撑脚高度可调. 筛孔直径选取Mönkäre等[23 ] 确定的细粒组分与粗粒组分直径划分界限20 mm,孔距取半径的3倍,筛孔呈正三角形分布. 筛筒转速在15~75 r/min内可连续自由调整. ...
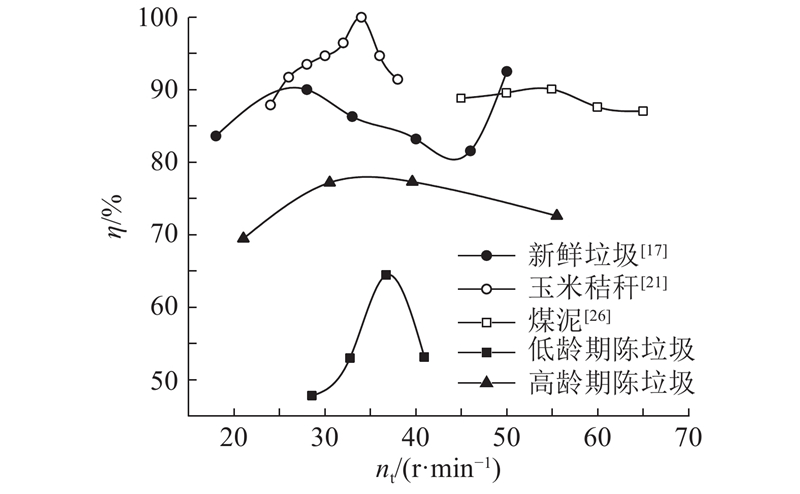
... 由物料运动模式的定性描述可知,陈垃圾滚筒筛筛分效率随着筛筒转速的提高,呈现先增后减的规律. 这个规律不仅出现在陈垃圾原料上,其他种类物料的滚筒筛筛分也有类似现象的记录,如新鲜垃圾筛分[17 ] 、秸秆筛分[21 ] 、煤泥筛分[26 ] 等,但记录陈垃圾转速与筛分效率关系试验的文献数据较少. 在不同转速下的室内小型滚筒筛筛分试验中,对陈垃圾的筛分指标进行记录、计算其筛分效率,并对比试验结果与前述几类非陈垃圾原料试验的典型结果,如图12 所示. 不同种类物料在同一转速下的筛分效率差距很大,这是由于物料本身属性(摩擦因数、黏聚力、级配等)、滚筒筛运行参数(转速、筒径、孔径等)、试验方法(试验时长、入料方式)均不同. 同一物料筛分效率随转速呈现先增后减的趋势均有所体现. ...
3
... 如图1 所示,陈垃圾物料在滚筒筛内的运动模式主要有3种,可以按转速由小到大分为滚落运动、抛落运动、圆周运动. 图中,δ 为物料位置角,即物料质心到滚筒筛中心轴的垂线与竖直方向所成夹角. 每个模式各自的运动特点如表1 所示[14 ,17 ] .表中,δ max 为物料最大位置角,n t 为滚筒筛转速,η 为筛分效率. ...
... 试验设备在参考李兵等[17 ,21 -22 ] 的设计基础上,结合本研究所于我国多地现场陈垃圾筛分工程经验改进的室内小型滚筒筛,如图7 所示. 滚筒筛驱动方式:利用380 V、2.2 kW电机驱动,通过变速比为1∶5的手轮变速器带动齿轮转动,齿轮通过链条传动至滚筒筛中轴上的齿轮带动筒体旋转,滚筒筛筒体再通过摩擦力带动陈垃圾原料筛分. 滚筒筛筒体尺寸参数:半径为0.5 m,筒体长为2.0 m,筒壁厚为5 mm,筒壁与中轴通过总计20根支撑轴形成稳定结构. 筒体两侧设置挡板,使得筛下物可汇聚至下端,减少细粒散落率,提升试验精度. 筒口为一端封闭一端开放,开放端设有导料板,开放端下部撑脚高度可调. 筛孔直径选取Mönkäre等[23 ] 确定的细粒组分与粗粒组分直径划分界限20 mm,孔距取半径的3倍,筛孔呈正三角形分布. 筛筒转速在15~75 r/min内可连续自由调整. ...
... 由物料运动模式的定性描述可知,陈垃圾滚筒筛筛分效率随着筛筒转速的提高,呈现先增后减的规律. 这个规律不仅出现在陈垃圾原料上,其他种类物料的滚筒筛筛分也有类似现象的记录,如新鲜垃圾筛分[17 ] 、秸秆筛分[21 ] 、煤泥筛分[26 ] 等,但记录陈垃圾转速与筛分效率关系试验的文献数据较少. 在不同转速下的室内小型滚筒筛筛分试验中,对陈垃圾的筛分指标进行记录、计算其筛分效率,并对比试验结果与前述几类非陈垃圾原料试验的典型结果,如图12 所示. 不同种类物料在同一转速下的筛分效率差距很大,这是由于物料本身属性(摩擦因数、黏聚力、级配等)、滚筒筛运行参数(转速、筒径、孔径等)、试验方法(试验时长、入料方式)均不同. 同一物料筛分效率随转速呈现先增后减的趋势均有所体现. ...
3
... 考虑到抛落运动模式是由一段在筛面圆周上的运动叠加一段空中抛落运动而成的,为了统一描述,本研究中在圆周上的运动包含以上3种模式在单元体未离开筛面时的所有运动. 由于原料沿轴向运动可用螺距与转速进行简单计算[18 ] ,本研究暂不追加考虑此方向上的运动. ...
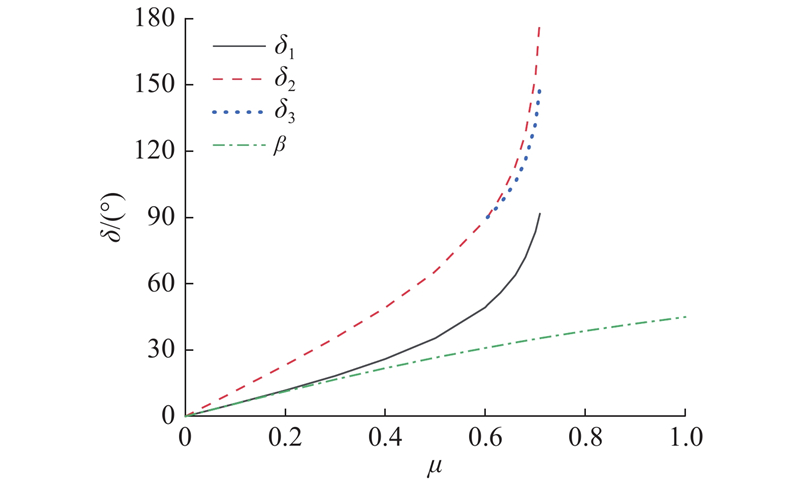
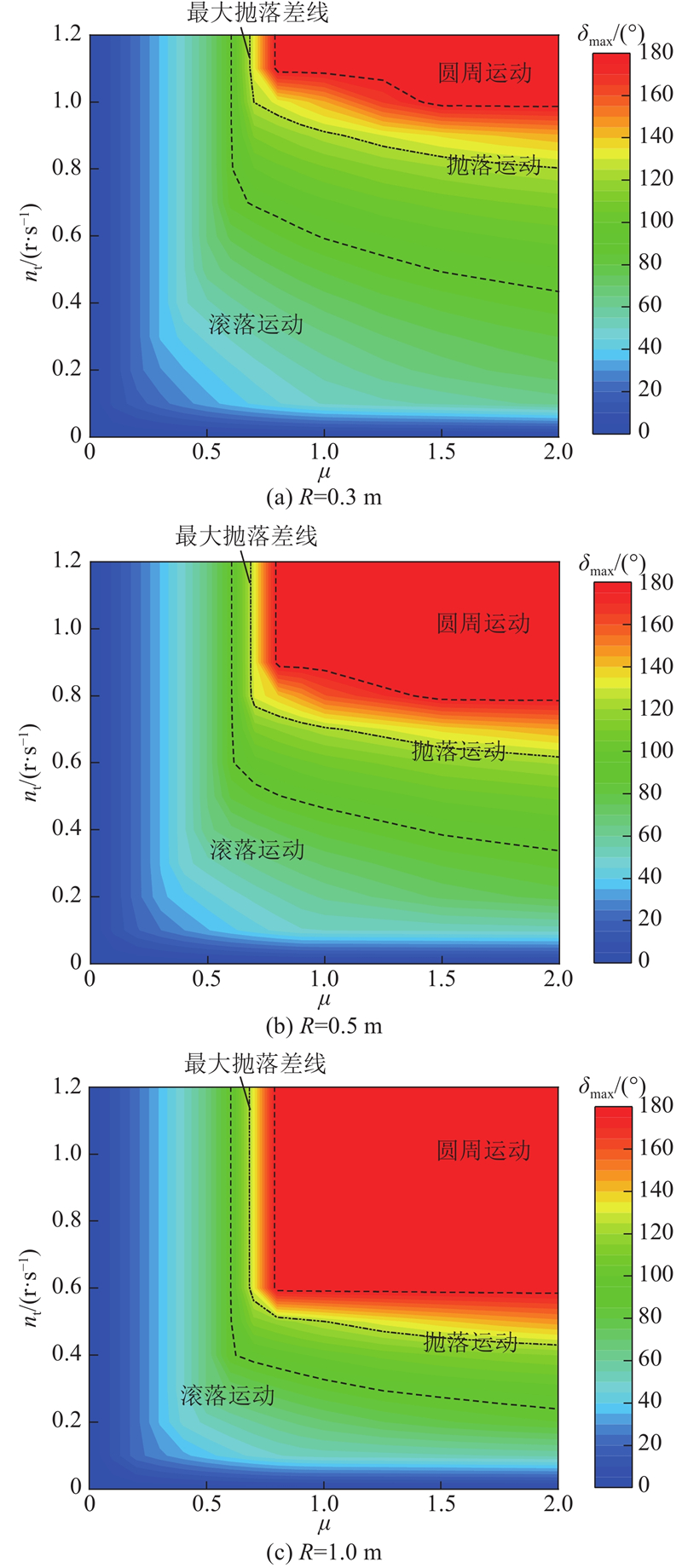
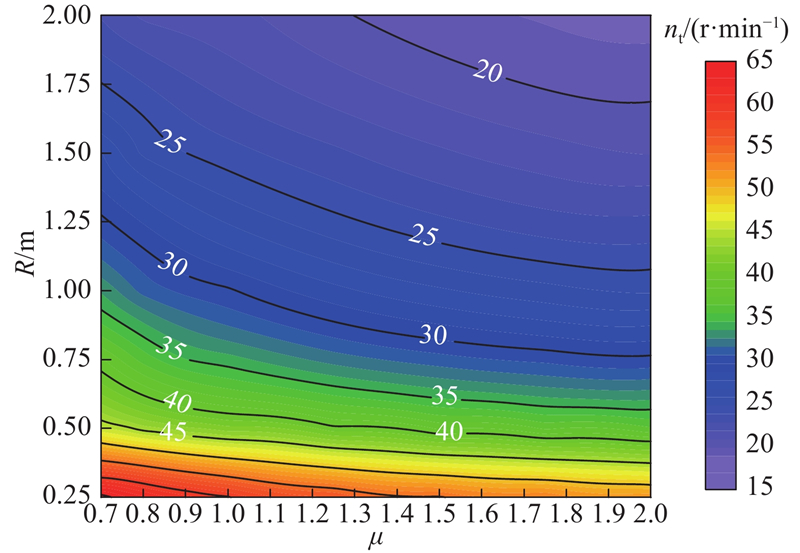
... 目前常见的垃圾滚筒筛直径有0.6、1.0 、2.0 m等,故除前述R =0.5 m以外,另外计算R =0.3 m,R =1.0 m的云图情况,如图6 所示. 由图可知:1) 最大角δ max 随着动摩擦因数μ 与滚筒筛转速n t 各自的增大而增大,若以90°与180°为分界线,陈垃圾在滚筒筛中的运动模式在图中可以分为3个区域,即滚落运动区、抛落运动区和圆周运动区. 2) 最大角等值点在云图上表现为先沿直线下降后沿斜率变化并向右下角移动. 这表明在μ 一定的情况下,转速足够大时符合标准工况,此时运动模式与转速具体值无关,转速不足时符合一般工况,此时运动模式与转速有关. 张大卫[18 ] 指出,满足物体抛落差最大的情况筛分效率最高,此时抛出角约为125.3°,将该等值线标在图6 中可发现该曲线大致位于抛落运动区的中间部分. 3) 标准工况与一般工况的分界线在图中表现为先同向变化后异向变化. 这是由于当μ 较小时,μ 增大将引起滑动平衡角δ 1 变大,而更大的δ 1 需要更大的转速才能满足,两者同向变化;当μ 较大时,由于物料运动最大角δ max 在达到180°后即做圆周运动,δ max 已不能再增大,而μ 增大使得满足可使物料进入圆周运动的转速需求降低,两者异向变化. 4) 半径R 越大,圆周运动区越大,滚落运动区与抛落运动区越小. 这是由于半径越大,物料在倾角较小的部分加速的长度越长,运动同样角度能提升的线速度越多,最大角也随之增长. 并且出于同样的原因,半径越大,标准工况的区域也更大,一般工况的区域则更小. ...
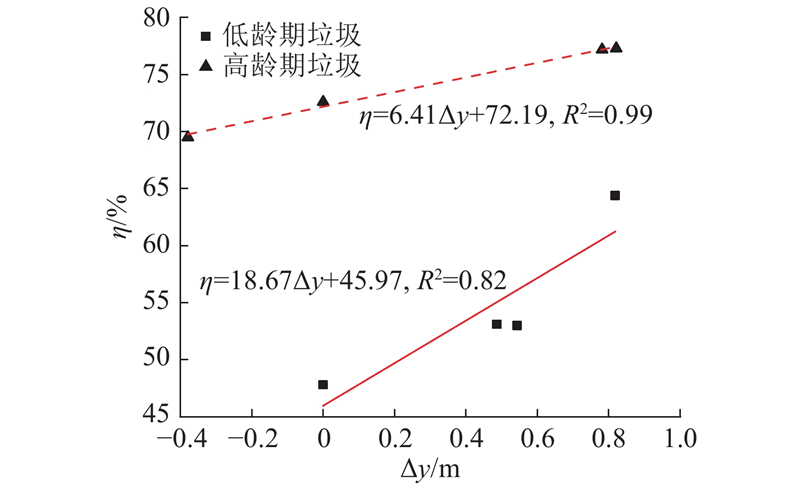
... 考虑使用抛落差大小作为评价筛分效率的方法. 抛落差指物料在抛落运动中抛出点到接收点的竖直距离差,可以由函数计算[18 ] : ...
3
... 考虑到抛落运动模式是由一段在筛面圆周上的运动叠加一段空中抛落运动而成的,为了统一描述,本研究中在圆周上的运动包含以上3种模式在单元体未离开筛面时的所有运动. 由于原料沿轴向运动可用螺距与转速进行简单计算[18 ] ,本研究暂不追加考虑此方向上的运动. ...
... 目前常见的垃圾滚筒筛直径有0.6、1.0 、2.0 m等,故除前述R =0.5 m以外,另外计算R =0.3 m,R =1.0 m的云图情况,如图6 所示. 由图可知:1) 最大角δ max 随着动摩擦因数μ 与滚筒筛转速n t 各自的增大而增大,若以90°与180°为分界线,陈垃圾在滚筒筛中的运动模式在图中可以分为3个区域,即滚落运动区、抛落运动区和圆周运动区. 2) 最大角等值点在云图上表现为先沿直线下降后沿斜率变化并向右下角移动. 这表明在μ 一定的情况下,转速足够大时符合标准工况,此时运动模式与转速具体值无关,转速不足时符合一般工况,此时运动模式与转速有关. 张大卫[18 ] 指出,满足物体抛落差最大的情况筛分效率最高,此时抛出角约为125.3°,将该等值线标在图6 中可发现该曲线大致位于抛落运动区的中间部分. 3) 标准工况与一般工况的分界线在图中表现为先同向变化后异向变化. 这是由于当μ 较小时,μ 增大将引起滑动平衡角δ 1 变大,而更大的δ 1 需要更大的转速才能满足,两者同向变化;当μ 较大时,由于物料运动最大角δ max 在达到180°后即做圆周运动,δ max 已不能再增大,而μ 增大使得满足可使物料进入圆周运动的转速需求降低,两者异向变化. 4) 半径R 越大,圆周运动区越大,滚落运动区与抛落运动区越小. 这是由于半径越大,物料在倾角较小的部分加速的长度越长,运动同样角度能提升的线速度越多,最大角也随之增长. 并且出于同样的原因,半径越大,标准工况的区域也更大,一般工况的区域则更小. ...
... 考虑使用抛落差大小作为评价筛分效率的方法. 抛落差指物料在抛落运动中抛出点到接收点的竖直距离差,可以由函数计算[18 ] : ...
1
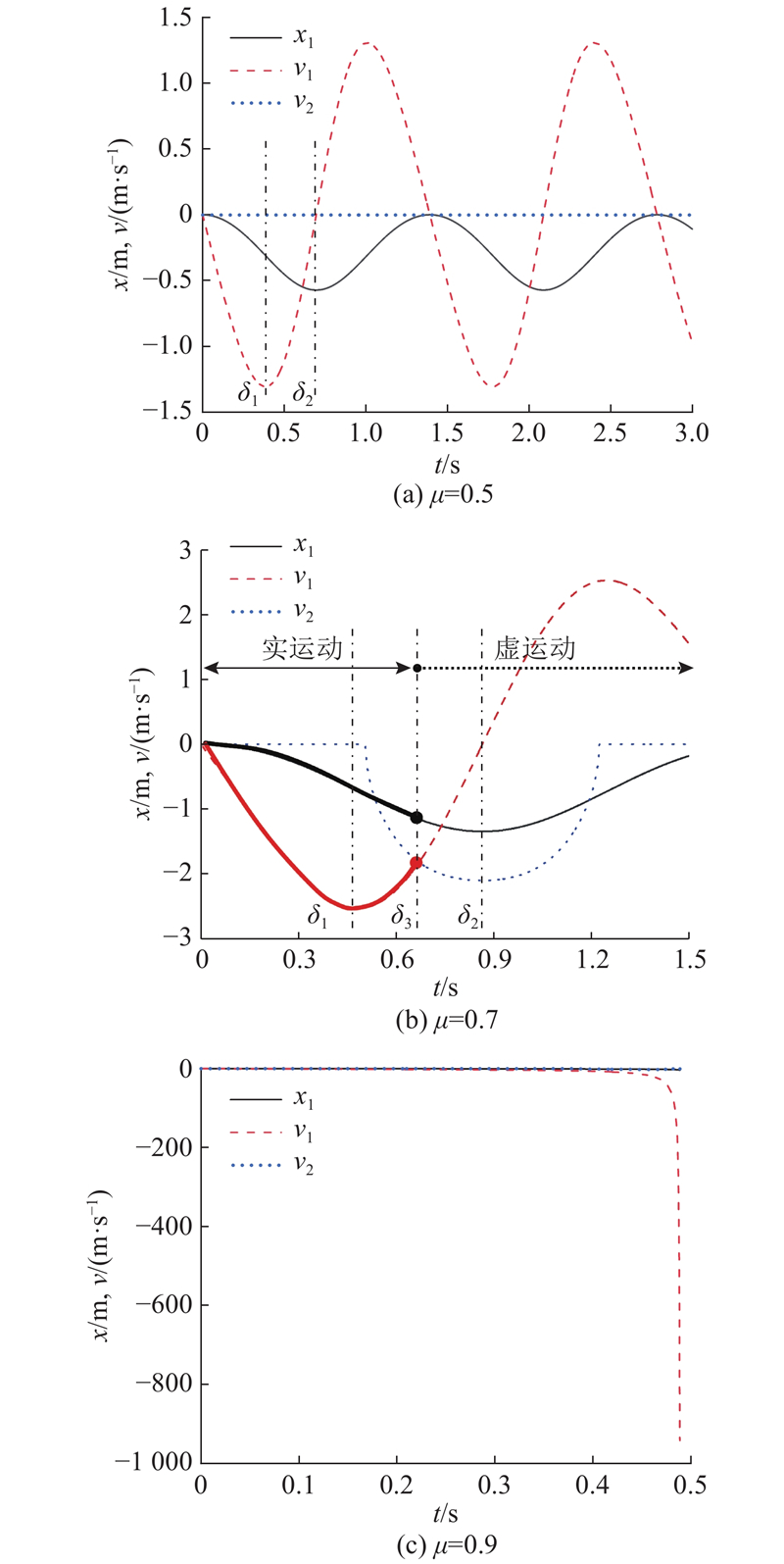
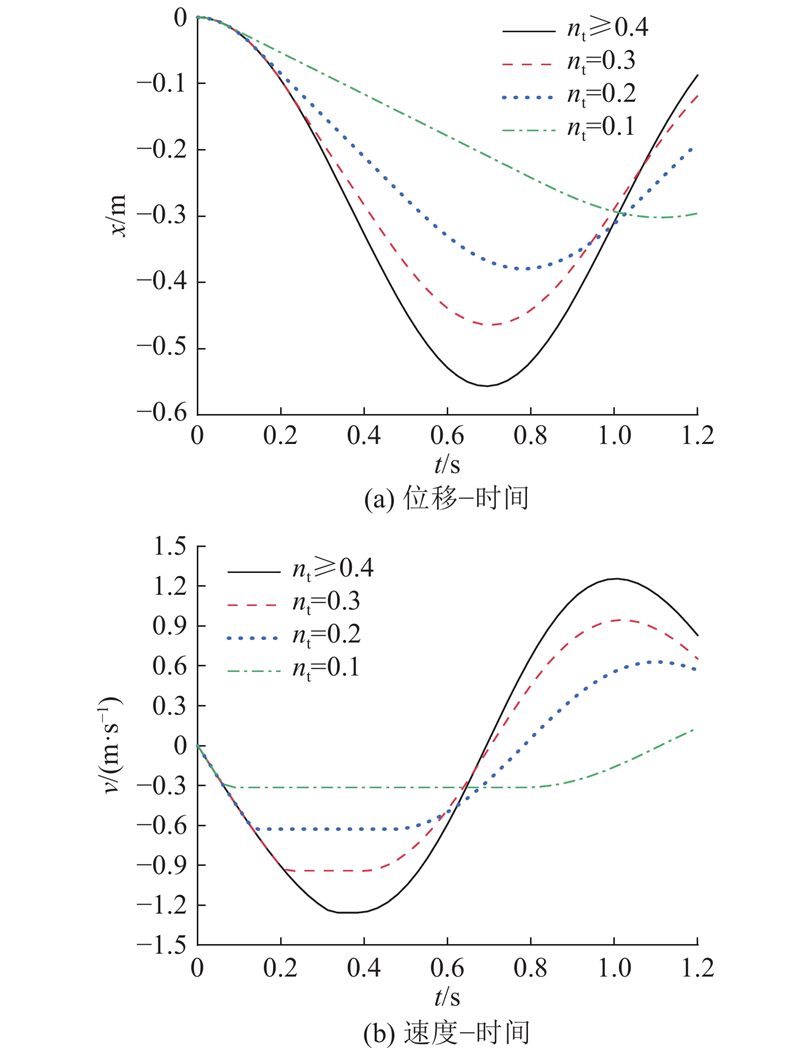
... 式(2)是切向运动位移x 关于时间t 的二阶非线性微分方程,求解析解比较困难,多数情况下只能利用级数或者有限元解法解答[19 -20 ] . 以下通过分析特定旋转角时的受力解构滚筒筛内物料运动理论,并通过Matlab的常微分方程刚性求解器进行求解. 将式(2)的显式解记作 ...
1
... 式(2)是切向运动位移x 关于时间t 的二阶非线性微分方程,求解析解比较困难,多数情况下只能利用级数或者有限元解法解答[19 -20 ] . 以下通过分析特定旋转角时的受力解构滚筒筛内物料运动理论,并通过Matlab的常微分方程刚性求解器进行求解. 将式(2)的显式解记作 ...
1
... 式(2)是切向运动位移x 关于时间t 的二阶非线性微分方程,求解析解比较困难,多数情况下只能利用级数或者有限元解法解答[19 -20 ] . 以下通过分析特定旋转角时的受力解构滚筒筛内物料运动理论,并通过Matlab的常微分方程刚性求解器进行求解. 将式(2)的显式解记作 ...
1
... 式(2)是切向运动位移x 关于时间t 的二阶非线性微分方程,求解析解比较困难,多数情况下只能利用级数或者有限元解法解答[19 -20 ] . 以下通过分析特定旋转角时的受力解构滚筒筛内物料运动理论,并通过Matlab的常微分方程刚性求解器进行求解. 将式(2)的显式解记作 ...
秸秆类生物质原料筛分除杂试验及滚筒筛改进
2
2016
... 试验设备在参考李兵等[17 ,21 -22 ] 的设计基础上,结合本研究所于我国多地现场陈垃圾筛分工程经验改进的室内小型滚筒筛,如图7 所示. 滚筒筛驱动方式:利用380 V、2.2 kW电机驱动,通过变速比为1∶5的手轮变速器带动齿轮转动,齿轮通过链条传动至滚筒筛中轴上的齿轮带动筒体旋转,滚筒筛筒体再通过摩擦力带动陈垃圾原料筛分. 滚筒筛筒体尺寸参数:半径为0.5 m,筒体长为2.0 m,筒壁厚为5 mm,筒壁与中轴通过总计20根支撑轴形成稳定结构. 筒体两侧设置挡板,使得筛下物可汇聚至下端,减少细粒散落率,提升试验精度. 筒口为一端封闭一端开放,开放端设有导料板,开放端下部撑脚高度可调. 筛孔直径选取Mönkäre等[23 ] 确定的细粒组分与粗粒组分直径划分界限20 mm,孔距取半径的3倍,筛孔呈正三角形分布. 筛筒转速在15~75 r/min内可连续自由调整. ...
... 由物料运动模式的定性描述可知,陈垃圾滚筒筛筛分效率随着筛筒转速的提高,呈现先增后减的规律. 这个规律不仅出现在陈垃圾原料上,其他种类物料的滚筒筛筛分也有类似现象的记录,如新鲜垃圾筛分[17 ] 、秸秆筛分[21 ] 、煤泥筛分[26 ] 等,但记录陈垃圾转速与筛分效率关系试验的文献数据较少. 在不同转速下的室内小型滚筒筛筛分试验中,对陈垃圾的筛分指标进行记录、计算其筛分效率,并对比试验结果与前述几类非陈垃圾原料试验的典型结果,如图12 所示. 不同种类物料在同一转速下的筛分效率差距很大,这是由于物料本身属性(摩擦因数、黏聚力、级配等)、滚筒筛运行参数(转速、筒径、孔径等)、试验方法(试验时长、入料方式)均不同. 同一物料筛分效率随转速呈现先增后减的趋势均有所体现. ...
秸秆类生物质原料筛分除杂试验及滚筒筛改进
2
2016
... 试验设备在参考李兵等[17 ,21 -22 ] 的设计基础上,结合本研究所于我国多地现场陈垃圾筛分工程经验改进的室内小型滚筒筛,如图7 所示. 滚筒筛驱动方式:利用380 V、2.2 kW电机驱动,通过变速比为1∶5的手轮变速器带动齿轮转动,齿轮通过链条传动至滚筒筛中轴上的齿轮带动筒体旋转,滚筒筛筒体再通过摩擦力带动陈垃圾原料筛分. 滚筒筛筒体尺寸参数:半径为0.5 m,筒体长为2.0 m,筒壁厚为5 mm,筒壁与中轴通过总计20根支撑轴形成稳定结构. 筒体两侧设置挡板,使得筛下物可汇聚至下端,减少细粒散落率,提升试验精度. 筒口为一端封闭一端开放,开放端设有导料板,开放端下部撑脚高度可调. 筛孔直径选取Mönkäre等[23 ] 确定的细粒组分与粗粒组分直径划分界限20 mm,孔距取半径的3倍,筛孔呈正三角形分布. 筛筒转速在15~75 r/min内可连续自由调整. ...
... 由物料运动模式的定性描述可知,陈垃圾滚筒筛筛分效率随着筛筒转速的提高,呈现先增后减的规律. 这个规律不仅出现在陈垃圾原料上,其他种类物料的滚筒筛筛分也有类似现象的记录,如新鲜垃圾筛分[17 ] 、秸秆筛分[21 ] 、煤泥筛分[26 ] 等,但记录陈垃圾转速与筛分效率关系试验的文献数据较少. 在不同转速下的室内小型滚筒筛筛分试验中,对陈垃圾的筛分指标进行记录、计算其筛分效率,并对比试验结果与前述几类非陈垃圾原料试验的典型结果,如图12 所示. 不同种类物料在同一转速下的筛分效率差距很大,这是由于物料本身属性(摩擦因数、黏聚力、级配等)、滚筒筛运行参数(转速、筒径、孔径等)、试验方法(试验时长、入料方式)均不同. 同一物料筛分效率随转速呈现先增后减的趋势均有所体现. ...
1
... 试验设备在参考李兵等[17 ,21 -22 ] 的设计基础上,结合本研究所于我国多地现场陈垃圾筛分工程经验改进的室内小型滚筒筛,如图7 所示. 滚筒筛驱动方式:利用380 V、2.2 kW电机驱动,通过变速比为1∶5的手轮变速器带动齿轮转动,齿轮通过链条传动至滚筒筛中轴上的齿轮带动筒体旋转,滚筒筛筒体再通过摩擦力带动陈垃圾原料筛分. 滚筒筛筒体尺寸参数:半径为0.5 m,筒体长为2.0 m,筒壁厚为5 mm,筒壁与中轴通过总计20根支撑轴形成稳定结构. 筒体两侧设置挡板,使得筛下物可汇聚至下端,减少细粒散落率,提升试验精度. 筒口为一端封闭一端开放,开放端设有导料板,开放端下部撑脚高度可调. 筛孔直径选取Mönkäre等[23 ] 确定的细粒组分与粗粒组分直径划分界限20 mm,孔距取半径的3倍,筛孔呈正三角形分布. 筛筒转速在15~75 r/min内可连续自由调整. ...
Characterization of fine fraction mined from two Finnish landfills
1
2016
... 试验设备在参考李兵等[17 ,21 -22 ] 的设计基础上,结合本研究所于我国多地现场陈垃圾筛分工程经验改进的室内小型滚筒筛,如图7 所示. 滚筒筛驱动方式:利用380 V、2.2 kW电机驱动,通过变速比为1∶5的手轮变速器带动齿轮转动,齿轮通过链条传动至滚筒筛中轴上的齿轮带动筒体旋转,滚筒筛筒体再通过摩擦力带动陈垃圾原料筛分. 滚筒筛筒体尺寸参数:半径为0.5 m,筒体长为2.0 m,筒壁厚为5 mm,筒壁与中轴通过总计20根支撑轴形成稳定结构. 筒体两侧设置挡板,使得筛下物可汇聚至下端,减少细粒散落率,提升试验精度. 筒口为一端封闭一端开放,开放端设有导料板,开放端下部撑脚高度可调. 筛孔直径选取Mönkäre等[23 ] 确定的细粒组分与粗粒组分直径划分界限20 mm,孔距取半径的3倍,筛孔呈正三角形分布. 筛筒转速在15~75 r/min内可连续自由调整. ...
1
... 在滚筒筛试验前后利用电子天平对陈垃圾质量进行称重,并对筛上物、筛下物按规定粒径进行人工分拣分别称重,可以测试其筛分效率. 滚筒筛筛分效率在不同的文献、工程中有不同的计算方法,目前常用的计算方法主要有2类:量效率、总效率. 量效率计算方法是滚筒筛筛下细粒的质量除以垃圾原料中所有能通过相应筛孔的量.总效率为在量效率的基础上减去修正值[24 -25 ] . 总效率具体计算式为 ...
1
... 在滚筒筛试验前后利用电子天平对陈垃圾质量进行称重,并对筛上物、筛下物按规定粒径进行人工分拣分别称重,可以测试其筛分效率. 滚筒筛筛分效率在不同的文献、工程中有不同的计算方法,目前常用的计算方法主要有2类:量效率、总效率. 量效率计算方法是滚筒筛筛下细粒的质量除以垃圾原料中所有能通过相应筛孔的量.总效率为在量效率的基础上减去修正值[24 -25 ] . 总效率具体计算式为 ...
1
... 由物料运动模式的定性描述可知,陈垃圾滚筒筛筛分效率随着筛筒转速的提高,呈现先增后减的规律. 这个规律不仅出现在陈垃圾原料上,其他种类物料的滚筒筛筛分也有类似现象的记录,如新鲜垃圾筛分[17 ] 、秸秆筛分[21 ] 、煤泥筛分[26 ] 等,但记录陈垃圾转速与筛分效率关系试验的文献数据较少. 在不同转速下的室内小型滚筒筛筛分试验中,对陈垃圾的筛分指标进行记录、计算其筛分效率,并对比试验结果与前述几类非陈垃圾原料试验的典型结果,如图12 所示. 不同种类物料在同一转速下的筛分效率差距很大,这是由于物料本身属性(摩擦因数、黏聚力、级配等)、滚筒筛运行参数(转速、筒径、孔径等)、试验方法(试验时长、入料方式)均不同. 同一物料筛分效率随转速呈现先增后减的趋势均有所体现. ...
1
... 由物料运动模式的定性描述可知,陈垃圾滚筒筛筛分效率随着筛筒转速的提高,呈现先增后减的规律. 这个规律不仅出现在陈垃圾原料上,其他种类物料的滚筒筛筛分也有类似现象的记录,如新鲜垃圾筛分[17 ] 、秸秆筛分[21 ] 、煤泥筛分[26 ] 等,但记录陈垃圾转速与筛分效率关系试验的文献数据较少. 在不同转速下的室内小型滚筒筛筛分试验中,对陈垃圾的筛分指标进行记录、计算其筛分效率,并对比试验结果与前述几类非陈垃圾原料试验的典型结果,如图12 所示. 不同种类物料在同一转速下的筛分效率差距很大,这是由于物料本身属性(摩擦因数、黏聚力、级配等)、滚筒筛运行参数(转速、筒径、孔径等)、试验方法(试验时长、入料方式)均不同. 同一物料筛分效率随转速呈现先增后减的趋势均有所体现. ...
Evolution of saturated hydraulic conductivity with compression and degradation for municipal solid waste
1
2017
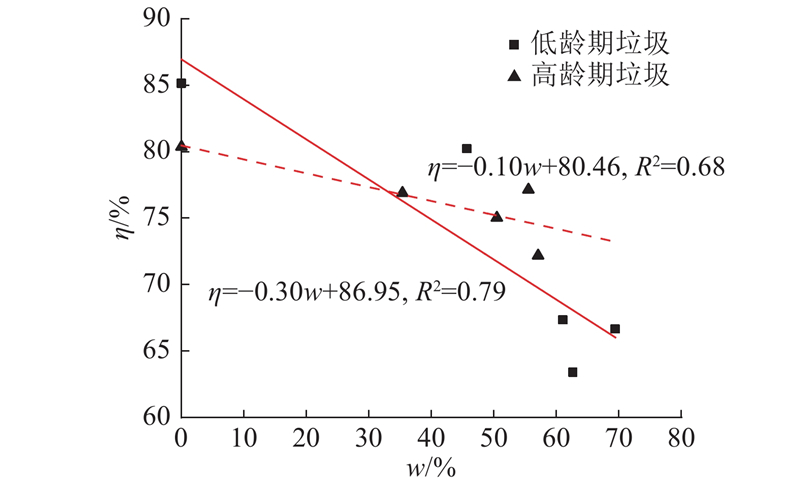
... 将陈垃圾使用70℃烘箱加热去除水分,以防止有机物燃烧损失[27 ] . 设置未加热、加热1 h、加热2 h、加热4 h与加热48 h(烘干)5组对照试验,测试其水的质量分数w ,并在36 r/min转速下对不同龄期陈垃圾进行筛分试验. 试验结果表明同物料在不同水的质量分数下抛出角误差极值在10°以内,但筛分效果随着水的质量分数减小有变佳的趋势. 这表明陈垃圾水的质量分数对其运动模式影响较小,对筛分效率影响较大. 试验结果如图15 所示. 由试验结果可知,筛分效率随着水的质量分数的减小呈现上升的趋势,但两者的线性关系不显著. 完全脱水的原料相比未进行脱水处理的原料,低龄期垃圾筛分效率提高18.4%,高龄期垃圾筛分效率提高8.2%. 其中,低龄期垃圾筛分效率对于水的质量分数的变动敏感性比高龄期垃圾高,线性变动敏感性约为其3倍. 试验证明,在滚筒筛筛分前,对原料进行脱水处理,一定程度上有利于筛分效率的提高. ...