卷吸速度为任意方向的椭圆接触弹流润滑复合迭代解法
2
2014
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
... 接触区压力和油膜厚度分布由雷诺方程求解得到[1, 14-15]. 为了提高计算效率,在不关注接触界面微观润滑和摩擦特性的情况下,采用赫兹接触压力近似油膜压力[16],油膜厚度计算采用Chittenden等[23]提出的等温任意速度矢量点接触中心油膜厚度公式为 ...
卷吸速度为任意方向的椭圆接触弹流润滑复合迭代解法
2
2014
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
... 接触区压力和油膜厚度分布由雷诺方程求解得到[1, 14-15]. 为了提高计算效率,在不关注接触界面微观润滑和摩擦特性的情况下,采用赫兹接触压力近似油膜压力[16],油膜厚度计算采用Chittenden等[23]提出的等温任意速度矢量点接触中心油膜厚度公式为 ...
双圆弧谐波减速器共轭啮合区混合润滑分析
1
2018
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
双圆弧谐波减速器共轭啮合区混合润滑分析
1
2018
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
基于Circular模型的大剪应变率点接触弹流界面滑移数值分析
0
2018
基于Circular模型的大剪应变率点接触弹流界面滑移数值分析
0
2018
An adhesive wear model for helical gears in line-contact mixed elastohydrodynamic lubrication
0
2019
The effect of surface roughness on friction and film thickness in transition from EHL to mixed lubrication
1
2018
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
Film thickness and asperity load formulas for line-contact elastohydrodynamic lubrication with provision for surface roughness
1
2012
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
On the effect of surface roughness in point-contact EHL: formulas for film thickness and asperity load
1
2015
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
Mixed elastohydrodynamic lubrication line-contact formulas with different surface patterns
1
2014
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
An engineering approach for rapid evaluation of traction coefficient and wear in mixed EHL
1
2015
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
Prediction of oil-film thickness and shape in elliptical point contacts under combined rolling and sliding motion
1
2000
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
Simplified multigrid technique for the numerical solution to the steady-state and transient EHL line contacts and the arbitrary entrainment EHL point contacts
2
2001
... 为了验证具有卷吸速度夹角的点接触油膜厚度预测结果,给出2种工况下油膜厚度随卷吸夹角 $ {\theta _{\text{e}}} $的变化趋势,并与Stahl等[12]的实验结果进行对比,如图9所示. 测试夹角 $ {\theta _{\text{e}}} $分别为0°、7.63°、16.10°、26.57°,润滑油参数与文献[30]一致,工况1的参数为 $ {R_x} $=12.7 mm, $ {R_y} $=31.6 mm, $ {p_{\text{h}}} $=0.512 GPa, $ {u_{\text{e}}} $=0.5 m/s, $ E' $ =123.90 GPa;工况2的参数为 $ {R_x} $=4.0 mm, $ {R_y} $=12.7 mm, $ {p_{\text{h}}} $=1.03 GPa, $ {u_e} $=0.3 m/s, $ E' $=123.90 GPa. 由图可知,当卷吸速度为0.5 m/s时,中心油膜厚度随着卷吸速度夹角 $ {\theta _{\text{e}}} $增大而减小. Chittenden公式[23]与Gupta系数修正[31]得到的油膜厚度与实验结果趋势一致,但考虑入口区热影响,迭代得到的油膜厚度与Stahl等[12]的实验结果更为吻合. 当卷吸速度减小到0.3m/s时(工况2),入口区热影响不显著,3种情况下的油膜预测值与实验数据相近. 图9中的油膜厚度预测值误差不超过5.0%,为了进一步验证更大卷吸速度夹角下油膜厚度的预测情况,将本研究数值结果与已有研究结果进行比较,如表1所示. 计算参数为 $ {R_x} $=20.0 mm, $ {R_y} $=56.8 mm, $ {p_{\text{h}}} $=0.3 GPa, $ {u_e} $=0.57 m/s, $ E' $=228.3 GPa, $ {\eta _0} $=0.08 Pa·s, $ \alpha $=2.1×10−8 Pa−1. 由表1可知,在卷吸速度夹角0~90°,油膜厚度随卷吸速度夹角增大而减小,由于雷诺方程数值求解方法不同,文献中的中心油膜厚度有一定的差异. 考虑入口区热影响的油膜厚预测结果与文献[11]、[13]、[33]的结论接近,相比文献[13]结果的最大偏差为7.3%. ...
... Central oil film thickness corresponding to entrainment angle in different calculation methods
Tab.1 | 计算方法 | hc/nm |
| θe= 0° | θe= 45° | θe= 90° |
| 文献[11] | 495.3 | 440.0 | 375.3 |
| 文献[33] | 457.0 | 419.0 | 393.0 |
| 文献[13] | 457.0 | 415.0 | 357.8 |
| 本研究 | 461.5 | 429.9 | 383.2 |
具有卷吸速度矢量点接触摩擦系数的实验研究相对较少,Pu等[20]采用椭球−盘接触实验研究卷吸速度大小和卷吸速度夹角对点接触摩擦系数的影响,实验参数为 $ {\theta _{\text{e}}} $=22.5°, $ {R_x} $=16 mm, $ {R_y} $=45.5 mm, $ {p_{\text{h}}} $=0.73 GPa, $ {\sigma _{{\text{RMS}}}} $=0.3 μm, $ {\eta _0} $=0.08 Pa·s, $ \alpha $=2.10 ×10−8 Pa−1, $ E' $=210.0 GPa. 如图10所示研究不同热影响因素下的摩擦系数、接触区最大温升 $ \Delta {T_{{\text{f}},\max }} $以及入口区温升 $ \Delta {T_{{\text{in}}}} $随卷吸速度的变化情况,并与Pu等[20]的实验结果进行对比. 由图可知,卷吸速度在0.1 m/s~10 m/s时,摩擦系数预测结果与实验数据在变化趋势上一致. 卷吸速度大于1m/s时,接触区温升显著,忽略接触区温升导致摩擦系数预测结果偏大. 与图7不同,当转速大于3 m/s时,入口区温升对摩擦系数的影响较为明显. 考虑入口区和接触区热影响的摩擦系数在高速工况下与Pu等[20]实验结果吻合较好,但在混合润滑和边界润滑状态下( $ {u_e} $= 0.1~1 m/s),摩擦系数预测结果偏离实验数据明显,最大误差为27.8%. 原因是式(15)中的载荷百分比函数 ${f_\varLambda }$是关于膜厚比 $\varLambda$的函数,根据文献[33]的研究可知,在边界润滑和混合润滑状态下,粗糙度形貌类型(如横向和径向粗糙纹理)以及纹理方向与卷吸速度的夹角对膜厚比 $\varLambda$影响较为显著,式(11)未能考虑粗糙形貌的影响. ...
Theoretical and experimental investigations on EHL point contacts with different entrainment velocity directions
3
2013
... 为了验证具有卷吸速度夹角的点接触油膜厚度预测结果,给出2种工况下油膜厚度随卷吸夹角 $ {\theta _{\text{e}}} $的变化趋势,并与Stahl等[12]的实验结果进行对比,如图9所示. 测试夹角 $ {\theta _{\text{e}}} $分别为0°、7.63°、16.10°、26.57°,润滑油参数与文献[30]一致,工况1的参数为 $ {R_x} $=12.7 mm, $ {R_y} $=31.6 mm, $ {p_{\text{h}}} $=0.512 GPa, $ {u_{\text{e}}} $=0.5 m/s, $ E' $ =123.90 GPa;工况2的参数为 $ {R_x} $=4.0 mm, $ {R_y} $=12.7 mm, $ {p_{\text{h}}} $=1.03 GPa, $ {u_e} $=0.3 m/s, $ E' $=123.90 GPa. 由图可知,当卷吸速度为0.5 m/s时,中心油膜厚度随着卷吸速度夹角 $ {\theta _{\text{e}}} $增大而减小. Chittenden公式[23]与Gupta系数修正[31]得到的油膜厚度与实验结果趋势一致,但考虑入口区热影响,迭代得到的油膜厚度与Stahl等[12]的实验结果更为吻合. 当卷吸速度减小到0.3m/s时(工况2),入口区热影响不显著,3种情况下的油膜预测值与实验数据相近. 图9中的油膜厚度预测值误差不超过5.0%,为了进一步验证更大卷吸速度夹角下油膜厚度的预测情况,将本研究数值结果与已有研究结果进行比较,如表1所示. 计算参数为 $ {R_x} $=20.0 mm, $ {R_y} $=56.8 mm, $ {p_{\text{h}}} $=0.3 GPa, $ {u_e} $=0.57 m/s, $ E' $=228.3 GPa, $ {\eta _0} $=0.08 Pa·s, $ \alpha $=2.1×10−8 Pa−1. 由表1可知,在卷吸速度夹角0~90°,油膜厚度随卷吸速度夹角增大而减小,由于雷诺方程数值求解方法不同,文献中的中心油膜厚度有一定的差异. 考虑入口区热影响的油膜厚预测结果与文献[11]、[13]、[33]的结论接近,相比文献[13]结果的最大偏差为7.3%. ...
... [12]的实验结果更为吻合. 当卷吸速度减小到0.3m/s时(工况2),入口区热影响不显著,3种情况下的油膜预测值与实验数据相近. 图9中的油膜厚度预测值误差不超过5.0%,为了进一步验证更大卷吸速度夹角下油膜厚度的预测情况,将本研究数值结果与已有研究结果进行比较,如表1所示. 计算参数为 $ {R_x} $=20.0 mm, $ {R_y} $=56.8 mm, $ {p_{\text{h}}} $=0.3 GPa, $ {u_e} $=0.57 m/s, $ E' $=228.3 GPa, $ {\eta _0} $=0.08 Pa·s, $ \alpha $=2.1×10−8 Pa−1. 由表1可知,在卷吸速度夹角0~90°,油膜厚度随卷吸速度夹角增大而减小,由于雷诺方程数值求解方法不同,文献中的中心油膜厚度有一定的差异. 考虑入口区热影响的油膜厚预测结果与文献[11]、[13]、[33]的结论接近,相比文献[13]结果的最大偏差为7.3%. ...
... (3)不同工况下,油膜厚度和摩擦系数预测结果相对实验结果(Paouris等[30]、Stahl等[12]、Pu等[20])的最大误差为分别为14.2%和28.5%,但其整体变化趋势与实验数据具有较好的一致性,摩擦系数简化计算方法的可靠性得以验证. ...
A theoretical analysis of the mixed elastohydrodynamic lubrication in elliptical contacts with an arbitrary entrainment angle
5
2014
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
... [13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
... 为了验证具有卷吸速度夹角的点接触油膜厚度预测结果,给出2种工况下油膜厚度随卷吸夹角 $ {\theta _{\text{e}}} $的变化趋势,并与Stahl等[12]的实验结果进行对比,如图9所示. 测试夹角 $ {\theta _{\text{e}}} $分别为0°、7.63°、16.10°、26.57°,润滑油参数与文献[30]一致,工况1的参数为 $ {R_x} $=12.7 mm, $ {R_y} $=31.6 mm, $ {p_{\text{h}}} $=0.512 GPa, $ {u_{\text{e}}} $=0.5 m/s, $ E' $ =123.90 GPa;工况2的参数为 $ {R_x} $=4.0 mm, $ {R_y} $=12.7 mm, $ {p_{\text{h}}} $=1.03 GPa, $ {u_e} $=0.3 m/s, $ E' $=123.90 GPa. 由图可知,当卷吸速度为0.5 m/s时,中心油膜厚度随着卷吸速度夹角 $ {\theta _{\text{e}}} $增大而减小. Chittenden公式[23]与Gupta系数修正[31]得到的油膜厚度与实验结果趋势一致,但考虑入口区热影响,迭代得到的油膜厚度与Stahl等[12]的实验结果更为吻合. 当卷吸速度减小到0.3m/s时(工况2),入口区热影响不显著,3种情况下的油膜预测值与实验数据相近. 图9中的油膜厚度预测值误差不超过5.0%,为了进一步验证更大卷吸速度夹角下油膜厚度的预测情况,将本研究数值结果与已有研究结果进行比较,如表1所示. 计算参数为 $ {R_x} $=20.0 mm, $ {R_y} $=56.8 mm, $ {p_{\text{h}}} $=0.3 GPa, $ {u_e} $=0.57 m/s, $ E' $=228.3 GPa, $ {\eta _0} $=0.08 Pa·s, $ \alpha $=2.1×10−8 Pa−1. 由表1可知,在卷吸速度夹角0~90°,油膜厚度随卷吸速度夹角增大而减小,由于雷诺方程数值求解方法不同,文献中的中心油膜厚度有一定的差异. 考虑入口区热影响的油膜厚预测结果与文献[11]、[13]、[33]的结论接近,相比文献[13]结果的最大偏差为7.3%. ...
... ]的结论接近,相比文献[13]结果的最大偏差为7.3%. ...
... Central oil film thickness corresponding to entrainment angle in different calculation methods
Tab.1 | 计算方法 | hc/nm |
| θe= 0° | θe= 45° | θe= 90° |
| 文献[11] | 495.3 | 440.0 | 375.3 |
| 文献[33] | 457.0 | 419.0 | 393.0 |
| 文献[13] | 457.0 | 415.0 | 357.8 |
| 本研究 | 461.5 | 429.9 | 383.2 |
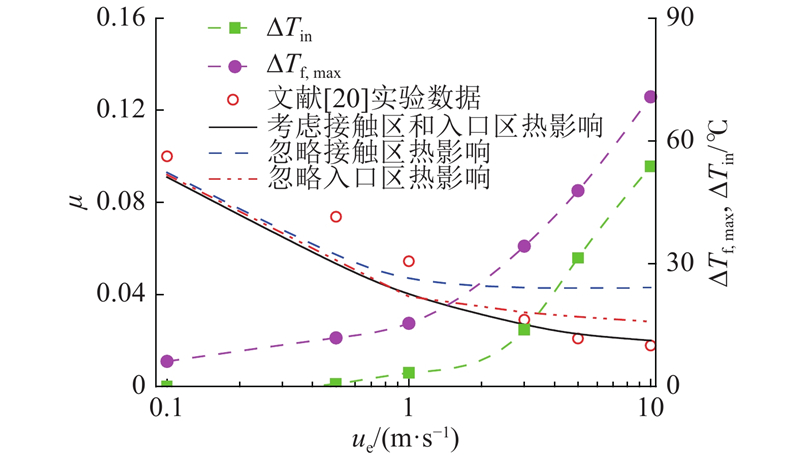
具有卷吸速度矢量点接触摩擦系数的实验研究相对较少,Pu等[20]采用椭球−盘接触实验研究卷吸速度大小和卷吸速度夹角对点接触摩擦系数的影响,实验参数为 $ {\theta _{\text{e}}} $=22.5°, $ {R_x} $=16 mm, $ {R_y} $=45.5 mm, $ {p_{\text{h}}} $=0.73 GPa, $ {\sigma _{{\text{RMS}}}} $=0.3 μm, $ {\eta _0} $=0.08 Pa·s, $ \alpha $=2.10 ×10−8 Pa−1, $ E' $=210.0 GPa. 如图10所示研究不同热影响因素下的摩擦系数、接触区最大温升 $ \Delta {T_{{\text{f}},\max }} $以及入口区温升 $ \Delta {T_{{\text{in}}}} $随卷吸速度的变化情况,并与Pu等[20]的实验结果进行对比. 由图可知,卷吸速度在0.1 m/s~10 m/s时,摩擦系数预测结果与实验数据在变化趋势上一致. 卷吸速度大于1m/s时,接触区温升显著,忽略接触区温升导致摩擦系数预测结果偏大. 与图7不同,当转速大于3 m/s时,入口区温升对摩擦系数的影响较为明显. 考虑入口区和接触区热影响的摩擦系数在高速工况下与Pu等[20]实验结果吻合较好,但在混合润滑和边界润滑状态下( $ {u_e} $= 0.1~1 m/s),摩擦系数预测结果偏离实验数据明显,最大误差为27.8%. 原因是式(15)中的载荷百分比函数 ${f_\varLambda }$是关于膜厚比 $\varLambda$的函数,根据文献[33]的研究可知,在边界润滑和混合润滑状态下,粗糙度形貌类型(如横向和径向粗糙纹理)以及纹理方向与卷吸速度的夹角对膜厚比 $\varLambda$影响较为显著,式(11)未能考虑粗糙形貌的影响. ...
重载下准双曲面齿轮传动界面润滑机理分析
2
2015
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
... 接触区压力和油膜厚度分布由雷诺方程求解得到[1, 14-15]. 为了提高计算效率,在不关注接触界面微观润滑和摩擦特性的情况下,采用赫兹接触压力近似油膜压力[16],油膜厚度计算采用Chittenden等[23]提出的等温任意速度矢量点接触中心油膜厚度公式为 ...
重载下准双曲面齿轮传动界面润滑机理分析
2
2015
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
... 接触区压力和油膜厚度分布由雷诺方程求解得到[1, 14-15]. 为了提高计算效率,在不关注接触界面微观润滑和摩擦特性的情况下,采用赫兹接触压力近似油膜压力[16],油膜厚度计算采用Chittenden等[23]提出的等温任意速度矢量点接触中心油膜厚度公式为 ...
Effect of contact path on the mixed lubrication performance, friction and contact fatigue in spiral bevel gears
2
2018
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
... 接触区压力和油膜厚度分布由雷诺方程求解得到[1, 14-15]. 为了提高计算效率,在不关注接触界面微观润滑和摩擦特性的情况下,采用赫兹接触压力近似油膜压力[16],油膜厚度计算采用Chittenden等[23]提出的等温任意速度矢量点接触中心油膜厚度公式为 ...
Prediction of mechanical gear mesh efficiency of hypoid gear pairs
2
2010
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
... 接触区压力和油膜厚度分布由雷诺方程求解得到[1, 14-15]. 为了提高计算效率,在不关注接触界面微观润滑和摩擦特性的情况下,采用赫兹接触压力近似油膜压力[16],油膜厚度计算采用Chittenden等[23]提出的等温任意速度矢量点接触中心油膜厚度公式为 ...
Improvements in the mixed elastohydrodynamic lubrication and in the efficiency of hypoid gears
1
2020
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
Prediction of friction-related power losses of hypoid gear pairs
1
2007
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
计及齿面摩擦的弧齿锥齿轮动态特性
1
2020
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
计及齿面摩擦的弧齿锥齿轮动态特性
1
2020
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
Friction and flash temperature prediction of mixed lubrication in elliptical contacts with arbitrary velocity vector
8
2016
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
... 具有卷吸速度矢量点接触摩擦系数的实验研究相对较少,Pu等[20]采用椭球−盘接触实验研究卷吸速度大小和卷吸速度夹角对点接触摩擦系数的影响,实验参数为 $ {\theta _{\text{e}}} $=22.5°, $ {R_x} $=16 mm, $ {R_y} $=45.5 mm, $ {p_{\text{h}}} $=0.73 GPa, $ {\sigma _{{\text{RMS}}}} $=0.3 μm, $ {\eta _0} $=0.08 Pa·s, $ \alpha $=2.10 ×10−8 Pa−1, $ E' $=210.0 GPa. 如图10所示研究不同热影响因素下的摩擦系数、接触区最大温升 $ \Delta {T_{{\text{f}},\max }} $以及入口区温升 $ \Delta {T_{{\text{in}}}} $随卷吸速度的变化情况,并与Pu等[20]的实验结果进行对比. 由图可知,卷吸速度在0.1 m/s~10 m/s时,摩擦系数预测结果与实验数据在变化趋势上一致. 卷吸速度大于1m/s时,接触区温升显著,忽略接触区温升导致摩擦系数预测结果偏大. 与图7不同,当转速大于3 m/s时,入口区温升对摩擦系数的影响较为明显. 考虑入口区和接触区热影响的摩擦系数在高速工况下与Pu等[20]实验结果吻合较好,但在混合润滑和边界润滑状态下( $ {u_e} $= 0.1~1 m/s),摩擦系数预测结果偏离实验数据明显,最大误差为27.8%. 原因是式(15)中的载荷百分比函数 ${f_\varLambda }$是关于膜厚比 $\varLambda$的函数,根据文献[33]的研究可知,在边界润滑和混合润滑状态下,粗糙度形貌类型(如横向和径向粗糙纹理)以及纹理方向与卷吸速度的夹角对膜厚比 $\varLambda$影响较为显著,式(11)未能考虑粗糙形貌的影响. ...
... [20]的实验结果进行对比. 由图可知,卷吸速度在0.1 m/s~10 m/s时,摩擦系数预测结果与实验数据在变化趋势上一致. 卷吸速度大于1m/s时,接触区温升显著,忽略接触区温升导致摩擦系数预测结果偏大. 与图7不同,当转速大于3 m/s时,入口区温升对摩擦系数的影响较为明显. 考虑入口区和接触区热影响的摩擦系数在高速工况下与Pu等[20]实验结果吻合较好,但在混合润滑和边界润滑状态下( $ {u_e} $= 0.1~1 m/s),摩擦系数预测结果偏离实验数据明显,最大误差为27.8%. 原因是式(15)中的载荷百分比函数 ${f_\varLambda }$是关于膜厚比 $\varLambda$的函数,根据文献[33]的研究可知,在边界润滑和混合润滑状态下,粗糙度形貌类型(如横向和径向粗糙纹理)以及纹理方向与卷吸速度的夹角对膜厚比 $\varLambda$影响较为显著,式(11)未能考虑粗糙形貌的影响. ...
... [20]实验结果吻合较好,但在混合润滑和边界润滑状态下( $ {u_e} $= 0.1~1 m/s),摩擦系数预测结果偏离实验数据明显,最大误差为27.8%. 原因是式(15)中的载荷百分比函数 ${f_\varLambda }$是关于膜厚比 $\varLambda$的函数,根据文献[33]的研究可知,在边界润滑和混合润滑状态下,粗糙度形貌类型(如横向和径向粗糙纹理)以及纹理方向与卷吸速度的夹角对膜厚比 $\varLambda$影响较为显著,式(11)未能考虑粗糙形貌的影响. ...
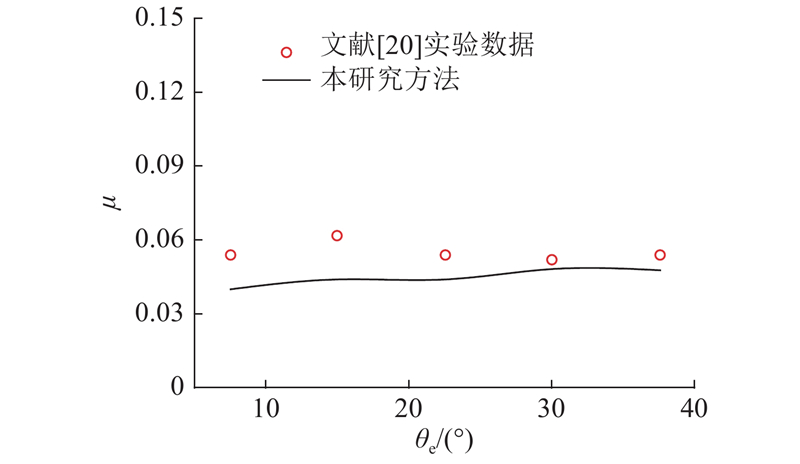
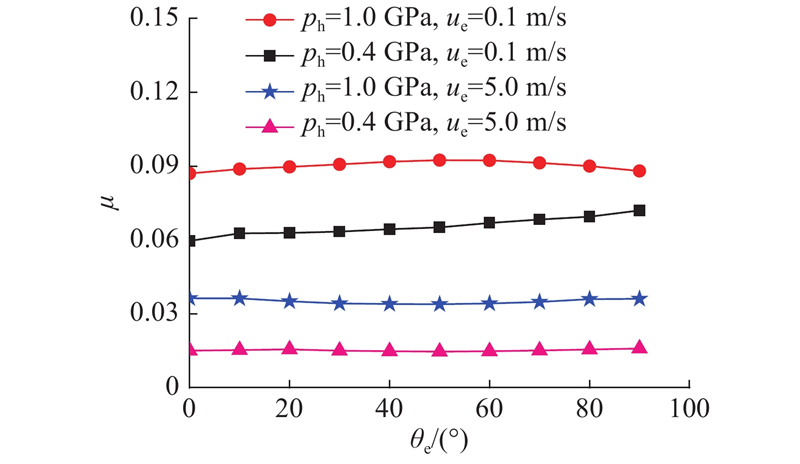
... 如图11所示,在不同卷吸速度夹角下,Pu等[20]摩擦系数实验结果和数值结果对比情况,卷吸速度 $ {u_{\text{e}}} $=1 m/s, 卷吸速度夹角 $ {\theta _{\text{e}}} $变化范围为7.5°~37.5°,其他参数与图10保持一致. 由图可知,摩擦系数随卷吸速度夹角变化没有明显的规律,且摩擦系数在当 $ {\theta _{\text{e}}} $=7.5°~37.5°时的变化不大,最大预测误差28.5%,但数值结果变化趋势与实验研究[20]一致. 图11中的相对滑动速度的大小随卷吸速度夹角变化影响着摩擦系数,且实验测试的卷吸速度夹角范围较窄. 为了研究卷吸速度夹角单一因素对摩擦系数的影响,将卷吸速度和相对滑动速度设为定值,摩擦系数随卷吸速度夹角的变化情况如图12所示. 在低速重载工况下( $ {u_{\text{e}}} $=0.1 m/s, $ {p_{\text{h}}} $=0.40 GPa),油膜厚度 $ {h_{\text{c}}} $随 $ {\theta _{\text{e}}} $增大而减小,导致摩擦系数随 $ {\theta _{\text{e}}} $增加单调递增;在重载( $ {p_{\text{h}}} $=1.0 GPa)和高速工况下( $ {u_{\text{e}}} $=5.0 m/s),受入口区和接触区热影响,摩擦系数变化趋势未表现出单调性,且摩擦系数在 $ {\theta _{\text{e}}} $= 0°~90°范围内变化不大,这与Pu等[20]的实验结论以及Wang等[34]的理论结果一致. ...
... [20]一致. 图11中的相对滑动速度的大小随卷吸速度夹角变化影响着摩擦系数,且实验测试的卷吸速度夹角范围较窄. 为了研究卷吸速度夹角单一因素对摩擦系数的影响,将卷吸速度和相对滑动速度设为定值,摩擦系数随卷吸速度夹角的变化情况如图12所示. 在低速重载工况下( $ {u_{\text{e}}} $=0.1 m/s, $ {p_{\text{h}}} $=0.40 GPa),油膜厚度 $ {h_{\text{c}}} $随 $ {\theta _{\text{e}}} $增大而减小,导致摩擦系数随 $ {\theta _{\text{e}}} $增加单调递增;在重载( $ {p_{\text{h}}} $=1.0 GPa)和高速工况下( $ {u_{\text{e}}} $=5.0 m/s),受入口区和接触区热影响,摩擦系数变化趋势未表现出单调性,且摩擦系数在 $ {\theta _{\text{e}}} $= 0°~90°范围内变化不大,这与Pu等[20]的实验结论以及Wang等[34]的理论结果一致. ...
... [20]的实验结论以及Wang等[34]的理论结果一致. ...
... (3)不同工况下,油膜厚度和摩擦系数预测结果相对实验结果(Paouris等[30]、Stahl等[12]、Pu等[20])的最大误差为分别为14.2%和28.5%,但其整体变化趋势与实验数据具有较好的一致性,摩擦系数简化计算方法的可靠性得以验证. ...
3
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
... 油膜入口区温升会降低润滑油黏度[21],影响中心油膜厚度. 入口区流体剪切率和压力较小,温升通常较低,但当卷吸速度或润滑油黏度较大时,入口区热影响较为显著[21]. 在弹流润滑状态下,Greenwood等[29]给出入口区油膜厚度方向( $ z $轴)的能量方程 ...
... [21]. 在弹流润滑状态下,Greenwood等[29]给出入口区油膜厚度方向( $ z $轴)的能量方程 ...
2
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
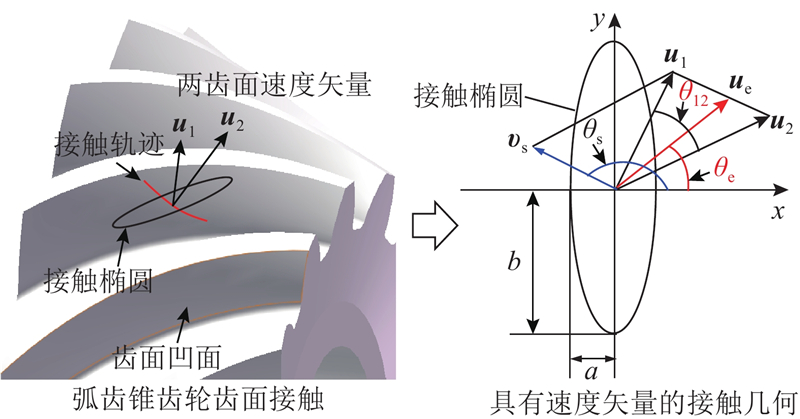
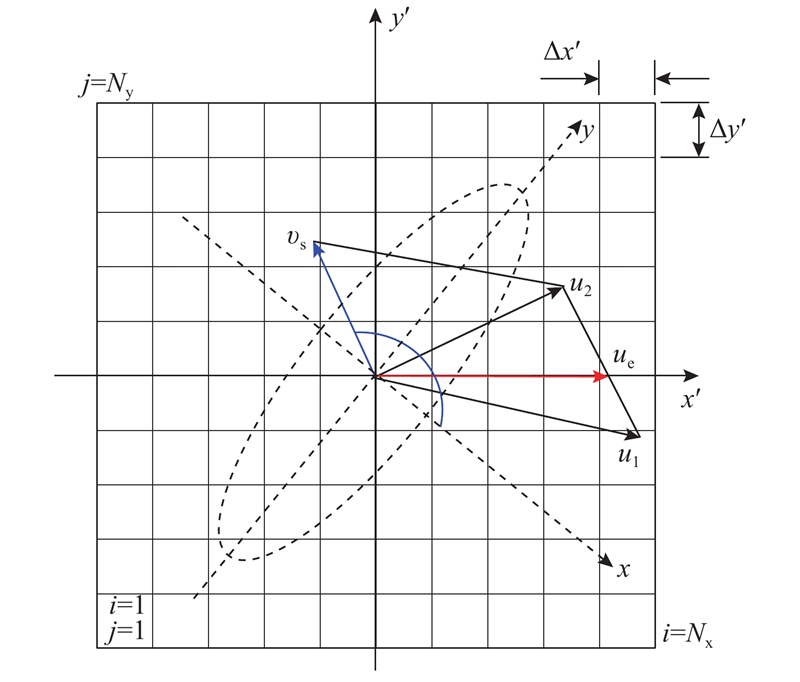
... 由图1可知,速度矢量 $ {{\boldsymbol{u}}_1} $、 $ {{\boldsymbol{u}}_2} $的大小和方向变化会引起相对滑动速度矢量 $ {{\boldsymbol{v}}_{\text{s}}} $和卷吸速度矢量 $ {{\boldsymbol{u}}_{\text{e}}} $的变化. 根据式(2),流体剪切力求解以滑动速度矢量为坐标轴方向. 以弧齿锥齿轮和准双曲面齿轮啮合为例,速度矢量 $ {{\boldsymbol{v}}_{\text{s}}} $和 $ {{\boldsymbol{u}}_{\text{e}}} $随齿面啮合位置变化[22]. Houpert[26]通过对滑动速度矢量 $ {{\boldsymbol{v}}_{\text{s}}} $沿 $ x $和 $ y $轴分解,对J-T非线性黏弹性流变模型[27]进行非线性方程组替换,提出流体剪切快速求解方法. 本研究采用类似的方法,将式(2)沿如图2所示的 $ x' $和 $ y' $轴求解.图中,Nx、Ny分别为x'、y'轴方向的网格线,则式(2)改写为 ...
2
... 润滑状态下的摩擦系数和油膜厚度预测需求解雷诺方程、膜厚方程以及流变方程等,数值过程复杂[1],难以实现此类传动或接触问题的高效分析. 王家序等[2-5]对卷吸速度与赫兹接触主轴重合的点、线接触润滑、摩擦特性进行大量的分析,提出膜厚和粗糙峰接触载荷比经验公式[6-7],实现线接触[8]和点接触[9]摩擦系数计算方法在工程上的简便应用. 卷吸速度与接触椭圆主轴成夹角的润滑和摩擦特性研究相对较少,具有代表性的如Jalali-Vahid等[10-13]的工作. 这些研究均基于雷诺方程求解,其数值计算耗时,尤其在粗糙峰接触的混合润滑状态[13-14], 难以实现弧齿锥齿轮和准双曲面齿轮传动油膜厚度和摩擦系数的高效分析[15]. 为此,Kolivand等[16]将准双曲面齿轮的点接触工况简化为线接触,Simon[17]忽略卷吸夹角的影响,Xu等[18-19]采用线接触摩擦系数经验公式. 采用线接触简化不符合点接触真实工况,忽略卷吸速度夹角和入口区温升导致膜厚度和摩擦系数预测偏差[20-21],因此目前应用于弧齿锥齿轮和准双曲面齿轮传动的摩擦系数经验公式误差较大[22]. ...
... 由图1可知,速度矢量 $ {{\boldsymbol{u}}_1} $、 $ {{\boldsymbol{u}}_2} $的大小和方向变化会引起相对滑动速度矢量 $ {{\boldsymbol{v}}_{\text{s}}} $和卷吸速度矢量 $ {{\boldsymbol{u}}_{\text{e}}} $的变化. 根据式(2),流体剪切力求解以滑动速度矢量为坐标轴方向. 以弧齿锥齿轮和准双曲面齿轮啮合为例,速度矢量 $ {{\boldsymbol{v}}_{\text{s}}} $和 $ {{\boldsymbol{u}}_{\text{e}}} $随齿面啮合位置变化[22]. Houpert[26]通过对滑动速度矢量 $ {{\boldsymbol{v}}_{\text{s}}} $沿 $ x $和 $ y $轴分解,对J-T非线性黏弹性流变模型[27]进行非线性方程组替换,提出流体剪切快速求解方法. 本研究采用类似的方法,将式(2)沿如图2所示的 $ x' $和 $ y' $轴求解.图中,Nx、Ny分别为x'、y'轴方向的网格线,则式(2)改写为 ...
A theoretical analysis of the isothermal elastohydrodynamic lubrication of concentrated contacts. II. General case, with lubricant entrainment along either principal axis of the Hertzian contact ellipse or at some intermediate angle
5
1985
... 接触区压力和油膜厚度分布由雷诺方程求解得到[1, 14-15]. 为了提高计算效率,在不关注接触界面微观润滑和摩擦特性的情况下,采用赫兹接触压力近似油膜压力[16],油膜厚度计算采用Chittenden等[23]提出的等温任意速度矢量点接触中心油膜厚度公式为 ...
... 式中:Q为无量纲载荷, $Q = {W \mathord{\left/ {\vphantom {W {\left( {E'R_{\text{e}}^2} \right)}}} \right. } {\left( {E'R_{\text{e}}^2} \right)}}$;Ue为无量纲卷吸速度, $ {U_{\text{e}}} = {{{\eta _0}\left| {{{\boldsymbol{u}}_{\text{e}}}} \right|} \mathord{\left/ {\vphantom {{{\eta _0}\left| {{{\boldsymbol{u}}_{\text{e}}}} \right|} {\left( {E'{R_{\text{e}}}} \right)}}} \right. } {\left( {E'{R_{\text{e}}}} \right)}} $;G为无量纲材料参数, $ G = \alpha E' $; $ W $为接触载荷; $ \alpha $为黏压系数; $ {\eta _0} $为润滑油的环境黏度; $ E' $为等效弹性模量;等效曲率半径 $ {R_{\text{s}}} $、 $ {R_{\text{e}}} $与综合曲率半径 $ {R_x} $、 $ {R_y} $相关,定义见文献 [23]. ...
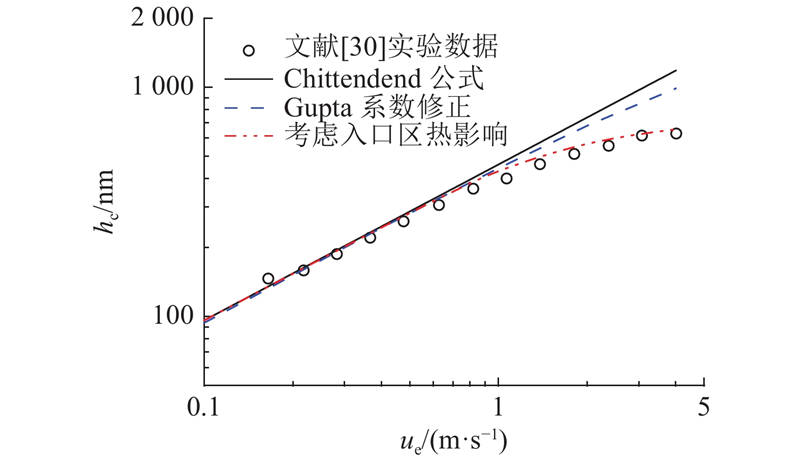
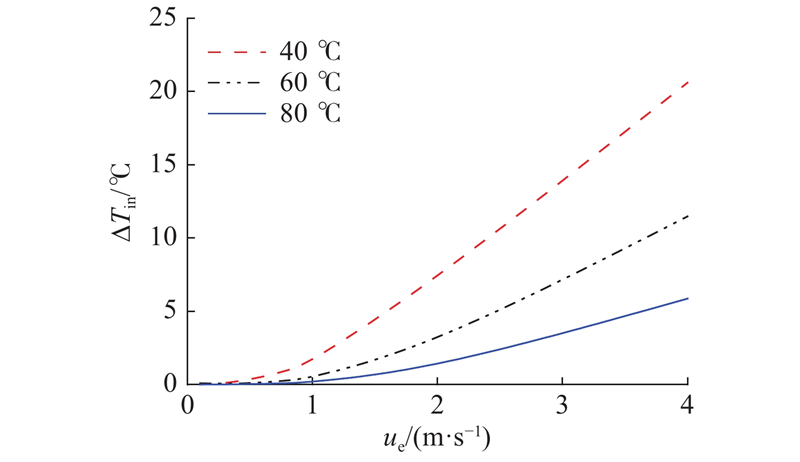
... 如图5所示对比Chittenden公式[23]、Gupta系数修正[31]以及考虑入口区温升对油膜厚度的预测情况. 测试载荷为W=17 N,滑滚比为SR=0.0. 由图可知Chittenden公式的膜厚预测结果随卷吸速度ue变化趋势与文献[30]的实验结果一致,在高速工况下(大于1 m/s时),该公式预测结果与实验数据偏差较大. 当卷吸速度为4 m/s时,Gupta系数修正和考虑入口区热影响使油膜厚度从1183.79 nm分别减小至988.91 nm和656.63 nm (实验结果为628.38 nm). 若考虑入口区热影响,油膜厚度最大预测误差为14.2%. 如图6所示为润滑油在不同温度下入口区的温升情况,工况与图5保持一致. 入口区温升随卷吸速度增大而升高,当油温在40 ℃时,卷吸速度从1 m/s变化至4 m/s,入口区温升由1.6 ℃升高至21.0 ℃,因此在高速工况下,入口区温升对中心油膜厚度影响较为显著. 由于入口温升与 $ h_{\text{c}}^4 $成正比,润滑油温度越高导致油膜厚度越低,则入口区温升越小,这与Paouris等[30]的研究结果一致. ...
... 为了验证具有卷吸速度夹角的点接触油膜厚度预测结果,给出2种工况下油膜厚度随卷吸夹角 $ {\theta _{\text{e}}} $的变化趋势,并与Stahl等[12]的实验结果进行对比,如图9所示. 测试夹角 $ {\theta _{\text{e}}} $分别为0°、7.63°、16.10°、26.57°,润滑油参数与文献[30]一致,工况1的参数为 $ {R_x} $=12.7 mm, $ {R_y} $=31.6 mm, $ {p_{\text{h}}} $=0.512 GPa, $ {u_{\text{e}}} $=0.5 m/s, $ E' $ =123.90 GPa;工况2的参数为 $ {R_x} $=4.0 mm, $ {R_y} $=12.7 mm, $ {p_{\text{h}}} $=1.03 GPa, $ {u_e} $=0.3 m/s, $ E' $=123.90 GPa. 由图可知,当卷吸速度为0.5 m/s时,中心油膜厚度随着卷吸速度夹角 $ {\theta _{\text{e}}} $增大而减小. Chittenden公式[23]与Gupta系数修正[31]得到的油膜厚度与实验结果趋势一致,但考虑入口区热影响,迭代得到的油膜厚度与Stahl等[12]的实验结果更为吻合. 当卷吸速度减小到0.3m/s时(工况2),入口区热影响不显著,3种情况下的油膜预测值与实验数据相近. 图9中的油膜厚度预测值误差不超过5.0%,为了进一步验证更大卷吸速度夹角下油膜厚度的预测情况,将本研究数值结果与已有研究结果进行比较,如表1所示. 计算参数为 $ {R_x} $=20.0 mm, $ {R_y} $=56.8 mm, $ {p_{\text{h}}} $=0.3 GPa, $ {u_e} $=0.57 m/s, $ E' $=228.3 GPa, $ {\eta _0} $=0.08 Pa·s, $ \alpha $=2.1×10−8 Pa−1. 由表1可知,在卷吸速度夹角0~90°,油膜厚度随卷吸速度夹角增大而减小,由于雷诺方程数值求解方法不同,文献中的中心油膜厚度有一定的差异. 考虑入口区热影响的油膜厚预测结果与文献[11]、[13]、[33]的结论接近,相比文献[13]结果的最大偏差为7.3%. ...
... (1)在高速工况时,任意卷吸速度夹角下, Chittendend公式[23]与Gupta系数修正[31]得到的中心油膜厚度偏大,考虑入口区温升显著提高油膜厚度的预测精度. ...
A rheological model for elastohydrodynamic contacts based on primary laboratory data
1
1979
... 流体的极限剪切应力 $ {\tau _{\text{L}}} $和黏度 $ \eta $受温度的影响,采用广泛应用的黏弹性非牛顿流体模型求解流体剪切力,表达式[24]为 ...
A computer program package for the prediction of EHL and mixed lubrication characteristics, friction, subsurface stresses and flash temperatures based on measured 3-D surface roughness
5
2001
... 式中: $ {\tau _{\text{L}}} $、 $ {G_\infty } $分别为极限切应力、极限切变模量,均可表示为压力 $ p $和温度 $ T $的函数,表达式见文献[25]. ...
... 式中: $ A $、 $ B $、 $ C $为方程系数, $A = {{\left| {{{\boldsymbol{u}}_{\text{e}}}} \right|{\tau _{\text{L}}}}}/{{{(G_\infty }\Delta x'{{\dot \gamma }_x)}}}$, $B = $ $ {{{\tau _{\text{L}}}}}/{{[\eta {{\dot \gamma }_x} {(1 + F_{xy}^2)^{0.5}]} }}$, $C = 1 + {{\left| {{{\boldsymbol{u}}_{\text{e}}}} \right|\tau _x^ * }}/{{{(G_\infty }\Delta x'{{\dot \gamma }_x)}}}$. 式(6)包含黏度,黏度为压力 $ p $和温度 $ {T_{\text{f}}} $的函数,表达式[25]为 ...
... 式中: $ {\mu _{\text{h}}} $为全膜润滑状态下的摩擦系数, ${f_\varLambda }$为油膜承担载荷比函数,表达式[25, 28]为 ...
... 具有任意速度矢量的点接触不可避免地存在相对滑动,接触区压力以及油膜剪切率较大时,接触区温升显著,影响流体极限剪切应力. 与流体剪切耦合的温升求解采用快速移动热源法,计算式[25]为 ...
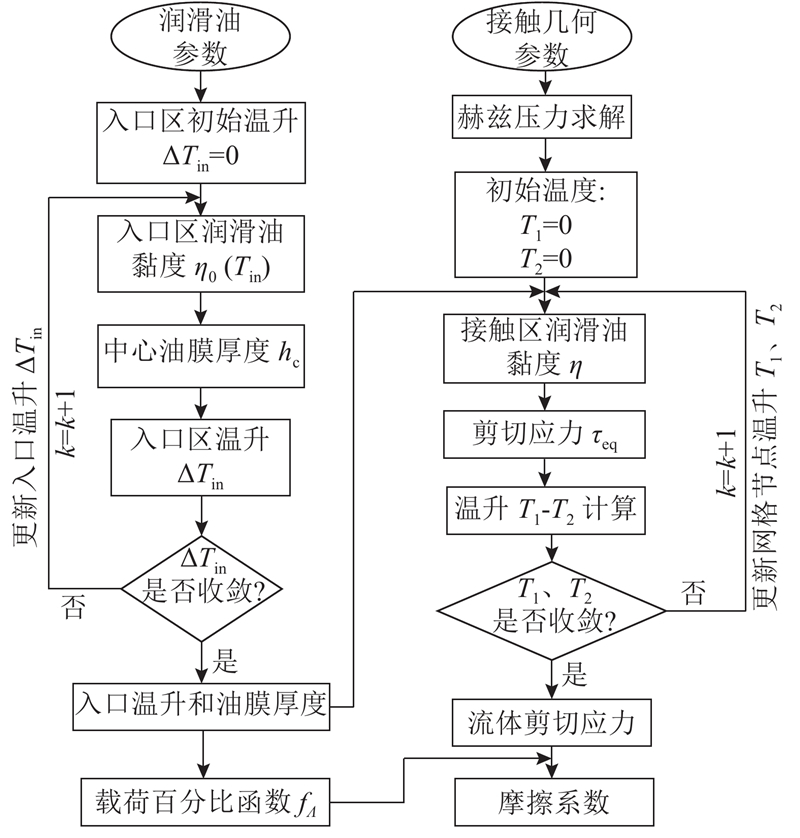
... 式中: $ {T_{1,i + 1}} $、 $ {T_{2,i + 1}} $为待求解温度, 润滑油黏度和极限剪切应力是关于温度的函数,因此摩擦系数与温升的求解要相互迭代[25],温度求解收敛后输出结果为流体切应力 $ {\tau _{{\text{eq}}}} $和温升 $ {T_1} $、 $ {T_2} $. ...
Fast numerical calculations of EHD sliding traction forces; application to rolling bearings
1
1985
... 由图1可知,速度矢量 $ {{\boldsymbol{u}}_1} $、 $ {{\boldsymbol{u}}_2} $的大小和方向变化会引起相对滑动速度矢量 $ {{\boldsymbol{v}}_{\text{s}}} $和卷吸速度矢量 $ {{\boldsymbol{u}}_{\text{e}}} $的变化. 根据式(2),流体剪切力求解以滑动速度矢量为坐标轴方向. 以弧齿锥齿轮和准双曲面齿轮啮合为例,速度矢量 $ {{\boldsymbol{v}}_{\text{s}}} $和 $ {{\boldsymbol{u}}_{\text{e}}} $随齿面啮合位置变化[22]. Houpert[26]通过对滑动速度矢量 $ {{\boldsymbol{v}}_{\text{s}}} $沿 $ x $和 $ y $轴分解,对J-T非线性黏弹性流变模型[27]进行非线性方程组替换,提出流体剪切快速求解方法. 本研究采用类似的方法,将式(2)沿如图2所示的 $ x' $和 $ y' $轴求解.图中,Nx、Ny分别为x'、y'轴方向的网格线,则式(2)改写为 ...
Shear behaviour of elastohydrodynamic oil films
1
1977
... 由图1可知,速度矢量 $ {{\boldsymbol{u}}_1} $、 $ {{\boldsymbol{u}}_2} $的大小和方向变化会引起相对滑动速度矢量 $ {{\boldsymbol{v}}_{\text{s}}} $和卷吸速度矢量 $ {{\boldsymbol{u}}_{\text{e}}} $的变化. 根据式(2),流体剪切力求解以滑动速度矢量为坐标轴方向. 以弧齿锥齿轮和准双曲面齿轮啮合为例,速度矢量 $ {{\boldsymbol{v}}_{\text{s}}} $和 $ {{\boldsymbol{u}}_{\text{e}}} $随齿面啮合位置变化[22]. Houpert[26]通过对滑动速度矢量 $ {{\boldsymbol{v}}_{\text{s}}} $沿 $ x $和 $ y $轴分解,对J-T非线性黏弹性流变模型[27]进行非线性方程组替换,提出流体剪切快速求解方法. 本研究采用类似的方法,将式(2)沿如图2所示的 $ x' $和 $ y' $轴求解.图中,Nx、Ny分别为x'、y'轴方向的网格线,则式(2)改写为 ...
Global and local analysis of gear scuffing tests using a mixed film lubrication model
2
2008
... 混合润滑状态下流体剪切与粗糙峰接触共存,接触区的边界摩擦系数 ${\mu {\rm{_b}}}$通过实验确定,本研究取 ${\mu {\rm{_b}}}$=0.13. Castro等[28]提出基于载荷分配的摩擦系数计算方法,表达式为 ...
... 式中: $ {\mu _{\text{h}}} $为全膜润滑状态下的摩擦系数, ${f_\varLambda }$为油膜承担载荷比函数,表达式[25, 28]为 ...
Inlet shear heating in elastohydrodynamic lubrication
1
1973
... 油膜入口区温升会降低润滑油黏度[21],影响中心油膜厚度. 入口区流体剪切率和压力较小,温升通常较低,但当卷吸速度或润滑油黏度较大时,入口区热影响较为显著[21]. 在弹流润滑状态下,Greenwood等[29]给出入口区油膜厚度方向( $ z $轴)的能量方程 ...
An analytical approach for prediction of elastohydrodynamic friction with inlet shear heating and starvation
8
2016
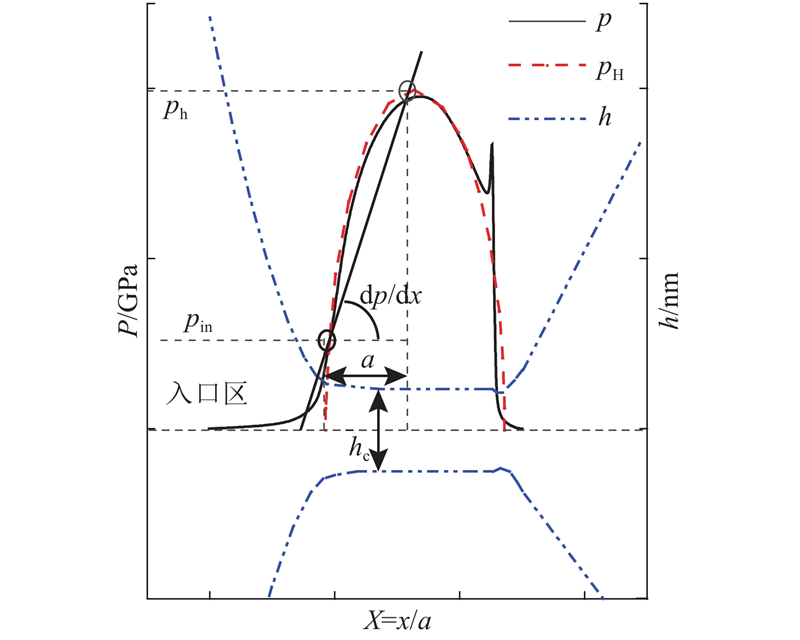
... 式中: $ {{{\text{d}}p} \mathord{\left/ {\vphantom {{{\text{d}}p} {{\text{d}}x}}} \right. } {{\text{d}}x}} $为压力梯度,采用如图3所示的入口区流体压力 $ {p_{{\text{in}}}} $和最大赫兹压力 $ {p_{\text{h}}} $近似计算. 图中,pH为赫兹接触压力分布;a为赫兹接触椭圆短半轴长度,根据文献[30]可知,入口区的压力 $ {p_{{\text{in}}}} \approx {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. } \alpha } $,即(dp/dx)|x=−a ≈ (ph−pin)/a. ...
... 为了验证摩擦系数简化算法在卷吸速度矢量与接触椭圆短轴重合情况下的正确性,对不同工况下点接触油膜厚度和摩擦系数进行预测,并与文献[30]中的球−盘实验结果进行对比. 算例中润滑油和材料参数与文献[30]的实验参数保持一致,主要参数为 $ {R_x} $= $ {R_y} $=9.525 mm,均方根粗糙度 $ {\sigma _{{\text{RMS}}}} $=3.25 nm, $ {\eta _0} $=0.092 Pa·s,黏压系数 $ \alpha $=1.61 ×10−8 Pa−1,等效弹性模量 $ E' $=116.90 GPa. ...
... ]中的球−盘实验结果进行对比. 算例中润滑油和材料参数与文献[30]的实验参数保持一致,主要参数为 $ {R_x} $= $ {R_y} $=9.525 mm,均方根粗糙度 $ {\sigma _{{\text{RMS}}}} $=3.25 nm, $ {\eta _0} $=0.092 Pa·s,黏压系数 $ \alpha $=1.61 ×10−8 Pa−1,等效弹性模量 $ E' $=116.90 GPa. ...
... 如图5所示对比Chittenden公式[23]、Gupta系数修正[31]以及考虑入口区温升对油膜厚度的预测情况. 测试载荷为W=17 N,滑滚比为SR=0.0. 由图可知Chittenden公式的膜厚预测结果随卷吸速度ue变化趋势与文献[30]的实验结果一致,在高速工况下(大于1 m/s时),该公式预测结果与实验数据偏差较大. 当卷吸速度为4 m/s时,Gupta系数修正和考虑入口区热影响使油膜厚度从1183.79 nm分别减小至988.91 nm和656.63 nm (实验结果为628.38 nm). 若考虑入口区热影响,油膜厚度最大预测误差为14.2%. 如图6所示为润滑油在不同温度下入口区的温升情况,工况与图5保持一致. 入口区温升随卷吸速度增大而升高,当油温在40 ℃时,卷吸速度从1 m/s变化至4 m/s,入口区温升由1.6 ℃升高至21.0 ℃,因此在高速工况下,入口区温升对中心油膜厚度影响较为显著. 由于入口温升与 $ h_{\text{c}}^4 $成正比,润滑油温度越高导致油膜厚度越低,则入口区温升越小,这与Paouris等[30]的研究结果一致. ...
... [30]的研究结果一致. ...
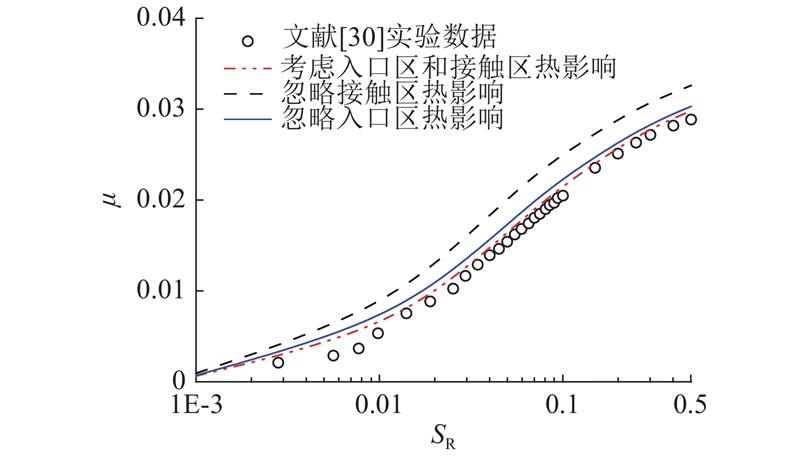
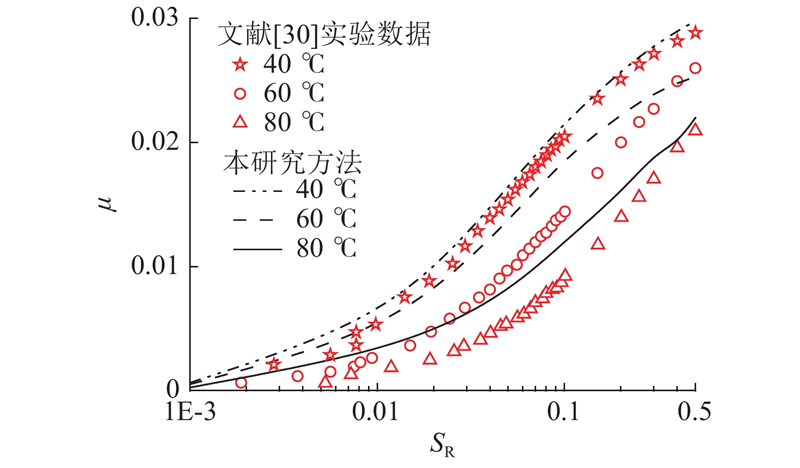
... 为了说明接触区温升和入口区温升对摩擦系数的影响,给出不同热影响因素下的摩擦系数并与文献[30]的实验结果进行对比如,图7所示. 测试工况为W=20 N, $ {u_{\text{e}}} $=2.5 m/s, $ {p_{\text{h}}} $=0.512 GPa,润滑油温度为40 ℃. 与油膜厚度变化趋势不同,入口区温升对摩擦系数影响较小,当滑滚比大于0.1时,忽略接触区温升会导致摩擦系数预测结果偏大,考虑热影响的摩擦系数与实验结果的最大误差为4.1%. 如图8所示为不同润滑油温度下摩擦系数预测结果,其他工况与图5保持一致. 由图可知,温度越大,摩擦系数越小,在60 ℃和80 ℃下的摩擦系数预测结果仍与实验结果具有良好的一致性. ...
... 为了验证具有卷吸速度夹角的点接触油膜厚度预测结果,给出2种工况下油膜厚度随卷吸夹角 $ {\theta _{\text{e}}} $的变化趋势,并与Stahl等[12]的实验结果进行对比,如图9所示. 测试夹角 $ {\theta _{\text{e}}} $分别为0°、7.63°、16.10°、26.57°,润滑油参数与文献[30]一致,工况1的参数为 $ {R_x} $=12.7 mm, $ {R_y} $=31.6 mm, $ {p_{\text{h}}} $=0.512 GPa, $ {u_{\text{e}}} $=0.5 m/s, $ E' $ =123.90 GPa;工况2的参数为 $ {R_x} $=4.0 mm, $ {R_y} $=12.7 mm, $ {p_{\text{h}}} $=1.03 GPa, $ {u_e} $=0.3 m/s, $ E' $=123.90 GPa. 由图可知,当卷吸速度为0.5 m/s时,中心油膜厚度随着卷吸速度夹角 $ {\theta _{\text{e}}} $增大而减小. Chittenden公式[23]与Gupta系数修正[31]得到的油膜厚度与实验结果趋势一致,但考虑入口区热影响,迭代得到的油膜厚度与Stahl等[12]的实验结果更为吻合. 当卷吸速度减小到0.3m/s时(工况2),入口区热影响不显著,3种情况下的油膜预测值与实验数据相近. 图9中的油膜厚度预测值误差不超过5.0%,为了进一步验证更大卷吸速度夹角下油膜厚度的预测情况,将本研究数值结果与已有研究结果进行比较,如表1所示. 计算参数为 $ {R_x} $=20.0 mm, $ {R_y} $=56.8 mm, $ {p_{\text{h}}} $=0.3 GPa, $ {u_e} $=0.57 m/s, $ E' $=228.3 GPa, $ {\eta _0} $=0.08 Pa·s, $ \alpha $=2.1×10−8 Pa−1. 由表1可知,在卷吸速度夹角0~90°,油膜厚度随卷吸速度夹角增大而减小,由于雷诺方程数值求解方法不同,文献中的中心油膜厚度有一定的差异. 考虑入口区热影响的油膜厚预测结果与文献[11]、[13]、[33]的结论接近,相比文献[13]结果的最大偏差为7.3%. ...
... (3)不同工况下,油膜厚度和摩擦系数预测结果相对实验结果(Paouris等[30]、Stahl等[12]、Pu等[20])的最大误差为分别为14.2%和28.5%,但其整体变化趋势与实验数据具有较好的一致性,摩擦系数简化计算方法的可靠性得以验证. ...
Viscoelastic effects in MIL-L-7808-type lubricant, part I: analytical formulation
4
1992
... Gupta等[31]通过研究入口区温升与油膜厚度,提出应用更为简便的油膜厚度系数 $ {\varphi _{\text{T}}} $修正等温油膜厚度 $ {h_{{\text{c}},{\text{iso}}}} $,即 ...
... 如图5所示对比Chittenden公式[23]、Gupta系数修正[31]以及考虑入口区温升对油膜厚度的预测情况. 测试载荷为W=17 N,滑滚比为SR=0.0. 由图可知Chittenden公式的膜厚预测结果随卷吸速度ue变化趋势与文献[30]的实验结果一致,在高速工况下(大于1 m/s时),该公式预测结果与实验数据偏差较大. 当卷吸速度为4 m/s时,Gupta系数修正和考虑入口区热影响使油膜厚度从1183.79 nm分别减小至988.91 nm和656.63 nm (实验结果为628.38 nm). 若考虑入口区热影响,油膜厚度最大预测误差为14.2%. 如图6所示为润滑油在不同温度下入口区的温升情况,工况与图5保持一致. 入口区温升随卷吸速度增大而升高,当油温在40 ℃时,卷吸速度从1 m/s变化至4 m/s,入口区温升由1.6 ℃升高至21.0 ℃,因此在高速工况下,入口区温升对中心油膜厚度影响较为显著. 由于入口温升与 $ h_{\text{c}}^4 $成正比,润滑油温度越高导致油膜厚度越低,则入口区温升越小,这与Paouris等[30]的研究结果一致. ...
... 为了验证具有卷吸速度夹角的点接触油膜厚度预测结果,给出2种工况下油膜厚度随卷吸夹角 $ {\theta _{\text{e}}} $的变化趋势,并与Stahl等[12]的实验结果进行对比,如图9所示. 测试夹角 $ {\theta _{\text{e}}} $分别为0°、7.63°、16.10°、26.57°,润滑油参数与文献[30]一致,工况1的参数为 $ {R_x} $=12.7 mm, $ {R_y} $=31.6 mm, $ {p_{\text{h}}} $=0.512 GPa, $ {u_{\text{e}}} $=0.5 m/s, $ E' $ =123.90 GPa;工况2的参数为 $ {R_x} $=4.0 mm, $ {R_y} $=12.7 mm, $ {p_{\text{h}}} $=1.03 GPa, $ {u_e} $=0.3 m/s, $ E' $=123.90 GPa. 由图可知,当卷吸速度为0.5 m/s时,中心油膜厚度随着卷吸速度夹角 $ {\theta _{\text{e}}} $增大而减小. Chittenden公式[23]与Gupta系数修正[31]得到的油膜厚度与实验结果趋势一致,但考虑入口区热影响,迭代得到的油膜厚度与Stahl等[12]的实验结果更为吻合. 当卷吸速度减小到0.3m/s时(工况2),入口区热影响不显著,3种情况下的油膜预测值与实验数据相近. 图9中的油膜厚度预测值误差不超过5.0%,为了进一步验证更大卷吸速度夹角下油膜厚度的预测情况,将本研究数值结果与已有研究结果进行比较,如表1所示. 计算参数为 $ {R_x} $=20.0 mm, $ {R_y} $=56.8 mm, $ {p_{\text{h}}} $=0.3 GPa, $ {u_e} $=0.57 m/s, $ E' $=228.3 GPa, $ {\eta _0} $=0.08 Pa·s, $ \alpha $=2.1×10−8 Pa−1. 由表1可知,在卷吸速度夹角0~90°,油膜厚度随卷吸速度夹角增大而减小,由于雷诺方程数值求解方法不同,文献中的中心油膜厚度有一定的差异. 考虑入口区热影响的油膜厚预测结果与文献[11]、[13]、[33]的结论接近,相比文献[13]结果的最大偏差为7.3%. ...
... (1)在高速工况时,任意卷吸速度夹角下, Chittendend公式[23]与Gupta系数修正[31]得到的中心油膜厚度偏大,考虑入口区温升显著提高油膜厚度的预测精度. ...
Effect of arbitrary entrainment angle in elastohydrodynamic lubrication elliptical and circular contacts
0
2020
Effect of surface topography associated with arbitrary velocity direction on the lubrication film thickness in elliptical contacts
3
2018
... 为了验证具有卷吸速度夹角的点接触油膜厚度预测结果,给出2种工况下油膜厚度随卷吸夹角 $ {\theta _{\text{e}}} $的变化趋势,并与Stahl等[12]的实验结果进行对比,如图9所示. 测试夹角 $ {\theta _{\text{e}}} $分别为0°、7.63°、16.10°、26.57°,润滑油参数与文献[30]一致,工况1的参数为 $ {R_x} $=12.7 mm, $ {R_y} $=31.6 mm, $ {p_{\text{h}}} $=0.512 GPa, $ {u_{\text{e}}} $=0.5 m/s, $ E' $ =123.90 GPa;工况2的参数为 $ {R_x} $=4.0 mm, $ {R_y} $=12.7 mm, $ {p_{\text{h}}} $=1.03 GPa, $ {u_e} $=0.3 m/s, $ E' $=123.90 GPa. 由图可知,当卷吸速度为0.5 m/s时,中心油膜厚度随着卷吸速度夹角 $ {\theta _{\text{e}}} $增大而减小. Chittenden公式[23]与Gupta系数修正[31]得到的油膜厚度与实验结果趋势一致,但考虑入口区热影响,迭代得到的油膜厚度与Stahl等[12]的实验结果更为吻合. 当卷吸速度减小到0.3m/s时(工况2),入口区热影响不显著,3种情况下的油膜预测值与实验数据相近. 图9中的油膜厚度预测值误差不超过5.0%,为了进一步验证更大卷吸速度夹角下油膜厚度的预测情况,将本研究数值结果与已有研究结果进行比较,如表1所示. 计算参数为 $ {R_x} $=20.0 mm, $ {R_y} $=56.8 mm, $ {p_{\text{h}}} $=0.3 GPa, $ {u_e} $=0.57 m/s, $ E' $=228.3 GPa, $ {\eta _0} $=0.08 Pa·s, $ \alpha $=2.1×10−8 Pa−1. 由表1可知,在卷吸速度夹角0~90°,油膜厚度随卷吸速度夹角增大而减小,由于雷诺方程数值求解方法不同,文献中的中心油膜厚度有一定的差异. 考虑入口区热影响的油膜厚预测结果与文献[11]、[13]、[33]的结论接近,相比文献[13]结果的最大偏差为7.3%. ...
... Central oil film thickness corresponding to entrainment angle in different calculation methods
Tab.1 | 计算方法 | hc/nm |
| θe= 0° | θe= 45° | θe= 90° |
| 文献[11] | 495.3 | 440.0 | 375.3 |
| 文献[33] | 457.0 | 419.0 | 393.0 |
| 文献[13] | 457.0 | 415.0 | 357.8 |
| 本研究 | 461.5 | 429.9 | 383.2 |
具有卷吸速度矢量点接触摩擦系数的实验研究相对较少,Pu等[20]采用椭球−盘接触实验研究卷吸速度大小和卷吸速度夹角对点接触摩擦系数的影响,实验参数为 $ {\theta _{\text{e}}} $=22.5°, $ {R_x} $=16 mm, $ {R_y} $=45.5 mm, $ {p_{\text{h}}} $=0.73 GPa, $ {\sigma _{{\text{RMS}}}} $=0.3 μm, $ {\eta _0} $=0.08 Pa·s, $ \alpha $=2.10 ×10−8 Pa−1, $ E' $=210.0 GPa. 如图10所示研究不同热影响因素下的摩擦系数、接触区最大温升 $ \Delta {T_{{\text{f}},\max }} $以及入口区温升 $ \Delta {T_{{\text{in}}}} $随卷吸速度的变化情况,并与Pu等[20]的实验结果进行对比. 由图可知,卷吸速度在0.1 m/s~10 m/s时,摩擦系数预测结果与实验数据在变化趋势上一致. 卷吸速度大于1m/s时,接触区温升显著,忽略接触区温升导致摩擦系数预测结果偏大. 与图7不同,当转速大于3 m/s时,入口区温升对摩擦系数的影响较为明显. 考虑入口区和接触区热影响的摩擦系数在高速工况下与Pu等[20]实验结果吻合较好,但在混合润滑和边界润滑状态下( $ {u_e} $= 0.1~1 m/s),摩擦系数预测结果偏离实验数据明显,最大误差为27.8%. 原因是式(15)中的载荷百分比函数 ${f_\varLambda }$是关于膜厚比 $\varLambda$的函数,根据文献[33]的研究可知,在边界润滑和混合润滑状态下,粗糙度形貌类型(如横向和径向粗糙纹理)以及纹理方向与卷吸速度的夹角对膜厚比 $\varLambda$影响较为显著,式(11)未能考虑粗糙形貌的影响. ...
... 具有卷吸速度矢量点接触摩擦系数的实验研究相对较少,Pu等[20]采用椭球−盘接触实验研究卷吸速度大小和卷吸速度夹角对点接触摩擦系数的影响,实验参数为 $ {\theta _{\text{e}}} $=22.5°, $ {R_x} $=16 mm, $ {R_y} $=45.5 mm, $ {p_{\text{h}}} $=0.73 GPa, $ {\sigma _{{\text{RMS}}}} $=0.3 μm, $ {\eta _0} $=0.08 Pa·s, $ \alpha $=2.10 ×10−8 Pa−1, $ E' $=210.0 GPa. 如图10所示研究不同热影响因素下的摩擦系数、接触区最大温升 $ \Delta {T_{{\text{f}},\max }} $以及入口区温升 $ \Delta {T_{{\text{in}}}} $随卷吸速度的变化情况,并与Pu等[20]的实验结果进行对比. 由图可知,卷吸速度在0.1 m/s~10 m/s时,摩擦系数预测结果与实验数据在变化趋势上一致. 卷吸速度大于1m/s时,接触区温升显著,忽略接触区温升导致摩擦系数预测结果偏大. 与图7不同,当转速大于3 m/s时,入口区温升对摩擦系数的影响较为明显. 考虑入口区和接触区热影响的摩擦系数在高速工况下与Pu等[20]实验结果吻合较好,但在混合润滑和边界润滑状态下( $ {u_e} $= 0.1~1 m/s),摩擦系数预测结果偏离实验数据明显,最大误差为27.8%. 原因是式(15)中的载荷百分比函数 ${f_\varLambda }$是关于膜厚比 $\varLambda$的函数,根据文献[33]的研究可知,在边界润滑和混合润滑状态下,粗糙度形貌类型(如横向和径向粗糙纹理)以及纹理方向与卷吸速度的夹角对膜厚比 $\varLambda$影响较为显著,式(11)未能考虑粗糙形貌的影响. ...
On the surface dimple phenomena in elliptical TEHL contacts with arbitrary entrainment
1
2003
... 如图11所示,在不同卷吸速度夹角下,Pu等[20]摩擦系数实验结果和数值结果对比情况,卷吸速度 $ {u_{\text{e}}} $=1 m/s, 卷吸速度夹角 $ {\theta _{\text{e}}} $变化范围为7.5°~37.5°,其他参数与图10保持一致. 由图可知,摩擦系数随卷吸速度夹角变化没有明显的规律,且摩擦系数在当 $ {\theta _{\text{e}}} $=7.5°~37.5°时的变化不大,最大预测误差28.5%,但数值结果变化趋势与实验研究[20]一致. 图11中的相对滑动速度的大小随卷吸速度夹角变化影响着摩擦系数,且实验测试的卷吸速度夹角范围较窄. 为了研究卷吸速度夹角单一因素对摩擦系数的影响,将卷吸速度和相对滑动速度设为定值,摩擦系数随卷吸速度夹角的变化情况如图12所示. 在低速重载工况下( $ {u_{\text{e}}} $=0.1 m/s, $ {p_{\text{h}}} $=0.40 GPa),油膜厚度 $ {h_{\text{c}}} $随 $ {\theta _{\text{e}}} $增大而减小,导致摩擦系数随 $ {\theta _{\text{e}}} $增加单调递增;在重载( $ {p_{\text{h}}} $=1.0 GPa)和高速工况下( $ {u_{\text{e}}} $=5.0 m/s),受入口区和接触区热影响,摩擦系数变化趋势未表现出单调性,且摩擦系数在 $ {\theta _{\text{e}}} $= 0°~90°范围内变化不大,这与Pu等[20]的实验结论以及Wang等[34]的理论结果一致. ...