(15) $ {C_{ij,k}} = \frac{{{A_{ij,k}}}}{{{T_{ij,{{d}}}}}}(\cos\; {\varphi _{ij,k}} + {\rm{i}}\sin {\varphi _{ij,k}});\;k = 1,2, \cdot \cdot \cdot ,{N \mathord{\left/ {\vphantom {N 2}} \right. } 2} + 1 .$
(18) $ {\phi _{ij,k}} = {\phi _{i{1},k}}(1 + {\mu _{ij,k}});\; k = 1,2, \cdot \cdot \cdot ,{N_{ij}}{,_{{\rm{fc}}}}. $
[1]
廖文义, 罗俊雄, 万绚. 隔震桥梁承受近断层地震之反应分析[J]. 地震工程与工程振动, 2001, 21(4): 102-108.
[本文引用: 1]
LIAO Wen-yi, LUO Jun-xiong, WAN Xuan. Responses of isolated bridges subjected to near-fault ground motions [J], Earthquake Engineering and Engineering Vibration , 2001, 21(4): 102-108.
[本文引用: 1]
[2]
JONSSON M H, BESSASON B, HAFLIDASON E Earthquake response of a base-isolated bridge subjected to strong near-fault ground motion
[J]. Soil Dynamics and Earthquake Engineering , 2010 , 30 (6 ): 447 - 455
DOI:10.1016/j.soildyn.2010.01.001
[3]
李小军, 贺秋梅, 亓兴军 地震动速度脉冲对大跨斜拉桥减震控制的影响
[J]. 应用基础与工程科学学报 , 2012 , 20 (2 ): 272 - 285
DOI:10.3969/j.issn.1005-0930.2012.02.011
LI Xiao-jun, HE Qiu-mei, QI Xing-jun Seismic mitigation control effects of long-span cable-stayed bridges to ground motions with velocity pulse
[J]. Journal of Basic Science and Engineering , 2012 , 20 (2 ): 272 - 285
DOI:10.3969/j.issn.1005-0930.2012.02.011
[4]
魏红一, 逯宗典, 王志强 近场简支梁铅芯橡胶支座隔震特性分析
[J]. 同济大学学报:自然科学版 , 2010 , 38 (1 ): 39 - 44
URL
WEI Hong-yi, LU Zong-dian, WANG Zhi-qiang Isolation characteristic analysis of simple supported bridge to near fault ground motions
[J]. Journal of Tongji University: Natural Science , 2010 , 38 (1 ): 39 - 44
URL
[5]
ZHONG J, JIANG L W, PANG Y T, et al Near-fault seismic risk assessment of simply supported bridges
[J]. Earthquake Spectra , 2020 , 36 (4 ): 1645 - 1669
DOI:10.1177/8755293020935145
[6]
CHWN X, LI J Z, GUAN Z G Fragility analysis of tall pier bridges subjected to near-fault pulse-like ground motions
[J]. Structure and Infrastructure Engineering , 2020 , 16 (8 ): 1082 - 1095
DOI:10.1080/15732479.2019.1683589
[本文引用: 1]
[8]
BOORE D M Stochastic simulation of high-frequency ground motions based on seismological models of the radiated spectra
[J]. Bulletin of the Seismological Society of America , 1983 , 73 (6 ): 1865 - 1894
URL
[本文引用: 4]
[11]
王海云, 谢礼立 近断层强地震动场预测
[J]. 地球物理学报 , 2009 , 52 (3 ): 703 - 711
URL
[本文引用: 1]
WANG Hai-yun, XIE Li-li Prediction of near-fault strong ground motion field
[J]. Chinese Journal of Geophysics , 2009 , 52 (3 ): 703 - 711
URL
[本文引用: 1]
[12]
孙吉泽, 俞言祥, 何金刚, 等 2013年乌鲁木齐M S 5.6和M S 5.1地震强地震动模拟研究
[J]. 地震学报 , 2017 , 39 (5 ): 751 - 763
DOI:10.11939/jass.2017.05.010
[本文引用: 1]
SUN Ji-ze, YU Yan-xiang, HE Jin-gang, et al Ground motion simulation of 2013 Ürümqi M S 5.6 and M S 5.1 earthquakes
[J]. Acta Seismologica Sinica , 2017 , 39 (5 ): 751 - 763
DOI:10.11939/jass.2017.05.010
[本文引用: 1]
[13]
李启成, 何书耕, 闵也, 等 用随机有限断层方法模拟 2016-11-13新西兰 MW 7.8地震
[J]. 大地测量与地球动力学 , 2019 , 39 (12 ): 1237 - 1242
URL
[本文引用: 1]
LI Qi-cheng, HE Shu-geng, MIN Ye, el al Simulation of Amberley New Zealand November 13, 2016 MW 7.8 earthquake using stochastic finite fault method
[J]. Journal of Geodesy and Geodynamics , 2019 , 39 (12 ): 1237 - 1242
URL
[本文引用: 1]
[14]
香川敬生 ハイブリッド合成法に用いる統計的グリーン関数法の長周期帯域への拡張
[J]. 日本地震工学会論文集 , 2004 , 4 (2 ): 21 - 32
DOI:10.5610/jaee.4.2_21
[本文引用: 2]
KAGAWA Takao Developing a stochastic Green ’s function method having more accuracy in long period range to be used in the hybrid method
[J]. Journal of Japan Association for Earthquake Engineering , 2004 , 4 (2 ): 21 - 32
DOI:10.5610/jaee.4.2_21
[本文引用: 2]
[15]
入倉孝次郎, 香川敬生, 関口春子. 経験的グリーン関数を用いた強震動予測方法の改良 [C]// 日本地震学会講演予稿集. Tokyo: 日本地震学会, 1997(2): B25.
[本文引用: 1]
IRIKURA Kojiro, KAGAWA Takao, SEKIGUCHI Haruko. Revision of the empirical Green ’s function method [C]// Program and abstracts of the Seismological Society of Japan . Tokyo: Seismological Society of Japan, 1997(2): B25.
[本文引用: 1]
[16]
佐藤智美 近地項と中間項を考慮した三成分統計的グリーン関数生成手法の高度化
[J]. 日本建築学会構造系論文集 , 2009 , 74 (638 ): 629 - 638
DOI:10.3130/aijs.74.629
[本文引用: 1]
SATOH Toshimi Improvement of generation method of three components of statistical Green's functions considering near-field and intermediate-field terms
[J]. Journal of Structural and Construction Engineering , 2009 , 74 (638 ): 629 - 638
DOI:10.3130/aijs.74.629
[本文引用: 1]
[17]
佐藤智美, 川瀬博, 佐藤俊明 ボアホール観測記録を用いた表層地盤同定手法による工学的基盤波の推定及びその統計的経時特性
[J]. 日本建築学会構造系論文集 , 1994 , 59 (461 ): 19 - 28
DOI:10.3130/aijs.59.19_3
[本文引用: 1]
SATOH Toshimi, KAWASE Hiroshi, SATO Toshiaki Engineering bedrock waves obtained through the identification analysis based on borehole records and their statistical envelope characteristics
[J]. Journal of Structural and Construction Engineering , 1994 , 59 (461 ): 19 - 28
DOI:10.3130/aijs.59.19_3
[本文引用: 1]
[18]
大崎順彦. 新地震動のスペクトル解析入門[M]. 東京: 鹿島出版会, 1994: 66-79.
[本文引用: 3]
[19]
HARTZELL S H, LEEDS A, FRANKEL A, et al Site response for urban Los Angeles using aftershocks of the Northridge earthquake
[J]. Bulletin of the Seismological Society of America , 1996 , 86 (1B ): S168 - S192
URL
[本文引用: 1]
[20]
野津厚. 統計的グリーン関数に近地項と中間項を導入するための簡便な方法 [C]// 第 12回日本地震工学シンポジウム. Tokyo: JEES, 2006: 190-193.
[本文引用: 1]
NOZU Atsushi. A simple scheme to introduce near-field and intermediate-field terms in stochastic Green’s functions [C]// Proceedings of the 12nd Japan Earthquake Engineering Symposium . Tokyo: JEES, 2006: 190-193.
[本文引用: 1]
[21]
WALD D J, HEATON T H, HUDNUT K W The slip history of the 1994 Northridge, California, earthquake determined from strong-motion, teleseismic, GPS, and leveling data
[J]. Bulletin of the Seismological Society of America , 1996 , 86 (1B ): S49 - S70
DOI:10.1785/BSSA08601B0S49
[本文引用: 1]
[22]
PEER. PEER strong ground motion databases [DB/OL]. [2020-12-29]. https://peer.berkeley.edu/peer-strong-ground-motion-databases.
[本文引用: 1]
[23]
谢旭, 王炎, 陈列 轨道约束对铁路减隔震桥梁地震响应的影响
[J]. 铁道学报 , 2012 , 34 (6 ): 75 - 82
DOI:10.3969/j.issn.1001-8360.2012.06.014
[本文引用: 1]
XIE Xu, WANG Yan, CHEN Lie Effect of rail restraints on seismic response of cushioning railway bridges
[J]. Journal of the China Railway Society , 2012 , 34 (6 ): 75 - 82
DOI:10.3969/j.issn.1001-8360.2012.06.014
[本文引用: 1]
1
... 近场地震动的周期特性、PGV/PGA、持时等参数对减隔震桥梁和非减隔震桥梁的地震反应均有显著的影响[1 -6 ] ,历史地震记录或者人工波虽然可以实现具有与弹性设计反应谱一致的反应谱特性,但不能直接反映地震断层参数,其周期特性、PGV/PGA和时历特性没有考虑潜在震源个性的影响,有可能导致桥梁地震反应计算结果不合理. ...
1
... 近场地震动的周期特性、PGV/PGA、持时等参数对减隔震桥梁和非减隔震桥梁的地震反应均有显著的影响[1 -6 ] ,历史地震记录或者人工波虽然可以实现具有与弹性设计反应谱一致的反应谱特性,但不能直接反映地震断层参数,其周期特性、PGV/PGA和时历特性没有考虑潜在震源个性的影响,有可能导致桥梁地震反应计算结果不合理. ...
Earthquake response of a base-isolated bridge subjected to strong near-fault ground motion
0
2010
地震动速度脉冲对大跨斜拉桥减震控制的影响
0
2012
地震动速度脉冲对大跨斜拉桥减震控制的影响
0
2012
Near-fault seismic risk assessment of simply supported bridges
0
2020
Fragility analysis of tall pier bridges subjected to near-fault pulse-like ground motions
1
2020
... 近场地震动的周期特性、PGV/PGA、持时等参数对减隔震桥梁和非减隔震桥梁的地震反应均有显著的影响[1 -6 ] ,历史地震记录或者人工波虽然可以实现具有与弹性设计反应谱一致的反应谱特性,但不能直接反映地震断层参数,其周期特性、PGV/PGA和时历特性没有考虑潜在震源个性的影响,有可能导致桥梁地震反应计算结果不合理. ...
Earthquake aftershocks as Green’s functions
1
1978
... 格林函数法根据断层破坏过程以及地震波传播过程模拟观测点地震动,自Hartzell[7 ] 提出经验格林函数法以来,在地震学领域得到迅速发展,在反演历史地震和强地震动模拟中得到广泛应用. 但是经验格林函数需要震源参数、传播路径和场地条件相同的小震记录,当缺乏小震记录时难以实现场地地震动的模拟. Boore[8 ] 提出用人工随机波替代小震记录的随机格林函数法,为设计地震动模拟提供了一种途径. 近年来,随机格林函数法模拟设计地震动的方法受到学者们的关注,如陶夏新等[9 ] 分析近断层强地震动的破裂方向性效应和上盘效应;王国新等[10 ] 预测沈阳地区近断层地震动的分布特性;王海云等[11 ] 用3个台站的地震记录校正随机格林函数,模拟 1997 年新疆伽师地震周围的近断层地震动分布;孙吉泽等[12 ] 模拟2013年乌鲁木齐 M S 5.6 和 M S 5.1 地震的强地震动分布;李启成等[13 ] 用基于动力学拐角模拟的随机有限断层法模拟2016年新西兰MW 7.8地震的地震动,得到较高的模拟精度. 有学者对随机格林法的地震动模拟进行一系列研究[14 -18 ] ,在实测数据分析的基础上对Boore[8 ] 提出的随机格林函数法进行许多改进,提高格林函数法的模拟精度. ...
Stochastic simulation of high-frequency ground motions based on seismological models of the radiated spectra
4
1983
... 格林函数法根据断层破坏过程以及地震波传播过程模拟观测点地震动,自Hartzell[7 ] 提出经验格林函数法以来,在地震学领域得到迅速发展,在反演历史地震和强地震动模拟中得到广泛应用. 但是经验格林函数需要震源参数、传播路径和场地条件相同的小震记录,当缺乏小震记录时难以实现场地地震动的模拟. Boore[8 ] 提出用人工随机波替代小震记录的随机格林函数法,为设计地震动模拟提供了一种途径. 近年来,随机格林函数法模拟设计地震动的方法受到学者们的关注,如陶夏新等[9 ] 分析近断层强地震动的破裂方向性效应和上盘效应;王国新等[10 ] 预测沈阳地区近断层地震动的分布特性;王海云等[11 ] 用3个台站的地震记录校正随机格林函数,模拟 1997 年新疆伽师地震周围的近断层地震动分布;孙吉泽等[12 ] 模拟2013年乌鲁木齐 M S 5.6 和 M S 5.1 地震的强地震动分布;李启成等[13 ] 用基于动力学拐角模拟的随机有限断层法模拟2016年新西兰MW 7.8地震的地震动,得到较高的模拟精度. 有学者对随机格林法的地震动模拟进行一系列研究[14 -18 ] ,在实测数据分析的基础上对Boore[8 ] 提出的随机格林函数法进行许多改进,提高格林函数法的模拟精度. ...
... [8 ]提出的随机格林函数法进行许多改进,提高格林函数法的模拟精度. ...
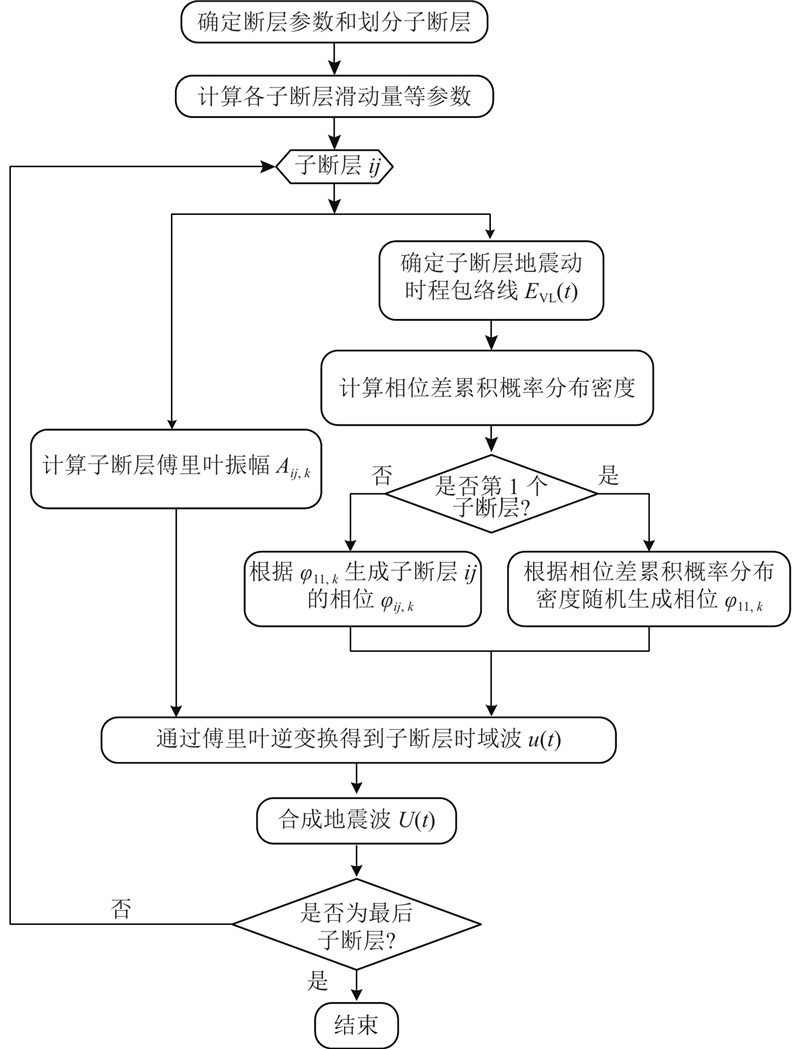
... 随机格林函数法模拟地震动的基本原理是把断层分成若干个滑动量不等的子断层,各子断层按照断层破裂方向依次发生滑动,并向周围辐射地震能量,观测点的地震动U (t )为各子断层辐射而至的地震动u (t )的叠加结果. 许多学者在Boore[8 ] 的研究基础上进行一系列改进,已初步具备合理模拟设计地震动的能力. 本研究采用入倉孝次郎等[15 ] 根据相似比提出的地震动时程合成方法,即: ...
... 由于Boore[8 ] 提出的模拟方法不考虑地震动的近场和中场影响,影响长周期地震动模拟精度,为此本研究采用佐藤智美[16 ] 提出的考虑近场和中场影响的修正加速度傅里叶谱 ...
近场强地震动模拟中对破裂的方向性效应和上盘效应的表达
1
2003
... 格林函数法根据断层破坏过程以及地震波传播过程模拟观测点地震动,自Hartzell[7 ] 提出经验格林函数法以来,在地震学领域得到迅速发展,在反演历史地震和强地震动模拟中得到广泛应用. 但是经验格林函数需要震源参数、传播路径和场地条件相同的小震记录,当缺乏小震记录时难以实现场地地震动的模拟. Boore[8 ] 提出用人工随机波替代小震记录的随机格林函数法,为设计地震动模拟提供了一种途径. 近年来,随机格林函数法模拟设计地震动的方法受到学者们的关注,如陶夏新等[9 ] 分析近断层强地震动的破裂方向性效应和上盘效应;王国新等[10 ] 预测沈阳地区近断层地震动的分布特性;王海云等[11 ] 用3个台站的地震记录校正随机格林函数,模拟 1997 年新疆伽师地震周围的近断层地震动分布;孙吉泽等[12 ] 模拟2013年乌鲁木齐 M S 5.6 和 M S 5.1 地震的强地震动分布;李启成等[13 ] 用基于动力学拐角模拟的随机有限断层法模拟2016年新西兰MW 7.8地震的地震动,得到较高的模拟精度. 有学者对随机格林法的地震动模拟进行一系列研究[14 -18 ] ,在实测数据分析的基础上对Boore[8 ] 提出的随机格林函数法进行许多改进,提高格林函数法的模拟精度. ...
近场强地震动模拟中对破裂的方向性效应和上盘效应的表达
1
2003
... 格林函数法根据断层破坏过程以及地震波传播过程模拟观测点地震动,自Hartzell[7 ] 提出经验格林函数法以来,在地震学领域得到迅速发展,在反演历史地震和强地震动模拟中得到广泛应用. 但是经验格林函数需要震源参数、传播路径和场地条件相同的小震记录,当缺乏小震记录时难以实现场地地震动的模拟. Boore[8 ] 提出用人工随机波替代小震记录的随机格林函数法,为设计地震动模拟提供了一种途径. 近年来,随机格林函数法模拟设计地震动的方法受到学者们的关注,如陶夏新等[9 ] 分析近断层强地震动的破裂方向性效应和上盘效应;王国新等[10 ] 预测沈阳地区近断层地震动的分布特性;王海云等[11 ] 用3个台站的地震记录校正随机格林函数,模拟 1997 年新疆伽师地震周围的近断层地震动分布;孙吉泽等[12 ] 模拟2013年乌鲁木齐 M S 5.6 和 M S 5.1 地震的强地震动分布;李启成等[13 ] 用基于动力学拐角模拟的随机有限断层法模拟2016年新西兰MW 7.8地震的地震动,得到较高的模拟精度. 有学者对随机格林法的地震动模拟进行一系列研究[14 -18 ] ,在实测数据分析的基础上对Boore[8 ] 提出的随机格林函数法进行许多改进,提高格林函数法的模拟精度. ...
近场强地震动合成方法研究及地震动模拟
1
2008
... 格林函数法根据断层破坏过程以及地震波传播过程模拟观测点地震动,自Hartzell[7 ] 提出经验格林函数法以来,在地震学领域得到迅速发展,在反演历史地震和强地震动模拟中得到广泛应用. 但是经验格林函数需要震源参数、传播路径和场地条件相同的小震记录,当缺乏小震记录时难以实现场地地震动的模拟. Boore[8 ] 提出用人工随机波替代小震记录的随机格林函数法,为设计地震动模拟提供了一种途径. 近年来,随机格林函数法模拟设计地震动的方法受到学者们的关注,如陶夏新等[9 ] 分析近断层强地震动的破裂方向性效应和上盘效应;王国新等[10 ] 预测沈阳地区近断层地震动的分布特性;王海云等[11 ] 用3个台站的地震记录校正随机格林函数,模拟 1997 年新疆伽师地震周围的近断层地震动分布;孙吉泽等[12 ] 模拟2013年乌鲁木齐 M S 5.6 和 M S 5.1 地震的强地震动分布;李启成等[13 ] 用基于动力学拐角模拟的随机有限断层法模拟2016年新西兰MW 7.8地震的地震动,得到较高的模拟精度. 有学者对随机格林法的地震动模拟进行一系列研究[14 -18 ] ,在实测数据分析的基础上对Boore[8 ] 提出的随机格林函数法进行许多改进,提高格林函数法的模拟精度. ...
近场强地震动合成方法研究及地震动模拟
1
2008
... 格林函数法根据断层破坏过程以及地震波传播过程模拟观测点地震动,自Hartzell[7 ] 提出经验格林函数法以来,在地震学领域得到迅速发展,在反演历史地震和强地震动模拟中得到广泛应用. 但是经验格林函数需要震源参数、传播路径和场地条件相同的小震记录,当缺乏小震记录时难以实现场地地震动的模拟. Boore[8 ] 提出用人工随机波替代小震记录的随机格林函数法,为设计地震动模拟提供了一种途径. 近年来,随机格林函数法模拟设计地震动的方法受到学者们的关注,如陶夏新等[9 ] 分析近断层强地震动的破裂方向性效应和上盘效应;王国新等[10 ] 预测沈阳地区近断层地震动的分布特性;王海云等[11 ] 用3个台站的地震记录校正随机格林函数,模拟 1997 年新疆伽师地震周围的近断层地震动分布;孙吉泽等[12 ] 模拟2013年乌鲁木齐 M S 5.6 和 M S 5.1 地震的强地震动分布;李启成等[13 ] 用基于动力学拐角模拟的随机有限断层法模拟2016年新西兰MW 7.8地震的地震动,得到较高的模拟精度. 有学者对随机格林法的地震动模拟进行一系列研究[14 -18 ] ,在实测数据分析的基础上对Boore[8 ] 提出的随机格林函数法进行许多改进,提高格林函数法的模拟精度. ...
近断层强地震动场预测
1
2009
... 格林函数法根据断层破坏过程以及地震波传播过程模拟观测点地震动,自Hartzell[7 ] 提出经验格林函数法以来,在地震学领域得到迅速发展,在反演历史地震和强地震动模拟中得到广泛应用. 但是经验格林函数需要震源参数、传播路径和场地条件相同的小震记录,当缺乏小震记录时难以实现场地地震动的模拟. Boore[8 ] 提出用人工随机波替代小震记录的随机格林函数法,为设计地震动模拟提供了一种途径. 近年来,随机格林函数法模拟设计地震动的方法受到学者们的关注,如陶夏新等[9 ] 分析近断层强地震动的破裂方向性效应和上盘效应;王国新等[10 ] 预测沈阳地区近断层地震动的分布特性;王海云等[11 ] 用3个台站的地震记录校正随机格林函数,模拟 1997 年新疆伽师地震周围的近断层地震动分布;孙吉泽等[12 ] 模拟2013年乌鲁木齐 M S 5.6 和 M S 5.1 地震的强地震动分布;李启成等[13 ] 用基于动力学拐角模拟的随机有限断层法模拟2016年新西兰MW 7.8地震的地震动,得到较高的模拟精度. 有学者对随机格林法的地震动模拟进行一系列研究[14 -18 ] ,在实测数据分析的基础上对Boore[8 ] 提出的随机格林函数法进行许多改进,提高格林函数法的模拟精度. ...
近断层强地震动场预测
1
2009
... 格林函数法根据断层破坏过程以及地震波传播过程模拟观测点地震动,自Hartzell[7 ] 提出经验格林函数法以来,在地震学领域得到迅速发展,在反演历史地震和强地震动模拟中得到广泛应用. 但是经验格林函数需要震源参数、传播路径和场地条件相同的小震记录,当缺乏小震记录时难以实现场地地震动的模拟. Boore[8 ] 提出用人工随机波替代小震记录的随机格林函数法,为设计地震动模拟提供了一种途径. 近年来,随机格林函数法模拟设计地震动的方法受到学者们的关注,如陶夏新等[9 ] 分析近断层强地震动的破裂方向性效应和上盘效应;王国新等[10 ] 预测沈阳地区近断层地震动的分布特性;王海云等[11 ] 用3个台站的地震记录校正随机格林函数,模拟 1997 年新疆伽师地震周围的近断层地震动分布;孙吉泽等[12 ] 模拟2013年乌鲁木齐 M S 5.6 和 M S 5.1 地震的强地震动分布;李启成等[13 ] 用基于动力学拐角模拟的随机有限断层法模拟2016年新西兰MW 7.8地震的地震动,得到较高的模拟精度. 有学者对随机格林法的地震动模拟进行一系列研究[14 -18 ] ,在实测数据分析的基础上对Boore[8 ] 提出的随机格林函数法进行许多改进,提高格林函数法的模拟精度. ...
2013年乌鲁木齐M S 5.6和M S 5.1地震强地震动模拟研究
1
2017
... 格林函数法根据断层破坏过程以及地震波传播过程模拟观测点地震动,自Hartzell[7 ] 提出经验格林函数法以来,在地震学领域得到迅速发展,在反演历史地震和强地震动模拟中得到广泛应用. 但是经验格林函数需要震源参数、传播路径和场地条件相同的小震记录,当缺乏小震记录时难以实现场地地震动的模拟. Boore[8 ] 提出用人工随机波替代小震记录的随机格林函数法,为设计地震动模拟提供了一种途径. 近年来,随机格林函数法模拟设计地震动的方法受到学者们的关注,如陶夏新等[9 ] 分析近断层强地震动的破裂方向性效应和上盘效应;王国新等[10 ] 预测沈阳地区近断层地震动的分布特性;王海云等[11 ] 用3个台站的地震记录校正随机格林函数,模拟 1997 年新疆伽师地震周围的近断层地震动分布;孙吉泽等[12 ] 模拟2013年乌鲁木齐 M S 5.6 和 M S 5.1 地震的强地震动分布;李启成等[13 ] 用基于动力学拐角模拟的随机有限断层法模拟2016年新西兰MW 7.8地震的地震动,得到较高的模拟精度. 有学者对随机格林法的地震动模拟进行一系列研究[14 -18 ] ,在实测数据分析的基础上对Boore[8 ] 提出的随机格林函数法进行许多改进,提高格林函数法的模拟精度. ...
2013年乌鲁木齐M S 5.6和M S 5.1地震强地震动模拟研究
1
2017
... 格林函数法根据断层破坏过程以及地震波传播过程模拟观测点地震动,自Hartzell[7 ] 提出经验格林函数法以来,在地震学领域得到迅速发展,在反演历史地震和强地震动模拟中得到广泛应用. 但是经验格林函数需要震源参数、传播路径和场地条件相同的小震记录,当缺乏小震记录时难以实现场地地震动的模拟. Boore[8 ] 提出用人工随机波替代小震记录的随机格林函数法,为设计地震动模拟提供了一种途径. 近年来,随机格林函数法模拟设计地震动的方法受到学者们的关注,如陶夏新等[9 ] 分析近断层强地震动的破裂方向性效应和上盘效应;王国新等[10 ] 预测沈阳地区近断层地震动的分布特性;王海云等[11 ] 用3个台站的地震记录校正随机格林函数,模拟 1997 年新疆伽师地震周围的近断层地震动分布;孙吉泽等[12 ] 模拟2013年乌鲁木齐 M S 5.6 和 M S 5.1 地震的强地震动分布;李启成等[13 ] 用基于动力学拐角模拟的随机有限断层法模拟2016年新西兰MW 7.8地震的地震动,得到较高的模拟精度. 有学者对随机格林法的地震动模拟进行一系列研究[14 -18 ] ,在实测数据分析的基础上对Boore[8 ] 提出的随机格林函数法进行许多改进,提高格林函数法的模拟精度. ...
用随机有限断层方法模拟 2016-11-13新西兰 MW 7.8地震
1
2019
... 格林函数法根据断层破坏过程以及地震波传播过程模拟观测点地震动,自Hartzell[7 ] 提出经验格林函数法以来,在地震学领域得到迅速发展,在反演历史地震和强地震动模拟中得到广泛应用. 但是经验格林函数需要震源参数、传播路径和场地条件相同的小震记录,当缺乏小震记录时难以实现场地地震动的模拟. Boore[8 ] 提出用人工随机波替代小震记录的随机格林函数法,为设计地震动模拟提供了一种途径. 近年来,随机格林函数法模拟设计地震动的方法受到学者们的关注,如陶夏新等[9 ] 分析近断层强地震动的破裂方向性效应和上盘效应;王国新等[10 ] 预测沈阳地区近断层地震动的分布特性;王海云等[11 ] 用3个台站的地震记录校正随机格林函数,模拟 1997 年新疆伽师地震周围的近断层地震动分布;孙吉泽等[12 ] 模拟2013年乌鲁木齐 M S 5.6 和 M S 5.1 地震的强地震动分布;李启成等[13 ] 用基于动力学拐角模拟的随机有限断层法模拟2016年新西兰MW 7.8地震的地震动,得到较高的模拟精度. 有学者对随机格林法的地震动模拟进行一系列研究[14 -18 ] ,在实测数据分析的基础上对Boore[8 ] 提出的随机格林函数法进行许多改进,提高格林函数法的模拟精度. ...
用随机有限断层方法模拟 2016-11-13新西兰 MW 7.8地震
1
2019
... 格林函数法根据断层破坏过程以及地震波传播过程模拟观测点地震动,自Hartzell[7 ] 提出经验格林函数法以来,在地震学领域得到迅速发展,在反演历史地震和强地震动模拟中得到广泛应用. 但是经验格林函数需要震源参数、传播路径和场地条件相同的小震记录,当缺乏小震记录时难以实现场地地震动的模拟. Boore[8 ] 提出用人工随机波替代小震记录的随机格林函数法,为设计地震动模拟提供了一种途径. 近年来,随机格林函数法模拟设计地震动的方法受到学者们的关注,如陶夏新等[9 ] 分析近断层强地震动的破裂方向性效应和上盘效应;王国新等[10 ] 预测沈阳地区近断层地震动的分布特性;王海云等[11 ] 用3个台站的地震记录校正随机格林函数,模拟 1997 年新疆伽师地震周围的近断层地震动分布;孙吉泽等[12 ] 模拟2013年乌鲁木齐 M S 5.6 和 M S 5.1 地震的强地震动分布;李启成等[13 ] 用基于动力学拐角模拟的随机有限断层法模拟2016年新西兰MW 7.8地震的地震动,得到较高的模拟精度. 有学者对随机格林法的地震动模拟进行一系列研究[14 -18 ] ,在实测数据分析的基础上对Boore[8 ] 提出的随机格林函数法进行许多改进,提高格林函数法的模拟精度. ...
ハイブリッド合成法に用いる統計的グリーン関数法の長周期帯域への拡張
2
2004
... 格林函数法根据断层破坏过程以及地震波传播过程模拟观测点地震动,自Hartzell[7 ] 提出经验格林函数法以来,在地震学领域得到迅速发展,在反演历史地震和强地震动模拟中得到广泛应用. 但是经验格林函数需要震源参数、传播路径和场地条件相同的小震记录,当缺乏小震记录时难以实现场地地震动的模拟. Boore[8 ] 提出用人工随机波替代小震记录的随机格林函数法,为设计地震动模拟提供了一种途径. 近年来,随机格林函数法模拟设计地震动的方法受到学者们的关注,如陶夏新等[9 ] 分析近断层强地震动的破裂方向性效应和上盘效应;王国新等[10 ] 预测沈阳地区近断层地震动的分布特性;王海云等[11 ] 用3个台站的地震记录校正随机格林函数,模拟 1997 年新疆伽师地震周围的近断层地震动分布;孙吉泽等[12 ] 模拟2013年乌鲁木齐 M S 5.6 和 M S 5.1 地震的强地震动分布;李启成等[13 ] 用基于动力学拐角模拟的随机有限断层法模拟2016年新西兰MW 7.8地震的地震动,得到较高的模拟精度. 有学者对随机格林法的地震动模拟进行一系列研究[14 -18 ] ,在实测数据分析的基础上对Boore[8 ] 提出的随机格林函数法进行许多改进,提高格林函数法的模拟精度. ...
... 用随机格林函数法模拟地震动时,采用满足地震动傅里叶谱条件和持时包络曲线的随机波模拟子断层的地震动. 这种方法采用随机的相位谱,模拟结果很难保证地震动的方向性效应. 对此,有学者提出一些解决办法,如香川敬生[14 ] 提出选择位移波形相似的相位谱作为子断层的地震动,这种方法是从大量随机相位谱中挑选符合要求的相位谱,计算过程过于烦琐. ...
ハイブリッド合成法に用いる統計的グリーン関数法の長周期帯域への拡張
2
2004
... 格林函数法根据断层破坏过程以及地震波传播过程模拟观测点地震动,自Hartzell[7 ] 提出经验格林函数法以来,在地震学领域得到迅速发展,在反演历史地震和强地震动模拟中得到广泛应用. 但是经验格林函数需要震源参数、传播路径和场地条件相同的小震记录,当缺乏小震记录时难以实现场地地震动的模拟. Boore[8 ] 提出用人工随机波替代小震记录的随机格林函数法,为设计地震动模拟提供了一种途径. 近年来,随机格林函数法模拟设计地震动的方法受到学者们的关注,如陶夏新等[9 ] 分析近断层强地震动的破裂方向性效应和上盘效应;王国新等[10 ] 预测沈阳地区近断层地震动的分布特性;王海云等[11 ] 用3个台站的地震记录校正随机格林函数,模拟 1997 年新疆伽师地震周围的近断层地震动分布;孙吉泽等[12 ] 模拟2013年乌鲁木齐 M S 5.6 和 M S 5.1 地震的强地震动分布;李启成等[13 ] 用基于动力学拐角模拟的随机有限断层法模拟2016年新西兰MW 7.8地震的地震动,得到较高的模拟精度. 有学者对随机格林法的地震动模拟进行一系列研究[14 -18 ] ,在实测数据分析的基础上对Boore[8 ] 提出的随机格林函数法进行许多改进,提高格林函数法的模拟精度. ...
... 用随机格林函数法模拟地震动时,采用满足地震动傅里叶谱条件和持时包络曲线的随机波模拟子断层的地震动. 这种方法采用随机的相位谱,模拟结果很难保证地震动的方向性效应. 对此,有学者提出一些解决办法,如香川敬生[14 ] 提出选择位移波形相似的相位谱作为子断层的地震动,这种方法是从大量随机相位谱中挑选符合要求的相位谱,计算过程过于烦琐. ...
1
... 随机格林函数法模拟地震动的基本原理是把断层分成若干个滑动量不等的子断层,各子断层按照断层破裂方向依次发生滑动,并向周围辐射地震能量,观测点的地震动U (t )为各子断层辐射而至的地震动u (t )的叠加结果. 许多学者在Boore[8 ] 的研究基础上进行一系列改进,已初步具备合理模拟设计地震动的能力. 本研究采用入倉孝次郎等[15 ] 根据相似比提出的地震动时程合成方法,即: ...
1
... 随机格林函数法模拟地震动的基本原理是把断层分成若干个滑动量不等的子断层,各子断层按照断层破裂方向依次发生滑动,并向周围辐射地震能量,观测点的地震动U (t )为各子断层辐射而至的地震动u (t )的叠加结果. 许多学者在Boore[8 ] 的研究基础上进行一系列改进,已初步具备合理模拟设计地震动的能力. 本研究采用入倉孝次郎等[15 ] 根据相似比提出的地震动时程合成方法,即: ...
近地項と中間項を考慮した三成分統計的グリーン関数生成手法の高度化
1
2009
... 由于Boore[8 ] 提出的模拟方法不考虑地震动的近场和中场影响,影响长周期地震动模拟精度,为此本研究采用佐藤智美[16 ] 提出的考虑近场和中场影响的修正加速度傅里叶谱 ...
近地項と中間項を考慮した三成分統計的グリーン関数生成手法の高度化
1
2009
... 由于Boore[8 ] 提出的模拟方法不考虑地震动的近场和中场影响,影响长周期地震动模拟精度,为此本研究采用佐藤智美[16 ] 提出的考虑近场和中场影响的修正加速度傅里叶谱 ...
ボアホール観測記録を用いた表層地盤同定手法による工学的基盤波の推定及びその統計的経時特性
1
1994
... 本研究采用考虑地震动传播过程中弥散效应的经验时程包络函数[17 ] ,即 ...
ボアホール観測記録を用いた表層地盤同定手法による工学的基盤波の推定及びその統計的経時特性
1
1994
... 本研究采用考虑地震动传播过程中弥散效应的经验时程包络函数[17 ] ,即 ...
3
... 格林函数法根据断层破坏过程以及地震波传播过程模拟观测点地震动,自Hartzell[7 ] 提出经验格林函数法以来,在地震学领域得到迅速发展,在反演历史地震和强地震动模拟中得到广泛应用. 但是经验格林函数需要震源参数、传播路径和场地条件相同的小震记录,当缺乏小震记录时难以实现场地地震动的模拟. Boore[8 ] 提出用人工随机波替代小震记录的随机格林函数法,为设计地震动模拟提供了一种途径. 近年来,随机格林函数法模拟设计地震动的方法受到学者们的关注,如陶夏新等[9 ] 分析近断层强地震动的破裂方向性效应和上盘效应;王国新等[10 ] 预测沈阳地区近断层地震动的分布特性;王海云等[11 ] 用3个台站的地震记录校正随机格林函数,模拟 1997 年新疆伽师地震周围的近断层地震动分布;孙吉泽等[12 ] 模拟2013年乌鲁木齐 M S 5.6 和 M S 5.1 地震的强地震动分布;李启成等[13 ] 用基于动力学拐角模拟的随机有限断层法模拟2016年新西兰MW 7.8地震的地震动,得到较高的模拟精度. 有学者对随机格林法的地震动模拟进行一系列研究[14 -18 ] ,在实测数据分析的基础上对Boore[8 ] 提出的随机格林函数法进行许多改进,提高格林函数法的模拟精度. ...
... 本研究根据相位差分的分布模拟地震动时程[18 ] . 子断层ij 破裂引起的观测点地震加速度时程的傅里叶谱可以表示为 ...
... 为了使式(15)的傅里叶系数经过逆变换后地震动时程与图1 的持时曲线吻合,采用合理的相位谱. 由于持时包络曲线与相位差分谱相似,相位差分分布如图2 (a)所示,如将相位差分谱等分成若干区段,可以得到如图2 (b)所示的相位差分谱累计概率分布密度P φ [18 ] . 其中相位差分定义为 ...
Site response for urban Los Angeles using aftershocks of the Northridge earthquake
1
1996
... 式中:Q (f )为与频率相关的传播路径衰减特性,具有地域性,本研究采用的计算式[19 ] 为 ...
1
... 近场和中场影响函数的计算式[20 ] 为 ...
1
... 近场和中场影响函数的计算式[20 ] 为 ...
The slip history of the 1994 Northridge, California, earthquake determined from strong-motion, teleseismic, GPS, and leveling data
1
1996
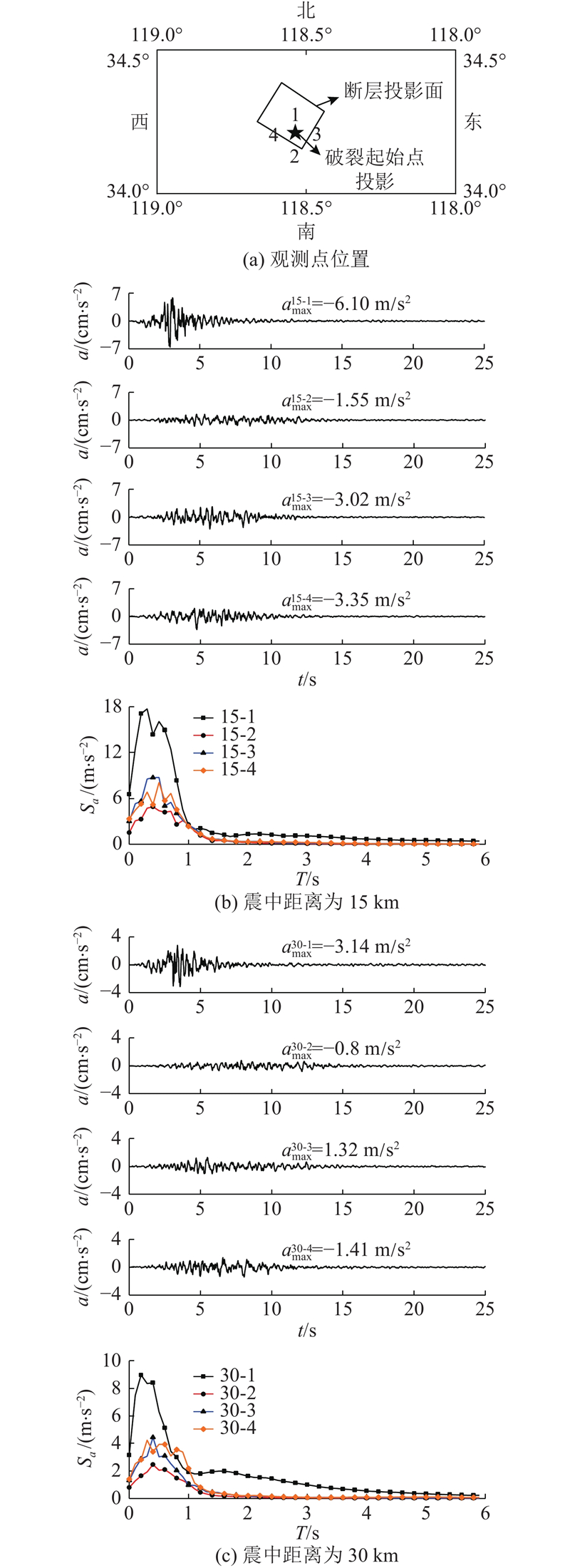
... 以1994年美国北岭地震为例. 地震震级为M6.7,震中位于北纬34.211°,西经118.546°,震源深度为17.5 km. 根据Wald等[21 ] 的反演结果,断层走向为122°,倾角为40°,平均滑动角为101°. 断层破裂面沿走向的长度为18 km,下倾宽度为21 km,破裂面积为378 km2 . 断层顶部的深度为5.0 km,断层底部的深度为20.4 km. 应力降取5 MPa,地震矩估计为1.3×1019 N·m,断层面上的平均滑动量为101.85 cm,最大滑动量约为3 m. 震源附近区域的介质密度为2.8 g/cm3 ,震源附近区域的剪切波速为3.7 km/s. 断层面上的破裂传播速度约为震源附近区域剪切波速的0.8倍,取为3.0 km/s. 凹凸体数为2,面积分别为58.5、8.4 km2 ,滑动量分别为2.016、1.779 m;凹凸体地震矩为5.116×1018 N·m. 背景区域面积为310.8 km2 ,滑动量为0.661 8 m,地震矩为7.884×1018 N·m. 如图4 所示为断层参数以及实测台站位置. 图中,OXYZ 为整体坐标系,X 为正北方向,Y 为正东方向,Z 为竖直向下方向,O 点为断层面左上角点在地面的投影,oxy 为断层面局部坐标系,o 点为断层面左上角点,x 为断层长度方向,y 为断层宽度方向,Q 点为断层面上破裂起始点的位置,ϕ s 为断层面走向,δ 为断层面倾角,L 为断层面长度,W 为断层面宽度,d t 为断层顶部埋深. ...
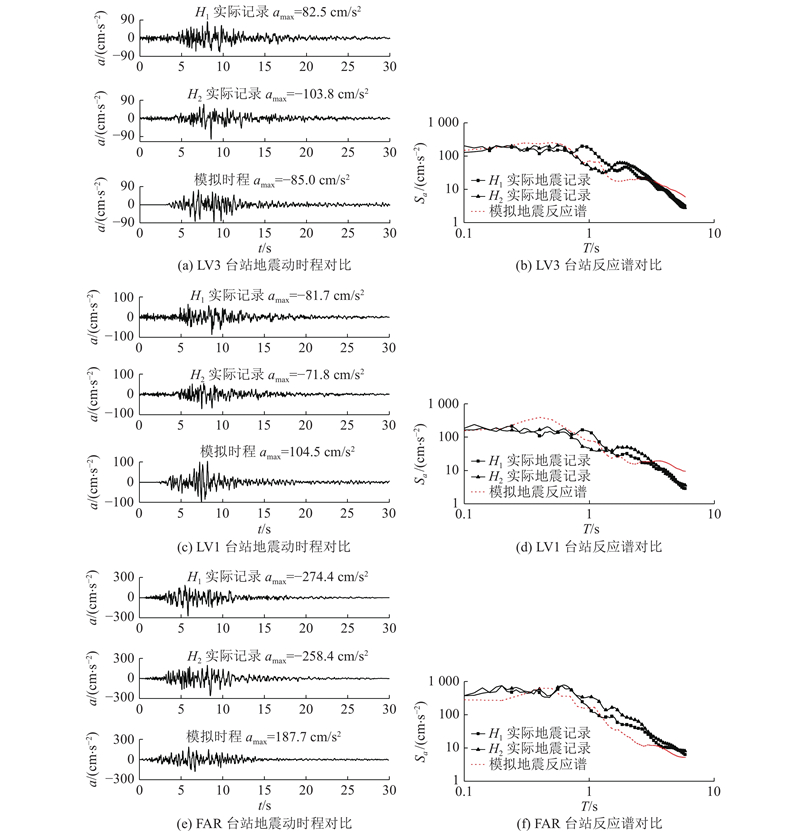
1
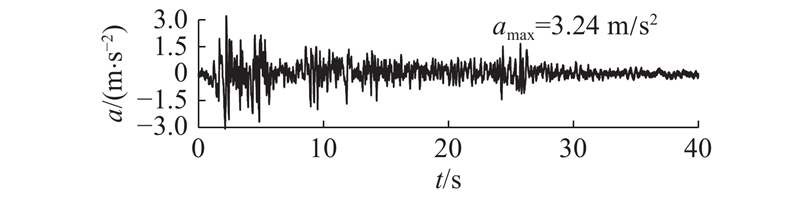
... 如图5 所示为北岭地震中3个台站模拟的地震动加速度时程和反应谱与相应实际记录的对比,计算时相位差分分32等分计算累计概率密度分布. 图中,t 为时间,a 为加速度,a max 为最大加速度,T 为周期,S a H 1 、H 2 分别为水平相互垂直的2个方向. 结果表明,无论是峰值加速度还是宽频域的反应谱,均有比较好的精度. 由于震源参数、传播路径以及场地条件的不确定性,以及计算方法的近似性,计算结果与实测结果多少存在差异. 实际地震记录取自文献[22 ]. ...
轨道约束对铁路减隔震桥梁地震响应的影响
1
2012
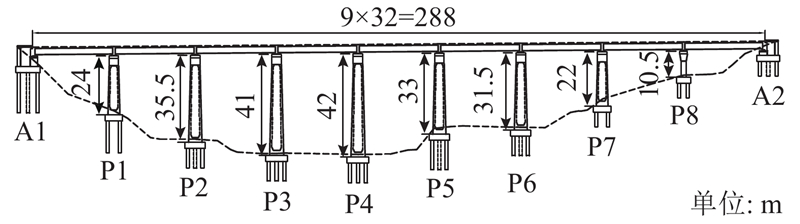
... 以如图6 所示的铁路减隔震桥梁[23 ] 为例. 桥梁为9 m×32 m的预应力混凝土简支箱结构,下部结构采用U型桥台双线圆端型空心桥墩. 桥墩编号从左至右依次为P1~P8,梁端桥台分别为A1、A2. 桥墩高度依次为24、35.5、41、42、33、31.5、22、10.5 m. 采用E型钢阻尼作为减震元件. 支座编号从左至右依次为B1~B18. 如图7 所示为桥梁−轨道一体化计算模型,取道床阻力系数为15 kN/m. ...
轨道约束对铁路减隔震桥梁地震响应的影响
1
2012
... 以如图6 所示的铁路减隔震桥梁[23 ] 为例. 桥梁为9 m×32 m的预应力混凝土简支箱结构,下部结构采用U型桥台双线圆端型空心桥墩. 桥墩编号从左至右依次为P1~P8,梁端桥台分别为A1、A2. 桥墩高度依次为24、35.5、41、42、33、31.5、22、10.5 m. 采用E型钢阻尼作为减震元件. 支座编号从左至右依次为B1~B18. 如图7 所示为桥梁−轨道一体化计算模型,取道床阻力系数为15 kN/m. ...