空间结构、铁路、高速公路等经常采用桁架作为主要承力结构，其杆件主要承受轴向拉压，能充分利用材料强度，增强结构刚度并减轻自重. 但空间桁架往往杆件数量多、体系冗余度大，同时存在不确定性因素如节点连接条件、外荷载分布、杆件截面不均匀等^[1]，使得准确评估桁架体系安全性的难度较大.

当前对于超静定桁架体系的安全评估主要基于可靠度理论，传统的桁架体系可靠度评估方法依赖复杂的失效模式判别^[2-4]，不利于实际应用. 长期服役的桁架可靠度主要取决于桁架力学属性及外荷载的变化，同时也影响着桁架的响应输出. 近年来，结构健康监测系统在各类工程结构中的应用日趋广泛^[5]，监测数据可以作为评估结构安全性的有用信息. 但由于传感器的布置有限，监测数据存在不完备性^[6]，人工智能方法为处理监测数据及进行安全评估提供了新的可能.

相比于传统的神经网络方法的“黑盒子”模式，贝叶斯网络（Bayesian networks，BN）^[7]为具有逻辑推理的人工智能方法. BN拓扑为有向无环图，用节点表示变量，联系各节点的有向弧代表节点间的相互逻辑关系，关系强度通过条件概率表（conditional probability table，CPT）或条件概率分布（conditional probability distribution，CPD）^[8-9]表征. 近年来BN在可靠性分析和风险评估上已有一定应用^[10-14]. BN类型有离散型、连续型及混合型^[15]，分别对应离散型、连续型和离散-连续混合的节点变量. 将桁架结构中各单元的最大应力处理成连续变量，可以精确推理出单元应力，有利于桁架结构的安全评估的准确性. 而对于桁架结构体系的安全性评估，将体系节点处理成离散型的状态（“安全”或“破坏”）更具实用性，可以直接得到体系的破坏概率.

BN的建立主要包含BN拓扑和其有向弧的CPT（或CPD）2个要素，均可以通过经验确定和基于观测数据参数学习方式得到^[16-19]. 前者主观性太强，有时缺乏客观依据，而后者在确定BN拓扑时容易导致节点间逻辑关系过于复杂或丢失，比如属于间接关系的节点被有向弧直接连接，或有直接父子关系的节点间不存在有向弧. 桁架结构是由杆件（梁）组成的格构体系，当外荷载作用在桁架结点（区别于BN节点）上时，各杆内力主要为轴向拉力或压力，交汇于一个结点上的内力合力作用于梁截面. 在给定外荷载形式下各杆件间的力学关系明确，体系力学模型易于建立. 因此，基于力学逻辑建立桁架结构的BN拓扑是可行且合理的方法. 在BN拓扑建立后，CPT和CPD可以通过观测数据进行参数学习得到.

本研究针对桁架结构安全性评估问题，提出嵌套力学BN方法. 将桁架结构各单元最大应力作为BN的连续型节点，而体系状态作为离散节点，通过对下平纵梁节点的离散化将2种类型的BN节点进行关联，形成嵌套力学BN. 首先，根据外荷载和桁架杆件内力分布情况，建立表述桁架单元间逻辑关系的构件层次BN拓扑；接着定义桁架体系为独立节点，将离散后的各下平纵梁单元节点与之相联系，建立体系层次的BN拓扑. 接着通过抽样样本和最大似然估计法对CPT和CPD进行学习，得到可以用于推理的嵌套力学BN. 提出的嵌套BN既能保证单元应力的评估精度，避免信息的损失，又能通过对体系安全评估的直观指标满足现实需求，具有更好的实用性.

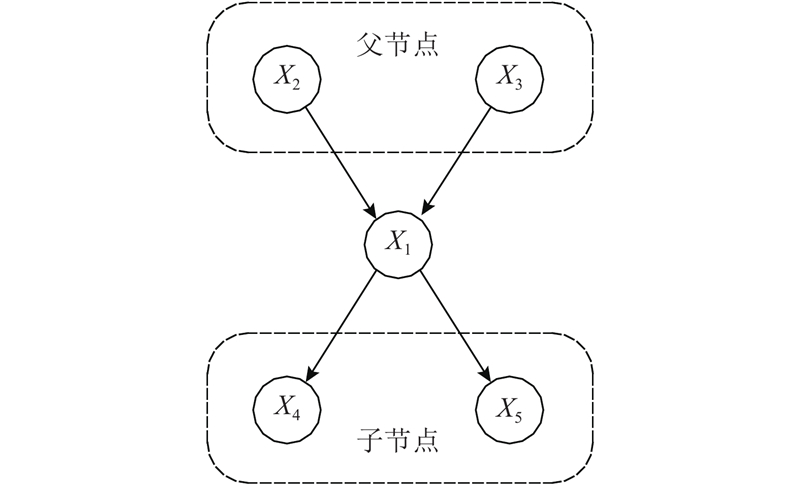
BN是形容各节点变量之间概率关系的图模型，由两部分构成：1）网络拓扑，为有向无环图；2）连接节点的有向弧，节点间逻辑关系通过有向弧由起因节点（父节点）指向结果节点（子节点），关系强度采用CPT（对应离散型）或CPD（对应连续型）描述.

BN节点的取值可以是离散的，也可以是连续的，离散型BN为最早提出且使用广泛的一种类型. 设离散型节点变量 ${X_i}$具有多种状态 ${x_{i,j}}\left( j = 1, $ $ 2, \cdots , n \right)$，其状态概率可以通过贝叶斯公式推理得到^[20]， ${X_i}$的所有状态的概率之和为1.0. 如图1所示，考虑 ${X_1}$之前的父节点集合F（包含 ${X_2}$、 ${X_3}$这2个父节点）和 $X$之后的子节点集合S（包含 ${X_4}$、 ${X_5}$这2个子节点）. 状态概率 $ {x_i}_{,j} $的“置信水平”表达式^[21]如下：

(1) $ P\left( {{x_{i,j}}{{|}}e} \right) \propto P\left( {{e^{\rm{S}}}{{|}}{x_{i,j}}} \right)P\left( {{x_{i,j}}{{|}}{e^{{\rm{F}}} }} \right) . $

式中： $e$为所有证据， ${e^{\rm{S}}}$为子节点证据， ${e^{\rm{F}}}$为父节点证据. 同一节点各状态概率之和为1.0，因此对节点各状态“置信水平”归一化后即可得到各状态概率.

离散型BN节点间逻辑关系强度通过CPT表示，CPT中元素为父节点状态组合下子节点的状态概率，可以通过对观测数据进行参数学习得到.

在实际工程中，连续变量普遍存在，对于连续型BN节点，可以将节点变量进行离散化，或考虑成服从某一分布的连续函数. 节点离散化若划分过粗将影响节点变量的分辨率，而划分过细容易出现极端概率情况，影响BN建模及推理. 因此在更高节点精度需求下，可以假设连续型BN节点服从高斯分布，设节点变量用 $ X = ({X_1},{X_2}, \cdots ,{X_n}) $表示，则均值向量 $ {\boldsymbol{\mu }} = \left[ {{\mu _1},{\mu _2}, \cdots ,{\mu _n}} \right] $和协方差矩阵 $ {\boldsymbol{S}}(n \times n) $中元素 $ {\mu _i} $和 $ {\sigma _{ij}} $可以表示为

(2) $ {\mu _i} = E({X_i}) , $

(3) $ {\sigma _{ij}} = E[({X_i} - {\mu _i})({X_j} - {\mu _j})] . $

父节点集合 $ {{\varPi}_i} $（共有 $ {f_i} $个节点）与子节点 $ {X_i} $相连的有向弧的CPD所服从分布^[22]如下：

(4) $ f\left( {{X_i}|{{\varPi}_i}} \right)\sim N\left( {{\mu _i} + \sum\limits_{j = 1}^{{f_i}} {{\beta _i}_j\left( {{x_j} - {\mu _j}} \right),\;{\nu _i}} } \right) .$

式中： $\; {\beta _{ij}}$为节点 $ {X_i} $和 $ {X_j} $（ $ {{\varPi}_i} $中）的回归系数，表示节点 $ {X_i} $和 $ {X_j} $的关系强度，若 $ {\beta _{ij}} = 0 $，表示 $ {X_j} $不是 $ {X_i} $的父节点；x_i为变量X_i的某个样本值； $ {\nu _i} $为 $ {X_i} $的条件方差. $ {\nu _i}$可以表达为

(5) $ {{{\nu }}_{{i}}} = {{{S}}_{{i}}} - {{\boldsymbol{S}}_{{{i}}{{\varPi}_{{i}}}}}{\boldsymbol{S}}_{{{\varPi}_{{i}}}}^{{{ - }}1}{\boldsymbol{S}}_{{{i}}{{\varPi}_{{i}}}}^{{\rm{T}}}. $

式中： $ {S_i} $为 $ {X_i} $的无条件方差， ${{\boldsymbol{S}}}_{{i{\varPi_i}}}$为 $ {X_i} $与 $ {{\varPi}_i} $中变量间的协方差向量， $ {\boldsymbol{S}}_{{{\varPi}_{{i}}}}^{} $为 $ {{\varPi}_i} $中变量的协方差矩阵.

BN的2个关键要素是网络的几何拓扑和CPT（或CPD），若各节点间逻辑关系明确，则可以直接建立拓扑，仅对CPT（或CPD）进行学习，以大幅减小所需的观测数据量. 学习CPT（或CPD）最常用最大似然估计法和贝叶斯方法，当观测数据数目较多时，最大似然法的收敛性质更佳，下面以一榀钢桁架结构为例进行说明.

工程桁架结构往往受恒荷载和活荷载的组合作用. 本研究以一下承式桁架桥结构为例，阐述力学BN模型的构建方法. 假设恒荷载为作用于下平纵梁的均布荷载，活荷载为沿下平纵梁移动的随机集中荷载. 以下将对组合荷载作用下的桁架结构力学BN进行说明.

为了评估桁架结构体系的安全性能，提出一种力学BN，节点变量包含离散型节点和连续型节点，为以下3种类型.

1）各单元最大应力（连续型）. 假设桁架结构破坏过程中杆件的破坏由材料强度控制，即暂不考虑失稳. 在钢桁架结构系统中，构件中的应力大小决定了材料所处的性能状态，进而影响桁架结构的安全性能. 与此同时，应变监测是桥梁健康监测系统中常见的监测类型，应力可以由应变推算得到，在监测数据处理过程中某时段内局部最大值亦为重要数据特征. 因此本研究将桁架结构划分为不同的单元，每个单元在恒荷载及移动荷载作用下的最大应力（分别指拉或压的最大应力）作为BN模型中的节点变量. 在BN建立过程中此类节点变量用高斯分布进行处理.

2）体系状态（离散型）. 为了获得表征体系的量化指标，设置1个离散型体系节点，具有“安全”和“破坏”2种状态，其状态概率之和为1.0，其状态概率可以作为体系安全评估的参考指标.

3）离散化的下平纵梁单元节点. 为了将连续型节点变量（各桁架单元节点）和离散型节点进行耦合建模，对体系节点的父节点（各下平纵梁单元）进行离散化. 考虑到钢材不同受力阶段是其安全性能的重要参考指标，因此离散化后的下平纵梁单元包含3种状态：“弹性”、“塑性”和“破坏”，其状态概率之和为1.0.

在桁架结构中交汇于同一结点的杆件会保持力学平衡，某一（部分）杆件内力水平的变化将直接影响其他杆件的受力情况. 同时，超静定桁架的某一（部分）杆件破坏后会形成新的桁架，在剩余杆件间发生内力重分配，形成新的力学平衡关系，往往使得与破坏相邻的杆件内力变大. 因此，BN中相邻单元间的逻辑关系可以通过有向弧表达，弧的方向可以根据其当前最大应力状况和材料极限应力来判断.

首先，以桁架结点为界限划分各个单元，包括杆件单元和梁单元. 令BN节点数等于桁架结构中单元数目，然后选取具代表性的荷载组合（恒荷载和移动荷载的样本均值）作用于桁架结构，令杆件i的最大应力σ_max与材料极限应力σ_b比值为 $ {\gamma _i} = {{{\sigma _{\max }}} / {{\sigma _{\rm{b}}}}} $，有向弧方向为 $ {\gamma _i} $大的杆件指向小的杆件，以此建立单元层次BN拓扑.

其次，由于本研究以一座实际桁架桥为背景进行BN建模，下纵梁主要承受车辆荷载，考虑到下平纵梁破坏将直接影响桁架桥的正常使用，因此BN拓扑中将离散化的下平纵梁单元节点作为体系节点的父节点，由此得到体系BN拓扑. 最后，将单元层次BN和体系BN相嵌套，合成为同时包含单元和体系节点的力学BN拓扑.

须说明的是，桁架结构中各构件节点也通过下平纵梁节点间接指向了体系节点，各构件节点的应力变化对体系安全性能的影响可以通过BN推理时信息随拓扑图的传递得到体现.

在确定桁架BN拓扑并定义了单元、体系节点后，须进一步确定节点间的CPD（连续节点）及CPT（离散节点）. 本研究采用数值模拟得到的观测数据学习CPD及CPT的参数. 考虑到杆件加工时截面几何尺寸不可避免地存在误差，定义各杆件的截面积为服从正态分布的随机变量. 在外荷载方面，设桁架下平纵梁均布荷载（恒荷载）为确定值，而作用于桁架下平纵梁的移动集中荷载（活荷载，如车辆荷载）在运营阶段存在幅值变化，考虑不确定性将外荷载设定为服从正态分布的随机变量. 构建一组BN观测数据的具体步骤如下：1）建立桁架的数值模型，对上述2种随机变量进行蒙特卡洛抽样，将得到的一组变量样本输入数值模型；2）计算恒荷载及活荷载在沿下平纵梁移动过程中各单元的最大应力；3）结合材料的本构关系判断各下平纵梁单元的状态：“弹性”、“塑性”或“破坏”；4）通过桁架下平纵梁的破坏与否来判断桁架结构体系的安全状态（“安全”或“破坏”）. 重复上述步骤获得 $ n $组用于CPD和CPT参数学习的观测数据；最后采用最大似然估计法，根据观测数据与变量参数间的相似程度判断观测数据与模型的拟合程度. 似然函数的一般形式为

(6) $ L(\theta ;D) = P(D|\theta ) = \prod\limits_{m=1}^M {P({x_i^m}|\theta )} . $

式中：D为观测数据集合； $\theta $为CPD和CPT中表示条件概率的参数； ${x_i^m}$为BN节点X_i的第m个观测数据， $M$为观测数据集合D中的数据量.

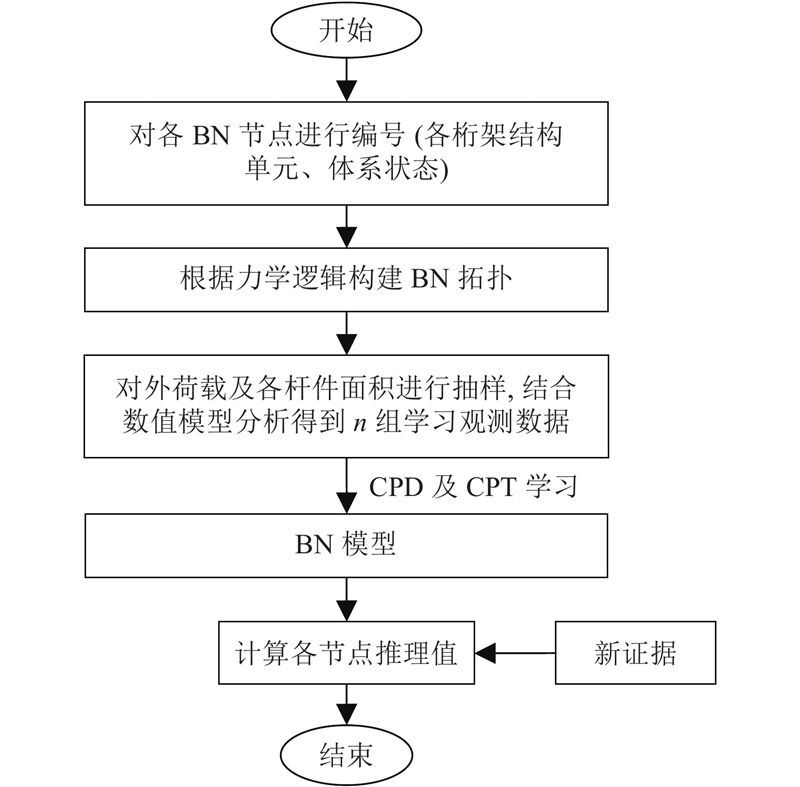
基于连续型BN的桁架安全性评估可以分为以下步骤（见图2）. 1）对各桁架结构单元、体系状态进行BN节点编号. 2）选取具有代表性的荷载组合（恒荷载和移动荷载的样本均值）作用于桁架结构，计算荷载移动过程中各杆件最大应力σ_max与极限应力σ_b的比值 $ {\gamma _i} = {{{\sigma _{\max }}} / {{\sigma _{\rm{b}}}}} $. 3）对于桁架中交汇于一点的相邻单元，其BN节点间通过有向弧连接，有向弧的方向为 $ {\gamma _i} $大的杆件指向 $ {\gamma _i} $小的杆件，依此类推. 对于相连于同一节点且 $ {\gamma _i} $大小相等的2个单元，以离顶层父节点近的杆件指向离顶层父节点远的杆件. 最后得到桁架单元层次的BN拓扑. 4）设置一个桁架体系状态节点，并将离散化的下平纵梁单元节点均通过有向弧指向体系节点，此时下平纵梁单元间没有联系，得到体系的BN拓扑. 再将体系BN与单元BN合并，形成嵌套拓扑模式. 5）使用2.3节介绍的方法获得 $ n $组用于CPD和CPT参数学习的观测数据，用于学习CPD和CPT的参数. 至此用于桁架安全性评估的力学BN构建完成. 6）在有新证据加入时，采用BN推理各单元的最大应力、下平纵梁单元状态概率和桁架体系状态概率.

须说明的是，用于CPD和CPT参数学习的观测数据来自于数值模拟，包括所有杆件和系统节点的不同状态，符合土木工程的实际情况（即结构具有唯一性，难以获取大量测试样本）. 而证据指的是实际观测中所获取的某个或部分节点（单元）状态信息，即在利用力学BN评估桁架安全性时，无须获取所有节点信息，增强了实用性.

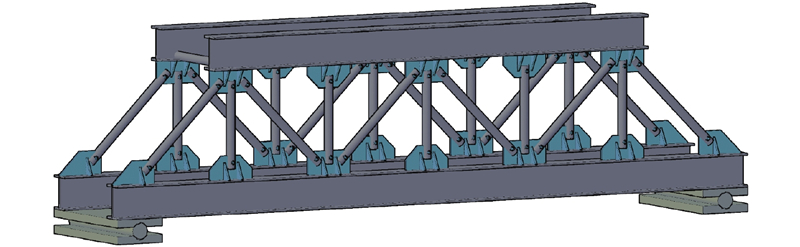
如图3所示，本研究采用一榀三维钢桁架模型验证所提出方法的可行性，此类桁架形式常见于铁路桥梁，具有典型性. 上、下平纵梁采用H型钢，高度h=100 mm，宽度w=100 mm，截面积A=2159 mm²，惯性矩I_x=3.86×10⁶ mm⁴，I_y=134×10⁶ mm⁴. 腹杆采用外径17 mm、内径13 mm的钢管，截面积为94 mm². 腹杆通过螺栓与节点板进行连接，连接处腹杆为实心，节点板焊接于上下平纵梁相应位置. 在杆件材料特性方面，弹性模量均值为188 GPa，屈服强度为365 MPa，极限抗拉强度为536 MPa. 如图4所示，在下平纵梁处作用均布恒荷载，g=120 kN/m；此外，还作用了一沿下平纵梁纵向移动的随机荷载Q，服从均值为60 kN的正态分布，以模拟行驶于桥上的车辆荷载.

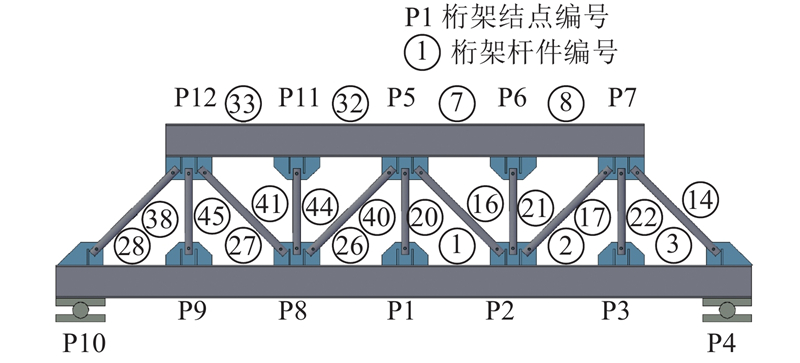
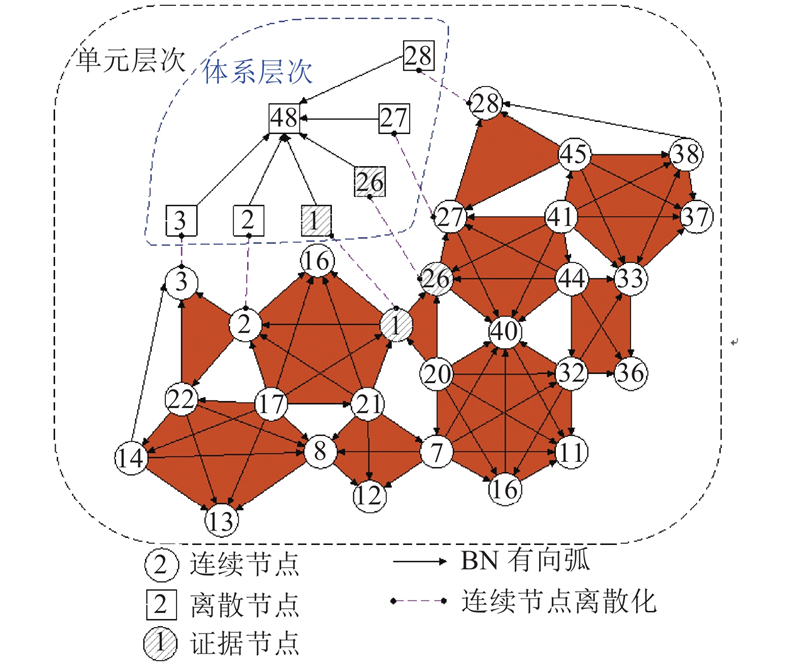
对桁架结构模型中各构件单元进行编号，如图5所示. 设BN节点编号①、②、③ $、\cdots、 $㊼分别表示桁架单元（杆、梁）①、②、③ $、\cdots、 $㊼， ${\boxed{48}}$节点定义为体系状态节点. 以桁架结构的正面一侧为例，分析其BN拓扑图.

首先，设恒荷载为g=120 kN/m，移动荷载为60 kN，计算荷载移动过程中各杆件的最大应力σ_max与材料极限应力σ_b的比值 $ {\gamma _i} = {{{\sigma _{\max }}}/ {{\sigma _{\rm{b}}}}} $. 由于各杆件是通过桁架结点进行连接的，在任一结点Pi上都会形成力的平衡关系，同一结点Pi相连的各杆件所对应的BN节点之间通过有向弧进行连接. 对图5中的桁架结点P1进行分析，与其连接的有3根杆件，编号为：①、⑳、㉖，这3个BN节点通过有向弧连接，有向弧的方向为γ大的指向小的杆件. 以此类推，以桁架结点Pi为单位，对每个桁架结点Pi进行拓扑分析，从而得到如图6所示单元层次的拓扑. 图中，橙色部分表明各单元节点连接于同一桁架结点Pi.

桁架体系节点编号为 ${\boxed{48}}$，为离散节点，包含2种状态：安全和破坏. 与此同时，离散化的下平纵梁节点包含3种状态：弹性、塑性和破坏. 下平纵梁的受力状态均对体系的安全性能有影响，因此代表下平纵梁的离散化节点 ${\boxed{\,1\,}}$、 ${\boxed{\,2\,}}$、 ${\boxed{\,3\,}}$、 ${\boxed{26}}$、 ${\boxed{27}}$、 ${\boxed{28}}$通过有向弧指向体系节点 ${\boxed{48}}$，以构建体系层次的BN拓扑. 最后，如图6所示，将单元BN拓扑和体系BN拓扑相结合，通过嵌套的方式得到用于桁架结构安全性评估的BN拓扑.

假设恒荷载g=120 kN/m，为确定值；移动荷载Q服从正态分布，均值为60 kN，标准差为18 kN（以90%概率落在区间 $ \left[ {0.5 \times 60,1.5 \times 60} \right] $ kN）；各桁架杆截面积A服从正态分布，均值为95 mm²，标准差为11.4 mm²（以90%概率落在区间 $ \left[ 0.8 \times 95, $ $ 1.2 \times 95 \right] $ mm²）. 为了简化分析，定义杆件材料本构为双线性随动强化模型，切线模量取弹性模量的0.2倍，即 $188 \times 0.2 = 37.6$ GPa.

对截面积和外荷载进行抽样，结合有限元分析得到不同样本下各单元最大应力. 随后对各下平纵梁单元进行状态划分：“弹性”、“塑性”或“破坏”，同时根据当前下平纵梁单元的状态判断桁架状态为“安全”或“破坏”. 然后将所有单元最大应力、下平纵梁状态和体系节点状态作为1组观测数据，并以同样方法获取了10000组观测数据，用于学习连续型BN节点的CPD参数及离散型节点的CPT参数.

为了验证BN安全评估的效果，构建一组参考数据，各参数为确定值. 当移动荷载为60 kN时，通过数值模拟计算出各单元最大应力和体系状态，获得1组数据（48个节点），用于对比BN模型的推理结果. 在荷载移动过程中，单元⑰、⑲、㉑、㉒、㉔、㉕、㊶、㊸、㊹、㊺、㊻、㊼陆续进入塑性，下平纵梁均为弹性状态，体系的状态为安全.

为了模拟在实践中受监测成本和安装条件的限制而只能监测部分构件的情况，选取下平纵梁跨中的3个梁单元以及1个内力较大的杆单元作为已知证据点，分别为节点①、④、㉖、㊸. 假设其中4个节点变量（节点①、④、㉖的最大应力均为178.5 MPa，节点㊸的最大应力为382.2 MPa）是已知的.

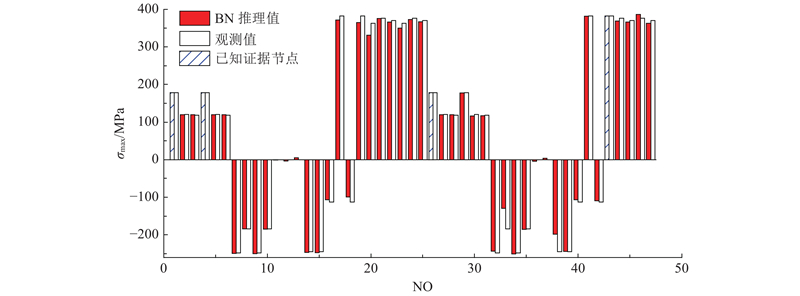
将已知节点变量作为证据输入BN模型中，对其他节点进行BN推理，将得到的结果与有限元分析结果进行对比，如图7所示. 图中， ${\sigma _{\max }} $为最大应力，NO为节点编号，1~10、26~35号节点为上下平纵梁单元编号，11~25、36~47号节点为各杆件单元节点，采用决定系数 ${R^2}$^[23]来表征BN推理值和观测值的符合程度， ${R^2} = 0.999\;2$，非常接近1.0，表明本研究方法对各单元最大应力的推理值与观测值较符合. 此外，由图7可知，对于纵梁单元的评估结果较为准确，这是由于已知证据节点多为纵梁单元节点，在BN拓扑中纵梁单元节点和已知节点的路径较短，评估效果最好. 其次，图中数根单元的应力均大于250 MPa，相对更为危险. 其中应力评估误差较大的单元为⑳号杆单元，观测值为362.4 MPa，而BN推理值为331.3 MPa，误差为8.6%，相对梁单元，杆单元对体系安全性影响更小，考虑经济性，在接受的范围内可以容许一定的误差. 与此同时，离散化后的下平纵梁单元状态概率如表1所示. 可以看出，下平纵梁单元的状态皆大概率为弹性，与图7中相应单元应力情况基本一致. 此时所推理的体系破坏概率为0.0%. 对单元应力、下平纵梁单元状态概率及体系状态概率的推理结果验证了本研究所提方法的可行性，且体系破坏概率可以为桁架结构的安全性能评估提供量化的参考指标.

（1）当外荷载作用形式明确时，桁架各杆件具有明确的力学关系，也是土木工程结构的特点，可以据此确定桁架构件层次BN拓扑，避免复杂的网络拓扑学习过程.

（2）在已知BN拓扑情况下，采用数值模拟得到的观测数据具有较好的完备性，避免了实际工程中因为成本因素无法监测所有构件的局限性，有利于CPD和CPT的学习，所建立的BN具有较好的推理能力.

（3）本研究方法可以仅根据部分杆件的状态监测结果，较为准确地推算其他单元的最大应力（决定系数 ${R^2} = 0.999\;2$，且离已知单元近的单元效果更佳）、桁架结构体系的状态概率. 观测证据所包含的杆件越多，体系安全性评估结果越准确，且离已知节点路径越短，评估效果越佳，具有较好的应用前景.

作为初步的创新性探索，本研究采用相对简单的桁架结构模型验证其可行性，便于方法示例和理解. 而本研究方法可以拓展于更复杂的结构体系，比如空间网格和受力状况不是特别明确的结构，因为力学BN模型的构建是基于大量样本学习，推理过程根据贝叶斯推断，具备一定的容错性. 当复杂结构在外荷载作用下的构件受力可以分析时，即可进行拓扑构建和参数学习. 当然，为了保证复杂桁架结构安全评估的精度，证据节点的选取和数量有待进一步研究（一般证据节点越多识别效果越好，离证据节点越近的杆件评估精度越好）.