随着微小卫星技术的高速发展,太阳敏感器作为卫星姿态控制系统的重要组成部分,已广泛应用于微小卫星太阳方位角的测量,太阳敏感器、磁强计和陀螺仪组成的联合定姿系统可以满足微小卫星中低精度定姿的要求[1-2]. 根据探测器种类不同,太阳敏感器主要分为图像传感器类数字式太阳敏感器与光电探测器类模拟式太阳敏感器[3]. 针对微纳卫星小体积、低成本与低功耗的要求,许多学者致力于研发适用于微纳卫星的新型太阳敏感器. Antonello等[4]研制基于精密加工针孔与互补金属氧化物半导体(complementary metal oxide semiconductor,CMOS)图像传感器的低成本小体积太阳敏感器,实现了66.2°×51.1°的视场与0.03°(1σ)的精度,其中σ为标准差. Wei等[5]基于图像传感器的剖面检测与检测器多路复用技术,实现了100°视场与0.01°(1σ)的精度. Abhilash等[6]基于双三角形光电探测器配合微机电系统(micro-electro-mechanical system,MEMS)加工狭缝式掩模孔,实现了±62°的视场与0.5°(1σ)的精度. 与数字式太阳敏感器相比,模拟式太阳敏感器一般精度较低,但结构、原理更简单,体积、重量、功耗与成本更占优势. 出于对星上资源的权衡,微小卫星更倾向于使用模拟式太阳敏感器[7-8].
四象限模拟太阳敏感器[9]具有极低功耗、极小体积、低复杂度、低成本与高可靠性,国内外多家单位均基于该原理研制了多种型号的太阳敏感器,已应用于多颗卫星中[10-12]. 由于探测器件抗高、低温与抗空间辐照性能特别优异,特别适合采用分体式设计应用于太阳能帆板的对日定向与跟踪过程[13]. 随着航天任务的日益复杂,要求四象限模拟太阳敏感器精度尽可能地提高,在不采用高功耗大体积高精度器件的前提下,实现微纳卫星中等精度定姿任务,满足太阳能帆板高精度对日定向与跟踪的要求. 实践证明,对太阳敏感器进行精确建模并作出相应误差补偿与精密标定,是一种廉价且有效提高精度的方法. Fan等[14]对编码式太阳敏感器的误差因素进行分析和仿真,建立包含结构误差和细码算法误差的误差补偿模型,提出相应的内、外参数精确建模的模型参数标定方法. 实验结果表明,精度平均提升了3倍. Yousefian等[15]分析6个光电二极管组成的太阳敏感器阵列,将系统误差分为制造误差、环境光散射与光电二极管模型误差,给出相应的校准程序与环境光模型,将敏感器精度从2.63°(1σ)降低为0.83°(1σ).
许多学者针对四象限模拟太阳敏感器,作了相应的分析建模工作. 冯邈等[16]通过建立5次曲面拟合方程,对四象限模拟太阳敏感器的太阳矢量输入值与测量值直接进行拟合,取得了±60°的视场与0.5°(1σ)的精度,但引入的参数过多,且模型缺乏实际含义,效果不理想. 王春宇等[17]针对装配环节偏差导致的四象限模拟太阳敏感器测量误差问题,提出对装配环节主要误差源进行定量分析的方法,但没有分析机械加工误差,也没有给出完备的补偿方法与补偿过程. 徐晓丹等[18]针对四象限模拟太阳敏感器硅光电池各象限的光生电流采集精度,分析测量链路各环节可能引入的误差,对各环节的综合误差进行标定和修正,从而有效提升了测量精度,但是各环节测试过程均采用实验测量方法,对设备要求精度较高,测试过程较繁琐.
针对上述研究的不足,本文从四象限模拟太阳敏感器的工作原理出发,分析光生电流的测量过程,对太阳光入射遮光罩后的投影关系进行建模. 考虑电流测量误差、机械误差与遮光罩误差,提出高精度的误差补偿方法. 针对标定测试生产工序,设计全流程自动化标定测试方法.
1. 结构与工作原理
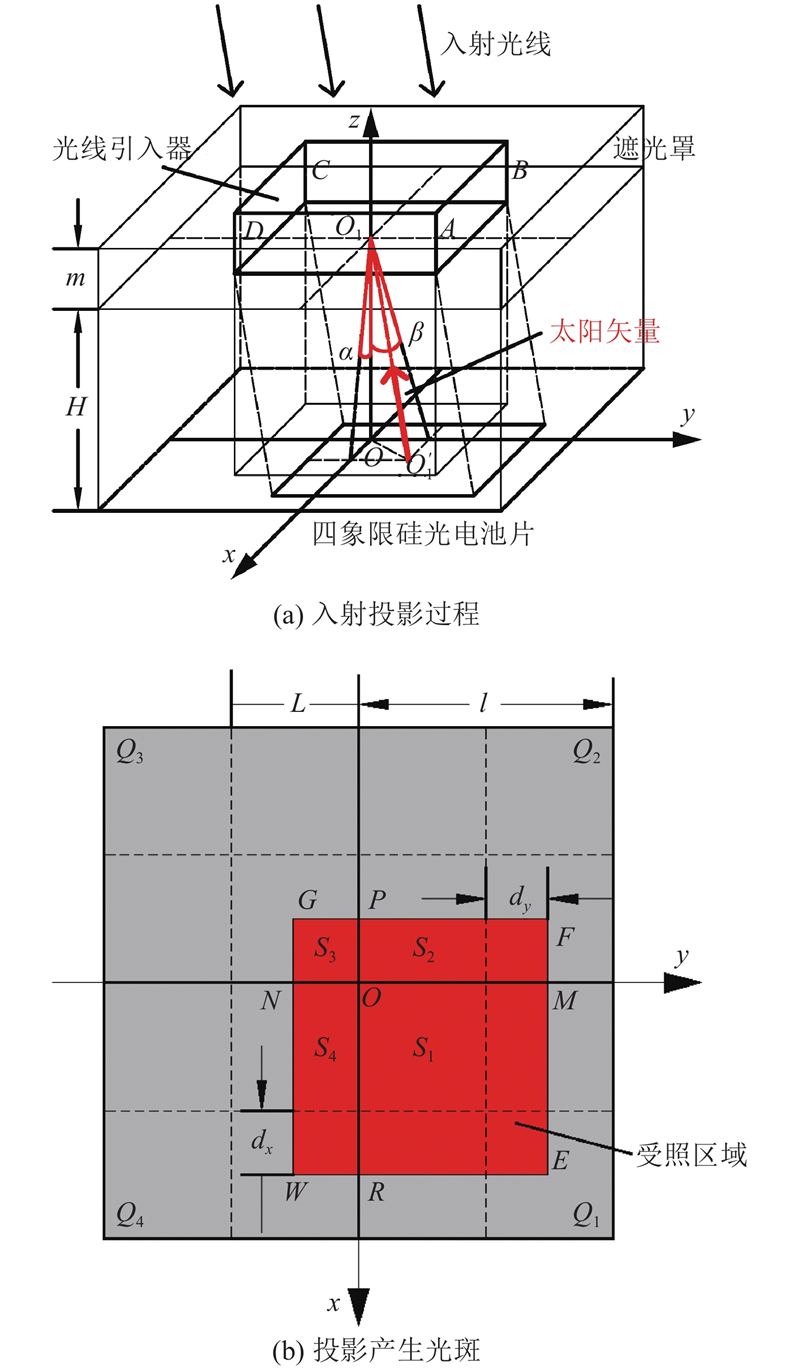
四象限模拟太阳敏感器(简称模拟太阳敏感器)底部是1片边长为2l的方形硅光电池片,被蚀刻为4片硅光电池片(Q1、Q2、Q3和Q4),中心点为O,如图1(a)所示,四象限硅光电池片构成1个Oxyz坐标系. 在四象限硅光电池正上方平行设置带有正方形光线引入器的遮光罩,光线引入器中心O1位于轴Oz上,且4边分别与轴Ox、Oy平行,A、B、C、D分别为光线引入器的4个角点,依次位于Oxy平面的第一、二、三、四象限.
图 1
图 1 四象限模拟太阳敏感器测量过程示意图
Fig.1 Schematic diagram of measurement process of four-quadrant analog sun sensor
式中:I1、I2、I3和I4为硅光电池片各象限光生电流,
联立方程组(1),可得中心坐标的计算公式为
定义太阳在Oxyz坐标系的位置为太阳矢量方向,定义图1为太阳光从第三象限入射,则有
式中:H为遮光罩光线引入器底面到电池片表面的距离,α为太阳矢量在xOz平面上的投影与z轴的夹角,β为太阳矢量在yOz平面上的投影与z轴的夹角,定义图1中α与β为正方向. 注意有2L≤l,否则在视场边缘会不满足上述投影关系与式(1)~(3). 由此可得,模拟太阳敏感器视场角为
2. 误差分析
探究模拟太阳敏感器的电流测量过程与太阳光的入射投影过程,分析电流测量误差、机械加工与安装误差与忽略遮光罩厚度导致误差的影响程度.
2.1. 电流测量误差
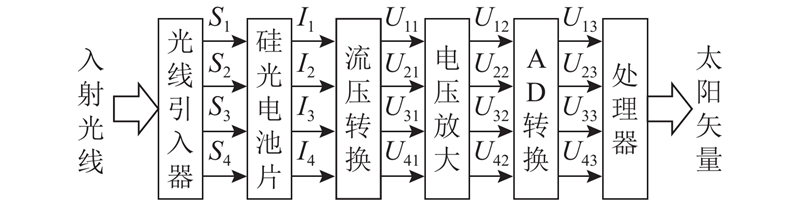
模拟太阳敏感器测量的基础是考虑四象限硅光电池片产生的光生电流能被精准测量且测量过程不存在差异性,实际的测量过程如图2所示.
图 2
图 2 模拟太阳敏感器光生电流的测量过程
Fig.2 Measurement process of analog sun sensor photocurrent
考虑电流测量误差的影响,可得
式中:Ii为四象限硅光电池片光生电流,Ui1为各象限流压转换后的电压,Ui2为各象限电压放大后的电压,Ui3为各象限模数转换后的电压,kij、bij为各象限测量过程的各项响应系数与系统偏置,vij为各象限测量过程中的系统噪声与测量误差,Si为各象限硅光电池片投影产生太阳光斑的面积,i=1,2,3,4,j=1,2,3,4,可以简化为
式中:响应系数
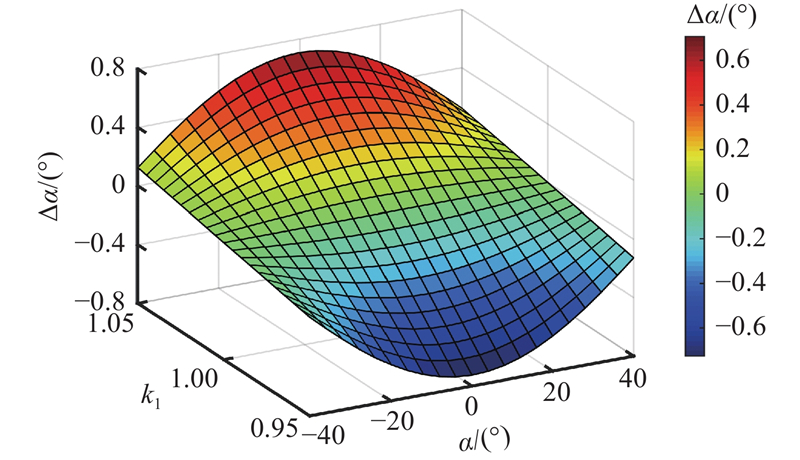
图 3
图 3 电池片1响应系数对模拟太阳敏感器精度影响
Fig.3 Influence of response coefficient of silicon photodiode 1 on precision of analog sun sensor
由此可见,四象限硅光电池片各探测回路响应系数的偏差将直接影响太阳敏感器的测量精度,应被精密测量或标定出来并加以补偿.
2.2. 机械加工与安装误差
模拟太阳敏感器的精度受机械加工精度与安装精度的共同影响. 遮光罩的机械加工精度往往不高,特别是在低成本器件上,加工误差不可忽略;安装工艺往往要求不高,意味着会引入较大的相对位置误差. 下面对各个过程的误差进行分析.
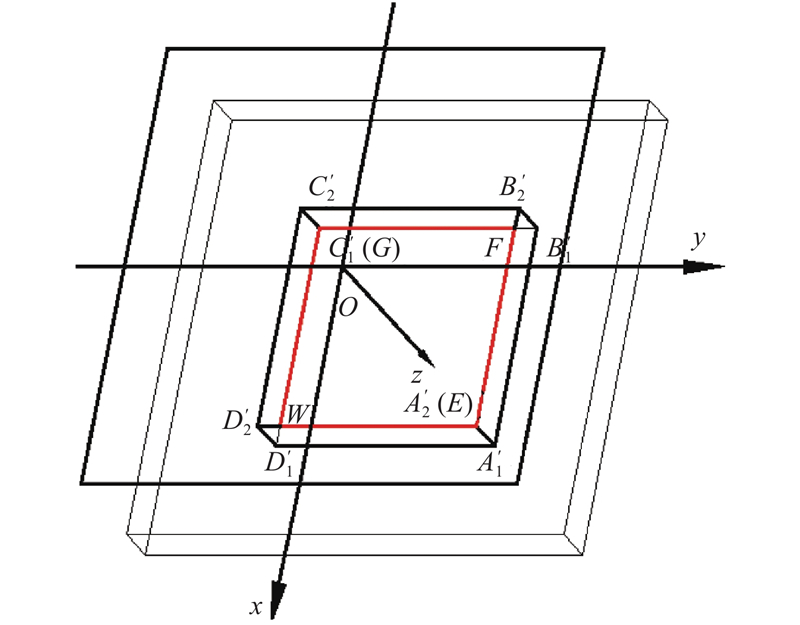
式中:A、B、C、D为A、B、C、D各点坐标向量,h为遮光罩光线引入器底面到硅光电池片表面的实际距离,L1为与光线引入器x轴平行的2条边长的一半,L2为光线引入器与y轴平行的2条边长的一半,dx0、dy0为光线引入器中心相对于硅光电池片中心的水平偏移.
在投影过程中,当太阳光线经过光线引入器时,考虑机械误差后投影形状仍为一个四边形,由此确定光线引入器的4个角点的投影位置,即可确定光斑投影分布. 投影过程可以采用以下矩阵表示:
由此可以得到遮光罩光线引入器的4个角点A、B、C、D经过偏移与投影后对应点E、F、G、W在Oxyz坐标系下的位置为
式中: E、F、G、W为E、F、G、W各点的坐标向量.
2.3. 忽略遮光罩厚度导致误差
光线引入器本身会设计斜台结构,以尽力消除厚度的影响,但是实际上边缘处的厚度相较于遮光罩高度h不可忽略[9]. 考虑太阳光从第三象限入射的情况,即当
式中: m为遮光罩厚度,
如图4所示,标注点均为 Oxy平面上的投影点,太阳光从第三象限入射,设投影四边形4个顶点为
图 4
图 4 太阳光从第三象限入射投影示意图(α = 25°,β = 25°)
Fig.4 Schematic diagram of sunlight incidence from third quadrant (α = 25°, β = 25°)
根据四边形的4个顶点坐标,可以计算出四边形面积. 在0≤α≤90 °,0≤β≤90 °的条件下,不考虑电流检测的差异,按照理想情况的式(1)~(3)可知,直接得到的测量值为
式中:α与β为实际的太阳入射角,
考虑到视场角会发生变化,式(4)退化为
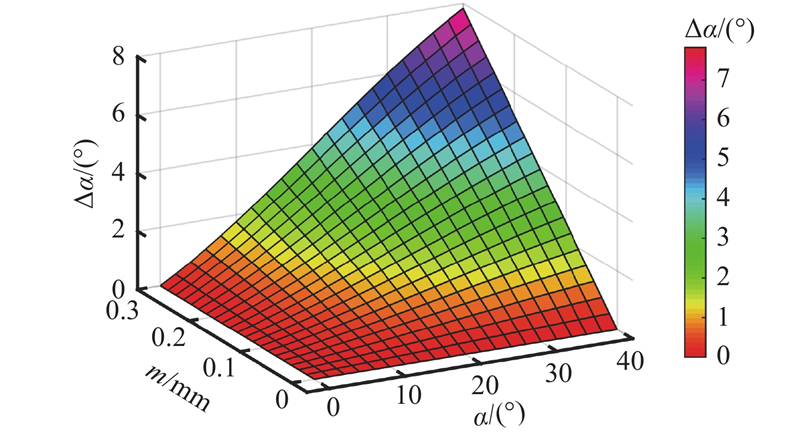
在−40°≤α≤40°,β=0°的条件下,取h=1 mm,L1=L2=1 mm,dx0=dy0=0,当式(13)中m变化时,对模拟太阳敏感器精度的影响如图5所示. 可以看出,m越大,对测量精度的影响越大,且α绝对值越大,作用越明显,同理对于β有类似结论. 为了保证模拟太阳敏感器视场,四象限硅光电池片的边长l限制了h,受加工条件的限制,m相对于h不可忽略.
图 5
图 5 遮光罩厚度对模拟太阳敏感器精度的影响
Fig.5 Influence of optical mask thickness on precision of analog sun sensor
结合式(14)与图5可以得出,遮光罩偏移误差、开孔误差、高度误差、遮光罩厚度对模拟太阳敏感器精度的影响复杂且明显,原有的测量公式会引入较大误差,需要对上述误差源进行控制与补偿.
3. 误差补偿方法
误差补偿是以模拟太阳敏感器的精确模型为基础,考虑各环节存在的误差,给出含有待定参数的矢量输出公式. 根据标定实验对待定参数进行整定,有效提高敏感器的精度.
根据式(6)对实际测量得到的各路电压Ui3进行比例系数与系统偏置的补偿:
根据式(2),可得
式中:Kx为x轴系数,Ky为y轴系数.
根据前面的结论,考虑误差源dx0、dy0、L1、L2、h、m,求解S1、S2、S3、S4的表达式,从而解算α、β与Kx、Ky之间的对应关系. 在根据所测得的电流之比计算太阳矢量时,不应采用待定量α与β作为判据,应根据Kx、Ky进行判断,由此解算公式为
利用式(15)~(17)可以补偿前述的电流测量误差、遮光罩偏移误差、开孔误差和高度误差,忽略遮光罩厚度导致误差对太阳敏感器精度的影响.
4. 标定流程设计
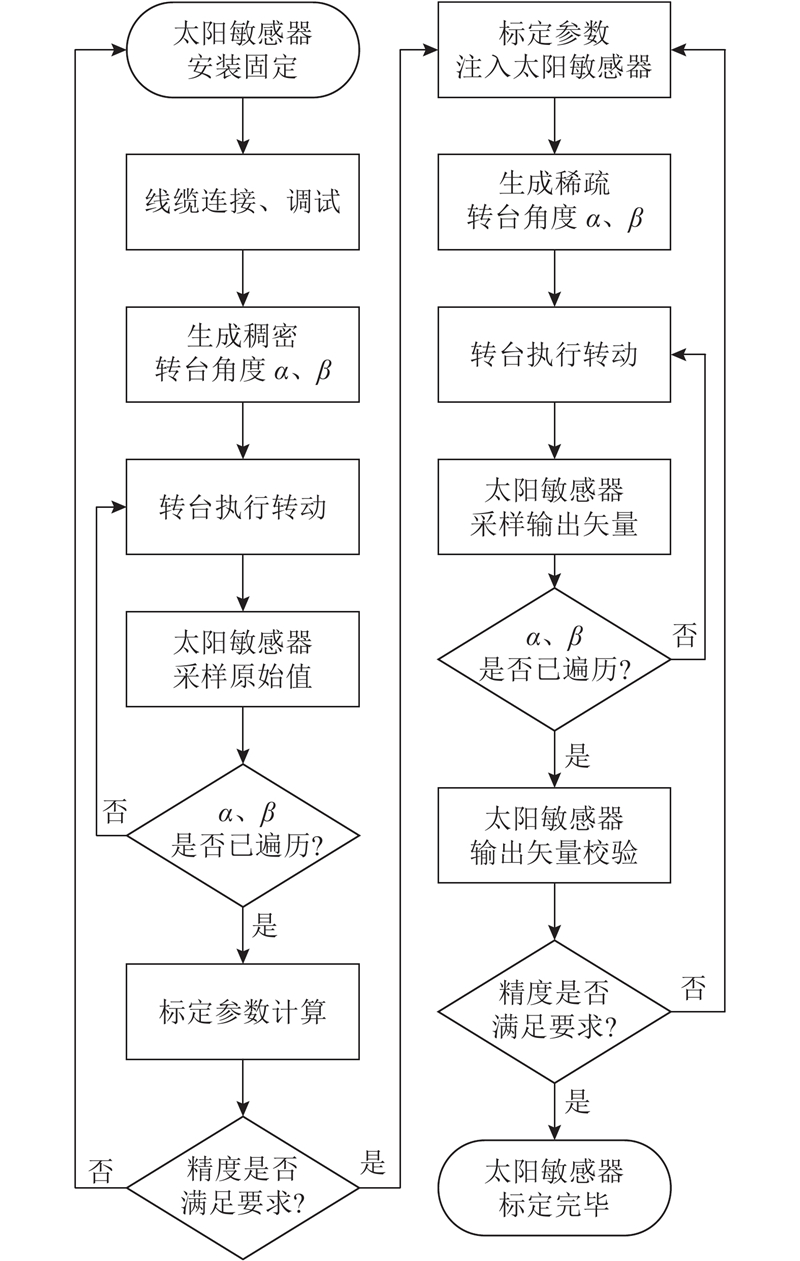
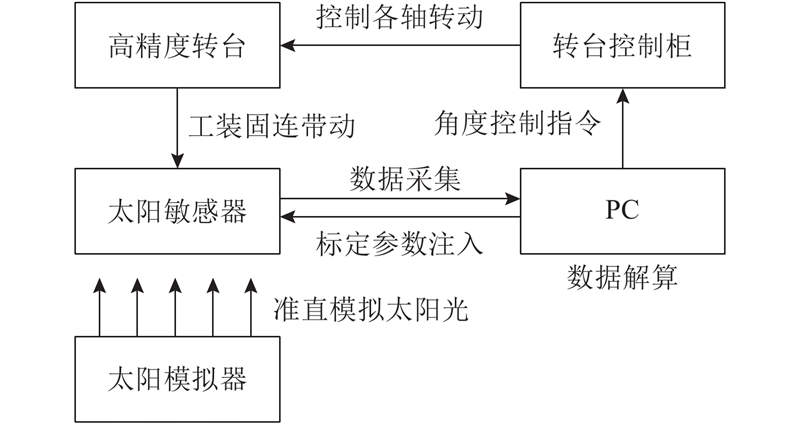
针对模拟太阳敏感器生产中的标定测试过程,设计全流程自动化标定与参数注入方法,具体的标定流程如图6所示. 该标定方案采用1台控制电脑同时连接并控制高精度转台与模拟太阳敏感器,通过程序设计实现自动化操作,保证动作序列的连贯性. 由此可以快速大批量地进行模拟太阳敏感器标定测试,为模拟太阳敏感器的低成本与大规模应用提供可靠依据.
图 6
图 6 模拟太阳敏感器的自动标定与参数注入流程
Fig.6 Calibration and parameter injection process of analog sun sensor
5. 实验结果
图 7
图 8
图 9
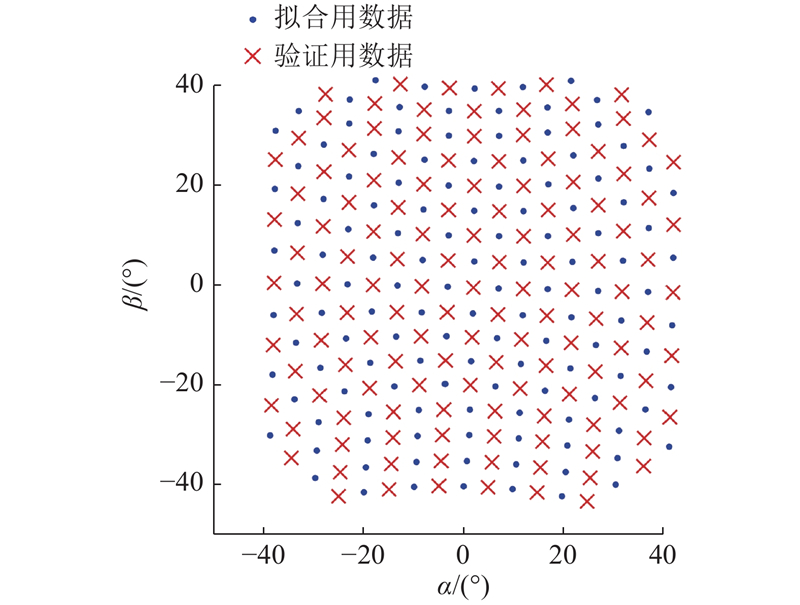
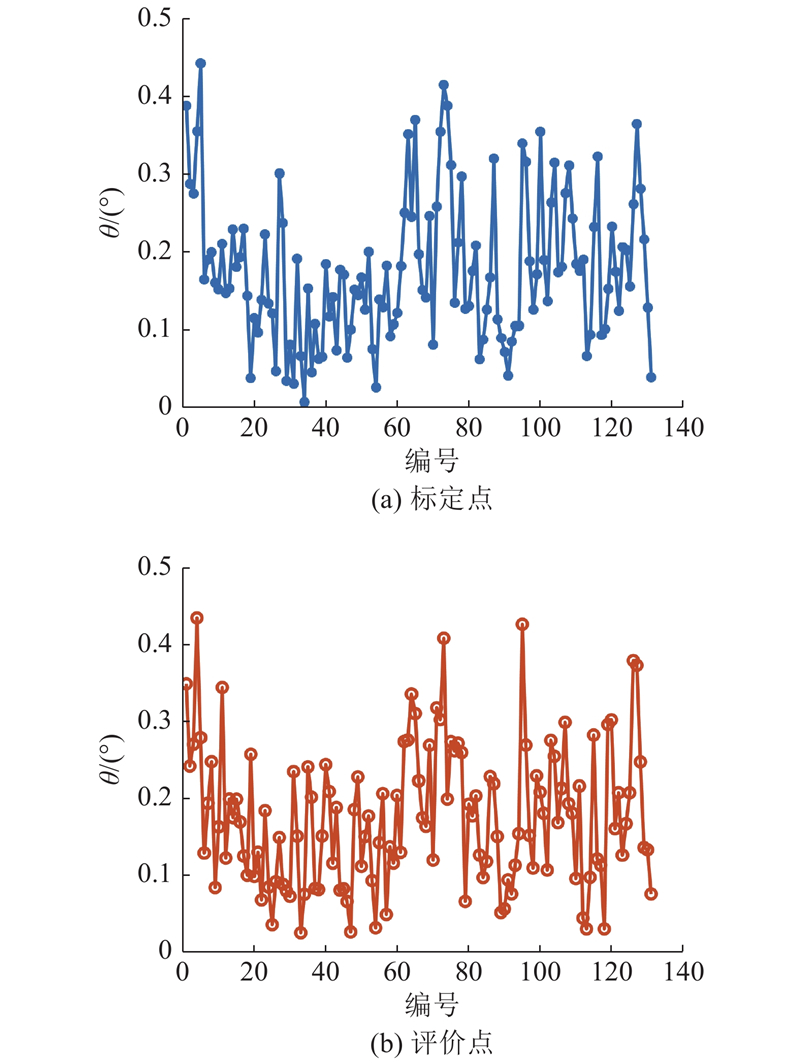
图 9 标定点和评价点的数据分布
Fig.9 Data distribution of calibration points and evaluation points
选取1批共10台模拟太阳敏感器进行实际测试,采用的模拟太阳敏感器均为按照文献[9]介绍的设计方案近期重新生产的产品. 实际测验的结果表明,应用自动化标定流程在8 h内完成了所有敏感器的标定与参数注入工序. 与原先的标定流程相比,全程自动化操作的标定效率有大幅度提升.
在标定过程中,模拟太阳敏感器每一个测试点的残差为
式中:V为实际输入的太阳矢量估计值;S为敏感器实际输出的太阳矢量测量值;偏差角θ为V与S之间的夹角,以θ作为残差.
在系统参数的拟合过程中,以最小化所有标定点的残差平方和为目标,求解待定系统参数的最优解,即最小化下式:
式中:t为所有测试点中用于标定后精度评价的标定点数量,J为代价函数[20].
在标定后精度评价过程中,每一个模拟太阳敏感器的标定后精度评价指标定义为
式中:Δθ为该模拟太阳模拟器的统计偏差角[19],n为所有测试点中用于标定后精度评价的评价点数量.
应用式(16)~(18),对太阳敏感器进行误差补偿. 某台模拟太阳敏感器的标定点与评价点的偏差角θ分布如图10所示. 可以看出,2组数据均呈随机分布,卡方检验证实2组数据均呈随机正态分布,证明拟合得到的系统参数具有较好的普适性. 该台模拟太阳敏感器的Δθ为0.154°.
图 10
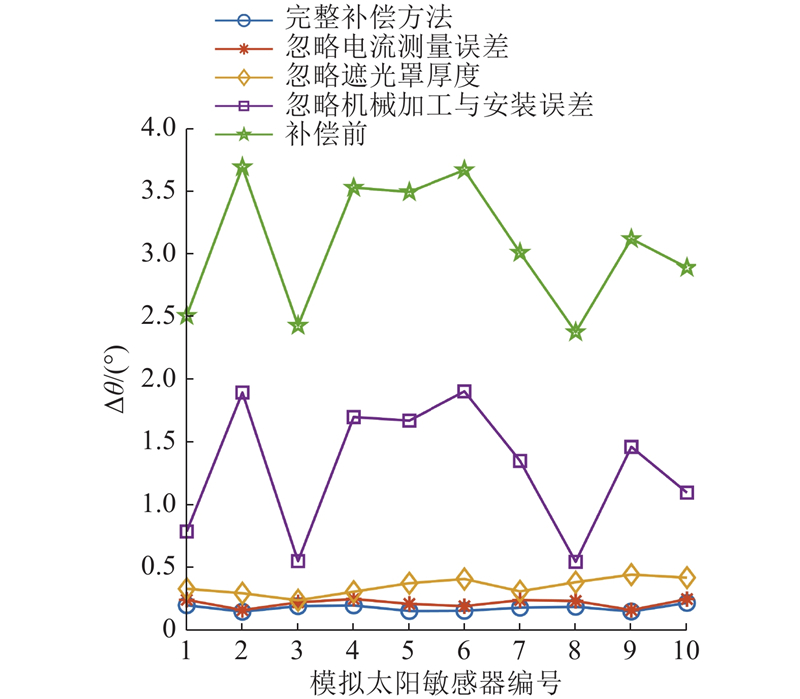
为了评估误差补偿方法的效果,设置5种工况:1)采用完整误差补偿方法;2)忽略电流测量误差的影响,即将ki均固定为1,bi均固定为经验值(该实验中选为100);3)忽略遮光罩厚度的影响,即将m固定为0;4)忽略机械加工与安装误差,即依据设计值,将L1、L2固定为1 mm,dx0与dy0固定为0,h固定为1 mm;5)同时忽略电流测量误差的影响、遮光罩厚度和机械加工与安装误差的影响,作为补偿前结果供参考. 5种工况均采用相同设置,开展迭代计算. 在每种工况下,对各台模拟太阳敏感器进行系统参数拟合,计算各组数据的统计偏差角Δθ. 为了评估各工况下模拟太阳敏感器的标定效果,计算每种工况下所有敏感器统计偏差角的均值
表 1 模拟太阳敏感器标定后的精度评估
Tab.1
| 补偿方法 | | σΔθ /(°) |
| 完整补偿方法 | 0.177 | 0.025 |
| 忽略电流测量误差 | 0.215 | 0.034 |
| 忽略遮光罩厚度 | 0.350 | 0.065 |
| 忽略机械加工与安装误差 | 1.296 | 0.525 |
| 补偿前 | 3.072 | 0.514 |
图 11
图 11 模拟太阳敏感器标定后的精度评估
Fig.11 Accuracy evaluation of analog sun sensor after calibration
6. 结 语
(1)在±40°范围内,10台模拟太阳敏感器补偿前平均精度为3.072°(1σ),补偿后平均精度达到0.177°(1σ),且波动较小,证明利用该误差补偿方法可以稳定、可靠地提高模拟太阳敏感器的精度.
(3)在模拟太阳敏感器的3种误差源中,对精度影响从大到小排序依次为机械加工与安装误差、忽略遮光罩厚度导致误差及电流测量误差,且机械加工与安装误差为主要误差来源.
在应用上述误差补偿方法之前,应控制误差源以尽量减小误差的影响. 误差补偿方法通过实验标定方法尽可能提高敏感器精度,不能解决前述误差引发的视场角退化问题. 四象限模拟太阳敏感器精度上限的来源是四象限硅光电池片光生电流测量电路的噪声,该噪声可以采用更先进的电路设计手段进行抑制,也可以采用后续滤波算法进行处理. 后续应依据高精度模型,优化结构与电路设计方案,减小加工误差与安装误差,设计精度更高的太阳敏感器.
参考文献
皮纳卫星姿控系统分层式故障检测
[J].
Hierarchical fault detection for nano-pico satellite attitude control system
[J].
Development of a low-cost sun sensor for nanosatellites
[J].DOI:10.1016/j.actaastro.2018.01.003 [本文引用: 1]
A highly accurate wireless digital sun sensor based on profile detecting and detector multiplexing technologies
[J].DOI:10.1016/j.ymssp.2016.05.004 [本文引用: 1]
Micro digital sun sensor with linear detector
[J].DOI:10.1063/1.4958696 [本文引用: 1]
基于太阳能电池板的皮卫星最优姿态确定算法
[J].DOI:10.3785/j.issn.1008-973X.2010.09.015 [本文引用: 1]
Optimal attitude determination method for pico-satellite using solar panels
[J].DOI:10.3785/j.issn.1008-973X.2010.09.015 [本文引用: 1]
四象限差动式模拟太阳敏感器设计
[J].DOI:10.3969/j.issn.1004-1699.2012.12.007 [本文引用: 4]
Design of four-quadrant analog sun sensor
[J].DOI:10.3969/j.issn.1004-1699.2012.12.007 [本文引用: 4]
Flexible attitude control design and on-orbit performance of the ZDPS-2 satellite
[J].DOI:10.1016/j.actaastro.2016.10.020 [本文引用: 1]
A filtered sun sensor for solar tracking in HCPV and CSP systems
[J].
Error modeling and calibration for encoded sun sensors
[J].DOI:10.3390/s130303217 [本文引用: 1]
Fabrication, characterization, and error mitigation of non-flat sun sensor
[J].DOI:10.1016/j.sna.2017.05.022 [本文引用: 1]
低成本小型无线自动太阳敏感器设计与实现
[J].DOI:10.3969/j.issn.1001-506X.2019.08.24 [本文引用: 2]
Design and realization of low-cost micro wireless automatic sun sensor
[J].DOI:10.3969/j.issn.1001-506X.2019.08.24 [本文引用: 2]
双轴模拟式太阳敏感器的误差源分析
[J].DOI:10.3969/j.issn.1674-1579.2016.01.008 [本文引用: 2]
Analysis of error sources existing in dual-axial analog sun sensor
[J].DOI:10.3969/j.issn.1674-1579.2016.01.008 [本文引用: 2]
双轴模拟式太阳敏感器测试链误差分析及修正
[J].
Error source analysis and compensation in test chain for dual-axial analog sun sensor
[J].
内外参数精确建模的太阳敏感器标定
[J].
Sun sensor calibration based on exact modeling with intrinsic and extrinsic parameters
[J].