浙江大学学报(工学版)

浙江大学学报(工学版), 2021, 55(10): 1968-1977 doi: 10.3785/j.issn.1008-973X.2021.10.019

机械与能源工程

基于人工神经网络的超临界小火焰模型研究

高正伟,, 金台, 宋昌成, 罗坤, 樊建人,

1. 浙江大学 能源清洁利用国家重点实验室，浙江 杭州 310027

2. 浙江大学 航空航天学院，浙江 杭州 310027

Application of artificial neural networks to supercritical flamelet model

GAO Zheng-wei,, JIN Tai, SONG Chang-cheng, LUO Kun, FAN Jian-ren,

1. State Key Laboratory of Clean Energy Utilization, Zhejiang University, Hangzhou 310027, China

2. School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 310027, China

通讯作者: 樊建人，男，教授，博导. orcid.org/0000-0002-6332-6441. E-mail： fanjr@zju.edu.cn

收稿日期: 2020-10-29  

基金资助: 国家重点研发计划资助项目（2016YFB0600102）

Received: 2020-10-29  

Fund supported: 国家重点研发计划资助项目（2016YFB0600102）

作者简介 About authors

高正伟（1993—），男，博士生，从事超临界燃烧的数值模拟研究.orcid.org/0000-0003-1455-3493.E-mail：gaozw@zju.edu.cn , E-mail：gaozw@zju.edu.cn

摘要

为了解决超临界小火焰燃烧模型数据库过于庞大，导致计算机内存不足和取值性能下降的问题，提出使用人工神经网络（ANN）进行建库的超临界小火焰/过程变量模型FPV-ANN. 在先验性分析及在超临界水热火焰的大涡模拟计算中发现，FPV-ANN方法在温度、组分和其他目标变量的分布与传统FPV方法得到的结果吻合，说明FPV-ANN方法的准确性与传统FPV方法一致. 由于人工神经网络小火焰库大小只有传统库的1%，FPV-ANN方法在大规模并行计算中消耗更少的计算机内存. FPV-ANN方法的计算速度比传统FPV方法提升了30%. 可以看出，提出的FPV-ANN方法具有更好的计算性能.

关键词： 小火焰模型 ; 燃烧模拟 ; 人工神经网络(ANN) ; 小火焰库建库方法 ; 计算性能

Abstract

Artificial neural networks (ANN) were utilized to build the library for the flamelet/progress variable (FPV) model and develop the FPV-ANN approach aiming at the problem that the enlarged lookup tables of the flamelet-based combustion model make the computer memory insufficient and slow down the interpolation process. Both the priori analysis and the large-eddy simulation of supercritical hydrothermal flames show that the distributions of temperature, species and other target variables obtained by FPV-ANN and classical FPV method achieve overall good agreement, verifying the accuracy of the FPV-ANN approach. Since the size of the ANN library is only 1% of the classical library, the use of FPV-ANN approach can produce a significant reduction in computer memory consumption during the large-scale parallel simulation. The computational speed of FPV-ANN approach is 30% faster than the classical FPV approach, which confirms that FPV-ANN approach has better computational performance.

Keywords： flamelet model ; combustion simulation ; artificial neural network (ANN) ; flamelet library construction method ; computational performance

PDF (1375KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

高正伟, 金台, 宋昌成, 罗坤, 樊建人. 基于人工神经网络的超临界小火焰模型研究. 浙江大学学报(工学版)[J], 2021, 55(10): 1968-1977 doi:10.3785/j.issn.1008-973X.2021.10.019

GAO Zheng-wei, JIN Tai, SONG Chang-cheng, LUO Kun, FAN Jian-ren. Application of artificial neural networks to supercritical flamelet model. Journal of Zhejiang University(Engineering Science)[J], 2021, 55(10): 1968-1977 doi:10.3785/j.issn.1008-973X.2021.10.019

基于查表（tabulated--based）的燃烧模型具有高效的特点，小火焰模型[1-2]（flamelet model）是其中的代表. 小火焰模型假设火焰面是由一组小火焰构成，且小火焰可以用一维简单火焰结构表示，故化学反应数据可以在流场模拟之前计算出来，制作成小火焰库. 在流场模拟过程中，火焰状态量直接从小火焰库中提取，避免了求解能量与组分输运方程. 小火焰模型可以在计算少量输运方程的情况下考虑详细的化学反应机理，得到了广泛研究[3-4].

传统小火焰库是一组多维结构化表格（multi-dimensional structed table）. 小火焰模型通过假设把火焰状态用数个特征量表征出来，特征量的个数通常是小火焰库的维度，小火焰库大小会随着维度的增加而指数型增大，增加计算机内存负担，也使得从数据库中取值性能下降. 这是小火焰方法的维度灾难（curse of dimensionality）[5].

近些年来，国内外学者开始探究小火焰模型的新型建库方法，其中基于人工神经网络（artificial neural network，ANN）的建库方法受到关注并开展相关研究. Matthias等[6]使用传统建库方法（结构化表格）和ANN网络的建库方法，分别模拟甲烷-氢气湍流火焰，提出建立人工神经网络的优化方法（OANNs). Emami等[7]研究层流小火焰模型的ANN建库方法，在非预混湍流CH4/H2/N2火焰的模拟研究中发现，使用ANN库方法的结果准确. Owoyele等[8]提出分组多目标ANN建库方法，这种方法根据组分之间的相互关系把组分进行分组，进而分别训练ANN库，在正十二烷液雾燃烧模拟中发现，这种方法可以准确捕捉熄灭、自着火、两阶段放热等现象. 近期，Zhang等[9]研究基于ANN的小火焰生成流行方法（flamelet generated manifolds，FGM），在液雾燃烧的模拟研究中发现，利用该FGM方法能够准确地预测组分及温度分布.

以上研究表明，基于人工神经网络的小火焰模型方法有很大潜力，但目前主要研究局限在常压的工况下，超临界燃烧下的小火焰模型相关研究很少. 在超临界燃烧中，由于理想气体假设不再适用，要在小火焰模型中耦合真实气体相关的物性模型. 在真实气体效应显著的区域，物理性质会在很小的时空间里出现剧烈变化. 在使用传统方法进行小火焰建库时，需要对各个维度的网格加密. 部分超临界燃烧工况中需要考虑多相燃烧、传热和压力脉动等，这需要提升小火焰库维度，这使得维度灾难问题更加严峻.

本文的主要目标是基于CFD开源数值模拟平台OpenFOAM[10]，发展适用于超临界燃烧的小火焰模型人工神经网络建库方法. 本文研究基于人工神经网络建库小火焰方法的计算精度与计算性能，与传统方法进行对比. 在笔者的前期工作中[11]，发展适用于超临界水热燃烧的小火焰/过程变量（FPV）方法，建立小火焰库. 本文的研究工作以该小火焰库为数据基础，采用人工神经网络建立小火焰库.

1. 数值方法

1.1. 超临界小火焰模型的数学描述

在稳态小火焰模型中，组分守恒和能量守恒方程在混合物分数空间下的表述为[1]

$ \frac{1}{2}\rho \chi \frac{{{\partial ^2}{{{w}}_i}}}{{\partial {Z^2}}} = - {\dot \omega _i} , $
(1)

$ \frac{1}{2}\rho \chi {c_p}\frac{{{\partial ^2}T}}{{\partial {Z^2}}} = \sum\limits_{i = 1}^{{n_{\rm{s}}}} {{h_k}{{\dot \omega }_i}} . $
(2)

式中：ρ为密度；χ为标量耗散率；wi为第i组分的质量分数； $ \dot{{\omega }_{i}} $为第i组分的生成速率；Z为混合物分数，采用Bilger定义方式[12]；cp为比定压热容； $ T $为温度； $ {h}_{i} $为第i组分的焓； ${n}_{{\rm{s}}}$为反应机理中的组分个数. 本文采用17个组分、54步化学反应的详细反应机理[13].

在超临界燃烧中，真实气体效应显著，需要修正小火焰方程中所需的热力学和动力学物性参数. 为了修正密度计算，使用Peng-Robinson状态方程（P-R EOS）[14]，热容与焓的计算公式可以根据P-R EOS的偏差函数（departure function）得到. 为了修正黏性与计算热导率，采用Chung等[15]提出的高压工况下的计算方法. Gao等[11]的研究发现，未考虑真实气体效应的小火焰模型会过高地预测火焰温度，错误地预测火焰位置. 本文基于软件FlameMaster[16]耦合相关的真实气体模型，开发小火焰求解器.

使用小火焰/过程变量模型（flamelet/progress variable，FPV）[17-18]. 化学状态量 $ \phi $由2个火焰特征量确定，表示为

$ \phi = \phi (Z,C). $
(3)

式中：C为过程变量，表示化学反应进程，由下式计算得到：

$ C = {w({{\rm{CO}}})} + {w({{\rm{C}}{{\rm{O}}_2}})} + {w({{{\rm{H}}_2}})}. $
(4)

其中， ${w({{\rm{CO}}})}$、 ${w({{\rm{C}}{{\rm{O}}_2}})}$和 ${w({{{\rm{H}}_2}})}$分别为组分CO、CO2和H2的质量分数.

采用预设概率密度函数（PDF）方法，描述湍流-燃烧耦合的影响[2]. 在大涡模拟中，使用 $ \;\beta $-PDF，考虑亚网格对混合分数 $ Z $的影响，这需要求解混合分数脉动 $ {Z}^{{'}{'}2} $的输运方程. 使用 $ \delta $-PDF，考虑亚网格对过程变量 $ C $的影响. 小火焰库中，化学状态量的Favre平均值表示为

$ \widetilde \phi = \phi (\widetilde Z,\widetilde {{{Z''}^2}},\widetilde C). $
(5)

在实现大涡模拟时，需要求解质量守恒方程、动量守恒方程、混合分数 $ Z $的输运方程、混合分数脉动 $ {Z}^{{'}{'}2} $的输运方程及过程变量 $ C $输运方程，表述为

$ \frac{{\partial \bar \rho }}{{\partial t}} + \frac{{\partial (\bar \rho \widetilde {{u_j}})}}{{\partial {x_j}}} = 0. $
(6)

$ \begin{split} & \frac{{\partial (\bar \rho \widetilde {{u_i}}\widetilde {{u_i}})}}{{\partial t}} + \frac{{\partial (\rho \widetilde {{u_i}}\widetilde {{u_j}})}}{{\partial {x_j}}} = - \frac{{\partial \bar p}}{{\partial {x_i}}} + \hfill \\ & \frac{\partial }{{\partial {x_j}}}\left[(\bar \mu + {\mu _{\rm{t}}})\left(\frac{{\partial \widetilde {{u_i}}}}{{\partial {x_j}}} + \frac{{\partial \widetilde {{u_j}}}}{{\partial {x_i}}} - \frac{2}{3}{\delta _{ij}}\frac{{\partial \widetilde {{u_k}}}}{{\partial {x_k}}}\right)\right]. \hfill \end{split} $
(7)

$ \frac{{\partial (\bar \rho \widetilde Z)}}{{\partial t}} + \frac{{\partial (\bar \rho \widetilde {{u_i}}\widetilde Z)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}\left[\left(\bar \rho \widetilde D + \frac{{{\mu _{\rm{t}}}}}{{{S}{{c}_{\text{t}}}}}\right)\frac{{\partial \widetilde Z}}{{\partial {x_i}}}\right]. $
(8)

$ \begin{split} & \frac{{\partial (\bar \rho \widetilde {{{Z''}^2}})}}{{\partial t}} + \frac{{\partial (\bar \rho \widetilde {{u_i}}\widetilde {{{Z''}^2}})}}{{\partial {x_i}}} = 2\frac{{{\mu _{\rm{t}}}}}{{{S}{{c}_{\text{t}}}}}{\left(\frac{{\partial \widetilde Z}}{{\partial {x_i}}}\right)^2} \times \hfill \\ & \frac{\partial }{{\partial {x_i}}}\left[\left(\bar \rho \widetilde D + \frac{{{\mu _{\rm{t}}}}}{{{S}{{c}_{\text{t}}}}}\right)\frac{{\partial \widetilde {{{Z''}^2}}}}{{\partial {x_i}}}\right] - \bar \rho \widetilde {\chi .} \hfill \end{split} $
(9)

$ \begin{array}{l} \dfrac{{\partial (\bar \rho \widetilde C)}}{{\partial t}} + \dfrac{{\partial (\bar \rho \widetilde {{u_i}}\widetilde C)}}{{\partial {x_i}}} = \hfill \dfrac{\partial }{{\partial {x_i}}}\left[\left(\bar \rho \widetilde D + \dfrac{{{\mu _{\rm{t}}}}}{{{S}{{c}_{\text{t}}}}}\right)\dfrac{{\partial \widetilde C}}{{\partial {x_i}}}\right] + \widetilde {{{\dot \omega }_{\rm{C}}}}. \hfill \end{array} $
(10)

式中： $\overline \phi $和 $\widetilde \phi $分别为变量 $\phi $的平均值和Favre平均值； $ {u}_{\text{­}i} $为 $ i $方向的速度； $ p $为压力； $ \mu $为动态黏性系数； $ {\mu }_{{\rm{t}}} $为亚格子涡黏性，用Smagorinsky模型[19]进行封闭； $ {\delta }_{ij} $为Kronecker delta函数； $ D $为标量的分子扩散系数，使用单位Lewis数假设进行计算； $ S{c}_{{\rm{t}}} $为湍流Schmit数，设置为0.7； $ \dot{{\omega }_{{\rm{C}}}} $为过程变量源项，需要从小火焰库中进行提取得到.

1.2. 传统建库方法

在传统的小火焰建库方法中，为每个化学状态量建立多维结构化表格（multi-dimensional structed table）. 它本质上是多维向量，每个维度代表一个火焰特征量，根据化学状态量的取值范围和所需精度进行离散，未在格子点上的值根据线性插值得到.

增加格子数量会提高小火焰库的准确度，但是会带来小火焰库过大、增加计算机内存开销以及取值速度下降的问题. 每个结构化表格均有3个维度，表征燃料/氧化剂的混合程度、反应与湍流的耦合影响和化学反应进程，分别用 $ Z $、 $ {Z}^{{'}{'}2} $和 $ C $表示. 在小火焰库中，一共为11个化学状态量（即目标变量）建立结构化表格，包括密度 $ \;\rho $、黏性系数 $ \;\mu $、热扩散系数 $ \alpha $、温度 $ T $、主要组分（CH3OH、O2、H2O、CO2、CO、H2）的质量分数以及过程变量源项 $ \dot{{\omega }_{{\rm{C}}}} $. 如表1所示为不同精度下小火焰库的大小. 可以看出，小火焰库的大小会随着各个维度上格子数量的增加而线性增长[5]. 在OpenFOAM中，使用MPI进行并行计算，每个计算核心都需要读取一整套小火焰库. 例如当采用64核心计算时，若使用4.8 GB的小火焰库，则将使用307.2 GB的计算机内存花费在存贮小火焰库上，给计算机系统造成严重负担.

表 1   不同精度下多维结构化表格小火焰库的大小

Tab.1  Size of flamelet libraries with various accuracies built with structed table method

案例 各维度上的格子数（ $ Z\times {Z}^{{'}{'}2}\times C $） 小火焰库大小/MB
1 150×10×50 60
2 300×25×300 600
3 600×50×600 4800

新窗口打开| 下载CSV


对每个标量各个维度上使用的格子数量是150×10×150，分别对应 $ Z $、 $ {Z}^{{'}{'}2} $和 $ C $，总大小约为60 MB. 为了方便表述，将使用传统小火焰库的FPV方法记为FPV-ST（FPV structed table）方法.

1.3. 人工神经网络建库方法

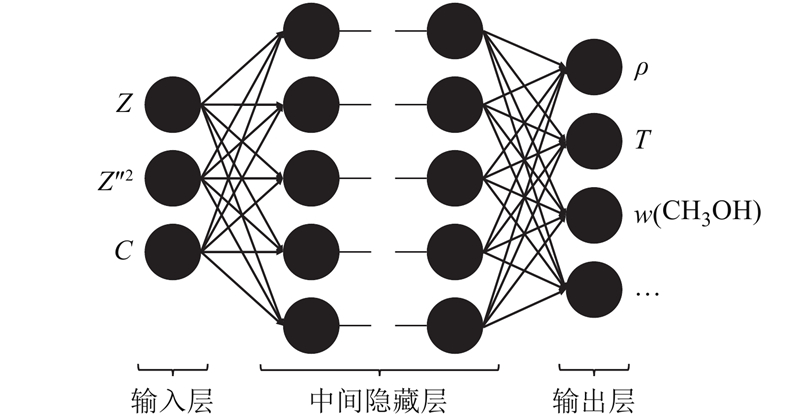
人工神经网络方法（ANN）的灵感来自生物神经网络，它由一组相互连接的人工神经元组成一个或多个输出与输入的网络. 人工神经元本质上是感知机，它由非线性激活函数和偏重组成. 使用的多层人工神经网络的结构如图1所示，它主要由以下3部分组成. 1）输入层，它是一组变量，在本文中它是3个火焰特征量. 2）中间隐藏层，它把输入层传入的数据通过传递函数传递到输出层. 3）输出层，用于输出目标变量，在本文中它是输运方程需要的物性参数（如密度、黏性系数等）以及组分质量分数和过程变量源项.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   人工神经网络的示意图

Fig.1   Schematic of architecture of artificial neural network


在本文的研究中，输入层有3个参数，即 $ Z $、 $ {Z}^{{'}{'}2} $和 $ C $. 输出层的目标变量一共有11个，与前文的传统建库方法相同，即密度 $\; \rho $、黏性系数 $ \;\mu $、热扩散系数 $ \alpha $、温度 $ T $、主要组分（CH3OH、O2、H2O、CO2、CO、H2）的质量分数以及过程变量源项 $ \dot{{\omega }_{{\rm{C}}}} $. 使用主流深度学习框架之一——TensorFlow[20]. 采用的人工神经网络包含5个中间隐藏层，每个隐藏层含有50个神经元，层与层之间采用密连接. 存储这样一个网络仅需约200 kB，不足传统小火焰库大小的1%，可以显著减少计算机内存开销.

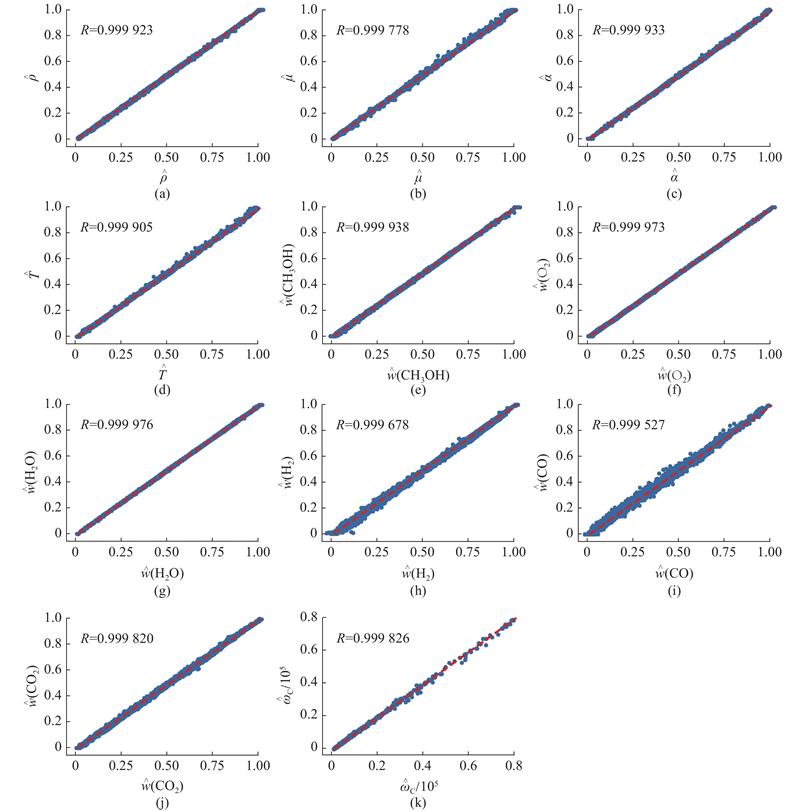
使用2个上述的人工神经网络. 第1个网络用于预测除 $ \dot{{\omega }_{{\rm{C}}}} $之外的10个变量，第2个网络用于预测 $ \dot{{\omega }_{{\rm{C}}}} $. 在第1个神经网络中，在数据输入网络进行训练前进行归一化处理，使其值分布在[0，1.0]，以加速网络训练. 在第2个网络中，未对 $ \dot{{\omega }_{{\rm{C}}}} $进行归一化，使用原数据直接训练，以提高预测精度. 在试验中发现，由于 $ \dot{{\omega }_{{\rm{C}}}} $的量级分布过大，为[−10，105]. 若使用归一化方法训练 $ \dot{{\omega }_{{\rm{C}}}} $，预测结果的相对误差尽管较小，但绝对误差难以控制，造成过程变量 $ C $的求解结果不正确，甚至输运方程计算不稳定. 对 $ \dot{{\omega }_{{\rm{C}}}} $不进行归一化，且为 $ \dot{{\omega }_{{\rm{C}}}} $单独配置一个神经网络进行训练，可以克服该问题，但是会使 $ \dot{{\omega }_{{\rm{C}}}} $的训练比较困难（训练时间长），且需要更大的人工神经网络（一个标量所需的网络与10个归一化的标量所需的网络相同）. 此外，2个网络的输入参数一致，均使用经过归一化处理的 $ Z $、 $ {Z}^{{'}{'}2} $和 $ C $.

一共有约23万组的训练数据，将其中85%作为训练集，15%作为测试集. 如图2所示为目标变量的回归分析图以及ANN预测结果与结构化表格中原始数据的相关系数. 图中，纵坐标表示结构化表格中的原始数据，横坐标表示ANN的预测结果. 在理想情况下，ANN可以准确地复现原始数据，散点分布在对角线上，即图2中虚线处. 从图2可以看出，各个变量原始值与预测值的相关系数均大于0.999，说明神经网络具有很高的精度，达到训练要求. 除 $ \dot{{\omega }_{{\rm{C}}}} $的变量的预测结果由同一个ANN得出，且变量经过归一化处理，故数据分布在[0，1.0]. $ \dot{{\omega }_{{\rm{C}}}} $由另一个ANN得出，且未进行归一化处理，故数据的量级分布较大. 为了方便表述，使用ANN小火焰库的FPV方法记为FPV-ANN方法.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   ANN训练结果：目标变量的回归分析图

Fig.2   ANNs training results: regression plots of target variables


1.4. 测试算例

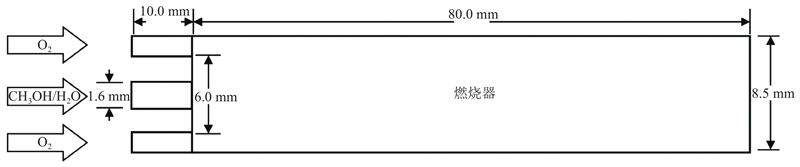
使用由瑞士苏黎世理工大学进行的超临界水热燃烧实验[21]作为测试算例，燃烧实验装置称作水冷壁面水热燃烧器（wall-cooled hydrothermal burner，WCHB）. 采用质量分数为16%的甲醇水溶液作为燃料，纯氧作为氧化剂. 实验的操作压力为25 MPa，燃料和氧化剂的入口温度为698 K，温度和压力均超过水的临界点（ $ {p}_{\mathrm{c}} $=22.04 MPa， $ {T}_{\mathrm{c}} $=647.14 K），处于超临界状态. WCHB的结构与尺寸如图3所示. 燃料由中轴处直径为1.6 mm的细管喷出，质量流量为2 g/s，氧气从外侧内径为6 mm、外径为8.5 mm的环中喷出，质量流量为0.62 g/s. 燃烧器壁面为700 K的等温壁面. 本文没有考虑等温冷壁面所带来的焓损失问题，此处带来的影响会在2.2节讨论. 使用三维结构化网格，网格量为3 $ \times $105. 在笔者之前的工作[22]中，证明了该网格对计算结果具有网格无关性，可以满足LES的解析要求.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   水热燃烧器WCHB的结构和尺寸示意图

Fig.3   Geometry and dimensions of injector and combustion chamber for WCHB


2. 结果和分析

2.1. FPV-ANN小火焰库精度分析

对FPV-ANN方法进行先验性分析. 具体方法如下. 将小火焰求解器计算得出的结果生成三维结构化表格（three-dimensional structured table），使用结构化表格的数据训练上述人工神经网络. 为了检测人工神经网络预测的准确性，使用从结构化表格中线性插值得到的预测值作为标的值，与ANN的预测值进行对比，可以避免与CFD模型相关的数值误差，直接对比2种建库方法所得出的结果.

如图4所示为目标变量在混合物分数 $ Z $维度上的先验结果，在 $ {Z}^{{'}{'}2} $和 $ C $维度上取随机值（ $ C $=0.117， $ {Z}^{{'}{'}2} $=0.15）. 可以看出，ANN的预测值与由结构化表中线性差值得到的值吻合很好，各曲线中的各峰值处有很好的预测. 在其他2个维度上进行先验性研究，得出与 $ Z $方向上一样的表现，此处不再赘述. 这些研究证明，该ANN库能够较准确地复现三维结构化表格的信息，以较高的精度代替CFD程序中的多维表格和插值方法.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   FPV-ANN方法目标变量在 $ Z $维度上的先验结果（ $ C $= 0.117， $ {Z}^{{'}{'}2} $=0.15）

Fig.4   Priori validation of FPV-ANN approach at dimension $ Z $ ( $ C $= 0.117, $ {Z}^{{'}{'}2} $=0.15)


2.2. FPV-ANN方法的大涡模拟研究

对FPV-ANN方法进行后验性分析. 具体方法如下：将1.1节生成的ANN小火焰库耦合入CFD软件OpenFOAM，实现在CFD迭代计算中，通过ANN预测获得相关热物性参数、组分分布以及过程变量反应源项的信息. 在传统FPV方法中，使用结构化表格中插值得到的信息. 经过CFD的迭代计算，2种小火焰库的取值差异被放大，故2个结果的差异比先验性分析中大，后验性分析中可以探究FPV-ANN方法与CFD耦合影响.

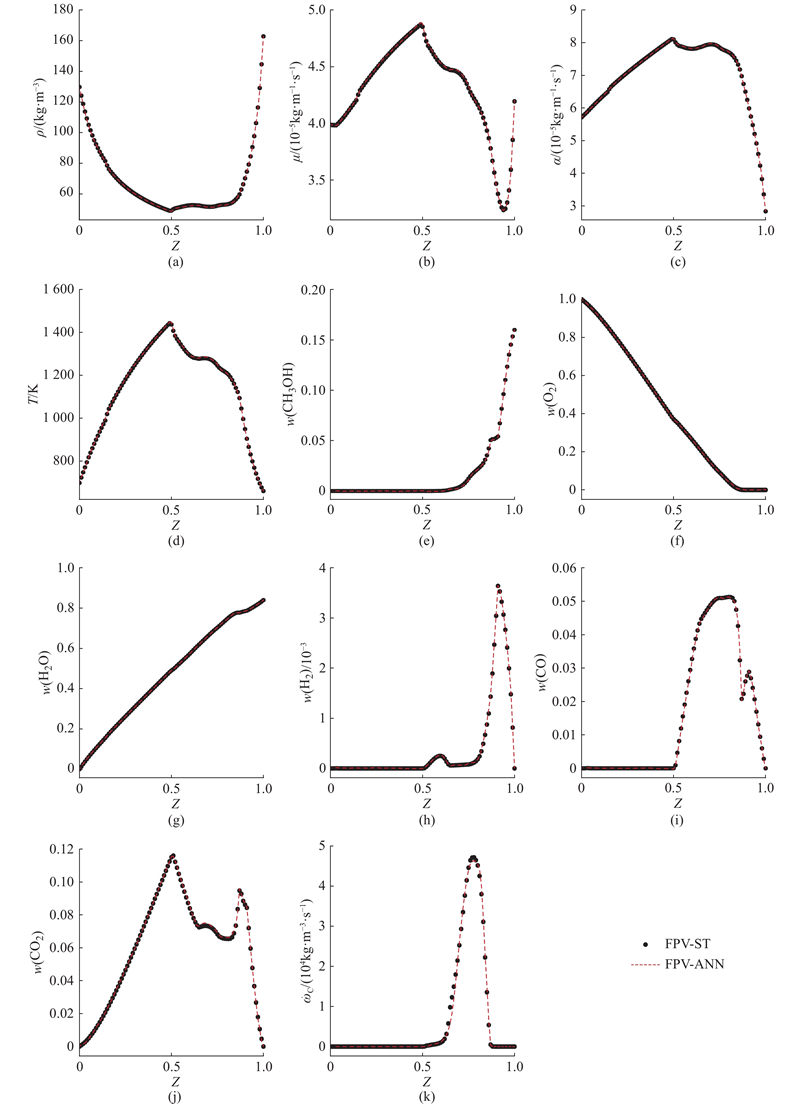
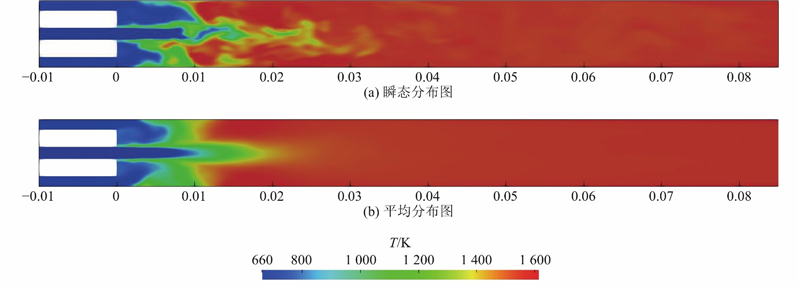
如图5所示为使用FPV-ANN方法得到的WCHB温度分布. 可以看出，在计算入口附近受到湍流的影响，火焰面十分褶皱. 火焰有一定的抬升高度，从图5（b）可以看出，抬升高度约为9 mm. 为了量化对比FPV-ANN与FPV-ST方法的结果，如图6所示为11个目标变量在中轴线上的时均分布. 如图6（d）所示为2种小火焰库方法在轴线处的温度，与实验测量的数据进行对比. 可以发现，2种方法的结果几乎一致，在燃烧器中前段与实验数据吻合得很好. 在燃烧器后段，模拟结果有明显的偏高. 这是由于在WCHB中使用的是水冷壁面，壁面为恒温700 K，有着强烈的壁面换热，造成燃烧器焓损失. 本文的FPV方法未考虑焓损失，小火焰库中的反应数据由绝热小火焰方程得到，故出现了这种误差. 解决该问题的方法是建立非绝热的小火焰库，增加一个维度表示焓损失，Gao等[22]进行了相关工作.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   FPV-ANN方法的温度分布

Fig.5   Contours of temperature obtained by FPV-ANN method


图 6

新窗口打开| 下载原图ZIP| 生成PPT

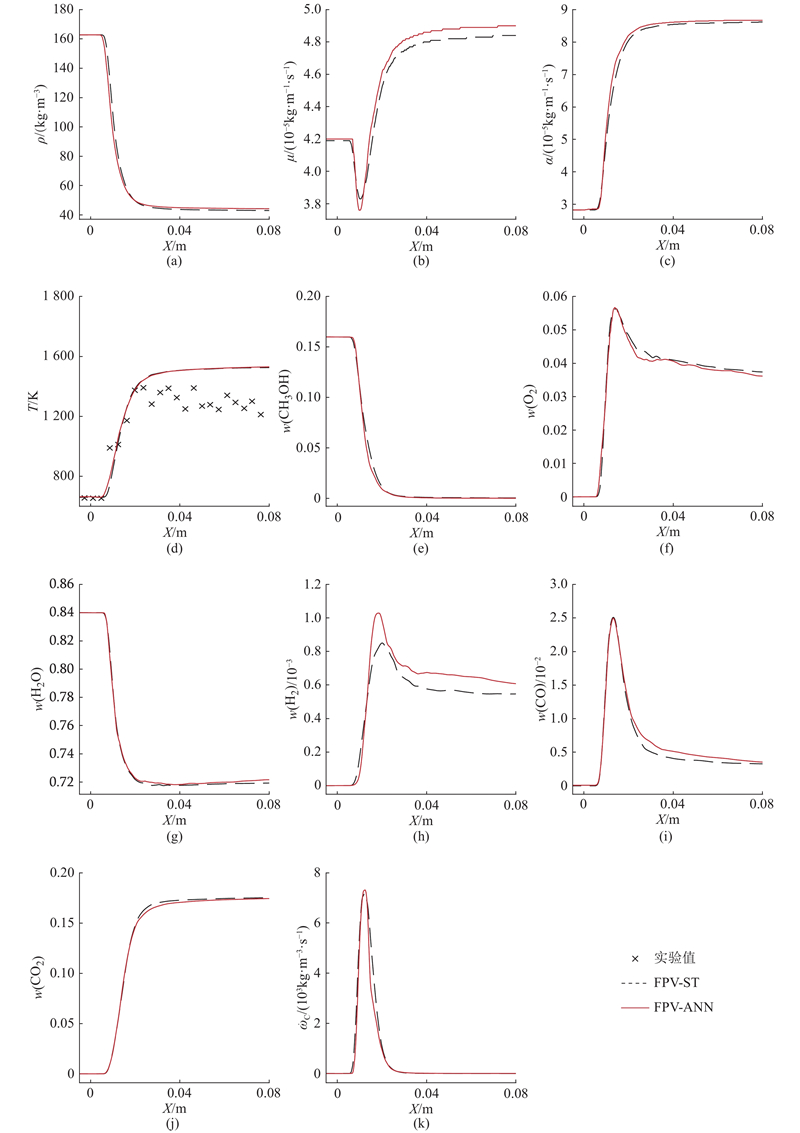
图 6   目标变量在中轴线上的时均分布

Fig.6   Time-averaged distributions of target variables along axis


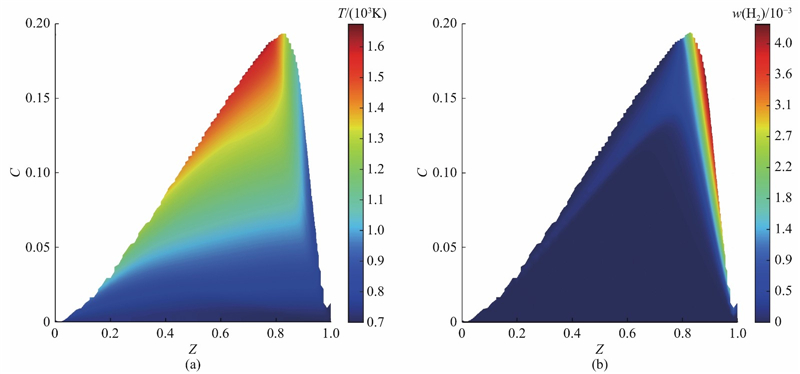
从图6（a）~（c）、（e）~（l）可以看出物性参数、各组分和过程变量源项在轴线上的分布，FPV-ANN方法与传统小火焰库的结果大体一致. 从图6（i）可以发现，FPV-ANN预测 H2在轴线上的分布与传统小火焰库的结果在趋势上一致，但是数值上有些偏差. 以下原因造成了这样的偏差：主要原因是H2质量分数在特征量空间分布不均. 如图7所示为当 $ {Z}^{{'}{'}2} $=0时温度及H2质量分数在 $ Z $- $ C $空间的分布. 可以看出，温度变化在 $ Z $- $ C $空间分布较均匀；H2质量分数的变化主要分布在局部狭长区域里，这种情况下，即使特征变量变化很小，也会给目标变量带来较大变化，这对神经网络学习分布规律造成困难. 由于H2质量分数低，在输入神经网络之前，进行归一化处理，H2质量分数从[0，0.004]放大到[0，1.0]，同时放大了分布规律中的噪声，使得神经网络难以准确把握分布规律. Gao等[11, 23-24]发现在后验计算中，输运方程源项的不同会放大后验的误差，本文中ANN库与传统库过程变量源项存在微小差异，差异经过迭代计算放大，是导致H2质量分数出现较明显偏差的原因.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   温度和H2质量分数在Z-C空间内的分布（ $ {Z}^{{'}{'}2} $=0）

Fig.7   Distributions of temperature and H2 mass fraction in Z-C space ( $ {Z}^{{'}{'}2} $=0)


总体上来看，FPV-ANN方法与传统的FPV-ST方法的准确性几乎一致，ANN小火焰库可以代替传统多维结构化表格方案，参与CFD迭代计算.

2.3. 计算性能分析

讨论FPV-ANN方法的计算性能，主要分成计算机内存使用和计算速度2个部分.

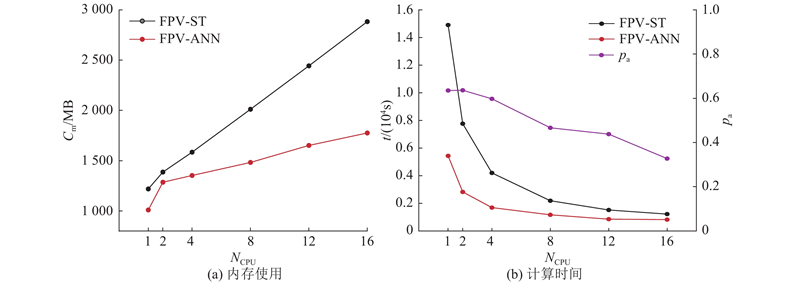
如图8（a）所示为在使用不同CPU数量NCPU进行并行计算下的内存使用量Cm. 可以发现，在并行计算中，2种FPV方法的内存使用量随着CPU数量的增加近似线性增长，这是由于MPI并行计算需要每个核心（进程）都存贮一套完整的小火焰库. 由于ANN小火焰库较小，从图8（a）可以看出，FPV-ANN方法内存增长的斜率较小，即增长速率较慢. 可以预见，在使用更多CPU进行并行计算数量时，使用FPV-ST方法很快会使计算机内存不堪重负. 使用FPV-ANN方法在大规模并行计算中的优势非常明显. 如图8（b）所示为使用不同CPU数量进行并行计算2 000个时间步的计算时间t. 图中，虚线表示使用ANN小火焰库相比传统小火焰库节省时间的比率pa. 可以发现，FPV-ANN方法的计算速度比FPV-ST方法节省时间30%以上. 综上所述，FPV-ANN方法的内存开销更小，计算速度更快，总体上具有更好的计算性能.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   FPV-ANN方法与FPV-ST方法的计算性能分析

Fig.8   Computational performance analysis of FPV-ANN and FPV-ST methods


3. 结　语

使用人工神经网络，解决了超临界小火焰燃烧模型数据库过于庞大、导致计算机内存不足和取值性能下降的问题. 基于开源软件OpenFOAM和TensorFlow，实现了基于人工神经网络建库的超临界小火焰模型FPV-ANN. 从先验性分析和后验性分析角度，研究该方法的准确性和计算性能，得出以下结论.

1）先验性分析显示，ANN小火焰库的预测结果与结构化表格的插值结果吻合很好，说明ANN库与传统库的精度一致. 在后验分析中，对WCHB超临界水热火焰进行大涡模拟计算发现，FPV-ANN方法在温度、组分和其他目标变量的分布与传统FPV方法得到的结果吻合，说明FPV-ANN方法的准确性与传统FPV方法一致.

2）由于ANN小火焰库大小只有传统库的1%，FPV-ANN方法在大规模并行计算中消耗更少的计算机内存. FPV-ANN方法的计算速度比传统FPV-ST方法快30%以上，说明FPV-ANN方法有很好的计算性能.

综上所述，本文使用ANN建库，与传统方法相比，能够在保证精度的同时减少内存消耗，提升计算速度，且理论上不存在维度灾难问题，可以更进一步研究更高维度的超临界小火焰模型.

参考文献

NORBERT P

Laminar diffusion flamelet models in non-premixed turbulent combustion

[J]. Progress in Energy and Combustion Science, 1984, 10 (3): 319- 339

DOI:10.1016/0360-1285(84)90114-X      [本文引用: 2]

NORBERT P. Turbulent combustion [M]. Cambridge: Cambridge University Press, 2000.

[本文引用: 2]

PITSCH H

Large-eddy simulation of turbulent combustion

[J]. Annual Review of Fluid Mechanics, 2006, 38: 453- 482

DOI:10.1146/annurev.fluid.38.050304.092133      [本文引用: 1]

BENOIT F, VEYNANTE D, CANDEL S

Modeling combustion chemistry in large eddy simulation of turbulent flames

[J]. Flow, Turbulence and Combustion, 2015, 94 (1): 3- 42

DOI:10.1007/s10494-014-9579-8      [本文引用: 1]

STEPHEN B P

Small scales, many species and the manifold challenges of turbulent combustion

[J]. Proceedings of the Combustion Institute, 2013, 34 (1): 1- 31

DOI:10.1016/j.proci.2012.09.009      [本文引用: 2]

MATTHIAS I, SCHMITT C, PITSCH H

Optimal artificial neural networks and tabulation methods for chemistry representation in LES of a bluff-body swirl-stabilized flame

[J]. Proceedings of the Combustion Institute, 2009, 32 (1): 1527- 1535

DOI:10.1016/j.proci.2008.06.100      [本文引用: 1]

EMAMI M D, FARD A E

Laminar flamelet modeling of a turbulent CH4/H2/N2 jet diffusion flame using artificial neural networks

[J]. Applied Mathematical Modelling, 2012, 36 (5): 2082- 2093

DOI:10.1016/j.apm.2011.08.012      [本文引用: 1]

OWOYELE O, KUNDU P, AMEEN M M, et al

Application of deep artificial neural networks to multi-dimensional flamelet libraries and spray flames

[J]. International Journal of Engine Research, 2020, 21 (1): 151- 168

DOI:10.1177/1468087419837770      [本文引用: 1]

ZHANG Y, XU S, ZHONG S, et al

Large eddy simulation of spray combustion using flamelet generated manifolds combined with artificial neural networks

[J]. Energy and AI, 2020, 2: 100021

DOI:10.1016/j.egyai.2020.100021      [本文引用: 1]

WELLER H G, TABOR G, JASAK H, et al

A tensorial approach to computational continuum mechanics using object-oriented techniques

[J]. Computers in Physics, 1998, 12 (6): 620- 631

DOI:10.1063/1.168744      [本文引用: 1]

GAO Z, WANG H, LUO K, et al

Evaluation of real-fluid flamelet/progress variable model for laminar hydrothermal flames

[J]. The Journal of Supercritical Fluids, 2019, 143: 232- 241

DOI:10.1016/j.supflu.2018.08.014      [本文引用: 3]

BILGER R W, STÅRNER S H, KEE R J

On reduced mechanisms for methane air combustion in non-premixed flames

[J]. Combustion and Flame, 1990, 80 (2): 135- 149

DOI:10.1016/0010-2180(90)90122-8      [本文引用: 1]

REN M, WANG S, ZHANG J, et al

Characteristics of methanol hydrothermal combustion: detailed chemical kinetics coupled with simple flow modeling study

[J]. Industrial and Engineering Chemistry Research, 2017, 56 (18): 5469- 5478

DOI:10.1021/acs.iecr.7b00886      [本文引用: 1]

PENG D Y, ROBINSON D B

A new two-constant equation of state

[J]. Industrial and Engineering Chemistry Fundamentals, 1976, 15 (1): 59- 64

DOI:10.1021/i160057a011      [本文引用: 1]

CHUNG T H, AJLAN M, LEE L L, et al

Generalized multiparameter correlation for nonpolar and polar fluid transport properties

[J]. Industrial and Engineering Chemistry Research, 1988, 27 (4): 671- 679

DOI:10.1021/ie00076a024      [本文引用: 1]

PITSCH H. FlameMaster: A C++ computer program for 0D combustion and 1D laminar flame calculations[EB/OL]. [2020-09-20]. https://www.itv.rwth-aachen.de/downloads/flamemaster/.

[本文引用: 1]

PIERCE C D, MOIN P. Progress-variable approach for large-eddy simulation of turbulent combustion [D]. Stanford: Stanford University, 2001.

[本文引用: 1]

PIERCE C D, MOIN P

Progress-variable approach for large-eddy simulation of non-premixed turbulent combustion

[J]. Journal of Fluid Mechanics, 2004, 504: 73

DOI:10.1017/S0022112004008213      [本文引用: 1]

SMAGORINSKY J

General circulation experiments with the primitive equations: I. the basic experiment

[J]. Monthly Weather Review, 1963, 91 (3): 99- 164

DOI:10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;2      [本文引用: 1]

ABADI M, BARHAM P, CHEN J, et al. Tensorflow: a system for large-scale machine learning [C]// 12th Symposium on Operating Systems Design and Implementation. Savannah, GA: USENIX, 2016: 265-283.

[本文引用: 1]

PRÍKOPSKÝ K. Characterization of continuous diffusion flames in supercritical water [D]. Zurich: Swiss Federal Institute of Technology, 2007.

[本文引用: 1]

GAO Z, WANG H, SONG C, et al

Large-eddy simulation of hydrothermal flames using extended flamelet/progress variable approach

[J]. The Journal of Supercritical Fluids, 2020, 163: 104843

DOI:10.1016/j.supflu.2020.104843      [本文引用: 2]

WEN X, WANG H, LUO Y, et al

Evaluation of flamelet/progress variable model for laminar pulverized coal combustion

[J]. Physics of Fluids, 2017, 29 (8): 083607

DOI:10.1063/1.4999335      [本文引用: 1]

IHME M, SEE Y C

Prediction of autoignition in a lifted methane/air flame using an unsteady flamelet/progress variable model

[J]. Combustion and Flame, 2010, 157 (10): 1850- 1862

DOI:10.1016/j.combustflame.2010.07.015      [本文引用: 1]

/

〈 〉