风荷载不同于行人荷载,本身没有明显的周期,不易引起共振. 大跨度柔性结构对风较敏感,抖振问题突出. 熊耀清等[6]采用简化的风荷载模式,对主跨为199 m的型钢组合加劲梁窄桥面人行悬索桥进行风振时域分析,通过风压考虑风荷载,忽略了自激力对抖振响应的影响. 刘健新等[7]对主跨为278 m的钢桁架加劲梁窄桥面悬索桥进行抖振时域分析,研究位移响应特点,对比自激力的影响,认为自激力具有减小桥梁竖向振动位移的作用. 陈代海等[8]根据主跨为276 m的钢桁架加劲梁窄桥面悬索桥抖振分析结果,得出与上述相反的结论. 既有研究主要以结构刚度大的钢桁架加劲梁悬索桥为对象,相对于柔性加劲梁悬索桥,抖振对舒适性的影响小.
本文以一座主跨为460 m的柔性人行悬索桥为对象,建立有限元模型并进行动力特性计算. 利用谱表示法,生成具有不同湍流强度的脉动风时程. 基于数值模拟识别的18个颤振导数,计算有理函数表达的自激力. 通过非线性抖振时域分析,探究并比较自激力与结构阻尼对抖振响应的影响. 计算桥梁在不同湍流强度下的振动响应,开展舒适性评价. 比较具有不同设计参数的中央扣与抗风缆对桥梁的减振效果. 结果为大跨度人行桥安全管理和设计提供参考.
1. 桥梁模型及计算方法
1.1. 桥梁计算模型
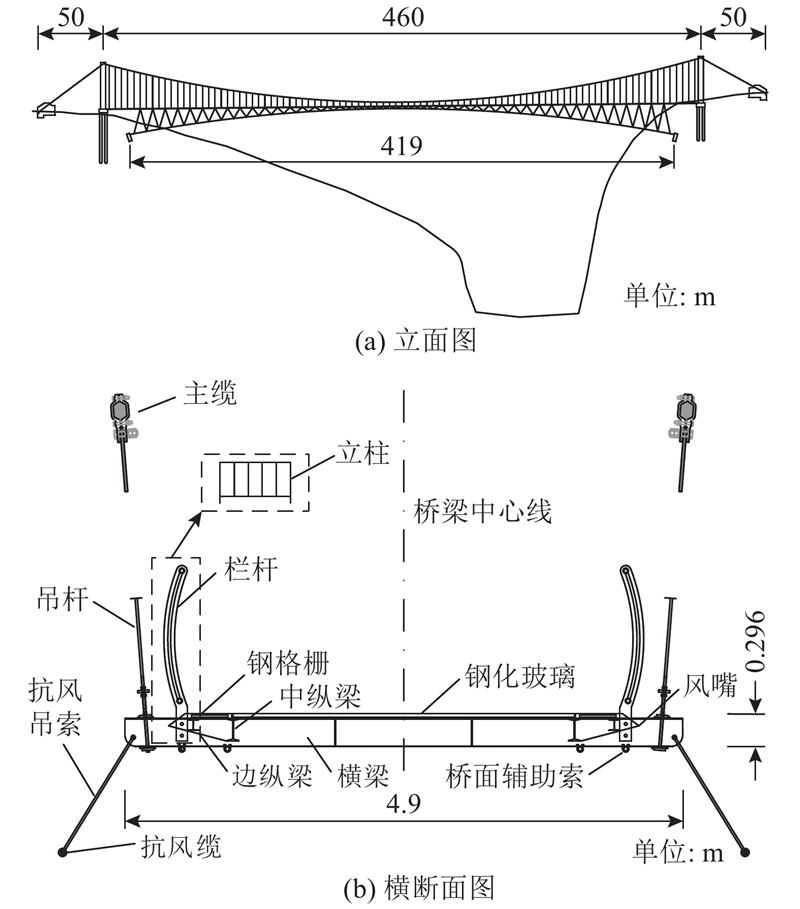
以图1所示的一座跨度为460 m的单跨地锚式人行悬索桥为对象进行分析. 桥梁宽为4.9 m,梁高为0.296 m. 桥塔采用钢筋混凝土结构,塔高36 m,塔柱底横向中心距为6 m,塔柱顶横向中心距为9.5 m. 主缆采用环氧钢绞线作为索股的空间索,垂直平面内的垂跨比为1/14.375. 吊杆采用圆形钢棒,标准间距为4.8 m,倾角为85.5°. 桥面采用型钢组成的水平框架,桥面中间铺设钢化玻璃,左、右两侧铺设钢格栅,格栅外侧为带立柱的栏杆. 为了增大结构的抗风性能,桥梁的左、右两侧对称设置抗风缆,桥面横梁底部设置4根钢丝绳辅助索,纵梁外侧设置风嘴. 抗风缆角度约为45°,抗风缆和辅助索张力为200 kN.
图 1
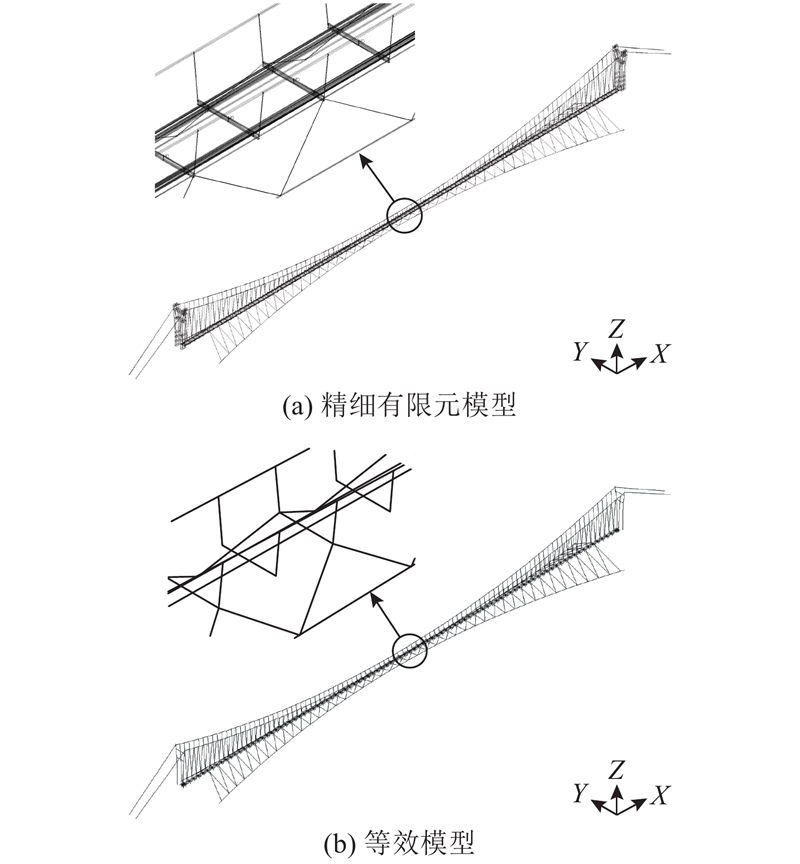
计算在通用有限元ANSYS15.0平台上开展. 主缆、吊杆、抗风缆、抗风吊索和桥面辅助索采用LINK180单元,初拉力通过初应变施加,桥塔和加劲梁采用BEAM188单元,钢格栅采用SHELL63单元,玻璃质量和质量惯性矩采用MASS21单元模拟. 如图2(a)所示为桥梁精细有限元模型,为了减少振动分析计算量,采用等效单主梁模型近似,如图2(b)所示. 等效模型的纵梁质量惯性矩通过附加质量惯性矩法获得[9],截面惯性矩根据悬臂梁法试算获得. 如表1所示为2种模型的主梁侧弯、竖弯和扭转前3阶动力特性计算结果的对比. 表中,fnat为自振频率. 2种模型的频率偏差小于6%,表明等效模型能够替代精细模型用于横风作用下的结构振动分析.
图 2
表 1 精细模型与等效模型动力特性对比
Tab.1
| 振型 | fnat /Hz | 偏差/% | |
| 精细模型 | 等效模型 | ||
| 1阶对称侧弯 | 0.160 2 | 0.162 3 | 1.3 |
| 1阶反对称侧弯与扭转 | 0.222 3 | 0.221 0 | −0.6 |
| 1阶反对称竖弯 | 0.247 9 | 0.235 5 | −5.0 |
| 1阶对称竖弯 | 0.282 7 | 0.275 4 | −2.6 |
| 1阶对称侧弯与扭转 | 0.288 4 | 0.305 9 | 6.0 |
| 2阶对称竖弯 | 0.394 6 | 0.381 8 | −3.2 |
| 1阶反对称扭转 | 0.398 2 | 0.382 5 | −4.0 |
| 1阶对称扭转 | 0.409 4 | 0.398 3 | −2.7 |
| 2阶对称扭转 | 0.520 7 | 0.503 5 | −3.3 |
1.2. 横风作用及桥梁运动方程以及计算流程
为了提高计算精度,桥梁抖振分析考虑自重、静风力、抖振力和自激力的作用,运动方程为
式中:M、C和K分别为结构质量矩阵、阻尼矩阵和刚度矩阵,Y为结构位移向量,Fg为结构自重,Fs为静风力,Fb为抖振力,Fse为自激力,上标“·”和“··”分别表示位移对时间的一阶导数和二阶导数. 以下分别阐述静风力、抖振力和自激力的计算方法.
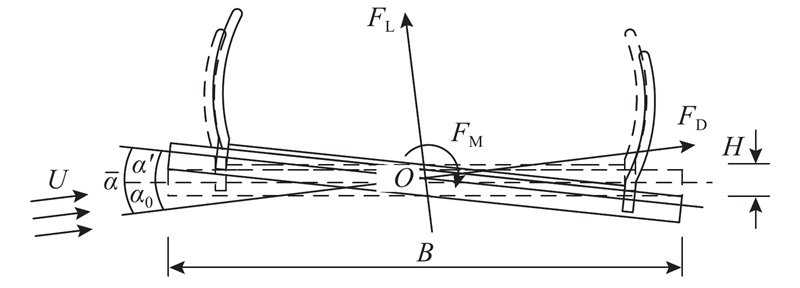
作用在主梁上的静风力通常分解到风轴坐标下,如图3所示. 图中,O为剪切中心;
图 3
式中:FD、FL和FM分别为风轴坐标下的静风阻力、升力和升力矩分量;ρ为空气密度,ρ=1.225 kg/m3;U为平均风速;CD、CL和CM分别为阻力系数、升力系数和升力矩系数;H为梁高;B为梁宽.
抖振力是由脉动风引起的. 根据准定常理论,单位长度的抖振力Fb三分量采用下式[10]计算:
式中:Db、Lb和Mb分别为抖振阻力、升力和升力矩,上标“′”表示三分力系数对攻角
自激力由流固耦合产生. 单位长度的自激力Fse三分量可以采用卷积[11]表示为
式中:Dse、Lse和Mse分别为自激阻力、升力和升力矩;Ijk (j=D、L、M,k=p、h、α)为单位脉冲响应函数;p、h和α分别为横向、竖向位移和扭转角.
以横向振动引起的自激阻力Dse,p为例,式(4)中的对应项通过傅里叶变换得到传递函数
式中:ω为圆频率,ADp1、ADp2、ADpi 、dDpi(dDpi≥0; i=3,···, m)为与频率无关的参数.
式(5)通过傅里叶逆变换,可得
式中:δ(t)为Dirac函数.
将式(6)代入式(4),化简后可得[12]
将式(4)中的其余卷积项表示为式(7)的形式,式(7)中的卷积项可以通过递推计算.
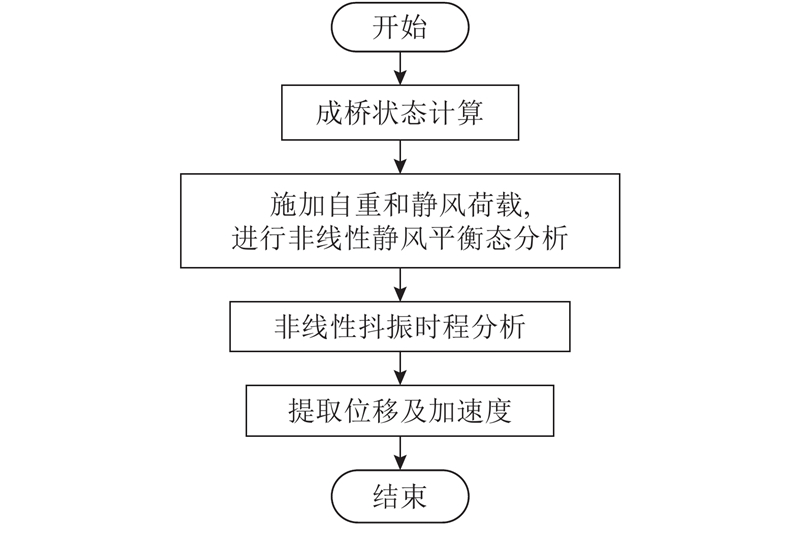
采用非线性振动分析计算桥梁时域抖振响应,通过APDL命令实现非线性迭代过程. 计算流程如图4所示. 计算过程包括桥梁成桥状态、静风作用下的平衡状态和非线性抖振时程分析等几个方面. 计算均考虑几何非线性的影响,静风力和抖振力中的风攻角均采用实时风攻角. 加劲梁考虑静风力、抖振力和自激力,桥塔和主缆只考虑静风阻力和抖振阻力,抗风缆和吊杆只考虑静风阻力. 自激力计算所采用的位移均为振动位移,不计静风位移.
图 4
图 4 非线性抖振时域分析的流程图
Fig.4 Flow chart of nonlinear buffeting analysis in time domain
2. 横向风作用下的桥梁振动响应
2.1. 脉动风模拟
水平横向和竖向风谱表示为
式中:Su(n, z)和Sw(n, z)分别为横向和竖向脉动风功率谱;n为脉动风频率;z为高度;σu和σw分别为横向和竖向脉动风标准差;Lu和Lw分别为横向和竖向湍流积分尺度,加劲梁基准高度为109.3 m,湍流积分长度为Lu=160 m,Lw=80 m[15].
相干函数采用Devenport提出的表达式[18]:
式中:r为两模拟点之间的距离,衰减系数λ取7.
脉动风模拟点布置如图5所示,模拟参数如表2所示,截止频率为2 Hz,频率分割数为2 048,时间间隔为0.25 s. 表中,ttot为总采样时长. 以主梁跨中横向脉动风为例,3种工况250 s内的脉动风模拟时程如图6(a)所示. 工况Ⅰ脉动风速为−2.9~3.3 m/s,工况Ⅱ脉动风速为−5.8~6.6 m/s,工况Ⅲ脉动风速为−8.7~10.0 m/s. 以工况Ⅱ的横桥向脉动风为例,开展风谱、相关函数和相干函数检验,结果如图6(b)~(e)所示. 图6(c)中,tint为时间间隔,Rj,k为模拟点j与模拟点k的相关函数,通过功率谱密度的傅里叶逆变换获得. 图6(d)中,cj,k为模拟点j与模拟点k的相干函数,K为折减频率,K=2πnB/U. 图6(e)中,ci,25为模拟点i(i=1,···,24)与模拟点25的相干函数. 模拟值与目标值吻合,表明模拟的风场有效、可靠.
图 5
表 2 脉动风模拟参数
Tab.2
| 脉动风编号 | 位置 | 模拟风速 | 模拟点数 | ttot /s |
| 1 | 主梁 | u | 49 | 50 176 |
| 2 | 主梁 | w | 49 | 50 176 |
| 3 | 南塔 | u | 10 | 10 240 |
| 4 | 北塔 | u | 10 | 10 240 |
| 5 | 主缆 | u | 49 | 50 176 |
图 6
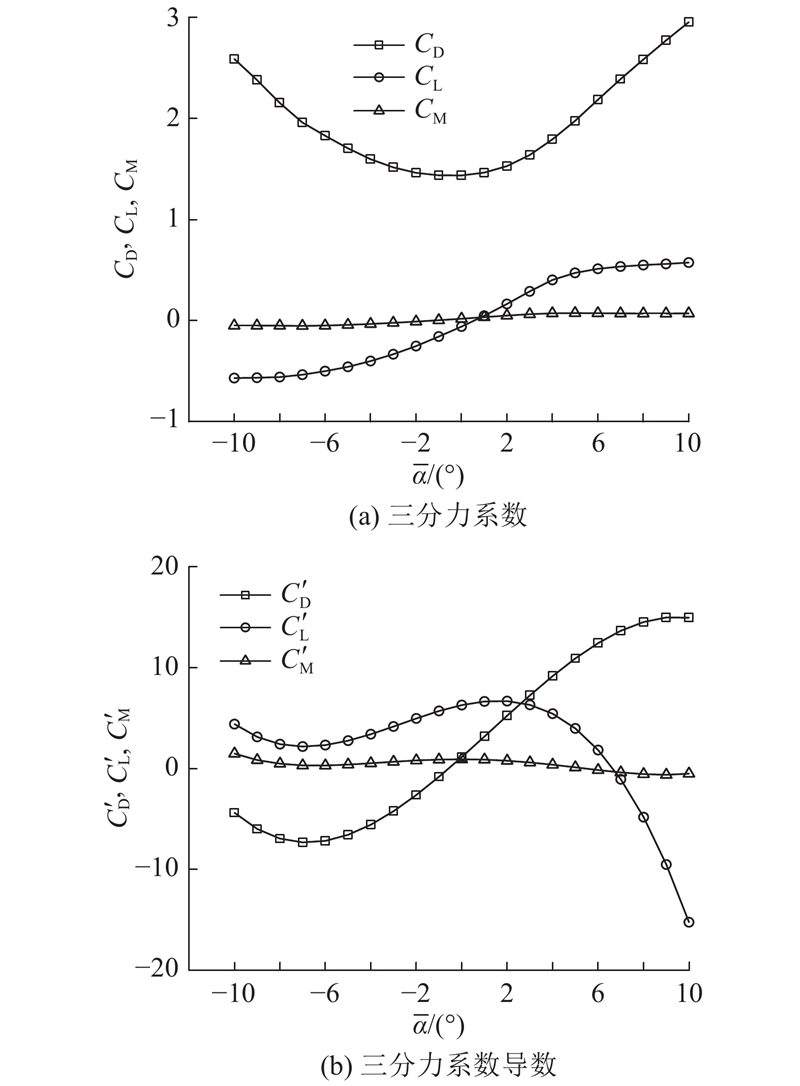
2.2. 风荷载参数
图 7
图 8
图 8 加劲梁三分力系数及导数
Fig.8 Aerostatic force coefficients and their derivatives of stiffening girder
图 9
图 9 加劲梁0°风攻角颤振导数
Fig.9 Flutter derivatives of stiffening girder at 0° wind attack angle
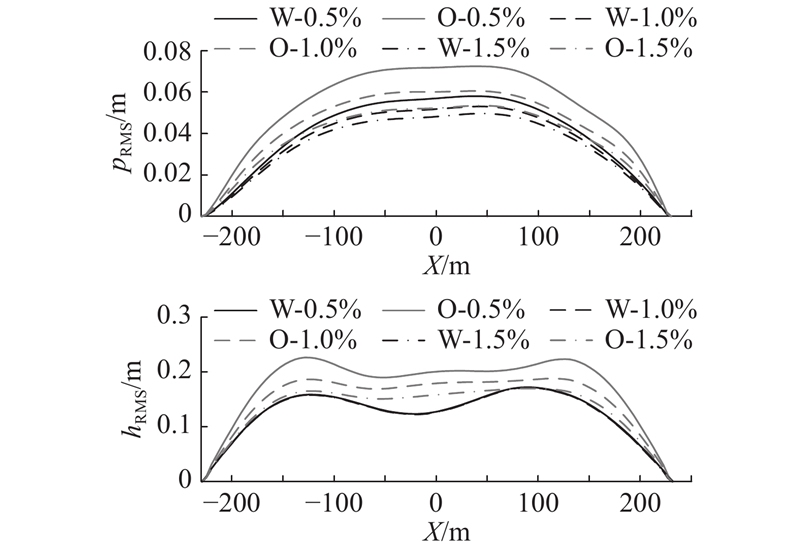
2.3. 自激力与结构阻尼对桥梁抖振响应的影响
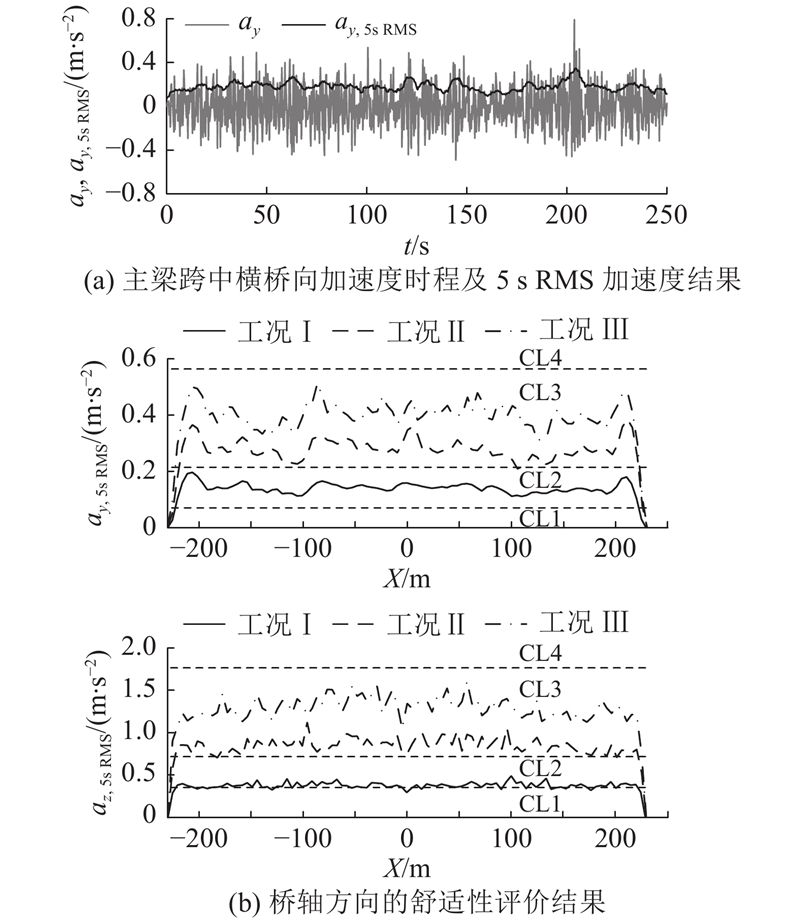
以工况Ⅱ为荷载条件,分别计算考虑自激力(W)和不考虑自激力(O)在结构阻尼比为0.5%、1.0%和1.5%情况下的抖振响应. 用W-0.5%表示考虑自激力且阻尼比为0.5%,O-0.5%表示不考虑自激力且阻尼比为0.5%. 计算采用Rayleigh阻尼,主梁断面中心位移均方根(RMS)沿桥梁轴向的分布如图10所示. 图中,X为桥梁轴向坐标,0表示跨中,
图 10
图 10 自激力与结构阻尼对主梁抖振位移响应的影响
Fig.10 Influence of self-excited force and structural damping on buffeting displacement responses of main girder
在不考虑自激力的情况下,结构阻尼比由0.5%增加到1%、1.5%,竖向抖振位移减小比例由17.0%增加到24.8%;横桥向抖振位移减小比例由16.5%增加到26.2%. 在考虑自激力的情况下,结构阻尼比由0.5%增加到1%、1.5%,竖向抖振位移减小比例由0.3%增加到0.5%;横桥向抖振位移减小比例由8.6%增加到14.5%. 结构阻尼对抖振响应影响显著,但是考虑自激力后竖向抖振位移响应对结构阻尼比不敏感,横桥向位移响应对结构阻尼比的敏感性降低.
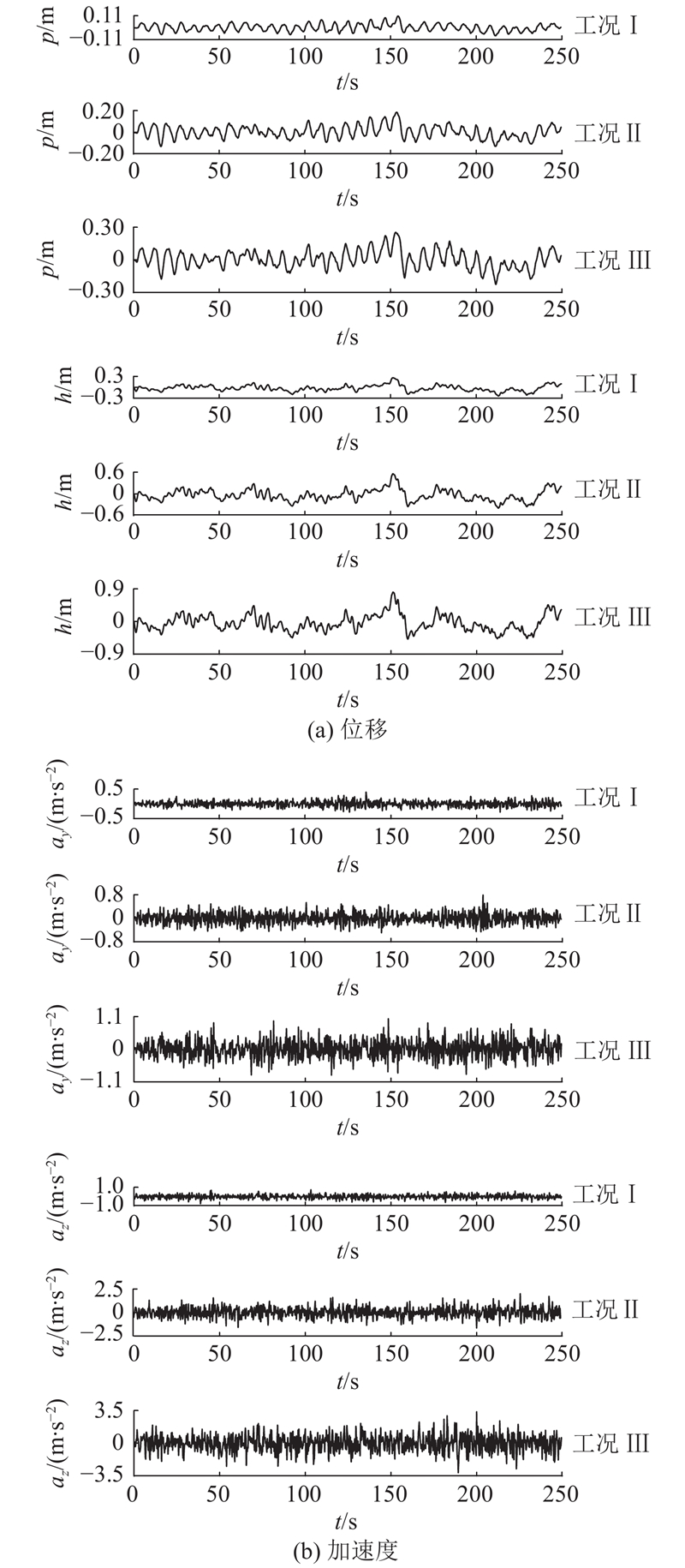
2.4. 不同湍流度下的桥梁抖振响应舒适性评价
鉴于自激力对抖振响应的影响明显,以下计算均考虑自激力的影响;结构阻尼比采用0.5%. 为了考虑主梁扭转振动对竖向响应的贡献,竖向响应均取主梁断面中心与吊杆下端点中的峰值响应最大点.
图 11
图 11 不同湍流强度下主梁跨中抖振响应比较
Fig.11 Comparison of buffeting responses at mid-span of main girder under different turbulence intensities
| 舒适性分级 | 舒适度 | ay,peak /(m·s−2) | az,peak /(m·s−2) |
| CL1 | 非常舒适 | <0.1 | <0.5 |
| CL2 | 中等舒适 | 0.1~0.3 | 0.5~1.0 |
| CL3 | 不太舒适 | 0.3~0.8 | 1.0~2.5 |
| CL4 | 不能忍受 | >0.8 | >2.5 |
图 12
图 12 加速度时程及舒适性评价的结果
Fig.12 Acceleration time history and comfort evaluation results
2.5. 抖振响应的减振措施
上述结果表明,大跨度柔性人行悬索桥在横风作用下会发生影响舒适性的振动,需要采取减振措施. 为了分析减振措施的效果,通过在原模型上设置中央扣和增大抗风缆面积2种措施,比较桥梁的抖振响应.
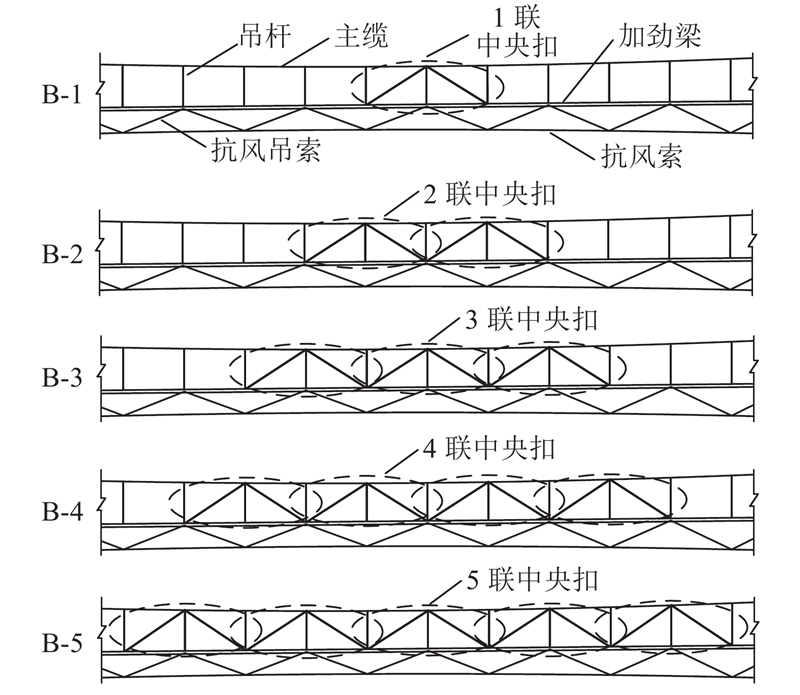
2.5.1. 中央扣
图 13
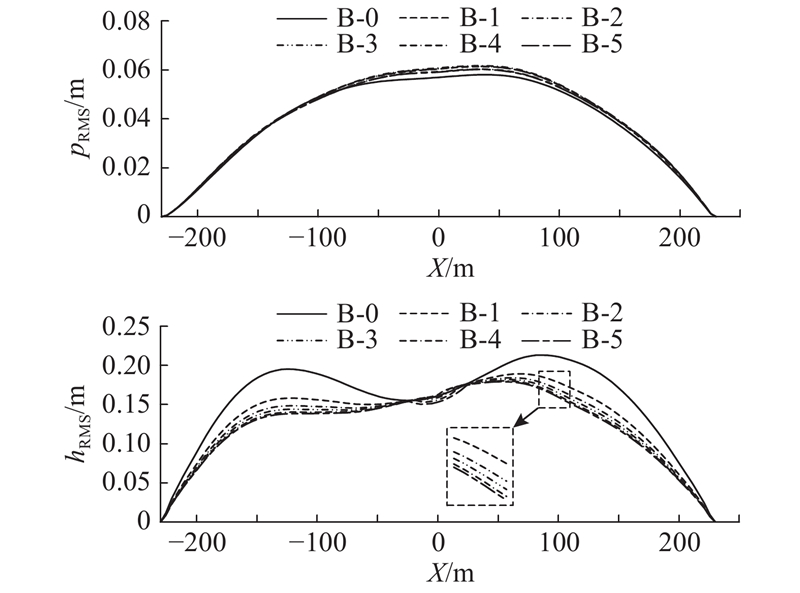
主梁位移响应沿桥梁轴向的分布如图14所示. 图中,B-0为原模型. 结果表明,中央扣具有较好的竖向减振效果,对1/4跨和3/4跨的竖向减振效果明显,对跨中的竖向减振作用较小;对横桥向无明显的减振效果. 设置1联中央扣,1/4跨和3/4跨竖向位移RMS分别减小18.7%、17.7%. 继续增加中央扣的数量,对应的减振效果不明显.
图 14
图 14 中央扣对主梁抖振位移响应的影响
Fig.14 Influence of central buckle on buffeting displacement responses of main girder
2.5.2. 增大抗风缆面积
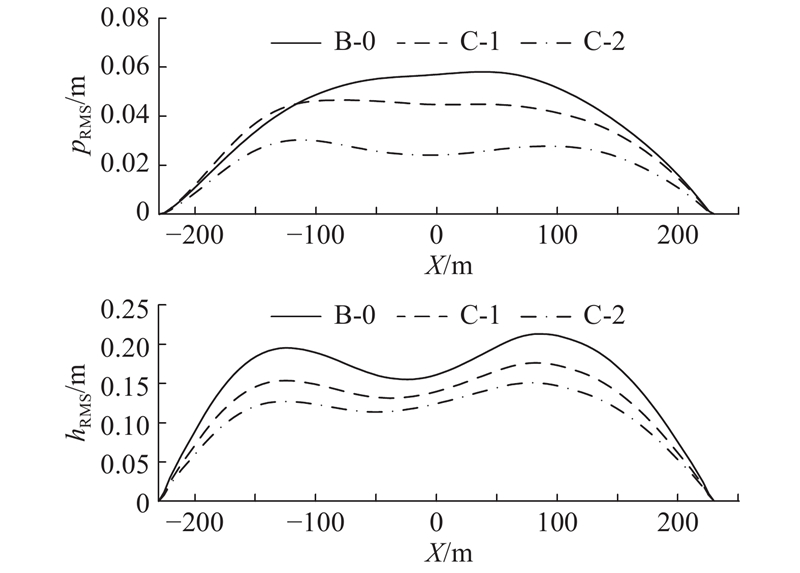
抗风缆可以增加结构的约束,提高结构刚度. 熊耀清等[6]认为抗风缆是有效的减振措施. 为了研究抗风缆断面面积对抖振响应的影响,对2种工况进行对比分析:抗风缆系统的截面积分别增加1倍(C-1)和2倍(C-2).
表 4 增大抗风缆面积后的桥梁动力特性
Tab.4
| 振型 | fnat /Hz | |
| C-1 | C-2 | |
| 1阶对称侧弯 | 0.197 6 | 0.222 8 |
| 1阶反对称侧弯与扭转 | 0.250 5 | 0.271 0 |
| 1阶反对称竖弯 | 0.256 8 | 0.271 0 |
| 1阶对称竖弯 | 0.280 1 | 0.282 6 |
| 1阶对称扭转 | 0.398 8 | 0.400 8 |
| 1阶反对称扭转 | 0.416 5 | 0.433 8 |
主梁位移响应沿桥梁轴向的分布如图15所示. 可知,增大抗风缆系统断面面积能够显著减小全桥竖向位移和跨中横桥向位移,当面积增加1倍和2倍时,跨中的横桥向位移RMS分别减小21.5%、57.7%,竖向位移RMS分别减小13.3%、22.9%.
图 15
图 15 抗风缆对主梁抖振位移响应的影响
Fig.15 Influence of wind-resistant cable on buffeting displacement responses of main girder
对象桥的振动舒适性由横桥向和竖向振动共同控制. 上述结果表明,增大抗风缆刚度对舒适性的改善效果比加中央扣的效果更好.
3. 结 论
(1)在15 m/s的平均风速下,大跨度人行悬索桥的自激力表现出明显的振动抑制作用,忽略自激力的影响将使抖振计算结果偏大. 在考虑自激力后,竖向振动对结构阻尼不敏感.
(2)抖振响应对湍流强度敏感,湍流强度变化50%,响应变化30%~68%,对舒适性评价结果的影响较大.
(3)适当设置中央扣对人行悬索桥具有较好的竖向减振效果. 增大抗风缆的截面积可以减小桥梁的竖向抖振响应,对跨中横桥向的抖振响应减振效果明显,是有效的减振措施.
参考文献
A method for predicting the lateral girder response of footbridges induced by pedestrians
[J].
The London millennium footbridge
[J].
人致荷载研究综述
[J].
A review of human-induced loads study
[J].
Formulation of human-structure interaction system models for vertical vibration
[J].DOI:10.1016/j.jsv.2016.05.015 [本文引用: 1]
Mitigation of human-induced vertical vibrations of footbridges through crowd flow control
[J].DOI:10.1002/stc.2266 [本文引用: 1]
大跨极窄人行悬索桥动力特性及风振响应研究
[J].
Research on dynamic characteristics and wind vibration response of a pedestrian large-span and slender suspension bridge
[J].
窄桥面悬索桥非线性抖振时域分析
[J].
Time domain analysis of nonlinear buffeting of narrow deck suspension bridges
[J].
大跨度窄桥面钢桁架悬索桥抖振影响因素分析
[J].DOI:10.3969/j.issn.1003-1995.2016.11.03 [本文引用: 1]
Influential factors analysis of buffeting for long-span narrow deck steel truss suspension bridge
[J].DOI:10.3969/j.issn.1003-1995.2016.11.03 [本文引用: 1]
悬索桥钢桁梁断面质量惯性矩简化计算方法
[J].
A simplified method for calculating mass moment of inertia of stiffening truss in suspension bridges
[J].
Advances in modeling of aerodynamic forces on bridge decks
[J].DOI:10.1061/(ASCE)0733-9399(2002)128:11(1193) [本文引用: 1]
New stochastic theory for bridge stability in turbulent flow. II
[J].DOI:10.1061/(ASCE)0733-9399(1995)121:1(102) [本文引用: 1]
桥梁气动自激力时域表达式的瞬态与极限特性
[J].
Limiting and transient characteristics of time-domain expressions for bridge self-excited aerodynamic forces
[J].
Simulation of ergodic multivariate stochastic processes
[J].DOI:10.1061/(ASCE)0733-9399(1996)122:8(778) [本文引用: 1]
Field measurement study of wind characteristics at different measuring positions in a mountainous valley
[J].DOI:10.1016/j.expthermflusci.2019.109991 [本文引用: 2]
Field measurement study on turbulence field by wind tower and windcube lidar in mountain valley
[J].DOI:10.1016/j.jweia.2019.104090 [本文引用: 1]
The spectrum of horizontal gustiness near the ground in high winds
[J].DOI:10.1002/qj.49708737208 [本文引用: 1]
Enhancement factors for the vertical response of footbridges subjected to stochastic crowd loading
[J].DOI:10.1016/j.compstruc.2012.03.006 [本文引用: 1]
Nonlinear buffeting response analysis of long-span suspension bridges with central buckle
[J].DOI:10.1007/s11803-010-0011-7 [本文引用: 1]