对于空心圆截面FRP杆,早期研究有Goodman等[8]的Boron-FRP圆管试验及Davis[6]的Boron-和Glass-FRP圆管试验. Davis[6]将考虑、不考虑剪切变形的屈曲荷载理论结果与试验结果进行比较,指出不考虑剪切变形会导致明显的误差. 近年来,Puente等[9]认为FRP的材性与高强度钢材相似,可以通过修订规范中高强度钢材的相对初弯曲表达式,进行FRP杆稳定承载力计算. 利用多种截面形式FRP杆件的试验结果,Zhan等[10]提出基于Ayrton-Perry公式[11-12]的临界荷载经验公式,Zhan等[13]提出计入剪切变形的临界荷载经验公式. 李喜来等[5]认为鉴于复合材料不具有塑性发展性能,可以采用Ayrton-Perry公式计算稳定承载力. 钱鹏等[14]和侯炜等[15]分别开展长细比从35到90和长细比从40到120的GFRP圆管轴压试验,分别提出相对初弯曲的线性拟合式和三次拟合式. 王虎长等[3]分析长细比从24到70的GFRP圆管,发现长细比小于50且大于临界长细比时,试验所得的屈曲应力小于欧拉临界应力,且长细比越小,偏离越大. 近几十年来,研究其他截面形式FRP杆在轴压下的力学行为. 例如Barbero等[16]进行工字形截面FRP杆轴压试验,提出可以利用木材的轴心受压杆承载力公式来表征稳定承载力. Zureick等[7]根据矩形截面和工字形截面FRP杆轴压试验结果,建议分析时应考虑剪切变形. Cardoso等[17]开展GFRP方管压杆轴压试验,提出稳定承载力的公式. 综上所述,大部分研究未考虑剪切变形对GFRP杆屈曲荷载的影响,部分研究采用经验模型或现象模型来反映该影响,理论支撑较薄弱.
本文采用Engesser剪切变形理论,推导考虑剪切变形和初弯曲的一般杆件临界荷载计算式. 将其推广应用到FRP圆管杆件时,考虑FRP材料的各向异性特征. 对4根具有不同相对长细比的GFRP圆管试件进行轴压试验,分析力学行为特征和破坏机理. 将试验结果和理论计算结果进行比较.
1. 考虑剪切变形和初弯曲的受压杆
1.1. 力学模型
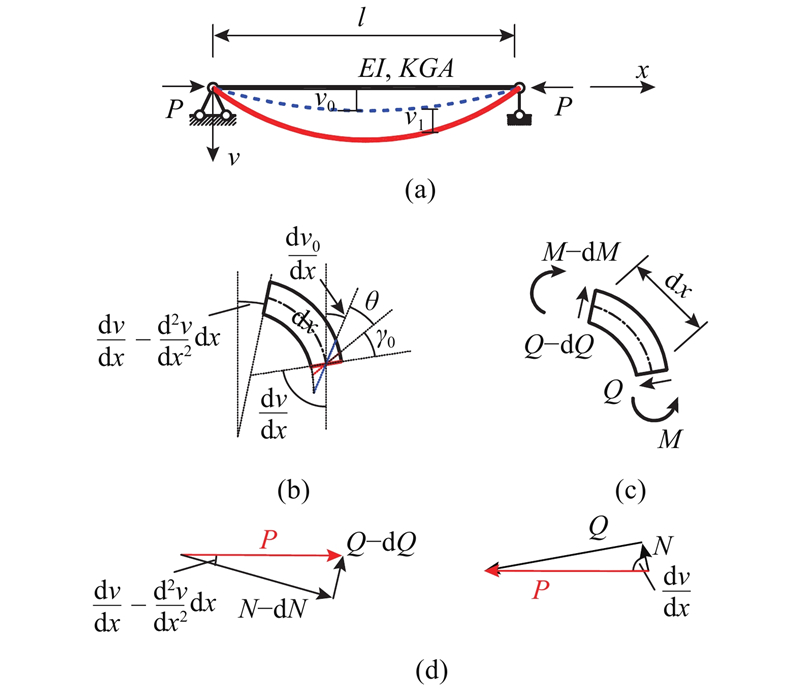
图 1
图 1 受压杆件的剪切变形、弯曲变形和内力
Fig.1 Internal forces, shear and flexural deformations of member under axial compression
如图1(b)所示,θ为弯曲转角,γ0为平均切应变. 横向总位移的增量
故几何方程为
弯矩M以下侧纤维受拉为正,剪切位移发生顺时针转动时剪力Q为正,则本构方程有
由图1(c)可得,平衡关系为
将式(5)代入式(4),利用本构方程和几何方程可得平衡方程为
1.2. 屈曲荷载和临界荷载
无初弯曲时,由式(6)可得
不考虑剪切变形时,该方程的解为经典的欧拉屈曲荷载Pcr,E,且
式中:
将式(8)代入式(9),则
式(10)即考虑剪切变形的Engesser屈曲荷载Pcr,Eng的表达式,表示为
式中:Pcr,S为弯曲刚度无穷大时的屈曲荷载,Pcr,S = KGA.
当初弯曲不为零时,利用式(7)的失稳模态对初弯曲进行展开,即有
式中:ai为对应于i阶失稳模态
式中:Pcr,E,i为对应于i阶失稳模态的屈曲荷载,Pcr,E,1=Pcr,E. 一阶展开式对屈曲荷载具有决定性影响,故式(6)可以写为
设特解
则
可见,当荷载P趋近于Pcr,Eng时,杆件横向位移趋于无穷大. 根据式(4)确定的弯曲变形和剪切变形之间的微分关系,利用式(13)可得剪切变形的表达式为
根据边缘纤维屈服准则可知,截面最大压应力不大于抗压强度fy,则
式中:
式(19)给出的横向位移放大系数(弯矩放大系数)β与文献[19]给出的由两端简支压杆所得的放大系数一致. 本文推导表明,式(19)适用于任意端部约束条件下的压杆.
设
式中:χ为稳定折减系数(稳定系数). 定义相对初弯曲
解为
或
式(23)在形式上和经典Ayrton-Perry临界荷载公式一致. 若取
2. GFRP圆管稳定承载力试验
2.1. 试验概述
采用长丝缠绕工艺制作GFRP圆管试件,参数见表1. 表中,D2为外径,T为壁厚,L为外包长度,Ls为端部加厚长度,Ts为端部增加的厚度,Lt为上、下端位移计测量点的间距. 该试件由内向外,按[04](4层0°铺层)进行纤维铺层. 按质量计算的纤维质量分数为72%. 端部加厚以防止端部复杂应力状态下的局部破坏,加厚部分由内向外按[9012](12层90°铺层)进行纤维铺层. 0°纤维铺层的纤维方向为试件纵轴线方向,90°纤维铺层的纤维方向为试件圆周向.
表 1 试件几何尺寸
Tab.1
| 试件 | D1 /mm | D2 /mm | T /mm | L /mm | Ls /mm | Ts /mm | Lt /mm |
| Z-1 | 60 | 68 | 4 | 1 295.5 | 50 | 4 | 1 100 |
| Z-2 | 60 | 68 | 4 | 1 943.2 | 50 | 4 | 1 700 |
| Z-3 | 60 | 68 | 4 | 2 591.0 | 50 | 4 | 2 400 |
| Z-4 | 60 | 68 | 4 | 3 238.7 | 50 | 4 | 3 000 |
如图2(a)所示为试验装置,加载设备为YAW-10000F型微机控制电液伺服多功能试验机. 为了保证安全,防止端部复杂应力条件下的试件内壁收缩,试件内壁受固定在加载面上的钢环约束,钢环高度为25 mm. 加载策略如下:预加载至试件估算承载力的30%,再卸载;按100 kN/min加载至估算承载力的70%,最后按0.1 mm/min进行位移控制加载.
图 2
图 2 轴压试验装置及测点布置
Fig.2 Experimental setup for compressive tests and layout of measuring points
如图2所示,近杆件上、下端处沿圆周方向均匀布置4个位移计. 位移测点编号D1表征由上端位移计D1-1和在同一母线的下端位移计D1-2所得的纵向相对位移. 应变测点位于试件中部,沿圆周向均匀布置4个测区,每个测区包含纵向和环向应变测点. SV1表示测区1的竖向应变,SH1表示测区1的环向应变.
表 2 材性试验结果
Tab.2
| 材料参数 | 数值 |
| E1c/MPa | 41 495 |
| E1t/MPa | 49 760 |
| E2c/MPa | 9 230 |
| E2t/MPa | 10 590 |
| G12/MPa | 3 220 |
| υ21c | 0.24 |
| Xt/MPa | 964.25 |
| Yt/MPa | 23.47 |
| Xc/MPa | 617.16 |
| Yc/MPa | 103.83 |
2.2. 试验结果
图3给出试件破坏形式. 长细比较小试件(Z-1和Z-2)表现出脆性破坏,即达到荷载峰值前无明显破坏现象,达到荷载峰值后截面局部出现破碎,承载力迅速丧失. 试件Z-1的2个破坏截面几乎同时出现并位于杆件的中下部,破坏截面Ⅰ的压应力较大侧发生了环向基体拉伸失效,和纵向纤维压缩失效,破坏截面Ⅱ也出现了纵向纤维压缩失效和环向基体拉伸失效. 试件Z-2的2个破坏截面出现在杆件接近底部约束的位置,破坏形式和Z-1相似. 具有较大长细比的试件(Z-3和Z-4)出现了较大的横向位移,横向位移整体形态和欧拉失稳的形态相似. 为了保证安全,试件Z-3和Z-4在荷载-位移曲线出现下降段后停止加载,肉眼无法观察到纤维及基体破坏,卸载后杆件基本回复到初始形态.
图 3
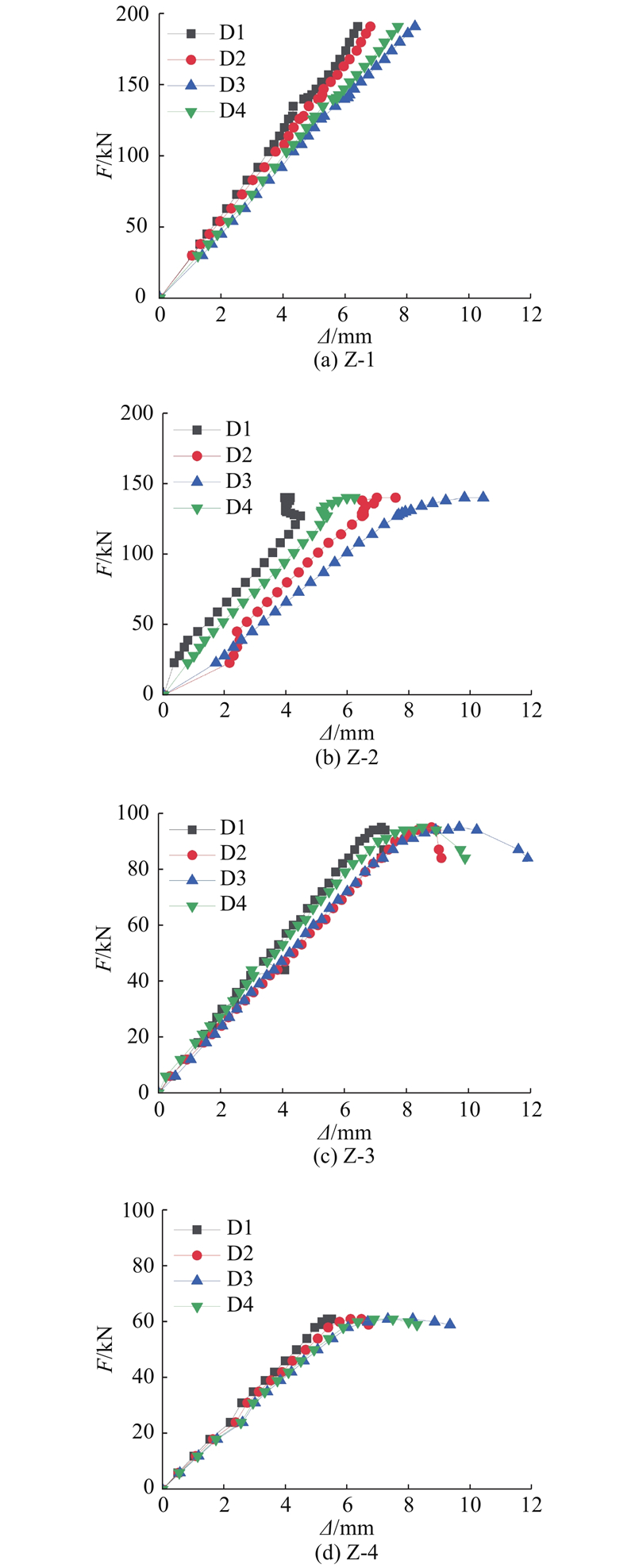
图4给出荷载F-相对纵向位移Δ曲线. 杆件沿圆周向的相对纵向位移不同,表明杆件存在制造安装引起的初弯曲和加载时没有完全对中(合力中心和形心不重合)引起的初偏心. 长细比较小的试件Z-1和Z-2(长细比分别为53和81)在荷载到达峰值后发生脆性破坏. 长细比较大的试件Z-3和Z-4(长细比分别为110和138)在荷载达到峰值后有一定的承载能力,位移曲线具有极值稳定曲线的特征. 试件Z-1和Z-2的弹性刚度较接近,表明长细比较小的试件受初弯曲和初偏心的影响较弱. 从弹性刚度来看,试件Z-3大于试件Z-4,且小于试件Z-2,反映出弹性刚度随着长细比的增加而减小,表明长杆受初弯曲和初偏心的影响较大.
图 4
图 4 荷载-纵向相对位移曲线
Fig.4 Curves of loading versus relative longitudinal displacement
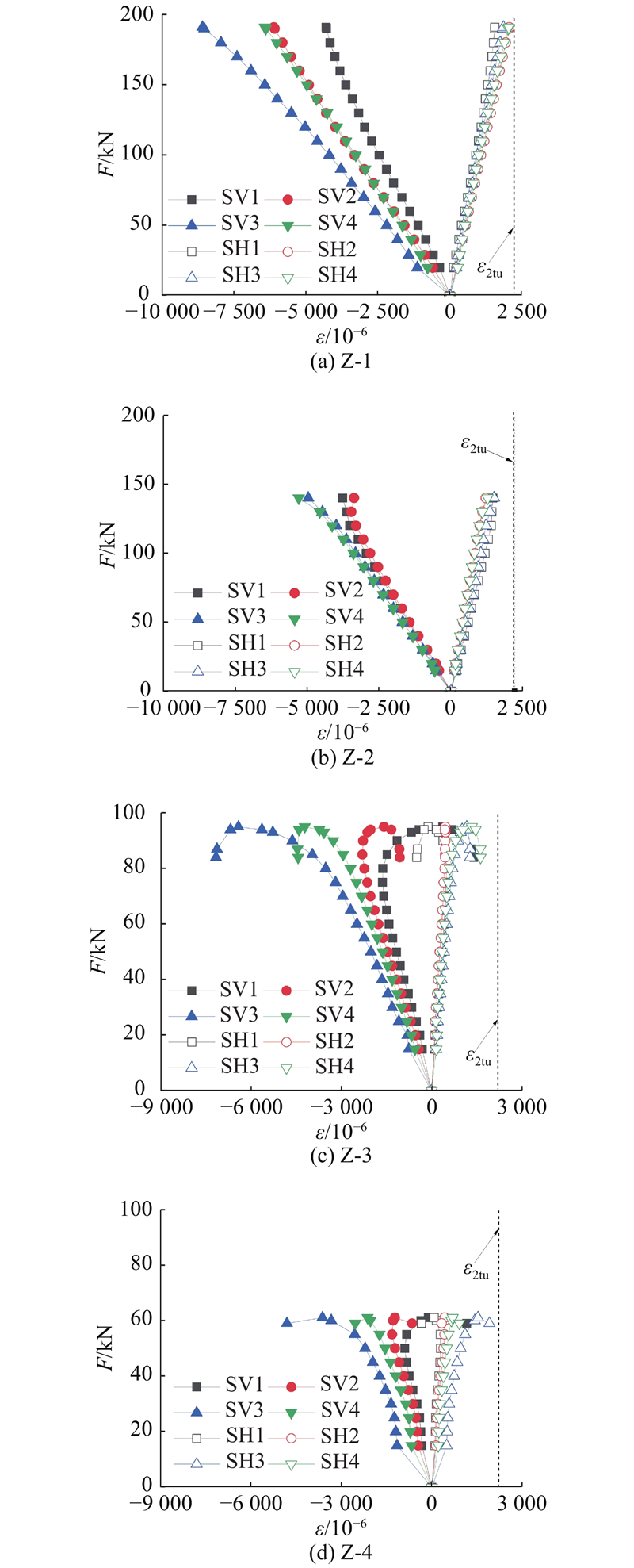
图5给出试件中部表面应变ε随荷载的变化. 纵向应变为压应变,环向应变为拉应变,两者比值在加载初期变化不大. 长细比较小的试件Z-1和Z-2在到达荷载峰值前的曲线基本为线弹性. 长细比较大的试件Z-3和Z-4在接近荷载峰值时表现出非弹性特征,应变分布受二阶矩的影响较明显,说明须考虑几何非线性致使的P-Δ效应. 应变沿圆周向分布的不均匀性表明了初弯曲和初偏心的存在.
图 5
纤维压缩的极限压应变ε1cu和基体拉伸的极限拉应变ε2tu为
3. 理论分析及讨论
各向异性材料的失效准则主要有最大应力、最大应变、Tsai-Wu准则[22]等. 由于试件的纤维方向和轴线方向一致,采用最大应变准则. 完善GFRP短管在轴心受压时,当纵向纤维发生压缩失效时,截面承载力P1u满足
式中:
根据板壳理论可知,外表面环向应变
式中:
将式(24)代入式(25)、(26),则
完善GFRP短管构件的截面承载力Pu为
考虑初弯曲后的最大压应变小于极限应变,则
即
比较式(17)、(31)可知,由式(29)确定的Pu和式(17)的fyA具有相同的物理含义. 由此,对于GFRP圆管构件,fy=Pu/A1.
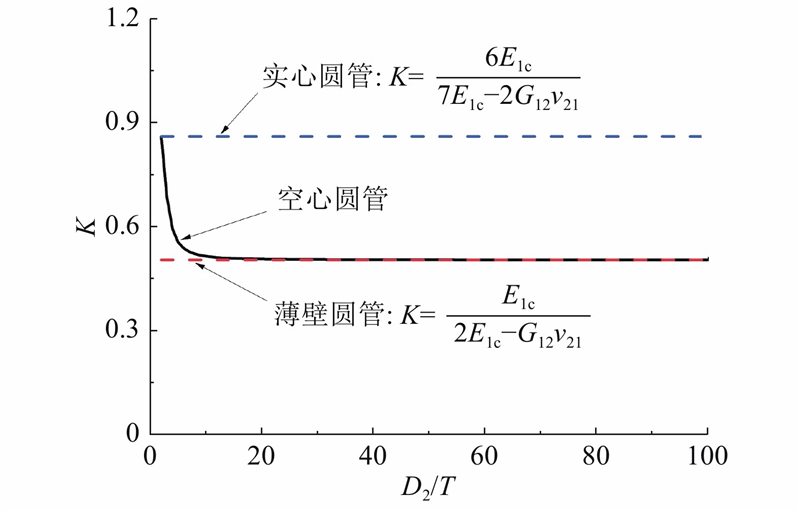
根据以上分析,可以利用式(21)、(22)计算GFRP圆管构件轴心受压稳定折减系数,此时
式中:m=D1/D2. 数值计算分析表明,文献[23]算式分母中的−27 m4应修订为+27 m4. 对于薄壁圆管,有m ≈ 1,此时
对于实心圆管,有m=0,此时
图 6
表3给出各试件极限承载力试验值、完善短构件截面承载力、稳定折减系数的理论(初弯曲幅值为l0/500)及试验值. 表中,l0为扣除受约束部分长度后的杆件长度,即l0= l −2 ls. 由式(34)可得K= 0.505,计算长度系数取μ = 0.5. 由式(28)可得P1u=496.3 kN,P2u=290.0 kN,故有Pu=290.0 kN. 根据Cardoso等[15]对短杆(λn≤0.7)、中长杆(0.7<λn<1.3)及长杆(λn≥1.3)的划分,长杆的破坏为整体失稳,短杆和中长杆可能会出现强度破坏. 由表3可知,试件Z-1和Z-2为中长杆,试件Z-3和Z-4为长杆,破坏现象符合Cardoso等[17]的破坏规律. 若简单地按照纵向纤维压缩失效所确定的截面承载力计算相对长细比,则这些试件均属于长杆.
表 3 稳定折减系数的理论和试验结果
Tab.3
| 试件 | l0 /mm | Pcr,E /kN | Pcr,Eng /kN | Pu /kN | λn | 理论值 | 试验值 | 误差/% | |||
| Pcr /kN | χ | Pcr /kN | χ | ||||||||
| Z-1 | 1195.5 | 473.8 | 347.7 | 290.0 | 0.913 | 208.1 | 0.717 | 191.0 | 0.659 | 8.9 | |
| Z-2 | 1843.2 | 199.3 | 173.0 | 290.0 | 1.30 | 135.8 | 0.468 | 140.0 | 0.483 | −3.0 | |
| Z-3 | 2491.0 | 109.1 | 100.7 | 290.0 | 1.70 | 86.6 | 0.299 | 95.0 | 0.328 | −8.8 | |
| Z-4 | 3138.7 | 68.7 | 65.3 | 290.0 | 2.11 | 58.5 | 0.202 | 61.0 | 0.210 | −4.2 | |
由表3可见,稳定折减系数的理论值和试验值较接近,两者之比的平均值为0.98,变异系数为6.7%,表明GFRP圆管构件可以用临界荷载估算极限承载力. 与稳定折减系数的试验值相比,试件Z-1的理论值偏大,其他试件的理论值偏小,这是由于试件Z-1的承载力较大,试验中加载端会产生一定的转动,减弱了约束.
为了便于比较,定义基于欧拉稳定承载力的相对长细比
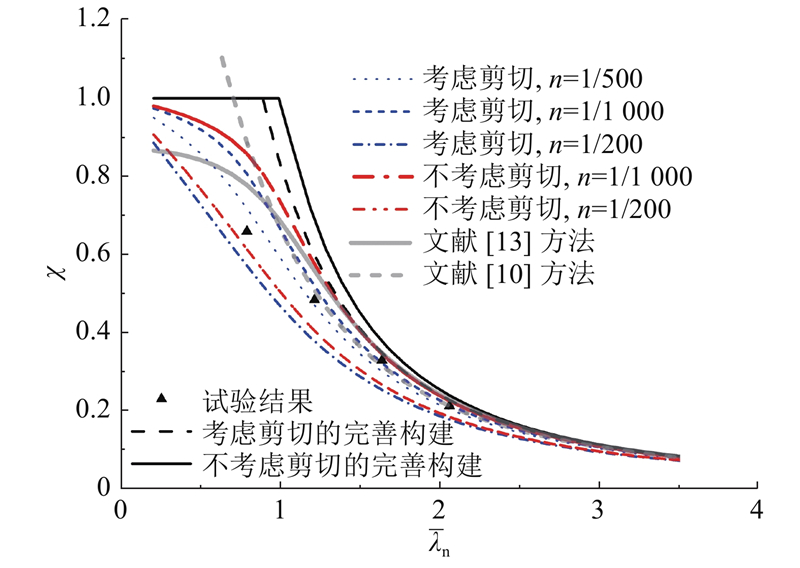
采用本文的试件参数,只改变GFRP圆管的长度和初弯曲率,可得稳定折减系数随
对于一般GFRP 压杆,Zhan等[10]给出的稳定折减系数公式为
Zhan等[10]给出稳定承载力的表达式:
可以重写为
根据式(36)、(38)所得的曲线如图7所示. 可见,它们较适合于长杆的稳定承载力预测.
图 7
图 7 稳定折减系数的理论和试验结果
Fig.7 Theoretical and experimental results of buckling reduction factor
4. 结 论
(1) GFRP构件的剪切刚度相对较小,计算屈曲荷载时应考虑剪切变形. 采用基于Engesser剪切变形理论的屈曲荷载相对保守. Engesser屈曲荷载、初弯曲幅值及荷载共同决定了杆件的横向位移幅.
(2) 试验结果表明,在确定完善GFRP短管的截面承载力时,应综合考虑试件轴向纤维压缩破坏和环向基体拉伸破坏. 基于最大应变准则得到的计算式能够较准确地反映试验破坏现象.
(3) 考虑剪切变形,推导基于最大应变准则的GFRP圆管杆件的临界荷载计算式. 计算结果与试验获得的轴压极限承载力接近,表明GFRP圆管构件可以用临界荷载估算极限承载力. 初弯曲率可取1/500,剪切系数按正交异性材料空心圆管确定.
(4) 非完善GFRP圆管杆件的轴心受压稳定折减系数随着初弯曲率的增大而减小. 剪切变形会对临界荷载产生不利影响,随着初弯曲率的减小变得明显.
参考文献
荆门换流站接地极工程玻璃钢构架真型试验
[J].DOI:10.3969/j.issn.1000-7229.2010.12.008 [本文引用: 2]
Full scale test of glass fiber reinforced plastic gantry for the earth electrode of Jingmen converter station
[J].DOI:10.3969/j.issn.1000-7229.2010.12.008 [本文引用: 2]
复合材料输电杆塔设计方法讨论
[J].
The discussion of designing fiber reinforce plastic transmission tower
[J].
玻璃钢复合材料轴压构杆稳定性分析
[J].DOI:10.3969/j.issn.1000-7229.2011.09.021 [本文引用: 1]
Stability analysis of axial compression component of FRP
[J].DOI:10.3969/j.issn.1000-7229.2011.09.021 [本文引用: 1]
FRP在工程结构中的应用与发展
[J].DOI:10.3321/j.issn:1000-131X.2006.03.004
Applications and development of fiber-reinforced polymer in engineering structures
[J].DOI:10.3321/j.issn:1000-131X.2006.03.004
复合材料杆塔压杆稳定计算方法研究
[J].DOI:10.3969/j.issn.1001-3598.2010.06.001 [本文引用: 2]
Study on the stability calculation method of compressive member in composites pole tower
[J].DOI:10.3969/j.issn.1001-3598.2010.06.001 [本文引用: 2]
Short-term behavior and design of fiber-reinforced polymeric slender members under axial compression
[J].DOI:10.1061/(ASCE)1090-0268(1997)1:4(140) [本文引用: 2]
Buckling of GFRP columns: an empirical approach to design
[J].DOI:10.1061/(ASCE)1090-0268(2006)10:6(529) [本文引用: 1]
Determination of critical loads for global buckling of axially loaded pultruded fiber-reinforced polymer members with doubly symmetric cross sections
[J].DOI:10.1177/1369433218759572 [本文引用: 3]
On the theoretical background of the generalization of Ayrton-Perry type resistance formulas
[J].
Complete generalization of the Ayrton-Perry formula for beam-column buckling problems
[J].
Determination of critical load for global flexural buckling in concentrically loaded pultruded FRP structural struts
[J].
GFRP管轴心受压性能的试验研究
[J].
Experimental study on GFRP pipes under axial compression
[J].
GFRP轴心受压构件的稳定性能
[J].DOI:10.3969/j.issn.1007-9629.2010.04.005 [本文引用: 2]
Stability of axial compression members of glass fiber-reinforced plastic (GFRP)
[J].DOI:10.3969/j.issn.1007-9629.2010.04.005 [本文引用: 2]
A phenomenological design equation for FRP columns with interaction between local and global buckling
[J].DOI:10.1016/0263-8231(94)90013-2 [本文引用: 1]
Compressive strength equation for GFRP square tube columns
[J].
Timoshenko beam-column buckling. does Dario stand the test?
[J].DOI:10.1016/j.engstruct.2008.09.010 [本文引用: 1]
A general theory of strength for anisotropic materials
[J].DOI:10.1177/002199837100500106 [本文引用: 1]
Shear coefficients for orthotropic beams
[J].DOI:10.1177/002199837300700411 [本文引用: 2]