[1]
LE B R, PÉNARD L, HAUET A, et al Gauging extreme floods on YouTube: application of LSPIV to home movies for the post-event determination of stream discharges
[J]. Hydrological Process , 2016 , 30 (1 ): 90 - 105
DOI:10.1002/hyp.10532
[本文引用: 2]
[2]
KASUGA K, HACHIYA H, KINOSITA T, et al Quantitative estimation of the ultrasound transmission characteristics for river flow measurement during a flood
[J]. Japanese Journal of Applied Physics , 2003 , 42 (5 ): 3212 - 3215
URL
[本文引用: 1]
[3]
LE C J, HAUET A, PIERREFEU G, et al Performance of image-based velocimetry (LSPIV) applied to flash-flood discharge measurements in mediterranean rivers
[J]. Journal of Hydrology , 2010 , 394 (1-2 ): 42 - 52
DOI:10.1016/j.jhydrol.2010.05.049
[本文引用: 4]
[4]
LEWIS Q W, RHOADS B L Resolving two-dimensional flow structure in rivers using large-scale particle image velocimetry: an example from a stream confluence
[J]. Water Resources Research , 2015 , 51 (10 ): 7977 - 7994
DOI:10.1002/2015WR017783
[本文引用: 1]
[5]
FUJITA I, NOTOYA Y, FURUTA T. Measurement of inundating flow from a broken embankment by using video images shoot from a media helicopter [C]// Proceedings of the International Conference on Fluvial Hydraulics . Villeurbanne: CRC Press, 2018: 06001.
[本文引用: 1]
[6]
FUJITA I, MUSTE M, KRUGER A Large-scale particle image velocimetry for flow analysis in hydraulic engineering applications
[J]. Journal of Hydraulic Research , 1998 , 36 (3 ): 397 - 414
DOI:10.1080/00221689809498626
[本文引用: 4]
[7]
DAL S S, PIZARRO A, SAMELA C, et al Exploring the optimal experimental setup for surface flow velocity measurements using PTV
[J]. Environmental Monitoring and Assessment , 2018 , 190 (8 ): 460
DOI:10.1007/s10661-018-6848-3
[本文引用: 4]
[8]
LEITÃO J P, PEÑA-HARO S, LÜTHI B, et al Urban overland runoff velocity measurement with consumer-grade surveillance cameras and surface structure image velocimetry
[J]. Journal of Hydrology , 2018 , 565 : 791 - 804
DOI:10.1016/j.jhydrol.2018.09.001
[本文引用: 3]
[9]
TAURO F, TOSI F, MATTOCCIA S, et al Optical tracking velocimetry (OTV): leveraging optical flow and trajectory-based filtering for surface streamflow observations
[J]. Remote Sensing , 2018 , 10 (12 ): 2010
DOI:10.3390/rs10122010
[本文引用: 4]
[10]
FUJITA I, WATANABLE H, TSUBAKI R Development of a non-intrusive and efficient flow monitoring technique: the space-time image velocimetry (STIV)
[J]. International Journal of River Basin Management , 2007 , 5 (2 ): 105 - 114
DOI:10.1080/15715124.2007.9635310
[本文引用: 3]
[11]
BACHARIDIS K, MOIROGIORGOU K, SIBETHEROS I A, et al. River flow estimation using video data [C]// 2014 IEEE International Conference on Imaging Systems and Techniques (IST) Proceedings. Santorini: IEEE, 2014: 173-178.
[本文引用: 4]
[12]
王万良, 邱虹, 郑建炜 基于压缩感知图像分析的河流表面流速估计方法
[J]. 水力发电学报 , 2018 , 37 (5 ): 69 - 79
DOI:10.11660/slfdxb.20180507
[本文引用: 3]
WANG Wan-liang, QIU Hong, ZHENG Jian-wei Estimation of river surface flow velocity through image analysis based on compressed sensing
[J]. Journal of Hydroelectric Engineering , 2018 , 37 (5 ): 69 - 79
DOI:10.11660/slfdxb.20180507
[本文引用: 3]
[13]
王万良, 杨胜兰, 赵燕伟, 等 基于条件边界平衡生成对抗网络的河流表面流速估测
[J]. 浙江大学学报:工学版 , 2019 , 53 (11 ): 2118 - 2128
DOI:10.3785/j.issn.1008-973X.2019.11.009
[本文引用: 1]
WANG Wan-liang, YANG Sheng-lan, ZHAO Yan-wei, et al Estimation of river surface flow velocity based on conditional boundary equilibrium generative adversarial network
[J]. Journal of Zhejiang University: Engineering Science , 2019 , 53 (11 ): 2118 - 2128
DOI:10.3785/j.issn.1008-973X.2019.11.009
[本文引用: 1]
[14]
KIM J, KIM J Estimation of water surface flow velocity in coastal video imagery by visual tracking with deep learning
[J]. Journal of Coastal Research , 2020 , 95 (Suppl.1 ): 522 - 526
URL
[本文引用: 3]
[16]
ZHANG Z, ZHOU Y, LI Y, et al. IP camera-based LSPIV system for on-line monitoring of river flow [C]// IEEE International Conference on Electronic Measurement Instruments . Yangzhou: IEEE, 2017: 357-363.
[本文引用: 2]
[17]
BASSET A B. A treatise on hydrodynamics: with numerous examples [M]. [S. l. ]: Deighton, Bell and Company, 1888.
[本文引用: 2]
[18]
HADAD T, GURKA R Effects of particle size, concentration and surface coating on turbulent flow properties obtained using PIV/PTV
[J]. Experimental Thermal and Fluid Science , 2013 , 45 : 203 - 212
DOI:10.1016/j.expthermflusci.2012.11.006
[本文引用: 1]
[19]
EICHENDORFF P, SCHLENKHOFF A. Continuous measurement of open channel discharge using a video data logger and subsequent LSPIV analysis [C]// EGU General Assembly Conference Abstracts . [S. l.]: Geophysical Research Abstracts (GRA), 2020: 18413.
[本文引用: 1]
[20]
ZHANG Z, WANG X, FAN T, et al River surface target enhancement and background suppression for unseeded LSPIV
[J]. Flow Measurement and Instrumentation , 2013 , 30 : 99 - 111
DOI:10.1016/j.flowmeasinst.2012.12.002
[本文引用: 1]
[21]
张振, 徐枫, 沈洁, 等 基于变高单应的单目视觉平面测量方法
[J]. 仪器仪表学报 , 2014 , 35 (8 ): 1860 - 1868
URL
[本文引用: 2]
ZHANG Zhen, XU Feng, SHEN Jie, et al Plane measurement method with monocular vision based on variable-height homography
[J]. Chinese Journal of Scientific Instrument , 2014 , 35 (8 ): 1860 - 1868
URL
[本文引用: 2]
[22]
LI W, LIAO Q, RAN Q Stereo-imaging LSPIV (SI-LSPIV) for 3D water surface reconstruction and discharge measurement in mountain river flows
[J]. Journal of Hydrology , 2019 , 578 : 124099
DOI:10.1016/j.jhydrol.2019.124099
[本文引用: 1]
[23]
WERELEY S T, GUI L, MEINHART C D Advanced algorithms for microscale particle image velocimetry
[J]. AIAA Journal , 2002 , 40 (6 ): 1047 - 1055
DOI:10.2514/2.1786
[本文引用: 1]
[24]
DOBSON D W, HOLLAND K T, CALANTONI J Fast, large-scale, particle image velocimetry-based estimations of river surface velocity
[J]. Computers and Geosciences , 2014 , 70 : 35 - 43
DOI:10.1016/j.cageo.2014.05.007
[本文引用: 1]
[25]
WEITBRECHT V, KÜHN G, JIRKA G H Large scale PIV measurements at the surface of shallow water flows
[J]. Flow Measurement and Instrumentation , 2002 , 13 (5-6 ): 237 - 245
DOI:10.1016/S0955-5986(02)00059-6
[本文引用: 1]
[26]
SCARANO F, RIETHMULLER M L Iterative multigrid approach in PIV image processing with discrete window offset
[J]. Experiments in Fluids , 1999 , 26 (6 ): 513 - 523
DOI:10.1007/s003480050318
[本文引用: 1]
[27]
SCARANO F Iterative image deformation methods in PIV
[J]. Measurement Science and Technology , 2001 , 13 (1 ): R1 - R19
URL
[本文引用: 1]
[28]
LIBERZON A, GURKA R, TAYLOR Z. OpenPIV [EB/OL]. [2021-08-28].https://github.com/OpenPIV.
[本文引用: 1]
[29]
LE C J, JODEAU M, HAUET A, et al. Image-based velocity and discharge measurements in field and laboratory river engineering studies using the free FUDAA-LSPIV software [C]// Proceedings of the International Conference on Fluvial Hydraulics. Lausanne: CRC Press, 2014.
[本文引用: 1]
[30]
THIELICKE W, STAMHUIS E. PIVlab–towards user-friendly, affordable and accurate digital particle image velocimetry in MATLAB [J/OL]. Journal of Open Research software , 2014, 2(1): e30[2021-08-28]. http://doi.org/10.5334/jors.bl.
[本文引用: 1]
[31]
PATALANO A, GARCÍA C M, RODRÍGUEZ A Rectification of image velocity results (RIVeR): a simple and user-friendly toolbox for large scale water surface particle image velocimetry (PIV) and particle tracking velocimetry (PTV)
[J]. Computers and Geosciences , 2017 , 109 : 323 - 330
DOI:10.1016/j.cageo.2017.07.009
[本文引用: 1]
[32]
PERKS M T, SASSO S F D, HAUET A, et al Towards harmonisation of image velocimetry techniques for river surface velocity observations
[J]. Earth System Science Data , 2020 , 12 (3 ): 1545 - 1559
DOI:10.5194/essd-12-1545-2020
[本文引用: 1]
[33]
PEARCE S, LJUBIČIĆ R, PEÑA-HARO S, et al An evaluation of image velocimetry techniques under low flow conditions and high seeding densities using unmanned aerial systems
[J]. Remote Sensing , 2020 , 12 (2 ): 232
DOI:10.3390/rs12020232
[本文引用: 1]
[34]
FUJITA I, DEGUCHI T, DOI K, et al. Development of KU-STIV: software to measure surface velocity distribution and discharge from river surface images [C]// Proceedings of the 37th IAHR World Congress . Kuala Lumpur: [s.n.], 2017: 5284-5292.
[本文引用: 1]
[35]
王慧斌, 董伟, 张振, 等 基于时空图像频谱的时均流场重建方法
[J]. 仪器仪表学报 , 2015 , 36 (3 ): 623 - 631
URL
[本文引用: 1]
WANG Hui-bin, DONG Wei, ZHANG Zhen, et al Time-averaged flow field reconstruction method based on spectrum of spatio-temporal image
[J]. Chinese Journal of Scientific Instrument , 2015 , 36 (3 ): 623 - 631
URL
[本文引用: 1]
[36]
张振, 周扬, 李旭睿, 等 图像法测流系统开发与应用
[J]. 水利信息化 , 2018 , (3 ): 7 - 13
URL
[本文引用: 1]
ZHANG Zhen, ZHOU Yang, LI Xu-rui, et al Development and application of an image-based flow measurement system
[J]. Water Resources Informatization , 2018 , (3 ): 7 - 13
URL
[本文引用: 1]
[37]
张振, 王慧斌, 严锡君, 等 时空图像测速法的敏感性分析及不确定度评估
[J]. 仪器仪表学报 , 2017 , 38 (7 ): 1763 - 1771
DOI:10.3969/j.issn.0254-3087.2017.07.025
[本文引用: 1]
ZHANG Zhen, WANG Hui-bin, YAN Xi-jun, et al Sensitivity analysis and uncertainty evaluation of space-time image velocimetry
[J]. Chinese Journal of Scientific Instrument , 2017 , 38 (7 ): 1763 - 1771
DOI:10.3969/j.issn.0254-3087.2017.07.025
[本文引用: 1]
[38]
BAEK J, LEE S J A new two-frame particle tracking algorithm using match probability
[J]. Experiments in Fluids , 1996 , 22 (1 ): 23 - 32
DOI:10.1007/BF01893303
[本文引用: 3]
[39]
TANG H, CHENG C, HONG C, et al An improved PTV system for large-scale physical river model
[J]. Journal of Hydrodynamics, Ser. B , 2008 , 20 (6 ): 669 - 678
DOI:10.1016/S1001-6058(09)60001-9
[本文引用: 2]
[40]
CIERPKA C, LÜTKE B, KÄHLER C J Higher order multi-frame particle tracking velocimetry
[J]. Experiments in Fluids , 2013 , 54 (5 ): 1533
DOI:10.1007/s00348-013-1533-3
[本文引用: 3]
[41]
OKAMOTO K, HASSAN Y, SCHMID W New tracking algorithm for particle image velocimetry
[J]. Experiments in Fluids , 1995 , 19 (5 ): 342 - 347
DOI:10.1007/BF00203419
[本文引用: 2]
[42]
ISHIKAWA M, MURAI Y, WADA A, et al A novel algorithm for particle tracking velocimetry using the velocity gradient tensor
[J]. Experiments in Fluids , 2000 , 29 (6 ): 519 - 531
DOI:10.1007/s003480000120
[本文引用: 1]
[43]
CHANG, JOHNNY, EDWARDS D, et al. Statistical estimation of fluid flow fields [C]// ECCV Workshop on Statistical Methods in Video Processing . Copenhagen: Springer, 2002.
[本文引用: 1]
[44]
PYTLAK R. Conjugate gradient algorithms in nonconvex optimization [M]. [S. l. ]: Springer Science and Business Media, 2008.
[本文引用: 1]
[45]
HÉAS P, HERZET C, MÉMIN E, et al Bayesian estimation of turbulent motion
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2012 , 35 (6 ): 1343 - 1356
[本文引用: 1]
[46]
HÉAS P, HERZET C, MÉMIN E Bayesian inference of models and hyperparameters for robust optical-flow estimation
[J]. IEEE Transactions on Image Processing , 2011 , 21 (4 ): 1437 - 1451
URL
[本文引用: 1]
[49]
BLACK M J, ANANDAN P The robust estimation of multiple motions: parametric and piecewise-smooth flow fields
[J]. Computer Vision and Image Understanding , 1996 , 63 (1 ): 75 - 104
DOI:10.1006/cviu.1996.0006
[本文引用: 1]
[50]
TSUBAKI R, FUJITA I, TSUTSUMI S Measurement of the flood discharge of a small-sized river using an existing digital video recording system
[J]. Journal of Hydro-environment Research , 2011 , 5 (4 ): 313 - 321
DOI:10.1016/j.jher.2010.12.004
[本文引用: 1]
[52]
高琪, 王成跃, 王洪平, 等 基于连续性条件的体PIV后处理技术
[J]. 北京航空航天大学学报 , 2013 , (5 ): 693 - 696
URL
[本文引用: 1]
Gao Qi, WANG Cheng-yue, WANG Hong-ping, et al Post-processing of volumetric PIV data based on continuity condition
[J]. Journal of Beijing University of Aeronautics and Astronautics , 2013 , (5 ): 693 - 696
URL
[本文引用: 1]
[53]
DRUAULT P, GUIBERT P, ALIZON F Use of proper orthogonal decomposition for time interpolation from PIV data
[J]. Experiments in Fluids , 2005 , 39 (6 ): 1009 - 1023
DOI:10.1007/s00348-005-0035-3
[本文引用: 1]
[54]
姚叶. 基于深度学习的流场数据后处理方法的研究[D]. 北京: 北京邮电大学, 2018: 15-27.
[本文引用: 1]
YAO Ye. Research of flow field data postprocessing methods based on deep learning [D]. Beijing: Beijing University of Posts and Telecommunications, 2018: 15-27.
[本文引用: 1]
Gauging extreme floods on YouTube: application of LSPIV to home movies for the post-event determination of stream discharges
2
2016
... 开展河流科学研究、监测和管控、及时有效的灾前预警措施能极大地降低山洪灾害带来的损失[1 ] . 河流流量监测是监管河流的核心部分. 传统仪器价格昂贵,侵入式测量会对河流流动产生一定干扰. 传统仪器需要水文专家在野外环境中手动布设,仪器调试需要丰富的水文专业知识. 另外,已布设仪器容易被水中的泥沙和漂浮物损坏,难以正常作业. 由于传统仪器不足,基于图像的河流测速方法开始在水文领域广泛运用. 其中的代表性方法是粒子图像测速技术(particle image velocimetry, PIV). 这种连续的、非侵入性和低成本的方法,结合光学、图像处理和计算机技术,获取高时空分辨率运动矢量,为流场的运动估计提供高精度保障. ...
... 该方法在许多场景中已被成功应用,如阿尔卑斯山的山洪流量测量[1 ] ,为水利工程应用的二维流场评估[4 ] ,日本大融雪洪水监测[5 ] . 自大尺度粒子图像测速(large-scale particle image velocimetry, LSPIV)[3 , 6 ] 提出后,各方法对河流表面测速的效果均有提升. 常见的河流测速算法有:LSPIV、大尺度粒子跟踪测速(large-scale particle tracking velocimetry, LSPTV)[7 ] 、表面结构图像测速(surface structure image velocimetry, SSIV)[8 ] 、光学跟踪测速(optical tracking velocimetry, OTV)[9 ] 、时空图像测速[10 ] 、基于概率的测速[11 ] 、基于机器学习的测速[12 -14 ] 等. 各种算法的概述及优缺点如表1 所示. ...
Quantitative estimation of the ultrasound transmission characteristics for river flow measurement during a flood
1
2003
... 传统的河流测速方案依赖布设在现场的速度测量工具,如流速计、声学多普勒流速剖面仪(acoustic doppler current profiler, ADCP)和超声仪(ultrasonic defectoscope)[2 ] . 其工作环境通常在待观测的目标水域范围内,超出测量最大值后,流量的确定通常依赖经验的水位−流量关系[3 ] ,往往导致流量预测中的非量化不确定性. ...
Performance of image-based velocimetry (LSPIV) applied to flash-flood discharge measurements in mediterranean rivers
4
2010
... 传统的河流测速方案依赖布设在现场的速度测量工具,如流速计、声学多普勒流速剖面仪(acoustic doppler current profiler, ADCP)和超声仪(ultrasonic defectoscope)[2 ] . 其工作环境通常在待观测的目标水域范围内,超出测量最大值后,流量的确定通常依赖经验的水位−流量关系[3 ] ,往往导致流量预测中的非量化不确定性. ...
... 该方法在许多场景中已被成功应用,如阿尔卑斯山的山洪流量测量[1 ] ,为水利工程应用的二维流场评估[4 ] ,日本大融雪洪水监测[5 ] . 自大尺度粒子图像测速(large-scale particle image velocimetry, LSPIV)[3 , 6 ] 提出后,各方法对河流表面测速的效果均有提升. 常见的河流测速算法有:LSPIV、大尺度粒子跟踪测速(large-scale particle tracking velocimetry, LSPTV)[7 ] 、表面结构图像测速(surface structure image velocimetry, SSIV)[8 ] 、光学跟踪测速(optical tracking velocimetry, OTV)[9 ] 、时空图像测速[10 ] 、基于概率的测速[11 ] 、基于机器学习的测速[12 -14 ] 等. 各种算法的概述及优缺点如表1 所示. ...
... Comparisons of image-based surface flow velocimetry method
Tab.1 算法 概述 优点 缺点 LSPIV[3 , 6 ] 在前一帧的查询区域和后一帧的搜索区域间进行相关分析操作. 查询区域和搜索区域根据流动情况人为定义. 相关系数最大的2个窗口对应最可能的位移. 相关分析操作主要分为空域互相关和快速傅里叶变换互相关 可以提供全局的表面流速场. 简单有效,是目前应用较广的技术 空域互相关计算量较大. 算法得到的是每个查询区域的平均速度,速度场分辨率不高 LSPTV[7 ] 包括粒子检测和跟踪共2个步骤. 获取图像中粒子的空间分布情况,并进一步获取粒子的亚像素质心位置. 在跟踪阶段,根据粒子动态特性和分配算法,匹配不同时间帧中的粒子质心,连接粒子质心以重建轨迹 在稀疏粒子的情况下表现良好. 相对于粒子图像测速,算出的流场速度具有真实物理意义 无法处理粒子浓度较高的情况,对部分设定参数较敏感 SSIV[8 ] 在LSPIV的相关分析操作的基础上,得到初步的全局速度矢量场,再利用表面流的特性对矢量场进行后处理. 其核心在于去除LSPIV结果中的错误矢量 对查询区域变化不敏感,在复杂光学环境(如阴影或眩光)中仍有较好的 互相关分析以及对矢量场进行后处理的过程计算量较大 OTV[9 ] 结合自动特征检测、Lucas-Kanade跟踪算法和基于轨迹的过滤方法.利用Fast算法检测水面目标角点特征,用基于图像金字塔的Lucas-Kanade稀疏光流跟踪算法跟踪以上特征,再对跟踪轨迹进行后处理 在表面目标特征稀疏、非恒定流情况时表现良好 所得速度场分辨率不高 STIV[10 ] 先合成时空图像,再利用傅里叶变换检测时空图像的纹理主方向,该主方向对应原图像序列的一维时均流速矢量 空间分辨率高、实时性强,可用于河流的实时 对复杂光照和水流环境的变化较为敏感 基于概率的测速 [11 ] 基于概率的图像测速方法.基于贝叶斯框架,在图像观测函数已知的情况下,估计像素速度矢量场的后验概率 可以得到稠密的光流矢量场 为了提高流场精度,须改进超参数估计以及描述条件概率分布的似然估计 基于机器学习的测速[12 -14 ] 基于有监督学习的机器学习表面流测速方法,主要进行水流表面特征的提取和流速的分类识别. 基于无监督学习的方法,利用非线性图像配准的思路计算表面速度矢量场 有效水流表面特征的 有监督学习方法需要大量数据. 无监督学习方法的研究较少,其测速精度仍需要经过更多实验的验证;该方法仅研究了海岸波浪的跟踪测速方案,其泛化性仍有待研究 SGSD[15 ] 在变分光流框架中加入流体物理约束. 利用标量输运方程计算光流场,引入扩散项补充小尺度流场特征 速度矢量场结果精度 流动轨迹重建中仍对异常值存在敏感性
2. 图像测速方法研究现状 图像测速方法包含5个主要步骤:1)水面示踪,2)图像采集,3)图像预处理,4)图像分析,5)流场后处理. ...
... 河流测速方法基于水面图像分析流场,其主要思想是假设河流表面的颗粒或水面特征遵循与流体相同的运动模式[3 ] ,同时反映真实的河流流动信息,水面模式如图1 所示. ...
Resolving two-dimensional flow structure in rivers using large-scale particle image velocimetry: an example from a stream confluence
1
2015
... 该方法在许多场景中已被成功应用,如阿尔卑斯山的山洪流量测量[1 ] ,为水利工程应用的二维流场评估[4 ] ,日本大融雪洪水监测[5 ] . 自大尺度粒子图像测速(large-scale particle image velocimetry, LSPIV)[3 , 6 ] 提出后,各方法对河流表面测速的效果均有提升. 常见的河流测速算法有:LSPIV、大尺度粒子跟踪测速(large-scale particle tracking velocimetry, LSPTV)[7 ] 、表面结构图像测速(surface structure image velocimetry, SSIV)[8 ] 、光学跟踪测速(optical tracking velocimetry, OTV)[9 ] 、时空图像测速[10 ] 、基于概率的测速[11 ] 、基于机器学习的测速[12 -14 ] 等. 各种算法的概述及优缺点如表1 所示. ...
1
... 该方法在许多场景中已被成功应用,如阿尔卑斯山的山洪流量测量[1 ] ,为水利工程应用的二维流场评估[4 ] ,日本大融雪洪水监测[5 ] . 自大尺度粒子图像测速(large-scale particle image velocimetry, LSPIV)[3 , 6 ] 提出后,各方法对河流表面测速的效果均有提升. 常见的河流测速算法有:LSPIV、大尺度粒子跟踪测速(large-scale particle tracking velocimetry, LSPTV)[7 ] 、表面结构图像测速(surface structure image velocimetry, SSIV)[8 ] 、光学跟踪测速(optical tracking velocimetry, OTV)[9 ] 、时空图像测速[10 ] 、基于概率的测速[11 ] 、基于机器学习的测速[12 -14 ] 等. 各种算法的概述及优缺点如表1 所示. ...
Large-scale particle image velocimetry for flow analysis in hydraulic engineering applications
4
1998
... 该方法在许多场景中已被成功应用,如阿尔卑斯山的山洪流量测量[1 ] ,为水利工程应用的二维流场评估[4 ] ,日本大融雪洪水监测[5 ] . 自大尺度粒子图像测速(large-scale particle image velocimetry, LSPIV)[3 , 6 ] 提出后,各方法对河流表面测速的效果均有提升. 常见的河流测速算法有:LSPIV、大尺度粒子跟踪测速(large-scale particle tracking velocimetry, LSPTV)[7 ] 、表面结构图像测速(surface structure image velocimetry, SSIV)[8 ] 、光学跟踪测速(optical tracking velocimetry, OTV)[9 ] 、时空图像测速[10 ] 、基于概率的测速[11 ] 、基于机器学习的测速[12 -14 ] 等. 各种算法的概述及优缺点如表1 所示. ...
... Comparisons of image-based surface flow velocimetry method
Tab.1 算法 概述 优点 缺点 LSPIV[3 , 6 ] 在前一帧的查询区域和后一帧的搜索区域间进行相关分析操作. 查询区域和搜索区域根据流动情况人为定义. 相关系数最大的2个窗口对应最可能的位移. 相关分析操作主要分为空域互相关和快速傅里叶变换互相关 可以提供全局的表面流速场. 简单有效,是目前应用较广的技术 空域互相关计算量较大. 算法得到的是每个查询区域的平均速度,速度场分辨率不高 LSPTV[7 ] 包括粒子检测和跟踪共2个步骤. 获取图像中粒子的空间分布情况,并进一步获取粒子的亚像素质心位置. 在跟踪阶段,根据粒子动态特性和分配算法,匹配不同时间帧中的粒子质心,连接粒子质心以重建轨迹 在稀疏粒子的情况下表现良好. 相对于粒子图像测速,算出的流场速度具有真实物理意义 无法处理粒子浓度较高的情况,对部分设定参数较敏感 SSIV[8 ] 在LSPIV的相关分析操作的基础上,得到初步的全局速度矢量场,再利用表面流的特性对矢量场进行后处理. 其核心在于去除LSPIV结果中的错误矢量 对查询区域变化不敏感,在复杂光学环境(如阴影或眩光)中仍有较好的 互相关分析以及对矢量场进行后处理的过程计算量较大 OTV[9 ] 结合自动特征检测、Lucas-Kanade跟踪算法和基于轨迹的过滤方法.利用Fast算法检测水面目标角点特征,用基于图像金字塔的Lucas-Kanade稀疏光流跟踪算法跟踪以上特征,再对跟踪轨迹进行后处理 在表面目标特征稀疏、非恒定流情况时表现良好 所得速度场分辨率不高 STIV[10 ] 先合成时空图像,再利用傅里叶变换检测时空图像的纹理主方向,该主方向对应原图像序列的一维时均流速矢量 空间分辨率高、实时性强,可用于河流的实时 对复杂光照和水流环境的变化较为敏感 基于概率的测速 [11 ] 基于概率的图像测速方法.基于贝叶斯框架,在图像观测函数已知的情况下,估计像素速度矢量场的后验概率 可以得到稠密的光流矢量场 为了提高流场精度,须改进超参数估计以及描述条件概率分布的似然估计 基于机器学习的测速[12 -14 ] 基于有监督学习的机器学习表面流测速方法,主要进行水流表面特征的提取和流速的分类识别. 基于无监督学习的方法,利用非线性图像配准的思路计算表面速度矢量场 有效水流表面特征的 有监督学习方法需要大量数据. 无监督学习方法的研究较少,其测速精度仍需要经过更多实验的验证;该方法仅研究了海岸波浪的跟踪测速方案,其泛化性仍有待研究 SGSD[15 ] 在变分光流框架中加入流体物理约束. 利用标量输运方程计算光流场,引入扩散项补充小尺度流场特征 速度矢量场结果精度 流动轨迹重建中仍对异常值存在敏感性
2. 图像测速方法研究现状 图像测速方法包含5个主要步骤:1)水面示踪,2)图像采集,3)图像预处理,4)图像分析,5)流场后处理. ...
... Fujita等[6 ] 将被校正的水面近似为倾斜的、表面粗糙度小的平面. 三维投影矩阵被简化为单应性矩阵 $ H $ $ Z $
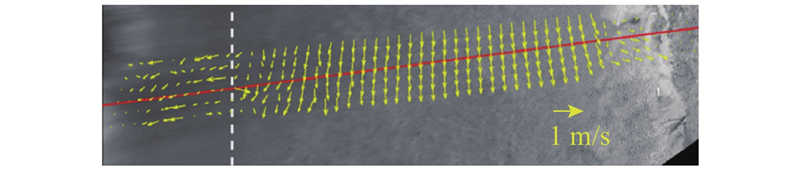
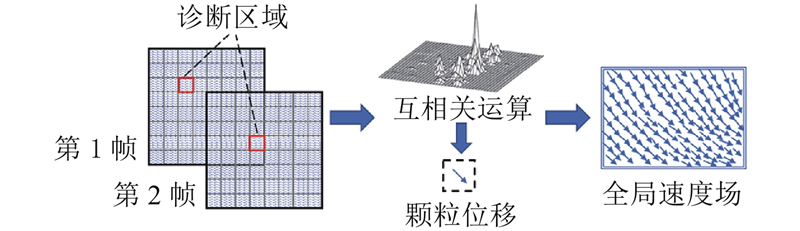
... LSPIV自Fujita等[6 ] 于1998年提出以来,已经成为目前应用较广的表面流图像测速方法,并在水文领域取得显著成效. 该方法计算的瞬时和平均速度与声波仪器测量值的偏差小于10%. 粒子图像测速基于欧拉框架描述流体运动,通过在下一连续的图像序列中搜寻最相似的图像模式,计算查询窗口内的整体粒子的平均位移,其流场计算结果如图4 所示. 该方法的关键是相关分析操作. 在相邻2帧图像的相应位置附近取一些查询窗口(窗口可人为设定),计算并查找2个时间戳下相关性最大的2个窗口. 速度矢量由位移矢量除以相应时间间隔可得. 二维离散互相关函数为 ...
Exploring the optimal experimental setup for surface flow velocity measurements using PTV
4
2018
... 该方法在许多场景中已被成功应用,如阿尔卑斯山的山洪流量测量[1 ] ,为水利工程应用的二维流场评估[4 ] ,日本大融雪洪水监测[5 ] . 自大尺度粒子图像测速(large-scale particle image velocimetry, LSPIV)[3 , 6 ] 提出后,各方法对河流表面测速的效果均有提升. 常见的河流测速算法有:LSPIV、大尺度粒子跟踪测速(large-scale particle tracking velocimetry, LSPTV)[7 ] 、表面结构图像测速(surface structure image velocimetry, SSIV)[8 ] 、光学跟踪测速(optical tracking velocimetry, OTV)[9 ] 、时空图像测速[10 ] 、基于概率的测速[11 ] 、基于机器学习的测速[12 -14 ] 等. 各种算法的概述及优缺点如表1 所示. ...
... Comparisons of image-based surface flow velocimetry method
Tab.1 算法 概述 优点 缺点 LSPIV[3 , 6 ] 在前一帧的查询区域和后一帧的搜索区域间进行相关分析操作. 查询区域和搜索区域根据流动情况人为定义. 相关系数最大的2个窗口对应最可能的位移. 相关分析操作主要分为空域互相关和快速傅里叶变换互相关 可以提供全局的表面流速场. 简单有效,是目前应用较广的技术 空域互相关计算量较大. 算法得到的是每个查询区域的平均速度,速度场分辨率不高 LSPTV[7 ] 包括粒子检测和跟踪共2个步骤. 获取图像中粒子的空间分布情况,并进一步获取粒子的亚像素质心位置. 在跟踪阶段,根据粒子动态特性和分配算法,匹配不同时间帧中的粒子质心,连接粒子质心以重建轨迹 在稀疏粒子的情况下表现良好. 相对于粒子图像测速,算出的流场速度具有真实物理意义 无法处理粒子浓度较高的情况,对部分设定参数较敏感 SSIV[8 ] 在LSPIV的相关分析操作的基础上,得到初步的全局速度矢量场,再利用表面流的特性对矢量场进行后处理. 其核心在于去除LSPIV结果中的错误矢量 对查询区域变化不敏感,在复杂光学环境(如阴影或眩光)中仍有较好的 互相关分析以及对矢量场进行后处理的过程计算量较大 OTV[9 ] 结合自动特征检测、Lucas-Kanade跟踪算法和基于轨迹的过滤方法.利用Fast算法检测水面目标角点特征,用基于图像金字塔的Lucas-Kanade稀疏光流跟踪算法跟踪以上特征,再对跟踪轨迹进行后处理 在表面目标特征稀疏、非恒定流情况时表现良好 所得速度场分辨率不高 STIV[10 ] 先合成时空图像,再利用傅里叶变换检测时空图像的纹理主方向,该主方向对应原图像序列的一维时均流速矢量 空间分辨率高、实时性强,可用于河流的实时 对复杂光照和水流环境的变化较为敏感 基于概率的测速 [11 ] 基于概率的图像测速方法.基于贝叶斯框架,在图像观测函数已知的情况下,估计像素速度矢量场的后验概率 可以得到稠密的光流矢量场 为了提高流场精度,须改进超参数估计以及描述条件概率分布的似然估计 基于机器学习的测速[12 -14 ] 基于有监督学习的机器学习表面流测速方法,主要进行水流表面特征的提取和流速的分类识别. 基于无监督学习的方法,利用非线性图像配准的思路计算表面速度矢量场 有效水流表面特征的 有监督学习方法需要大量数据. 无监督学习方法的研究较少,其测速精度仍需要经过更多实验的验证;该方法仅研究了海岸波浪的跟踪测速方案,其泛化性仍有待研究 SGSD[15 ] 在变分光流框架中加入流体物理约束. 利用标量输运方程计算光流场,引入扩散项补充小尺度流场特征 速度矢量场结果精度 流动轨迹重建中仍对异常值存在敏感性
2. 图像测速方法研究现状 图像测速方法包含5个主要步骤:1)水面示踪,2)图像采集,3)图像预处理,4)图像分析,5)流场后处理. ...
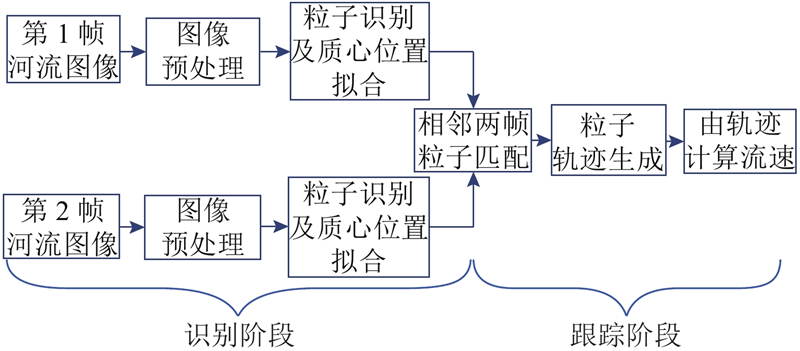
... LSPTV[7 ] 基于拉格朗日框架描述流体运动,粒子跟踪测速适用于处理较低粒子浓度的图像,以便于识别和跟踪单个粒子. 如图10 所示,预处理图像,提取目标粒子,利用图像增强手段(如区域生长法)强化粒子特征,计算构成该粒子的所有像素的质心位置定位该粒子的中心坐标. 粒子形状特征(区域面积,方向角等)被提取来帮助匹配相邻帧的粒子并重建轨迹. ...
... 在参数敏感性上,Dal等[7 ] 探索了不同粒子浓度、粒子逐帧位移,粒子直径以及跟踪最小帧数对跟踪效果的影响,并研究了不同的水力和形态条件下的最佳粒子播种密度和帧速率. ...
Urban overland runoff velocity measurement with consumer-grade surveillance cameras and surface structure image velocimetry
3
2018
... 该方法在许多场景中已被成功应用,如阿尔卑斯山的山洪流量测量[1 ] ,为水利工程应用的二维流场评估[4 ] ,日本大融雪洪水监测[5 ] . 自大尺度粒子图像测速(large-scale particle image velocimetry, LSPIV)[3 , 6 ] 提出后,各方法对河流表面测速的效果均有提升. 常见的河流测速算法有:LSPIV、大尺度粒子跟踪测速(large-scale particle tracking velocimetry, LSPTV)[7 ] 、表面结构图像测速(surface structure image velocimetry, SSIV)[8 ] 、光学跟踪测速(optical tracking velocimetry, OTV)[9 ] 、时空图像测速[10 ] 、基于概率的测速[11 ] 、基于机器学习的测速[12 -14 ] 等. 各种算法的概述及优缺点如表1 所示. ...
... Comparisons of image-based surface flow velocimetry method
Tab.1 算法 概述 优点 缺点 LSPIV[3 , 6 ] 在前一帧的查询区域和后一帧的搜索区域间进行相关分析操作. 查询区域和搜索区域根据流动情况人为定义. 相关系数最大的2个窗口对应最可能的位移. 相关分析操作主要分为空域互相关和快速傅里叶变换互相关 可以提供全局的表面流速场. 简单有效,是目前应用较广的技术 空域互相关计算量较大. 算法得到的是每个查询区域的平均速度,速度场分辨率不高 LSPTV[7 ] 包括粒子检测和跟踪共2个步骤. 获取图像中粒子的空间分布情况,并进一步获取粒子的亚像素质心位置. 在跟踪阶段,根据粒子动态特性和分配算法,匹配不同时间帧中的粒子质心,连接粒子质心以重建轨迹 在稀疏粒子的情况下表现良好. 相对于粒子图像测速,算出的流场速度具有真实物理意义 无法处理粒子浓度较高的情况,对部分设定参数较敏感 SSIV[8 ] 在LSPIV的相关分析操作的基础上,得到初步的全局速度矢量场,再利用表面流的特性对矢量场进行后处理. 其核心在于去除LSPIV结果中的错误矢量 对查询区域变化不敏感,在复杂光学环境(如阴影或眩光)中仍有较好的 互相关分析以及对矢量场进行后处理的过程计算量较大 OTV[9 ] 结合自动特征检测、Lucas-Kanade跟踪算法和基于轨迹的过滤方法.利用Fast算法检测水面目标角点特征,用基于图像金字塔的Lucas-Kanade稀疏光流跟踪算法跟踪以上特征,再对跟踪轨迹进行后处理 在表面目标特征稀疏、非恒定流情况时表现良好 所得速度场分辨率不高 STIV[10 ] 先合成时空图像,再利用傅里叶变换检测时空图像的纹理主方向,该主方向对应原图像序列的一维时均流速矢量 空间分辨率高、实时性强,可用于河流的实时 对复杂光照和水流环境的变化较为敏感 基于概率的测速 [11 ] 基于概率的图像测速方法.基于贝叶斯框架,在图像观测函数已知的情况下,估计像素速度矢量场的后验概率 可以得到稠密的光流矢量场 为了提高流场精度,须改进超参数估计以及描述条件概率分布的似然估计 基于机器学习的测速[12 -14 ] 基于有监督学习的机器学习表面流测速方法,主要进行水流表面特征的提取和流速的分类识别. 基于无监督学习的方法,利用非线性图像配准的思路计算表面速度矢量场 有效水流表面特征的 有监督学习方法需要大量数据. 无监督学习方法的研究较少,其测速精度仍需要经过更多实验的验证;该方法仅研究了海岸波浪的跟踪测速方案,其泛化性仍有待研究 SGSD[15 ] 在变分光流框架中加入流体物理约束. 利用标量输运方程计算光流场,引入扩散项补充小尺度流场特征 速度矢量场结果精度 流动轨迹重建中仍对异常值存在敏感性
2. 图像测速方法研究现状 图像测速方法包含5个主要步骤:1)水面示踪,2)图像采集,3)图像预处理,4)图像分析,5)流场后处理. ...
... 表面结构图像测速法(surface structure lmage velocimetry, SSIV)[8 ] 在粒子图像测速法的基础上结合河流表面的局部和全局特征进一步改进,效果如图16 所示. SSIV方法首先用相关分析操作得到初步的全局速度矢量场,再利用表面流特性2步过滤矢量场:1)SSIV提出局部过滤的思想,将每个矢量与其相邻的8个速度矢量进行对比,若矢量偏差过大,则会被直接抛弃;2)检测每个速度矢量与全局平均速度矢量是否存在较大偏差,大偏差矢量被认为是无效的. ...
Optical tracking velocimetry (OTV): leveraging optical flow and trajectory-based filtering for surface streamflow observations
4
2018
... 该方法在许多场景中已被成功应用,如阿尔卑斯山的山洪流量测量[1 ] ,为水利工程应用的二维流场评估[4 ] ,日本大融雪洪水监测[5 ] . 自大尺度粒子图像测速(large-scale particle image velocimetry, LSPIV)[3 , 6 ] 提出后,各方法对河流表面测速的效果均有提升. 常见的河流测速算法有:LSPIV、大尺度粒子跟踪测速(large-scale particle tracking velocimetry, LSPTV)[7 ] 、表面结构图像测速(surface structure image velocimetry, SSIV)[8 ] 、光学跟踪测速(optical tracking velocimetry, OTV)[9 ] 、时空图像测速[10 ] 、基于概率的测速[11 ] 、基于机器学习的测速[12 -14 ] 等. 各种算法的概述及优缺点如表1 所示. ...
... Comparisons of image-based surface flow velocimetry method
Tab.1 算法 概述 优点 缺点 LSPIV[3 , 6 ] 在前一帧的查询区域和后一帧的搜索区域间进行相关分析操作. 查询区域和搜索区域根据流动情况人为定义. 相关系数最大的2个窗口对应最可能的位移. 相关分析操作主要分为空域互相关和快速傅里叶变换互相关 可以提供全局的表面流速场. 简单有效,是目前应用较广的技术 空域互相关计算量较大. 算法得到的是每个查询区域的平均速度,速度场分辨率不高 LSPTV[7 ] 包括粒子检测和跟踪共2个步骤. 获取图像中粒子的空间分布情况,并进一步获取粒子的亚像素质心位置. 在跟踪阶段,根据粒子动态特性和分配算法,匹配不同时间帧中的粒子质心,连接粒子质心以重建轨迹 在稀疏粒子的情况下表现良好. 相对于粒子图像测速,算出的流场速度具有真实物理意义 无法处理粒子浓度较高的情况,对部分设定参数较敏感 SSIV[8 ] 在LSPIV的相关分析操作的基础上,得到初步的全局速度矢量场,再利用表面流的特性对矢量场进行后处理. 其核心在于去除LSPIV结果中的错误矢量 对查询区域变化不敏感,在复杂光学环境(如阴影或眩光)中仍有较好的 互相关分析以及对矢量场进行后处理的过程计算量较大 OTV[9 ] 结合自动特征检测、Lucas-Kanade跟踪算法和基于轨迹的过滤方法.利用Fast算法检测水面目标角点特征,用基于图像金字塔的Lucas-Kanade稀疏光流跟踪算法跟踪以上特征,再对跟踪轨迹进行后处理 在表面目标特征稀疏、非恒定流情况时表现良好 所得速度场分辨率不高 STIV[10 ] 先合成时空图像,再利用傅里叶变换检测时空图像的纹理主方向,该主方向对应原图像序列的一维时均流速矢量 空间分辨率高、实时性强,可用于河流的实时 对复杂光照和水流环境的变化较为敏感 基于概率的测速 [11 ] 基于概率的图像测速方法.基于贝叶斯框架,在图像观测函数已知的情况下,估计像素速度矢量场的后验概率 可以得到稠密的光流矢量场 为了提高流场精度,须改进超参数估计以及描述条件概率分布的似然估计 基于机器学习的测速[12 -14 ] 基于有监督学习的机器学习表面流测速方法,主要进行水流表面特征的提取和流速的分类识别. 基于无监督学习的方法,利用非线性图像配准的思路计算表面速度矢量场 有效水流表面特征的 有监督学习方法需要大量数据. 无监督学习方法的研究较少,其测速精度仍需要经过更多实验的验证;该方法仅研究了海岸波浪的跟踪测速方案,其泛化性仍有待研究 SGSD[15 ] 在变分光流框架中加入流体物理约束. 利用标量输运方程计算光流场,引入扩散项补充小尺度流场特征 速度矢量场结果精度 流动轨迹重建中仍对异常值存在敏感性
2. 图像测速方法研究现状 图像测速方法包含5个主要步骤:1)水面示踪,2)图像采集,3)图像预处理,4)图像分析,5)流场后处理. ...
... 图像采集的工作方式不尽相同,通常是用相机定义参数,再进行图像测速分析. 河流测速需要选择与流动相关的最佳相机采样频率(24、30、60 Hz)[16 ] . 当河流流速小时,改变采样频率以获取更有效的图像[11 ] . Tauro等[9 ] 分析了OTV对相机帧率变化的敏感性,不同频率(8~25 Hz)得到的平均速度没有统计学意义,因此在该实验条件下(平均流速0.47 m/s)OTV对采样频率不敏感[15 ] . ...
... 光跟踪测速法(optical tracking velocimety, OTV)[9 ] 利用基于图像金字塔的稀疏变分Lucas-Kanade(L-K)算法[48 ] 跟踪检测到的特征. 作为稀疏的一阶微分技术,L-K算法在数据项上同样假定图像强度 $ I\left(x,t\right) $ t 的函数,它是守恒的. 基于局部邻域(大小为n )内流速矢量不变假设,该邻域生成包含n 个方程的超定方程组,再由加权最小二乘原理求解,转化为最小化以下光流误差 ...
Development of a non-intrusive and efficient flow monitoring technique: the space-time image velocimetry (STIV)
3
2007
... 该方法在许多场景中已被成功应用,如阿尔卑斯山的山洪流量测量[1 ] ,为水利工程应用的二维流场评估[4 ] ,日本大融雪洪水监测[5 ] . 自大尺度粒子图像测速(large-scale particle image velocimetry, LSPIV)[3 , 6 ] 提出后,各方法对河流表面测速的效果均有提升. 常见的河流测速算法有:LSPIV、大尺度粒子跟踪测速(large-scale particle tracking velocimetry, LSPTV)[7 ] 、表面结构图像测速(surface structure image velocimetry, SSIV)[8 ] 、光学跟踪测速(optical tracking velocimetry, OTV)[9 ] 、时空图像测速[10 ] 、基于概率的测速[11 ] 、基于机器学习的测速[12 -14 ] 等. 各种算法的概述及优缺点如表1 所示. ...
... Comparisons of image-based surface flow velocimetry method
Tab.1 算法 概述 优点 缺点 LSPIV[3 , 6 ] 在前一帧的查询区域和后一帧的搜索区域间进行相关分析操作. 查询区域和搜索区域根据流动情况人为定义. 相关系数最大的2个窗口对应最可能的位移. 相关分析操作主要分为空域互相关和快速傅里叶变换互相关 可以提供全局的表面流速场. 简单有效,是目前应用较广的技术 空域互相关计算量较大. 算法得到的是每个查询区域的平均速度,速度场分辨率不高 LSPTV[7 ] 包括粒子检测和跟踪共2个步骤. 获取图像中粒子的空间分布情况,并进一步获取粒子的亚像素质心位置. 在跟踪阶段,根据粒子动态特性和分配算法,匹配不同时间帧中的粒子质心,连接粒子质心以重建轨迹 在稀疏粒子的情况下表现良好. 相对于粒子图像测速,算出的流场速度具有真实物理意义 无法处理粒子浓度较高的情况,对部分设定参数较敏感 SSIV[8 ] 在LSPIV的相关分析操作的基础上,得到初步的全局速度矢量场,再利用表面流的特性对矢量场进行后处理. 其核心在于去除LSPIV结果中的错误矢量 对查询区域变化不敏感,在复杂光学环境(如阴影或眩光)中仍有较好的 互相关分析以及对矢量场进行后处理的过程计算量较大 OTV[9 ] 结合自动特征检测、Lucas-Kanade跟踪算法和基于轨迹的过滤方法.利用Fast算法检测水面目标角点特征,用基于图像金字塔的Lucas-Kanade稀疏光流跟踪算法跟踪以上特征,再对跟踪轨迹进行后处理 在表面目标特征稀疏、非恒定流情况时表现良好 所得速度场分辨率不高 STIV[10 ] 先合成时空图像,再利用傅里叶变换检测时空图像的纹理主方向,该主方向对应原图像序列的一维时均流速矢量 空间分辨率高、实时性强,可用于河流的实时 对复杂光照和水流环境的变化较为敏感 基于概率的测速 [11 ] 基于概率的图像测速方法.基于贝叶斯框架,在图像观测函数已知的情况下,估计像素速度矢量场的后验概率 可以得到稠密的光流矢量场 为了提高流场精度,须改进超参数估计以及描述条件概率分布的似然估计 基于机器学习的测速[12 -14 ] 基于有监督学习的机器学习表面流测速方法,主要进行水流表面特征的提取和流速的分类识别. 基于无监督学习的方法,利用非线性图像配准的思路计算表面速度矢量场 有效水流表面特征的 有监督学习方法需要大量数据. 无监督学习方法的研究较少,其测速精度仍需要经过更多实验的验证;该方法仅研究了海岸波浪的跟踪测速方案,其泛化性仍有待研究 SGSD[15 ] 在变分光流框架中加入流体物理约束. 利用标量输运方程计算光流场,引入扩散项补充小尺度流场特征 速度矢量场结果精度 流动轨迹重建中仍对异常值存在敏感性
2. 图像测速方法研究现状 图像测速方法包含5个主要步骤:1)水面示踪,2)图像采集,3)图像预处理,4)图像分析,5)流场后处理. ...
... 目前,STIV方法的主要研究及应用集中于日本. Fujita等[10 ] 提出该方法并验证其有效性,同时开发KU-STIV商业软件,成功应用于日本诸多河流的测量方案[34 ] . 国内对于STIV方法的研究与应用尚处于初步阶段,主要集中在河海大学. 王慧斌等[35 ] 提出基于时空图像频谱的时均流场重建方法,基于傅里叶变换的自配准性质约束时空图像纹理和频谱主方向的关系,可以达到0.1°的测量精度. 张振等[36 ] 基于STIV方法开发图像法测流系统,目前已投入实际运行;张振等[37 ] 还对进行了时空图像测速法的敏感性分析及不确定度评估. 与LSPIV方法相比,STIV方法的显著优势是空间分辨率能够达到单像素水平,计算效率在前者的10倍以上,可实现高效河流测速. ...
4
... 该方法在许多场景中已被成功应用,如阿尔卑斯山的山洪流量测量[1 ] ,为水利工程应用的二维流场评估[4 ] ,日本大融雪洪水监测[5 ] . 自大尺度粒子图像测速(large-scale particle image velocimetry, LSPIV)[3 , 6 ] 提出后,各方法对河流表面测速的效果均有提升. 常见的河流测速算法有:LSPIV、大尺度粒子跟踪测速(large-scale particle tracking velocimetry, LSPTV)[7 ] 、表面结构图像测速(surface structure image velocimetry, SSIV)[8 ] 、光学跟踪测速(optical tracking velocimetry, OTV)[9 ] 、时空图像测速[10 ] 、基于概率的测速[11 ] 、基于机器学习的测速[12 -14 ] 等. 各种算法的概述及优缺点如表1 所示. ...
... Comparisons of image-based surface flow velocimetry method
Tab.1 算法 概述 优点 缺点 LSPIV[3 , 6 ] 在前一帧的查询区域和后一帧的搜索区域间进行相关分析操作. 查询区域和搜索区域根据流动情况人为定义. 相关系数最大的2个窗口对应最可能的位移. 相关分析操作主要分为空域互相关和快速傅里叶变换互相关 可以提供全局的表面流速场. 简单有效,是目前应用较广的技术 空域互相关计算量较大. 算法得到的是每个查询区域的平均速度,速度场分辨率不高 LSPTV[7 ] 包括粒子检测和跟踪共2个步骤. 获取图像中粒子的空间分布情况,并进一步获取粒子的亚像素质心位置. 在跟踪阶段,根据粒子动态特性和分配算法,匹配不同时间帧中的粒子质心,连接粒子质心以重建轨迹 在稀疏粒子的情况下表现良好. 相对于粒子图像测速,算出的流场速度具有真实物理意义 无法处理粒子浓度较高的情况,对部分设定参数较敏感 SSIV[8 ] 在LSPIV的相关分析操作的基础上,得到初步的全局速度矢量场,再利用表面流的特性对矢量场进行后处理. 其核心在于去除LSPIV结果中的错误矢量 对查询区域变化不敏感,在复杂光学环境(如阴影或眩光)中仍有较好的 互相关分析以及对矢量场进行后处理的过程计算量较大 OTV[9 ] 结合自动特征检测、Lucas-Kanade跟踪算法和基于轨迹的过滤方法.利用Fast算法检测水面目标角点特征,用基于图像金字塔的Lucas-Kanade稀疏光流跟踪算法跟踪以上特征,再对跟踪轨迹进行后处理 在表面目标特征稀疏、非恒定流情况时表现良好 所得速度场分辨率不高 STIV[10 ] 先合成时空图像,再利用傅里叶变换检测时空图像的纹理主方向,该主方向对应原图像序列的一维时均流速矢量 空间分辨率高、实时性强,可用于河流的实时 对复杂光照和水流环境的变化较为敏感 基于概率的测速 [11 ] 基于概率的图像测速方法.基于贝叶斯框架,在图像观测函数已知的情况下,估计像素速度矢量场的后验概率 可以得到稠密的光流矢量场 为了提高流场精度,须改进超参数估计以及描述条件概率分布的似然估计 基于机器学习的测速[12 -14 ] 基于有监督学习的机器学习表面流测速方法,主要进行水流表面特征的提取和流速的分类识别. 基于无监督学习的方法,利用非线性图像配准的思路计算表面速度矢量场 有效水流表面特征的 有监督学习方法需要大量数据. 无监督学习方法的研究较少,其测速精度仍需要经过更多实验的验证;该方法仅研究了海岸波浪的跟踪测速方案,其泛化性仍有待研究 SGSD[15 ] 在变分光流框架中加入流体物理约束. 利用标量输运方程计算光流场,引入扩散项补充小尺度流场特征 速度矢量场结果精度 流动轨迹重建中仍对异常值存在敏感性
2. 图像测速方法研究现状 图像测速方法包含5个主要步骤:1)水面示踪,2)图像采集,3)图像预处理,4)图像分析,5)流场后处理. ...
... 图像采集的工作方式不尽相同,通常是用相机定义参数,再进行图像测速分析. 河流测速需要选择与流动相关的最佳相机采样频率(24、30、60 Hz)[16 ] . 当河流流速小时,改变采样频率以获取更有效的图像[11 ] . Tauro等[9 ] 分析了OTV对相机帧率变化的敏感性,不同频率(8~25 Hz)得到的平均速度没有统计学意义,因此在该实验条件下(平均流速0.47 m/s)OTV对采样频率不敏感[15 ] . ...
... Bacharidis等 [11 ] 提出基于统计框架的河流流量图像监测方法. 该方法结合机器学习与光流技术,其中的光流场估计算法在Chang 等[43 ] 的方法基础上进行改进,使用贝叶斯框架为每个像素计算后验分布,提供最能描述像素运动的速度矢量,该矢量通过最大化等效的后验分布获得等效于最小化代价函数 ...
基于压缩感知图像分析的河流表面流速估计方法
3
2018
... 该方法在许多场景中已被成功应用,如阿尔卑斯山的山洪流量测量[1 ] ,为水利工程应用的二维流场评估[4 ] ,日本大融雪洪水监测[5 ] . 自大尺度粒子图像测速(large-scale particle image velocimetry, LSPIV)[3 , 6 ] 提出后,各方法对河流表面测速的效果均有提升. 常见的河流测速算法有:LSPIV、大尺度粒子跟踪测速(large-scale particle tracking velocimetry, LSPTV)[7 ] 、表面结构图像测速(surface structure image velocimetry, SSIV)[8 ] 、光学跟踪测速(optical tracking velocimetry, OTV)[9 ] 、时空图像测速[10 ] 、基于概率的测速[11 ] 、基于机器学习的测速[12 -14 ] 等. 各种算法的概述及优缺点如表1 所示. ...
... Comparisons of image-based surface flow velocimetry method
Tab.1 算法 概述 优点 缺点 LSPIV[3 , 6 ] 在前一帧的查询区域和后一帧的搜索区域间进行相关分析操作. 查询区域和搜索区域根据流动情况人为定义. 相关系数最大的2个窗口对应最可能的位移. 相关分析操作主要分为空域互相关和快速傅里叶变换互相关 可以提供全局的表面流速场. 简单有效,是目前应用较广的技术 空域互相关计算量较大. 算法得到的是每个查询区域的平均速度,速度场分辨率不高 LSPTV[7 ] 包括粒子检测和跟踪共2个步骤. 获取图像中粒子的空间分布情况,并进一步获取粒子的亚像素质心位置. 在跟踪阶段,根据粒子动态特性和分配算法,匹配不同时间帧中的粒子质心,连接粒子质心以重建轨迹 在稀疏粒子的情况下表现良好. 相对于粒子图像测速,算出的流场速度具有真实物理意义 无法处理粒子浓度较高的情况,对部分设定参数较敏感 SSIV[8 ] 在LSPIV的相关分析操作的基础上,得到初步的全局速度矢量场,再利用表面流的特性对矢量场进行后处理. 其核心在于去除LSPIV结果中的错误矢量 对查询区域变化不敏感,在复杂光学环境(如阴影或眩光)中仍有较好的 互相关分析以及对矢量场进行后处理的过程计算量较大 OTV[9 ] 结合自动特征检测、Lucas-Kanade跟踪算法和基于轨迹的过滤方法.利用Fast算法检测水面目标角点特征,用基于图像金字塔的Lucas-Kanade稀疏光流跟踪算法跟踪以上特征,再对跟踪轨迹进行后处理 在表面目标特征稀疏、非恒定流情况时表现良好 所得速度场分辨率不高 STIV[10 ] 先合成时空图像,再利用傅里叶变换检测时空图像的纹理主方向,该主方向对应原图像序列的一维时均流速矢量 空间分辨率高、实时性强,可用于河流的实时 对复杂光照和水流环境的变化较为敏感 基于概率的测速 [11 ] 基于概率的图像测速方法.基于贝叶斯框架,在图像观测函数已知的情况下,估计像素速度矢量场的后验概率 可以得到稠密的光流矢量场 为了提高流场精度,须改进超参数估计以及描述条件概率分布的似然估计 基于机器学习的测速[12 -14 ] 基于有监督学习的机器学习表面流测速方法,主要进行水流表面特征的提取和流速的分类识别. 基于无监督学习的方法,利用非线性图像配准的思路计算表面速度矢量场 有效水流表面特征的 有监督学习方法需要大量数据. 无监督学习方法的研究较少,其测速精度仍需要经过更多实验的验证;该方法仅研究了海岸波浪的跟踪测速方案,其泛化性仍有待研究 SGSD[15 ] 在变分光流框架中加入流体物理约束. 利用标量输运方程计算光流场,引入扩散项补充小尺度流场特征 速度矢量场结果精度 流动轨迹重建中仍对异常值存在敏感性
2. 图像测速方法研究现状 图像测速方法包含5个主要步骤:1)水面示踪,2)图像采集,3)图像预处理,4)图像分析,5)流场后处理. ...
... 近年来,机器学习方法开始被应用到河流表面测速领域,并取得了一定成效. 王万良等[12 ] 利用压缩感知来提取河流表面图像中的水流特征,如图15 所示,并从理论研究和实验验证2个角度证实该方法在河流表面测速上的有效性. 为了解决小差异河流图像的流速分类问题,王万良等[13 ] 引入生成对抗网络,生成更多的流速图像来增强数据,再利用多特征融合的卷积分类网络实现河流流速分类,该方法对于小差异河流图像具有较好的鲁棒性. ...
基于压缩感知图像分析的河流表面流速估计方法
3
2018
... 该方法在许多场景中已被成功应用,如阿尔卑斯山的山洪流量测量[1 ] ,为水利工程应用的二维流场评估[4 ] ,日本大融雪洪水监测[5 ] . 自大尺度粒子图像测速(large-scale particle image velocimetry, LSPIV)[3 , 6 ] 提出后,各方法对河流表面测速的效果均有提升. 常见的河流测速算法有:LSPIV、大尺度粒子跟踪测速(large-scale particle tracking velocimetry, LSPTV)[7 ] 、表面结构图像测速(surface structure image velocimetry, SSIV)[8 ] 、光学跟踪测速(optical tracking velocimetry, OTV)[9 ] 、时空图像测速[10 ] 、基于概率的测速[11 ] 、基于机器学习的测速[12 -14 ] 等. 各种算法的概述及优缺点如表1 所示. ...
... Comparisons of image-based surface flow velocimetry method
Tab.1 算法 概述 优点 缺点 LSPIV[3 , 6 ] 在前一帧的查询区域和后一帧的搜索区域间进行相关分析操作. 查询区域和搜索区域根据流动情况人为定义. 相关系数最大的2个窗口对应最可能的位移. 相关分析操作主要分为空域互相关和快速傅里叶变换互相关 可以提供全局的表面流速场. 简单有效,是目前应用较广的技术 空域互相关计算量较大. 算法得到的是每个查询区域的平均速度,速度场分辨率不高 LSPTV[7 ] 包括粒子检测和跟踪共2个步骤. 获取图像中粒子的空间分布情况,并进一步获取粒子的亚像素质心位置. 在跟踪阶段,根据粒子动态特性和分配算法,匹配不同时间帧中的粒子质心,连接粒子质心以重建轨迹 在稀疏粒子的情况下表现良好. 相对于粒子图像测速,算出的流场速度具有真实物理意义 无法处理粒子浓度较高的情况,对部分设定参数较敏感 SSIV[8 ] 在LSPIV的相关分析操作的基础上,得到初步的全局速度矢量场,再利用表面流的特性对矢量场进行后处理. 其核心在于去除LSPIV结果中的错误矢量 对查询区域变化不敏感,在复杂光学环境(如阴影或眩光)中仍有较好的 互相关分析以及对矢量场进行后处理的过程计算量较大 OTV[9 ] 结合自动特征检测、Lucas-Kanade跟踪算法和基于轨迹的过滤方法.利用Fast算法检测水面目标角点特征,用基于图像金字塔的Lucas-Kanade稀疏光流跟踪算法跟踪以上特征,再对跟踪轨迹进行后处理 在表面目标特征稀疏、非恒定流情况时表现良好 所得速度场分辨率不高 STIV[10 ] 先合成时空图像,再利用傅里叶变换检测时空图像的纹理主方向,该主方向对应原图像序列的一维时均流速矢量 空间分辨率高、实时性强,可用于河流的实时 对复杂光照和水流环境的变化较为敏感 基于概率的测速 [11 ] 基于概率的图像测速方法.基于贝叶斯框架,在图像观测函数已知的情况下,估计像素速度矢量场的后验概率 可以得到稠密的光流矢量场 为了提高流场精度,须改进超参数估计以及描述条件概率分布的似然估计 基于机器学习的测速[12 -14 ] 基于有监督学习的机器学习表面流测速方法,主要进行水流表面特征的提取和流速的分类识别. 基于无监督学习的方法,利用非线性图像配准的思路计算表面速度矢量场 有效水流表面特征的 有监督学习方法需要大量数据. 无监督学习方法的研究较少,其测速精度仍需要经过更多实验的验证;该方法仅研究了海岸波浪的跟踪测速方案,其泛化性仍有待研究 SGSD[15 ] 在变分光流框架中加入流体物理约束. 利用标量输运方程计算光流场,引入扩散项补充小尺度流场特征 速度矢量场结果精度 流动轨迹重建中仍对异常值存在敏感性
2. 图像测速方法研究现状 图像测速方法包含5个主要步骤:1)水面示踪,2)图像采集,3)图像预处理,4)图像分析,5)流场后处理. ...
... 近年来,机器学习方法开始被应用到河流表面测速领域,并取得了一定成效. 王万良等[12 ] 利用压缩感知来提取河流表面图像中的水流特征,如图15 所示,并从理论研究和实验验证2个角度证实该方法在河流表面测速上的有效性. 为了解决小差异河流图像的流速分类问题,王万良等[13 ] 引入生成对抗网络,生成更多的流速图像来增强数据,再利用多特征融合的卷积分类网络实现河流流速分类,该方法对于小差异河流图像具有较好的鲁棒性. ...
基于条件边界平衡生成对抗网络的河流表面流速估测
1
2019
... 近年来,机器学习方法开始被应用到河流表面测速领域,并取得了一定成效. 王万良等[12 ] 利用压缩感知来提取河流表面图像中的水流特征,如图15 所示,并从理论研究和实验验证2个角度证实该方法在河流表面测速上的有效性. 为了解决小差异河流图像的流速分类问题,王万良等[13 ] 引入生成对抗网络,生成更多的流速图像来增强数据,再利用多特征融合的卷积分类网络实现河流流速分类,该方法对于小差异河流图像具有较好的鲁棒性. ...
基于条件边界平衡生成对抗网络的河流表面流速估测
1
2019
... 近年来,机器学习方法开始被应用到河流表面测速领域,并取得了一定成效. 王万良等[12 ] 利用压缩感知来提取河流表面图像中的水流特征,如图15 所示,并从理论研究和实验验证2个角度证实该方法在河流表面测速上的有效性. 为了解决小差异河流图像的流速分类问题,王万良等[13 ] 引入生成对抗网络,生成更多的流速图像来增强数据,再利用多特征融合的卷积分类网络实现河流流速分类,该方法对于小差异河流图像具有较好的鲁棒性. ...
Estimation of water surface flow velocity in coastal video imagery by visual tracking with deep learning
3
2020
... 该方法在许多场景中已被成功应用,如阿尔卑斯山的山洪流量测量[1 ] ,为水利工程应用的二维流场评估[4 ] ,日本大融雪洪水监测[5 ] . 自大尺度粒子图像测速(large-scale particle image velocimetry, LSPIV)[3 , 6 ] 提出后,各方法对河流表面测速的效果均有提升. 常见的河流测速算法有:LSPIV、大尺度粒子跟踪测速(large-scale particle tracking velocimetry, LSPTV)[7 ] 、表面结构图像测速(surface structure image velocimetry, SSIV)[8 ] 、光学跟踪测速(optical tracking velocimetry, OTV)[9 ] 、时空图像测速[10 ] 、基于概率的测速[11 ] 、基于机器学习的测速[12 -14 ] 等. 各种算法的概述及优缺点如表1 所示. ...
... Comparisons of image-based surface flow velocimetry method
Tab.1 算法 概述 优点 缺点 LSPIV[3 , 6 ] 在前一帧的查询区域和后一帧的搜索区域间进行相关分析操作. 查询区域和搜索区域根据流动情况人为定义. 相关系数最大的2个窗口对应最可能的位移. 相关分析操作主要分为空域互相关和快速傅里叶变换互相关 可以提供全局的表面流速场. 简单有效,是目前应用较广的技术 空域互相关计算量较大. 算法得到的是每个查询区域的平均速度,速度场分辨率不高 LSPTV[7 ] 包括粒子检测和跟踪共2个步骤. 获取图像中粒子的空间分布情况,并进一步获取粒子的亚像素质心位置. 在跟踪阶段,根据粒子动态特性和分配算法,匹配不同时间帧中的粒子质心,连接粒子质心以重建轨迹 在稀疏粒子的情况下表现良好. 相对于粒子图像测速,算出的流场速度具有真实物理意义 无法处理粒子浓度较高的情况,对部分设定参数较敏感 SSIV[8 ] 在LSPIV的相关分析操作的基础上,得到初步的全局速度矢量场,再利用表面流的特性对矢量场进行后处理. 其核心在于去除LSPIV结果中的错误矢量 对查询区域变化不敏感,在复杂光学环境(如阴影或眩光)中仍有较好的 互相关分析以及对矢量场进行后处理的过程计算量较大 OTV[9 ] 结合自动特征检测、Lucas-Kanade跟踪算法和基于轨迹的过滤方法.利用Fast算法检测水面目标角点特征,用基于图像金字塔的Lucas-Kanade稀疏光流跟踪算法跟踪以上特征,再对跟踪轨迹进行后处理 在表面目标特征稀疏、非恒定流情况时表现良好 所得速度场分辨率不高 STIV[10 ] 先合成时空图像,再利用傅里叶变换检测时空图像的纹理主方向,该主方向对应原图像序列的一维时均流速矢量 空间分辨率高、实时性强,可用于河流的实时 对复杂光照和水流环境的变化较为敏感 基于概率的测速 [11 ] 基于概率的图像测速方法.基于贝叶斯框架,在图像观测函数已知的情况下,估计像素速度矢量场的后验概率 可以得到稠密的光流矢量场 为了提高流场精度,须改进超参数估计以及描述条件概率分布的似然估计 基于机器学习的测速[12 -14 ] 基于有监督学习的机器学习表面流测速方法,主要进行水流表面特征的提取和流速的分类识别. 基于无监督学习的方法,利用非线性图像配准的思路计算表面速度矢量场 有效水流表面特征的 有监督学习方法需要大量数据. 无监督学习方法的研究较少,其测速精度仍需要经过更多实验的验证;该方法仅研究了海岸波浪的跟踪测速方案,其泛化性仍有待研究 SGSD[15 ] 在变分光流框架中加入流体物理约束. 利用标量输运方程计算光流场,引入扩散项补充小尺度流场特征 速度矢量场结果精度 流动轨迹重建中仍对异常值存在敏感性
2. 图像测速方法研究现状 图像测速方法包含5个主要步骤:1)水面示踪,2)图像采集,3)图像预处理,4)图像分析,5)流场后处理. ...
... Kim等[14 ] 利用无监督学习的深度神经网络跟踪视频图像中的水流表面波浪. 该模型包含场景分离和图像配准2个阶段:1)自动编码器将场景分离,仅提取视频中波浪的动态信息,并消除外部环境因素(如环境光);2)空间变换网络对分离的波浪运动进行非线性图像配准以得到水面流速矢量. 该方法在海滩现场采集的测试图像数据集上进行验证,具有广阔的应用前景. ...
Optical flow for image-based river velocity estimation
3
2019
... Comparisons of image-based surface flow velocimetry method
Tab.1 算法 概述 优点 缺点 LSPIV[3 , 6 ] 在前一帧的查询区域和后一帧的搜索区域间进行相关分析操作. 查询区域和搜索区域根据流动情况人为定义. 相关系数最大的2个窗口对应最可能的位移. 相关分析操作主要分为空域互相关和快速傅里叶变换互相关 可以提供全局的表面流速场. 简单有效,是目前应用较广的技术 空域互相关计算量较大. 算法得到的是每个查询区域的平均速度,速度场分辨率不高 LSPTV[7 ] 包括粒子检测和跟踪共2个步骤. 获取图像中粒子的空间分布情况,并进一步获取粒子的亚像素质心位置. 在跟踪阶段,根据粒子动态特性和分配算法,匹配不同时间帧中的粒子质心,连接粒子质心以重建轨迹 在稀疏粒子的情况下表现良好. 相对于粒子图像测速,算出的流场速度具有真实物理意义 无法处理粒子浓度较高的情况,对部分设定参数较敏感 SSIV[8 ] 在LSPIV的相关分析操作的基础上,得到初步的全局速度矢量场,再利用表面流的特性对矢量场进行后处理. 其核心在于去除LSPIV结果中的错误矢量 对查询区域变化不敏感,在复杂光学环境(如阴影或眩光)中仍有较好的 互相关分析以及对矢量场进行后处理的过程计算量较大 OTV[9 ] 结合自动特征检测、Lucas-Kanade跟踪算法和基于轨迹的过滤方法.利用Fast算法检测水面目标角点特征,用基于图像金字塔的Lucas-Kanade稀疏光流跟踪算法跟踪以上特征,再对跟踪轨迹进行后处理 在表面目标特征稀疏、非恒定流情况时表现良好 所得速度场分辨率不高 STIV[10 ] 先合成时空图像,再利用傅里叶变换检测时空图像的纹理主方向,该主方向对应原图像序列的一维时均流速矢量 空间分辨率高、实时性强,可用于河流的实时 对复杂光照和水流环境的变化较为敏感 基于概率的测速 [11 ] 基于概率的图像测速方法.基于贝叶斯框架,在图像观测函数已知的情况下,估计像素速度矢量场的后验概率 可以得到稠密的光流矢量场 为了提高流场精度,须改进超参数估计以及描述条件概率分布的似然估计 基于机器学习的测速[12 -14 ] 基于有监督学习的机器学习表面流测速方法,主要进行水流表面特征的提取和流速的分类识别. 基于无监督学习的方法,利用非线性图像配准的思路计算表面速度矢量场 有效水流表面特征的 有监督学习方法需要大量数据. 无监督学习方法的研究较少,其测速精度仍需要经过更多实验的验证;该方法仅研究了海岸波浪的跟踪测速方案,其泛化性仍有待研究 SGSD[15 ] 在变分光流框架中加入流体物理约束. 利用标量输运方程计算光流场,引入扩散项补充小尺度流场特征 速度矢量场结果精度 流动轨迹重建中仍对异常值存在敏感性
2. 图像测速方法研究现状 图像测速方法包含5个主要步骤:1)水面示踪,2)图像采集,3)图像预处理,4)图像分析,5)流场后处理. ...
... 图像采集的工作方式不尽相同,通常是用相机定义参数,再进行图像测速分析. 河流测速需要选择与流动相关的最佳相机采样频率(24、30、60 Hz)[16 ] . 当河流流速小时,改变采样频率以获取更有效的图像[11 ] . Tauro等[9 ] 分析了OTV对相机帧率变化的敏感性,不同频率(8~25 Hz)得到的平均速度没有统计学意义,因此在该实验条件下(平均流速0.47 m/s)OTV对采样频率不敏感[15 ] . ...
... 亚网格尺度扩散测速法(subgrid scale diffusion, SGSD)[15 ] 在变分光流框架中加入流体物理约束. 将图像强度 $ {\boldsymbol{I}} $
2
... 水面特征来源于水面示踪物[16 ] ,如天然水面波、水面翻腾、涟漪或天然碎屑漂浮物. 若没有天然水面特征,可使用环保、惰性、可降解的人工材料(生态泡沫、木屑或自然漂浮可降解物). 根据不同环境选择合适的示踪物,其中,颗粒的形状和密度特性都是影响颗粒示踪的关键. ...
... 图像采集的工作方式不尽相同,通常是用相机定义参数,再进行图像测速分析. 河流测速需要选择与流动相关的最佳相机采样频率(24、30、60 Hz)[16 ] . 当河流流速小时,改变采样频率以获取更有效的图像[11 ] . Tauro等[9 ] 分析了OTV对相机帧率变化的敏感性,不同频率(8~25 Hz)得到的平均速度没有统计学意义,因此在该实验条件下(平均流速0.47 m/s)OTV对采样频率不敏感[15 ] . ...
2
... 良好示踪颗粒的选择,需要弄清河流中颗粒运动、流体流动和流体与颗粒间的瞬时相对速度三者之间的关系. 例如当示踪颗粒为球形颗粒时,Basset [17 ] 将受力、压力梯度和流体密度联系起来,其中雷诺数Re和颗粒瞬时相对速度满足斯托克斯(Stokes)阻力定律. Hadad等[18 ] 对湍流情况下PIV方法中的示踪粒子参数的影响进行研究,该研究测量在不同参数下标准流动的速度场,并统计对比对湍流量和速度导数的影响,发现Re越高,粒子参数对测量的影响越大,粒子尺寸对速度和加速度的影响最大,粒子浓度和化学处理不会独立影响结果. ...
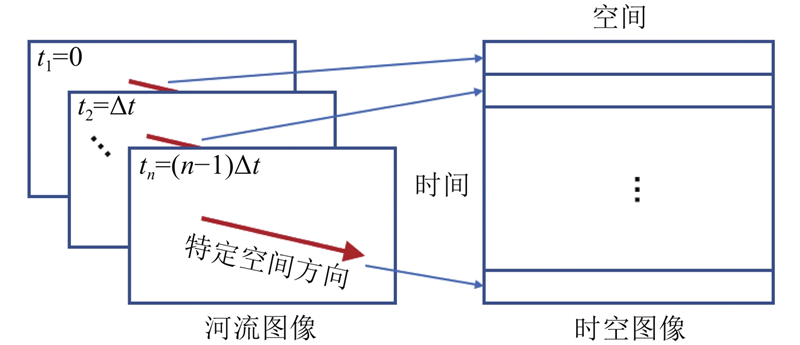
... 另一类特殊方法是时空图像测速法(space-time image velocimetry, STIV)[17 ] . 该方法基于质量守恒定律,假设目标运动轨迹满足连续性条件,即可同时在空间和时间组成的时空域上对该目标进行相关分析操作,得到具有高空间分辨率的一维时均流场矢量. 如图8 所示,若将图像中某一特定方向的一维像素值按照时间顺序排列成二维的时空图像,则该指定空间方向的时空域相关性将表现为对应方向的显著纹理特征. 该纹理特征的主方向和间隔表征着原指定空间方向的速度矢量. 如图9 所示,在河流测速中,常取顺流方向或平行河岸方向为该特定空间方向,原始图像中该方向上像素速度矢量的大小q 与时空图像中的纹理特征的关系可以表示为 ...
Effects of particle size, concentration and surface coating on turbulent flow properties obtained using PIV/PTV
1
2013
... 良好示踪颗粒的选择,需要弄清河流中颗粒运动、流体流动和流体与颗粒间的瞬时相对速度三者之间的关系. 例如当示踪颗粒为球形颗粒时,Basset [17 ] 将受力、压力梯度和流体密度联系起来,其中雷诺数Re和颗粒瞬时相对速度满足斯托克斯(Stokes)阻力定律. Hadad等[18 ] 对湍流情况下PIV方法中的示踪粒子参数的影响进行研究,该研究测量在不同参数下标准流动的速度场,并统计对比对湍流量和速度导数的影响,发现Re越高,粒子参数对测量的影响越大,粒子尺寸对速度和加速度的影响最大,粒子浓度和化学处理不会独立影响结果. ...
1
... 图像的预处理效果将直观影响图像分析结果,预处理阶段包括图像正射校正、消除镜头失真和滤波,或者去除阴影、眩光以增强粒子的示踪性[19 ] . ...
River surface target enhancement and background suppression for unseeded LSPIV
1
2013
... 如图2 所示,展示了在全光谱和近红外光谱下的河流表面情况. zhang等[20 ] 研制了近红外智能相机以实现图像采集和预处理工作. 根据示踪剂和河面的光学特性,将近红外(nar infrared, NIR)成像和空间高通滤波相结合,实现河流水面的目标增强和背景抑制,提高所估计运动矢量的峰值信噪比. ...
基于变高单应的单目视觉平面测量方法
2
2014
... 在采集原始图像后即可开展正射校正,如图3 所示,其目的在于联系世界坐标与相机二维投影,消除透视效果以加强速度场的分析,其转换关系[21 ] 为 ...
... 之后张振等[21 ] 提出基于变高单应的单目视觉平面测量方法,利用像差修正的直接线性变换法改善测量精度. Li等[22 ] 开发基于立体成像的LSPIV系统,重建三维地形和水面分布. ...
基于变高单应的单目视觉平面测量方法
2
2014
... 在采集原始图像后即可开展正射校正,如图3 所示,其目的在于联系世界坐标与相机二维投影,消除透视效果以加强速度场的分析,其转换关系[21 ] 为 ...
... 之后张振等[21 ] 提出基于变高单应的单目视觉平面测量方法,利用像差修正的直接线性变换法改善测量精度. Li等[22 ] 开发基于立体成像的LSPIV系统,重建三维地形和水面分布. ...
Stereo-imaging LSPIV (SI-LSPIV) for 3D water surface reconstruction and discharge measurement in mountain river flows
1
2019
... 之后张振等[21 ] 提出基于变高单应的单目视觉平面测量方法,利用像差修正的直接线性变换法改善测量精度. Li等[22 ] 开发基于立体成像的LSPIV系统,重建三维地形和水面分布. ...
Advanced algorithms for microscale particle image velocimetry
1
2002
... 自LSPIV被提出以来,关于LSPIV论文的主要区别在于引入不同的现有PIV相关分析方法. 在计算效率方面,空域相关分析操作需要较大的计算量以及有河流监测的实时性需求,因此更多频域的方法被引入河流测速中来. 如图6 所示,快速傅里叶变换(fast fourier transform, FFT)将PIV中的相关积分操作切换到频域下的乘法,再将乘法计算结果经过反傅里叶变换,即可得到空域下的相关分析结果[23 ] . 例如,Dobson等[24 ] 使用快速傅里叶变换互相关(fast fourier transform cross correlation, FFT-CC)方法计算速度矢量,计算效率更高. ...
Fast, large-scale, particle image velocimetry-based estimations of river surface velocity
1
2014
... 自LSPIV被提出以来,关于LSPIV论文的主要区别在于引入不同的现有PIV相关分析方法. 在计算效率方面,空域相关分析操作需要较大的计算量以及有河流监测的实时性需求,因此更多频域的方法被引入河流测速中来. 如图6 所示,快速傅里叶变换(fast fourier transform, FFT)将PIV中的相关积分操作切换到频域下的乘法,再将乘法计算结果经过反傅里叶变换,即可得到空域下的相关分析结果[23 ] . 例如,Dobson等[24 ] 使用快速傅里叶变换互相关(fast fourier transform cross correlation, FFT-CC)方法计算速度矢量,计算效率更高. ...
Large scale PIV measurements at the surface of shallow water flows
1
2002
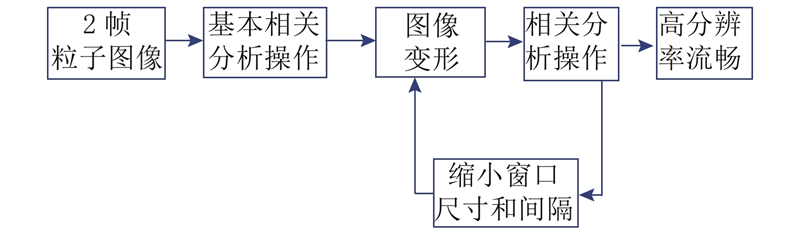
... 在计算精度上,Weitbrecht等[25 ] 将图像位移多重网格迭代算法[26 ] (window displacement iterative multigrid, WIDIM)引入河流表面流的测速中,从大的查询区域开始计算速度作为下个较小的查询区域的参考速度. 通过不断迭代,计算出更准确可靠的流速. Scarano[27 ] 对相关分析法进一步改进,提出图像变形多重网格迭代算法(window deformation iterative multigrid, WIDIM). 如图7 所示,先利用相关分析法得到粗分辨率的流场 $ {v}^{k}(x,y) $ $ \Delta {v}^{k}(x,y) $ k 为当前迭代轮数. 该算法有效地提升了相关分析法的计算精度、动态速度测量范围和流场空间分辨率. ...
Iterative multigrid approach in PIV image processing with discrete window offset
1
1999
... 在计算精度上,Weitbrecht等[25 ] 将图像位移多重网格迭代算法[26 ] (window displacement iterative multigrid, WIDIM)引入河流表面流的测速中,从大的查询区域开始计算速度作为下个较小的查询区域的参考速度. 通过不断迭代,计算出更准确可靠的流速. Scarano[27 ] 对相关分析法进一步改进,提出图像变形多重网格迭代算法(window deformation iterative multigrid, WIDIM). 如图7 所示,先利用相关分析法得到粗分辨率的流场 $ {v}^{k}(x,y) $ $ \Delta {v}^{k}(x,y) $ k 为当前迭代轮数. 该算法有效地提升了相关分析法的计算精度、动态速度测量范围和流场空间分辨率. ...
Iterative image deformation methods in PIV
1
2001
... 在计算精度上,Weitbrecht等[25 ] 将图像位移多重网格迭代算法[26 ] (window displacement iterative multigrid, WIDIM)引入河流表面流的测速中,从大的查询区域开始计算速度作为下个较小的查询区域的参考速度. 通过不断迭代,计算出更准确可靠的流速. Scarano[27 ] 对相关分析法进一步改进,提出图像变形多重网格迭代算法(window deformation iterative multigrid, WIDIM). 如图7 所示,先利用相关分析法得到粗分辨率的流场 $ {v}^{k}(x,y) $ $ \Delta {v}^{k}(x,y) $ k 为当前迭代轮数. 该算法有效地提升了相关分析法的计算精度、动态速度测量范围和流场空间分辨率. ...
1
... 自1999年以来,学者们开发并开源了各种PIV分析工具,包括OpenPIV[28 ] 、Fudaa-LSPIV[29 ] 、PIVlab[30 ] 、RIVeR[31 ] 等. 这些工具大多基于WIDIM算法或改进的相关分析法,除算法成熟可靠外,还提供友好的图形用户界面. Perks 等[32 -33 ] 直接引入这类开源工具,在不同应用或不同数据集中相互比较,并测试这些工具的总体效能. ...
1
... 自1999年以来,学者们开发并开源了各种PIV分析工具,包括OpenPIV[28 ] 、Fudaa-LSPIV[29 ] 、PIVlab[30 ] 、RIVeR[31 ] 等. 这些工具大多基于WIDIM算法或改进的相关分析法,除算法成熟可靠外,还提供友好的图形用户界面. Perks 等[32 -33 ] 直接引入这类开源工具,在不同应用或不同数据集中相互比较,并测试这些工具的总体效能. ...
1
... 自1999年以来,学者们开发并开源了各种PIV分析工具,包括OpenPIV[28 ] 、Fudaa-LSPIV[29 ] 、PIVlab[30 ] 、RIVeR[31 ] 等. 这些工具大多基于WIDIM算法或改进的相关分析法,除算法成熟可靠外,还提供友好的图形用户界面. Perks 等[32 -33 ] 直接引入这类开源工具,在不同应用或不同数据集中相互比较,并测试这些工具的总体效能. ...
Rectification of image velocity results (RIVeR): a simple and user-friendly toolbox for large scale water surface particle image velocimetry (PIV) and particle tracking velocimetry (PTV)
1
2017
... 自1999年以来,学者们开发并开源了各种PIV分析工具,包括OpenPIV[28 ] 、Fudaa-LSPIV[29 ] 、PIVlab[30 ] 、RIVeR[31 ] 等. 这些工具大多基于WIDIM算法或改进的相关分析法,除算法成熟可靠外,还提供友好的图形用户界面. Perks 等[32 -33 ] 直接引入这类开源工具,在不同应用或不同数据集中相互比较,并测试这些工具的总体效能. ...
Towards harmonisation of image velocimetry techniques for river surface velocity observations
1
2020
... 自1999年以来,学者们开发并开源了各种PIV分析工具,包括OpenPIV[28 ] 、Fudaa-LSPIV[29 ] 、PIVlab[30 ] 、RIVeR[31 ] 等. 这些工具大多基于WIDIM算法或改进的相关分析法,除算法成熟可靠外,还提供友好的图形用户界面. Perks 等[32 -33 ] 直接引入这类开源工具,在不同应用或不同数据集中相互比较,并测试这些工具的总体效能. ...
An evaluation of image velocimetry techniques under low flow conditions and high seeding densities using unmanned aerial systems
1
2020
... 自1999年以来,学者们开发并开源了各种PIV分析工具,包括OpenPIV[28 ] 、Fudaa-LSPIV[29 ] 、PIVlab[30 ] 、RIVeR[31 ] 等. 这些工具大多基于WIDIM算法或改进的相关分析法,除算法成熟可靠外,还提供友好的图形用户界面. Perks 等[32 -33 ] 直接引入这类开源工具,在不同应用或不同数据集中相互比较,并测试这些工具的总体效能. ...
1
... 目前,STIV方法的主要研究及应用集中于日本. Fujita等[10 ] 提出该方法并验证其有效性,同时开发KU-STIV商业软件,成功应用于日本诸多河流的测量方案[34 ] . 国内对于STIV方法的研究与应用尚处于初步阶段,主要集中在河海大学. 王慧斌等[35 ] 提出基于时空图像频谱的时均流场重建方法,基于傅里叶变换的自配准性质约束时空图像纹理和频谱主方向的关系,可以达到0.1°的测量精度. 张振等[36 ] 基于STIV方法开发图像法测流系统,目前已投入实际运行;张振等[37 ] 还对进行了时空图像测速法的敏感性分析及不确定度评估. 与LSPIV方法相比,STIV方法的显著优势是空间分辨率能够达到单像素水平,计算效率在前者的10倍以上,可实现高效河流测速. ...
基于时空图像频谱的时均流场重建方法
1
2015
... 目前,STIV方法的主要研究及应用集中于日本. Fujita等[10 ] 提出该方法并验证其有效性,同时开发KU-STIV商业软件,成功应用于日本诸多河流的测量方案[34 ] . 国内对于STIV方法的研究与应用尚处于初步阶段,主要集中在河海大学. 王慧斌等[35 ] 提出基于时空图像频谱的时均流场重建方法,基于傅里叶变换的自配准性质约束时空图像纹理和频谱主方向的关系,可以达到0.1°的测量精度. 张振等[36 ] 基于STIV方法开发图像法测流系统,目前已投入实际运行;张振等[37 ] 还对进行了时空图像测速法的敏感性分析及不确定度评估. 与LSPIV方法相比,STIV方法的显著优势是空间分辨率能够达到单像素水平,计算效率在前者的10倍以上,可实现高效河流测速. ...
基于时空图像频谱的时均流场重建方法
1
2015
... 目前,STIV方法的主要研究及应用集中于日本. Fujita等[10 ] 提出该方法并验证其有效性,同时开发KU-STIV商业软件,成功应用于日本诸多河流的测量方案[34 ] . 国内对于STIV方法的研究与应用尚处于初步阶段,主要集中在河海大学. 王慧斌等[35 ] 提出基于时空图像频谱的时均流场重建方法,基于傅里叶变换的自配准性质约束时空图像纹理和频谱主方向的关系,可以达到0.1°的测量精度. 张振等[36 ] 基于STIV方法开发图像法测流系统,目前已投入实际运行;张振等[37 ] 还对进行了时空图像测速法的敏感性分析及不确定度评估. 与LSPIV方法相比,STIV方法的显著优势是空间分辨率能够达到单像素水平,计算效率在前者的10倍以上,可实现高效河流测速. ...
图像法测流系统开发与应用
1
2018
... 目前,STIV方法的主要研究及应用集中于日本. Fujita等[10 ] 提出该方法并验证其有效性,同时开发KU-STIV商业软件,成功应用于日本诸多河流的测量方案[34 ] . 国内对于STIV方法的研究与应用尚处于初步阶段,主要集中在河海大学. 王慧斌等[35 ] 提出基于时空图像频谱的时均流场重建方法,基于傅里叶变换的自配准性质约束时空图像纹理和频谱主方向的关系,可以达到0.1°的测量精度. 张振等[36 ] 基于STIV方法开发图像法测流系统,目前已投入实际运行;张振等[37 ] 还对进行了时空图像测速法的敏感性分析及不确定度评估. 与LSPIV方法相比,STIV方法的显著优势是空间分辨率能够达到单像素水平,计算效率在前者的10倍以上,可实现高效河流测速. ...
图像法测流系统开发与应用
1
2018
... 目前,STIV方法的主要研究及应用集中于日本. Fujita等[10 ] 提出该方法并验证其有效性,同时开发KU-STIV商业软件,成功应用于日本诸多河流的测量方案[34 ] . 国内对于STIV方法的研究与应用尚处于初步阶段,主要集中在河海大学. 王慧斌等[35 ] 提出基于时空图像频谱的时均流场重建方法,基于傅里叶变换的自配准性质约束时空图像纹理和频谱主方向的关系,可以达到0.1°的测量精度. 张振等[36 ] 基于STIV方法开发图像法测流系统,目前已投入实际运行;张振等[37 ] 还对进行了时空图像测速法的敏感性分析及不确定度评估. 与LSPIV方法相比,STIV方法的显著优势是空间分辨率能够达到单像素水平,计算效率在前者的10倍以上,可实现高效河流测速. ...
时空图像测速法的敏感性分析及不确定度评估
1
2017
... 目前,STIV方法的主要研究及应用集中于日本. Fujita等[10 ] 提出该方法并验证其有效性,同时开发KU-STIV商业软件,成功应用于日本诸多河流的测量方案[34 ] . 国内对于STIV方法的研究与应用尚处于初步阶段,主要集中在河海大学. 王慧斌等[35 ] 提出基于时空图像频谱的时均流场重建方法,基于傅里叶变换的自配准性质约束时空图像纹理和频谱主方向的关系,可以达到0.1°的测量精度. 张振等[36 ] 基于STIV方法开发图像法测流系统,目前已投入实际运行;张振等[37 ] 还对进行了时空图像测速法的敏感性分析及不确定度评估. 与LSPIV方法相比,STIV方法的显著优势是空间分辨率能够达到单像素水平,计算效率在前者的10倍以上,可实现高效河流测速. ...
时空图像测速法的敏感性分析及不确定度评估
1
2017
... 目前,STIV方法的主要研究及应用集中于日本. Fujita等[10 ] 提出该方法并验证其有效性,同时开发KU-STIV商业软件,成功应用于日本诸多河流的测量方案[34 ] . 国内对于STIV方法的研究与应用尚处于初步阶段,主要集中在河海大学. 王慧斌等[35 ] 提出基于时空图像频谱的时均流场重建方法,基于傅里叶变换的自配准性质约束时空图像纹理和频谱主方向的关系,可以达到0.1°的测量精度. 张振等[36 ] 基于STIV方法开发图像法测流系统,目前已投入实际运行;张振等[37 ] 还对进行了时空图像测速法的敏感性分析及不确定度评估. 与LSPIV方法相比,STIV方法的显著优势是空间分辨率能够达到单像素水平,计算效率在前者的10倍以上,可实现高效河流测速. ...
A new two-frame particle tracking algorithm using match probability
3
1996
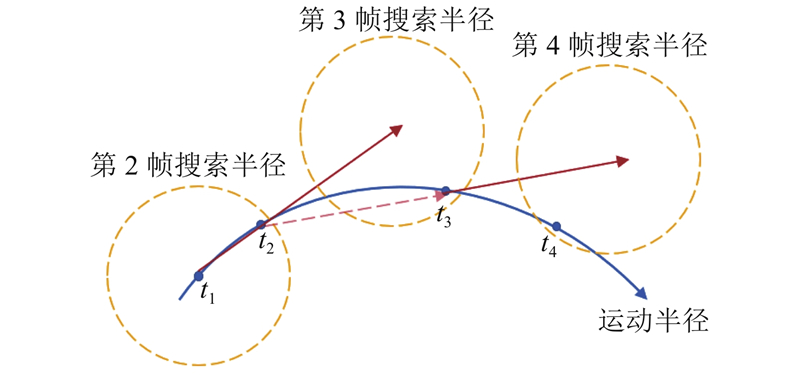
... 目前,大部分LSPTV算法都是基于不同的粒子跟踪算法重建粒子轨迹的. 按照粒子跟踪所用图像的帧数,分为2帧法[38 ] 、3帧法[39 ] 、4帧法[40 ] . 其中4帧法由于跟踪精度较高,经常被用在各种跟踪测速场景中. 原理是基于粒子速度变化连续性,利用上一帧的速度估计,减小下一帧最近邻搜索的搜索半径[40 ] . 如图11 所示,确定粒子图像在2帧(间隔足够小)间的位移,在第3帧中使用前2帧已估计的速度缩小搜索区域. 由于前一时刻的速度矢量估计可以有效指正下一帧的运动方向,该方法可以满足更大时间间隔,更大动态速度范围的流场测量. 同样方法用到后续帧,可形成完整的粒子运动轨迹并求得粒子速度矢量. ...
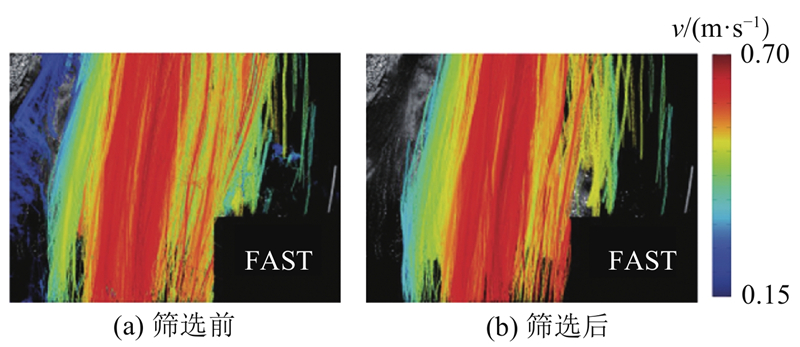
... 通常多帧跟踪方法在流速低的情况下表现得更好. 在大流速(如洪流)时,为了减小时滞影响,多使用2帧粒子跟踪法[38 ] . Tang等 [39 ] 使用3帧PTV算法监测黄河模型表面流的流速,并相比传统的4帧PTV算法和2帧PTV算法,可识别多帧图像粒子以减小噪声,使误差更小,效果更优. Cierpka等[40 ] 验证利用4个或更多粒子信息,即使在高种子浓度下,也能极大地提高粒子配对的可靠性. 此外,使用矢量重定位和基于轨迹拟合的高阶速度估计,进一步提高粒子跟踪准确性,效果如图12 所示. ...
... 粒子匹配策略可分为单独研究单个粒子的匹配算法(如最近邻法、4帧法)和结合附近粒子研究单个粒子的匹配算法(如弹簧模型法[41 ] 、概率匹配跟踪[38 ] 、基于速度梯度张量的跟踪[42 ] 等)2类. ...
An improved PTV system for large-scale physical river model
2
2008
... 目前,大部分LSPTV算法都是基于不同的粒子跟踪算法重建粒子轨迹的. 按照粒子跟踪所用图像的帧数,分为2帧法[38 ] 、3帧法[39 ] 、4帧法[40 ] . 其中4帧法由于跟踪精度较高,经常被用在各种跟踪测速场景中. 原理是基于粒子速度变化连续性,利用上一帧的速度估计,减小下一帧最近邻搜索的搜索半径[40 ] . 如图11 所示,确定粒子图像在2帧(间隔足够小)间的位移,在第3帧中使用前2帧已估计的速度缩小搜索区域. 由于前一时刻的速度矢量估计可以有效指正下一帧的运动方向,该方法可以满足更大时间间隔,更大动态速度范围的流场测量. 同样方法用到后续帧,可形成完整的粒子运动轨迹并求得粒子速度矢量. ...
... 通常多帧跟踪方法在流速低的情况下表现得更好. 在大流速(如洪流)时,为了减小时滞影响,多使用2帧粒子跟踪法[38 ] . Tang等 [39 ] 使用3帧PTV算法监测黄河模型表面流的流速,并相比传统的4帧PTV算法和2帧PTV算法,可识别多帧图像粒子以减小噪声,使误差更小,效果更优. Cierpka等[40 ] 验证利用4个或更多粒子信息,即使在高种子浓度下,也能极大地提高粒子配对的可靠性. 此外,使用矢量重定位和基于轨迹拟合的高阶速度估计,进一步提高粒子跟踪准确性,效果如图12 所示. ...
Higher order multi-frame particle tracking velocimetry
3
2013
... 目前,大部分LSPTV算法都是基于不同的粒子跟踪算法重建粒子轨迹的. 按照粒子跟踪所用图像的帧数,分为2帧法[38 ] 、3帧法[39 ] 、4帧法[40 ] . 其中4帧法由于跟踪精度较高,经常被用在各种跟踪测速场景中. 原理是基于粒子速度变化连续性,利用上一帧的速度估计,减小下一帧最近邻搜索的搜索半径[40 ] . 如图11 所示,确定粒子图像在2帧(间隔足够小)间的位移,在第3帧中使用前2帧已估计的速度缩小搜索区域. 由于前一时刻的速度矢量估计可以有效指正下一帧的运动方向,该方法可以满足更大时间间隔,更大动态速度范围的流场测量. 同样方法用到后续帧,可形成完整的粒子运动轨迹并求得粒子速度矢量. ...
... [40 ]. 如图11 所示,确定粒子图像在2帧(间隔足够小)间的位移,在第3帧中使用前2帧已估计的速度缩小搜索区域. 由于前一时刻的速度矢量估计可以有效指正下一帧的运动方向,该方法可以满足更大时间间隔,更大动态速度范围的流场测量. 同样方法用到后续帧,可形成完整的粒子运动轨迹并求得粒子速度矢量. ...
... 通常多帧跟踪方法在流速低的情况下表现得更好. 在大流速(如洪流)时,为了减小时滞影响,多使用2帧粒子跟踪法[38 ] . Tang等 [39 ] 使用3帧PTV算法监测黄河模型表面流的流速,并相比传统的4帧PTV算法和2帧PTV算法,可识别多帧图像粒子以减小噪声,使误差更小,效果更优. Cierpka等[40 ] 验证利用4个或更多粒子信息,即使在高种子浓度下,也能极大地提高粒子配对的可靠性. 此外,使用矢量重定位和基于轨迹拟合的高阶速度估计,进一步提高粒子跟踪准确性,效果如图12 所示. ...
New tracking algorithm for particle image velocimetry
2
1995
... 粒子匹配策略可分为单独研究单个粒子的匹配算法(如最近邻法、4帧法)和结合附近粒子研究单个粒子的匹配算法(如弹簧模型法[41 ] 、概率匹配跟踪[38 ] 、基于速度梯度张量的跟踪[42 ] 等)2类. ...
... 结合附近粒子研究单个粒子的匹配算法,即匹配过程同时考虑部分邻近粒子的特征,主要利用局部粒子群体运动的相似性. 例如,弹簧模型[41 ] 假设前后2帧图像中局部粒子群发生旋转和剪切,形状近似不变,局部粒子之间的弹簧由自由状态变成挤压或拉伸状态,再根据胡克定律由形变量计算局部粒子群间弹簧的平均压力. 对前1帧图像的局部粒子群,计算后1帧图像中可能存在每个粒子群组合的平均压力,选择其中平均压力最小的粒子群. 弹簧法的优点是测速精度高,且因考虑局部粒子群结构,可以处理较为复杂的流场结构;缺点是计算成本巨大,计算速度非常慢. 该方法可适用于具有复杂流场结构但无实时性需求的场景(如旋涡,剪切流). ...
A novel algorithm for particle tracking velocimetry using the velocity gradient tensor
1
2000
... 粒子匹配策略可分为单独研究单个粒子的匹配算法(如最近邻法、4帧法)和结合附近粒子研究单个粒子的匹配算法(如弹簧模型法[41 ] 、概率匹配跟踪[38 ] 、基于速度梯度张量的跟踪[42 ] 等)2类. ...
1
... Bacharidis等 [11 ] 提出基于统计框架的河流流量图像监测方法. 该方法结合机器学习与光流技术,其中的光流场估计算法在Chang 等[43 ] 的方法基础上进行改进,使用贝叶斯框架为每个像素计算后验分布,提供最能描述像素运动的速度矢量,该矢量通过最大化等效的后验分布获得等效于最小化代价函数 ...
1
... 在优化策略上,该方法使用Pytlak 等[44 ] 提出的标准共轭梯度算法最小化代价函数,最终得到全局平滑流场,分类提取主要的运动趋势,通过速度区域和图像变换计算流场平均速度. ...
Bayesian estimation of turbulent motion
1
2012
... 基于贝叶斯框架的测速方案的难点在于先验模型和似然模型的选择上. 为了克服这一难题并提升测流精度,已有研究提出了不同的似然模型和改进超参数估计[45 ] . 例如,Héas等[46 ] 提出3层模型,第1层使用经典后验概率估计初始流速场,第2层通过对运动变量的边缘化处理,得到合适的超参数,第3层根据前面的计算结果选择适合本图像数据的似然和先验运动模型. ...
Bayesian inference of models and hyperparameters for robust optical-flow estimation
1
2011
... 基于贝叶斯框架的测速方案的难点在于先验模型和似然模型的选择上. 为了克服这一难题并提升测流精度,已有研究提出了不同的似然模型和改进超参数估计[45 ] . 例如,Héas等[46 ] 提出3层模型,第1层使用经典后验概率估计初始流速场,第2层通过对运动变量的边缘化处理,得到合适的超参数,第3层根据前面的计算结果选择适合本图像数据的似然和先验运动模型. ...
Determining optical flow
1
1981
... 基于变分框架的图像测速方法假设整幅图像是关于空间位置的连续像素函数,且在相邻时间间隔足够小的情况下,像素灰度的变化也足够小. 其核心步骤在于光流场的计算[47 ] ,利用像素强度的时空导数计算光流矢量,其计算的基本等式(数据项 $ {f}_{{\rm{d}}{\rm{a}}{\rm{t}}{\rm{a}}} $
Lucas-Kanade 20 years on: a unifying framework
1
2004
... 光跟踪测速法(optical tracking velocimety, OTV)[9 ] 利用基于图像金字塔的稀疏变分Lucas-Kanade(L-K)算法[48 ] 跟踪检测到的特征. 作为稀疏的一阶微分技术,L-K算法在数据项上同样假定图像强度 $ I\left(x,t\right) $ t 的函数,它是守恒的. 基于局部邻域(大小为n )内流速矢量不变假设,该邻域生成包含n 个方程的超定方程组,再由加权最小二乘原理求解,转化为最小化以下光流误差 ...
The robust estimation of multiple motions: parametric and piecewise-smooth flow fields
1
1996
... 该模型由数据项 ${\rm{\Psi }}\left(\left\| {{{\partial {\boldsymbol{I}}}/{\partial t}+\nabla {{I}}\cdot{{\omega}} -{D}_{t}\Delta {{I}}}^{2}} \right\|\right)$ $ \alpha {\text{‖}\nabla \omega \text{‖}}^{2} $ $ {\rm{\Psi }} $ [49 ] . $ {D}_{t} $ $ {\rm{\Omega }} $
Measurement of the flood discharge of a small-sized river using an existing digital video recording system
1
2011
... 流场后处理主要是对数据图像进行滤波处理,旨在消除和修正不合理和错误的流场速度矢量[50 ] . 现有的流场后处理方法可以分为4类,即基于滤波的流场后处理,基于物理约束的流场后处理,基于POD的流场后处理,基于深度学习的流场后处理. ...
二维数字滤波在物理模型流场测量系统中的应用
1
2007
... 此外,二维数字滤波方法也是流场结果中常用的后处理方法[51 ] ,将时域内的二维数据基于离散快速傅里叶变换转换到频域内,通过低频分量,削弱高频分量(如Butterworth低通滤波法),修正流场中的错误矢量. 由于数据的所有非平稳成分都会被平滑处理,另外滤波的截止频率直接决定了处理后的流场矢量结果,对流场精度有较大的影响. ...
二维数字滤波在物理模型流场测量系统中的应用
1
2007
... 此外,二维数字滤波方法也是流场结果中常用的后处理方法[51 ] ,将时域内的二维数据基于离散快速傅里叶变换转换到频域内,通过低频分量,削弱高频分量(如Butterworth低通滤波法),修正流场中的错误矢量. 由于数据的所有非平稳成分都会被平滑处理,另外滤波的截止频率直接决定了处理后的流场矢量结果,对流场精度有较大的影响. ...
基于连续性条件的体PIV后处理技术
1
2013
... 根据测量获得的流场结果,引入物理约束的流场矢量修正方法[52 ] . 针对不可压缩流,由于真实的流体流动满足连续性方程 $ \nabla \cdot \boldsymbol{U}={\bf{0}} $
基于连续性条件的体PIV后处理技术
1
2013
... 根据测量获得的流场结果,引入物理约束的流场矢量修正方法[52 ] . 针对不可压缩流,由于真实的流体流动满足连续性方程 $ \nabla \cdot \boldsymbol{U}={\bf{0}} $
Use of proper orthogonal decomposition for time interpolation from PIV data
1
2005
... 本征正交分解(proper orthogonal decomposition, POD)是提取离散数据特征信息的重要数学方法[53 ] . 该方法分解得到模态的排序方式是能量从高到低的,需要处理的流场中低阶模态的能量占比高于高阶模态. 当错误矢量较多时,会增加高阶模态下的能量,进而改变能量占比. 该方法主要利用低阶模态重构流场,通过计算与真实流场间的偏差,由3σ 准则过滤偏差,在全局下识别错误流场矢量校正差值,通过迭代后得到精度较高的速度场. 其优点是流场中的错误矢量在POD过程中对于大尺度结构的低阶模态影响较小,其流场精细程度与适用性较高. ...
1
... 基于深度学习的后处理是新兴的流场处理方法,主要是将流场的二维数据转变为需要的图像格式,利用图像回归的方法,完成像素回归计算[54 ] . 常用的算法是全卷积网络,利用最后的反卷积层对之前提取的特征图进行上采样,逐渐把数据恢复为图像的输入尺寸,在保留原始信息的同时,对特征图进行逐像素分类,最终结果是各像素点带有标签的尺寸不变的输出图像. 其优点是在保证精度的情况下,极大地缩短了流场计算时间,具有较好的泛化性能. ...
1
... 基于深度学习的后处理是新兴的流场处理方法,主要是将流场的二维数据转变为需要的图像格式,利用图像回归的方法,完成像素回归计算[54 ] . 常用的算法是全卷积网络,利用最后的反卷积层对之前提取的特征图进行上采样,逐渐把数据恢复为图像的输入尺寸,在保留原始信息的同时,对特征图进行逐像素分类,最终结果是各像素点带有标签的尺寸不变的输出图像. 其优点是在保证精度的情况下,极大地缩短了流场计算时间,具有较好的泛化性能. ...