陆上风机结构在其20~25年的设计使用周期内,大约需要经历107~108次循环荷载[9]. Huang等[10-11]通过数值模拟和理论推导的方法开展风机结构的关键参数计算,分析风机结构自振频率对塔架直径、壁厚、上部结构质量以及基础刚度等因素的敏感程度. 其中,结构自振频率对基础刚度的变化十分敏感,基础刚度在外界荷载作用下会发生变化. Michel等[12]通过数值分析,对不同地基土下的浅基础动刚度、陆上风机自振频率展开分析,计算发现浅基础动刚度、陆上风机自振频率对地基土刚度的变化十分敏感. 柯世堂等[13-14]针对陆上风机塔架底部不同边界条件,展开相应风致响应、地震响应研究,发现在风、地震荷载下,不同的基础刚度对陆上风机结构动力特性和动力响应影响较大. 因此,研究长期循环荷载作用下风机支撑结构动力特性的演变规律是当前风电发展背景下的关键问题. Bhattacharya等[15-18]针对海上风机支撑结构开展室内1∶100缩尺模型试验,得出不同地基下海上风机支撑结构在长期运行下的动力特性演变规律. 目前对风机支撑结构动力特性的发展规律研究主要集中在海上风机支撑结构,对于陆上风机支撑结构长期动力特性演变规律的研究相对较少. Oliveira等[19]通过对陆上风机的现场长期监测,得到一段时间内陆上风机动力特性发展规律. Zhao等[20]通过现场监测对陆上风机不同运行工况下的动力特性展开研究,为风机结构的设计奠定基础.
针对陆上风机支撑结构的动力特性,本文搭建陆上风机支撑结构动力特性试验平台,对风电场中3.4 MW级别风机支撑结构进行1∶50缩尺,开展顶部集中质量−塔架−基础−上部结构一体化的长期循环荷载作用下结构动力特性演变规律试验研究,并利用数值模拟和基础转角监测,从基础周围土颗粒运移规律的角度对试验结果给予机理性解释.
1. 工程背景
目前陆上风电场的风机基础形式主要为重力式基础. 风电场以及3.4 MW风机的相关参数如表1所示.
表 1 3.4 MW风机的相关参数
Tab.1
| 参数 | 符号 | 数值 | 单位 |
| 轮毅高度 | L | 90 | m |
| 叶轮直径 | Db | 140.36 | m |
| 叶轮转速 | n | 6~12 | r/min |
| 年平均风速 | v | 7.2 | m/s |
| 切入风速 | vin | 2.5 | m/s |
| 切出风速 | vout | 20 | m/s |
| 塔架上部直径 | Dt | 3.8 | m |
| 塔架下部直径 | Db | 4.6 | m |
| 基础埋深 | HF | 4 | m |
| 基础底部直径 | D | 19.6 | m |
| 上部结构质量 | M1 | 233 | t |
| 塔架质量 | M2 | 280 | t |
| 基础质量 | M3 | 1350 | t |
| 荷载作用高度 | LF | 85 | m |
| 湍流系数 | I | 15 | % |
2. 陆上风机室内缩尺试验设计
2.1. 相似性理论与缩尺模型
2.1.1. 相似性理论
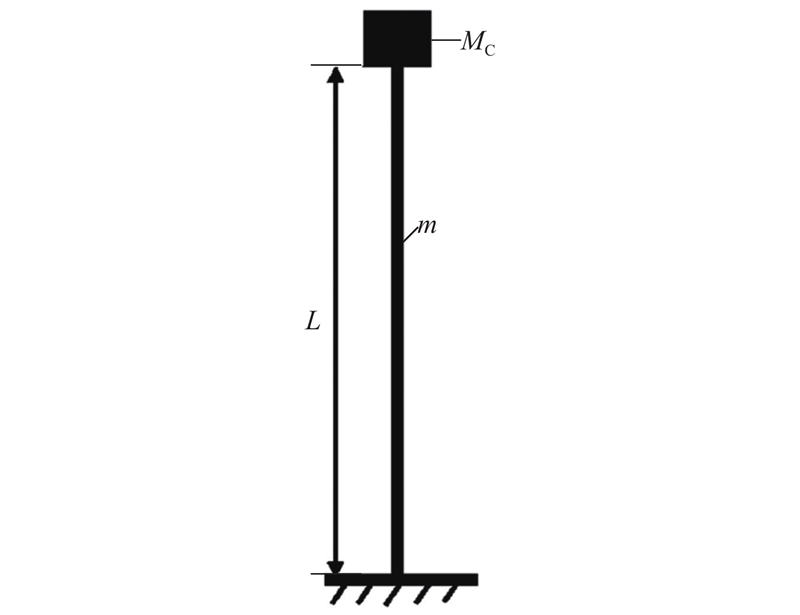
在建立风机模型相似性理论的过程中,进一步简化风机结构整体,如图1所示. 在该简化模型中,风机塔架简化为受轴向力作用且底部固定支撑的Euler-Bernoulli梁. 假设梁的抗弯刚度EI及单位长度质量m沿高度L不变,在梁的横向运动过程中轴向力的大小和方向不变. 塔顶机舱、轮毂和叶片等效为与悬臂梁刚性连接的集中质量块MC. 一般忽略梁的轴向振动,因此在简化计算模型中未加入基础−土对上部结构的约束.
图 1
表 2 相似性理论无量纲化关系
Tab.2
| 物理意义 | 无量纲化关系 | 比例大小 |
| 几何相似 | L/D | 1∶50 |
| 质量相似 | M1∶M2∶M3 | 1∶1.2∶5.78 |
| 荷载作用高度相似 | LF/D | 1∶50 |
| 基底应变相似 | H/GD2 | -- |
| 荷载频率相似 | fF/fn-in | -- |
本文提出重力式基础下基底土体的应变相似. 由于基底土体的不均匀应变累积会导致基础倾斜,可利用基础转角相似表征基底土体的应变相似. 基础转角相似引用文献[6]提出的埋置基础转置刚度公式进行推导计算.
式中:
在试验前期设计阶段,由式(1)再根据几何相似可以控制
式中:
2.1.2. 陆上风机支撑结构缩尺模型
结合相似性理论对陆上3.4 MW风机支撑结构进行整体缩尺,根据试验平台的规格,经过计算拟定1∶50的几何相似比尺. 模型结构基于上述简化模型,把叶轮、轮毂、机舱等效为相应的质量块固定于塔顶. 在试验设计准备阶段,通过确定模型几何相似比尺和地基土切变模量相似比尺,根据现场原位的风荷载幅值,获得模型结构承受的水平荷载幅值;通过改变模型试验中模型几何尺寸和地基土切变模量,调整模型结构承受的水平荷载幅值,以保证试验的正常进行;通过动力特性相似比尺,拟定试验过程中循环荷载频率. 基于相似性理论中的基底应变相似以及动力特性相似比尺,将试验中各工况下模型结构的动力特性、动力响应推算反演至遵循相同相似性理论的原型结构. 搭建的陆上风机支撑结构动力特性试验平台及相关尺寸如图2所示,土体参数见表3.
图 2
表 3 试验土基本物理力学参数
Tab.3
| 物理量 | 符号 | 数值 | 单位 |
| 比重 | Gs | 2.622 | |
| 中值粒径 | d50 | 0.16 | mm |
| 最大孔隙比 | emax | 0.943 | |
| 最小孔隙比 | emin | 0.60 | |
| 相对密实度 | Dr | 60 | % |
| 土体切变模量 | G | 12.2 | MPa |
2.2. 风荷载简化与计算
工程中计算风荷载,通常将总风速
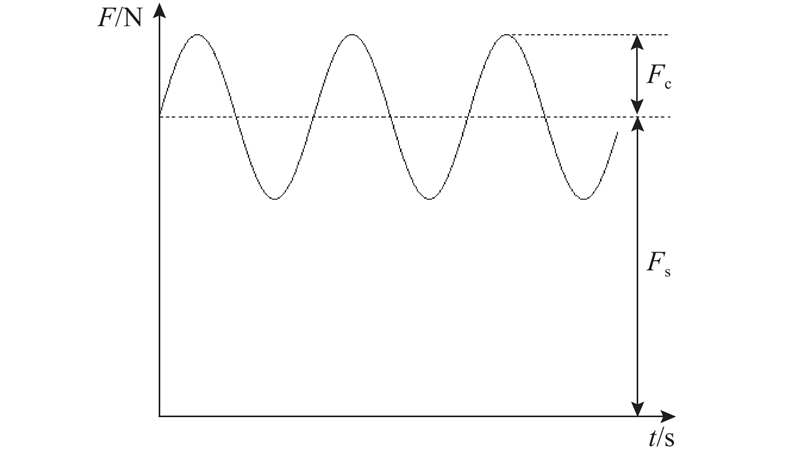
实际的脉动风荷载是离散随机的,因此简化脉动风荷载,根据最大脉动风速和频率将脉动风荷载简化为简谐荷载形式. 该荷载形式简单,可以很好地复刻脉动风荷载的动力性质. 脉动风速的大小取决于平均风速和湍流强度. 一般地,脉动风速视为平稳的高斯随机过程. 风速标准偏差
风在风机转子上的作用力
式中:
式中:
2.3. 模型试验设计
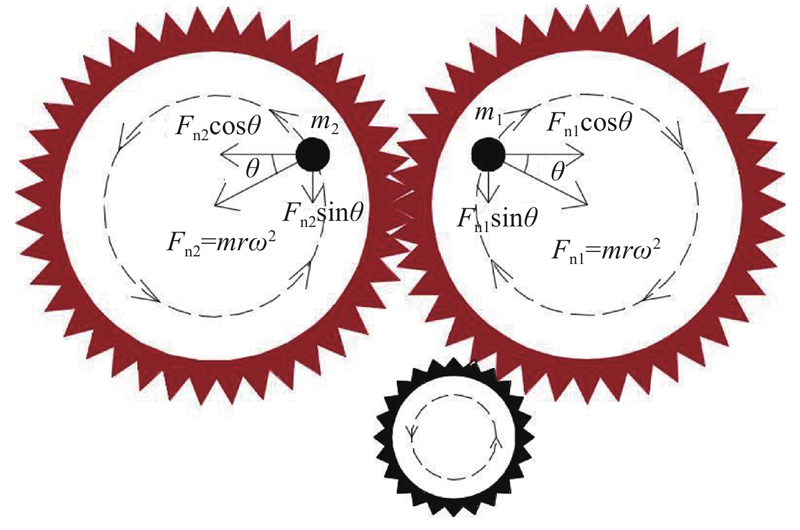
2.3.1. 循环动力加载装置
图 3
2.3.2. 陆上风机动力特性表征
使用结构的自振频率和阻尼比表征结构的动力特性. 通过对结构顶部采集的自由振动时程衰减信号[23]进行快速傅里叶变换,转化到频域内相应的功率谱密度函数,通过筛选频域内的峰值获得结构自振频率.
结构阻尼比[19]是表征结构动力特性的另一重要指标. 通过筛选衰减信号中的正峰值,对筛选出的峰值点进行拟合,得到结构阻尼比
式中:
2.3.3. 室内模型试验方案
表 4 室内模型试验方案
Tab.4
| 工况 | Fc/Fs | Hdyn/GD2 | fF/fn-in | N |
| CLT-1 | 0.267 | 5.40×10−6 | 1.5 | 1 628 992 |
| CLT-2 | 0.356 | 7.08×10−6 | 1.5 | 1 700 432 |
| CLT-3 | 0.445 | 9.00×10−6 | 1.5 | 1 377 834 |
| CLT-4 | 0.506 | 1.02×10−5 | 1.5 | 1 382 974 |
| CLT-5 | 0.356 | 7.08×10−6 | 0.5 | 2 773 040 |
| CLT-6 | 0.356 | 7.08×10−6 | 1.25 | 1 340 919 |
| CLT-7 | 0.356 | 7.08×10−6 | 1.875 | 2 450 498 |
图 4
3. 模型试验结果和分析
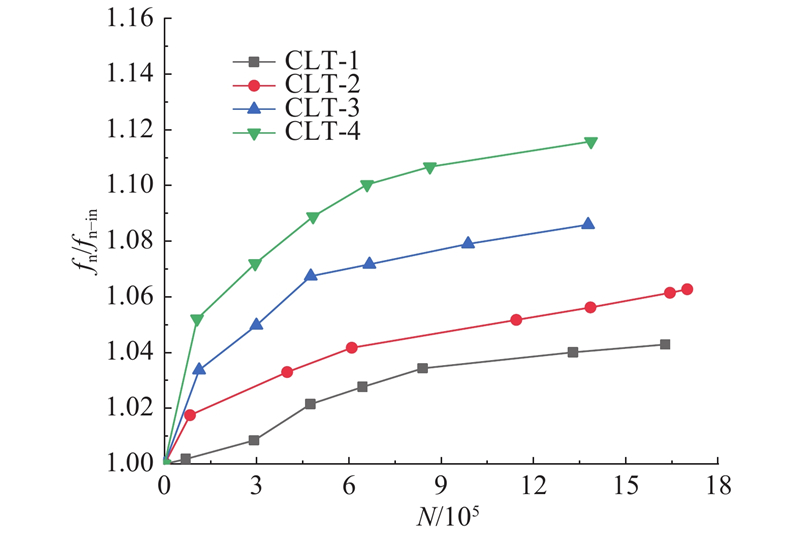
3.1. 结构自振频率
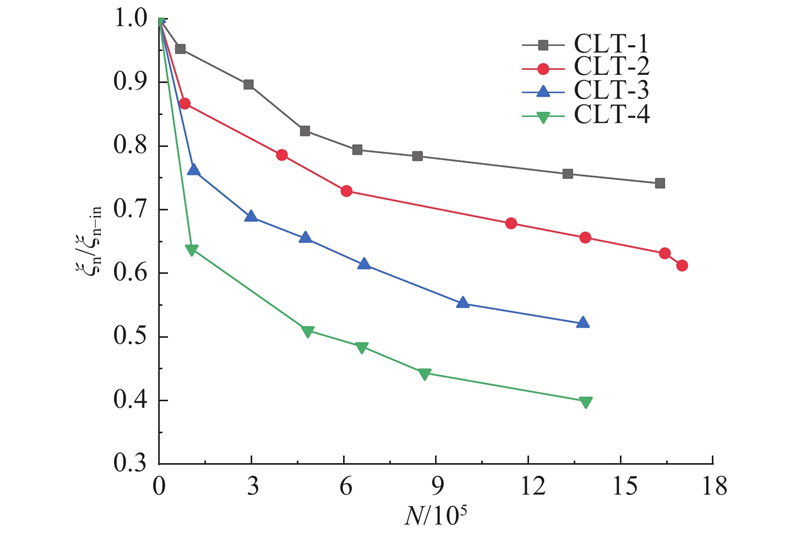
图 5
图 5 结构自振频率随循环加载次数变化关系图(CLT-1~CLT-4)
Fig.5 Change of natural frequency with number of cycles (CLT-1~CLT-4)
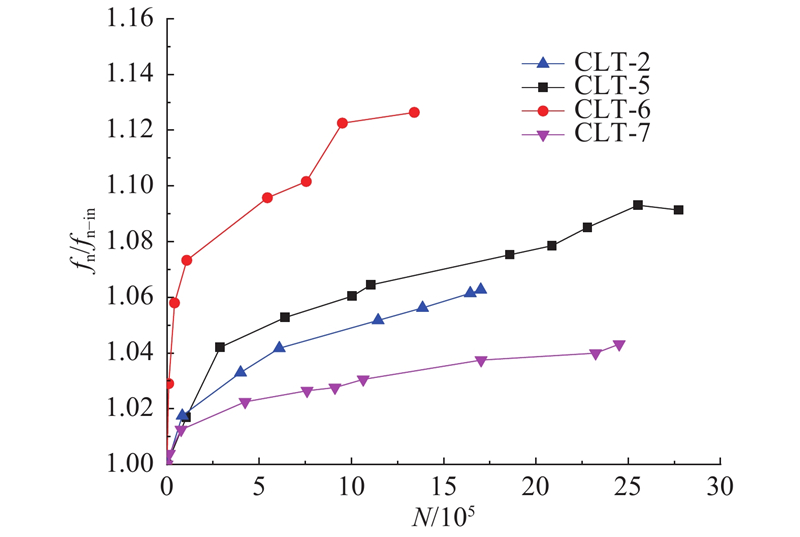
如图6所示为工况CLT-2、CLT-5~CLT-7中结构自振频率比与循环加载次数的关系. 从图可以看出,4组试验的主要变量是反映外界荷载频率的无量纲值(fn/fn-in). 4条曲线的发展规律基本与工况CLT-1~CLT-4的发展规律相同;具体表现为随着循环加载的进行,结构自振频率比不断增大,但在循环加载后期,结构自振频率比进入平稳发展阶段. 图中结构自振频率增长的速率及幅度对无量纲荷载频率值(fF/fn-in)十分敏感. 工况CLT-6中结构自振频率发展相比其余工况存在陡增的现象. 而工况CLT-7中结构自振频率发展相比其余工况更加稳定、平缓.
图 6
图 6 结构自振频率随循环加载次数变化关系图 (CLT-2,CLT-5~CLT-7)
Fig.6 Change of natural frequency with number of cycles (CLT-2, CLT-5~CLT-7)
3.2. 结构阻尼比
图 7
图 7 结构阻尼比随循环加载次数变化关系图(CLT-1~CLT-4)
Fig.7 Change of damping ratio with number of cycles (CLT-1~CLT-4)
在工况CLT-1~CLT-4中,CLT-1相比其余工况其动力特性发展曲线更加平缓. 即当反映基底土体应变水平的无量纲值(Hdyn/GD2)控制在5×10-6左右时,结构动力特性发展较为平缓,动力稳定性更高. 在工况CLT-2、CLT-5~CLT-7中,CLT-6相比其余工况动力特性发展更加陡峭;CLT-7相比其余工况表现出更好的动力稳定性,即当无量纲荷载频率值(fF/fn-in)幅值为1.25时,结构动力稳定性较差,容易引起共振现象;反之,当该值越远离幅值1,结构动力稳定性较好. 因此,结构运行期间控制基底土体应变水平以及考虑荷载频率对结构动力稳定性的影响尤为重要.
3.3. 模型试验机理分析
在试验过程中发现,基础周边局部区域在基础倾斜和基础−土相互摩擦作用下发生土颗粒运移,土体表面出现土颗粒流失的现象. 表现形式为土体表面随着循环加载的进行,在模型结构迎风面土体逐渐形成与基础底面直径相似的圆环形凹陷面,而模型结构背风面土体在循环加载过程中未出现明显凹陷面.
如图8所示为工况CLT-5试验过程中,结构迎风面区域基础周围土体的凹陷面演变情况. 由图可以看出,在循环加载初期,土体表面形成较浅的凹陷面雏形,但并不明显. 随着循环加载次数增加,基础产生较为明显的倾斜,土体表面凹陷区域逐渐加深,且在迎风面区域土体出现隆起的现象.
图 8
试验中基础主要承受弯矩,弯矩导致基底压力分布不均匀. 为了得到基础底部土体在结构运行下的受荷轨迹,并进一步验证试验结果与上述现象,本文基于ABAQUS有限元软件进行数值建模分析. 建立模型基础−土相互作用数值模型,由于数值模型的目的是作为辅助手段,获得模型基础底面土体在运行期间的应力状态,结合后续的基础转角监测,从土颗粒运移角度出发,揭示模型结构循环过程动力特性的演变规律,解释上文所示的循环过程中,基础周围土体发生凹陷的现象. 因此,土体采用线弹性本构,E=35 MPa,μ=0.3;基础采用线弹性本构,E=210 GPa,μ=0.3;基础和土体接触法向采用硬接触,切向采用罚接触,接触系数0.5. 建立隐式动态分析步进行计算分析. 在基础顶面施加荷载
式中:Mtotal为作用在基础顶面的总弯矩,
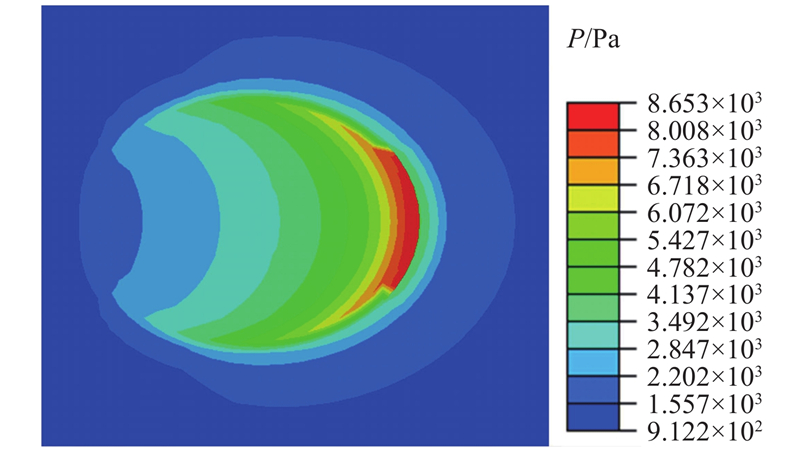
计算得到如图9所示的基底压力分布图. 图中,P为基底压力. 从图中可以看到基底土体基本处于受压的受荷状态;基底压力分布不均匀,其中在背风面范围土体出现较大的应力集中现象,在迎风面范围位置土体受到的压力最小.
图 9
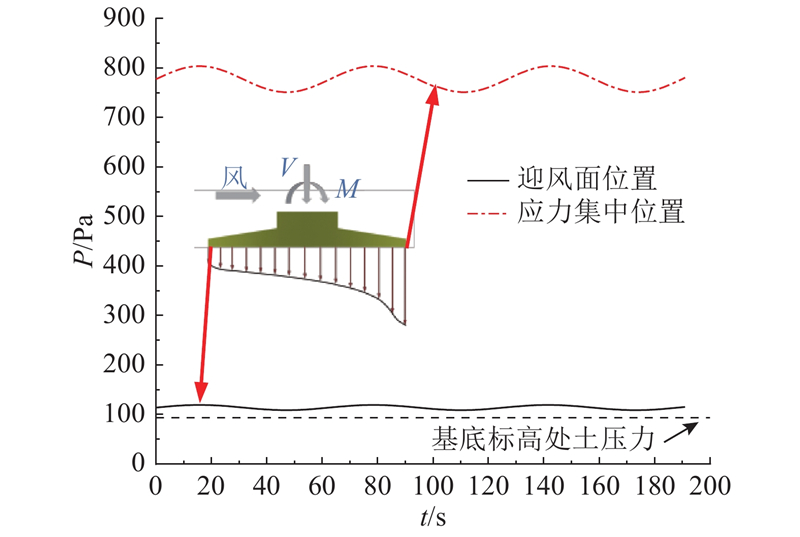
如图10所示为基底背风面压力最大处和迎风面压力最小处位置的基底土压力时程分布图,图中,虚线为该场地基底深度下的土压力. 由图可以看到,在循环弯矩作用下选择的2个位置的基底土压力均高于图中参考线,表明在循环弯矩作用下,基础底面土体均处于循环受压的状态,未发生基底脱开现象.
图 10
图 10 循环荷载下基底土体压力时程曲线
Fig.10 Time-history curve of base soil pressure under cyclic loading
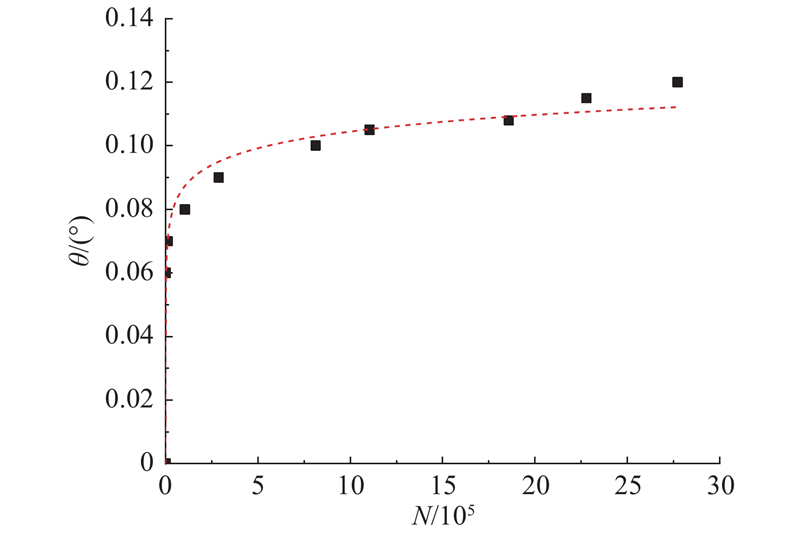
在试验过程中每隔一段时间用倾角仪测量基础顶面的转角,得到如图11所示的循环加载过程基础转角发展图. 由图中可以看到,在循环加载初期,基础倾斜变化明显,存在一段较陡的增加阶段;在循环加载后期,基础转角的增幅逐渐趋于稳定,基础转角随着循环加载的进行缓慢地增加.
图 11
图 11 基础转角随循环加载次数变化关系图(CLT-5)
Fig.11 Change of inclination of the foundation with number of cycles (CLT-5)
综上所述,基底土体在不均匀的循环压载下,产生不同程度的应变累积,使得基础产生倾斜. 基础倾斜程度随着循环加载的进行不断增大,为了保证基底始终与土体接触,脱开面上部区域土颗粒发生较大范围的运移,转移至基底脱开位置,在土层表面形成凹陷区域. 随着循环加载的进行,土层表面凹陷区域逐渐加深. 同时,基底土体在持续循环压载下,孔隙比逐渐减小,土体相对密实度增大,导致基础刚度逐渐增大,使得结构自振频率进一步增大(结构阻尼比减小). 因此,结构动力特性的演变从本质上来说是由基底土体在循环压载下的应变累积造成的.
4. 结 论
(1)在砂土地基中,陆上风机运行期间结构自振频率随着循环加载次数增加而增加,结构阻尼比发展则相反. 且结构阻尼比发展速率、幅度远大于结构自振频率相应发展规律.
(2)陆上风机运行期间控制基底土体应变水平对结构的动力稳定特性具有重要意义. 试验发现将反映基底土体应变水平的无量纲值(Hdyn/GD2)控制在5×10−6以内时,结构动力稳定性高,结构动力特性发展平稳、缓慢,在循环加载过程不存在明显的拐点.
(3)陆上风机结构动力特性的演变实际上是由基底土体的应变累积所造成的. 基底土体在循环加载过程中主要承受不均匀的循环压载,使得基底土体相对密实度增大引起基础刚度的增大,进而使得结构自振频率的增大及结构阻尼比的减小.
(4)模型试验中地基土未考虑不同相对密实度的土质和其他类型的土质,未来计划开展各类地基土下的结构动力特性试验,完善本文试验结果.
参考文献
导管架基础海上风机动力响应数值分析
[J].
Numerical analysis of dynamic responses of jacket supported offshore wind turbines
[J].
中国中长期风电发展路线图
[J].DOI:10.3969/j.issn.1003-2355.2012.03.001 [本文引用: 1]
Roadmap of China wind power development in a long-term
[J].DOI:10.3969/j.issn.1003-2355.2012.03.001 [本文引用: 1]
我国陆上风电场风机基础形式分析
[J].DOI:10.3969/j.issn.1009-6825.2014.29.045 [本文引用: 1]
Research of wind turbine foundation types of onshore wind power station in China
[J].DOI:10.3969/j.issn.1009-6825.2014.29.045 [本文引用: 1]
A comparative study of three onshore wind turbine foundation solutions
[J].DOI:10.1016/j.compgeo.2017.08.022 [本文引用: 1]
Natural frequencies of wind turbines on monopile foundations in clayey soils: a probabilistic approach
[J].DOI:10.1016/j.compgeo.2012.01.010 [本文引用: 1]
Static, seismic and stability analyses of a prototype wind turbine steel tower
[J].DOI:10.1016/S0141-0296(02)00021-4 [本文引用: 1]
Dynamics of offshore wind turbines supported on two foundation
[J].
Pile-grid foundations of onshore wind turbines considering soil-structure-interaction under seismic loading
[J].DOI:10.1016/j.soildyn.2018.03.009 [本文引用: 1]
考虑土−结构相互作用大型风力发电结构风致响应分析
[J].
Analysis on wind-induced responses of large wind power structures considering soil-structure interaction
[J].
考虑土−结构相互作用的风力发电机塔架地震响应分析
[J].
Seismic response analysis of wind turbine tower with soil-structure interaction
[J].
Observed dynamic soil-structure interaction in scale testing of offshore wind turbine foundations
[J].DOI:10.1016/j.soildyn.2013.07.012 [本文引用: 1]
Dynamic soil-structure interaction of monopile supported wind turbines in cohesive soil
[J].DOI:10.1016/j.soildyn.2013.01.015
海上风机支撑结构动力特性模型试验研究
[J].DOI:10.3969/j.issn.1000-0844.2014.04.0797 [本文引用: 1]
Scaled model test study of the dynamic behavior of an offshore wind turbine support structure
[J].DOI:10.3969/j.issn.1000-0844.2014.04.0797 [本文引用: 1]
Model tests on the long-term dynamic performance of offshore wind turbines founded on monopiles in sand
[J].DOI:10.1115/1.4030682 [本文引用: 1]
Continuous dynamic monitoring of an onshore wind turbine
[J].DOI:10.1016/j.engstruct.2018.02.030 [本文引用: 2]
Analysis of vibration monitoring data of an onshore wind turbine under different operational conditions
[J].DOI:10.1016/j.engstruct.2019.110071 [本文引用: 2]
Similitude relationship for physica modelling of monopile-supported offshore wind turbines
[J].DOI:10.1680/ijpmg.2011.11.2.58 [本文引用: 1]
An innovative cyclic loading device to study long term performance of offshore wind turbines
[J].DOI:10.1016/j.soildyn.2015.12.008 [本文引用: 1]