由于墙趾处混凝土高度的非线性和不对称性,传统的钢板混凝土组合剪力墙在地震作用下易造成墙趾处塑性应变累积. 当混凝土的抗拉应力超过抗拉强度时,裂缝开始出现,导致剪力墙净截面面积和惯性矩减小,抗侧刚度降低[1],墙趾受拉侧应力主要由钢板提供[2]. 当钢板达到屈服应力时,墙趾处的塑性应变积累速度加快,混凝土在反复荷载作用下破碎剥落,导致脆性破坏,结构功能受到严重影响[3]. 不同形式的钢板混凝土组合剪力墙拟静力试验[4]均表明:墙趾混凝土的脆性破坏对墙体的侧移刚度、延性、耗能性能等均有显著影响. 此外,对地震破坏的研究[5]表明:即使考虑延性设计,剪力墙仍有混凝土的压碎[6]和墙体底部纵向钢筋的局部屈曲问题[7]. 同时,剪力墙震后的修复[8]、重建[9]、评估[10]等工作也十分烦琐复杂. 因此,有必要对剪力墙韧性提升进行深入研究.
目前用于修复墙趾处混凝土脆性破坏的方法主要有2种. 1)为墙趾处混凝土裹上“外套”,使混凝土处于三向受压的约束状态,以提高混凝土的强度和延性. 纤维增强聚合物(fiber reinforced polymer,FRP)因其低密度、高抗拉强度的优异性能常被作为“外套”用以修复混凝土.FRP修复后剪力墙的拟静力试验[11]表明:采用FRP材料作为护套时,其强度相较于普通剪力墙提升约30%. 由于FRP在拉伸状态下表现出的非线性特征,FRP修复墙的耗能能力无法完全恢复[12],且在使用FRP混凝土构件的裂缝处,容易出现材料脱粘现象. 此外,钢带也常作为“外套”被用于构件的修复工作. 墙体表面粘贴正交扁钢的拟静力试验[13]表明:修复后的墙体骨架曲线具有较长的塑性发展阶段,耗能能力和延性均有明显提升. 但该方法在施工时难以保证锚固的可靠性,一旦失效,将会造成墙底抬起,产生更加严重的破坏. 2)置换高延性的材料以提高墙趾处的变形能力,如纤维增强混凝土(fiber reinforced concrete,FRC)和水泥基复合材料(engineered cementitious composites,ECC). 对在剪力墙墙趾处采用FRC代替传统混凝土的拟静力试验[14]表明:该技术能够在显著提升墙体极限承载力的同时,较好地限制墙体极限状态下的损伤. 对采用ECC置换的剪力墙的拟静力试验[15]表明:修复前后承载力基本一致,且修复后ECC与钢筋能够保持良好的变形协调,增强构件的延性与耗能能力. 虽然2种不同材料置换混凝土的修复方法均有较好的修复效果,但是修复耗时都很长,且FRC和ECC材料相对昂贵,在实际工程推广中具有一定的困难.
1. 试件设计
1.1. 剪力墙试件设计
表 1 试件钢材的力学性能
Tab.1
| 材料 | Es/105 MPa | Fy /MPa | Fu /MPa |
| 8钢筋 | 2.06 | 313 | 450 |
| 16钢筋 | 2.00 | 420 | 550 |
| Q235钢板 | 2.09 | 315 | 470 |
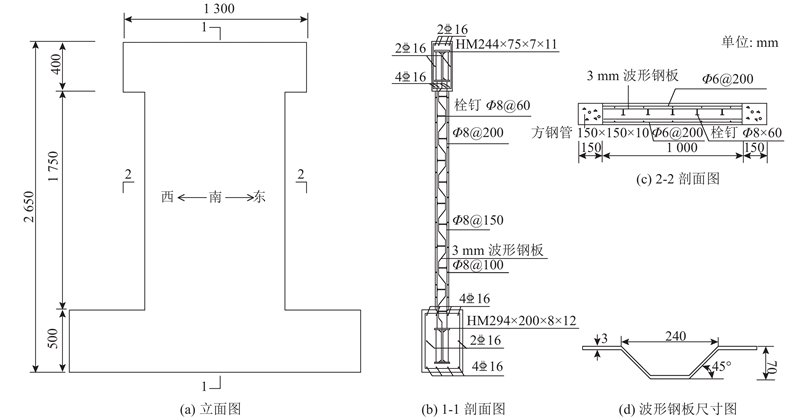
图 1
1.2. 塑性铰发展高度的确定
根据剪力墙可更换部件的修复原则,震损后试件的修复须先确定剪力墙墙趾处破坏区域和塑性开展区域. 参考Paulay等[18]提出的剪力墙的等效塑性区域高度经验公式,可更换区域高度计算公式为
式中:hc为可更换区域高度,hp塑性铰区域高度,hw为剪力墙截面宽度,H为剪力墙墙体高度. 代入剪力墙尺寸数据得到hp=337 mm,考虑到更换构件方便性,选取hc=350 mm.
1.3. 可更换墙趾部件设计
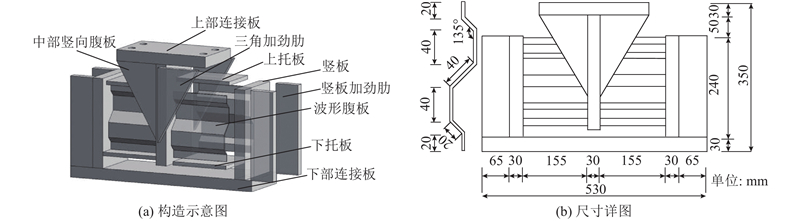
图 2
图 2 可更换阻尼器尺寸及构造
Fig.2 Specific dimensions and construction of replaceable damper
图 3
2. 加载装置及加载制度
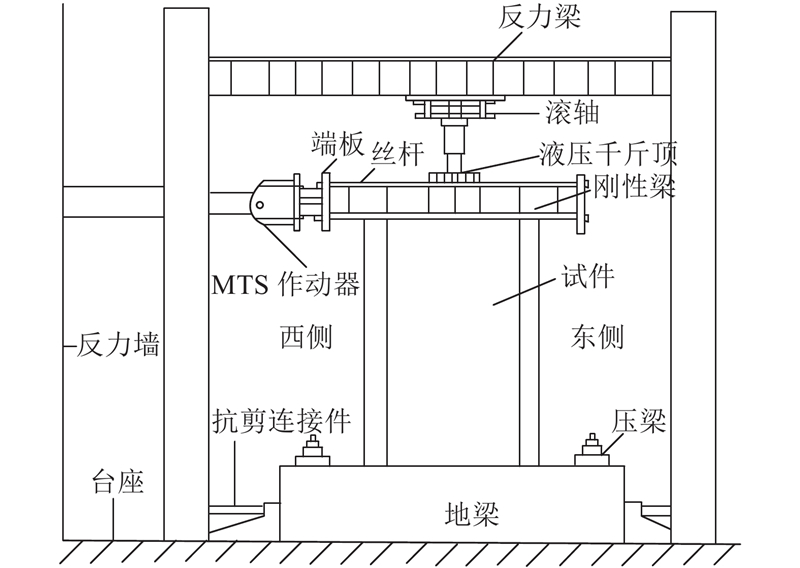
试验在西安建筑科技大学结构与抗震实验室进行. 由压梁和抗剪连接件将试件底部固定,刚性梁垫块放置于试件顶部,用以均匀分担竖向荷载. 试件加载梁由丝杆和端板与MTS(mechanical testing simulation)作动器相连,对试件施加往复推力,加载装置如图4所示.
图 4
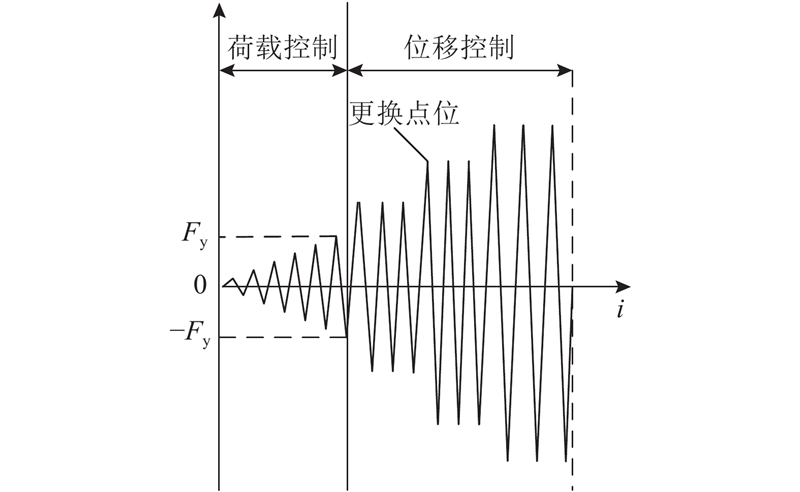
试验参照文献[19]的规定进行加载. 对构件先施加竖向荷载,并保持固定,再由MTS对试件施加水平荷载. 加载制度如图5所示. 图中,i为加载循环的次数. 加载过程分2个阶段控制. 1)荷载控制加载:加载初期采用力控制分级加载,荷载F增量为50 kN,每级循环一次. 2)位移控制加载:当荷载−位移曲线出现明显转折时,定义转折点对应位移
图 5
3. 试验现象及破坏机理分析
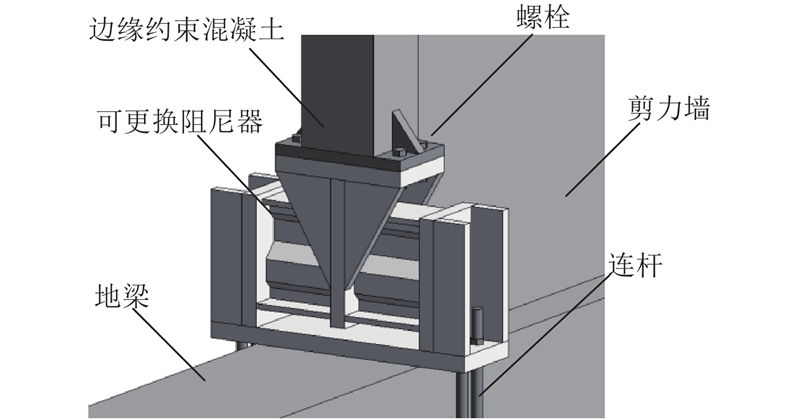
对试件施加荷载时,定义推为正,拉为负. 试验分3个阶段进行,规定修复前横向波形钢板混凝土组合剪力墙试件编号为CSPCW-H0. 对剪力墙墙趾损伤部位采用可更换阻尼器进行修复,边缘约束构件方钢管下端焊接钢板,并通过螺栓与阻尼器上部连接板相连,阻尼器下部连接板通过丝杆固定在地梁上,螺栓级别为12.9级,其连接方式如图6所示. 修复后带可更换阻尼器的剪力墙试件编号为RCSPCW-H1. 当修复后试件加载至位移角为1.25%时,拆除更换阻尼器,更换阻尼器后的试件编号为RCSPCW-H2.
图 6
图 6 可更换阻尼器与试件的连接示意图
Fig.6 Connection diagram of replaceable damper and specimen
3.1. 试验现象
3.1.1. CSPCW-H0试验现象
初始加载时,CSPCW-H0的荷载−位移曲线为直线. 当位移角为+0.2%时,出现第一条斜裂缝,裂缝自墙底向上发展,与水平方向约呈45°夹角. 当位移角为+0.4%时,东侧方钢管内部发出声响,但墙体外观没明显现象,仅地梁出现少许裂缝. 当位移角为−0.8%时,地梁裂缝明显增多,荷载位移曲线出现少量偏移. 当位移角为−0.94%时,东侧方钢管柱柱脚处发出一声巨响,柱脚从地梁拔动,试件发生脆性破坏. 墙体位移角超过0.5%,已达到文献[21]关于中度损伤的定义,墙体承受多遇地震. 此时墙体位移处在混凝土剥落位移和钢材屈服位移之间,属于可修复范围,将此损伤定义为初始损伤.
3.1.2. RCSPCW-H1试验现象
对RCSPCW-H1施加水平推力. 当位移角为+0.12%时,墙底出现第一条裂缝,裂缝与水平约呈15°夹角向西侧开展. 当为+0.4%时,在距离地梁顶部约15 cm处,从墙体西侧蔓延出一条水平裂缝,长度约为36 cm. 同时,在距离地梁顶部约40 cm处出现较短斜裂缝,斜裂缝与水平方向呈约35°夹角. 当位移角为+0.55%时,西侧墙趾阻尼器左上角区域应变过大,阻尼器开始屈服. 当位移角为−1.5%时,两侧阻尼器都已屈服,墙体出现较多斜裂缝. 此时试件的层间位移角为−1.5%,停止加载,更换金属阻尼器.
3.1.3. RCSPCW-H2试验现象
对RCSPCW-H2重新加载,由于未处理已出现的加载裂缝,加载初期,已损伤裂缝继续发展. 当位移角为−0.8%时,RCSPCW-H2的荷载−位移曲线出现转折,墙体屈服,改为位移控制加载. 当位移角为+1.4%时,西侧墙趾混凝土少许剥落,墙趾混凝土开始进入受压破坏状态. 当位移角为−1.7%时,剪力墙西侧墙趾处波形钢板开始屈服,此时阻尼器波形腹板有较大鼓曲,东侧阻尼器波形腹板发生撕裂,两侧墙趾处混凝土出现大块脱落现象. 继续加载至位移角为−2.1%,金属阻尼器翼缘板断裂,阻尼器完全破坏,退出工作,试验结束. 各阶段试件破坏形态,如图7所示.
图 7
3.2. 破坏机理分析
1)RCSPCW-H1的开裂荷载比CSPCW-H0的小. 主要原因是RCSPCW-H1加入阻尼器后,试件初试刚度降低,较小的荷载也会导致原有裂缝继续开展.
2)在裂缝开展过程中,修复前后试件的裂缝发展情况完全不同. CSPCW-H0自第一条斜裂缝起,出现的均是与水平夹角约为45°的斜向裂缝,RCSPCW-H1、RCSPCW-H2则先在可更换墙趾区域内出现水平裂缝,然后在此高度以上区域出现与水平方向约35°夹角的斜裂缝. 主要原因是CSPCW-H0的边缘约束构件与墙体刚度不匹配,墙体在受水平荷载作用时,边缘约束构件底部产生塑性铰,构件表现为框架受力特征,因此产生剪切斜裂缝. RCSPCW-H1、RCSPCW-H2减弱了边缘约束构件的刚度,在受水平荷载时,结构表现为悬臂梁受力特性. 当转过一定角度后,阻尼器为墙体提供一定的侧向刚度,墙体受弯剪复合作用,水平裂缝开始斜向发展,最终在墙底交汇.
3)在水平荷载作用下,RCSPCW-H1、RCSPCW-H2均发生弯曲型破坏,破坏征兆明显,且具有较好的延性特征. 具体表现:首先在墙体可更换墙趾高度区域出现水平裂缝,且随着荷载增加,可更换墙趾高度区域水平裂缝发展为斜裂缝,金属阻尼器开始屈服;当到达峰值荷载时,墙趾混凝土开始剥落,阻尼器产生局部变形;当到达极限荷载时,墙体底部裂缝贯通,墙趾混凝土剥落,金属阻尼器发生撕裂,墙趾箍筋弯曲变形,最终试件破坏.
4. 试验结果与分析
4.1. 滞回曲线
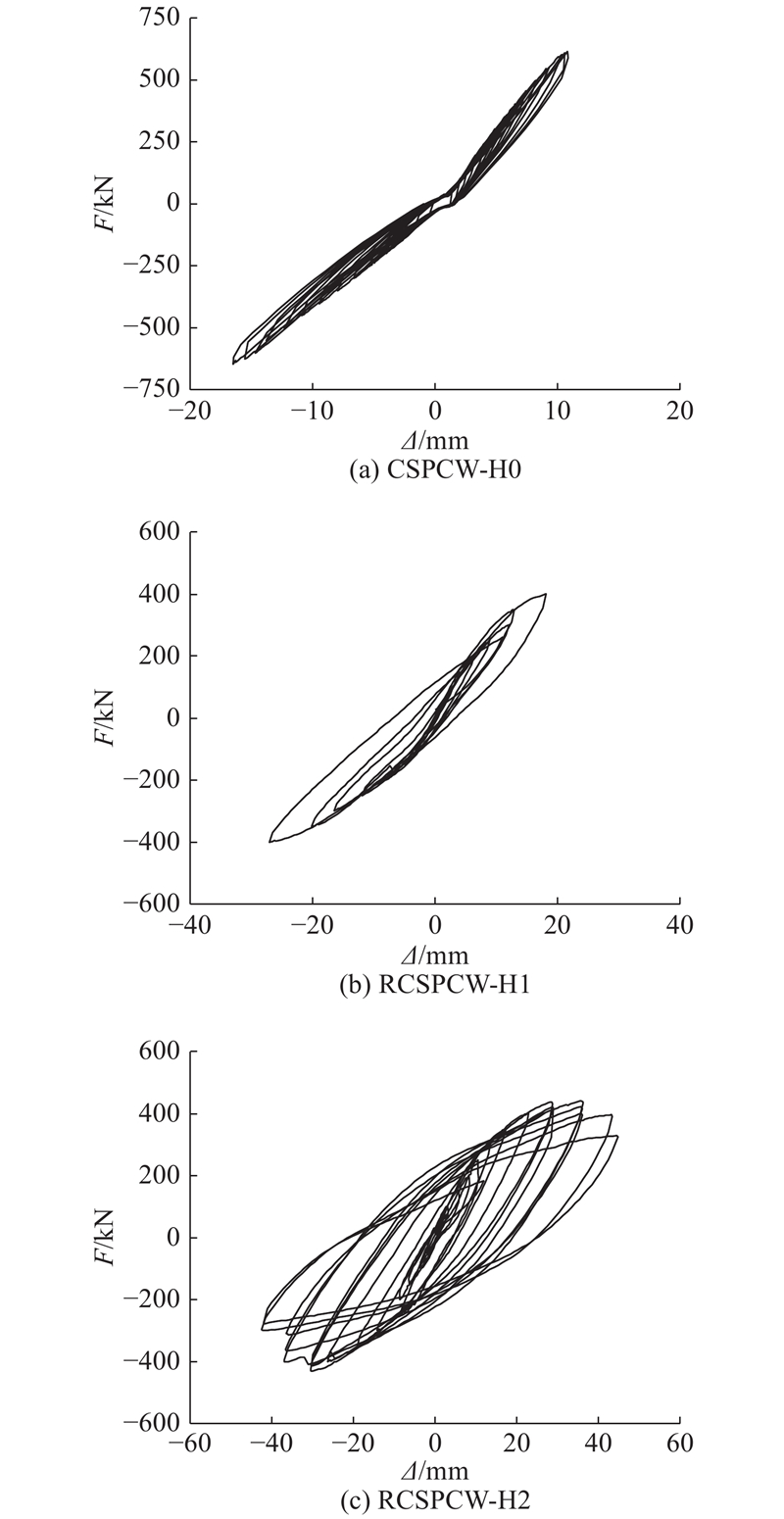
如图8所示为CSPCW-H0、RCSPCW-H1、RCSPCW-H2的滞回曲线. 图中,
图 8
4.2. 骨架曲线
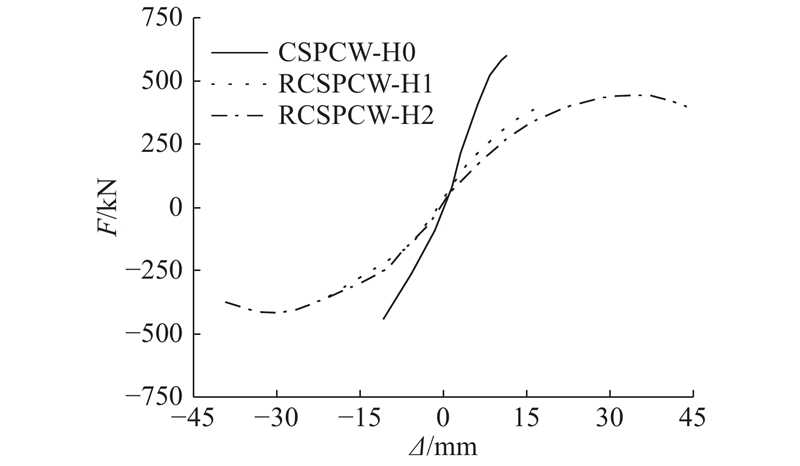
如图9所示为CSPCW-H0、RCSPCW-H1、RCSPCW-H2的骨架曲线. 由图可知:1)CSPCW-H0刚达到屈服强度就突然发生破坏,骨架曲线没有平直段,延性较差;RCSPCW-H1、RCSPCW-H2的骨架曲线有较长的平直段,在位移不断增长的情况下,承载力变化较小,表现出较好的延性特征. 2)RCSPCW-H1的骨架曲线上升趋势较平缓,几乎达到试件的峰值荷载. 在加载至层间位移角1.25%之前,RCSPCW-H2的骨架曲线与RCSPCW-H1基本重合,说明更换阻尼器的可行性. 随后RCSPCW-H2在经历较长平直段后,承载力开始下降,表现出较好的延性. 说明更换阻尼器后,试件的抗震性能较好.
图 9
4.3. 刚度退化
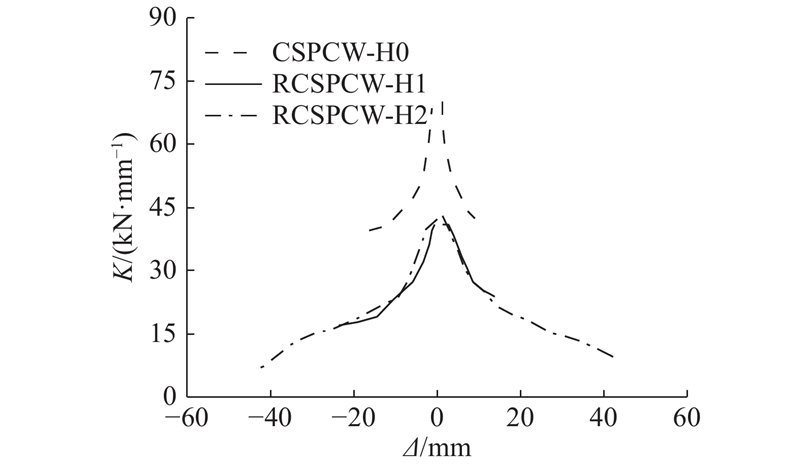
如图10所示为CSPCW-H0、RCSPCW-H1、RCSPCW-H2的刚度退化曲线. 图中,K为环线刚度. 由图可知:1)与CSPCW-H0相比,RCSPCW-H1、RCSPCW-H2,初始刚度较小,为修复前刚度的60%左右. 原因是采用金属阻尼器置换墙趾后,降低了边缘约束构件的刚度. 2)与CSPCW-H0相比,RCSPCW-H1、RCSPCW- H2刚度退化速率较低,且RCSPCW-H1、RCSPCW-H2的刚度退化曲线几乎重合,说明在墙趾放置拉压型阻尼器能将试件的损伤区域集中在阻尼器上,又因为金属材料的塑性远高于混凝土材料的塑性,所以RCSPCW-H1、RCSPCW-H2的刚度退化速率较低.
图 10
4.4. 延性与耗能能力分析
表 2 特征点的荷载和位移
Tab.2
| 试件 | Fcr/mm | | Fy/kN | | FP/kN | | Fu/kN | | μ |
| CSPCW-H0 | +250 | +8.102 | +5410.420 | +10.24 | +6010.85 | +10.61 | / | / | / |
| CSPCW-H0 | −250 | −5.410 | −544.160 | −18.68 | −647.52 | −16.50 | / | / | / |
| RCSPCW-H1 | +150 | +8.105 | +821.160 | +14.00 | / | / | / | / | / |
| RCSPCW-H1 | −150 | −5.180 | −812.200 | −14.54 | / | / | / | / | / |
| RCSPCW-H2 | / | / | +826.101 | +18.50 | +488.50 | +86.17 | +8100.62 | +48.88 | 8.21 |
| RCSPCW-H2 | / | / | −806.108 | −18.84 | −481.16 | −80.58 | −866.41 | −810.65 | 2.87 |
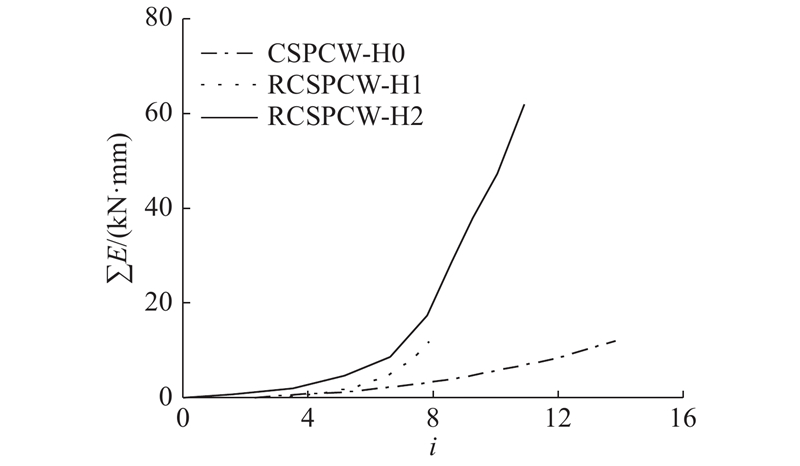
用每级荷载下滞回环的面积表示墙体的耗能能力. 如图11所示为CSPCW-H0、RCSPCW-H1、RCSPCW-H2的累积耗能能力对比结果. 图中,
图 11
图 11 试件的累积耗能能力比较
Fig.11 Accumulation energy consumption comparison of specimen
5. 有限元模拟
5.1. 有限元模型
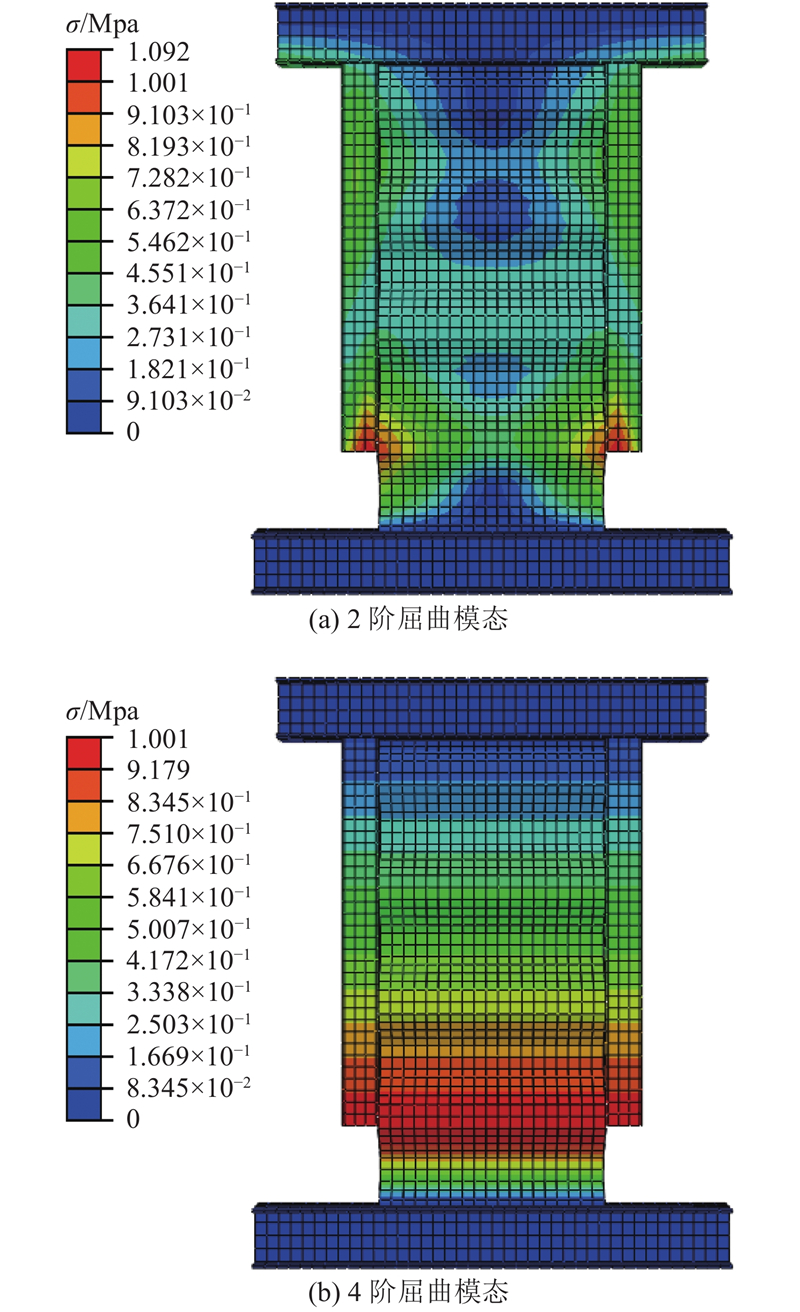
对RCSPCW-H2进行模拟时,须考虑RCSPCW-H1加载过程中对剪力墙波形钢板和边缘约束带来的应力累积效应,还须考虑更换阻尼器时带来的损伤,本文根据更换后的现象以及初始变形位置,以模型剪力墙波形钢板厚度的3%为初始缺陷,引入第2、4阶屈曲模态,其模态形式如图12所示。图中,σ为应力.
图 12
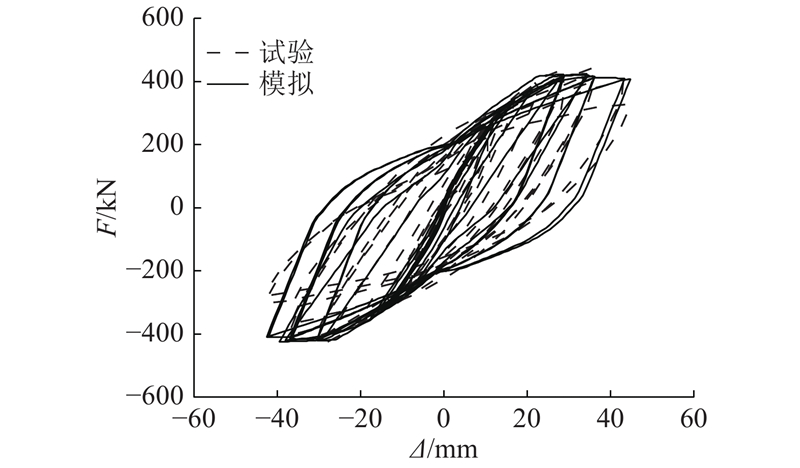
5.2. 模拟分析结果与试验结果对比
图 13
图 13 RCSPCW-H2的试验和模拟滞回曲线对比
Fig.13 Hysteresis curve comparison of RCSPCW-H2 test and simulation
表 3 RCSPCW-H2峰值载荷的试验和模拟结果对比
Tab.3
| | Fp/kN | e/% |
| +431.78 | +433.5 | 0.40 |
| −431.78 | −431.16 | 0.14 |
6. 有效抗侧刚度分析
由试验分析可知,在反复荷载作用下,转角阻尼器能够集中耗散能量,使得剪力墙的抗侧刚度降低,推迟了构件的屈服位移. 本节通过控制变量法,探讨不同影响因素对带阻尼器横波钢板剪力墙抗侧刚度的规律.
6.1. 有效抗侧计算公式
6.1.1. 有效抗侧刚度比
不同参数对剪力墙抗侧刚度的影响主要通过有效刚度抗侧刚度比k表示,计算公式为
式中:Ie为剪力墙截面的有效惯性矩;Ig为剪力墙截面未开裂的几何惯性矩;Ki为剪力墙有效刚度,Ki=Py/
计算构件有效抗侧刚度比时须进行如下假设:1)在参数研究中无法考虑剪力墙先前遭受地震的损伤情况,因此,不考虑剪力墙先前的地震损伤. 2)阻尼器在大位移下可能会发生屈曲失稳,本研究无法考虑这种情况,默认阻尼器受力为理想状态.
6.1.2. 阻尼器刚度
在计算阻尼器波形钢板的刚度时可参考文献[25],其计算公式为
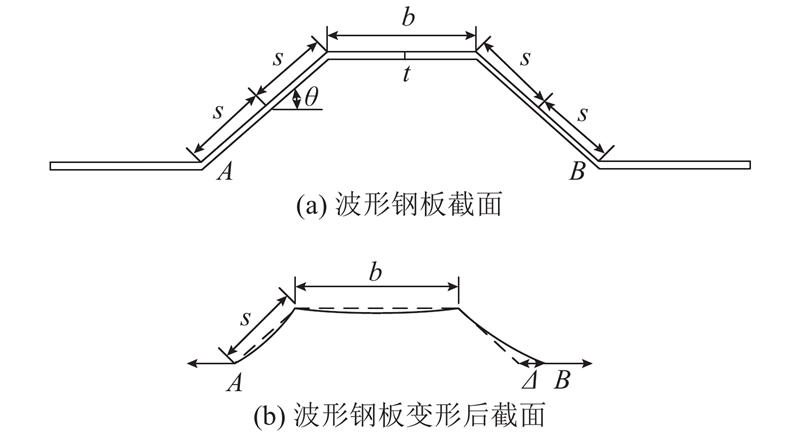
式中:KD为波纹钢板在轴向力和弯矩共同作用下的刚度,KN为波纹钢板在轴向力作用下的刚度,KM为波纹钢板在弯矩作用下的刚度,b为波峰宽度,s为波脊变形长度,取值未变形波脊一半. 参数示意如图14所示. 图中,A、B为参考点.
图 14
图 14 阻尼器波形钢板简化受力模型
Fig.14 Simplified mechanical model of corrugated steel plate of corner dampers
6.1.3. 边缘约束刚度
边缘约束方钢管构件的刚度KT计算公式为
式中:Ec为混凝土弹性模量,Is、Ic分别为钢筋截面和混凝土截面惯性矩,Eeff为钢管混凝土柱的有效弹性模量,Ieff为钢管混凝土柱的有效截面惯性矩,Leff为挖孔后实际边缘约束高度,As、Ac分别为钢筋和混凝土的截面面积;C1为影响系数.
6.1.4. 阻尼器与边缘约束构件刚度比
阻尼器与边缘约束构件刚度比k′计算公式为
6.2. 参数取值
建立81个模型,对轴压比n(0.1,0.2,0. 3)、剪跨比λ(1.5,2.0,3.0)、体积含钢率ρ(2.28%,3.02%,3.81%)、阻尼器与边缘约束构件刚度比k′(6.63%,9.89%,13.2%)进行变参分析.
6.3. 分析结果
根据模拟及计算,将结果汇总于表4,分析各个参数对墙体结构有效抗侧刚度比的影响.
表 4 不同参数下剪力墙的有效抗侧刚度比
Tab.4
| ρ/% | k'/% | k/% | ||||||||
| n=0.1,λ=1.5 | n=0.1,λ=2.0 | n=0.1,λ=2.5 | n=0.2,λ=1.5 | n=0.2,λ=2.0 | n=0.2,λ=2.5 | n=0.3,λ=1.5 | n=0.3,λ=2.0 | n=0.3,λ=2.5 | ||
| 2.28 | 6.63 | 11.59 | 12.79 | 14.09 | 15.22 | 17.39 | 20.01 | 17.45 | 19.15 | 21.00 |
| 2.28 | 9.89 | 12.81 | 14.11 | 15.52 | 16.52 | 19.20 | 21.98 | 19.23 | 21.08 | 23.09 |
| 2.28 | 13.20 | 14.14 | 15.55 | 17.09 | 17.31 | 20.97 | 23.77 | 21.17 | 23.19 | 25.39 |
| 3.05 | 6.63 | 12.37 | 13.63 | 15.00 | 16.30 | 19.94 | 23.82 | 18.57 | 20.37 | 22.32 |
| 3.05 | 9.89 | 13.65 | 15.03 | 16.52 | 17.79 | 22.11 | 26.29 | 20.46 | 22.42 | 24.54 |
| 3.05 | 13.20 | 15.06 | 16.56 | 18.18 | 18.73 | 24.14 | 28.33 | 22.52 | 24.66 | 26.98 |
| 3.81 | 6.63 | 13.38 | 14.73 | 16.20 | 17.29 | 22.91 | 29.06 | 20.27 | 22.21 | 24.32 |
| 3.81 | 9.89 | 14.77 | 16.24 | 17.83 | 18.72 | 25.31 | 31.56 | 22.31 | 24.43 | 26.73 |
| 3.81 | 13.20 | 16.28 | 17.89 | 19.62 | 19.68 | 27.07 | 33.87 | 24.56 | 26.87 | 29.37 |
6.3.1. 轴压比影响
修复墙的有效刚度随着轴向荷载的增加而增大,这与传统混凝土剪力墙的试验规律保持一致[26]. 轴向荷载的施加能够有效地提高修复墙的承载能力,试件的有效抗侧刚度相应提高. 随着轴压比的增加,剪力墙的有效抗侧刚度比也会增加. 在一定剪跨比,修复墙的有效抗侧刚度比随轴压比的增大而增大. 当轴压比从0.1增加到0.2、0.3时,λ=1.5的墙,有效刚度比分别平均增加约31%、51%. λ=2.0的墙,其有效侧向刚度比分别平均增加约45%、50%. λ=2.5的墙,其有效侧向刚度比分别平均增加约58%、49%.
6.3.2. 剪跨比的影响
对于具有相同体积含钢率和阻尼器和边缘约束刚度比的修复墙,其有效抗侧刚度比随剪跨比的增加而增加. 在n=0.1下,剪跨比从1.5增加到2.0、2.5,修复墙的有效抗侧刚度比分别平均增加约10%、21%. 在n=0.2下,有效抗侧刚度比分别平均增加约26%、51%. 在0.3轴向荷载下,分别平均增加约10%、21%.
6.3.3. 体积含钢率的影响
当修复墙的体积含钢率从2.28%增加到3.81%时,在一定剪跨比下,当n=0.1时,修复墙有效抗侧刚度比平均增加约16%. 当n=0.2时,修复墙的有效抗侧刚度比平均增加约29%. 当n=0.3时,这一指标平均增加约16%. 在一定轴压比下,当λ=1.5时,修复墙的有效刚度比平均增加约16%. 当λ=2.0时,修复墙的刚度比平均增加约29%. 当λ=3.0时,这一指标平均增加约16%.
6.3.4. 阻尼器与边缘约束刚度比的影响
当阻尼器与边界约束刚度比从6.63%增加到13.2%时,在一定剪跨比下,当n=0.1时,修复墙的有效刚度比平均增加约21%. 当n=0.2时,修复墙的有效抗侧刚度比平均增加约17%. 在n=0.3下,这一指标平均增加约21%. 在一定轴压比下,当λ=1.5时,修复墙有效抗侧刚度比平均增加约19%. 当λ=2.0时,修复墙的刚度比平均增加约21%. 当λ=2.5时,这一指标平均增加约20%.
6.4. 参数相关性
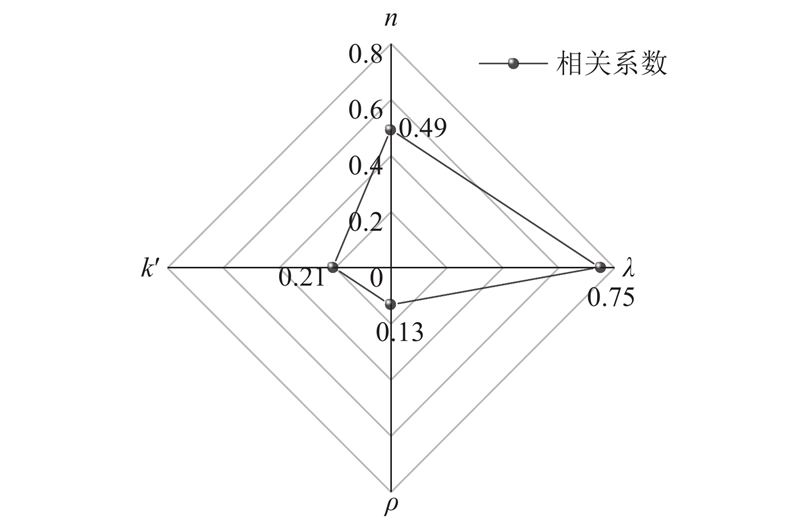
用SPSS软件计算4个影响参数与有效抗侧刚度的相关性. 如图15所示为修复墙各参数与有效抗侧刚度比的相关性分析结果. 由图可知,轴压比和剪跨比对修复墙的影响较大,体积含钢率和阻尼器与边缘约束刚度比的对修复墙影响较小.
图 15
图 15 修复后剪力墙影响参数相关性分析
Fig.15 Parameter correlation analysis of repaired shear wall
7. 结 论
(1)对剪力墙墙趾采用阻尼器进行置换能够实现中震下的快速修复,且改造后墙体遭受罕遇地震后,通过更换阻尼器可基本恢复使用功能.
(2)带阻尼器横波钢板混凝土组合剪力墙在拟静力试验中,阻尼器先于墙身受损,发挥集中耗能作用;使得剪力墙构件延性与耗能能力提升明显,抗震性能更优越.
(3)墙体破坏的模拟结果与试验结果基本吻合,变参结果显示:轴压比和剪跨比对墙体的抗侧刚度影响相较于体积含钢率和阻尼器与边缘约束刚度比显著. 4个参数中,剪跨比影响最大,体积含钢率影响最小.
(4)本文仅做了1组关于横波钢板混凝土组合剪力墙可更换的试验,未考虑阻尼器相关性能对整体可更换的影响,下一步计划引入多组试验进行对比,为后续实际设计提供更充分的理论基础.
参考文献
Lateral stiffness of concrete shear walls for tall buildings
[J].
Lateral stiffness of shear walls with openings
[J].DOI:10.1061/(ASCE)0733-9445(2006)132:11(1846) [本文引用: 1]
Confinement behavior of rectangular reinforced concrete prisms simulating wall boundary elements
[J].DOI:10.1061/(ASCE)ST.1943-541X.0001682 [本文引用: 1]
波形钢板−混凝土组合剪力墙抗震性能试验研究
[J].
Experimental research on seismic behavior of corrugated sheet plate-concrete composite shear walls
[J].
A statistical analysis of reinforced concrete wall buildings damaged during the 2010, Chile earthquake
[J].DOI:10.1016/j.engstruct.2014.10.014 [本文引用: 1]
Damage and implications for seismic design of RC structural wall buildings
[J].DOI:10.1193/1.4000047 [本文引用: 1]
近50年剪力墙结构震害及其对抗震设计的启示
[J].
Earthquake damages to shear wall structure in last fifty years and seismic design enlightenment
[J].
An innovative methodology for seismic retrofitting of existing RC buildings by metal shear panels
[J].
结构抗震设计的新概念——可恢复功能结构
[J].
New concept of structural seismic design: earthquake resilient structures
[J].
Cyclic tests on seismically damaged reinforced concrete walls strengthened using fiber-reinforced polymer reinforcement
[J].
Tests on seismically damaged reinforced concrete structural walls repaired using fiber-reinforced polymers
[J].DOI:10.1061/(ASCE)CC.1943-5614.0000110 [本文引用: 1]
低强度砖砌体粘钢-聚合物砂浆加固抗震性能试验
[J].
Experimental study on strengthening method of low strength brick masonry using steel plate and polymer mortar
[J].
RC structural wall with unbonded tendons strengthened with high-performance fiber-reinforced concrete
[J].DOI:10.1617/s11527-013-0180-8 [本文引用: 1]
ECC修复震损剪力墙抗震性能试验研究
[J].
Experimental test on aseismic behavior of damaged reinforced concrete shear wall repaired with ECC
[J].
Experimental study on seismic behavior of steel plate reinforced concrete composite shear wall
[J].
Experimental study and numerical simulation of replaceable corrugated steel plate-concrete composite shear walls
[J].DOI:10.1016/j.soildyn.2019.105827 [本文引用: 1]
结构抗震实验方法进展
[J].DOI:10.3321/j.issn:1000-131X.2004.10.003 [本文引用: 1]
Developments of seismic testing methods for structures
[J].DOI:10.3321/j.issn:1000-131X.2004.10.003 [本文引用: 1]
混凝土损伤塑性模型参数计算方法及试验验证
[J].
Parameter calculation method and experimental verification for concrete damage plastic model
[J].
钢筋混凝土结构的钢筋滞回模型
[J].
Steel hysteretic model of reinforced concrete structures
[J].
Simulation of accordion effect in corrugated steel web with concrete flanges
[J].
Effect of axial loads in the seismic behavior of reinforced concrete walls with unconfined wall boundaries
[J].DOI:10.1016/j.engstruct.2014.04.047 [本文引用: 1]