近年来，随着计算机水平的迅速发展，计算流体动力学（computational fluid dynamics，CFD）技术被广泛应用于船舶水动力性能的研究中. 与势流理论相比，CFD能够更好地求解流体的流动特性，从而更精确地求解船舶水动力性能. 杨帆等^[1]对某油船线型进行设计并基于CFD方法对船舶阻力进行数值模拟研究. 高鉴^[2]基于纳维斯托克斯雷诺时均方法（Reynolds average Navier-Stokes，RANS）及流体体积法（volumn of fluid, VOF）造波技术实现了DTMB 5512船在顶浪条件下的运动及黏性流场模拟. Rosetti等^[3]通过CFD技术模拟浮式生产、储油、卸油装置（floating production, storage and offloading unit, FPSO）在横浪下的甲板上浪.

船舶在服役期间都处于波浪的作用当中，波浪会诱导船舶产生六自由度运动，进而影响船舶航行安全性和人员及装备工作效率. 当某一海域的天气状况发生突变时，风向改变，而原先的风浪或涌浪仍继续传播，海面上会出现大范围的十字交叉状的方形波浪. 当船舶航行到双向波浪叠加的波峰或波谷时，须格外关注船舶的航行安全性，目前已经发现较多由双向波浪引起的船舶事故案例^[4]. Mathieu等^[5]基于势流理论和水池模型试验研究某LNG船在双向波中的水动力性能，结果表明双向波浪的耦合作用对于二阶慢漂力及系泊系统受力有较大影响. 因此，准确预报船舶在双向波浪中的运动响应是必要的^[6].

目前，耐波性理论主要用于预报规则波和长峰不规则波中船舶及海洋结构物的运动响应. 然而真实海况是三维短峰波，船舶在长峰波和短峰波中的运动响应和受力情况有较大的差异^[7-9]. 迄今，一些研究者已经建立了多向波的CFD模拟技术. 例如，Wang等^[10]采用CFD开源模型REEF3D模拟多向不规则波. Cao等^[11]等采用OpenFOAM建立基于NS方程和有限体积法（finite volume method，FVM）的非线性多向不规则波的数值模拟方法. 但是目前对于船舶在多向波中运动响应的研究相对较少，该研究对于保证实船在真实海况中的航行安全性具有重要实际意义.

本研究基于CFD技术建立双向波浪的数值模拟方法，分析船舶在双向波浪中的运动特性，并将船舶在单向波与双向波中的运动响应进行对比研究. 可以为船舶在方向波浪中的航行安全性评估提供方法及安全航行应对措施.

以标准船型S175集装箱船为研究对象，船模缩尺比取1∶40. 基于CFD商业软件STAR-CCM+建立的三维几何模型如图1所示. S175模型的主尺度及模型参数如表1所示.

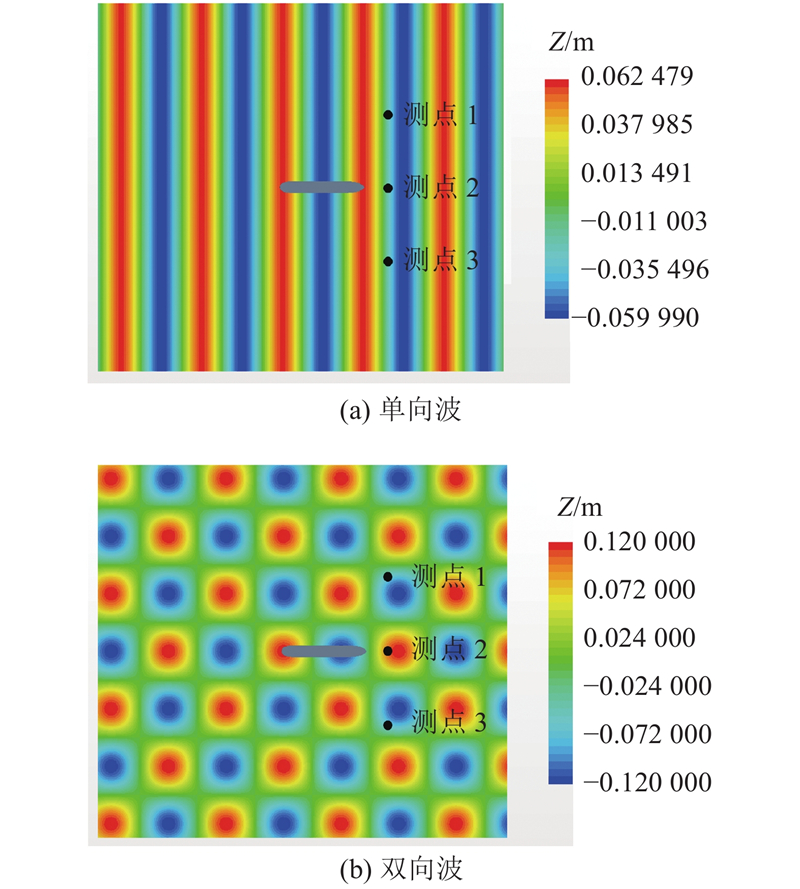
为了对比研究船舶在单向波与双向波中运动响应的差异性，涉及的计算工况如表2所示，相应的浪向角定义如图2所示. 表中，α为浪向角， $\varepsilon $为相位差，λ为波长，H为波高，F_n为航速. 为了研究船舶大幅运动和甲板上浪现象，单向规则波的波长范围取λ/L=0.6~2.0，波高取120 mm（实船波高4.8 m），符合规则波的线性假设. 双向波由2个正交的规则波叠加而成，当子波波长不同时，波浪叠加的波峰波谷与船舶相互作用位置也会发现改变，为了简化处理，本研究仅考虑2个子波的波高相同、波长相同，且相位差为0的情况，子波波浪参数与单向波的相同，以直观地比较船舶在单向波和双向波中的运动响应.

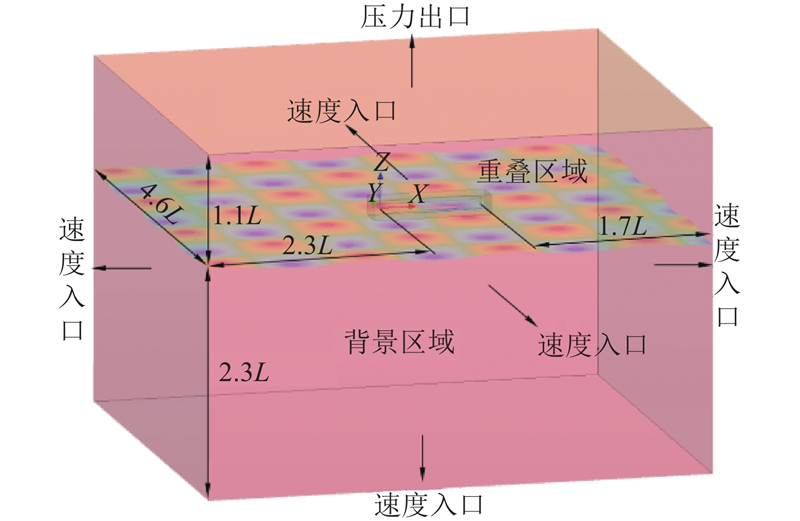
在数值计算中采用有限体积法离散控制方程，采用Realizable k-ε湍流模型，选用三维非定常隐式求解器和欧拉多相流模型，对流项离散采用二阶迎风格式，采用SIMPLE算法求解压力耦合方程，采用二阶时间离散格式进行计算，时间步长取0.005 s. 自由波面采用流体体积法追踪捕捉. 由于船舶在双向波中运动的不对称性，须建立整船及全部流体域模型，流体域坐标原点设在船舶中纵剖面、艉柱和吃水的交点，根据ITTC的推荐建议^[12]，流体域尺寸定为：−2.3L<x<2.7L，−2.3L<y<2.3L，−2.3L<z<1.1L.

流体域包括背景区域和重叠区域两部分，流体域划分及边界条件定义如图3所示. 流体域四周垂直壁面和底部采用速度入口边界条件，顶部采用压力出口边界条件. 采用动量源造波方法，在流体域四周边界施加波力（wave forcing），波力范围内的波浪强迫保持目标轮廓，同时也可以避免波浪在边界处发生反射. 在纳维-斯托克斯方程中额外添加的源项如下：

(1) ${q_\phi } = - \gamma \rho (\phi - {\phi ^*}).$

式中：γ为力系数，从力区域内缘处的0平稳过渡到边界（力区域外缘）处的最大值10；ρ为流体密度；φ为输运方程当前解；φ^*为输运方程所趋近的解.

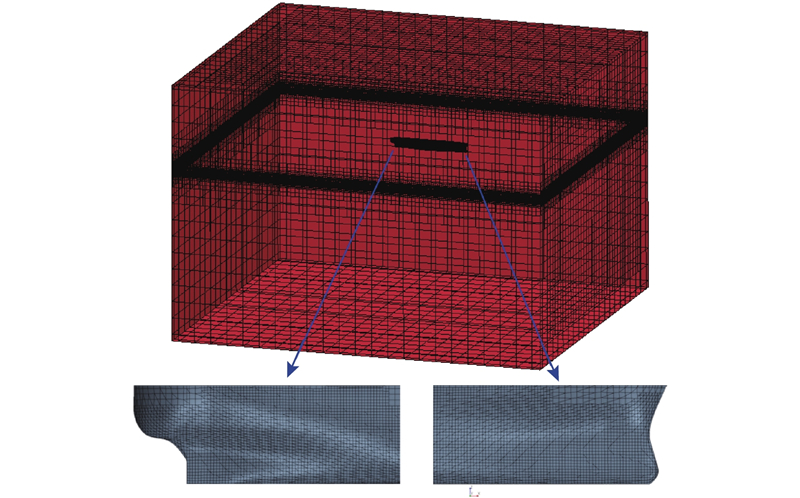
采用切割体非结构化网格对流体域进行划分，为了精确捕捉自由液面和船体周围的湍流流动变化，在自由液面以及船体周围进行局部加密. 在波高范围内设置16层网格，在波长范围内设置70~90层网格. 船体外壳设为不可滑移壁面，设置5层边界层网格（船体表面的壁面y+值为30~100）. 针对不同波长，流体域的网格单元总数也会有所变化，网格总数为380~560万. 在船体周围设置重叠区域，尺寸为5.1 m×1.2 m×0.9 m，区域外边界设置成重叠面，为了便于重叠区域和背景区域在重叠边界处插值传递数据，重叠边界附近4~5层网格的网格尺寸保持一致. 采用DFBI模块对船舶自由度运动进行模拟，在计算过程中释放横摇、纵摇和垂荡3个自由度，在计算初始时刻船舶处于静水正浮状态. 流体域的整体网格划分如图4所示，船体周围的网格划分如图5所示.

如图6所示为基于CFD模拟的单向及双向波浪示例图. 图中，Z为水面高度. 选取船艏前方L/6处的3个位置的波浪进行测量与分析，测点1~3在流体域中的坐标分别为（5.1，4）、（5.1，0）、（5.1，−4）. 须说明的是，在船舶耐波性CFD模拟中，通过设置流场相对大地坐标系的平动速度来实现船舶的前进速度，因此浪高仪具有与船舶相同的前进速度，监测的波面高程为遭遇波浪. 如图7、8所示分别为CFD模拟单向波和双向波中不同浪向角的初始化波形图.

如图9所示为单向规则波λ/L=1.0工况下船舶以不同浪向角航行时测点2处的遭遇波浪时历曲线. 图中，ζ为波幅. 给出了考虑船体兴波干扰的实际监测波高数据和理论值的对比情况. 可以看出，不同浪向下监测的波高曲线与理论值较吻合，且CFD模拟的波高时历曲线较稳定，未出现明显的波浪衰减与反射现象. 不同浪向角下的波浪遭遇周期不同，但幅值保持一致.

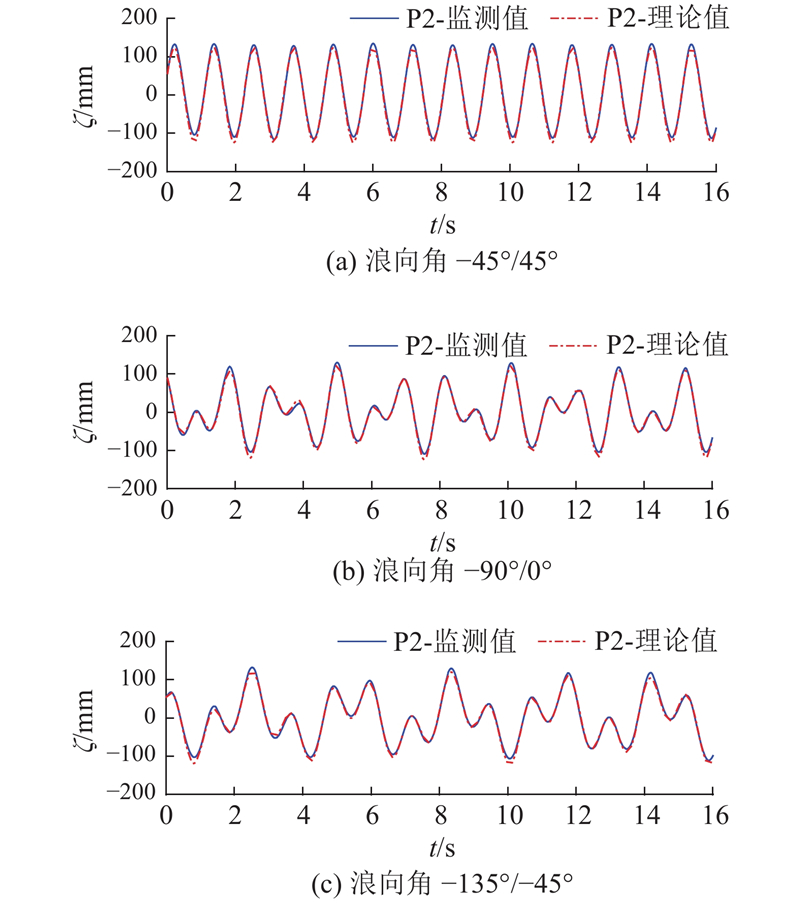
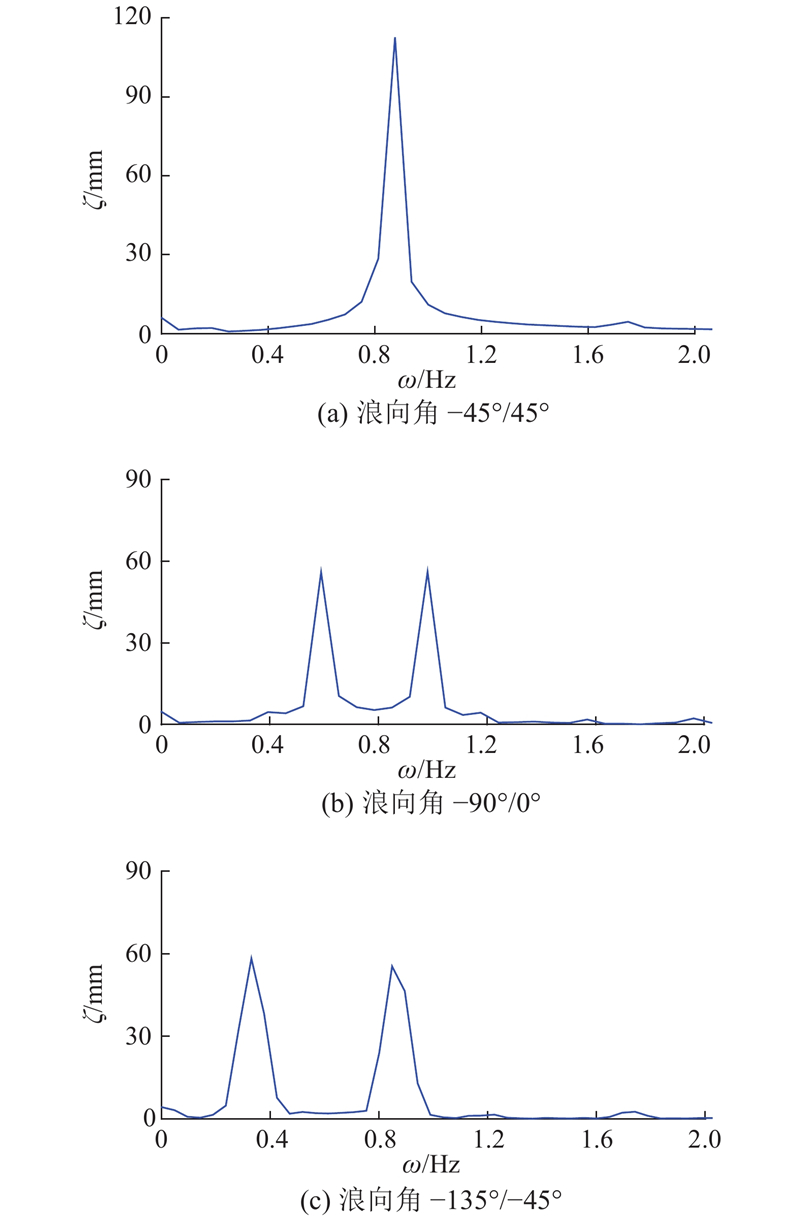
如图10、11所示分别为方形双向波λ/L=1.0工况下船舶以不同浪向角航行时测点2处的遭遇波浪时历曲线和相应的傅里叶变换频域结果. 图中，ω为遭遇频率. 可以看出，监测的波高曲线与理论值较吻合，且CFD模拟的波高时历曲线较稳定. 当方形波浪关于船舶航线对称（−45°/45°）时，由于两子波与船舶航向夹角相同，波浪遭遇频率也相同，船舶遭遇波浪呈现出规则波特征，谱曲线的谱峰峰值由两子波幅值叠加，谱峰频率等于两成分规则波的遭遇频率（0.876 Hz）. 但是当方形波浪关于船舶航向不对称时，两子波与船舶航向夹角均不相同，遭遇频率也有所差异，因此船舶遭遇波浪呈现出双色不规则特征. 谱曲线的谱峰频率对应于两成分规则波各自的遭遇频率，在浪向角−90°/0°和−135°/−45°工况下的遭遇频率分别为0.625 Hz/1.002 Hz和0.313 Hz/0.874 Hz.

如图12所示为船舶在方形波浪中（λ/L=1.0）以不同浪向角航行时的横摇 $\varphi $、纵摇θ、垂荡z响应时历曲线. 可以看出，船舶在浪向角−45°/45°工况下的纵摇和垂荡响应呈现规则波特征，与船舶遭遇的波浪形式相同. 横摇响应小于0.3°可以忽略不计，这是网格划分不对称因素引起的微小横向扰动. 另一方面，船舶在浪向角−90°/0°和−135°/−45°工况下的纵摇和垂荡呈现双色不规则特征. 由于横向或斜向成分入射波的作用，船舶横摇响应较明显，例如在−90°/0°双向波中的横摇幅值为16°.

首先将船舶在方形波浪中以合成迎浪−45°/45°航行的对称运动响应与单向规则波中以迎浪0°航行的对称运动响应进行对比；然后将船舶在方形波浪中以合成艏斜浪−90°/0°和合成横浪−135°/−45°航行的不对称运动响应与单向规则波中以艏斜浪−45°和横浪−90°航行的不对称运动响应分别进行对比.

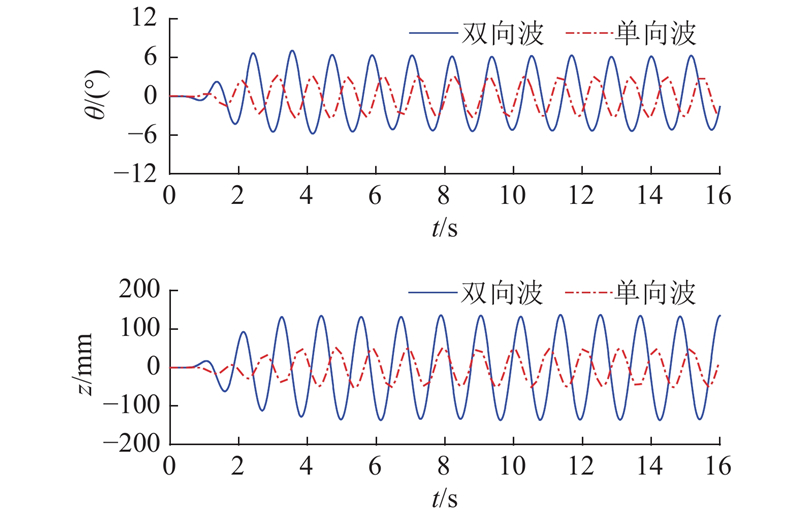
如图13所示为船舶在双向波浪−45°/45°浪向角和单向波浪0°浪向角中航行于不同波长工况下的纵摇与垂荡的运动响应幅值算子对比情况. 图中，k为波数. 可以看出，在λ/L<1.5时，2种波浪条件下的船舶纵摇幅值均随波长增大而增加. 在λ/L=1.5工况下，双向波浪中的纵摇幅值是单向波浪中的1.35倍. 双向波浪条件下的垂荡幅值随波长增加先增大后减小并在λ/L=1.1处达到最大值147 mm，是单向波浪中垂荡值的2.3倍.

如图14所示为λ/L=1.0情况下船舶在双向波浪−45°/45°浪向角与单向波浪0°浪向角中航行的纵摇与垂荡时历曲线对比. 如图15所示为相应工况下船舶发生大幅摇荡过程中的自由面波形及甲板上浪情况对比. 可以看出，船舶在双向波浪中的纵向运动响应比单向波中的明显增大，尤其是在双向波浪中船舶垂荡幅值是单向波中的2.7倍. 尽管两成分波叠加使得合成波浪的最大波高是单向规则波的2倍，但由于非线性因素作用，船舶运动响应增加大于2倍. 在单向波中航行，船舶未出现甲板上浪现象，而双向波中的甲板上浪较严重. 总之，当船舶以浪向角−45°/45°航行且航线与方形波浪场对称时，须重点关注航行安全性.

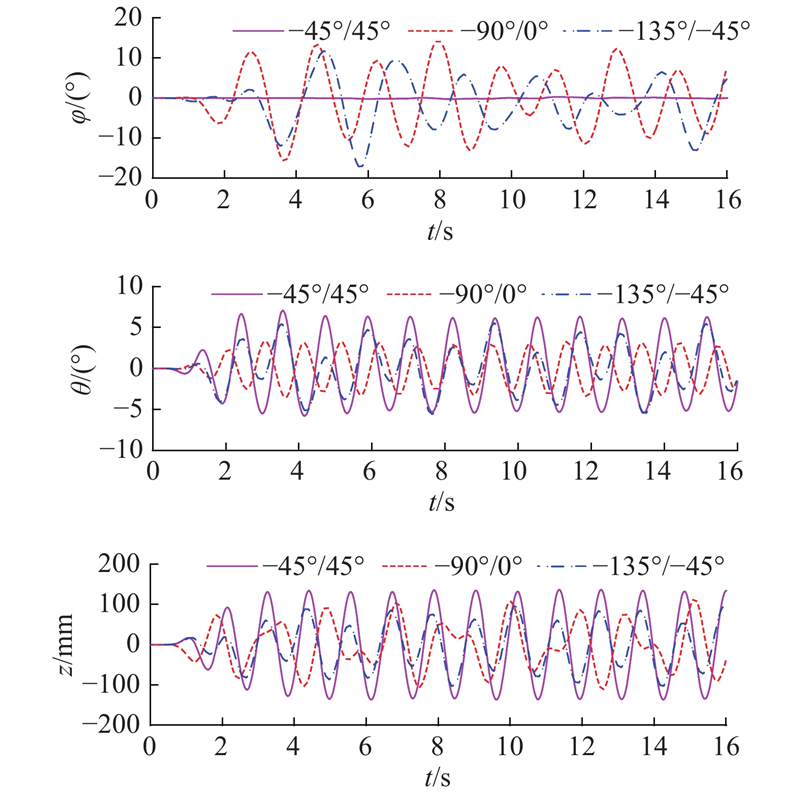
如图16所示为λ/L=1.0情况下船舶在双向波浪−90°/0°及−135°/−45°浪向角与单向波浪−45°及−90°浪向角中航行的横摇、纵摇与垂荡时历曲线对比. 从双向波浪−90°/0°与单向波浪−45°的对比结果可以看出，两者的纵摇和垂荡幅值相差不大，但双向波中的横摇运动为16°，而单向波中的横摇幅值仅为4°. 此外，由双向波浪−135°/−45°与单向波浪−90°的对比结果可以看出，两者的横摇和垂荡幅值相差不大，但双向波中的纵摇运动较明显，使得船舶产生艏部入水砰击和甲板上浪现象.

如图17所示为上述工况对应的船舶大幅运动及甲板上浪现象的对比图，图中均选取甲板上浪最严重的时刻. 可以看出，由于船舶在双向波浪−135°/−45°中航行时发生了大幅纵摇运动，此工况下的甲板上浪较严重. 船舶在单向波−45°中航行时也发生了明显的甲板上浪现象，而船舶在双向波浪−90°/0°中航行时未发生甲板上浪.

根据上述分析可以发现，船舶在方形波浪中航行时可以产生大幅横摇或纵摇响应，进而严重威胁船舶航行安全性. 因此，提出船舶遭遇方形波浪时的应对策略具有重要现实意义. 须对船舶在方形波浪中安全航行方案进行探索与研究.

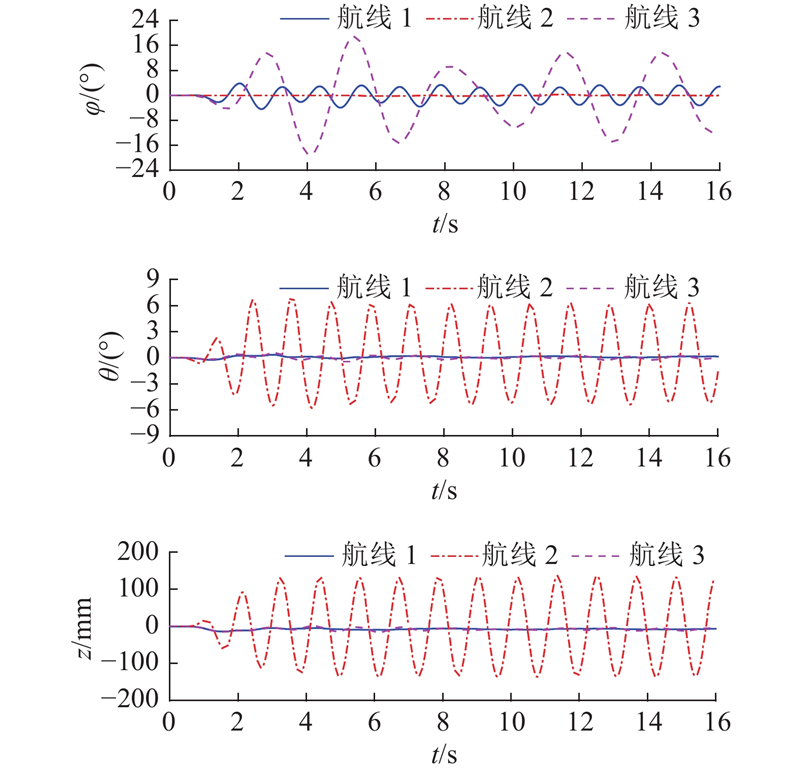
根据双向波浪的传播特性可以发现，在波浪场中存在由驻点组成的直线，此直线上的波高始终为零. 当船舶航向与两成分波的夹角为−45°/45°时，遭遇波浪为单色规则波，且波幅取决于航线位置并分布于0~2ζ范围内. 在4.1节研究了船舶航行于最大波峰谷线（即最危险工况）下的运动响应. 接下来研究当船舶航行于波幅始终为0的驻点组成的直线上时的运动响应. 为此，选取的船舶以浪向角−45°/45°航行的3条航线如图18所示. 图中，航线1为船舶迎浪经过驻点线，航线2为船舶迎浪经过最大波峰谷线，航线3为船舶随浪经过驻点线.

如图19所示为船舶以上述3种航线航行时的运动响应时历曲线对比. 可以看出，在航线2中，船舶产生了大幅纵向运动，由于左右舷侧波浪的对称性，横摇运动为零. 在航线3中，尽管船舶纵摇和垂荡运动较小，但是产生了大幅横摇运动（幅值为18°）. 这是由于舷侧波浪的交替变化频率较低，接近横摇固有频率引起了共振现象. 在航线1中船舶的纵摇和垂荡运动几乎为零，且横摇幅度较小约为4°.

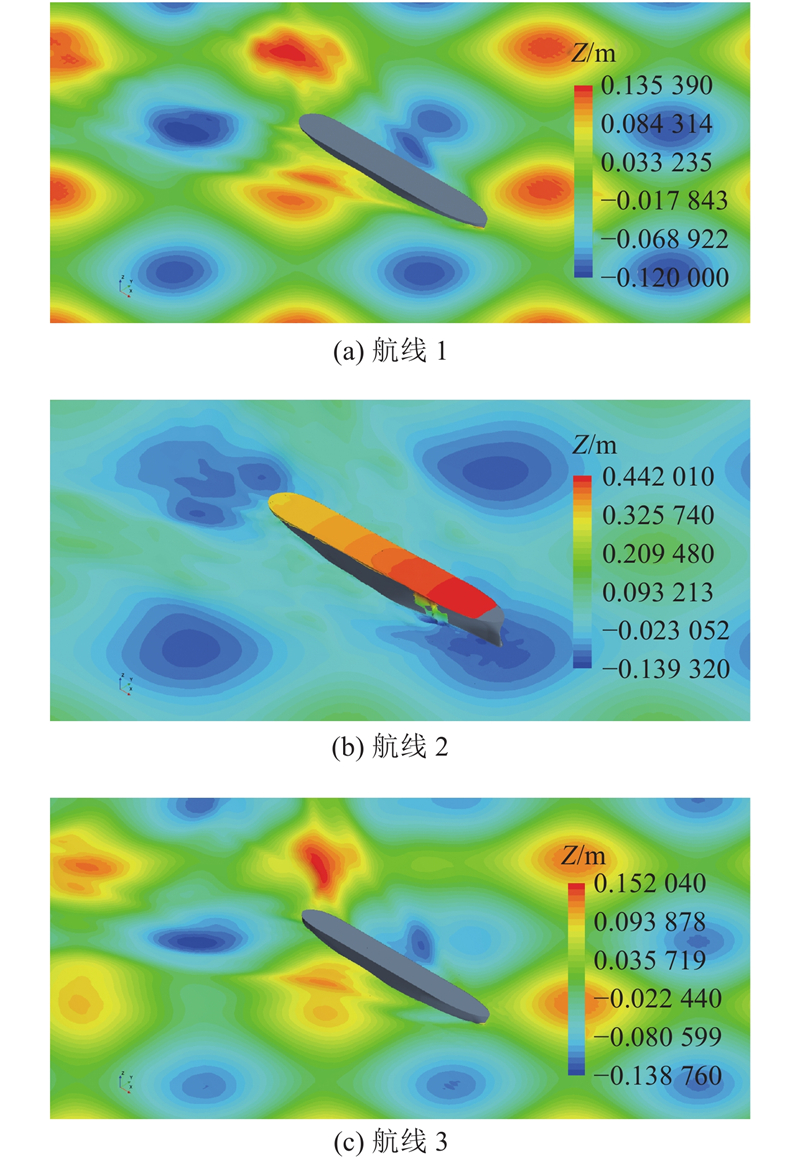
如图20所示为船舶航行于上述3种航线时的船体运动及甲板上浪现象的对比图，图中均选取了船体运动幅度最大或甲板上浪最严重的时刻. 可以看出，在航线1中船舶稳速直航，仅发生了轻微的横摇；在航线2中船舶发生了大幅纵向运动和甲板上浪；在航线3中船舶发生了大幅横摇运动. 因此，当船舶遭遇方形波浪时，最有利的航行方案为选择沿驻点线迎浪航行（航线1）并尽快驶离方形波浪区域.

（1）当方形波浪关于船舶航线对称时，两子波的遭遇频率相同，遭遇波浪呈现出规则波的单峰特征；当方形波浪关于船舶航向不对称时，两子波的遭遇频率有所差异，船舶遭遇波浪呈现出双色不规则特征.

（2）当船舶对称航行于方形波浪中时，可能产生大幅纵向运动，在船舶共振区域，垂荡响应幅值可能比在单向波中的大超过2倍，同时伴随着严重的甲板上浪现象；当船舶不对称航行于方形波浪中时，可能产生大幅横摇及纵向运动，其中横摇角最大可达16°.

（3）当船舶遭遇方形波浪时，最有利的安全航行方案为选择沿方形波浪场的驻点线迎浪航行（航线1）并尽快驶离方形波浪区域.

（4）本研究从数值计算角度探究船舶在方形波浪中的运动特性，尚未开展相应的水池模型试验. 按照所定义的波浪方向，仅考虑子波波长一样的工况，当考虑不同波长时，波浪叠加后方形波浪的波峰波谷与船舶的相互位置会发生改变，船舶的运动状态须进一步研究.