社会经济的发展带动城市地下空间的拓展,地下工程邻近既有地下管线的情况越来越常见. 在此背景下,存在很多邻近已建地下管线的隧道工程,其盾构掘进过程会造成周围地层变形,会进一步改变邻近管线周边土的应力应变场,导致管线发生破裂及泄露,威胁到管线的安全运营. 如何评价盾构开挖对邻近管线的影响已经成为目前地下工程领域的一大研究热点.
有很多学者就盾构开挖对邻近管线的影响进行深入研究. 分析方法主要分为3类. 第1类是实验模拟方法,Vorster 等[1-2]通过模型试验研究隧道施工对邻近埋地管道变形和力学特性的影响;王海涛等[3]基于某实际工程进行室内模型实验,对地铁隧道钻爆法施工对邻近埋地管道的影响开展研究;第2类是利用大型商业有限元软件来模拟盾构开挖对邻近管线的影响,此类模拟技术具有费用低、可以准确模拟施工过程的特点,在工程研究中得到广泛应用[4-7]. 第3类是理论解析法,理论解析主要是基于盾构开挖对既有邻近管线“施加”附加作用力,在附加作用力下管线发生相应的应力应变. 理论分析法相比于实验和有限元法更能定量判断管线变形是否满足规范所规定的变形范围,但现有的理论解析都是采用两阶段分析法:第1阶段分析邻近开挖在既有管线上所引起的附加应力或周围土体变形;第2阶段将得到的附加应力作用在隧道上,计算在相应的弹性地基上的变形响应. 对于第1阶段,Loganathan等[8]提出能够预测盾构隧道施工引起地层位移的三维计算公式,之后其因具有良好的计算精度而被广泛应用于二阶段法中;魏纲等[9]研究顶管开挖引起邻近管道隆起以及管道极限弯矩、理论弯矩的计算方法;刘晓强等[10]采用能量变分的方法研究隧道开挖对上覆既有管线的影响,该方法与工程实测以及离心机数据较吻合;基于单参数的Winker地基梁,Attewell等[11]利用Winkler模型模拟管-土之间的相互作用,张陈蓉等[12]利用改进Winkler地基模型,模拟管道接口对计算结果的非连续影响,得到管道位移和弯矩的解析解. Winkler地基模型由于计算简单且物理意义明确而被广泛应用,但该模型也存在明显缺陷,即地基模型无法考虑土体之间的剪切影响,而在地下管线的变形计算中,管线的变形刚度较小,此时忽略土体之间的剪切变形影响对管线变形计算影响较大. 为了考虑土体之间的剪切变形影响,已有不少学者考虑用双参数Pasternak弹性地基模型[13]来预测地下空间隧道管线的影响;Zhang等[14]基于两级时域算法得到邻近开挖对邻近桩基附加应力的影响,再将梁体简化成Euler-Bernoulli梁搁置在Pasternak地基模型上得到邻近开挖引起的桩基水平位移解析解;张恒等[15]利用Pasternak地基模型对盾构施工引起邻近管线变形进行解析分析,得到管线变形和内力解析方程;可文海等[16]改进Pasternak地基模型的参数计算方法,提高Pasternak地基模型的计算精度,计算所得数据与实测数据较吻合;林存刚等[17]利用Pasternak地基模型研究盾构开挖对地下非连续性管线的影响,得到非连续性管线变形及内力解析解;何小龙等[18]将管线简化成Euler-Bernoulli梁搁置在Pasternak地基模型上研究基坑开挖对邻近管线的影响,并与工程实测数据对比验证其理论的准确性. 为了更加精确地预测地下空间土与结构相互作用的内力和变形,Kerr[19]提出三参数Kerr地基模型;Zhang等[20]利用Kerr地基模型研究盾构开挖对邻近桩基的影响分析,并与Winkler地基模型进行对比,验证Kerr地基模型的优越性. 宗翔[21]将隧道简化成铁木辛柯梁搁置在Kerr地基模型上得到基坑开挖导致既有隧道变形的解析解. 张冬梅等[22]将隧道分别简化成Euler-Bernoulli梁和Timoshenko梁放在Kerr地基模型上,利用函数叠加法得到隧道纵向位移解析解,并对2种情况进行对比,说明考虑隧道剪切变形的合理性.
上述文献均说明盾构开挖会引起邻近管线的较大变形,然而盾构引起的邻近管线受力是三维空间的问题,已有文献考虑到土与结构的空间受力问题,Zhang等[23]将桩基简化成Pasternak地基模型并考虑桩土三维空间作用下盾构开挖对邻近桩基的影响作用,验证桩土三维空间作用更能精确地预测桩基变形. 本研究在前人基础上,考虑隧道与既有管线间夹角的影响,利用Loganathan公式得到管线轴线处土体自由位移场,将管线简化成Euler-Bernoulli梁搁置在Kerr地基模型上得到管线变形控制方程,提出剪切层弯矩的假设,利用差分法得到控制方程的解析解,在此基础上进一步考虑管线侧向土体影响,得到考虑管线侧向土体影响下盾构隧道引起上覆管线竖向变形的差分解. 将本研究差分解与已有工程案例及相关文献进行对比,验证本研究方法的正确性和准确性. 系统分析隧道开挖地层损失率、土体弹性模量、管线与隧道相对夹角的变化对管线竖向位移的影响,分析结果对于实际工程具有一定借鉴意义.
1. 自由位移场求解
1.1. 盾构开挖引起的土体自由位移场
1998年Loganathan等[8]提出的盾构开挖引起邻近土体自由位移场公式被广泛应用于工程实践,隧道开挖引起邻近土体自由位移场的竖向位移可以表示为
式中:R为隧道半径,H为隧道轴线深度,x为管线到隧道中心线的水平距离,z为距地表垂直距离,ε0为等效地层损失比,ν为土体泊松比.
1.2. 盾构开挖引起既有管线轴线位置的土体自由竖向位移
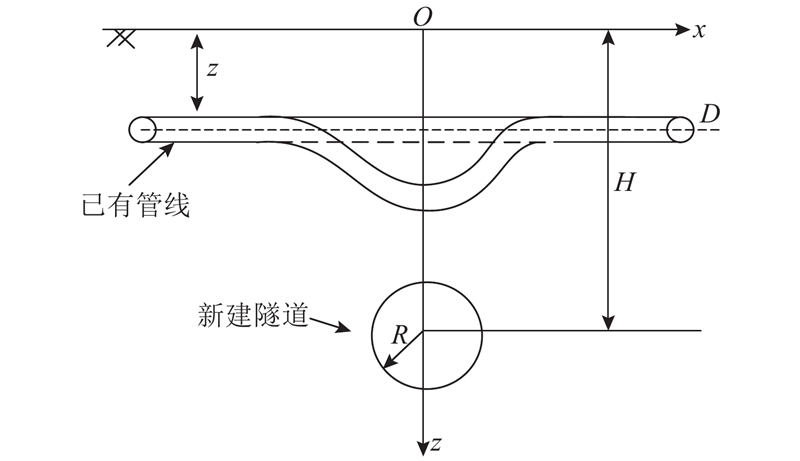
图 1
图 1 盾构隧道开挖对已有管线影响的简化模型
Fig.1 Simplified model for influence of shield tunneling on existing pipeline
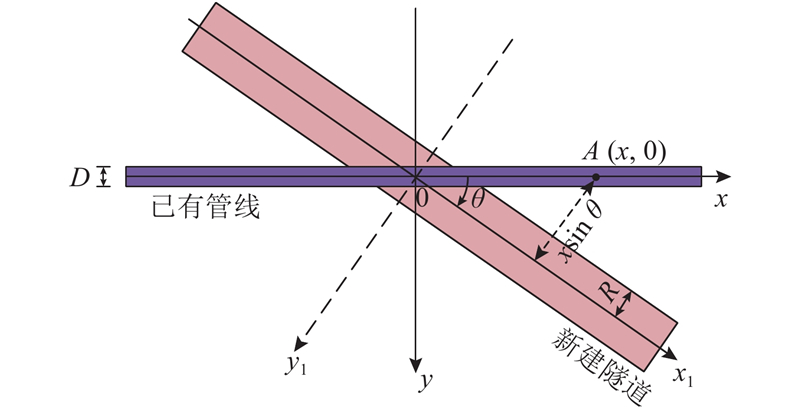
图 2
2. 理论分析
2.1. Kerr地基模型下不考虑管线侧向土体影响的简化计算方法
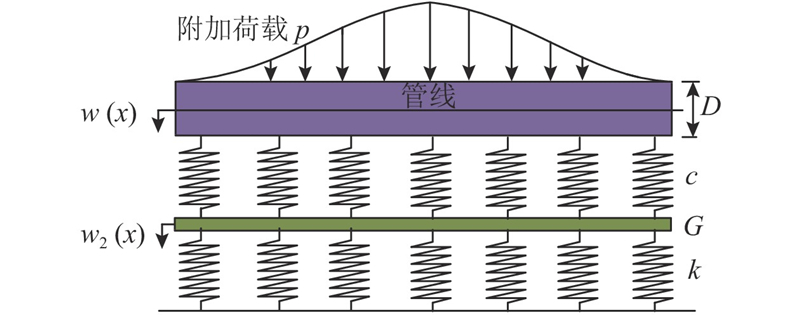
Kerr地基模型相比Pasternak地基模型增加了上层弹簧刚度c,更能准确预测地层变形,如图3所示. 基于Kerr地基模型,进行如下假设:1)假定土体为均匀、连续、各向同性的半无限空间弹性体,暂不考虑土体分层情况,隧道变形已经稳定;2)管线为一根直径为D、抗弯刚度为EI的纵向圆形截面Euler-Bernoulli梁,管线-地层相互作用通过Kerr地基模型考虑;3)管线与土体紧密接触,其变形和土体变形协调一致;4)已建管线轴线处土体自由位移场符合Loganathan公式(或修正后的Loganathan公式).
图 3
假设作用在管线上的荷载为p,在该荷载作用下管线竖向挠度为
式中:w1为上层弹簧的变形量,w2为剪切层变形量. 假设管线以及剪切层上侧的应力分别为
式中:k为下层弹簧刚度.
对于剪切层[13],有
式中:G为剪切层刚度.
通过式(2)、(4),可以得到
管线平衡方程为
将式(6)、(7)代入式(8),可以得到Kerr地基模型下不考虑管线侧向土体作用的控制方程:
利用差分法可以将式(9)差分为
式中:i=0,1,2
式中:l=L/n,L为管线水平向长度.
将式(11)~(16)代入式(10),可以得到
式中:W=c+k.
pi可以表示为
式中:
结合管线边界条件,得到剪切层竖向位移w2解析矩阵为
为了消去6个虚拟单元,可以根据实际两端边界条件进行简化,无限长管线两端受到基坑开挖的影响较小,可以将两端简化成2个自由端,这样可知管线自由端弯矩剪力均为0:
式中:MS为本研究假设的剪切层弯矩表达形式,MS0、MSn分别为管线两端剪切层的弯矩,M0、Mn分别为管线两端弯矩,Q0、Qn分别为管线两端剪力. 那么,K的表达式为
此时,通过式(19)即可以得到Kerr地基模型下不考虑管线侧向土体影响时剪切层变形w2(x)的差分解,利用式(7)即可以得到隧道开挖导致的邻近管线竖向位移w(x)的差分解.
2.2. Kerr地基模型下考虑管线侧向土体影响的简化计算方法
盾构隧道施工过程对邻近管线的影响是时空问题. 忽略对时间的考虑,考虑管线受力的三维空间问题. 隧道盾构过程引起的土体附加应力,一部分直接作用在管线上,一部分作用在管线地基上,管线侧向土体的变形与管线变形不一致,会导致侧向土体与管线存在相互作用. 基于文献[23]中Pasternak地基模型下考虑侧向土体作用下盾构开挖对邻近桩基水平向变形的情况,进一步针对Kerr地基模型下考虑侧向土体影响的管土相互作用机理进行讨论.
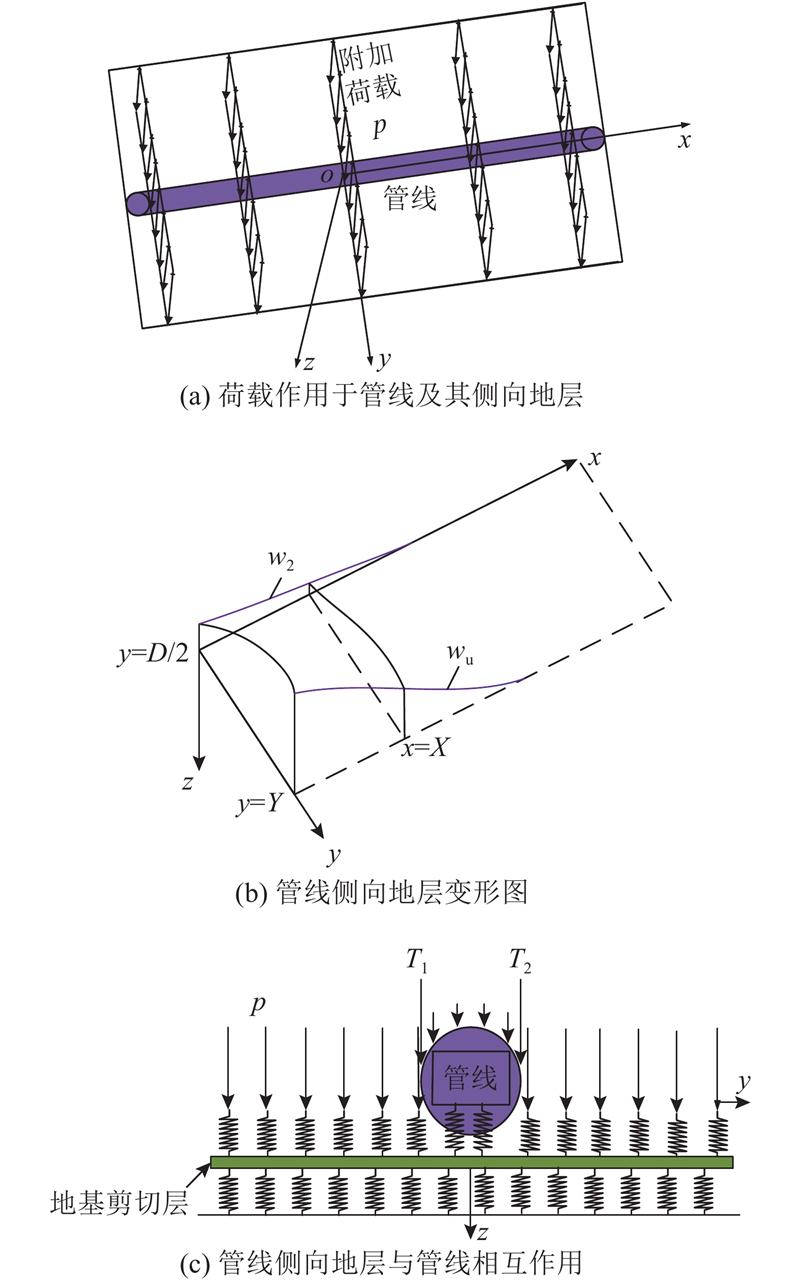
考虑侧向土体影响的管线变形与内力,进行以下假设:1)管线下方及侧向地层参数不变;2)侧向土体对管线作用力通过如图4所示剪切层提供的T1和T2,分别作用在管线两侧;3)管线与管线上侧剪切层位移变形一致;4)附加荷载p(x)以均布荷载形式作用在管线侧向土体上,且假设其宽度较大.
图 4
为了简化管线的侧向土体影响,将管线的三维侧向土体问题转化成二维问题进行考虑,对于任一与yoz平面平行的x=X平面,侧向地层剪切层平衡方程为
式中:
对于y≥D/2的情况,式(23)通解为
式中:χ1为通解系数.
若y=y0平面相当远处的地层剪切变形为wu,那么式(23)特解为wu,式(23)解为
利用边界条件:当y=D/2时,侧向地层剪切层与管线上侧剪切层变形wu相等,则
将式(26)代入式(25),得到
则在x=X平面内侧向地层对管线的作用力为
在y=y0平面求解相当远处的地层剪切变形wu,如图4(b)所示. 剪切层平衡方程为
通过以上分析,考虑管线侧向土体对管线的受荷平衡方程为
式中:
将式(7)、(27)、(31)代入式(30),整理得到
式中:wu由式(29)计算得出.
式(29)差分形式如下:
当管线两端均自由时,两端的边界条件满足:
由边界条件可知,当管线两端自由时,有
式中:
由式(35)可以得到剪切层位移wu的解析. 通过式(32)可以得到w2的解析,式(32)的差分形式可以表示为
式中:
根据管线两端的边界条件,可以消除−3、−2、−1、n+1、n+2、n+3节点,得到管线剪切层沉降位移:
式中:Kl为土体刚度矩阵,其值可以通过边界条件确定.
考虑到管线两端自由无约束作用,
此时,通过式(39)便可以得到Kerr地基模型下考虑管线侧向土体影响时剪切层变形w2(x)的差分解,利用式(7)即可以得到隧道开挖导致邻近管线竖向位移w(x)的差分解.
至此,2种情况下管线竖向位移w(x)都已经得到,根据Euler-Bernoulli梁理论可知,管线转角、弯矩、剪力分别如下:
2.3. Kerr地基模型参数确定
Kerr地基模型参数的确定对于计算结果的正确性起到关键作用,根据简化弹性空间法[24]可以得到
式中:ES为土体弹性模量,z为地基模型底部深度.
简化弹性空间法虽然操作简便,但由于引入许多假设,计算精度不高,故须调整各个参数取值来满足实测要求. 为了得到更精确的计算结果,现拟将参数c取值为c=nck(nc为下层弹簧调节系数),其他参数不变,本研究基于隧道开挖引起上覆管线的工况,利用有限元软件模拟的方法进一步确定nc的参考值. 采用的参数如下:R=3.0 m,H=20 m,z0=10 m,ε0=1%,ES=10 MPa,ν=0.33,D=3.0 m,EI=5×1010 kN·m,θ=90°.
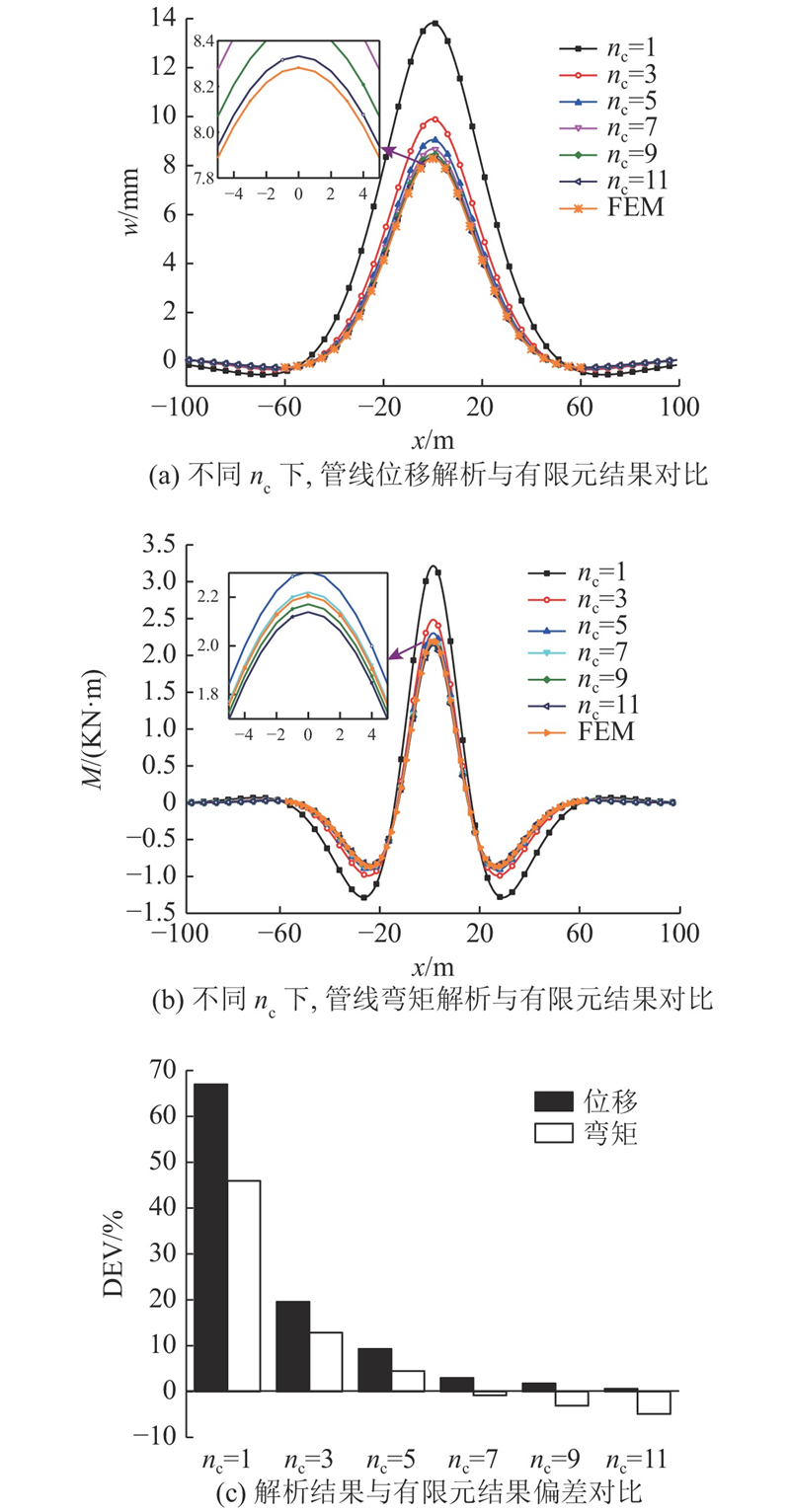
为了得到合理参数nc的取值,将上述工程概况下Kerr地基模型计算得到的管线位移和弯矩结果与有限元模拟结果进行对比,有限元模拟采用PLAXIS 3D,隧道及管线均采用板单元模拟. 考虑到管线和隧道相互垂直以及管线两端自由的情况,为了消除边界效应对案例的影响,模型尺寸为600 m×600 m×40 m. 由图5可知,随着nc的增大,管线位移会逐渐减小且趋于稳定值,但其弯矩有继续减小的趋势. 定义偏差DEV=(解析解数据−有限元数据)/有限元数据. 由图5(c)可以看出,对于管线最大位移来说,随着nc逐渐增大,解析解数据逐渐接近有限元数据,且有无限接近的趋势;对于管线的最大弯矩来说,随着nc逐渐增大,解析解数据值逐渐接近有限元值,但当nc>7时,其数据偏差又有增大趋势. 为了使本研究解析解管线位移偏差与弯矩偏差均能取得较小值,选择nc=7较适合本研究工况,此时管线位移偏差为2.98%,管线弯矩偏差为−0.82%.
图 5
图 5 本研究方法解析结果与有限元结果对比图
Fig.5 Comparison of analytical results of proposed method with finite element results
3. 算例验证
3.1. 工程实例
深圳地铁一期工程益田站至香蜜湖站区间隧道全长约为1540 m,采用2台土压平衡盾构机分别进行左右线隧道的施工. 隧道轴线埋深为12.0~15.0 m. 盾构机刀盘外径为6190 mm,盾壳外径为6140 mm. 隧道外径为6000 mm,隧道内径为5500 mm. 盾构在里程RK8+750处近距离垂直下穿一条大管径电缆管线,管线材质为混凝土. 管线外径为3.0 m,壁厚为0.12 m,埋深为7.2 m[25],本工程所取参数如表1所示. 吴为义[25]基于本工程概况建立FLAC 3D数值仿真模拟,与已有弹性地基梁理论计算结果比较,FLAC 3D计算结果更加接近实测数据;张恒等[15]等对本工程进行进一步研究,结果表明考虑侧向土体作用的Pasternak地基模型比不考虑侧向土体的Pasternak地基模型更加接近实测数据,本研究在张恒等[15]的基础上推导将管线放在Kerr地基模型上的变形响应.
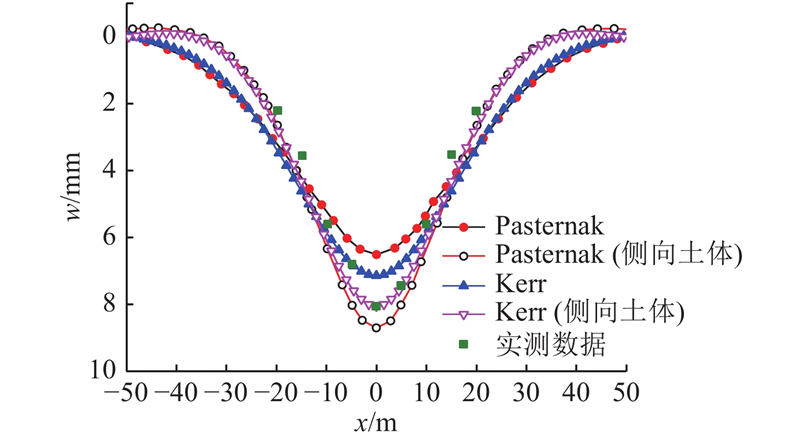
如图6所示,本研究所提出的Kerr地基模型计算得到的结果比张恒等[15]基于Pasternak地基模型得到的计算结果更加符合工程实际,考虑侧向土体作用的Kerr地基模型也比Pasternak地基模型更加精准. 对比文献[15]可知,Pasternak地基模型和Kerr地基模型明显优于Winkler地基模型,若以最大沉降值定义:偏差=(解析解数据−实测值)/实测值,则Kerr地基模型上的管线位移偏差为−11.5%,优于Pasternak地基模型上管线位移偏差(−19.5%);在考虑侧向土体作用时,Kerr地基模型上的管线位移偏差为0.2%,明显优于Pasternak地基模型上管线位移偏差(7.5%). 因此,Kerr地基模型相比于Pasternak地基模型更能准确反映管土之间的相互作用,而考虑侧向土体的Kerr地基模型更加精确,尤其是在计算隧道轴线附近的管线位移时,考虑管线侧向土体影响的计算结果更接近实测数据.
表 1 深圳地铁工程实例计算参数
Tab.1
| R/m | H/m | z/m | ε0/% | ES/MPa | v | D/m | EI/(kN·m2) |
| 3.0 | 14.4 | 8.7 | 0.84 | 8.2 | 0.3 | 3.0 | 5.87×107 |
图 6
图 6 管线位移计算及实测数据对比
Fig.6 Comparison of calculated and measured results of deformation of pipeline
3.2. 离心机试验
表 2 离心机试验参数
Tab.2
| R/m | H/m | z/m | ε0/% | ES/MPa | v | D/m | EI/(kN·m2) |
| 2.25 | 11.25 | 4.165 | 2 | 19.52 | 0.23 | 1.19 | 3.363×106 |
如图7所示为采用不同的计算方法得到的管线竖向位移曲线及离心机模拟数据. 可以看出,考虑侧向土体位移的Kerr地基模型更接近于离心机模拟数据. 对于邻近开挖引起管线变形响应来说,控制管线的最大变形是至关重要的,若以最大沉降定义:偏差=(解析解数据−离心机数据)/离心机数据,则Kerr地基模型的管线位移偏差为−13.3%,刘晓强方法计算得到的管线位移偏差为8.3%. 在考虑侧向土体的位移时,Kerr地基模型精度明显增强,管线位移偏差仅为0.12%,最大值基本上完全吻合. 在考虑离心机模拟的其他数据点时,考虑侧向土体影响的Kerr地基模型计算得到的管线位移结果和离心机数据基本一致,进一步说明本研究方法的可靠性,也进一步说明,在分析管-土相互作用时,不能忽略侧向土体的作用.
图 7
图 7 管线位移计算及离心机数据对比曲线
Fig.7 Comparison of calculated and centrifuge model test results of deformation of pipeline
4. 参数分析
为了研究地层损失率、土体弹性模量、管线与隧道夹角等参数对计算结果的影响,以深圳地铁一期工程益田站至香蜜湖站区间隧道工程的基本工况为基本参数. 采用本研究提出的考虑侧向土体三维作用效应的方法进行计算,在研究某一参数对管-土相互作用的影响时,其余参数不变.
4.1. 不同地层损失率对管道受力变形的影响
为了研究不同地层损失率对管道受力变形的影响,考虑到实际工况中隧道开挖引起的地层损失率普遍为1%~2%,选取几组与实际工况接近的地层损失率数据,分别取地层损失率ε0=0.8%、1.2%、1.6%、2.0%、2.4%进行参数分析.
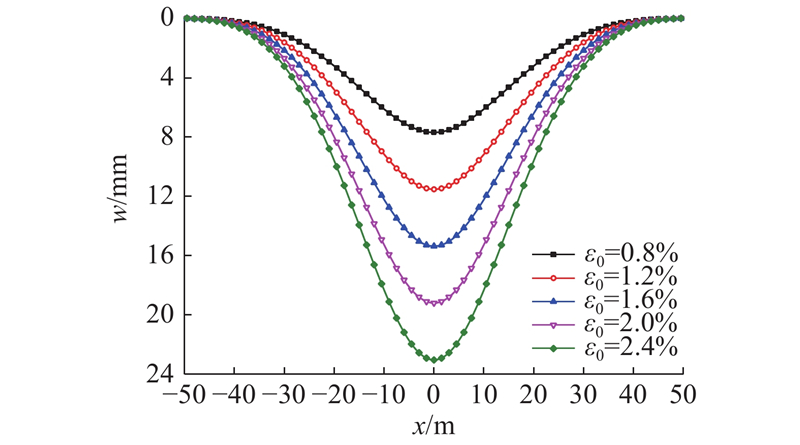
如图8所示为管线与隧道地层损失率情况下的隧道竖向位移图. 可以看出,地层损失率越大,管线的竖向位移也会随之增大,且增长速度较快,地层损失率每增加0.4%,管线的竖向位移均会增加20%以上,说明地层损失率是管线变形的控制性因素,在实际工程中要尽量控制地层损失率以减小已有管线的变形.
图 8
图 8 不同地层损失率下管线竖向位移
Fig.8 Pipeline vertical deformation with different volume losses ratios
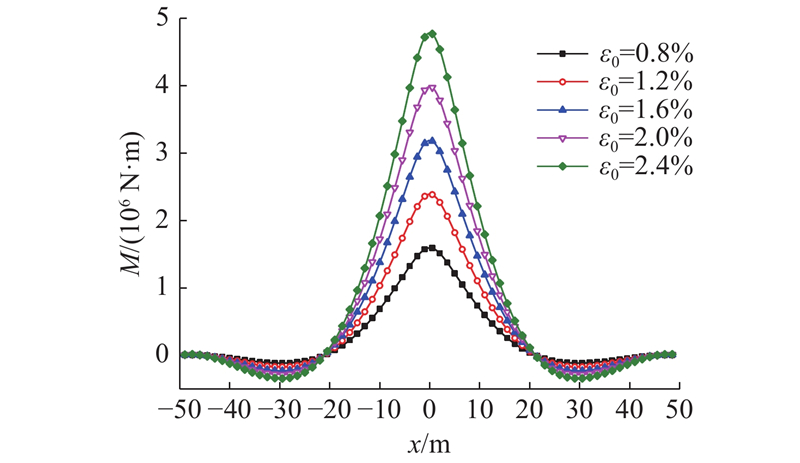
如图9所示为管线在不同的地层损失率下隧道开挖引起的管线弯矩变化曲线图. 可以看出,随着地层损失率的增大,管线的弯矩也会增大,且增大的速率较快,地层损失率每增加0.4%,管线的弯矩均会增加25%以上,说明隧道开挖的地层损失率对已有管线弯矩变化为敏感因素,在实际工程中,要尽可能减小隧道开挖造成的地层损失率,保证隧道结构受到的弯矩在合理范围内.
图 9
4.2. 不同土体弹性模量对管道受力变形的影响
为了研究不同土体弹性模量对管道受力变形的影响,分别取土体弹性模量ES=1.2、5.2、10.2、20.2、40.2 MPa进行分析.
如图10所示为不同土体弹性模量情况下的隧道竖向位移图. 可以看出,土体弹性模量越大,管线的竖向位移也会随之增大,这是由于土体弹性模量的增大,土体的弹簧系数c、k以及剪切系数G也会随之增大,管-土相互作用增强,但是随着土体弹性模量的继续增大,管线竖向位移增速放缓,说明管线变形会随着土体弹性模量的增大而增大,但其增速逐渐放缓.
如图11所示为不同土体弹性模量情况下的隧道弯矩图. 可以看出,随着地层损失率的增大,管线的弯矩也会增大,且增大的速率较快,说明土体弹性模量的变化对已有管线弯矩影响较大,在实际工程中,要尽可能选择在土体弹性模量较小的土层进行盾构开挖,保证隧道结构受到的弯矩在合理范围内.
图 10
图 10 不同土体弹性模型下管线竖向位移
Fig.10 Pipeline vertical deformation in different soil elastic modulus
图 11
4.3. 不同相交角度对管道受力变形的影响
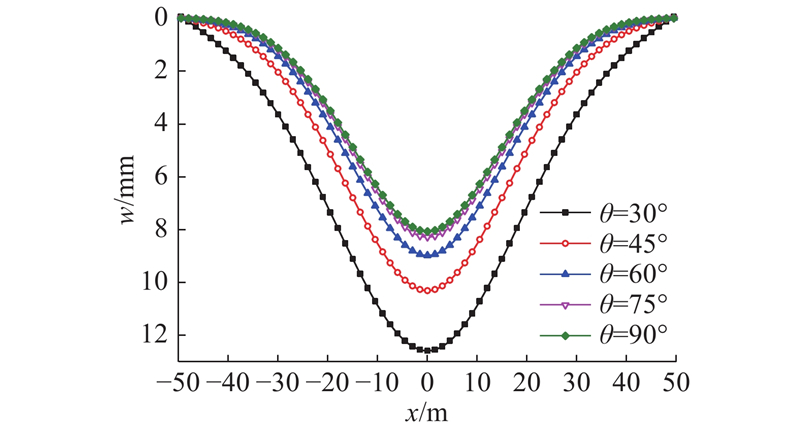
为了研究管线与隧道夹角变化对管道受力变形的影响,分别取夹角θ=90º、75º、60º、45º、30º进行分析.
如图12所示为管线与隧道在不同夹角情况下的隧道竖向位移. 可以看出,管线与隧道的夹角从30º增大到90º,隧道的竖向位移逐渐减小,且减小速率逐渐放缓,因为在隧道开挖过程中,隧道轴线正上方的地层沉降较大,而随着夹角的增大,管线与隧道相对位置由“重合”变成垂直,此时管线受到地层沉降的影响越来越小.
图 12
图 12 不同相交角度下管线竖向位移
Fig.12 Pipeline vertical deformation in different cross angles
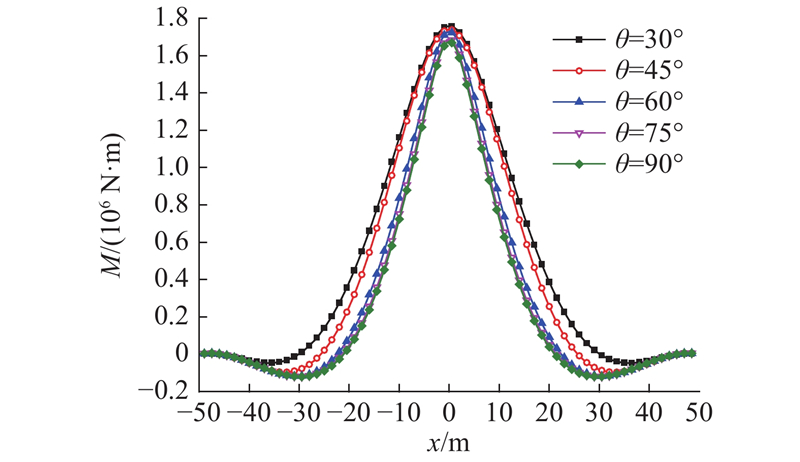
如图13所示为管线与隧道在不同夹角情况下的隧道弯矩. 可以看出,管线受到的最大弯矩随着夹角的增大而逐渐减小,这是由于管线与隧道的相对位置从平行逐渐变成垂直,管线的受力从“均布荷载”逐渐转换成“集中荷载”,但是这种效应对管线弯矩变化的影响较小.
图 13
5. 结 论
(1)将管线简化成Euler-Bernoulli梁搁置在三参数Kerr地基模型上,提出剪切层弯矩计算的假设,随后考虑管线侧向土体影响,采用有限差分法以及管线两端的边界条件得到管线纵向变形半解析解.
(2)在深圳地铁一号线案例中,本研究方法计算得到的最大沉降与实测最大沉降仅偏差0.2%,明显优于Pasternak地基模型下管线最大沉降偏差(7.5%);在Voster离心机试验中,本研究方法计算得到的最大位移与离心机最大位移仅偏差0.12%,明显优于刘晓强方法计算得到的管线最大位移偏差(8.3%),2个案例均说明本研究方法更具有优越性.
(3)隧道开挖对既有管线纵向受力变形不同影响因素的研究结果表明,随着地层损失率以及土体弹性模量的增大,隧道开挖均会引起上覆管线竖向位移和弯矩的增大;管线与隧道夹角的增大会引起上覆管线位移和弯矩的减小.
提出基于Kerr地基模型考虑侧向土体影响下盾构隧道引起上覆管线变形响应简化计算解析. 但是在简化计算中未考虑管土之间非线性作用的情况,也未考虑到隧道和管线之间土体为非均质土体的情况,这是今后须关注的方向.
参考文献
黄土地层盾构隧道施工的掘进试验研究
[J].DOI:10.3969/j.issn.1000-6915.2013.09.002 [本文引用: 1]
Laboratory test on shield tunneling in loss strata
[J].DOI:10.3969/j.issn.1000-6915.2013.09.002 [本文引用: 1]
地铁隧道钻爆法施工对邻近埋地管道影响的模型试验研究
[J].
Model test study on the influence of subway tunnel drilling and blasting method on adjacent buried pipeline
[J].
暗挖隧道施工对平行地下管线性状影响研究
[J].
Influence of tunneling construction on buried pipelines paralleled with running tunnel
[J].
盾构法施工引起邻近地下管线位移分析
[J].DOI:10.3321/j.issn:1000-8993.2005.09.014
Analysis of the displacements of underground pipelines caused by shield construction
[J].DOI:10.3321/j.issn:1000-8993.2005.09.014
地铁区间隧道施工对近邻管线影响的三维数值模拟
[J].
3D numerical simulation one ffect of tunnel construction on adjacent pipeline
[J].
过街隧道施工对地下影响的三维数值模拟
[J].
3D numerical simulation of effect of underground urban street-passage tunnel construction on adjacent pipeline
[J].
Analytical prediction for tunneling-induced ground movements in clays
[J].DOI:10.1061/(ASCE)1090-0241(1998)124:9(846) [本文引用: 2]
顶管施工对邻近地下管线的影响预测分析
[J].DOI:10.3969/j.issn.1000-7598.2009.03.045 [本文引用: 1]
Prediction for response of adjacent pipelines induced by pipe jacking construction
[J].DOI:10.3969/j.issn.1000-7598.2009.03.045 [本文引用: 1]
隧道穿越引起地下管线竖向位移的能量变分分析方法
[J].
Energy variational solution for settlement of buried pipeline induced by tunneling
[J].
隧道开挖对邻近非连续接口地埋管线的影响分析
[J].
Responses of adjacent underground jointed pipelines induced by tunneling
[J].
Time-domain analyses for pile deformation induced by adjacent excavation considering influences of viscoelastic mechanism
[J].DOI:10.1016/j.tust.2018.12.020 [本文引用: 1]
盾构隧道开挖引起既有管线的竖向变形
[J].
The vertical deformation of the pipeline caused by the shield tunnel excavation
[J].
盾构隧道下穿管道施工引起的管-土相互作用研究
[J].
Research on upper pipeline-soil interaction induced by shield tunneling
[J].
基于Pasternak地基的盾构隧道开挖非连续地下管线的挠曲
[J].
Evaluation method for effect of tunneling on underground jointed pipelines
[J].
考虑管土分离的基坑开挖引起邻近地下管线位移分析
[J].
Analysis of pipeline displacement induced by adjoining foundation pit excavation considering pipeline-soil separation
[J].
A study of a new foundation model
[J].DOI:10.1007/BF01174308 [本文引用: 1]
Analytical solution for tunnel-soil-pile interaction mechanics based on Kerr foundation model
[J].DOI:10.1007/s12205-019-0791-x [本文引用: 1]
基坑开挖卸载引起下卧已建隧道的纵向变形研究
[J].
Study of longitudinal deformation of existing tunnel due to above excavation unloading
[J].
盾构隧道掘进引起上方已建隧道的纵向变形研究
[J].
Longitudinal deformation of existing tunnel due to underlying shield tunneling
[J].
Simplified solution for tunnel-soil-pile interaction in Pasternak’s foundation model
[J].