当静电场作用在两相不相溶的液体时，由于两相流体间电特性的差异，悬浮在连续相中的离散液滴在界面处因产生切向与法向应力而发生变形^[1-3]. 液滴的这种静电变形的现象在很多工程场合均有涉及，如乳化液的电破乳、液液电萃取、两相不相溶液体的电分散、微流控技术中的电润湿（Electrowetting）等等^[4-9]. 因此，有关液滴电变形特性的研究一直是电流体力学领域中的主要研究点之一. 自Taylor等^[1-2]较早开展了液滴变形的理论研究并分别建立了液滴理想介电模型和漏电介质模型以来，许多学者在上述理论基础上采用各种方法对液滴变形进行了更深入的理论及实验研究. 其中在理论模拟及数值计算方面，Sherwood^[10]采用边界积分法求解拉普拉斯方程及N-S方程获得电场分布及流场分布，并分析了电参数对液滴变形的影响. Basaran等^[11]采用Bernoulli方程与液滴内部速度势及液滴外部电势的Laplace方程数值求解，对导电液滴的非线性振荡及破碎行为进行了研究. Baygents等^[12]提出适用于液滴大变形的电动模型（electrokinetic model）. 危卫等^[13]将电场力作为源项添加进N-S方程中，并采用流体体积模型（volume of fluid model，VOF）方法，对外加均匀电场与非均匀电场时中性漏电液滴和带电液滴的变形行为进行分析. 近些年来，分子动力学（molecular dynamics simulation，MD）、耗散粒子动力学（dissipative particle dynamics simulation，DPD）及光滑粒子动力学（smoothed particle hydrodynamics，SPH）等方法在液滴动力学特性的模拟中得到较多应用，在某些情况下取得较好效果^[14-16]，如Wang等^[14]采用分子动力学方法模拟电场作用下2个相近的导电纳米液滴的聚结和反弹特性，结果表明两液滴聚结或反弹取决于临界场强及临界锥角. 白莉等^[16-17]分别采用光滑粒子动力学及耗散粒子动力学方法对电场中液滴的变形进行模拟，揭示了液滴的变形及振荡特性. 此外，陈庆国等^[18-26]对液滴变形的模拟也有所涉及. 上述研究所采用的方法不同，在适用范围、计算过程的复杂性及与实际情况的相符性上各有千秋. 如O'Konski^[2]根据理想介电模型建立的液滴变形表达式只能预测液滴的扁长形（prolate）变形. Taylor^[1]的漏电介模型能对液滴扁长及扁平形（oblate）变形进行预测，但其变形度总是随 $a{E^2}$（a为液滴半径，E为场强）线性变化. Ajayi等^{[3, 10-12]}在液滴大变形模拟方面取得较大进展，但有些模型复杂，计算量大. MD、DPD、SPH等方法为无网格法，可避免液滴极大变形时网格扭曲造成的精度破坏问题，非常适合模拟液滴的变形及聚结，但理论基础目前尚不完善，且计算量极大.

本研究基于液滴单元变形的思路，从单元变形过程中的守恒方程出发，建立液滴的电变形数值计算模型. 该模型虽然仅适合计算液滴小变形过程，但是不用求解复杂的N-S方程及麦克斯韦方程，且模型的力学概念明晰、计算及编程简单，可用于对液滴扁长形变形、扁平形变形及液滴聚结过程的模拟.

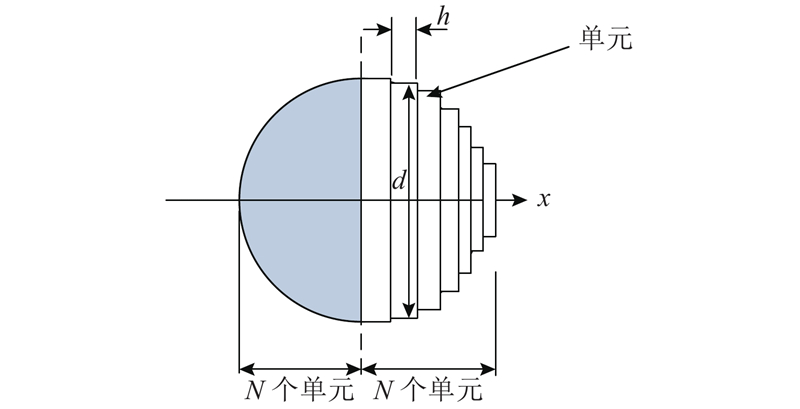
当电场作用于液液系统时，连续相中的离散液滴发生极化，在液滴表面产生极化电荷. 在极化电荷作用下，液滴发生变形，沿电场方向被拉长，形成椭球形状. 为了描述液滴的变形，现考虑单个离散液滴，如图1所示. 将液滴沿x轴方向用2N+1个x轴节点将液滴划分为2N个微小单元（液滴左右各N个单元），每个微小单元近似看为长度为h，直径为d的薄圆柱体. 这样，一个球形液滴就用一个个彼此相连的圆柱体单元来近似.

假定电场方向为水平方向（x轴方向），液滴沿水平方向被拉长，位于液滴左、右半球的单元分别产生向左、向右的水平速度，使得每个圆柱体单元的直径逐渐变小，长度逐渐变长. 对每个单元，变形前后可建立水平方向的动量方程

(1) $\frac{{{{\rm{d}}( {mv} )}}}{{{\rm{d}}t}} = {F_1} + {F_2 } + {F_3} + {F_4}.$

式中：m为单元质量，t为时间，v为因单元变形所产生的水平速度， ${F_1}$、 ${F_2 }$、 ${F_3}$、 ${F_4}$分别为单元变形过程中所受静电力、表面张力、压力及阻力在水平方向的投影.

式（1）的关键是方程右边单元所受各种力的模化. 为了使分析过程简单，做如下假设。1）在变形过程中，每个单元所携带的极化电荷保持不变（即不考虑液滴变形后表面电荷的重新分布）. 在液滴变形不是太大时，假设1）可以接受. 2）单元断面上水平速度均匀分布. 在上述假设基础上，力的模化处理如下. ${F_1}$包括单元所受外电场力及单元之间的静电相互作用力，即

(2) ${F_1} = {F_{\rm{E}}} + {F_{\rm{K}}}.$

式中： ${F_{\rm{E}}}$为单元所受外电场力， ${F_{\rm{K}}}$为单元之间的静电相互作用力. 假如单元所带电荷为q，单元所受外电场力可表达为

(3) ${F_{\rm{E}}} = qE.$

式中： $E$为电场强度； $q$为单元所带电荷，可由液滴表面电荷密度确定：对球形介质施加电场，介质表面产生极化电荷，极化电荷密度可表达为^[1-2]

(4) ${\sigma _{\rm{q}}} = 3{\varepsilon _0}\frac{{{\varepsilon _{{\rm{in}}}} - {\varepsilon _{{\rm{out}}}}}}{{{\varepsilon _{{\rm{in}}}} + 2{\varepsilon _{{\rm{out}}}}}}E\cos \theta .$

式中： ${\sigma _{\rm{q}}}$为电荷密度， ${\varepsilon _0}$为真空介电常数， ${\varepsilon _{{\rm{in}}}}$、 ${\varepsilon _{{\rm{out}}}}$分别为离散滴和周围连续相的相对介电常数， $\theta $为液滴表面法线方向和外电场方向的夹角. 由式（4）可确定各单元表面电荷密度. 如图1所示，假定用每个单元右端面的坐标代替单元位置，则单元 ${{j}}$所处的 $\theta $角可表达为

(5) $\cos \;{\theta _j} = \frac{{{x_j} - {x_0}}}{R}$

式中：R为球形液滴半径， ${x_j}$为单元 $j$的水平坐标， ${{{x}}_0}$为球心水平坐标. 由式（4）、（5）可确定每个单元的电荷密度. 由式（4）可知，液滴左右两面电荷符号相反. 由于假设液滴单元电荷在变形中保持不变，每个单元所带电荷量可表达为

(6) ${q_j} = {\sigma _{qj}}\frac{ {\text{π}} }{4}{d_j}^2{h_j}$

式中： ${d_j}$为圆柱单元直径， ${h_j}$为单元长度.

单元之间的静电相互作用力可表达为

(7) ${F_{\rm{k}}} = \sum\limits_{i \ne j}^N {\frac{{{q_i}{q_j}}}{{4{\text{π}} {\varepsilon _0}{\varepsilon _{{\rm{out}}}}{r_{i,j}}^2}}} $

式中： ${r_{i,j}}$为 $i$单元与 $j$单元之间的距离. 如图2所示为单元之间关系示意. 图中， ${F_{\rm{k}}}$的水平分力 ${F_{{\rm{k}}j}}$可表达为

(8) $ \begin{split} {F_{{\rm{k}}j}} =& \displaystyle\sum\limits_{i \ne j}^N {\dfrac{{{q_i}{q_j}}}{{4\text{π} {\varepsilon _0}{\varepsilon _{{\rm{out}}}}{r_{i,j}}^2}}} {\rm{cos}} \beta = \\ &\displaystyle\sum\limits_{i \ne j}^N {\frac{{{q_i}{q_j}}}{{4\text{π} {\varepsilon _0}{\varepsilon _{{\rm{out}}}}{x_m}{{_{i,j}}^2}}}} \dfrac{\dfrac{{{d_i} - {d_j}}}{2}}{{\sqrt {{{\left( {{x_{mi}} - {x_{mj}}} \right)}^2} + {{\left( {\dfrac{{{d_i} - {d_j}}}{2}} \right)}^2}} }}. \end{split} $

式中： ${x_{{m_{i,j}}}}$为单元 $i$与单元 $j$的中心点水平间距， ${x_m}$为单元中心水平坐标， $\;\beta $为单元 $i$表面中心与单元 $j$表面中心的连线与水平方向夹角. 由式（4）可知，液滴左、右两部分电荷极性相反，因此液滴右半球单元与左半球单元之间的相互作用力为吸引力.由图2还可看出，单元 $j$所受界面张力在水平方向投影 ${F_2 }$可近似表达为

(9) $ \begin{split} {F_2 }_j =& \sigma \text{π} \left( {{d_{j + 1}} - {d_j}} \right) \cos \alpha \approx \\ & \sigma \text{π} \left( {{d_{j + 1}} - {d_j}} \right)\dfrac{{{h_j}}}{{\sqrt {{h_j}^2 + {{\left( {\dfrac{{{d_j} - {d_{j + 1}}}}{2}} \right)}^2}} }}. \end{split} $

式中： $\sigma $为液滴与连续相间的界面张力系数， $\alpha $为液面切线与水平方向夹角. 式（8）的界面张力为负，与电场力方向相反. 用 $ p$表示压强. 假定液滴外压强为0，则单元所受水平方向压力可表达为

(10) ${F_{{3_j}}} = \left( {{p_{j - 1}} - {p_{j + 1}}} \right)\frac{\text{π} }{4}{d_j}^2 + {p_j}\frac{\text{π} }{4}\left( {{d_j}^2 - {d_{j + 1}}^2} \right).$

${F_4}$包括：1）单元圆柱界面所受摩擦阻力 ${F_\tau } $，2）单元之间直径变化所引起的局部阻力 ${F_{{\xi}} }$.

(11) ${F_4} = {F_\tau } + {F_\xi }.$

其中

(12) ${F_\tau } = \tau \text{π} {d_j}{h_j}.$

式中： $\tau $为界面摩擦应力. $\tau $可近似采用直径为 ${d_j}$的圆管内层流时壁面摩擦应力计算. 对于圆管流动，壁面摩擦应力为

(13) $\tau = \lambda \frac{{{\rho _{{\rm{in}}}}{v_j}^2}}{8}.$

式中： $\lambda $为沿程阻力系数， ${\;\rho _{\rm{in}}}$为离散液滴密度， ${v_j} $为流速. 对于层流

(14) $ \begin{array}{l} \lambda = \dfrac{{64}}{{{{Re}} }}.\\ {{Re}} = \dfrac{{{\rho _{{\rm{in}}}}{v_j}{d_j}}}{{{\mu _{{\rm{in}}}}}}. \end{array}$

式中： ${{Re}} $为雷诺数， ${\mu _{\rm{in}}}$为离散液滴动力黏度.

因单元直径变化所引起的局部压强损失为

(15) $ \begin{array}{l}\varDelta {p_j} = \xi \dfrac{1}{2}{\rho _{{\rm{in}}}}{v_{j + 1}}^2. \end{array}$

其中

$\xi = 0.5\left( {1 - \dfrac{{{A_{j + 1}}}}{{{A_j}}}} \right) = 0.5\left( {1 - \dfrac{{{d_{j + 1}}^2}}{{{d_j}^2}}} \right).$

式中： $\xi $为局部阻力系数， ${A_{j + 1}}$、 ${A_j}$分别为 $j + 1$和 $j$单元的断面面积. 式（14）中局部损失的压强是局部阻力作用的结果，故局部阻力为

(16) ${F_\xi } = \varDelta {p_j}\frac{\text{π} }{4}{d_j}^2.$

由式（10）、（11）、（15）可确定单元阻力 ${F_4}$，阻力方向与单元运动方向相反.

在单元变形过程中，由于产生了纵向（水平）速度，在不同时刻，单元的压强会产生变化. 由式（1）求得单元新时刻的速度后，单元新时刻的压强可由伯努利方程求得

(17) ${p_j}^{t + {\rm{d}}t} = {p_j}^t + \frac{1}{2}{\rho _{{\rm{in}}}}\left( {{v_j}^t - {v_j}^{t + {\rm{d}}t}} \right).$

式中：上标 $t + {\rm{d}}t$、 $t$分别代表新时刻和旧时刻值. 由式（1）可求得单元不同时刻的速度. 由单元速度可求得单元端面位置及单元长度的变化

(18) ${\rm{d}}{h_j} = {v_j}{\rm{d}}t.$

(19) ${x_j}^{t + {\rm{d}}t} = {x_j}^t + {\rm{d}}{h_j}.$

根据变形过程中质量守恒，可求得新时刻单元的直径

(20) ${d_j}^{t + {\rm{d}}t} = {d_j}^t\sqrt {\frac{{{h_j}^t}}{{{h_j}^{t + {\rm{d}}t}}}} .$

由单元的端面位置及直径，可确定不同时刻液滴的形状. 各单元的变形不是彼此孤立的，相同时刻，各单元之间的速度还应满足连续性方程，故

(21) ${v_{j + 1}} = {v_j}{\left( {\frac{{{d_j}}}{{{d_{j + 1}}}}} \right)^2}.$

各个单元新时刻的参数求得后，通过式（20），对单元速度进行更新及修正，将各单元的变形紧密联系起来.

当电场作用于液液两相系统时，两相邻离散液滴产生聚结现象^[27-28]. 液滴的电聚结可用于乳化液的破乳. 产生电聚结主要原因有：1）离散液滴的电变形，即液滴沿电场方向被拉长，使得2个临近的液滴容易接触而聚结；2）电偶聚结，即由于两相临液滴在相临一侧的电荷极性相反，相邻2个液滴形成电偶极子，在电场作用下因相互吸引而相向运动直至发生聚结^[28-29]. 本文数值模型也可用于2个临近液滴的电聚结过程模拟.

计算中需要考虑液滴的变形及两液滴因相互吸引而产生的相向运动. 液滴的变形可采用前文所述方法计算，对于电偶聚结所引起的两液滴相互吸引运动，可用液滴运动方程求解，并将求解的液滴位移叠加在液滴变形计算的每个单元的位移中即可. 如不考虑液滴的重力、浮力（液滴为水平运动）及视质量力，对于相近两液滴中的任一液滴，可建立简单的运动方程

(22) $m\frac{{{\rm{d}}{\rm{V}}}}{{{\rm{d}}t}} = {F_{{\rm{dd}}}} + {F_{{\rm{qe}}}},$

(23) $\frac{{{\rm{d}}s}}{{{\rm{d}}t}} = V.$

式中：V为液滴因静电吸引而产生的运动速度， ${F_{{\rm{dd}}}}$为液滴运动所受阻力， ${F_{{\rm{qe}}}}$为因电偶聚而产生的静电吸引力， $s$为液滴位移.

对电偶聚结的静电吸引力，Davis等^{[28, 30]}给出几个表达式. 这里采用Pedersen^[30]的偶极模型计算. 假如2个液滴中心水平坐标相同，则静电吸引力可表达为

(24) ${F_{{\rm{rad}}}} = \frac{{24\text{π} {\varepsilon _0}{\varepsilon _{{\rm{out}}}}{R_1}^3{R_2}^3{E^2}}}{{{d_{12}}^4}}.$

式中： ${R_1}$、 ${R_2}$分别为2个临近液滴的半径， ${d_{12}}$为2个临近液滴的中心间距.

液滴所受阻力用斯托克斯阻力公式计算，但要考虑液滴变形为椭球而给予修正，修正的阻力可表达为^[31]

(25) ${F_{{\rm{dd}}}} = 6\text{π} {\mu _{{\rm{out}}}}V{R_1}{\left( {1 - {e^2}} \right)^{1/6}}.$

式中：e为液滴因变形而产生的离心率，表达为^[31-32]：

(26) $e = \sqrt {1 - \frac{{{b^2}}}{{{a^2}}}} .$

式中： $b$、 $a$分别为液滴变形后的短半径和长半径. 采用相同的时间步长，对式（1）及（21）、（22）同时进行数值求解. 在每个时间步，将液滴变形运动及因吸引而产生的平动进行叠加，即式（22）所计算位移与式（18）的单元变形位移，获得不同时刻两相邻液滴的位置及形状.

本文采用有限差分法求解数值模型. 对于单液滴变形，只需求解单元变形方程，即式（1）~（20）；对于液滴聚结模拟，2个临近液滴均需要划分单元，2个液滴划分的单元数相同，须同时求解单元变形及液滴偶极吸引带来的平动，即式（1）~（25）. 在每个时间步内，液滴偶极吸引运动所需的 $e$，可由当前时间步的液滴变形计算结果提供，而每个时间步计算的吸引运动的平动位移要叠加在液滴变形的每个单元位移中，这样就可实现2个液滴聚结过程模拟. 需要指出的是，由于液滴表面电荷密度分布不均，且接近液滴两端处的单元直径变化剧烈，单元长度不是等距分布，从液滴中心到两端，单元长度按一定等比缩减，以保证每个单元所携带电荷大致相当、并使得每个单元均具有不大的离散误差.

求解式（1）~（25）的必要初始条件如下. 初始时刻，液滴为球形，所有液滴单元位置（即x坐标）可由液滴直径及式（5）确定. 每个单元初始直径及长度取决于计算时所取的离散单元数. 所有单元的变形速度为0，单元所带电荷可由式（4）确定. 单元所受界面张力与内部压力保持平衡，故每个单元内部压强均为 ${{2\sigma } / {{R}}}$（二维为 ${\sigma / {{R}}}$）. 单元所受静电力可由单元初始位置及式（2）、（3）及（7）确定. 对于双液滴聚结模拟，还需要给出2个液滴的初始中心间距，2个液滴的初始平动速度可假设为0，电偶聚结的初始吸引力可由2个液滴初始间距及式（23）确定. 计算时，液滴外部压力取为0.

用3个算例分析本文模型的预测特性.

算例1：对文献[33]的实验结果预测

如图3所示为本文模型预测的液滴形状与Eow等^[33]实验的比较. 在文献[33]的实验中离散液滴（直径为1.2 mm）为掺有染料的水，表面张力为0.045 N/m，黏度为0.001 14 ${{\rm{P}}_{\rm{a}}} \cdot {\rm{s}}$，密度为998 kg/m³，相对介电常数为80；连续相为葵花籽油，表面张力为0.034 N/m，黏度为0.0472 ${{\rm{P}}_{\rm{a}}} \cdot {\rm{s}}$，密度为922 kg/m³，相对介电常数为4.9. 油水界面张力为0.016 N/m. 图3清楚地演示了在场强作用下，液滴沿电场方向（水平方向）被拉长而变为椭球的趋势. 比较图3（a）、（b）可知，预测的液滴形状与实验的基本相符. Eow等^[33]采用椭球液滴的长短径之比表征液滴的变形程度，在电场强度为100、200、300 KV/m时，实测液滴的长短轴径之比分别约为1.05、1.12、1.32，本文模型预测的结果分别为1.027、1.079、1.24. 预测的变形度D分别为0.0113、0.0362、0.0989，预测最大相对误差为6.06%，预测值与实验值较为接近. 采用文献[2]的模型预测D分别为0.0092、0.0366、0.0824. 文献[2]的模型预测结果偏小，与之相比本文模型预测结果更好. 变形度D的定义为^[1]

(27) $D = \frac{{L - B}}{{L + B}}.$

式中：L，B分别为液滴沿电场方向及垂直电场方向的轴长.如果D为正，表明液滴沿电场方向被拉长，液滴变形为扁长形；如果D为负，则表明液滴沿垂直于电场方向被拉长，液滴变形为扁平形.

算例2：对文献[32]实验结果的预测

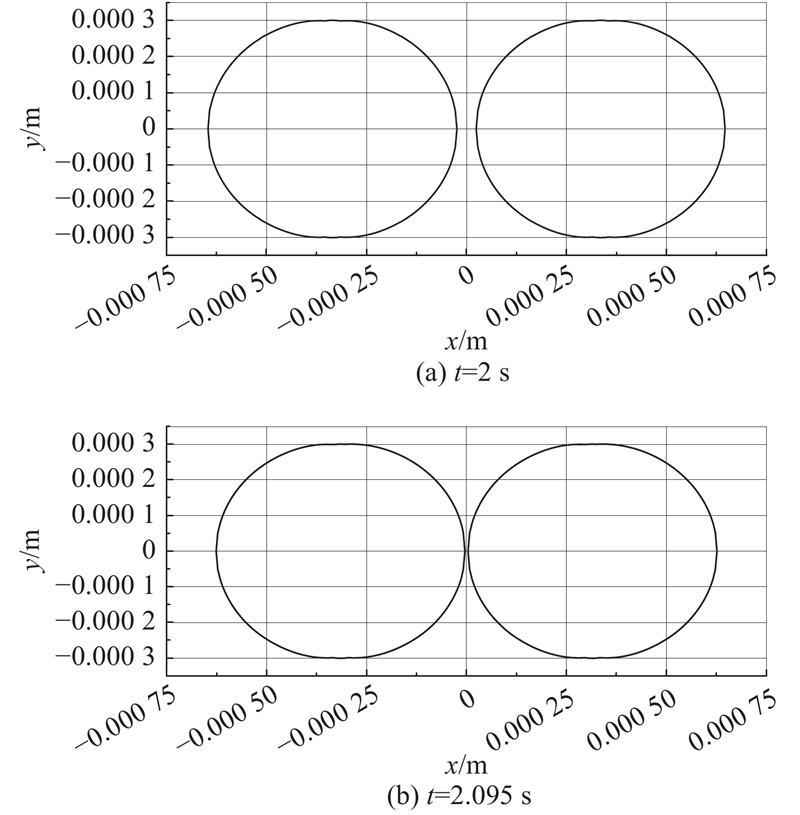
如图4所示为文献[32]的液滴聚结实验照片. 实验介质为葵花籽油（连续相）和水（离散液滴）. 葵花籽油的黏度为0.085 ${\rm{Pa}} \cdot {\rm{s}}$，密度为892 kg/m³，表面张力0.033 N/m；水的密度为998 kg/m³，表面张力为0.069 N/m. 2个液滴的直径分别为0.615 mm，2个液滴的初始中心间距（施加电场之前）为0.99 mm. 由图可见，施加水平方向的场强（E=186 400 V/m）后，2个液滴变形. 由于施加场强不大，且液滴初始直径较小，液滴变形不明显，变形后液滴长短轴径之比约1.068~1.072. 还可看到，由于偶极聚结，2个液滴因相互吸引产生相向运动而逐渐靠近，至2.5 s后聚合为大液滴，2个液滴相邻界面接触的时间约为2.46~2.50 s. 如图5所示为本文模型对文献[32]实验结果的预测. 图5较为清晰地演示了2个液滴的变形及因偶极吸引而产生的相向运动趋势. 预测的液滴变形后液滴长短轴径之比为1.041 9. 2 s后，预测的2个液滴相邻液面间距为 $4.799\;9 \times {10^{ - 5}}\;{\rm{m}}$，2个液滴界面接触的时间在2.095 s之后，模拟结果与文献[32]的实验结果大体相符. 图5的模拟仅限于对2个液滴从初始时刻至界面接触阶段的模拟，没有考虑界面接触后的聚合过程. 相对而言，预测液滴界面接触的时间要低于实验值，原因可能是实测的油黏度稍高，也可能是计算时的时间步长稍大（本算例时间步长为5×10⁻⁶ s）. 由于时间步长的选取与单元尺寸密切相关，如单元尺寸较小，时间步长也必须小，否则数值计算过程会失稳. 因为本算例液滴尺寸较小，2个液滴的初始间距相对较大，模拟聚结所花费的时间极长，为了适当提高计算效率，本算例单元尺寸（2个液滴均划分为200个单元）及时间步长取值偏大. 如果适当缩短时间步长及单元尺寸（划分更多的单元），预测偏差将减小.

算例3：对液滴扁平形变形的模拟

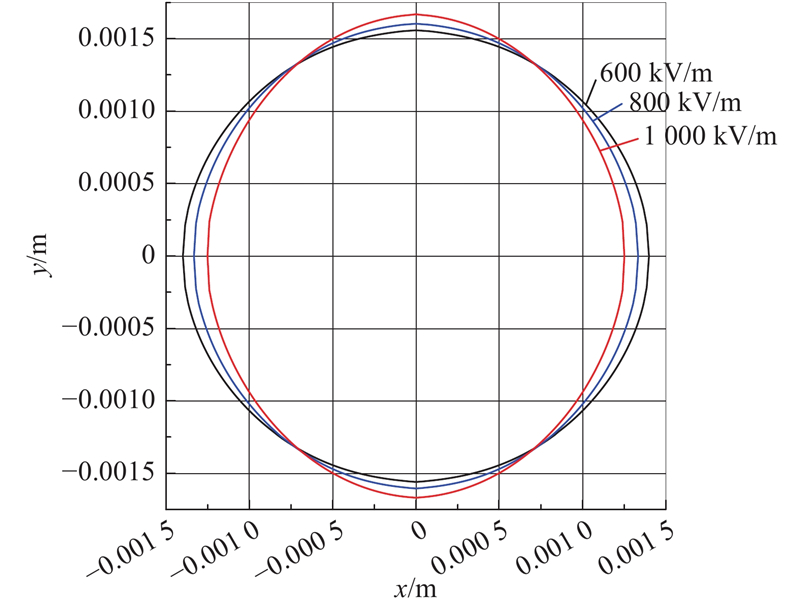
算例1、2均是针对液滴的扁长形变形的模拟. 本算例对液滴扁平形变形进行模拟. 如图6所示为在3种水平方向场强下液滴的变形模拟（液滴初始直径为3 mm）. 模拟计算时的两相流体的物理参数：连续相相对介电常数为6，密度为998 kg/m³，黏度为0.001 1 Pa·s；离散液滴相对介电常数为2.5，密度为922 kg/m³，黏度为0.04 Pa·s. 两相间界面张力为0.016 N/m. 图6清晰表明施加水平场强后，液滴在垂直方向出现变形趋势. 随着场强的增大，在垂直方向的变形逐渐增大. 在600、800、1 000 kV/m水平场强作用下，D分别为−0.054 6、−0.093 1、−0.148.

以上3个算例表明，本文所建立的液滴变形数值模型具有一定的可行性及较宽的适用范围，可用于单液滴变形预测，也可用于双液滴聚结预测；可用于液滴的扁长形变形模拟，也可用于液滴的扁平形变形模拟. 算例1、2的结果表明，本文模型对液滴变形程度的预测结果与实验值符合较好（最大相对误差为6.06%），对液滴聚结过程的模拟与实验结果大体相符，预测的聚结时间稍低于实验值（相对误差为16.2%）. 本文从液滴单元变形过程中的守恒方程出发来建立计算模型，避免计算N-S方程和麦克斯韦方程，计算更加方便，编程更加容易，可为研究液滴电变形机理提供一定参考. 如果在现有基础上进一步提高单元阻力模化精度及单元离散精度，该方法将具有较好的适用性.

（1）基于单元变形的思路，通过单元变形过程中的守恒方程，建立了电场中离散液滴的变形数值计算模型，并采用有限差分法编制了模型的数值计算程序，对几种参数下的液滴变形过程进行了模拟计算. 计算结果与相关实验结果的比较表明，所建模型对液滴变形的预测与实验较为接近.

（2）将所建模型与偶极聚结模型相耦合，可实现对2个液滴电聚结过程的模拟. 模拟结果与相关实验结果的比较表明，本文模型同样适用于对液滴电聚结过程的预测. 相对而言，预测的液滴聚结时间比实验结果稍短（相对误差为16.2%）.

（3）计算结果表明，本文模型可用于对液滴扁平形变形过程的模拟.

（4）本文模型所采用的液滴表面电荷密度是基于圆形液滴的表面电荷分布，在液滴变形较大时，模型计算的滴表面电荷分布与实际情况有较大出入，因此，本文模型不适合对液滴大变形的预测.